 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【数B】ベクトル:平行四辺形状のマス目上にあるベクトルを表そう!

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
Adプラ数学B問題606
次に図示された2つのベクトル$\overrightarrow{p},\overrightarrow{q}$を$\overrightarrow{a},\overrightarrow{b}$で表せ。
この動画を見る
Adプラ数学B問題606
次に図示された2つのベクトル$\overrightarrow{p},\overrightarrow{q}$を$\overrightarrow{a},\overrightarrow{b}$で表せ。
【物理】電磁気:コンデンサー② 紛らわしい「コンデンサー内部への2種類の挿入」を分かりやすく解説してみた

【受験算数】仕事算:9人ですると20日かかる仕事があります。この仕事を12人ですると□日で終わります。□にあてはまる数字は?【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
教材:
#予習シ#予習シ算数・小5下#中学受験教材#仕事に関する問題
指導講師:
理数個別チャンネル
問題文全文(内容文):
9人ですると20日かかる仕事があります。この仕事を12人ですると□日で終わります。□にあてはまる数字は?
この動画を見る
9人ですると20日かかる仕事があります。この仕事を12人ですると□日で終わります。□にあてはまる数字は?
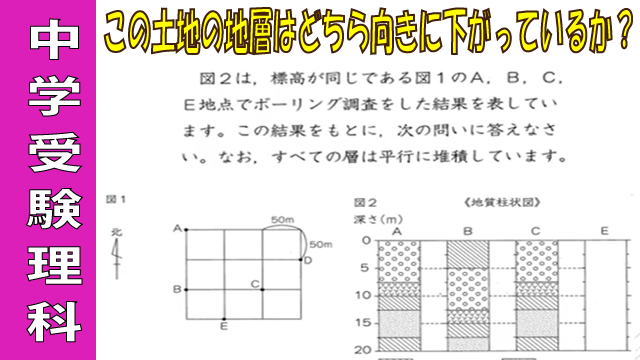
【中学受験理科】地学:ボーリング調査③地面は水平、地層はナナメ8方向
単元:
#理科(中学受験)#地学分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
図2は、標高が同じである図1のA, B, C, E地点でボーリング調査をした結果を表しています。この結果をもとに、次の問いに答えなさい。なお、すべての層は平行に堆積しています。
①この土地の地層は、どちらの方角へ下がっていますか。8方向で答えなさい。
②D地点で火山灰の層が見られるのは、地表から何mの深さですか。
③E地点の地質柱状図をかきなさい。
※柱状図は動画内に記載。
この動画を見る
図2は、標高が同じである図1のA, B, C, E地点でボーリング調査をした結果を表しています。この結果をもとに、次の問いに答えなさい。なお、すべての層は平行に堆積しています。
①この土地の地層は、どちらの方角へ下がっていますか。8方向で答えなさい。
②D地点で火山灰の層が見られるのは、地表から何mの深さですか。
③E地点の地質柱状図をかきなさい。
※柱状図は動画内に記載。
【受験理科】地学:ボーリング調査③地面は水平、地層はナナメ8方向

単元:
#理科(中学生)#地学
指導講師:
理数個別チャンネル
問題文全文(内容文):
図2は、標高が同じである図1のA, B, C, E地点でボーリング調査をした結果を表しています。この結果をもとに、次の問いに答えなさい。なお、すべての層は平行に堆積しています。
①この土地の地層は、どちらの方角へ下がっていますか。8方向で答えなさい。
②D地点で火山灰の層が見られるのは、地表から何mの深さですか。
③E地点の地質柱状図をかきなさい。
※柱状図は動画内に記載。
この動画を見る
図2は、標高が同じである図1のA, B, C, E地点でボーリング調査をした結果を表しています。この結果をもとに、次の問いに答えなさい。なお、すべての層は平行に堆積しています。
①この土地の地層は、どちらの方角へ下がっていますか。8方向で答えなさい。
②D地点で火山灰の層が見られるのは、地表から何mの深さですか。
③E地点の地質柱状図をかきなさい。
※柱状図は動画内に記載。
【数Ⅱ】三角関数:3倍角の公式笑っちゃう覚え方

【数学】確率:センター試験(平成30年)本試

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#センター試験・共通テスト関連#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
1枚のコインを最大で5回投げるゲームを行う。このゲームでは、1回投げるごとに表が出たら持ち点に2点を加え、裏が出たら持ち点に -1点を加える。はじめの持ち点は0点とし、ゲーム終了のルールを次のように定める。
・持ち点が再び0点になった場合は、その時点で終了する。
・持ち点が再び0点にならない場合は、コインを5回投げ終わった時点で終了する。
(1) コインを2回投げ終わって持ち点が -2点である確率は □
である。また、コインを2回投げ終わって持ち点が1点である確率は □
である。
(2) 持ち点が再び0点になることが起こるのは、コインを
□ 回投げ終わったときである。コインを □回投げ終わって持ち点が0点になる確率は
□である。
(3) ゲームが終了した時点で持ち点が4点である確率は □である。
(4) ゲームが終了した時点で持ち点が4点であるとき、コインを2回投げ終わって持ち点が1点である条件付き確率は□である。
この動画を見る
1枚のコインを最大で5回投げるゲームを行う。このゲームでは、1回投げるごとに表が出たら持ち点に2点を加え、裏が出たら持ち点に -1点を加える。はじめの持ち点は0点とし、ゲーム終了のルールを次のように定める。
・持ち点が再び0点になった場合は、その時点で終了する。
・持ち点が再び0点にならない場合は、コインを5回投げ終わった時点で終了する。
(1) コインを2回投げ終わって持ち点が -2点である確率は □
である。また、コインを2回投げ終わって持ち点が1点である確率は □
である。
(2) 持ち点が再び0点になることが起こるのは、コインを
□ 回投げ終わったときである。コインを □回投げ終わって持ち点が0点になる確率は
□である。
(3) ゲームが終了した時点で持ち点が4点である確率は □である。
(4) ゲームが終了した時点で持ち点が4点であるとき、コインを2回投げ終わって持ち点が1点である条件付き確率は□である。
【英語リスニング】 1分30秒の英語リスニングトレーニング

【中学数学】数学用語チェック絵本vol.1正負の数

単元:
#数学(中学生)#中1数学#正の数・負の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
中学1年生 正負の数の用語を総チェック!先生オリジナルキャラクターたちと一緒に覚えていこう!
この動画を見る
中学1年生 正負の数の用語を総チェック!先生オリジナルキャラクターたちと一緒に覚えていこう!
【数C】ベクトルが「等しい」とは??

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#アドバンスプラス#アドバンスプラス数Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
|vec(a)|=5であるvec(a)がある。
(1) vec(a)と同じ向きの単位ベクトルを、vec(a)を用いて表せ。
(2) vec(a)と平行で、大きさが3のベクトルを、vec(a)を用いて表せ。
この動画を見る
|vec(a)|=5であるvec(a)がある。
(1) vec(a)と同じ向きの単位ベクトルを、vec(a)を用いて表せ。
(2) vec(a)と平行で、大きさが3のベクトルを、vec(a)を用いて表せ。
【数B】ベクトル:ベクトルが「等しい」とは??

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\overrightarrow{a}=(4,1-5),\overrightarrow{b}=(2m,1)$が等しいとき,$l,m$の値を求めよ.
この動画を見る
$\overrightarrow{a}=(4,1-5),\overrightarrow{b}=(2m,1)$が等しいとき,$l,m$の値を求めよ.
【物理】電磁気:コンデンサー① コンデンサー嫌い必見!コンデンサーがよく分かるイメージ、徹底解説!

【英語】中1 頻度をあらわす副詞をどこに置く?

単元:
#英語(中学生)#英語(高校生)#英文法#中1英語#形容詞・副詞#形容詞・副詞
指導講師:
理数個別チャンネル
問題文全文(内容文):
always, usually, often, sometimes, neverなどのいわゆる「頻度をあらわす副詞」をどこに置くか確認します。
この動画を見る
always, usually, often, sometimes, neverなどのいわゆる「頻度をあらわす副詞」をどこに置くか確認します。
【数C】ベクトルの大きさ、単位ベクトルとは??

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#アドバンスプラス#アドバンスプラス数Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
|vec(a)|=5であるvec(a)がある。
(1) vec(a)と同じ向きの単位ベクトルを、vec(a)を用いて表せ。
(2) vec(a)と平行で、大きさが3のベクトルを、vec(a)を用いて表せ。
この動画を見る
|vec(a)|=5であるvec(a)がある。
(1) vec(a)と同じ向きの単位ベクトルを、vec(a)を用いて表せ。
(2) vec(a)と平行で、大きさが3のベクトルを、vec(a)を用いて表せ。
【数B】ベクトルの大きさ、単位ベクトルとは??

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\vert \overrightarrow{a}\vert=5$である$\overrightarrow{a}$がある。
(1) $\overrightarrow{a}$と同じ向きの単位ベクトルを、$\overrightarrow{a}$を用いて表せ。
(2) $\overrightarrow{a}$と平行で、大きさが3のベクトルを、$\overrightarrow{a}$を用いて表せ。
この動画を見る
$\vert \overrightarrow{a}\vert=5$である$\overrightarrow{a}$がある。
(1) $\overrightarrow{a}$と同じ向きの単位ベクトルを、$\overrightarrow{a}$を用いて表せ。
(2) $\overrightarrow{a}$と平行で、大きさが3のベクトルを、$\overrightarrow{a}$を用いて表せ。
【物理】電磁気:電位と電場② 丸暗記厳禁!超似てる4公式を超絶分かりやすくイメージさせてみた

【受験算数】流水算通過算:(基本❹)2つの差を考える通過算

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#流水算、通過算
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある電車が、長さ280mの鉄橋を通過するのに25秒かかり、長さ920mのトンネルを通過するのに1分5秒かかりました。これについて、次の問いに答えなさい。
(1)この電車の速さは毎秒何mですか。
(2)この電車の長さは何mですか。
この動画を見る
ある電車が、長さ280mの鉄橋を通過するのに25秒かかり、長さ920mのトンネルを通過するのに1分5秒かかりました。これについて、次の問いに答えなさい。
(1)この電車の速さは毎秒何mですか。
(2)この電車の長さは何mですか。
【数B】ベクトル:ベクトルの基本⑩三角形の面積の公式2パターン

【数C】ベクトルの基本⑩三角形の面積の公式2パターン

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ベクトルを用いた三角形の面積の公式
この動画を見る
ベクトルを用いた三角形の面積の公式
【英語】時制:時制の注意すべきポイント[未来完了]

単元:
#英語(高校生)#英文法#中3英語#時制#現在完了(継続、経験、完了・結果)
指導講師:
理数個別チャンネル
問題文全文(内容文):
時制の12種類の中から、苦手な人の多い未来完了形についての解説動画です。
この動画を見る
時制の12種類の中から、苦手な人の多い未来完了形についての解説動画です。
【英語】この名詞は何から来ている?

単元:
#英語(高校生)#英文法#名詞・冠詞・代名詞#勉強法・その他#その他
指導講師:
理数個別チャンネル
問題文全文(内容文):
大学入試の長文で長頻出の単語のうち、名詞⇔動詞の語形変化が特徴的なものを扱っています。
この動画を見る
大学入試の長文で長頻出の単語のうち、名詞⇔動詞の語形変化が特徴的なものを扱っています。
【受験算数】平面図形:黒い角度の和を求めよう

単元:
#算数(中学受験)#平面図形#角度と面積
教材:
#予習シ#予習シ算数・小5下#中学受験教材#平面図形と比
指導講師:
理数個別チャンネル
問題文全文(内容文):
黒い角度の和はいくつでしょう。
この動画を見る
黒い角度の和はいくつでしょう。
【受験算数】平面図形:Xの角度を秒殺で求めよう

単元:
#算数(中学受験)#平面図形#角度と面積
教材:
#予習シ#予習シ算数・小5下#中学受験教材#平面図形と比
指導講師:
理数個別チャンネル
問題文全文(内容文):
Xの角度の大きさを求めよう
この動画を見る
Xの角度の大きさを求めよう
【受験算数】流水算・通過算:(基本❸)流れるプールの流水算

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#流水算、通過算
指導講師:
理数個別チャンネル
問題文全文(内容文):
1周200mの流れるプールで、A君は流れに沿って泳ぐと1周するのに2分30秒かかり、流れに逆らって泳ぐと5分かかります。これについて、次の問いに答えなさい。
(1)このプールの流れの速さは、毎分何ですか。
(2)A君が自分のゴムボートを手放して流れに逆らって泳ぎ始めると、流れてくる自分のゴムボートに出会うのは何分何秒後ですか。
この動画を見る
1周200mの流れるプールで、A君は流れに沿って泳ぐと1周するのに2分30秒かかり、流れに逆らって泳ぐと5分かかります。これについて、次の問いに答えなさい。
(1)このプールの流れの速さは、毎分何ですか。
(2)A君が自分のゴムボートを手放して流れに逆らって泳ぎ始めると、流れてくる自分のゴムボートに出会うのは何分何秒後ですか。
【受験算数】流水算・通過算:(基本❷)流水算とグラフ

単元:
#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#流水算、通過算
指導講師:
理数個別チャンネル
問題文全文(内容文):
川上のP地から18km離れた川下のQ地へ船Aが進みました。はじめはエンジンを止めた状態で、途中からエンジンを動かして進みました。右のグラフは、P地を出発してからの時間と距離の関係を表したものです。これについて、次の問いに答えなさい。
(1)この船が静水を進む速さは時速何kmですか。
(2)船Bは、船AがP地を出発するのと同時にQ値を出発し、P地に向かいます。船Bの静水時の速さは時速19.5kmです。その運行の様子をグラフにかきなさい。
(3)船Aが船Bとすれ違うのは、P地から何mのところですか。
この動画を見る
川上のP地から18km離れた川下のQ地へ船Aが進みました。はじめはエンジンを止めた状態で、途中からエンジンを動かして進みました。右のグラフは、P地を出発してからの時間と距離の関係を表したものです。これについて、次の問いに答えなさい。
(1)この船が静水を進む速さは時速何kmですか。
(2)船Bは、船AがP地を出発するのと同時にQ値を出発し、P地に向かいます。船Bの静水時の速さは時速19.5kmです。その運行の様子をグラフにかきなさい。
(3)船Aが船Bとすれ違うのは、P地から何mのところですか。
【地理】政令指定都市の紹介2

【地理】政令指定都市の紹介1

単元:
#社会(中学受験)#社会(中学生)#地理#地理
指導講師:
理数個別チャンネル
問題文全文(内容文):
全国に20ある政令指定都市、すべて覚えていますか?
今回はざっくりとこの20都市を紹介していきます。
※この動画は前編です。後編もぜひご覧ください。
この動画を見る
全国に20ある政令指定都市、すべて覚えていますか?
今回はざっくりとこの20都市を紹介していきます。
※この動画は前編です。後編もぜひご覧ください。
【受験算数】場合の数:ぬり分けの問題~全色使う場合!【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
{赤,青,黄,緑}のうちの何色かを使って、右の図のア~エの4つの部分を、となり合う部分が同じ色にならないようにぬり分けます。4色全部を使うとき、色のぬり方は何通りありますか。
この動画を見る
{赤,青,黄,緑}のうちの何色かを使って、右の図のア~エの4つの部分を、となり合う部分が同じ色にならないようにぬり分けます。4色全部を使うとき、色のぬり方は何通りありますか。
【受験算数】場合の数:ぬり分けの問題~4色から3色選んでぬり分けるなら何通り?【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
{赤,青,黄,緑}のうちの何色かを使って、右の図のア~エの4つの部分を、となり合う部分が同じ色にならないようにぬり分けます。3色ちょうどを使うとき、色のぬり方は何通りありますか。
この動画を見る
{赤,青,黄,緑}のうちの何色かを使って、右の図のア~エの4つの部分を、となり合う部分が同じ色にならないようにぬり分けます。3色ちょうどを使うとき、色のぬり方は何通りありますか。
【中学数学】数学検定3級:問題6(27)~(30)

単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題6.次の問いに答えなさい。
(27) 正九角形の1つの内角の大きさは何度ですか。
(28) 3枚の硬貨を同時に投げるとき、3枚とも裏が出る確率を求めなさい。ただし、硬貨の表と裏の出方は同様に確からしいものとする。
(29) yはxの2乗に比例し、x=-6のときy=18です。x=8のときのyの値を求めなさい。
(30) 3点A,B,Cが円Oの周上にあります。∠OCB=28°のとき、∠xの大きさは何度ですか。
この動画を見る
問題6.次の問いに答えなさい。
(27) 正九角形の1つの内角の大きさは何度ですか。
(28) 3枚の硬貨を同時に投げるとき、3枚とも裏が出る確率を求めなさい。ただし、硬貨の表と裏の出方は同様に確からしいものとする。
(29) yはxの2乗に比例し、x=-6のときy=18です。x=8のときのyの値を求めなさい。
(30) 3点A,B,Cが円Oの周上にあります。∠OCB=28°のとき、∠xの大きさは何度ですか。




