 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【受験算数】平面図形:辺の長さと面積比1-1
単元:
#算数(中学受験)#平面図形#平面図形その他
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
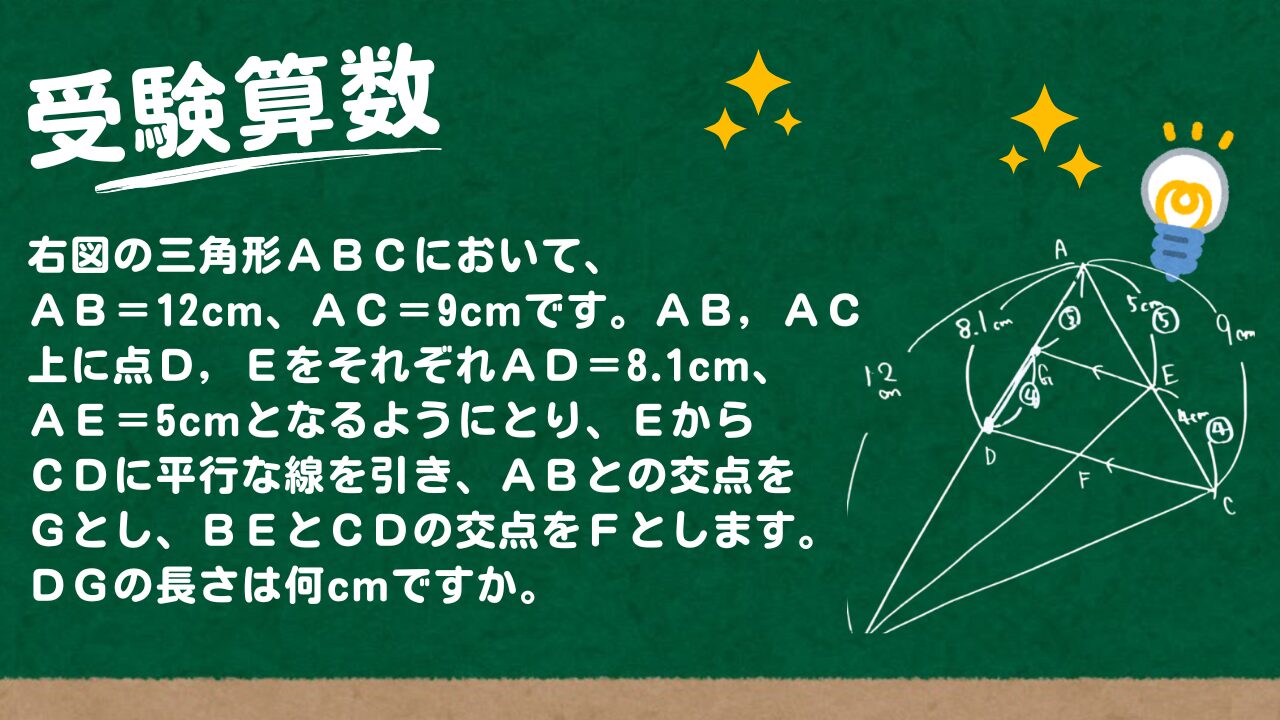
右図の三角形ABCにおいて、AB=12cm、AC=9cmです。AB,AC上に点D,EをそれぞれAD=8.1cm、AE=5cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、BEとCDの交点をFとします。次の問いに応えなさい。
(1)DGの長さは何cmですか。
この動画を見る
右図の三角形ABCにおいて、AB=12cm、AC=9cmです。AB,AC上に点D,EをそれぞれAD=8.1cm、AE=5cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、BEとCDの交点をFとします。次の問いに応えなさい。
(1)DGの長さは何cmですか。
【公民(現社)】今更聞けない『SDGs』!『ESG投資』もゼロから解説!

単元:
#社会(高校生)#現代社会
指導講師:
理数個別チャンネル
問題文全文(内容文):
今更人に聞けないSDGsとは何か?経済の観点から、ESG投資とは何かを4分で解説しています。
高校入試の記述問題で狙われるかも…!
この動画を見る
今更人に聞けないSDGsとは何か?経済の観点から、ESG投資とは何かを4分で解説しています。
高校入試の記述問題で狙われるかも…!
【受験理科】飽和と水溶液②『溶解度と水溶液問題』

単元:
#理科(中学受験)#化学分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)80℃の水100gにホウ酸を溶けるだけ溶かした後に温度を20℃に下げた時、何gのホウ酸の結晶が出てくるか?
(2)80℃の水100gにホウ酸を20gだけ溶かした後に温度を20度に下げた時、何gのホウ酸の結晶が出てくるか?
(3)80℃の水200gにホウ酸を溶けるだけ溶かした後に温度を20℃に下げた時、何gのホウ酸の結晶が出てくるか?
(4)60℃の水300gに食塩を溶けるだけ溶かした後に温度を60℃に保ったまま水を100gだけ蒸発させる時、何gの食塩の結晶が出てくるか?
(5)80℃の水100gに食塩を25gだけ溶かした後に、温度を80℃に保ったまま水を50gだけ蒸発させる時、何gの食塩の結晶が出てくるか?
※溶解度の表は動画中に表記しています。
この動画を見る
(1)80℃の水100gにホウ酸を溶けるだけ溶かした後に温度を20℃に下げた時、何gのホウ酸の結晶が出てくるか?
(2)80℃の水100gにホウ酸を20gだけ溶かした後に温度を20度に下げた時、何gのホウ酸の結晶が出てくるか?
(3)80℃の水200gにホウ酸を溶けるだけ溶かした後に温度を20℃に下げた時、何gのホウ酸の結晶が出てくるか?
(4)60℃の水300gに食塩を溶けるだけ溶かした後に温度を60℃に保ったまま水を100gだけ蒸発させる時、何gの食塩の結晶が出てくるか?
(5)80℃の水100gに食塩を25gだけ溶かした後に、温度を80℃に保ったまま水を50gだけ蒸発させる時、何gの食塩の結晶が出てくるか?
※溶解度の表は動画中に表記しています。
【英語】今更誰にも聞けない『補語』を3分半でおさらい!

単元:
#英語(高校生)#英文法#品詞と文型、句と節#中2英語#形容詞・副詞#文型(第1文型、第2文型、第3文型、第4文型、第5文型)
指導講師:
理数個別チャンネル
問題文全文(内容文):
『補語』がなんなのか知らない人に、『目的語』との差異・区別の仕方を教えるよ!
この動画を見る
『補語』がなんなのか知らない人に、『目的語』との差異・区別の仕方を教えるよ!
【数A】なんと1分で求められる!?一橋2020大問1(1)10の10乗を2020で割ったあまりを求める

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
10の10乗を2020で割ったあまりを求めよ
この動画を見る
10の10乗を2020で割ったあまりを求めよ
【受験理科】地学:ボーリング調査②地面はナナメ、地層は水平
単元:
#理科(中学受験)#地学分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
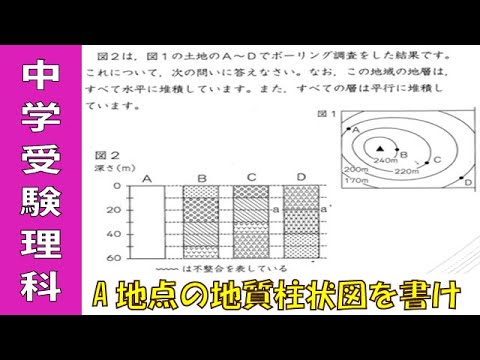
(1)B地点を何mほるとa-a'面になりますか。
(2)火山灰の層の厚さは何mですか?
(3)A地点の地質柱状図をかきなさい。
※柱状図は動画内に記載
この動画を見る
(1)B地点を何mほるとa-a'面になりますか。
(2)火山灰の層の厚さは何mですか?
(3)A地点の地質柱状図をかきなさい。
※柱状図は動画内に記載
【物理】電磁気:電位と電場① 電荷、電気量、電位ってなんだ?力学と比較して超絶分かりやすく解説してみた

【英語】英文法:形容詞と副詞の区別

単元:
#英語(中学生)#英語(高校生)#英文法#品詞と文型、句と節#中1英語#形容詞・副詞
指導講師:
理数個別チャンネル
問題文全文(内容文):
形容詞・副詞の区別を例文を使って説明します。
この動画を見る
形容詞・副詞の区別を例文を使って説明します。
【数A】modの計算法則を分かりやすく説明します

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
modの計算法則をわかりやすく説明します。(証明付き!)
この動画を見る
modの計算法則をわかりやすく説明します。(証明付き!)
【受験理科】地学:ボーリング調査①地面は水平、地層はナナメ

単元:
#理科(中学受験)#地学分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)この地域の地層は、どちらの方角からどちらの方角へ100mにつき何m下がっていますか。
(2)D地点で火山灰の層がみられるのは、地表から何mの深さですか。
(3)E地点の地質柱状図をかきなさい。
※柱状図は動画内に記載。
この動画を見る
(1)この地域の地層は、どちらの方角からどちらの方角へ100mにつき何m下がっていますか。
(2)D地点で火山灰の層がみられるのは、地表から何mの深さですか。
(3)E地点の地質柱状図をかきなさい。
※柱状図は動画内に記載。
【高校物理】力学(単振動):単振動「ばね付きの板にのせた物体」を力エネ保を使わずに鮮やかに解説してみた!

単元:
#物理#力学#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
軽いつる巻きばねの一端を地面につけ, 他端に質量Mの板をつけて,その上に質量mのおもりをのせたら,ばねが xo だけ縮んだ位置O(板の下面)でつりあった。この位置からさらに2xoだけ押し縮めてはなすと, ばねが伸び, ある位置でおもりは板から離れた。 0を原点, 鉛直上向きにx軸をとる。重力加速度の大きさをgとする。
(1) 板が座標xの点を通る瞬間の加速度a,および, 板とおもりが及ぼしあう力の大きさNを求めよ。
(2) おもりが板から離れるときの位置x1と,おもりの速さを求めよ。
(3) 運動を始めてから,おもりが板から離れるまでの時間t1を求めよ。
この動画を見る
軽いつる巻きばねの一端を地面につけ, 他端に質量Mの板をつけて,その上に質量mのおもりをのせたら,ばねが xo だけ縮んだ位置O(板の下面)でつりあった。この位置からさらに2xoだけ押し縮めてはなすと, ばねが伸び, ある位置でおもりは板から離れた。 0を原点, 鉛直上向きにx軸をとる。重力加速度の大きさをgとする。
(1) 板が座標xの点を通る瞬間の加速度a,および, 板とおもりが及ぼしあう力の大きさNを求めよ。
(2) おもりが板から離れるときの位置x1と,おもりの速さを求めよ。
(3) 運動を始めてから,おもりが板から離れるまでの時間t1を求めよ。
【物理】力学:単振動「ばね付きの板にのせた物体」を力エネ保を使わずに鮮やかに解説してみた!

単元:
#物理#力学#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
軽いつる巻きばねの一端を地面につけ, 他端に質量Mの板をつけて,その上に質量mのおもりをのせたら,ばねが xo だけ縮んだ位置O(板の下面)でつりあった。この位置からさらに2xoだけ押し縮めてはなすと, ばねが伸び, ある位置でおもりは板から離れた。 0を原点, 鉛直上向きにx軸をとる。重力加速度の大きさをgとする。
(1) 板が座標xの点を通る瞬間の加速度a,および, 板とおもりが及ぼしあう力の大きさNを求めよ。
(2) おもりが板から離れるときの位置x1と,おもりの速さを求めよ。
(3) 運動を始めてから,おもりが板から離れるまでの時間t1を求めよ。
この動画を見る
軽いつる巻きばねの一端を地面につけ, 他端に質量Mの板をつけて,その上に質量mのおもりをのせたら,ばねが xo だけ縮んだ位置O(板の下面)でつりあった。この位置からさらに2xoだけ押し縮めてはなすと, ばねが伸び, ある位置でおもりは板から離れた。 0を原点, 鉛直上向きにx軸をとる。重力加速度の大きさをgとする。
(1) 板が座標xの点を通る瞬間の加速度a,および, 板とおもりが及ぼしあう力の大きさNを求めよ。
(2) おもりが板から離れるときの位置x1と,おもりの速さを求めよ。
(3) 運動を始めてから,おもりが板から離れるまでの時間t1を求めよ。
【日本史】応仁の乱より少し前のお話

地質時代の怖い覚え方

【日本史】応仁の乱(チーム山名)

【中学数学】文字式:文字式のルールをすべて確認!

【英語】followに気をつけろ!

単元:
#英語(高校生)#英文解釈#大学入試過去問(英語)#学校別大学入試過去問解説(英語)
指導講師:
理数個別チャンネル
問題文全文(内容文):
知っているようで知らないfollowについて解説します 。
①Australia was followed by South Africa in the late 1990s, (センター試験2016)
②Naturally it follows that people who look honest, particularly (it seems) those with fresh, youthful, cherubic faces, make better liars.(慶應・文 2015)
この動画を見る
知っているようで知らないfollowについて解説します 。
①Australia was followed by South Africa in the late 1990s, (センター試験2016)
②Naturally it follows that people who look honest, particularly (it seems) those with fresh, youthful, cherubic faces, make better liars.(慶應・文 2015)
【数Ⅱ】中高一貫校問題集3(数式・関数編)394:図形と式:軌跡と方程式:2直線の交点の軌跡(直交する場合)

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
教材:
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
mが実数全体を取って動くとき、x+my-1=0,mx-y+2m=0の交点Pの軌跡を求めよ
この動画を見る
mが実数全体を取って動くとき、x+my-1=0,mx-y+2m=0の交点Pの軌跡を求めよ
【数学】中高一貫校用問題集:図形と式:軌跡と方程式:2直線の交点の軌跡(直交する場合)

単元:
#数Ⅰ#数Ⅱ#図形と計量#図形と方程式#数学(高校生)
教材:
#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
mが実数全体を取って動くとき、$x+my-1=0,mx-y+2m=0$の交点Pの軌跡を求めよ
この動画を見る
mが実数全体を取って動くとき、$x+my-1=0,mx-y+2m=0$の交点Pの軌跡を求めよ
【数Ⅱ】三角関数積⇒和の公式笑っちゃう覚え方

【受験算数】速さと比3:(練習❺)時計算の基本3【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#速さ#点の移動・時計算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#速さと比(3)
指導講師:
理数個別チャンネル
問題文全文(内容文):
太郎君のお母さんは、午前10時20分ごろ、時計の両針が反対方向に一直線に並んでいるときに外出しました。家にもどってきたのは午後0時30分過ぎで、このときも時計の両針が反対方向に一直線に並んでいました。これについて、次の問いに答えなさい。
(1)お母さんが外出から戻ってきたのは、午後何時何分ですか。
(2)お母さんが外出していた間に、時計の短針が動いた角度は何度ですか。
この動画を見る
太郎君のお母さんは、午前10時20分ごろ、時計の両針が反対方向に一直線に並んでいるときに外出しました。家にもどってきたのは午後0時30分過ぎで、このときも時計の両針が反対方向に一直線に並んでいました。これについて、次の問いに答えなさい。
(1)お母さんが外出から戻ってきたのは、午後何時何分ですか。
(2)お母さんが外出していた間に、時計の短針が動いた角度は何度ですか。
【数Ⅰ】相互関係式笑っちゃう覚え方

【英語】現在・現在進行時制のポイント

単元:
#英語(中学生)#英語(高校生)#英文法#中1英語#時制#現在進行形(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
現在・現在進行時制のポイントを解説していきます.
この動画を見る
現在・現在進行時制のポイントを解説していきます.
【化学】有機化学:東北大学を解いてみた(2022年第3問)Part 2

単元:
#化学#大学入試過去問(化学)#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2022:東北大入試(改題) 問1~5
炭素,水素,酸素のみからなる芳香族化合物A1molを水酸化ナトリウム水溶液で
完全に加水分解し希塩酸酸性にしたところ,化合物B,C,Dが1molずつ得られた。
CとDは炭素,水素,酸素からなる分子量150以下の共通の分子式を持つ物質で
200mgを完全燃焼させると,CO₂528mg,H₂O216mgのみが生じた。
Cはヨードホルム反応陽性であり,Dは陰性であった。また,CとDはどちらも
金属ナトリウムと反応し水素を発生した。
Cには不斉炭素原子が2つあり,水素を付加させ分子量が2.0増えたEが生成する。
Cに濃硫酸を作用させると,分子量が18減った化合物が得られた。
Dは炭素原子5個以上から成る環状構造をもち,酸化させて得られた分子量がDから
2.0減った化合物Fは銀鏡反応を示した。
この動画を見る
2022:東北大入試(改題) 問1~5
炭素,水素,酸素のみからなる芳香族化合物A1molを水酸化ナトリウム水溶液で
完全に加水分解し希塩酸酸性にしたところ,化合物B,C,Dが1molずつ得られた。
CとDは炭素,水素,酸素からなる分子量150以下の共通の分子式を持つ物質で
200mgを完全燃焼させると,CO₂528mg,H₂O216mgのみが生じた。
Cはヨードホルム反応陽性であり,Dは陰性であった。また,CとDはどちらも
金属ナトリウムと反応し水素を発生した。
Cには不斉炭素原子が2つあり,水素を付加させ分子量が2.0増えたEが生成する。
Cに濃硫酸を作用させると,分子量が18減った化合物が得られた。
Dは炭素原子5個以上から成る環状構造をもち,酸化させて得られた分子量がDから
2.0減った化合物Fは銀鏡反応を示した。
【英語】入試最頻出の強調構文を掴む!

単元:
#英語(高校生)#英文法#英文解釈#構文#接続詞#否定表現・特別な表現#その他
指導講師:
理数個別チャンネル
問題文全文(内容文):
大学入試や模試でこれでもか!というくらい良く出される強調構文のポイントについての解説動画です。おさえるべきポイントと出されるパターンについてお話します。
この動画を見る
大学入試や模試でこれでもか!というくらい良く出される強調構文のポイントについての解説動画です。おさえるべきポイントと出されるパターンについてお話します。
【受験算数】平面図形:折り紙のここ何度?【予習シリーズ算数・小5下】
単元:
#算数(中学受験)#平面図形#角度と面積
教材:
#予習シ#予習シ算数・小5下#中学受験教材#平面図形と比
指導講師:
理数個別チャンネル
問題文全文(内容文):
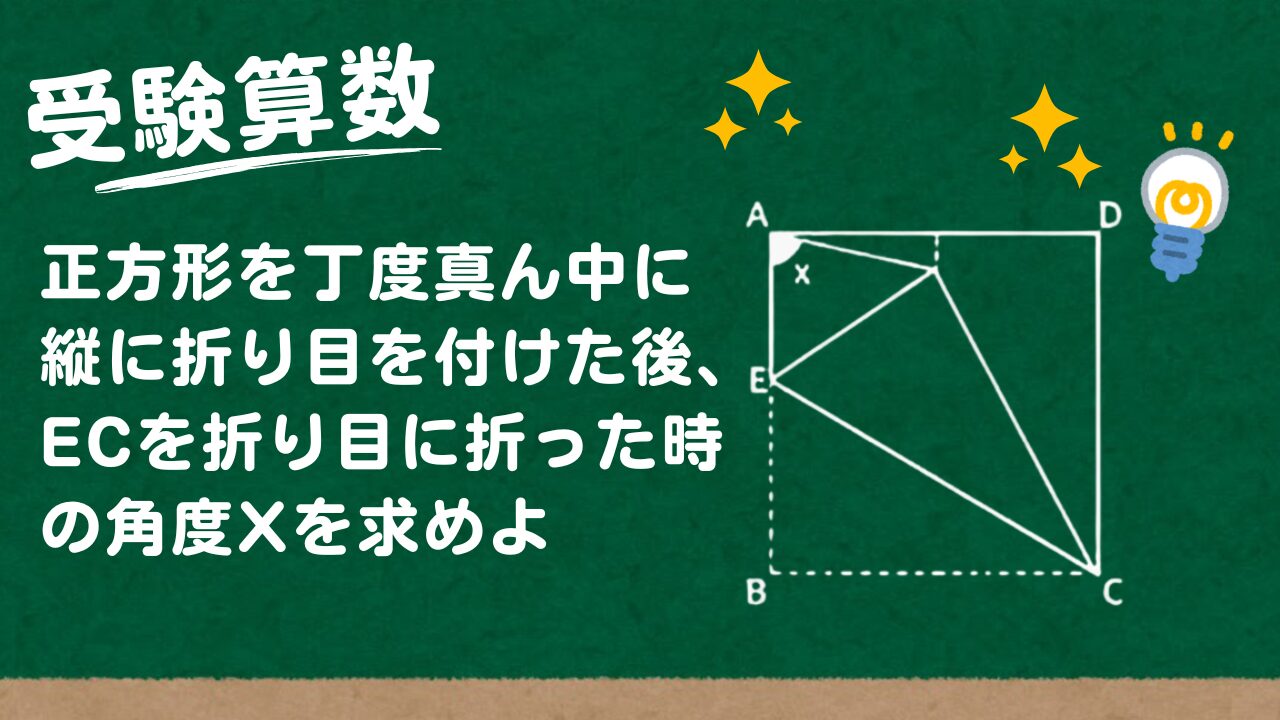
正方形を丁度真ん中に縦に折り目を付けた後、ECを折り目に折った時の角度Xを求めよ
この動画を見る
正方形を丁度真ん中に縦に折り目を付けた後、ECを折り目に折った時の角度Xを求めよ
【受験算数】速さと比3:(練習❹)時計算の基本2【予習シリーズ演習問題集・小5下】

単元:
#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#速さと比(3)
指導講師:
理数個別チャンネル
問題文全文(内容文):
7時と8時の間で、時計の両針が作る角の大きさについて、次の問いに答えなさい。
(1)時計の両針が重なるのは、7時何分ですか。
(2)時計の両針が反対側で一直線になるのは、7時何分ですか。
(3)時計の両針の作る角の大きさが2回目に60度になるのは、7時何分ですか。
この動画を見る
7時と8時の間で、時計の両針が作る角の大きさについて、次の問いに答えなさい。
(1)時計の両針が重なるのは、7時何分ですか。
(2)時計の両針が反対側で一直線になるのは、7時何分ですか。
(3)時計の両針の作る角の大きさが2回目に60度になるのは、7時何分ですか。
【公民・現代社会】憲法改正手続きはこんなにヤバい!?衆議院優越もチェック!

単元:
#社会(中学受験)#社会(中学生)#社会(高校生)#現代社会#公民#公民
指導講師:
理数個別チャンネル
問題文全文(内容文):
憲法改正ってよく聞くけど手続きはこんなに大変!
衆議院の優越ってあるのかな?確認しよう
この動画を見る
憲法改正ってよく聞くけど手続きはこんなに大変!
衆議院の優越ってあるのかな?確認しよう
【数C】ベクトルの基本⑨最小値を求めたいときの絶対値の2乗

【数B】ベクトル:ベクトルの基本⑨最小値を求めたいときの絶対値の2乗

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
aベクトル$+tb$ベクトルの絶対値の最小値を取るtの値について
この動画を見る
aベクトル$+tb$ベクトルの絶対値の最小値を取るtの値について




