 数学を数楽に
数学を数楽に
 数学を数楽に
数学を数楽に
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
整数問題 大阪星光学院

単元:
#計算と数の性質#数の性質その他#数学(中学生)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2b^2=a^2c^2+27$を満たす自然数a,b,cの組をすべて求めよ。
大阪星光学院高等学校
この動画を見る
$a^2b^2=a^2c^2+27$を満たす自然数a,b,cの組をすべて求めよ。
大阪星光学院高等学校
下2021ケタ目の数は? C

単元:
#計算と数の性質#数の性質その他#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$30^{2020}$の下2021ケタ目の数は?
この動画を見る
$30^{2020}$の下2021ケタ目の数は?
2001を素因数分解せよ 土佐高校

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{676} = ?$
2001を素因数分解せよ。
2011土佐高等学校
この動画を見る
$\sqrt{676} = ?$
2001を素因数分解せよ。
2011土佐高等学校
三平方の定理?いやいや〇〇でしょ A
単元:
#数学(中学生)#中2数学#中3数学#三平方の定理#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
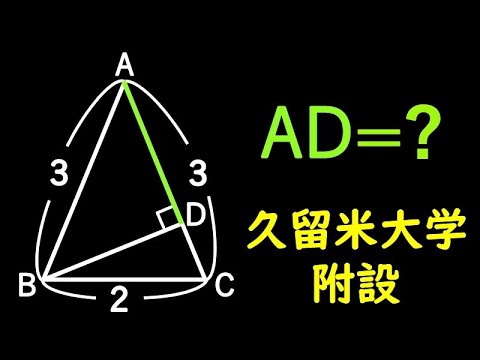
AD=?
*図は動画内参照
久留米大学附設高等学校
この動画を見る
AD=?
*図は動画内参照
久留米大学附設高等学校
互いに素の個数と和 慶應志木

単元:
#計算と数の性質#数の性質その他#数学(中学生)#文章題#文章題その他#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
1から123までの自然数のうち123と互いに素であるものの個数とその総和を求めよ。
慶應義塾志木高等学校
この動画を見る
1から123までの自然数のうち123と互いに素であるものの個数とその総和を求めよ。
慶應義塾志木高等学校
反比例と2次方程式 B
単元:
#数学(中学生)#中1数学#中3数学#2次方程式#比例・反比例#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
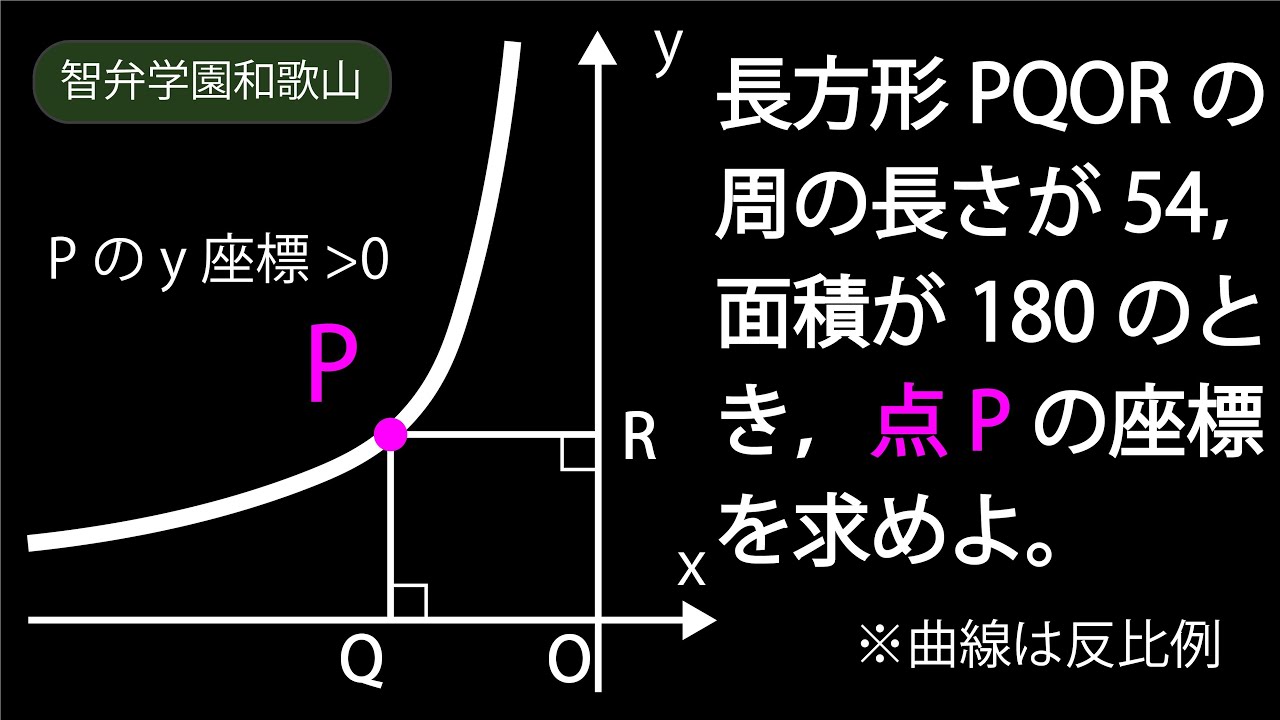
長方形PQORの周の=54、面積=180
点Pの座標は?
(点Pのy座標>0)
*図は動画内参照
智辯学園和歌山高等学校
この動画を見る
長方形PQORの周の=54、面積=180
点Pの座標は?
(点Pのy座標>0)
*図は動画内参照
智辯学園和歌山高等学校
ビンゴの確率 ラ・サール B

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
カード1⃣~9⃣から無造作に3枚取り出し、書かれている数字のマスを塗る。
縦、横、斜めのいずれか1列が塗りつぶされる確率は?
ラ・サール高等学校
この動画を見る
カード1⃣~9⃣から無造作に3枚取り出し、書かれている数字のマスを塗る。
縦、横、斜めのいずれか1列が塗りつぶされる確率は?
ラ・サール高等学校
三平方の定理の利用 成城学園
単元:
#数学(中学生)#中3数学#三平方の定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
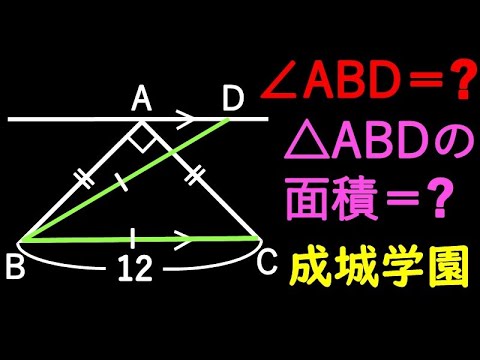
$\angle ABD=?$
$△ABD=?$
*図は動画内参照
成城学園高等学校
この動画を見る
$\angle ABD=?$
$△ABD=?$
*図は動画内参照
成城学園高等学校
相似 三平方の定理 芝浦工大柏
単元:
#数学(中学生)#中3数学#相似な図形#三平方の定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
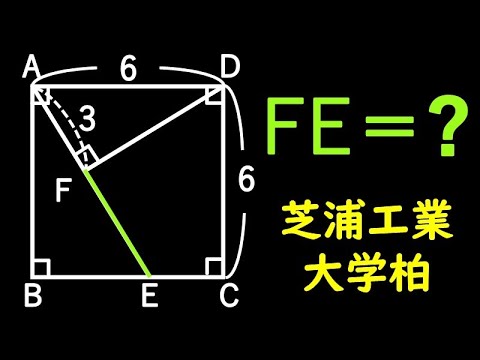
四角形ABCDは正方形
EF=?
*図は動画内参照
芝浦工業大学柏高等学校
この動画を見る
四角形ABCDは正方形
EF=?
*図は動画内参照
芝浦工業大学柏高等学校
三角比と二次不等式

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$のとき次の不等式
$4\cos^2\theta-4\sin\theta-1 \lt 0$を満たす$\theta$の範囲は?
この動画を見る
$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$のとき次の不等式
$4\cos^2\theta-4\sin\theta-1 \lt 0$を満たす$\theta$の範囲は?
三角比と二次関数の最大最小

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$のとき$y=\cos^2\theta+\sin\theta$の$y$の最大値と最小値を求めよ。
また、そのときの$\theta$の値を求めよ。
この動画を見る
$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$のとき$y=\cos^2\theta+\sin\theta$の$y$の最大値と最小値を求めよ。
また、そのときの$\theta$の値を求めよ。
2乗の数を5で割った余りの個数(整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$n$を30以下の正の整数とする。
$n^2$を$5$で割ったときの余りが1となるのはいくつあるか求めよ。
$\begin{array}{c|c|c|c|c|c|c|c|c|c|c|}
\hline
n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\
\hline
n^2 & & & & & & & & & & \\
\hline
余り & & & & & & & & & & \\
\hline
\end{array}$
出典:2003年筑波大学附属高等学校
この動画を見る
$n$を30以下の正の整数とする。
$n^2$を$5$で割ったときの余りが1となるのはいくつあるか求めよ。
$\begin{array}{c|c|c|c|c|c|c|c|c|c|c|}
\hline
n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\
\hline
n^2 & & & & & & & & & & \\
\hline
余り & & & & & & & & & & \\
\hline
\end{array}$
出典:2003年筑波大学附属高等学校
傍接円に関する問題
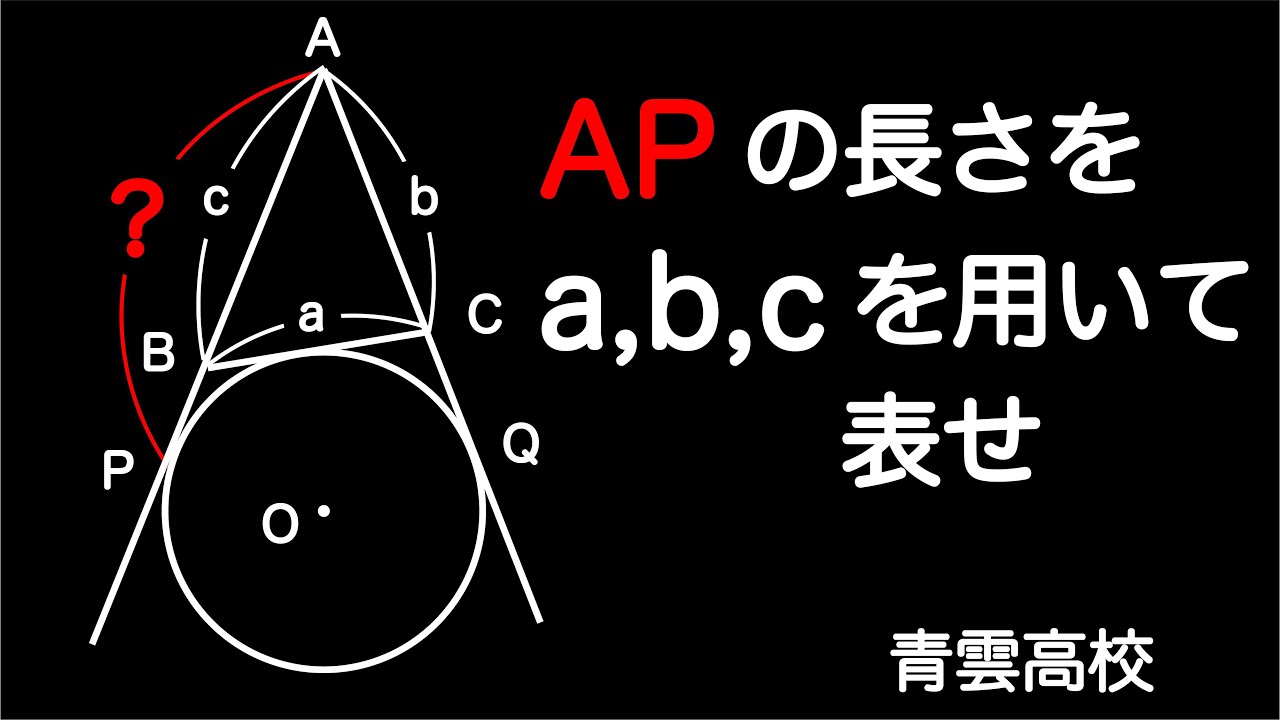
単元:
#数学(中学生)#中3数学#高校入試過去問(数学)#青雲高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、$\textrm{AP}$の長さを$a,b,c$で表せ。
出典:2002年青雲高等学校 高校入試
この動画を見る
動画内の図を参照し、$\textrm{AP}$の長さを$a,b,c$で表せ。
出典:2002年青雲高等学校 高校入試
傾きについて!(高校入試数学)

立方体に内部にできる三角形の面積
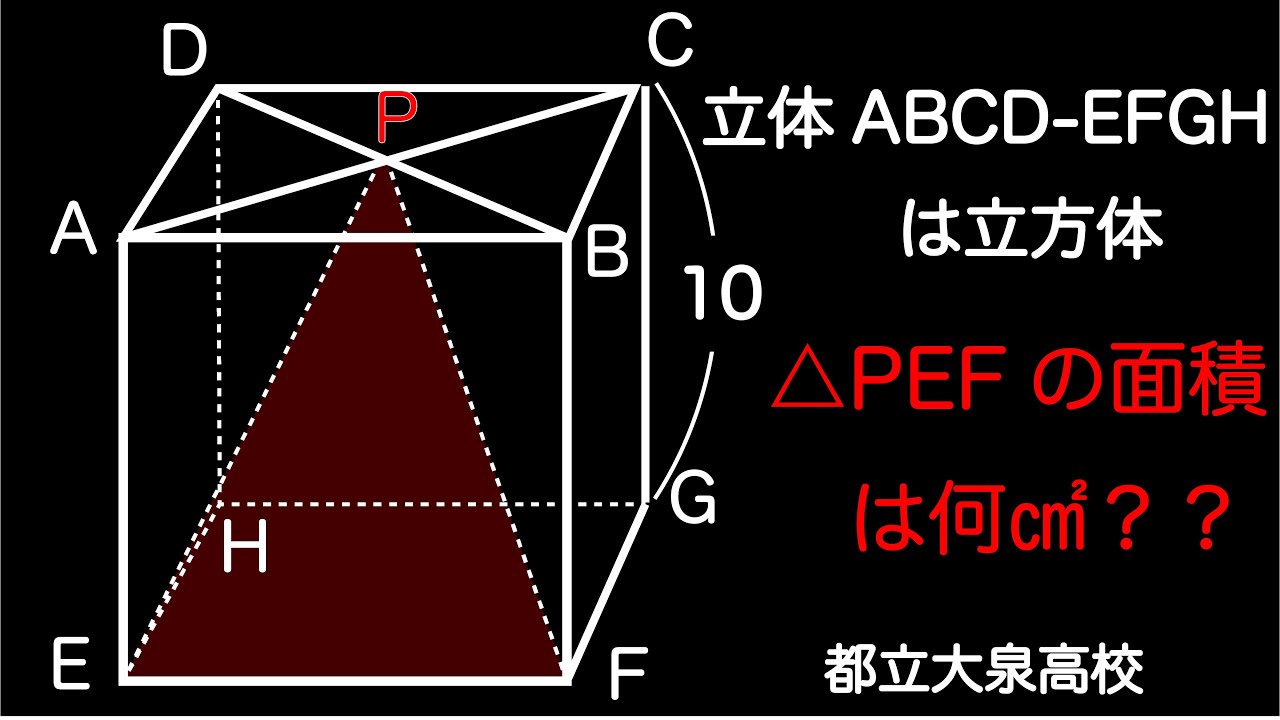
単元:
#数学(中学生)#中1数学#空間図形
指導講師:
数学を数楽に
問題文全文(内容文):
立体$ABCD-DFGH$は立方体
$\triangle PEF$の面積は何$cm^2$??
出典:東京都立大泉高等学校
この動画を見る
立体$ABCD-DFGH$は立方体
$\triangle PEF$の面積は何$cm^2$??
出典:東京都立大泉高等学校
二つの円と三平方!!(都立西)

日比谷高校の角度を求める問題!!
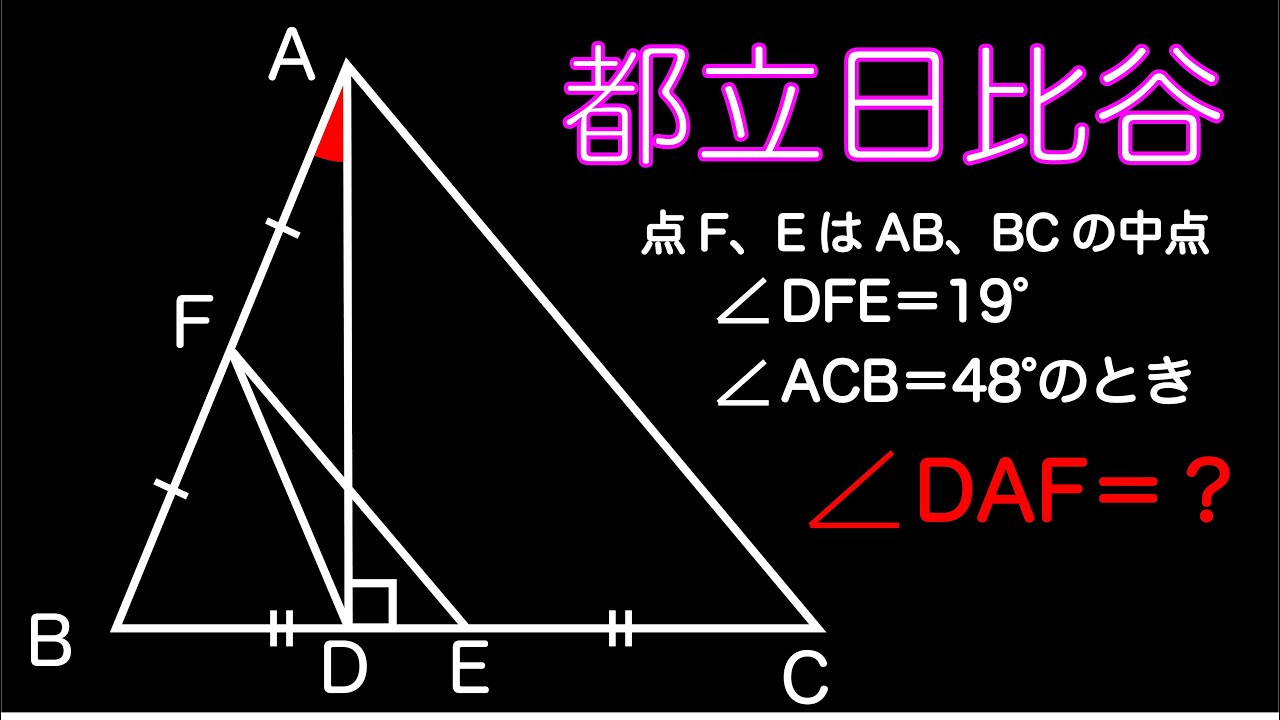
単元:
#数学(中学生)#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
点$F,E$は$AB,BC$の中点
$\angle DFE=19^{ \circ }$
$\angle ACB=48^{ \circ }$のとき
$\angle DAF=??$
出典:東京都立日比谷高等学校
この動画を見る
点$F,E$は$AB,BC$の中点
$\angle DFE=19^{ \circ }$
$\angle ACB=48^{ \circ }$のとき
$\angle DAF=??$
出典:東京都立日比谷高等学校
平面ベクトルと空間ベクトル

筆算したら負けですよ🤗慶應女子

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#高校入試過去問(数学)#慶應義塾女子高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$\displaystyle \frac{86^2-2\times86\times77+77^2}{15^2}+\displaystyle \frac{15^2+2\times15\times13+13^2}{35^2}$
出典:慶應義塾女子
この動画を見る
$\displaystyle \frac{86^2-2\times86\times77+77^2}{15^2}+\displaystyle \frac{15^2+2\times15\times13+13^2}{35^2}$
出典:慶應義塾女子
空間座標の導入!!

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点$P(2,3,4)$に対して
(1)$xy$平面に関して対称な点の座標は( , , )
(2)$yz$平面に関して対称な点の座標は( , , )
(3)$zx$平面に関して対称な点の座標は( , , )
(4)$x$軸平面に関して対称な点の座標は( , , )
(5)$y$軸平面に関して対称な点の座標は( , , )
(6)$z$軸平面に関して対称な点の座標は( , , )
(7)原点平面に関して対称な点の座標は( , , )
この動画を見る
点$P(2,3,4)$に対して
(1)$xy$平面に関して対称な点の座標は( , , )
(2)$yz$平面に関して対称な点の座標は( , , )
(3)$zx$平面に関して対称な点の座標は( , , )
(4)$x$軸平面に関して対称な点の座標は( , , )
(5)$y$軸平面に関して対称な点の座標は( , , )
(6)$z$軸平面に関して対称な点の座標は( , , )
(7)原点平面に関して対称な点の座標は( , , )
普通に計算したら面白くないですよ

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\{3^3\div(-7)^3\}\times\{7^2\div(-3)^2\}+(\displaystyle \frac{7}{3}-\displaystyle \frac{3}{7})\div(\displaystyle \frac{3}{7}-\displaystyle \frac{7}{3})$
出典:都立両国高校
この動画を見る
$\{3^3\div(-7)^3\}\times\{7^2\div(-3)^2\}+(\displaystyle \frac{7}{3}-\displaystyle \frac{3}{7})\div(\displaystyle \frac{3}{7}-\displaystyle \frac{7}{3})$
出典:都立両国高校
2012明大明治の問題!
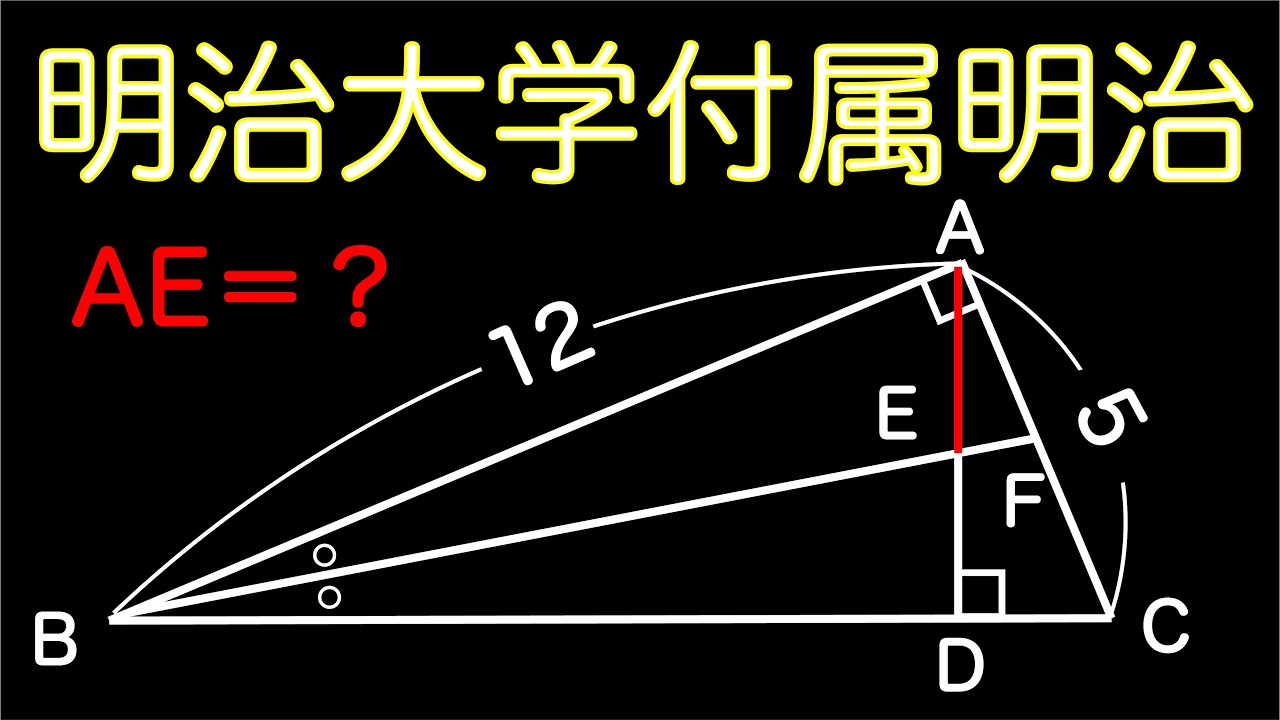
単元:
#数学(中学生)#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、AEの長さを求めよ。
出典:2012年明治大学付属明治高等学校
この動画を見る
動画内の図を参照し、AEの長さを求めよ。
出典:2012年明治大学付属明治高等学校
2直線の交点の位置ベクトル(3通りの説明)

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
数学を数楽に
問題文全文(内容文):
$\overrightarrow{ OA }=\vec{ a },\overrightarrow{ OB }=\vec{ b }$のとき
$\overrightarrow{ OP }$を$\vec{ a },\vec{ b }$で表せ。
この動画を見る
$\overrightarrow{ OA }=\vec{ a },\overrightarrow{ OB }=\vec{ b }$のとき
$\overrightarrow{ OP }$を$\vec{ a },\vec{ b }$で表せ。
内分の位置ベクトル

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
数学を数楽に
問題文全文(内容文):
(1)$\vec{ P }$を$\vec{ a },\vec{ b }$で表せ
(2)$\overrightarrow{ OQ }=\displaystyle \frac{3\vec{ a }+2\vec{ b }}{9}$のとき点$Q$はどこ?
この動画を見る
(1)$\vec{ P }$を$\vec{ a },\vec{ b }$で表せ
(2)$\overrightarrow{ OQ }=\displaystyle \frac{3\vec{ a }+2\vec{ b }}{9}$のとき点$Q$はどこ?
面積比!!
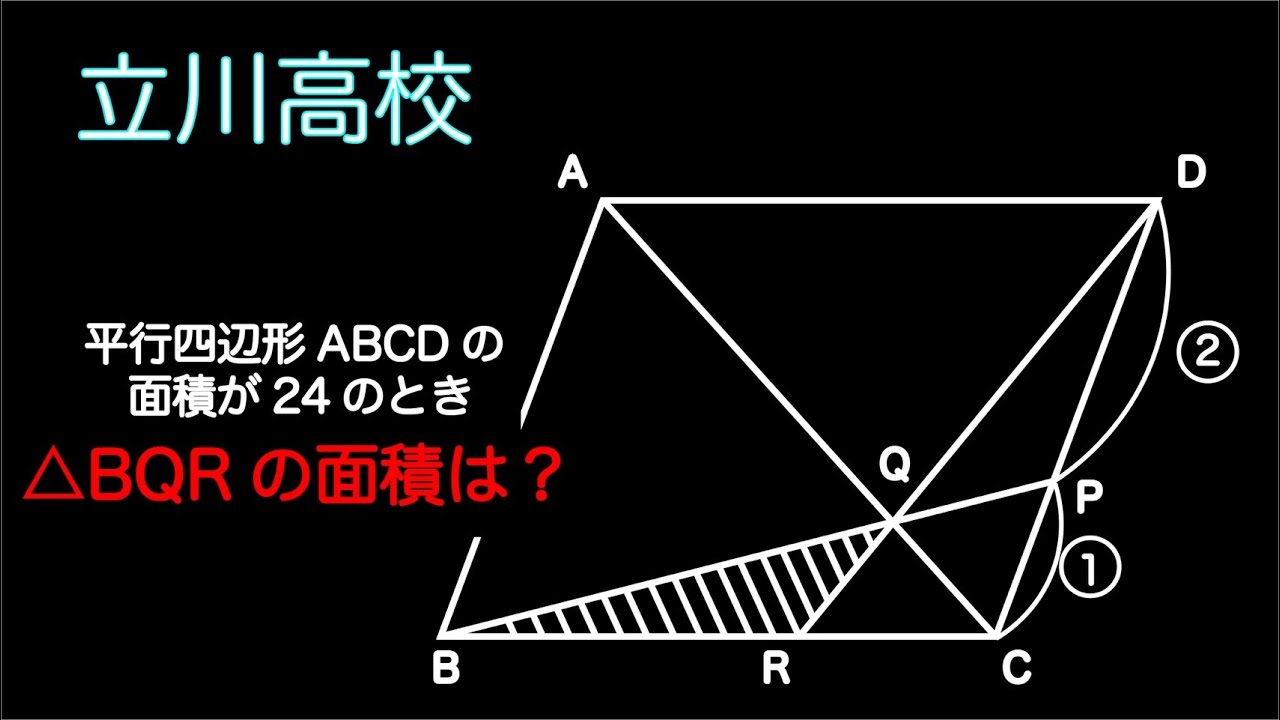
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#東京都立立川高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図の斜線部分の面積を求めよ
出典:2004年都立立川高校
この動画を見る
動画内の図の斜線部分の面積を求めよ
出典:2004年都立立川高校
✖️チョイスヘキサゴン!!(バッテンでチョイスして壁差ゴン!!)

内積と三角形の面積

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
数学を数楽に
問題文全文(内容文):
$\triangle \textrm{OAB}$の面積を求めよ。
この動画を見る
$\triangle \textrm{OAB}$の面積を求めよ。
ベクトルの内積とは??

ベクトルの導入

灘高校の小問 その3
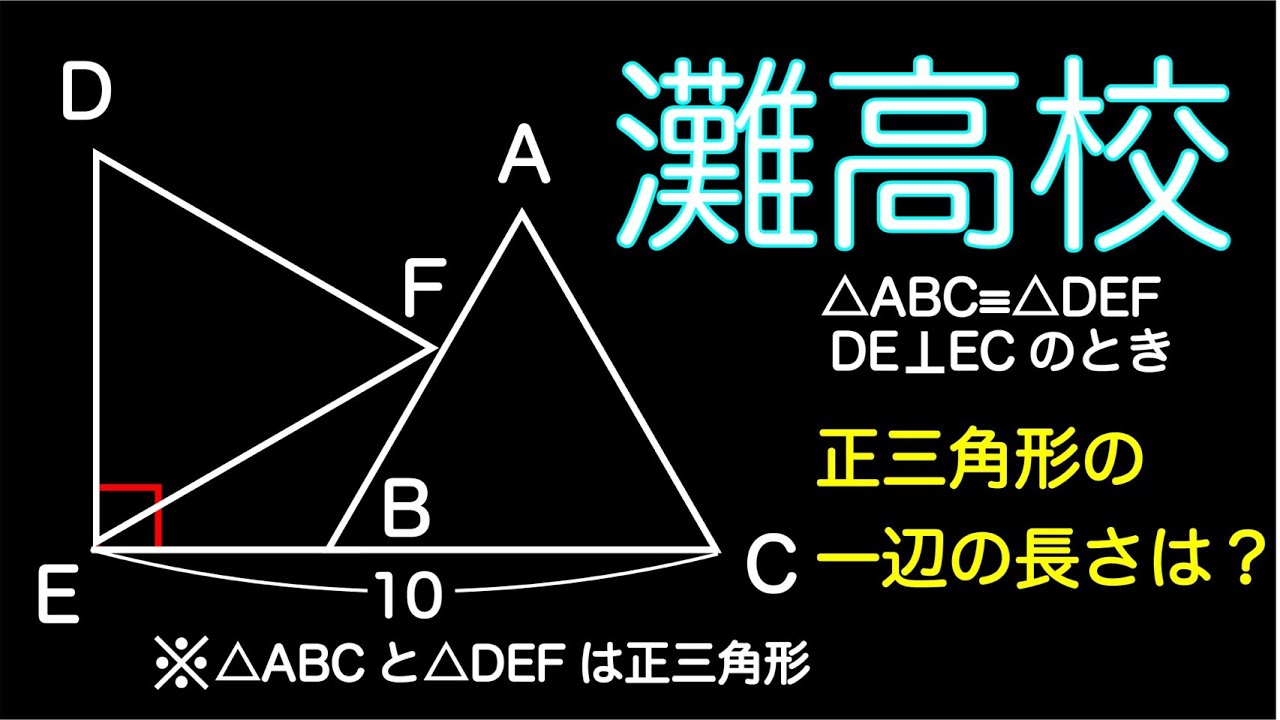
単元:
#数学(中学生)#中2数学#平行と合同#高校入試過去問(数学)#灘高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$\triangle \textrm{ABC} \equiv \triangle \textrm{FDE}$
正三角形の一辺の長さは?
この動画を見る
$\triangle \textrm{ABC} \equiv \triangle \textrm{FDE}$
正三角形の一辺の長さは?





