鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
指数方程式
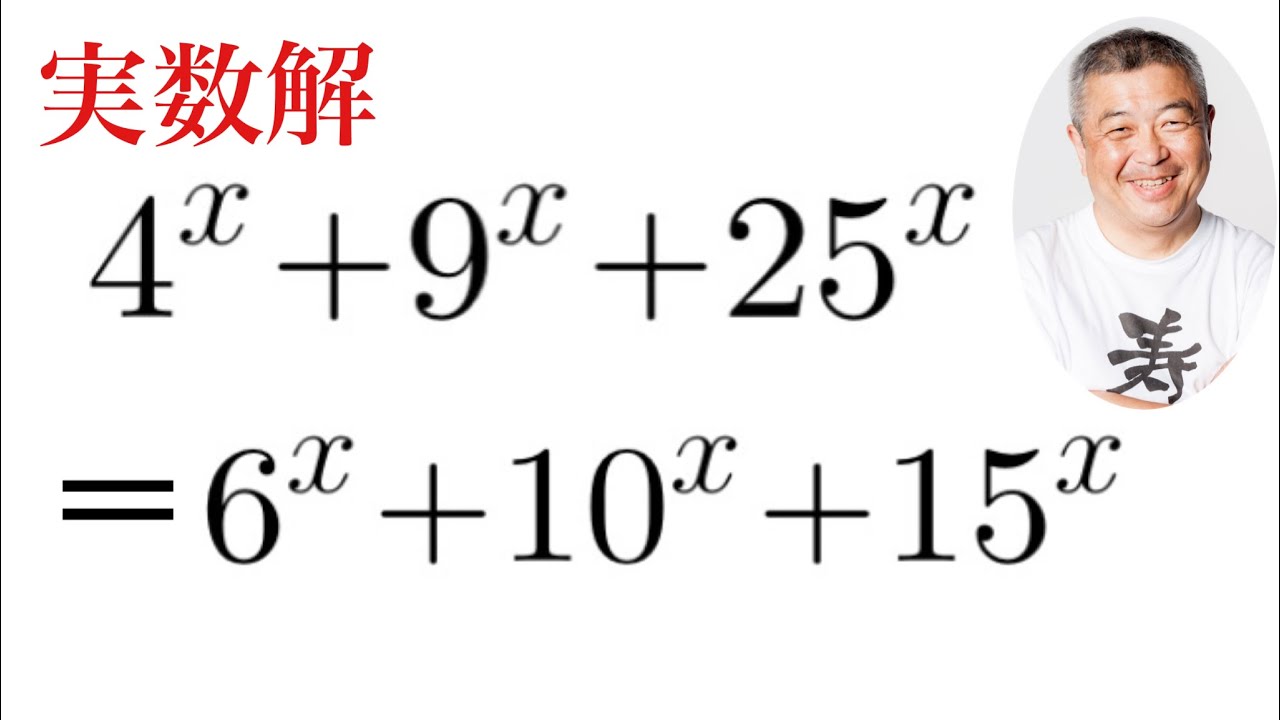
単元：
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ 4^x+9^x+25^x=6^x+10^x+15^x$
これの実数解を求めよ.
この動画を見る
$ 4^x+9^x+25^x=6^x+10^x+15^x$
これの実数解を求めよ.
近畿大（医）やっぱり出た２０２３年問題
単元：
#数A#大学入試過去問(数学)#整数の性質#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ a,n$は整数$(n \geqq2)a$から始まる連続n個の整数の和が2023となる$(a,n)$の組は,
(1)全部で何通りか?
(2)a,nともに奇数は何通りか?
近畿大(医)過去問
この動画を見る
$ a,n$は整数$(n \geqq2)a$から始まる連続n個の整数の和が2023となる$(a,n)$の組は,
(1)全部で何通りか?
(2)a,nともに奇数は何通りか?
近畿大(医)過去問
藤田医科大 ドモアブルの定理
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#数学(高校生)#藤田医科大学#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(1+i)^n=(1-i)n$をみたす2023以下の自然数nの個数を答えよ.
2023藤田医科大過去問
この動画を見る
$(1+i)^n=(1-i)n$をみたす2023以下の自然数nの個数を答えよ.
2023藤田医科大過去問
中学生も挑戦して！関西医科 因数分解
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(a+1)(a-1)(b+1)(b-1)=4ab$をみたす整数を求めよ．$(a,b)(a<b)$
関西医科大過去問
この動画を見る
$(a+1)(a-1)(b+1)(b-1)=4ab$をみたす整数を求めよ．$(a,b)(a<b)$
関西医科大過去問
立命館大 整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ 55x^2+2xy+y^2=2007$をみたす整数(x,y)をすべて求めよ.
立命館大過去問
この動画を見る
$ 55x^2+2xy+y^2=2007$をみたす整数(x,y)をすべて求めよ.
立命館大過去問
東京医科大 ３乗根の不等式
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ \sqrt[3]{n+1}-\sqrt[3]{n}<\dfrac{1}{48}$を満たす最小の自然数nを求めよ.
東京医科大過去問
この動画を見る
$ \sqrt[3]{n+1}-\sqrt[3]{n}<\dfrac{1}{48}$を満たす最小の自然数nを求めよ.
東京医科大過去問
算数できない投資情報誌の記者の記事が医大の入試問題に 小学生もチャレンジしてね！
単元：
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
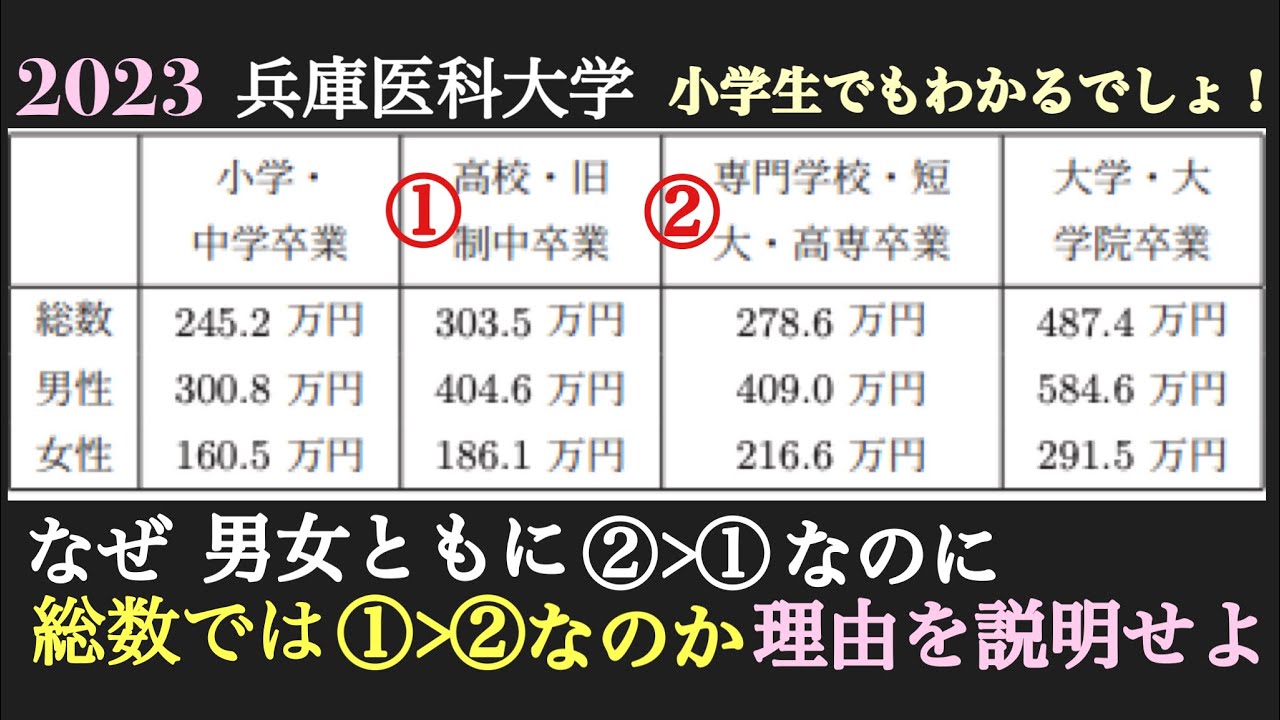
次の文章は,「貯蓄額や所得の多い少ないは「学歴」と関係あるのか？」という記事^1からの抜粋である。表は厚生労働省の令和元年国民生活基礎調査から,学歴ごとの平均所得金額(15歳以上の雇用者1人あたり)をまとめたものです。(中略)
男性・女性ともに専門学校・短大・高専卒の方が所得金額が多いのに,総数となると高校・旧制中卒の方が多いのは統計上の謎です。
男性の所得金額も女性の所得金額もともに,専門学校・短大・高専卒業の方が,高校・旧制中卒業より多いのに,総数(男性+女性)では,逆転した結果になっている。これはどうしてか?説明しなさい。
医大入試問題過去問
この動画を見る
次の文章は,「貯蓄額や所得の多い少ないは「学歴」と関係あるのか？」という記事^1からの抜粋である。表は厚生労働省の令和元年国民生活基礎調査から,学歴ごとの平均所得金額(15歳以上の雇用者1人あたり)をまとめたものです。(中略)
男性・女性ともに専門学校・短大・高専卒の方が所得金額が多いのに,総数となると高校・旧制中卒の方が多いのは統計上の謎です。
男性の所得金額も女性の所得金額もともに,専門学校・短大・高専卒業の方が,高校・旧制中卒業より多いのに,総数(男性+女性)では,逆転した結果になっている。これはどうしてか?説明しなさい。
医大入試問題過去問
虚数係数の二次方程式
単元：
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(1-i)x^2+(3k-6i)x+8-5ki+2i=0$が実数解をもつような整数ｋとそのときの解を求めよ.
愛知大過去問
この動画を見る
$(1-i)x^2+(3k-6i)x+8-5ki+2i=0$が実数解をもつような整数ｋとそのときの解を求めよ.
愛知大過去問
数１基本問題２０２３
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
自然数$(x,y)$の組をすべて求めよ.
$12x^2-xy-5x-y^2-10y+2023=0$
この動画を見る
自然数$(x,y)$の組をすべて求めよ.
$12x^2-xy-5x-y^2-10y+2023=0$
基本対称式 あれで出そうよ
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha+\beta+\delta=1 \\
\alpha\beta+\beta\delta+\delta\alpha=2,
\alpha\beta\delta=3
\end{array}
\right.
\end{eqnarray}$
を満たすとき,
①$\dfrac{1}{\alpha^2}+\dfrac{1}{\beta^2}+\dfrac{1}{\delta^2}$
②$\dfrac{1}{\alpha^3}+\dfrac{1}{\beta^3}+\dfrac{1}{\delta^3}$の値を求めよ.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha+\beta+\delta=1 \\
\alpha\beta+\beta\delta+\delta\alpha=2,
\alpha\beta\delta=3
\end{array}
\right.
\end{eqnarray}$
を満たすとき,
①$\dfrac{1}{\alpha^2}+\dfrac{1}{\beta^2}+\dfrac{1}{\delta^2}$
②$\dfrac{1}{\alpha^3}+\dfrac{1}{\beta^3}+\dfrac{1}{\delta^3}$の値を求めよ.
26次式の因数分解
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
因数分解せよ.
$\displaystyle \sum_{n=0}^{26} x^n=1+x+x^2+････+x^{26}$
この動画を見る
因数分解せよ.
$\displaystyle \sum_{n=0}^{26} x^n=1+x+x^2+････+x^{26}$
長崎大（医、他）虚数方程式
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学#数C#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$Z^4=-8-8\sqrt{3}i$
これを解け.
長崎大(医,他)過去問
この動画を見る
$Z^4=-8-8\sqrt{3}i$
これを解け.
長崎大(医,他)過去問
見掛け倒しの「どっちがでかい？」
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
どちらが大きいか?
$P_{2022} vs P_{2023}$
$P_n$はサイコロをn回ふって出た目の和が7の倍数になる確率を求めよ.
この動画を見る
どちらが大きいか?
$P_{2022} vs P_{2023}$
$P_n$はサイコロをn回ふって出た目の和が7の倍数になる確率を求めよ.
はじめしゃちょーの宝くじ710万円購入210万円当選を数学的に考える
単元：
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
はじめしゃちょーの宝くじ710万円購入210万円当選を数学的に考えていきます.
この動画を見る
はじめしゃちょーの宝くじ710万円購入210万円当選を数学的に考えていきます.
素数問題
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
素数$(p,q)$の組をすべて求めよ.
$-p^3+4p^2+7p-1=q^2$
この動画を見る
素数$(p,q)$の組をすべて求めよ.
$-p^3+4p^2+7p-1=q^2$
整数問題
単元：
#数Ⅰ#数A#数と式#式の計算（整式・展開・因数分解）#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
nを自然数とする.
$(4n-1)^{2n+1}+(4n+1)^{2n-1}$は$32n^2$で割り切れることを示せ.
この動画を見る
nを自然数とする.
$(4n-1)^{2n+1}+(4n+1)^{2n-1}$は$32n^2$で割り切れることを示せ.
ナイスな整数問題
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
nを自然数とする.
$(4n-1)^{2n+1}+(4n+1)^{2n-1}$は$8n$で割り切れることを示せ.
この動画を見る
nを自然数とする.
$(4n-1)^{2n+1}+(4n+1)^{2n-1}$は$8n$で割り切れることを示せ.
灘中2023 の素因数分解と合同式を使えば秒殺
単元：
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性（周期算・方陣算・数列・日暦算・N進法）#灘中学校
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\begin{array}{|c|c|c|c|c}
① & ② & ③ & ④& ⑤& \\
1234 & 5678 & 9123 & 4567&8912&3････\\
\end{array}$
1から9を繰り返し並べ,4つずつに区切る.
2023の4つの数の和を求めよ.
2023灘中過去問
この動画を見る
$\begin{array}{|c|c|c|c|c}
① & ② & ③ & ④& ⑤& \\
1234 & 5678 & 9123 & 4567&8912&3････\\
\end{array}$
1から9を繰り返し並べ,4つずつに区切る.
2023の4つの数の和を求めよ.
2023灘中過去問
2023共通テスト数学 １A 第１問
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)#共通テスト
指導講師：
鈴木貫太郎
問題文全文(内容文)：
第一問,
$\vert x+6 \vert \leqq 2$
$\Box \leqq x \leqq \Box$
$\vert (1-\sqrt3)(a-b)(c-d)+6 \vert 2$
$\Box \leqq (a-b)(c-d) \leqq \boxed{①}$
$(a-b)(c-d)=①$でさらに$(a-c)(b-d)=-3+\sqrt3 $なら $(a-d)(c-b)=\Box $
20232共通テスト過去問
この動画を見る
第一問,
$\vert x+6 \vert \leqq 2$
$\Box \leqq x \leqq \Box$
$\vert (1-\sqrt3)(a-b)(c-d)+6 \vert 2$
$\Box \leqq (a-b)(c-d) \leqq \boxed{①}$
$(a-b)(c-d)=①$でさらに$(a-c)(b-d)=-3+\sqrt3 $なら $(a-d)(c-b)=\Box $
20232共通テスト過去問
整式の剰余 xの２０２３乗
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x^{2023}を\displaystyle \sum_{n=1}^{16} x^n=1+x+x^2+････+x^{16}$で割った余りを求めよ.
この動画を見る
$ x^{2023}を\displaystyle \sum_{n=1}^{16} x^n=1+x+x^2+････+x^{16}$で割った余りを求めよ.
自作の整数問題 効率よく絞り込め
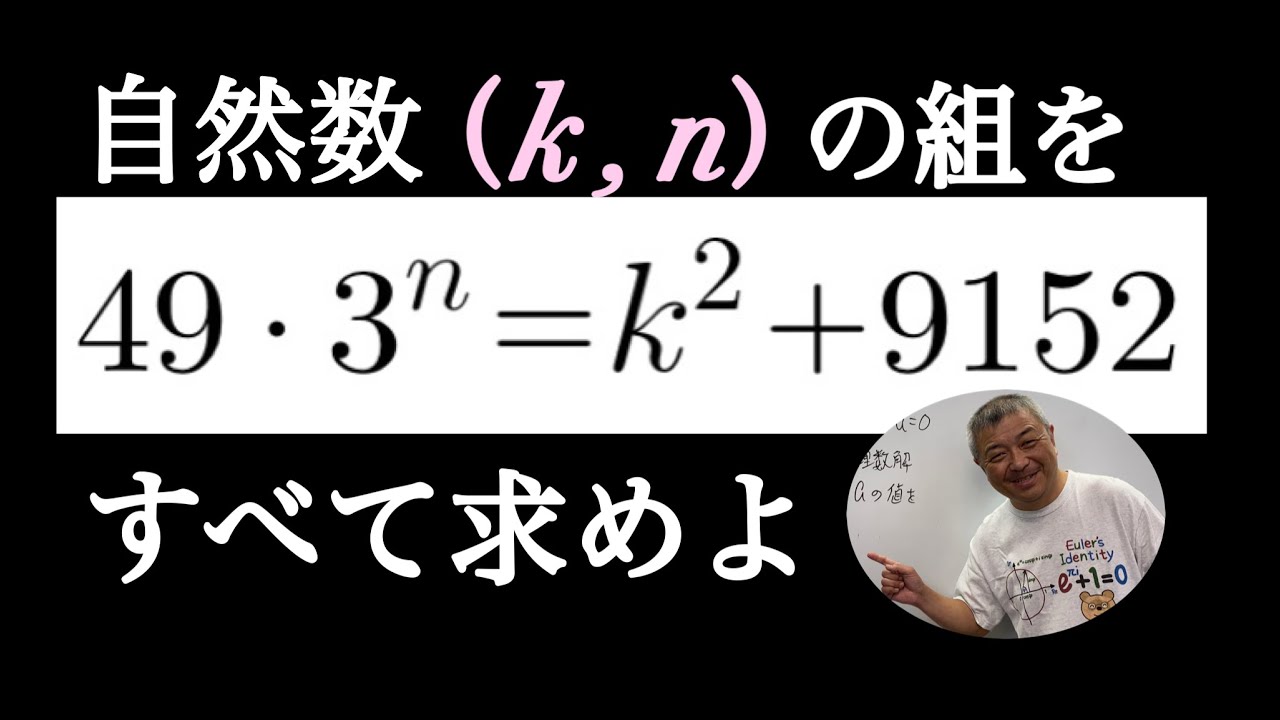
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
k,nを自然数とする.
$49・3^n=k^2+9152$
自然数(k,n)の組をすべて求めよ.
この動画を見る
k,nを自然数とする.
$49・3^n=k^2+9152$
自然数(k,n)の組をすべて求めよ.
宮崎大 整数問題基本
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
素数Pを2進法で表したらすべての位の数が1でk桁であったkは素数であることを示せ.
宮崎大過去問
この動画を見る
素数Pを2進法で表したらすべての位の数が1でk桁であったkは素数であることを示せ.
宮崎大過去問
大阪公立大 ７の８０乗の下５桁
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#学校別大学入試過去問解説(数学)#数学(高校生)#大阪公立大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ 7^{80}$の下5桁を求めよ.
大阪公立大過去問
この動画を見る
$ 7^{80}$の下5桁を求めよ.
大阪公立大過去問
積分の基本問題
単元：
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$y=x(x-2)^2$と$y=kx(0<k<4)$とで囲まれる2つの部分の面積が等しい.$k=\Box$を求めよ.
愛知学院大(薬,歯)過去問
この動画を見る
$y=x(x-2)^2$と$y=kx(0<k<4)$とで囲まれる2つの部分の面積が等しい.$k=\Box$を求めよ.
愛知学院大(薬,歯)過去問
学習院大 二次不等式
単元：
#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ f(x)=x^2+2(a-5)x+a^2-11a+26$
$f(x)a$を満たす実数xが存在するようなaの範囲を求めよ.
学習院大過去問
この動画を見る
$ f(x)=x^2+2(a-5)x+a^2-11a+26$
$f(x)a$を満たす実数xが存在するようなaの範囲を求めよ.
学習院大過去問
整式の剰余 ２通りの解法で 中京大
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ 3x^{3n+2}をx^2+x+1$で割った余りを求めよ.
中京大過去問
この動画を見る
$ 3x^{3n+2}をx^2+x+1$で割った余りを求めよ.
中京大過去問
解けるように作られた指数方程式
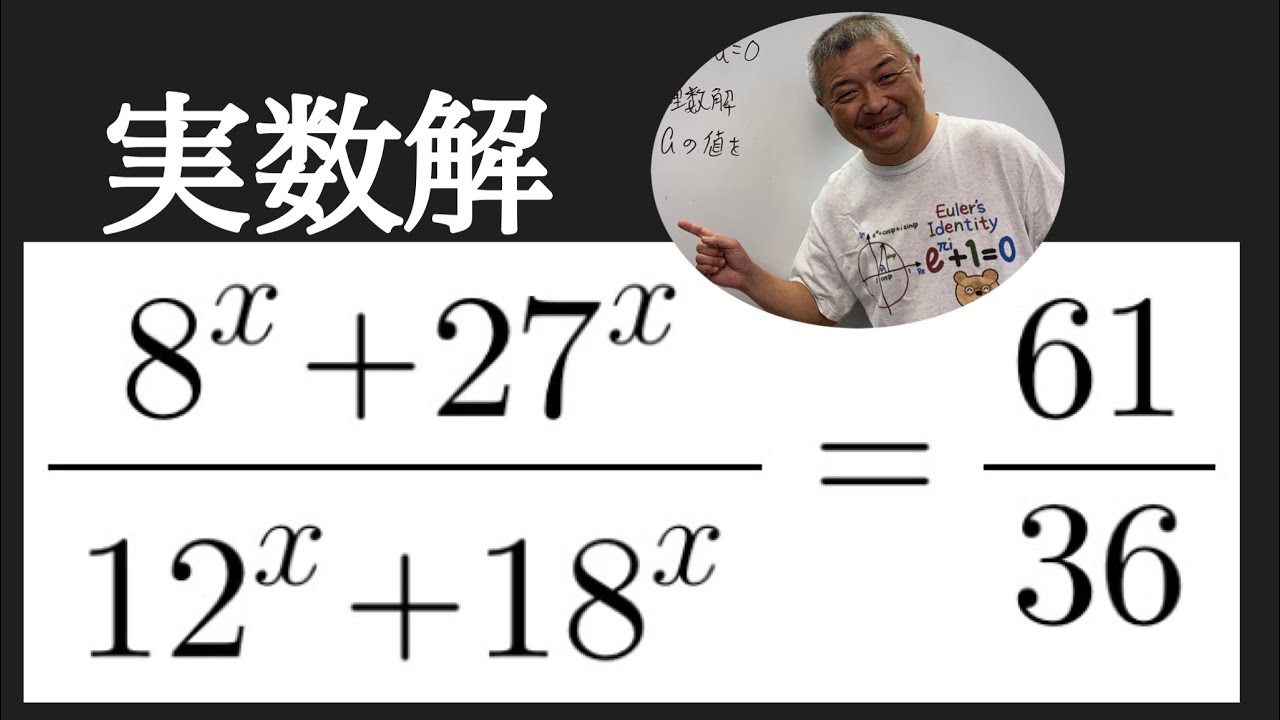
単元：
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$実数解 $\dfrac{8^x+27^x}{12^x+18^x}=\dfrac{61}{36}$
これを求めよ.
この動画を見る
$実数解 $\dfrac{8^x+27^x}{12^x+18^x}=\dfrac{61}{36}$
これを求めよ.
因数分解
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x(y^3-z^3)+y(z^3-x^3)+z(x^3-y^3)$
これを因数分解せよ.
創価大過去問
この動画を見る
$ x(y^3-z^3)+y(z^3-x^3)+z(x^3-y^3)$
これを因数分解せよ.
創価大過去問
ホッケースティック恒等式
単元：
#数A#整数の性質#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
a,b,cは0以上の整数であり,$a+b+c \leqq 11$となる.
(a,b,c)の組は何通りか?
この動画を見る
a,b,cは0以上の整数であり,$a+b+c \leqq 11$となる.
(a,b,c)の組は何通りか?
東海高校 ただの連立方程式だけど‥‥
単元：
#数学(中学生)#中２数学#連立方程式#高校入試過去問(数学)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
連立方程式を解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
(\sqrt5-1)x+y=\sqrt5-1 \\
x+(\sqrt5+1)y=\sqrt5+1
\end{array}
\right.
\end{eqnarray}$
東海高校過去問
この動画を見る
連立方程式を解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
(\sqrt5-1)x+y=\sqrt5-1 \\
x+(\sqrt5+1)y=\sqrt5+1
\end{array}
\right.
\end{eqnarray}$
東海高校過去問