 鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
指数方程式
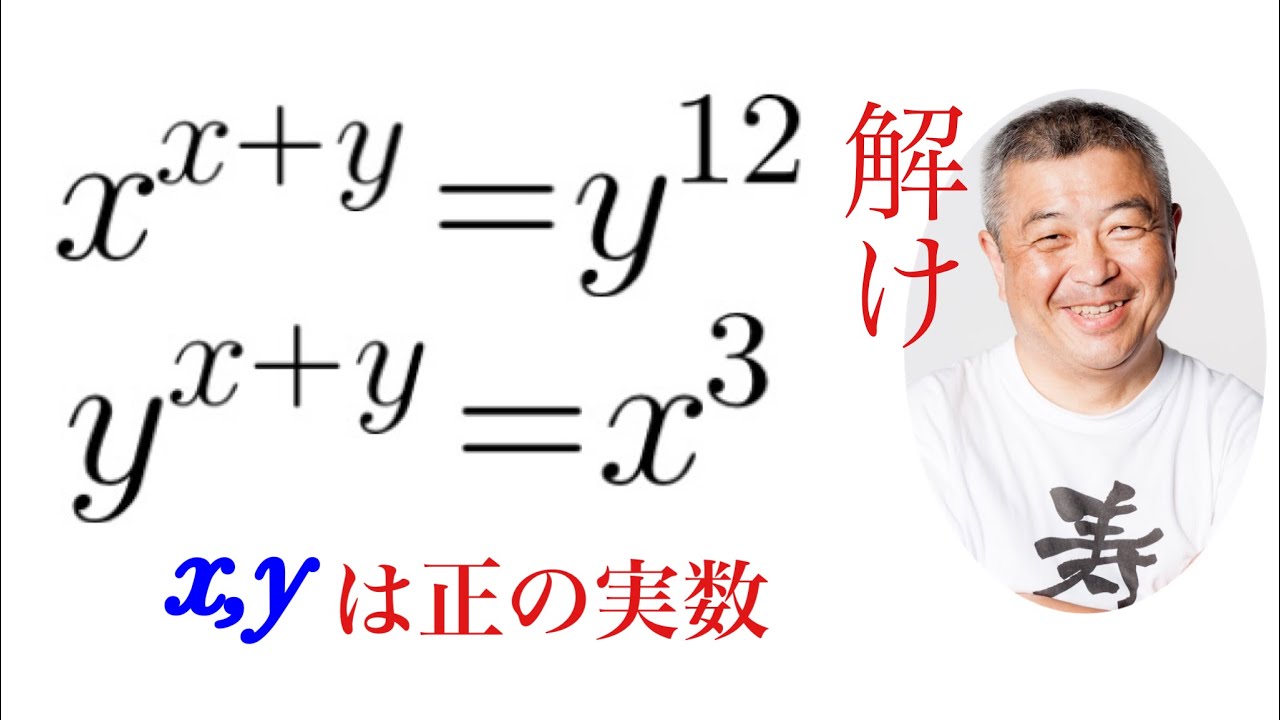
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yは正の実数である.
$x^{x+y}=y^{12},y^{x+y}=x^3$
これを解け.
この動画を見る
x,yは正の実数である.
$x^{x+y}=y^{12},y^{x+y}=x^3$
これを解け.
整数問題
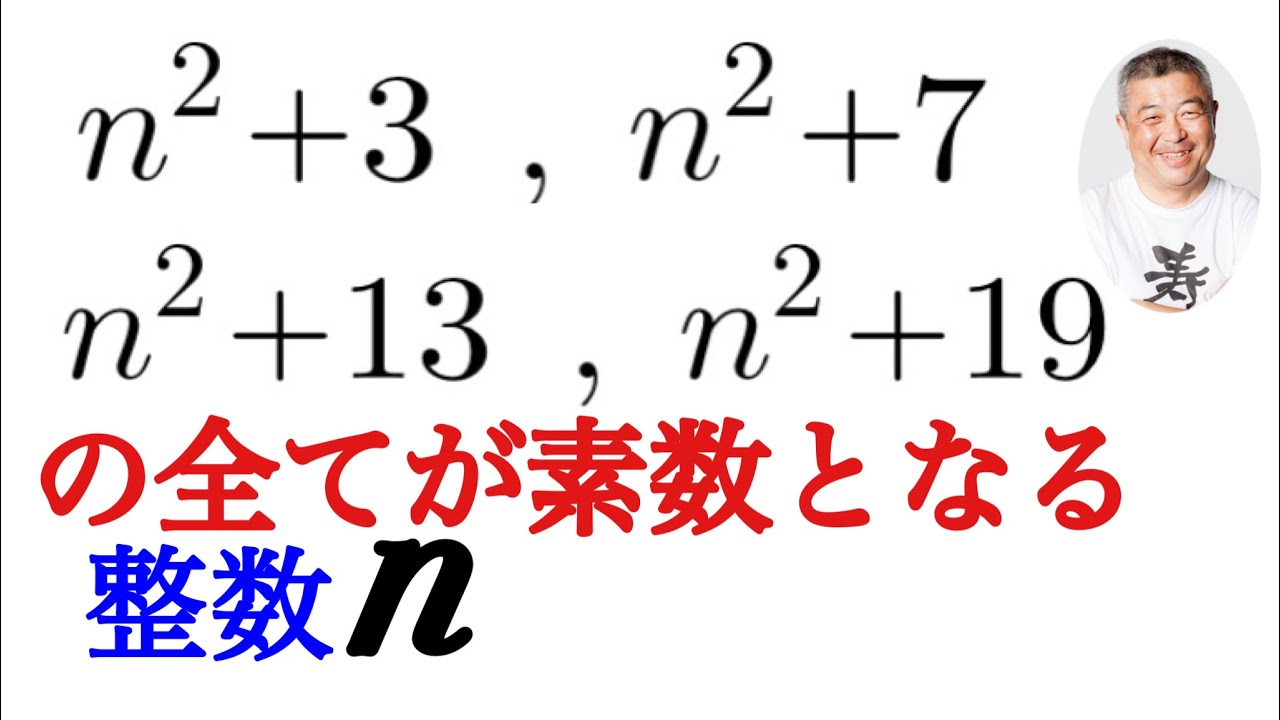
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ n^2+3,n^2+7,n^2+13,n^2+19$のすべてが素数となる整数nをすべて求めよ.
この動画を見る
$ n^2+3,n^2+7,n^2+13,n^2+19$のすべてが素数となる整数nをすべて求めよ.
解けるようにできた4次方程式 要工夫
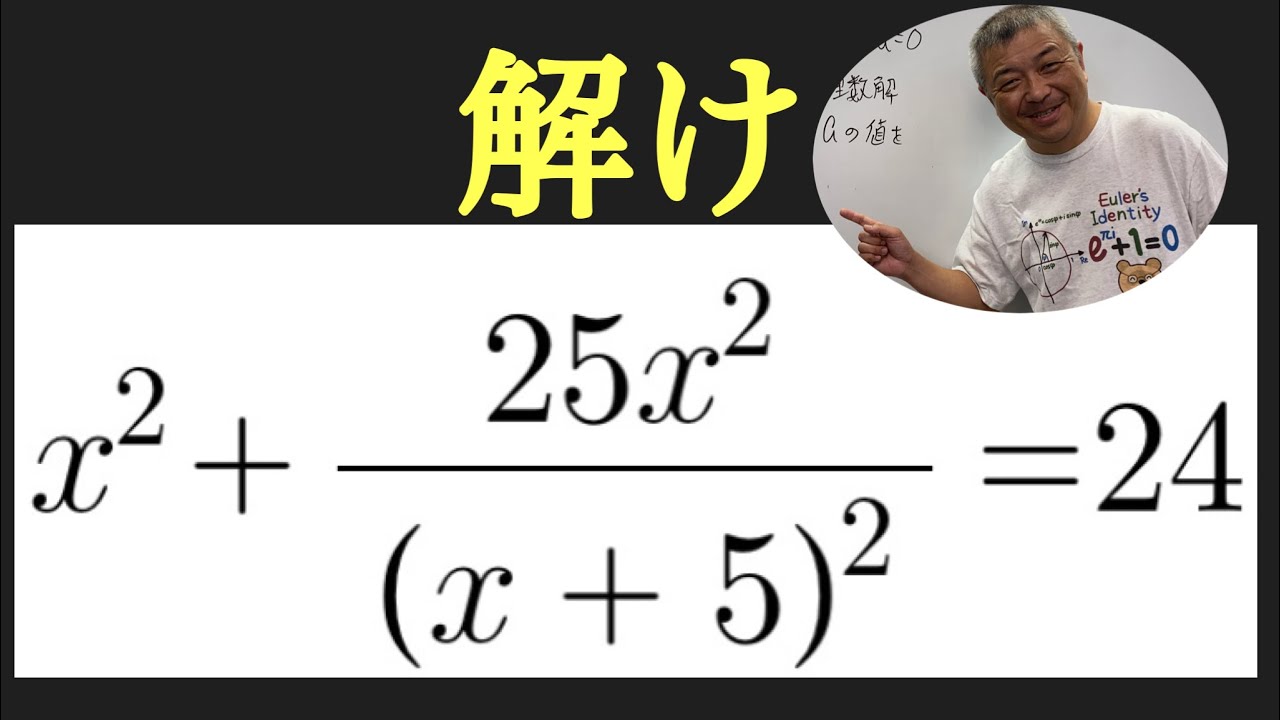
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^2+\dfrac{25x^2}{(x+5)^2}=24$
これを解け.
この動画を見る
$ x^2+\dfrac{25x^2}{(x+5)^2}=24$
これを解け.
ただの分数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{3}{m}+\dfrac{4}{n}=\dfrac{1}{12}$,自然数(m,n)をすべて求めよ.
ただし,$\dfrac{3}{m},\dfrac{4}{m}$は既約分数である.
この動画を見る
$ \dfrac{3}{m}+\dfrac{4}{n}=\dfrac{1}{12}$,自然数(m,n)をすべて求めよ.
ただし,$\dfrac{3}{m},\dfrac{4}{m}$は既約分数である.
素数になる2次式

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ n^2-54n+504$が素数となる自然数nをすべて求めよ.
この動画を見る
$ n^2-54n+504$が素数となる自然数nをすべて求めよ.
ベトナム数学オリンピック
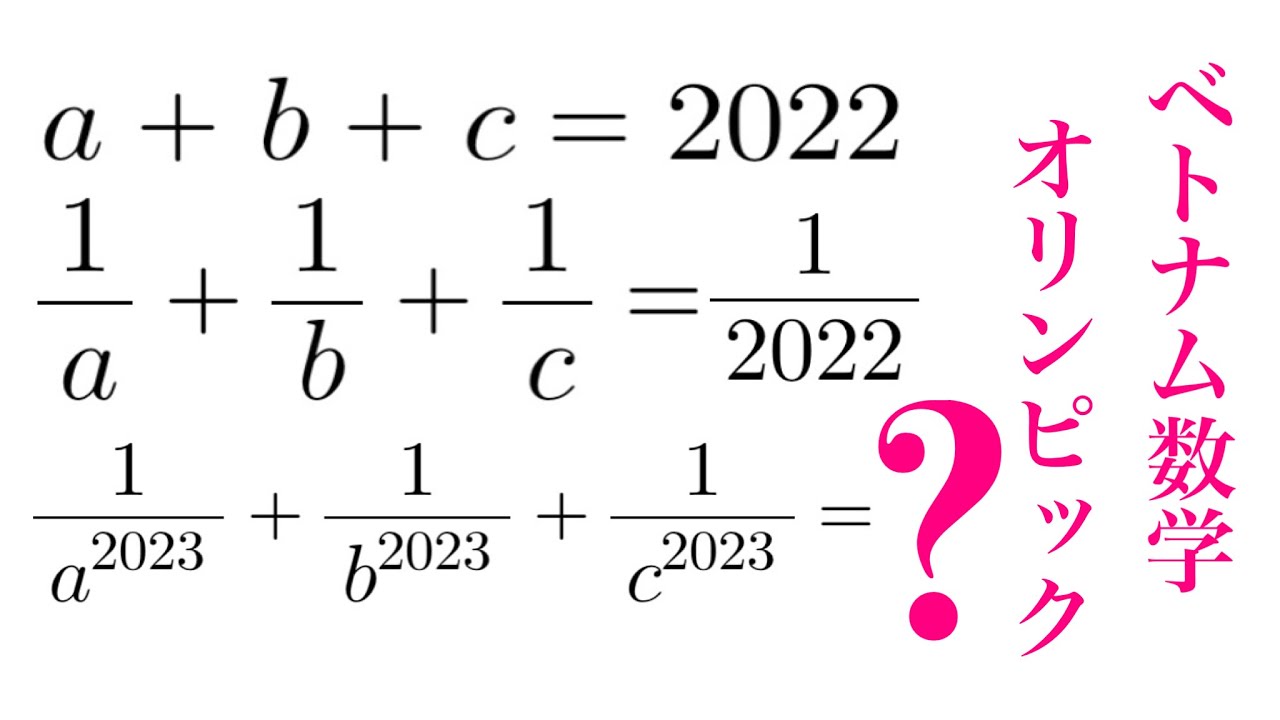
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a+b+c=2022$
$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{2022}$
$\dfrac{1}{a^{2023}}+\dfrac{1}{b^{2023}}+\dfrac{1}{c^{2023}}=?$
これを解け.
ベトナム数学オリンピック過去問
この動画を見る
$ a+b+c=2022$
$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{2022}$
$\dfrac{1}{a^{2023}}+\dfrac{1}{b^{2023}}+\dfrac{1}{c^{2023}}=?$
これを解け.
ベトナム数学オリンピック過去問
ガウス記号の二次方程式

見掛け倒しの「どっちがでかい?」

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt[5]{5!}$ vs $\sqrt[6]{6!}$
どちらが大きいか?
この動画を見る
$ \sqrt[5]{5!}$ vs $\sqrt[6]{6!}$
どちらが大きいか?
0.9999999‥‥=1?

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$A,B$は1桁の自然数である.これを解け.
$\sqrt{0.AAA・・・・・・}=0.BBB・・・・・・$
この動画を見る
$A,B$は1桁の自然数である.これを解け.
$\sqrt{0.AAA・・・・・・}=0.BBB・・・・・・$
指数の基本問題
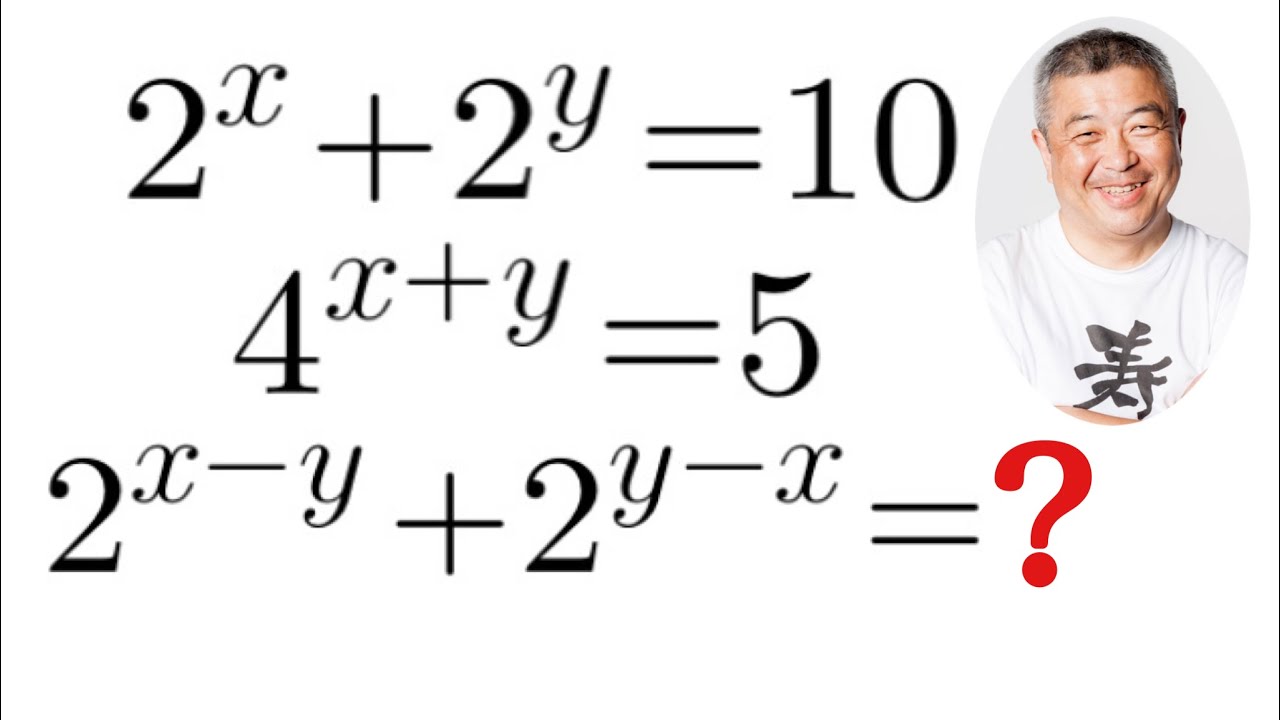
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yは実数である.
$2^x+2^y=10,4^{x+y}=5,2^{x-y}+2^{y-x}=?$
これを解け.
この動画を見る
x,yは実数である.
$2^x+2^y=10,4^{x+y}=5,2^{x-y}+2^{y-x}=?$
これを解け.
指数の基本
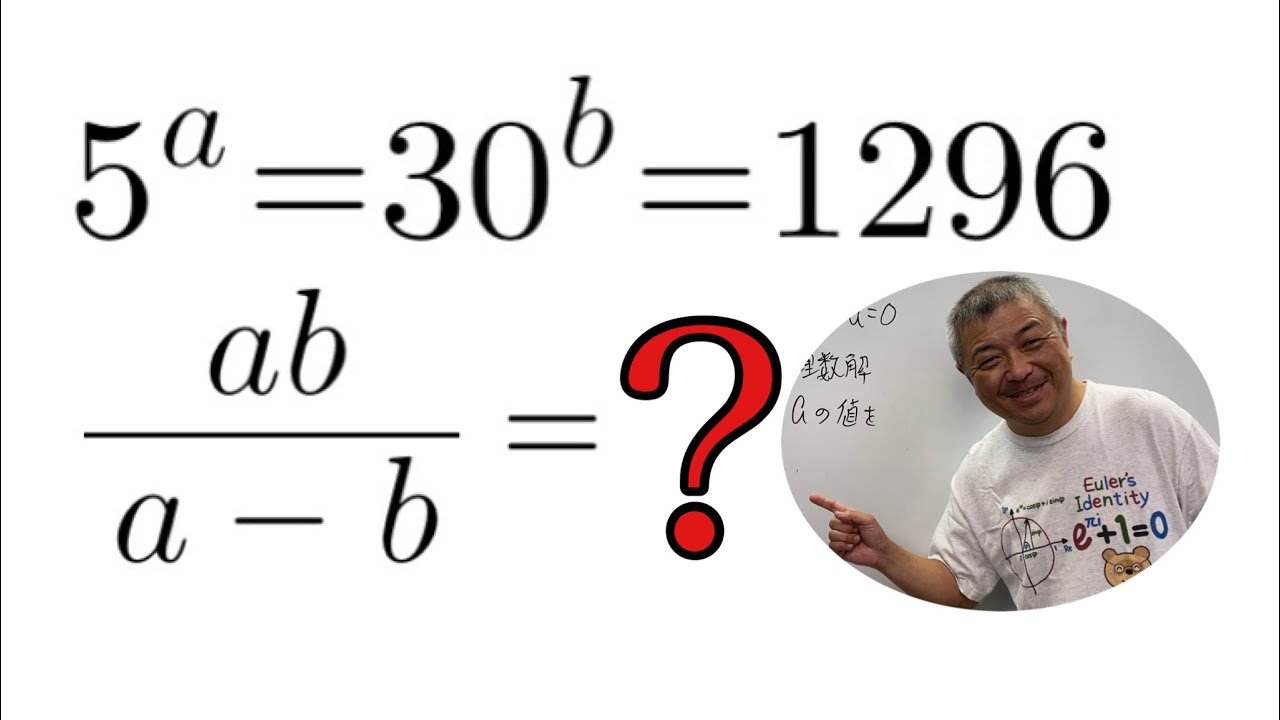
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 5^a=30^b=1296,\dfrac{ab}{a-b}$の値を求めよ.
この動画を見る
$ 5^a=30^b=1296,\dfrac{ab}{a-b}$の値を求めよ.
面白不等式

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
m,nは自然数である.
$\dfrac{57}{158}\lt \dfrac{m}{n}\lt \dfrac{25}{68}$
mの最小値を求めよ.
この動画を見る
m,nは自然数である.
$\dfrac{57}{158}\lt \dfrac{m}{n}\lt \dfrac{25}{68}$
mの最小値を求めよ.
ざ・一次不定方程式 合同式で楽々

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数x,yについて、$97x+83y=23$を満たす整数解x,yの一般解を求めよ.
この動画を見る
整数x,yについて、$97x+83y=23$を満たす整数解x,yの一般解を求めよ.
すっきりするただの計算問題

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x=\sqrt2+1$のとき,
$\dfrac{x^7-x}{x^8+1}$の値を求めよ.
この動画を見る
$ x=\sqrt2+1$のとき,
$\dfrac{x^7-x}{x^8+1}$の値を求めよ.
ただの約分

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{1+2+3+4+8+・・・・・・+2^{2024}}{1+8+64+512+・・・・・・+2^{2022}}$
これを計算せよ.
この動画を見る
$ \dfrac{1+2+3+4+8+・・・・・・+2^{2024}}{1+8+64+512+・・・・・・+2^{2022}}$
これを計算せよ.
合同式と組み合わせの公式

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
${}_{30} \mathrm{ C }_{15}$を31で割った余りを求めよ.
この動画を見る
${}_{30} \mathrm{ C }_{15}$を31で割った余りを求めよ.
3乗根をはずせ

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt[3]{77-20\sqrt{13}}$
これの3乗根を外せ.
この動画を見る
$ \sqrt[3]{77-20\sqrt{13}}$
これの3乗根を外せ.
平方して下3桁が同じ数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
次のような自然数をすべて求めよ.
①2桁の自然数を2乗したら下2桁が同じ数を求めよ.
②3桁の自然数を2乗したら下3桁が同じ数を求めよ.
この動画を見る
次のような自然数をすべて求めよ.
①2桁の自然数を2乗したら下2桁が同じ数を求めよ.
②3桁の自然数を2乗したら下3桁が同じ数を求めよ.
東海大 数1

単元:
#数Ⅰ#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 0\lt x\lt 2$で$x$と$x^2$の小数部分が同じであるxを求めよ.
東海大過去問
この動画を見る
$ 0\lt x\lt 2$で$x$と$x^2$の小数部分が同じであるxを求めよ.
東海大過去問
平方数にならない式

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
nを自然数とする.
$n(n+1)(n+2)(n+3)$は平方数でないことを示せ.
この動画を見る
nを自然数とする.
$n(n+1)(n+2)(n+3)$は平方数でないことを示せ.
整数問題 基本問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
nを整数とする.
$n^8-6n^6+9n^4-4n^2$は720の倍数であることを示せ.
この動画を見る
nを整数とする.
$n^8-6n^6+9n^4-4n^2$は720の倍数であることを示せ.
整数の基本問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
m,nを自然数とし$(m \gt n)$,pを素数とする.
$\dfrac{1}{m}+\dfrac{1}{n}=\dfrac{1}{p}$のとき,
mは偶数であることを示せ.
この動画を見る
m,nを自然数とし$(m \gt n)$,pを素数とする.
$\dfrac{1}{m}+\dfrac{1}{n}=\dfrac{1}{p}$のとき,
mは偶数であることを示せ.
x,yの2次式の値の範囲

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yは実数とする.
$x^2+2y^2-4y=2$を満たすとき,
$x+4y^2-8y$の値の範囲を求めよ.
この動画を見る
x,yは実数とする.
$x^2+2y^2-4y=2$を満たすとき,
$x+4y^2-8y$の値の範囲を求めよ.
5次式の因数分解 R15中学生はご遠慮ください

単元:
#数Ⅰ#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^5+16x+32$
これを因数分解(整数係数)せよ.
この動画を見る
$ x^5+16x+32$
これを因数分解(整数係数)せよ.
山形大 ナイスな問題

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#山形大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \alpha=\cos36°+i\sin36°$とする.
(1)$(x-1)(x-\alpha)(x-\alpha^2)・・・・・・(x-\alpha^9)$を計算せよ.
(2)$(x-1)(x-\alpha^2)(x-\alpha^4)(x-\alpha^6)(x-\alpha^8)$を計算せよ.
(3)$(x-\alpha)(x-\alpha^3)(x-\alpha^7)(x-\alpha^9)$を計算せよ.
(4)(3)を用いて\alpha+\dfrac{1}{\alpha}を計算せよ.
山形大過去問
この動画を見る
$ \alpha=\cos36°+i\sin36°$とする.
(1)$(x-1)(x-\alpha)(x-\alpha^2)・・・・・・(x-\alpha^9)$を計算せよ.
(2)$(x-1)(x-\alpha^2)(x-\alpha^4)(x-\alpha^6)(x-\alpha^8)$を計算せよ.
(3)$(x-\alpha)(x-\alpha^3)(x-\alpha^7)(x-\alpha^9)$を計算せよ.
(4)(3)を用いて\alpha+\dfrac{1}{\alpha}を計算せよ.
山形大過去問
5次方程式
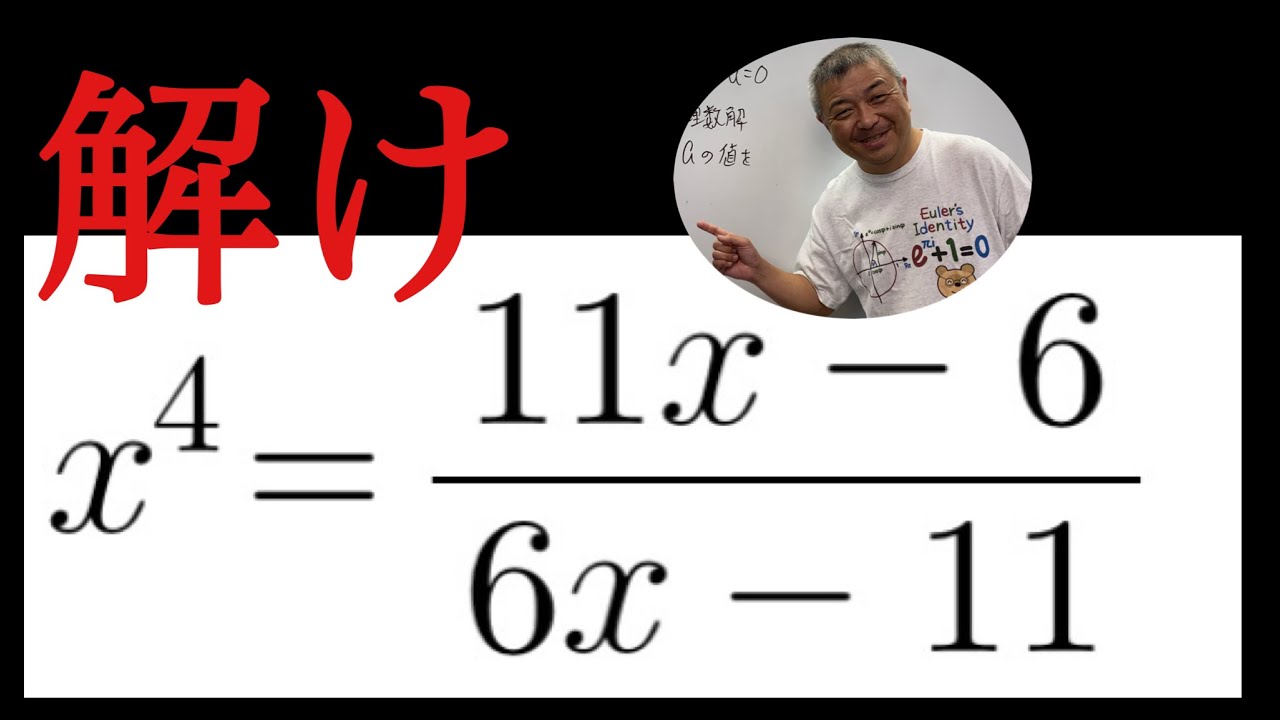
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^4=\dfrac{11x^6}{6x-11}$
これを解け.
この動画を見る
$ x^4=\dfrac{11x^6}{6x-11}$
これを解け.
素因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$64000001$を素因数分解すると3つの素因数分解をもつ.
$pqr(p \lt q \lt r)q$の値を求めよ.
この動画を見る
$64000001$を素因数分解すると3つの素因数分解をもつ.
$pqr(p \lt q \lt r)q$の値を求めよ.
数学オリンピック予選

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#解と判別式・解と係数の関係#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
有理数係数の2次方程式
$ x^{2n}+a_1x^{2n-1}+a_2x^{2n-2}+$
$・・・・・・+a_{2n-1}x+a_{2n}=0$
の解はすべて$x^2+5x+7=0$の解にもなっている.
$a_1$の値を求めよ.
この動画を見る
有理数係数の2次方程式
$ x^{2n}+a_1x^{2n-1}+a_2x^{2n-2}+$
$・・・・・・+a_{2n-1}x+a_{2n}=0$
の解はすべて$x^2+5x+7=0$の解にもなっている.
$a_1$の値を求めよ.
連立3元3次方程式
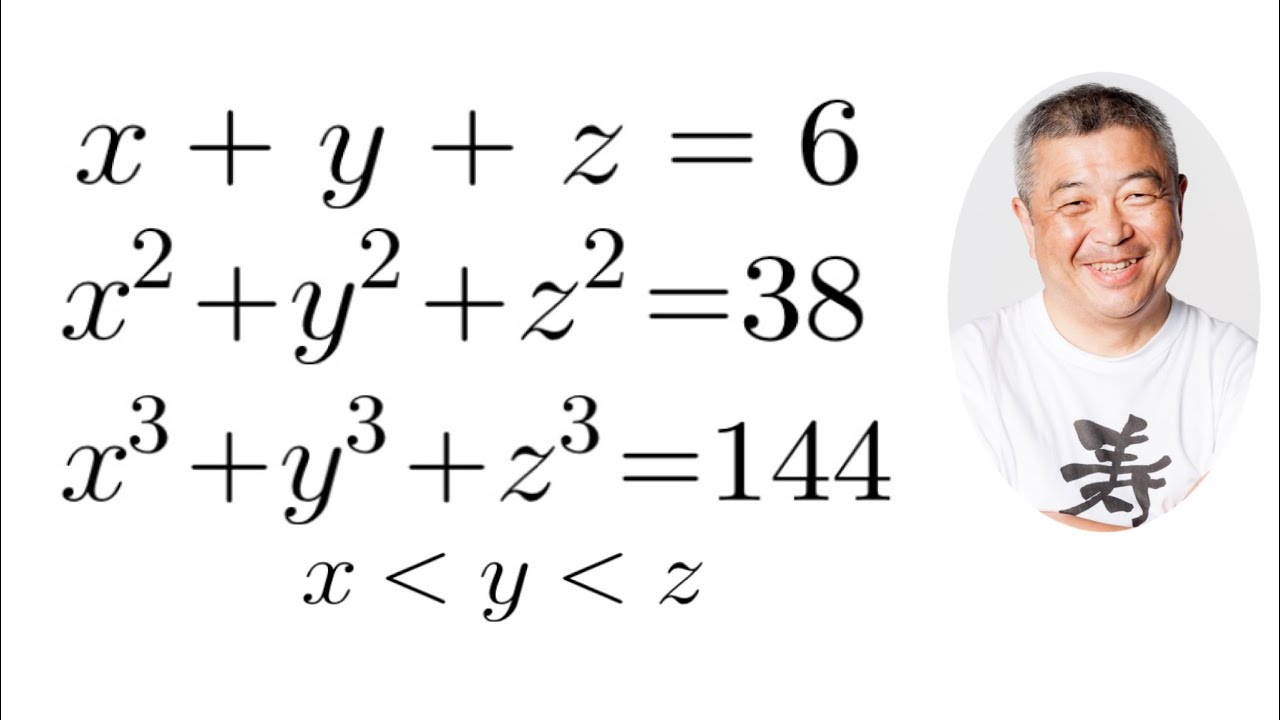
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\lt y\lt z$とする.これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+z=6 \\
x^2+y^2+z^2=38 \\\
x^3+y^3+z^3=144
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$x\lt y\lt z$とする.これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+z=6 \\
x^2+y^2+z^2=38 \\\
x^3+y^3+z^3=144
\end{array}
\right.
\end{eqnarray}$
アジア太平洋数学オリンピックのナイスな整数問題

単元:
#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
a,b,cは自然数である.
$a^2+b+c,a+b^2+c,a+b+c^2$
この3つのすべてが平方数になることはないことを示せ.
アジア太平洋数学オリンピック過去問
この動画を見る
a,b,cは自然数である.
$a^2+b+c,a+b^2+c,a+b+c^2$
この3つのすべてが平方数になることはないことを示せ.
アジア太平洋数学オリンピック過去問



