 鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
対数方程式 華麗に解こう

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$3^{\log_2 x}+3^{\log_2 \frac{8}{x}}=12$
この動画を見る
これを解け.
$3^{\log_2 x}+3^{\log_2 \frac{8}{x}}=12$
国際数学オリンピック 積和

単元:
#積分とその応用#不定積分#定積分#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\cos\dfrac{\pi}{7}-\cos\dfrac{2\pi}{7}+\cos\dfrac{3\pi}{7}=\dfrac{1}{2}$を示せ.
国際数学オリンピック
この動画を見る
$\cos\dfrac{\pi}{7}-\cos\dfrac{2\pi}{7}+\cos\dfrac{3\pi}{7}=\dfrac{1}{2}$を示せ.
国際数学オリンピック
トルコJr数学オリンピック

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解$(x,y)$を求めよ.
$2x^2+y^2+7=2(x+1)(y+1)$
トルコJr数学オリンピック
この動画を見る
実数解$(x,y)$を求めよ.
$2x^2+y^2+7=2(x+1)(y+1)$
トルコJr数学オリンピック
瞬殺!かいぶん数

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$を自然数とする.
$n^8+2n^7+3n^6+4n^5+5n^4+4n^3+3n^2+$
$2n+1$は素数でないことを示せ.
この動画を見る
$n$を自然数とする.
$n^8+2n^7+3n^6+4n^5+5n^4+4n^3+3n^2+$
$2n+1$は素数でないことを示せ.
4次方程式
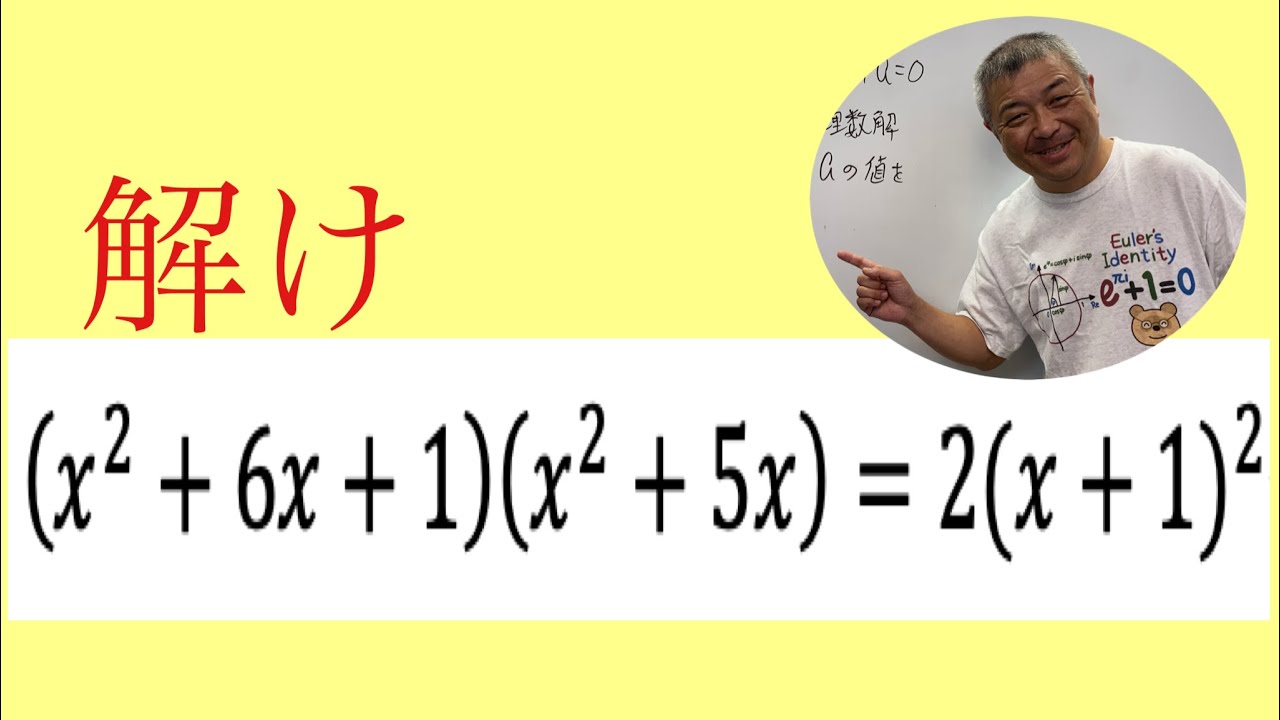
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$(x^2+6x+1)(x^2+5x)=2(x+1)^2$
この動画を見る
これを解け.
$(x^2+6x+1)(x^2+5x)=2(x+1)^2$
ただの累乗根方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\sqrt[x]{4096}-\sqrt[\frac{x}{2}]{2^{3x-6}}+12=0$
この動画を見る
これを解け.
$\sqrt[x]{4096}-\sqrt[\frac{x}{2}]{2^{3x-6}}+12=0$
指数タワー 7で割った余りは?

連立二元二次方程式
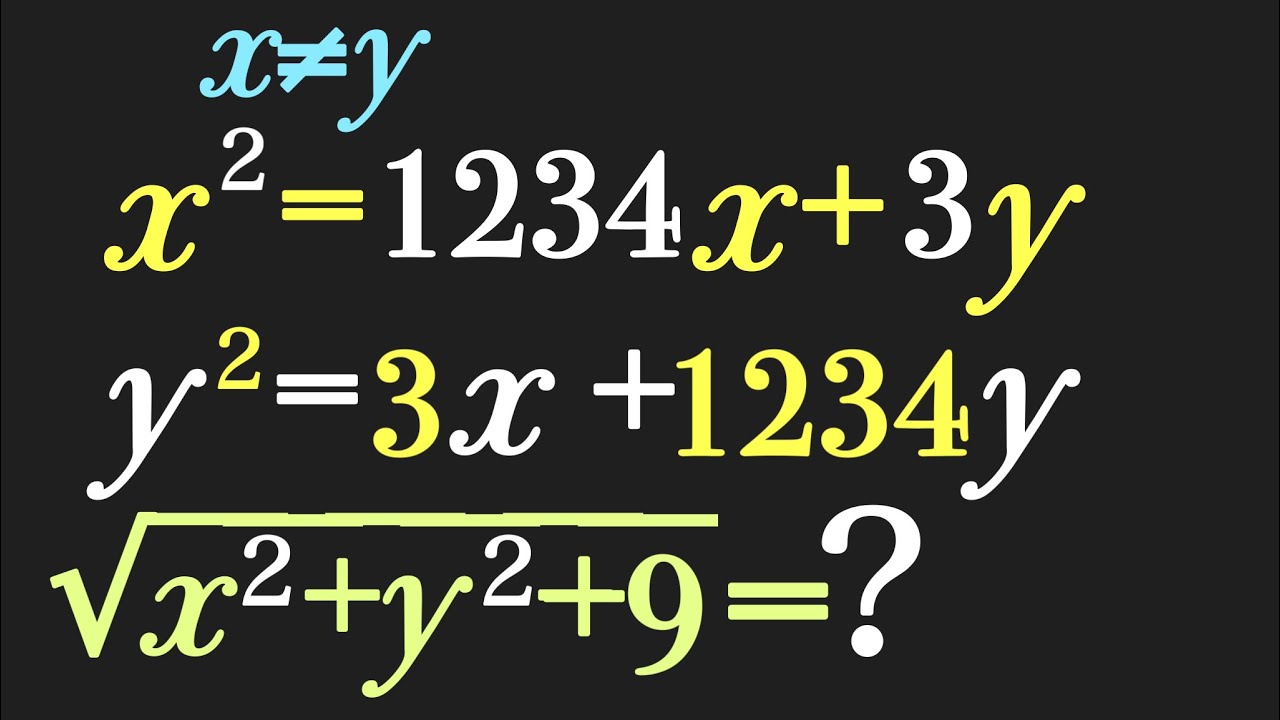
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x\neq y$である.
$x^2=1234x+3y$
$y^2=3x+1234y$
$\sqrt{x^2+y^2+9}=?$
この動画を見る
これを解け.$x\neq y$である.
$x^2=1234x+3y$
$y^2=3x+1234y$
$\sqrt{x^2+y^2+9}=?$
有名問題だよ(多分)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt[n]{n}$が最大となる自然数$n$を求めよ.
この動画を見る
$\sqrt[n]{n}$が最大となる自然数$n$を求めよ.
4の累乗の和で平方数を作れ

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c,n$は自然数である.
$4^a+4^b+4^c=n^2$
$10\lt a\lt b\lt c$を満たす$(a,b,c)$を1組与えよ.
この動画を見る
$a,b,c,n$は自然数である.
$4^a+4^b+4^c=n^2$
$10\lt a\lt b\lt c$を満たす$(a,b,c)$を1組与えよ.
整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
${}_{70} \mathrm{C}_{35}$を$71$で割った余りを求めよ.
${}_{50} \mathrm{C}_{25}$を$51$で割った余りを求めよ.
この動画を見る
${}_{70} \mathrm{C}_{35}$を$71$で割った余りを求めよ.
${}_{50} \mathrm{C}_{25}$を$51$で割った余りを求めよ.
古畑任三郎/刑事コロンボ問題

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\displaystyle \lim_{x\to \infty}\dfrac{[2x^2-x+3]}{x^2}$
この動画を見る
これを解け.
$\displaystyle \lim_{x\to \infty}\dfrac{[2x^2-x+3]}{x^2}$
華麗に解こう

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$a+b+c=4$
$a^2+b^2+c^2=10$
$a^3+b^3+c^3=22$
$a^4+b^4+c^4=?$
この動画を見る
これを解け.
$a+b+c=4$
$a^2+b^2+c^2=10$
$a^3+b^3+c^3=22$
$a^4+b^4+c^4=?$
指数タワー どっちがでかいの?

対数関数の微分公式
変わった指数方程式
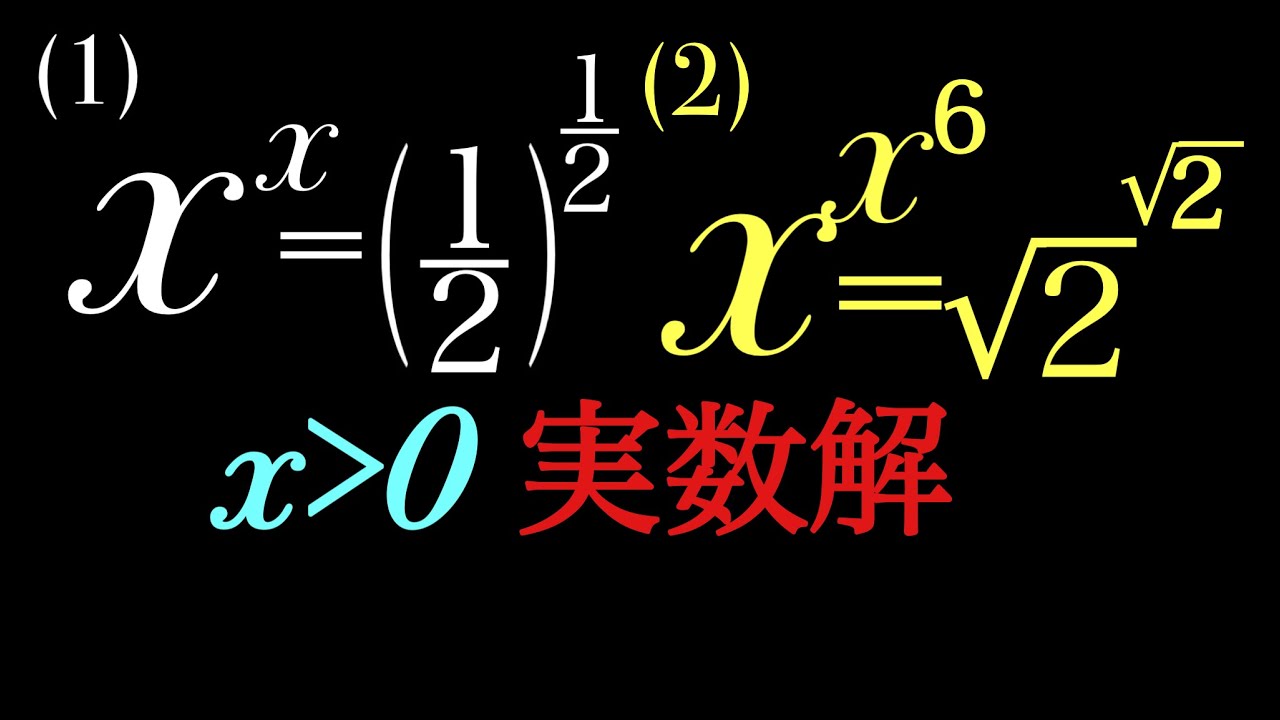
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\gt 0$である.これを解け.
(1)$x^x=\left(\dfrac{1}{2}\right)^{\frac{1}{2}}$
(2)$x^{x^6}=\sqrt2^{\sqrt2}$
この動画を見る
$x\gt 0$である.これを解け.
(1)$x^x=\left(\dfrac{1}{2}\right)^{\frac{1}{2}}$
(2)$x^{x^6}=\sqrt2^{\sqrt2}$
どっちがでかい?階乗の累乗根

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きい?
$\sqrt[8]{8!}$ VS $\sqrt[7]{7!}$
この動画を見る
どちらが大きい?
$\sqrt[8]{8!}$ VS $\sqrt[7]{7!}$
自分で考えろ!

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$42\times 37$の計算の様々なやり方に関して解説していきます.
この動画を見る
$42\times 37$の計算の様々なやり方に関して解説していきます.
素因数分解

奇数の平方の逆数の和になぜかあれが登場
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$n\to \infty$である.
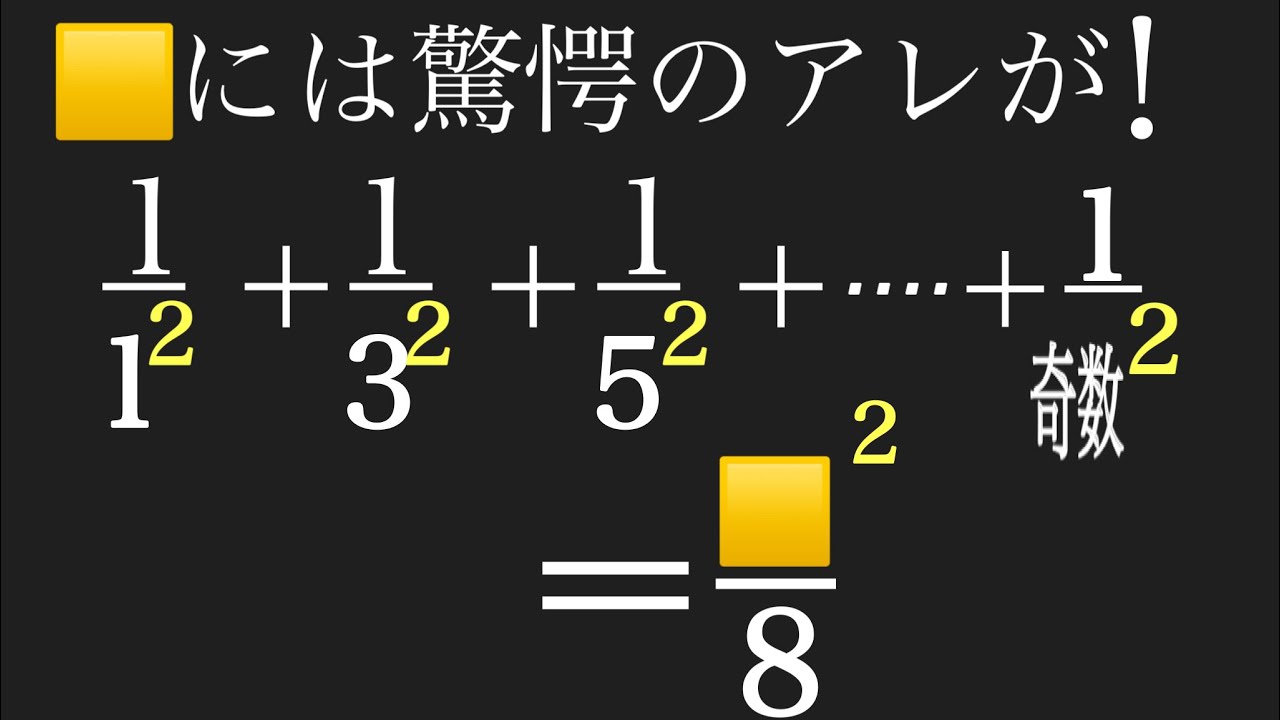
$\dfrac{1}{1^2}+\dfrac{1}{3^2}+\dfrac{1}{5^2}+\dfrac{1}{7^2}+・・・・・・$
$+\dfrac{1}{(2n-1)^2}=\dfrac{\Box^2}{8}$
この動画を見る
これを解け.$n\to \infty$である.
$\dfrac{1}{1^2}+\dfrac{1}{3^2}+\dfrac{1}{5^2}+\dfrac{1}{7^2}+・・・・・・$
$+\dfrac{1}{(2n-1)^2}=\dfrac{\Box^2}{8}$
どっちがでかい?

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?$ e\fallingdotseq 2,71$
$6^{\sqrt7}$ VS $7^{\sqrt6}$
この動画を見る
どちらが大きいか?$ e\fallingdotseq 2,71$
$6^{\sqrt7}$ VS $7^{\sqrt6}$
累乗の桁数

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2^{1000}$は$m$桁
$5^{1000}$は$n$桁
$m+n=\boxed{?}$
この動画を見る
$2^{1000}$は$m$桁
$5^{1000}$は$n$桁
$m+n=\boxed{?}$
ドラゴン桜 東大模試数学

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^3+b^3-3ab=2020$を満たす自然数$a,b$は存在するか.
東大模試過去問
この動画を見る
$a^3+b^3-3ab=2020$を満たす自然数$a,b$は存在するか.
東大模試過去問
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^{2x^2-1}+2・3^{(x+1)^2}-5・3^{4(x+1)}=0$
この動画を見る
実数解を求めよ.
$3^{2x^2-1}+2・3^{(x+1)^2}-5・3^{4(x+1)}=0$
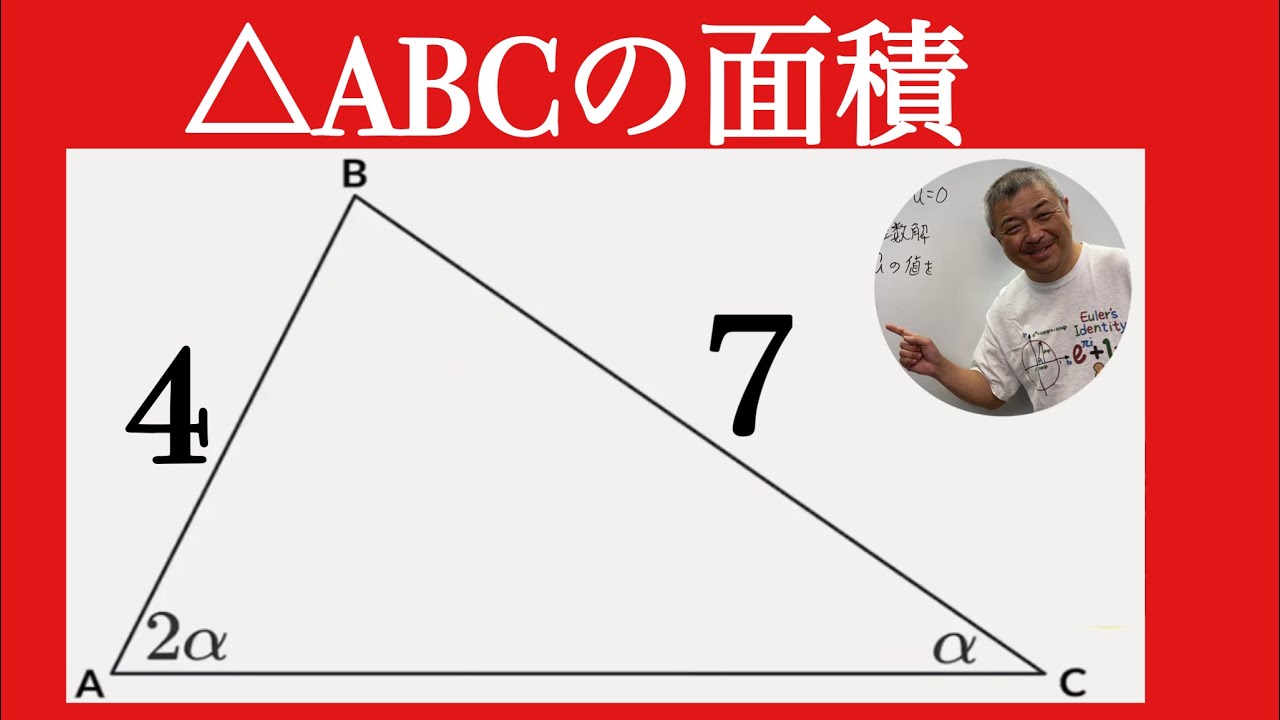
三角形の面積
ガウス記号 剰余

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$を自然数とする.
$\left[\dfrac{4^n}{5}\right]$を$6$で割った余りを求めよ.
この動画を見る
$n$を自然数とする.
$\left[\dfrac{4^n}{5}\right]$を$6$で割った余りを求めよ.
琉球大 積分 計算の工夫

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=2x^3-3x^2-6x+7$
$f(x)$は$\alpha,\beta(\alpha \lt \beta)$で極値をもつ.
$f(x)$と$x$軸で囲まれた領域で$\alpha\leqq x\leqq \beta$の部分の面積を求めよ.
2021琉球大過去問
この動画を見る
$f(x)=2x^3-3x^2-6x+7$
$f(x)$は$\alpha,\beta(\alpha \lt \beta)$で極値をもつ.
$f(x)$と$x$軸で囲まれた領域で$\alpha\leqq x\leqq \beta$の部分の面積を求めよ.
2021琉球大過去問
佐賀大(医)3次方程式の解の公式その2
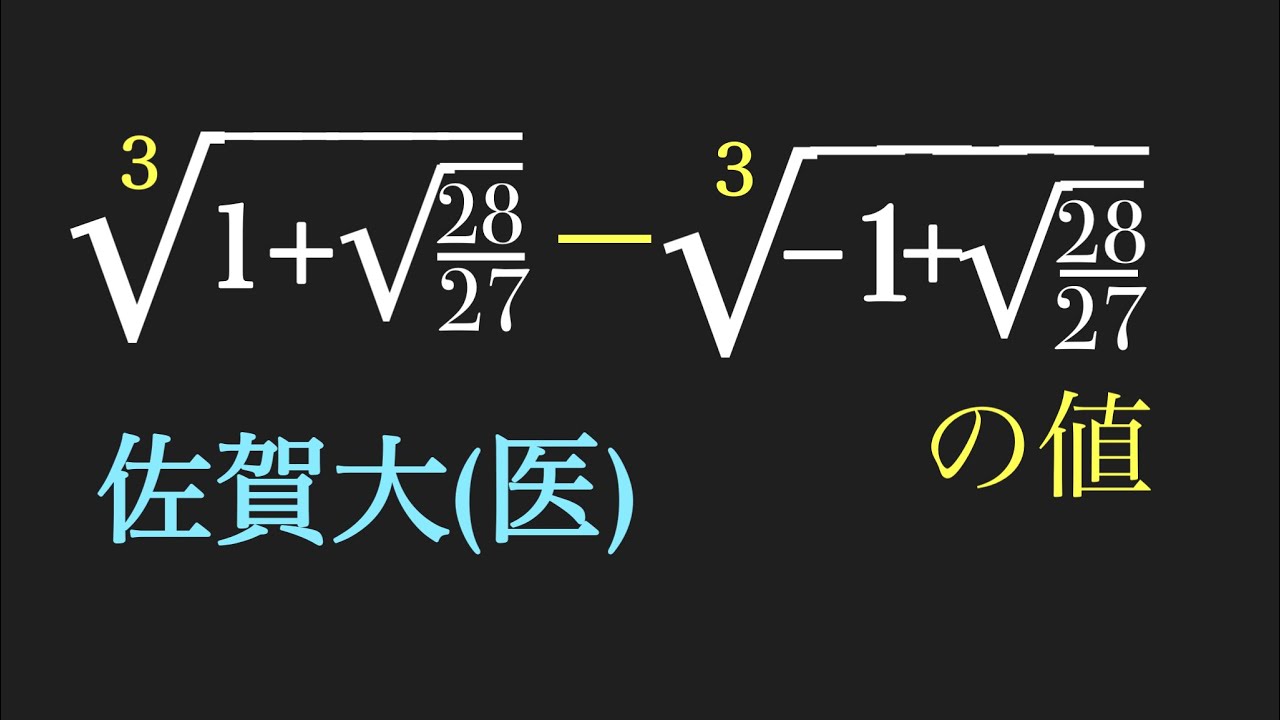
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3+px-q=0$
$\alpha-\beta=q,\alpha\beta=\left(\dfrac{p}{3}\right)^3$
$\sqrt[3]{\alpha}-\sqrt[3]{\beta}$は解である.
$\sqrt[3]{1+\sqrt{\dfrac{28}{27}}}-\sqrt[3]{-1+\sqrt{\dfrac{28}{27}}}$の値を求めよ.
佐賀大(医)過去問
この動画を見る
$x^3+px-q=0$
$\alpha-\beta=q,\alpha\beta=\left(\dfrac{p}{3}\right)^3$
$\sqrt[3]{\alpha}-\sqrt[3]{\beta}$は解である.
$\sqrt[3]{1+\sqrt{\dfrac{28}{27}}}-\sqrt[3]{-1+\sqrt{\dfrac{28}{27}}}$の値を求めよ.
佐賀大(医)過去問
佐賀大(医)3次方程式の解の公式
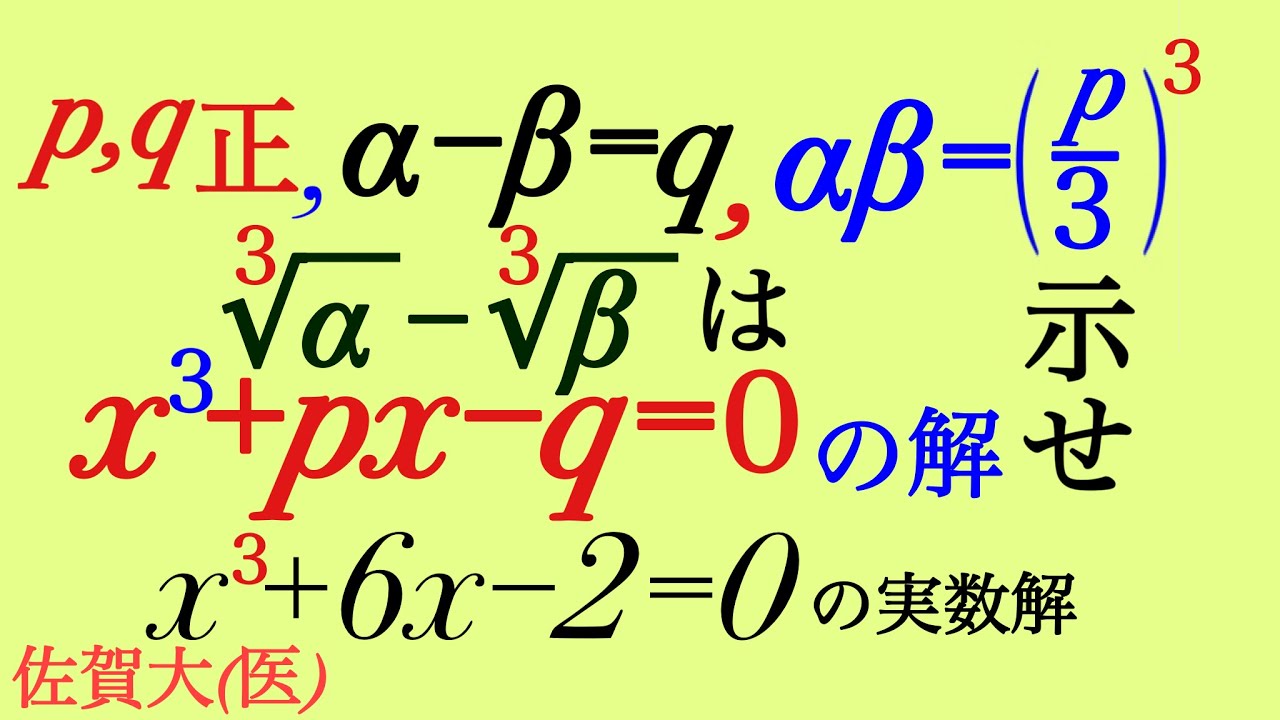
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha,\beta$は正の実数である.
(1)$p,q$正, $\alpha-\beta=q$,$\alpha\beta=\left(\dfrac{p}{3}\right)^3$
$\sqrt[3]{\alpha}-\sqrt[3]{\beta}$は$x^3+px-q=0$の解であることを示せ.
(2)$x^3+6x-2=0$の実数解を求めよ.
2020佐賀大(医)過去問
この動画を見る
$\alpha,\beta$は正の実数である.
(1)$p,q$正, $\alpha-\beta=q$,$\alpha\beta=\left(\dfrac{p}{3}\right)^3$
$\sqrt[3]{\alpha}-\sqrt[3]{\beta}$は$x^3+px-q=0$の解であることを示せ.
(2)$x^3+6x-2=0$の実数解を求めよ.
2020佐賀大(医)過去問
連立3元3次方程式
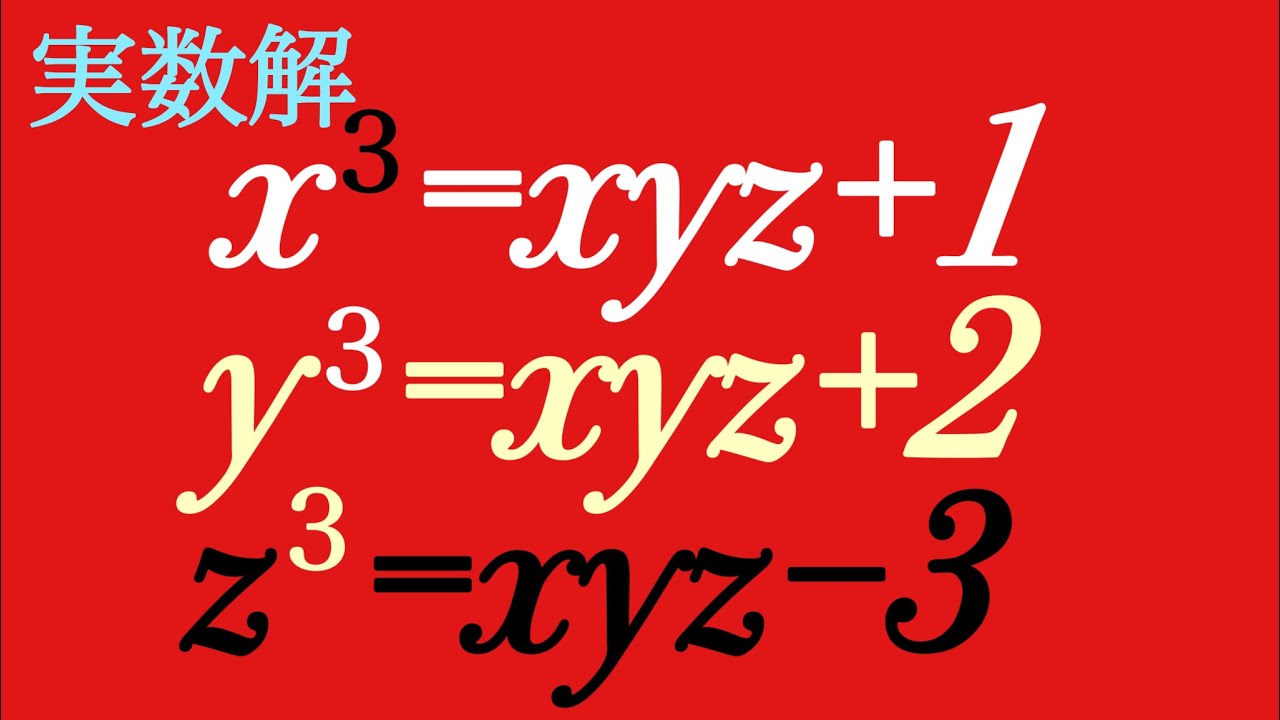
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3=xyz+1\\y^3=xyz+2 \\
z^3=xyz-3
\end{array}
\right.
\end{eqnarray}$
この動画を見る
実数解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3=xyz+1\\y^3=xyz+2 \\
z^3=xyz-3
\end{array}
\right.
\end{eqnarray}$



