 鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
帯広畜産大 漸化式 高校数学 Japanese university entrance exam questions

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
帯広畜産大学過去問題
初項~第n項までの和を$S_n$とする。
一般項$a_n$を求めよ。
$S_n = 9- \frac{1}{2}a_n-\frac{1}{3^{n-2}}$
この動画を見る
帯広畜産大学過去問題
初項~第n項までの和を$S_n$とする。
一般項$a_n$を求めよ。
$S_n = 9- \frac{1}{2}a_n-\frac{1}{3^{n-2}}$
大阪大 微分 立命館 数式 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#大阪大学#立命館大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
立命館大学過去問題
a,b実数 次の式が成り立つa,bを求めよ。
$a^2+10b^2-6ab-2b= -1$
大阪大学過去問題
(1,0)を通り、$y=x^4-2x^2+1$に接する直線の方程式をすべて求めよ。
この動画を見る
立命館大学過去問題
a,b実数 次の式が成り立つa,bを求めよ。
$a^2+10b^2-6ab-2b= -1$
大阪大学過去問題
(1,0)を通り、$y=x^4-2x^2+1$に接する直線の方程式をすべて求めよ。
大阪教育大 整式の剰余 複素数 Japanese university entrance exam questions

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#複素数#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$\omega$を方程式$x^2+x+1-0$の解を1つとする.
$(\omega+1)^{12}$の値を求めよ.
(2)$(x+1)^{12}$を$x^3-1$で割った余りを求めよ.
大阪教育大過去問
この動画を見る
(1)$\omega$を方程式$x^2+x+1-0$の解を1つとする.
$(\omega+1)^{12}$の値を求めよ.
(2)$(x+1)^{12}$を$x^3-1$で割った余りを求めよ.
大阪教育大過去問
信州大学 整数問題 Japanese university entrance exam questions

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
信州大学過去問題
$4^{2n-1}+3^{n+1}$は13の倍数であることを示せ。(n自然数)
この動画を見る
信州大学過去問題
$4^{2n-1}+3^{n+1}$は13の倍数であることを示せ。(n自然数)
信州大学 整数問題 Japanese university entrance exam questions

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
大阪教育大学過去問題
(1)ωを方程式$x^2+x+1=0$の解を1つとする。$(ω+1)^{12}$の値を求めよ。
(2)$(x+1)^{12}$を$x^3-1$で割った余りを求めよ。
この動画を見る
大阪教育大学過去問題
(1)ωを方程式$x^2+x+1=0$の解を1つとする。$(ω+1)^{12}$の値を求めよ。
(2)$(x+1)^{12}$を$x^3-1$で割った余りを求めよ。
京都大 三角関数 4次方程式 高校数学 大学受験 Japanese university entrance exam questions Kyoto University

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#三角関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2014京都大学過去問題
$0 \leqq θ < 90^\circ \quad$xについての4次方程式
$\{ x^2-2(cosθ)x-cosθ+1 \} x$
$\{ x^2-2(tanθ)x+3 \} = 0$は虚数解を少なくとも1つ持つことを示せ。
この動画を見る
2014京都大学過去問題
$0 \leqq θ < 90^\circ \quad$xについての4次方程式
$\{ x^2-2(cosθ)x-cosθ+1 \} x$
$\{ x^2-2(tanθ)x+3 \} = 0$は虚数解を少なくとも1つ持つことを示せ。
立教大 立体図形・関数最大値 信州大 指数方程式 高校数学 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#信州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
立教大学過去問題
底面の直径が6高さが12の円錐に図のように円柱が内接している。円柱の体積の最大値
*図は動画内参照
信州大学過去問題
$2^{3x+2}-13・2^{2x}+11・2^x-2=0$を解け
この動画を見る
立教大学過去問題
底面の直径が6高さが12の円錐に図のように円柱が内接している。円柱の体積の最大値
*図は動画内参照
信州大学過去問題
$2^{3x+2}-13・2^{2x}+11・2^x-2=0$を解け
東北大 常用対数 桁数と最高位の数字 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2006東北大学過去問題
$6^n$が39桁の自然数になるとき、自然数nを求めよ。
その場合のnに対する$6^n$の最高位の数字を求めよ。
$log_{10}2=0.3010$
$log_{10}3=0.4771$
この動画を見る
2006東北大学過去問題
$6^n$が39桁の自然数になるとき、自然数nを求めよ。
その場合のnに対する$6^n$の最高位の数字を求めよ。
$log_{10}2=0.3010$
$log_{10}3=0.4771$
連続n個の自然数の積はn!で割り切れる。岩手大 整数・因数分解 高校数学 Japanese university entrance exam questions

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
岩手大学過去問題
a,b,cは連続した自然数
$a^2b+a^2c+ab^2+b^2c+bc^2+ac^2+2abc$は6の倍数であることを示せ。
この動画を見る
岩手大学過去問題
a,b,cは連続した自然数
$a^2b+a^2c+ab^2+b^2c+bc^2+ac^2+2abc$は6の倍数であることを示せ。
同志社大・早稲田(商) 式の計算 高校数学 Japanese university entrance exam questions

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
同志社大学過去問題
$x+y+z=3 , \quad \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{3}$のとき
(1)$(x-3)(y-3)(z-3)$の値
(2)$x^3+y^3+z^3$の値
早稲田大学過去問題
$x^3+\frac{1}{x^3}=52$を満たす$x^4+\frac{1}{x^4}$の値
この動画を見る
同志社大学過去問題
$x+y+z=3 , \quad \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{3}$のとき
(1)$(x-3)(y-3)(z-3)$の値
(2)$x^3+y^3+z^3$の値
早稲田大学過去問題
$x^3+\frac{1}{x^3}=52$を満たす$x^4+\frac{1}{x^4}$の値
弘前大 三乗根の数の処理 高校数学 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2005弘前大学過去問題
$a={}^3 \sqrt{\sqrt{\frac{65}{64}}+1} - {}^3 \sqrt{\sqrt{\frac{65}{64}}-1}$
(1)aは整数を係数とする3次方程式の解であることを示せ
(2)aは整数でないことを証明せよ。
この動画を見る
2005弘前大学過去問題
$a={}^3 \sqrt{\sqrt{\frac{65}{64}}+1} - {}^3 \sqrt{\sqrt{\frac{65}{64}}-1}$
(1)aは整数を係数とする3次方程式の解であることを示せ
(2)aは整数でないことを証明せよ。
東大 整数問題 高校数学 大学入試 Japanese university entrance exam questions Tokyo University

単元:
#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
東京大学過去問題
m自然数
$5m^4$の下2桁として現れる数をすべて求めよ。
この動画を見る
東京大学過去問題
m自然数
$5m^4$の下2桁として現れる数をすべて求めよ。
広島大学 整数問題 高校数学 大学入試 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#広島大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2010広島大学
4で割ると余りが1である自然数全体の集合をAとする。
(1)m,nを0以上の整数とする。
m+nが偶数ならば$3^m7^n$はAに属し、m+nが奇数なら$3^m7^n$はAに属さないことを証明せよ。
(2)$3^{2m+1}7^{2n+1}$の正の約数のうちAに属する数の総和
この動画を見る
2010広島大学
4で割ると余りが1である自然数全体の集合をAとする。
(1)m,nを0以上の整数とする。
m+nが偶数ならば$3^m7^n$はAに属し、m+nが奇数なら$3^m7^n$はAに属さないことを証明せよ。
(2)$3^{2m+1}7^{2n+1}$の正の約数のうちAに属する数の総和
宇都宮大学 漸化式 高校数学 大学入試 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#大学入試解答速報
指導講師:
鈴木貫太郎
問題文全文(内容文):
宇都宮大学過去問題
$a_1=1 \quad$初項~第n項までの和を$S_n$
$a_{n+1}=9a_n -4S_n$
(1)一般項$a_n$を求めよ。
(2)$S_n$をnで表せ。
この動画を見る
宇都宮大学過去問題
$a_1=1 \quad$初項~第n項までの和を$S_n$
$a_{n+1}=9a_n -4S_n$
(1)一般項$a_n$を求めよ。
(2)$S_n$をnで表せ。
e^πとπ^e どっちがでかい?

単元:
#数Ⅱ#指数関数と対数関数#微分法と積分法#指数関数#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$e^π$と$π^e$どっちがでかい?
この動画を見る
$e^π$と$π^e$どっちがでかい?
弘前大 三角関数 正十角形の面積 高校数学 大学入試 Japanese university entrance exam questions

単元:
#数Ⅱ#複素数と方程式#複素数平面#三角関数#複素数#三角関数とグラフ#複素数平面#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
弘前大学過去問題
(1)$sin5θ=16sin^5θ-20sin^3θ+5sinθ$を示せ。
(2)半径1の円に内接する正十角形の面積を求めよ。
この動画を見る
弘前大学過去問題
(1)$sin5θ=16sin^5θ-20sin^3θ+5sinθ$を示せ。
(2)半径1の円に内接する正十角形の面積を求めよ。
一橋大学 三次関数の最大値 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#一橋大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2007一橋大学過去問題
aを定数とし、$f(x)=x^3-3ax^2+a$とする。
$x \leqq 2$の範囲でf(x)の最大値が105となるようなaをすべて求めよ。
この動画を見る
2007一橋大学過去問題
aを定数とし、$f(x)=x^3-3ax^2+a$とする。
$x \leqq 2$の範囲でf(x)の最大値が105となるようなaをすべて求めよ。
千葉大 整数問題 高校数学 Japanese university entrance exam questions

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
千葉大学過去問題
30!について
(1)$2^k$で割ったとき商が整数となる最大のkの値
(2)末尾に0がいくつ並ぶか
(3)1の位から左に見ていき最初にあらわれる0以外の数は何か
この動画を見る
千葉大学過去問題
30!について
(1)$2^k$で割ったとき商が整数となる最大のkの値
(2)末尾に0がいくつ並ぶか
(3)1の位から左に見ていき最初にあらわれる0以外の数は何か
旭川医大(N進法)弘前大(医)数列 高校数学 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#数列#旭川医科大学#数学(高校生)#弘前大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
旭川医科大学過去問題
$0.2\dot{2}\dot{1}_{(3)}$
十進法の分数に
弘前大学過去問題
$x_n=2^{n-1}n$
初項~n項の和
この動画を見る
旭川医科大学過去問題
$0.2\dot{2}\dot{1}_{(3)}$
十進法の分数に
弘前大学過去問題
$x_n=2^{n-1}n$
初項~n項の和
東京海洋大学 三角関数 最大最小 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#三角関数とグラフ#接線と増減表・最大値・最小値#東京海洋大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
東京海洋大学過去問題
$y=2\cos^3x+2\sin^3x+3 \cos x \sin x-3$
$\cos x-3 \sin x$
$0 \leqq x \leqq 2π$のときのyの最大値、最小値およびその時のxの値
この動画を見る
東京海洋大学過去問題
$y=2\cos^3x+2\sin^3x+3 \cos x \sin x-3$
$\cos x-3 \sin x$
$0 \leqq x \leqq 2π$のときのyの最大値、最小値およびその時のxの値
東大 場合の数 高校数学 Japanese university entrance exam questions Tokyo University

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#場合の数#場合の数#東京大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
nを正の整数とし、n個のボールを3つの箱に分けて入れる問題を考える。ただし、1個のボ ールも入らない箱があってもよいものとする。以下に述べる4つの場合について、それぞれ 相異なる入れ方の総数を求めたい。
(1) 1からnまで異なる番号のついたこのボールを、A、B、Cと区別された3つの箱に入れる場合、その入れ方は全部で何通りあるか。
(2)互いに区別のつかないn個のボールを、A、B、Cと区別された3つの箱に入れる場合、その入れ方は全部で何通りあるか。
(3) 1からnまで異なる番号のついたn個のボールを、区別のつかない3つの箱に入れる場合、その入れ方は全部で何通りあるか。
(4)nが6の倍数6mであるとき、n個の互いに区別のつかないボールを、区別のつかない3つ の箱に入れる場合、その入れ方は全部で何通りあるか。
この動画を見る
nを正の整数とし、n個のボールを3つの箱に分けて入れる問題を考える。ただし、1個のボ ールも入らない箱があってもよいものとする。以下に述べる4つの場合について、それぞれ 相異なる入れ方の総数を求めたい。
(1) 1からnまで異なる番号のついたこのボールを、A、B、Cと区別された3つの箱に入れる場合、その入れ方は全部で何通りあるか。
(2)互いに区別のつかないn個のボールを、A、B、Cと区別された3つの箱に入れる場合、その入れ方は全部で何通りあるか。
(3) 1からnまで異なる番号のついたn個のボールを、区別のつかない3つの箱に入れる場合、その入れ方は全部で何通りあるか。
(4)nが6の倍数6mであるとき、n個の互いに区別のつかないボールを、区別のつかない3つ の箱に入れる場合、その入れ方は全部で何通りあるか。
千葉大学 整数問題 高校数学 Japanese university entrance exam questions

単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#指数関数#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2003千葉大学過去問題
x,y,z,nは自然数
$x^2=7^{2n}(y^2+10z^2)$が成り立っている
(1)平方数を3で割った余りは0か1を示せ
(2)yzは3の倍数であることを示せ。
(3)y,zが共に素数のときxをnを用いて表せ。
この動画を見る
2003千葉大学過去問題
x,y,z,nは自然数
$x^2=7^{2n}(y^2+10z^2)$が成り立っている
(1)平方数を3で割った余りは0か1を示せ
(2)yzは3の倍数であることを示せ。
(3)y,zが共に素数のときxをnを用いて表せ。
東北大 三次方程式 相異三実根 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#東北大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
東北大学過去問題
$2x^3-3(a+b)x^2+6abx-2a^2b=0$が相異3実根をもつとき
(a,b)の範囲を図示せよ。
この動画を見る
東北大学過去問題
$2x^3-3(a+b)x^2+6abx-2a^2b=0$が相異3実根をもつとき
(a,b)の範囲を図示せよ。
京都大 図形(基礎)高校数学 Japanese university entrance exam questions Kyoto University

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#京都大学#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
京都大学過去問題
1辺の長さが1の正四面体OABCのBC上に点PをとりBPの長さをxとする
(1)OAPをxで表せ。
(2)OAPの最小値
*図は動画内参照
この動画を見る
京都大学過去問題
1辺の長さが1の正四面体OABCのBC上に点PをとりBPの長さをxとする
(1)OAPをxで表せ。
(2)OAPの最小値
*図は動画内参照
弘前大 微分 最小値 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)#弘前大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
弘前大学過去問題
$f(x) = x^3-(3a-2)x^2-8ax \quad (a>0)$
$-3\leqq x \leqq 3a$における最小値
この動画を見る
弘前大学過去問題
$f(x) = x^3-(3a-2)x^2-8ax \quad (a>0)$
$-3\leqq x \leqq 3a$における最小値
和歌山大 三項間漸化式 半角の公式 高校数学 Japanese university entrance exam questions
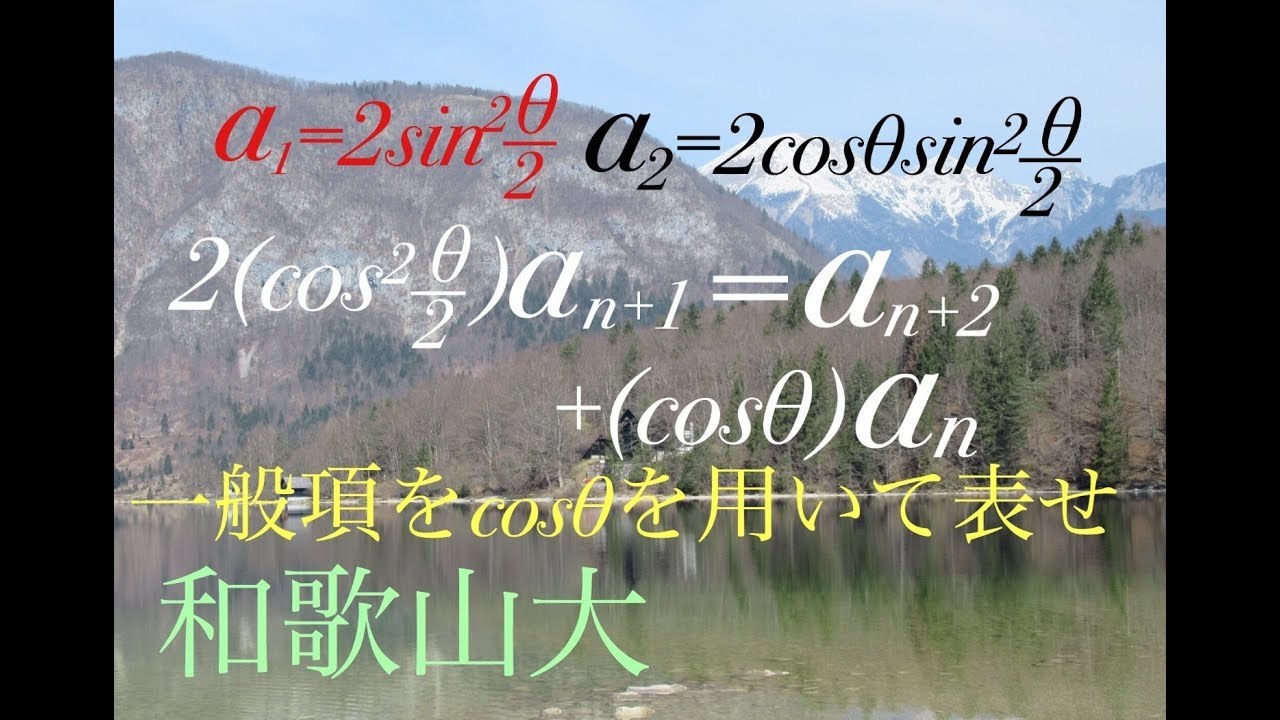
単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#三角関数#三角関数とグラフ#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#和歌山大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
和歌山大学過去問題
$a_1=2\sin^2\frac{θ}{2}$,$a_2=2\cosθ\sin^2\frac{θ}{2}$
$2(cos^2\frac{θ}{2})a_{n+1}=a_{n+2}+(\cosθ)a_n$
$a_n$を$\cosθ$を用いて表せ。
この動画を見る
和歌山大学過去問題
$a_1=2\sin^2\frac{θ}{2}$,$a_2=2\cosθ\sin^2\frac{θ}{2}$
$2(cos^2\frac{θ}{2})a_{n+1}=a_{n+2}+(\cosθ)a_n$
$a_n$を$\cosθ$を用いて表せ。
京都大 整数問題 高校数学 Japanese university entrance exam questions Kyoto University

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
'96京都大学過去問題
m,nは自然数で、m<nを満たすものとする。
$m^n+1,n^m+1$がともに10の倍数となるm,nを1組与えよ。
この動画を見る
'96京都大学過去問題
m,nは自然数で、m<nを満たすものとする。
$m^n+1,n^m+1$がともに10の倍数となるm,nを1組与えよ。
京都大 史上最短の入試問題 tan1°は有理数か 高校数学 Japanese university entrance exam questions Kyoto University

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
史上最短問題文 tan1°は有理数か?(京大入試)
この動画を見る
史上最短問題文 tan1°は有理数か?(京大入試)
慶應(医)空間 直線&平面の方程式 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#三角関数#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#慶應義塾大学#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
慶応義塾大学過去問題
直線 $l:6-x=\frac{y+5}{2}=2-z$と
平面$α:z+y-z-1=0$
(1)lとαの交点の座標
(2)lを含み平面αに垂直な平面πの方程式
(3)lと、平面αとπの交線のなす角をθ(0°$\leqq$θ$\leqq$90°)
cosθの値
この動画を見る
慶応義塾大学過去問題
直線 $l:6-x=\frac{y+5}{2}=2-z$と
平面$α:z+y-z-1=0$
(1)lとαの交点の座標
(2)lを含み平面αに垂直な平面πの方程式
(3)lと、平面αとπの交線のなす角をθ(0°$\leqq$θ$\leqq$90°)
cosθの値
北海道大学 数1 高校数学 Japanese university entrance exam questions

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#数学(高校生)#北海道大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
北海道大学過去問題
$\frac{1}{x}$の小数部分が$\frac{x}{2}$に等しくなるような正の数xをすべて求めよ。
ただし、正の数aの小数部分とは、aを超えない最大の整数nとの差$a-n$のことをいう。
この動画を見る
北海道大学過去問題
$\frac{1}{x}$の小数部分が$\frac{x}{2}$に等しくなるような正の数xをすべて求めよ。
ただし、正の数aの小数部分とは、aを超えない最大の整数nとの差$a-n$のことをいう。



