鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
立教大のナイスな問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023立教大学過去問題
$A=\frac{10^{40}-3^{10}}{9997}$,$B=\frac{10^{36}-3^{9}}{9997}$
①Aの１の位の数
②A-3Bを素因数分解
③AとBの最大公約数
この動画を見る
2023立教大学過去問題
$A=\frac{10^{40}-3^{10}}{9997}$,$B=\frac{10^{36}-3^{9}}{9997}$
①Aの１の位の数
②A-3Bを素因数分解
③AとBの最大公約数
確率 中央大（商）
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2020中央大学過去問題
$1,2,2^2,2^3,\cdots,2^{n-1}$
の数字が1つずつ書かれたn枚のカードから1枚をとり出して
その数をX,それを戻してもう1枚とり出してその数をYとする
①X=2Yとなる確率
②XがYの倍数となる確率
この動画を見る
2020中央大学過去問題
$1,2,2^2,2^3,\cdots,2^{n-1}$
の数字が1つずつ書かれたn枚のカードから1枚をとり出して
その数をX,それを戻してもう1枚とり出してその数をYとする
①X=2Yとなる確率
②XがYの倍数となる確率
文系積分の基本 中央大(文学部)
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#中央大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2021中央大学過去問題
$y=x(x-1)^2 \cdots$①
$y=kx \cdots$②
①と②は異なる3点で交わり、①と②とで囲まれる2つの部分の面積が等しい
kの値
この動画を見る
2021中央大学過去問題
$y=x(x-1)^2 \cdots$①
$y=kx \cdots$②
①と②は異なる3点で交わり、①と②とで囲まれる2つの部分の面積が等しい
kの値
立方の差でも平方の和でも表せる素数を探せ
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$37=4^3-3^3=1^2+6^2$のように
素数$=b^3-a^3=c^2+d^2$(a,b,c,dは自然数)と表せる
素数を37以外に探せ
この動画を見る
$37=4^3-3^3=1^2+6^2$のように
素数$=b^3-a^3=c^2+d^2$(a,b,c,dは自然数)と表せる
素数を37以外に探せ
中央大 三項間漸化式
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023中央大学過去問題
$a_n=(2+\sqrt{3})^n+(2-\sqrt{3})^n$
①$a_{n+2}+a_n=4a_{n+1}$を示せ
②$a_{n+1}+a_n$は3の倍数であることを示せ
③$a_{2023}$を3で割った余り
この動画を見る
2023中央大学過去問題
$a_n=(2+\sqrt{3})^n+(2-\sqrt{3})^n$
①$a_{n+2}+a_n=4a_{n+1}$を示せ
②$a_{n+1}+a_n$は3の倍数であることを示せ
③$a_{2023}$を3で割った余り
基本問題 明治大
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
明治大学過去問題
$ab_{(6)}=123_{(a)}$
a,bの値を求めよ
この動画を見る
明治大学過去問題
$ab_{(6)}=123_{(a)}$
a,bの値を求めよ
整数問題 明治大
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
明治大学 過去問
nを自然数とする.
$9n^5+15n^4+10n^3-4n$
が30の倍数であること示せ
この動画を見る
明治大学 過去問
nを自然数とする.
$9n^5+15n^4+10n^3-4n$
が30の倍数であること示せ
上智大 連立漸化式
単元：
#大学入試過去問(数学)#漸化式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
上智大学過去問題
$a_1 =0,b_1=6$
$a_{n+1}=\frac{a_n+b_n}{2}$,$b_{n+1}=a_n$
点Pの$(a_n,b_n)$はある直線上にある。その式は？
$n \to \infty$のときの$P_n$
この動画を見る
上智大学過去問題
$a_1 =0,b_1=6$
$a_{n+1}=\frac{a_n+b_n}{2}$,$b_{n+1}=a_n$
点Pの$(a_n,b_n)$はある直線上にある。その式は？
$n \to \infty$のときの$P_n$
青山学院大
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
【青山学院大 過去問】
AとB対戦
Aが勝つ確率$\displaystyle \frac{2}{3}$
Bが勝つ確率$\displaystyle \frac{1}{3}$
最大7試合でどちらかが4勝した時点で終了
第6試合で決着する確率
この動画を見る
【青山学院大 過去問】
AとB対戦
Aが勝つ確率$\displaystyle \frac{2}{3}$
Bが勝つ確率$\displaystyle \frac{1}{3}$
最大7試合でどちらかが4勝した時点で終了
第6試合で決着する確率
e話
単元：
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$e=\displaystyle\lim_{n \to \infty}(1+\frac{1}{n})^n$
$\displaystyle\lim_{n \to -\infty}(1+\frac{1}{n})^n=e$を示せ
この動画を見る
$e=\displaystyle\lim_{n \to \infty}(1+\frac{1}{n})^n$
$\displaystyle\lim_{n \to -\infty}(1+\frac{1}{n})^n=e$を示せ
青山学院大 放物線の中の四角形
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#青山学院大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
青山学院大学過去問題
$f(x)=-x^2+4x$
原点O,A(4,0),P(p,f(p)),Q(q,f(q)) (0<p<q<4)
四角形OAQPの面積の最大値
この動画を見る
青山学院大学過去問題
$f(x)=-x^2+4x$
原点O,A(4,0),P(p,f(p)),Q(q,f(q)) (0<p<q<4)
四角形OAQPの面積の最大値
青山学院大 放物線の中の四角形
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#図形の性質#図形と計量#一次不等式（不等式・絶対値のある方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(x)=-x^2+4x$
原点$O,A(4,0),P(p,f_{(p)}),Q(q,f_{(q)})$ $(0\lt p\lt q\lt 4)$
四角形$OAQP$の面積の最大値を求めよ.
青山学院大過去問
この動画を見る
$f(x)=-x^2+4x$
原点$O,A(4,0),P(p,f_{(p)}),Q(q,f_{(q)})$ $(0\lt p\lt q\lt 4)$
四角形$OAQP$の面積の最大値を求めよ.
青山学院大過去問
青山学院大 微分の基礎
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#青山学院大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
青山学院大学過去問題
$C:y=x^2$
A(-1,1),B(4,16)
放物線C上にx座標が
$t(-1<t<4)$である点P
直線AB上にx座標がtである点Qととる。
△APQの面積の最大値とそのときのtの値
この動画を見る
青山学院大学過去問題
$C:y=x^2$
A(-1,1),B(4,16)
放物線C上にx座標が
$t(-1<t<4)$である点P
直線AB上にx座標がtである点Qととる。
△APQの面積の最大値とそのときのtの値
文系積分の基本 法政大
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#法政大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
法政大学過去問題
a<0
$f(x)=\frac{1}{3}x^3-\frac{a+2}{2}x^2+2ax-\frac{7}{6}$
f(x)はx軸と接する
f(x)とx軸とで囲まれた面積
この動画を見る
法政大学過去問題
a<0
$f(x)=\frac{1}{3}x^3-\frac{a+2}{2}x^2+2ax-\frac{7}{6}$
f(x)はx軸と接する
f(x)とx軸とで囲まれた面積
積分の基本 工夫しようか
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#法政大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
【法政大 過去問】
$f(x)=x^3-2x^2+2x-|2x^2-2x|$
とx軸とで囲まれた面積を求めよ.
この動画を見る
【法政大 過去問】
$f(x)=x^3-2x^2+2x-|2x^2-2x|$
とx軸とで囲まれた面積を求めよ.
漸化式 関西医科大
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#関西医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2021関西医科大学過去問題
$a_1=\frac{1}{13}$ n=1,2,・・・自然数
$5a_{n+1}=10a_n-a_{n+1}・a_n$
一般項$a_n$を求めよ
この動画を見る
2021関西医科大学過去問題
$a_1=\frac{1}{13}$ n=1,2,・・・自然数
$5a_{n+1}=10a_n-a_{n+1}・a_n$
一般項$a_n$を求めよ
関西医科大 分数不等式 整数問題
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2022関西医科大学過去問題
$f(x)=\frac{6x^2+17x+10}{3x-2}$
①$f(x)>0$をみたすxの範囲
②f(n)が正の整数となる整数n
この動画を見る
2022関西医科大学過去問題
$f(x)=\frac{6x^2+17x+10}{3x-2}$
①$f(x)>0$をみたすxの範囲
②f(n)が正の整数となる整数n
関西医科大 対数方程式の基礎
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2020関西医科大学過去問題
$\log_4(2x^2)-\log_x4+\frac{1}{2}=0$
この動画を見る
2020関西医科大学過去問題
$\log_4(2x^2)-\log_x4+\frac{1}{2}=0$
三角関数の極限
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
関西医科大学過去問題
$\displaystyle\lim_{(x \to \pi)}\frac{sinx}{x^2-\pi^2}$
この動画を見る
関西医科大学過去問題
$\displaystyle\lim_{(x \to \pi)}\frac{sinx}{x^2-\pi^2}$
ただの連立方程式だよね
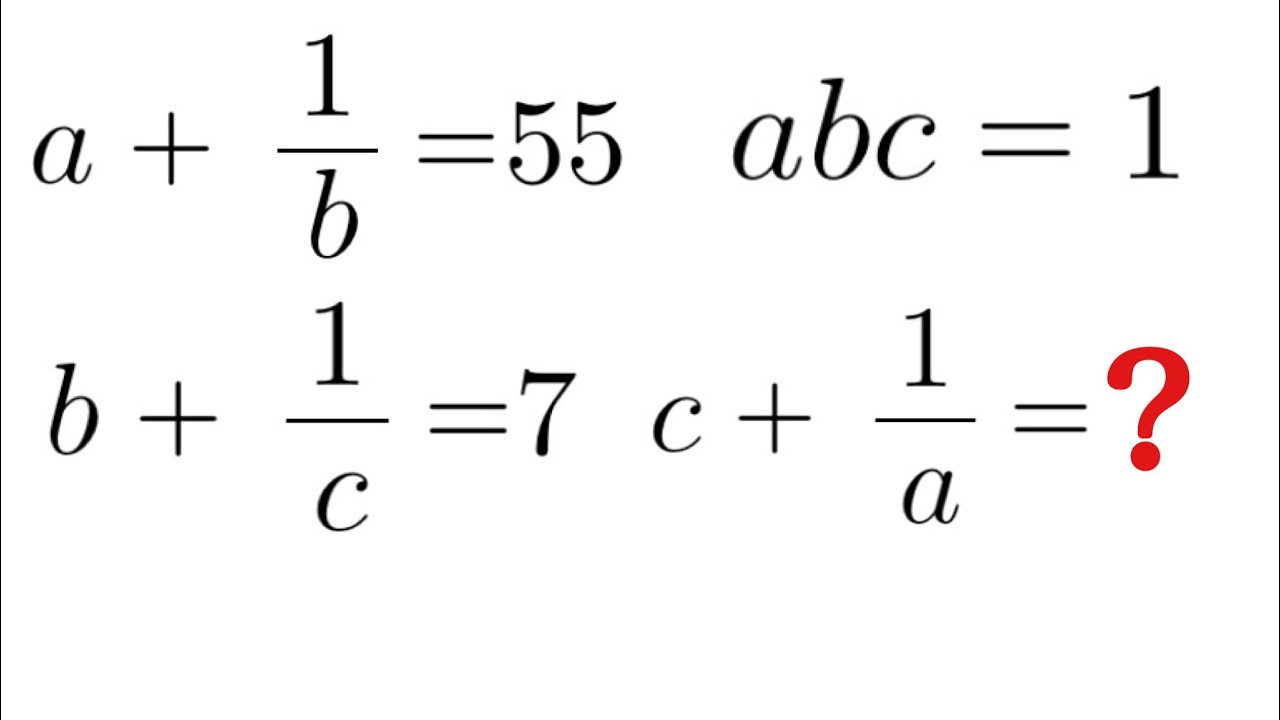
単元：
#数学(中学生)#中２数学#連立方程式#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$abc=1$
$a+\frac{1}{b}=55$
$b+\frac{1}{c}=7$
$C+\frac{1}{a}=?$
この動画を見る
$abc=1$
$a+\frac{1}{b}=55$
$b+\frac{1}{c}=7$
$C+\frac{1}{a}=?$
特性方程式を解いてる場合じゃないよ
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#広島大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
A,B,C,Dの5人がパス回しをする。
Aから始めて、ボールを持った人は等しい確率で自分以外の人にパスを出す。
ｎ回目にBがボールを持っている確率は？
この動画を見る
A,B,C,Dの5人がパス回しをする。
Aから始めて、ボールを持った人は等しい確率で自分以外の人にパスを出す。
ｎ回目にBがボールを持っている確率は？
広島大 対数の証明問題
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#広島大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$p,q$を異なる自然数とするとき、
$P log_2 3$と$q log_2 3$の小数部分は異なることを証明せよ。
この動画を見る
$p,q$を異なる自然数とするとき、
$P log_2 3$と$q log_2 3$の小数部分は異なることを証明せよ。
東京医科大 楽ちん問題
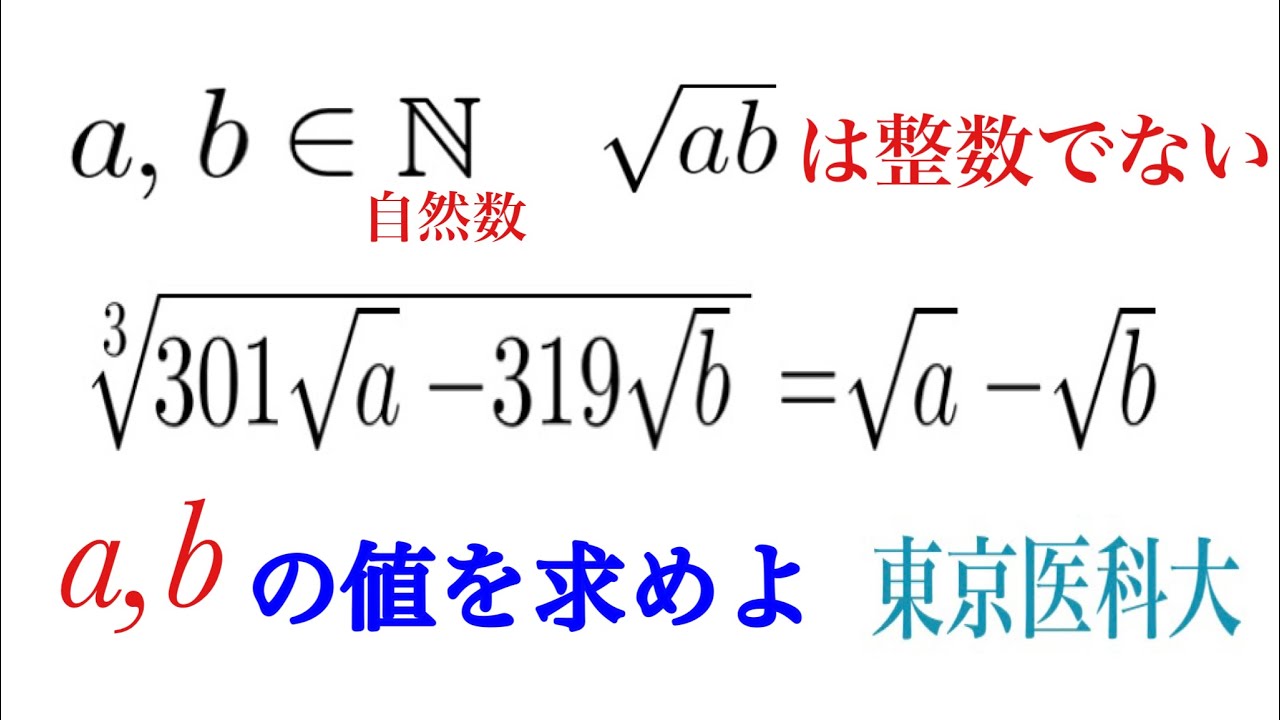
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科大学#東京医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a,b$は自然数であり、$\sqrt{ab}$は整数でないとき、
$\sqrt[3]{301\sqrt{a}-319\sqrt{b}}=\sqrt{a}-\sqrt{b}$
をみたす$a,b$を求めよ。
この動画を見る
$a,b$は自然数であり、$\sqrt{ab}$は整数でないとき、
$\sqrt[3]{301\sqrt{a}-319\sqrt{b}}=\sqrt{a}-\sqrt{b}$
をみたす$a,b$を求めよ。
東京医科大 見掛け倒しな問題
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#数B#東京医科大学#東京医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$1008$の正の約数$n$個を大きい順に並べた数列を
$a_1,a_2･･････,a_n$とし、$S(x)$を$S(x)=\displaystyle \sum_{k=1}^n a_k^x $とする。
①$S(0)$ ②$S(1)$ ③$S(-1)$ ④$\dfrac{S(2)}{S(1)}$
この動画を見る
$1008$の正の約数$n$個を大きい順に並べた数列を
$a_1,a_2･･････,a_n$とし、$S(x)$を$S(x)=\displaystyle \sum_{k=1}^n a_k^x $とする。
①$S(0)$ ②$S(1)$ ③$S(-1)$ ④$\dfrac{S(2)}{S(1)}$
いろんな要素いっぱいの良問 日本医科大
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\left(\frac{3}{2}x+\frac{3}{2}x+1 \right)^{n+2}$
を展開したときの$x^3$の係数を$Am$とする。
①$\displaystyle \lim_{ n \to x } \dfrac{1}{n^4}\displaystyle \sum_{k=1}^n A_k$
②$\displaystyle \lim_{ n \to (x) } \displaystyle \sum_{k=1}^n \dfrac{1}{A_n}$
日本医科大過去問
この動画を見る
$\left(\frac{3}{2}x+\frac{3}{2}x+1 \right)^{n+2}$
を展開したときの$x^3$の係数を$Am$とする。
①$\displaystyle \lim_{ n \to x } \dfrac{1}{n^4}\displaystyle \sum_{k=1}^n A_k$
②$\displaystyle \lim_{ n \to (x) } \displaystyle \sum_{k=1}^n \dfrac{1}{A_n}$
日本医科大過去問
合同式の基本
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
${3^{3}}^{2023}$を11で割ったあまりは？
この動画を見る
${3^{3}}^{2023}$を11で割ったあまりは？
大阪医科大 確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#大阪医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
黒石3個と白石7個を一列に並べる。
この列が、「2つ以上の連続した白石の両端に黒石がある」という部分を含む確率は？
大阪医科大過去問
この動画を見る
黒石3個と白石7個を一列に並べる。
この列が、「2つ以上の連続した白石の両端に黒石がある」という部分を含む確率は？
大阪医科大過去問
整数問題
単元：
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$n$を自然数とするとき、
$2^{3n-2}+3^n$は5の倍数であることを
数学的帰納法によって証明せよ。
会津大過去問
この動画を見る
$n$を自然数とするとき、
$2^{3n-2}+3^n$は5の倍数であることを
数学的帰納法によって証明せよ。
会津大過去問
答えは０通り⁉️
単元：
#数A#大学入試過去問(数学)#場合の数と確率#整数の性質#場合の数#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
100円玉、50円玉、10円玉で3000面を支払うのは何通りか？
産業医科大過去問
この動画を見る
100円玉、50円玉、10円玉で3000面を支払うのは何通りか？
産業医科大過去問
産業医科大 区分求積法を使わなくても出せるよ
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#産業医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }\dfrac{1^4+2^4+3^4+････+n^4}{n^5}$
これを求めよ。
産業医科大過去問
この動画を見る
$\displaystyle \lim_{ n \to \infty }\dfrac{1^4+2^4+3^4+････+n^4}{n^5}$
これを求めよ。
産業医科大過去問