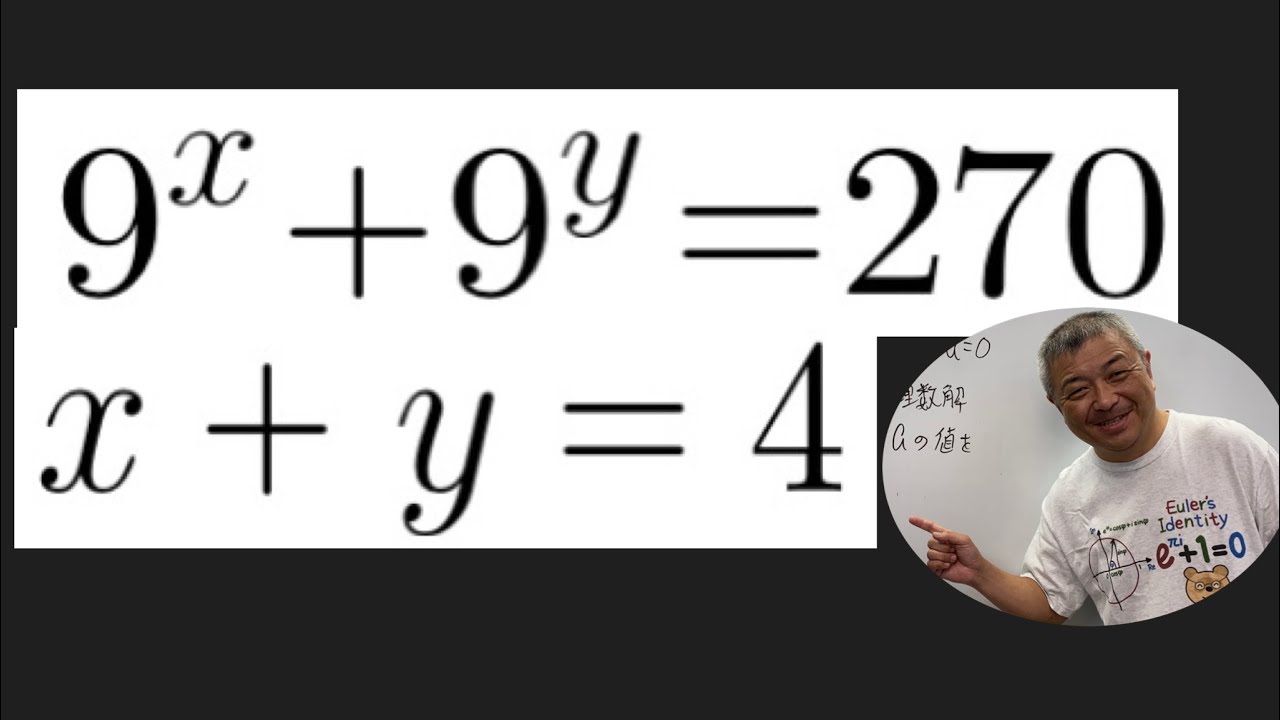鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
産業医科大 三角比の計算
単元：
#数Ⅰ#大学入試過去問(数学)#複素数平面#図形と計量#三角比（三角比・拡張・相互関係・単位円）#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#数C#産業医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=?$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=?$
これらを求めよ。
産業医科大過去問
この動画を見る
$\cos\dfrac{2}{7}\pi+\cos\dfrac{4}{7}\pi+\cos\dfrac{8}{7}\pi=?$
$\sin\dfrac{2}{7}\pi+\sin\dfrac{4}{7}\pi+\sin\dfrac{8}{7}\pi=?$
これらを求めよ。
産業医科大過去問
早稲田大 みんな大好きBBB
単元：
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\displaystyle \sum_{i=6}^{\infty} \dfrac{1800}{(n-5)(n-4)(n-1)n}$
これを求めよ。
早稲田大過去問
この動画を見る
$\displaystyle \sum_{i=6}^{\infty} \dfrac{1800}{(n-5)(n-4)(n-1)n}$
これを求めよ。
早稲田大過去問
電卓アプリで遊んでみた
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$n$は自然数であるとする。
$N=1^n+2^n+3^n+･･････+2024^n$
$N$が8の倍数となる$n$の条件を求めよ。
この動画を見る
$n$は自然数であるとする。
$N=1^n+2^n+3^n+･･････+2024^n$
$N$が8の倍数となる$n$の条件を求めよ。
誘導がなければ素晴らしい解法も出てくるんじゃね？
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#大阪教育大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
点Pは原点を出発して,「確率pで+1,確率1-pで+2」の移動を繰り返す.
ただし$0\leqq p \leqq 1$とする.このような移動を繰り返して自然数nの点に到達する確率を$p_n$と表す.次の問に答えよ.
(1)$p_1,p_2,p_3$を$p$を用いて表せ.
(2)$p_n,p_{n+1},p_{n+2}$の間の関係式を求めよ.
(3)$a_n=p_{n+1}-p_n(n \geqq 1)$とおくとき,数列${a_n}$が満たす漸化式を求めよ.
(4)pとnを用いて,一般項$p_n$を表せ.
(5)数列${p_n}$の極限を調べよ.
この動画を見る
点Pは原点を出発して,「確率pで+1,確率1-pで+2」の移動を繰り返す.
ただし$0\leqq p \leqq 1$とする.このような移動を繰り返して自然数nの点に到達する確率を$p_n$と表す.次の問に答えよ.
(1)$p_1,p_2,p_3$を$p$を用いて表せ.
(2)$p_n,p_{n+1},p_{n+2}$の間の関係式を求めよ.
(3)$a_n=p_{n+1}-p_n(n \geqq 1)$とおくとき,数列${a_n}$が満たす漸化式を求めよ.
(4)pとnを用いて,一般項$p_n$を表せ.
(5)数列${p_n}$の極限を調べよ.
超不人気！確率漸化式だよ
単元：
#数Ⅰ#数列#漸化式#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
点Pは原点を出発して確率$p(0\leqq P\leqq 1)$で$+1$, $1-p$で$+2$進む.
自然数nの地点に到達する確率$P_n$を求めよ.
大阪教育大過去問
この動画を見る
点Pは原点を出発して確率$p(0\leqq P\leqq 1)$で$+1$, $1-p$で$+2$進む.
自然数nの地点に到達する確率$P_n$を求めよ.
大阪教育大過去問
あれを使って解こう！大阪教育大
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#大阪教育大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
xを実数とする。
$x^8(y-x^2)\geqq 4$のとき、$x(x+y)\geqq 4$を示せ.
大阪教育大過去問
この動画を見る
xを実数とする。
$x^8(y-x^2)\geqq 4$のとき、$x(x+y)\geqq 4$を示せ.
大阪教育大過去問
指数方程式の解の配置 弘前大
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$4^x-2^{x+1}a+8a-15=0$の解が次の条件を満たす$a$の範囲を求めよ.
(1)ただ1つの実数解をもつとき
(2)相異なる2つの実数解がともに1以上のとき
弘前大過去問
この動画を見る
$4^x-2^{x+1}a+8a-15=0$の解が次の条件を満たす$a$の範囲を求めよ.
(1)ただ1つの実数解をもつとき
(2)相異なる2つの実数解がともに1以上のとき
弘前大過去問
二項定理 弘前大
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(1+x)^n$を展開したときの次数が奇数の項の係数の和を求めよ.
弘前大過去問
この動画を見る
$(1+x)^n$を展開したときの次数が奇数の項の係数の和を求めよ.
弘前大過去問
フツーにやっても出るけどね三次方程式解と係数の関係
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^3+2x^2+3x+4=0$の３つの解を$\alpha,\beta,\delta$としたとき、
次の３つを解にもつ３次方程式を作れ.
(1)$\dfrac{1}{\alpha},\dfrac{1}{\beta},\dfrac{1}{\delta}$
(2)$\dfrac{1}{\alpha^2},\dfrac{1}{\beta^2},\dfrac{1}{\delta^2}$
この動画を見る
$x^3+2x^2+3x+4=0$の３つの解を$\alpha,\beta,\delta$としたとき、
次の３つを解にもつ３次方程式を作れ.
(1)$\dfrac{1}{\alpha},\dfrac{1}{\beta},\dfrac{1}{\delta}$
(2)$\dfrac{1}{\alpha^2},\dfrac{1}{\beta^2},\dfrac{1}{\delta^2}$
ざ・漸化式 高知大
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(2n+2)a_n-na_{n+1}-3n-6=0$
(1)一般項$a_n$を求めよ.
(2)$\displaystyle \sum_{k=1}^n a_k$
高知大過去問
この動画を見る
$(2n+2)a_n-na_{n+1}-3n-6=0$
(1)一般項$a_n$を求めよ.
(2)$\displaystyle \sum_{k=1}^n a_k$
高知大過去問
ざ・整式の剰余 様々な解法
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
整式$P(x)$を$(x-2)^2$で割るとあまりは$6x-1$であり,
$(x+1)$で割るとあまりは2である.
$P(x)$を$(x-2)^2(x+1)$で割ったあまりはいくつか？求めよ.
この動画を見る
整式$P(x)$を$(x-2)^2$で割るとあまりは$6x-1$であり,
$(x+1)$で割るとあまりは2である.
$P(x)$を$(x-2)^2(x+1)$で割ったあまりはいくつか？求めよ.
高校生からのDM
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$N=1^n+2^n+3^n+････+2025^n$
Nはn(自然数)の値がいくつでも素数になり得ないことを示せ.
この動画を見る
$N=1^n+2^n+3^n+････+2025^n$
Nはn(自然数)の値がいくつでも素数になり得ないことを示せ.
４次方程式の解と係数の関係？
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(x+1)(x+2)(x+3)(x+4)=4$の4つの解を$\alpha,\beta,\delta,\zeta$とするとき,
$\alpha^3+\beta^3+\delta^3+\zeta^3$の値を求めよ.
この動画を見る
$(x+1)(x+2)(x+3)(x+4)=4$の4つの解を$\alpha,\beta,\delta,\zeta$とするとき,
$\alpha^3+\beta^3+\delta^3+\zeta^3$の値を求めよ.
ただの整式の割り算
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(3x^3-4x^2+10x+4)^2$を$x^2-2x+4$で割ったあまりを求めよ.$
この動画を見る
$(3x^3-4x^2+10x+4)^2$を$x^2-2x+4$で割ったあまりを求めよ.$
長崎大 複素数と整数の融合問題
単元：
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#整数の性質#約数・倍数・整数の割り算と余り・合同式#複素数#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$m,n$を整数とする.
$\alpha=m+\sqrt7 ni$,
$\alpha^3=225+2\sqrt7 i$
(1)$x^3=1$を解け.
(2)$m,n$を求めよ.
(3)$Z^3=225+2\sqrt7 i$を解け.
長崎大過去問
この動画を見る
$m,n$を整数とする.
$\alpha=m+\sqrt7 ni$,
$\alpha^3=225+2\sqrt7 i$
(1)$x^3=1$を解け.
(2)$m,n$を求めよ.
(3)$Z^3=225+2\sqrt7 i$を解け.
長崎大過去問
埼玉大 直方体の最大値
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#埼玉大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
三辺の和が9cmで表面積が$48m^2$の直方体の体積の最大値を求めよ.
長崎大過去問
この動画を見る
三辺の和が9cmで表面積が$48m^2$の直方体の体積の最大値を求めよ.
長崎大過去問
41万部のベストセラー「おみやげ算」
埼玉大 ３次不等式と不等式の証明
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#指数関数と対数関数#微分法と積分法#恒等式・等式・不等式の証明#指数関数#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(1)(n+1)^3\gt n^3+(n-1)^3$を満たす最大の整数$n$を求めよ.
(2)$n=(1)$の解,$x\gt 0$のとき
$(n+1)^{x+3}\gt n^{x+3}+(n-1)^{x+3}$を証明せよ.
埼玉大過去問
この動画を見る
$(1)(n+1)^3\gt n^3+(n-1)^3$を満たす最大の整数$n$を求めよ.
(2)$n=(1)$の解,$x\gt 0$のとき
$(n+1)^{x+3}\gt n^{x+3}+(n-1)^{x+3}$を証明せよ.
埼玉大過去問
埼玉大（経済）典型的な連立漸化式
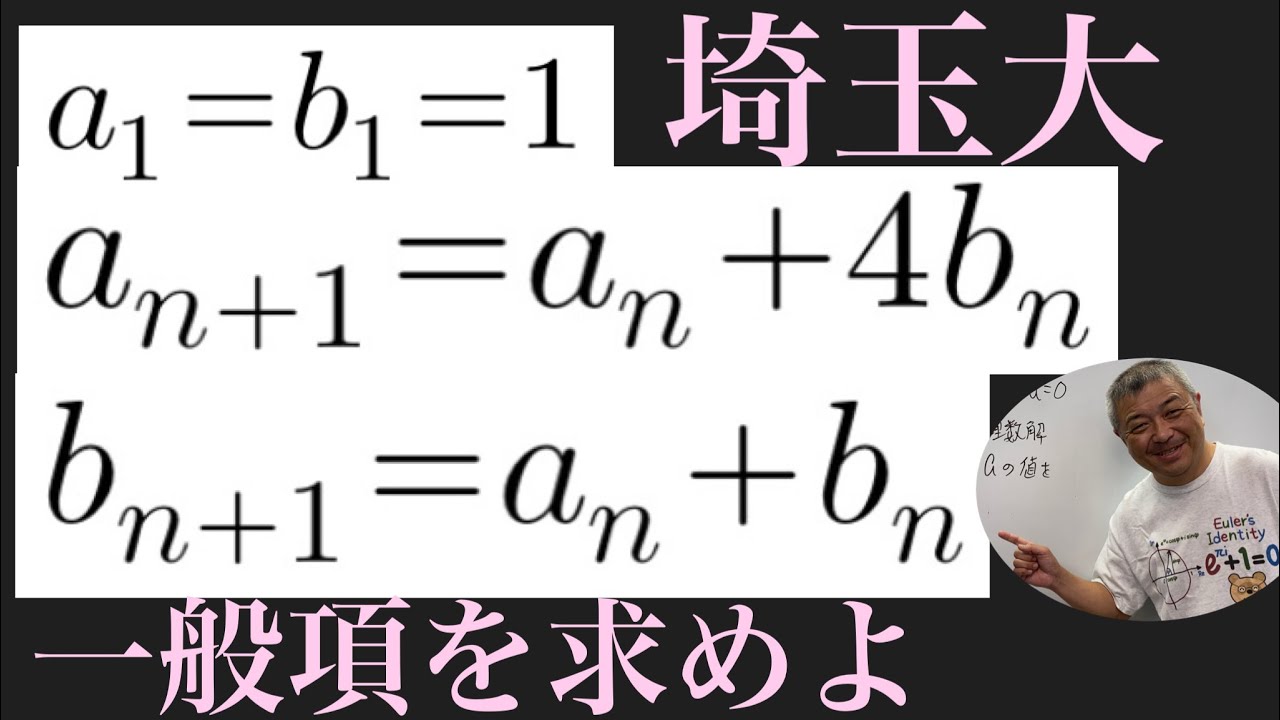
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a_n$の一般項
$a_1=b_1=1$
$a_{n+1}=a_n+4b_n$
$b_{n+1}=a_n+b_n$を求めよ.
埼玉大過去問
この動画を見る
$a_n$の一般項
$a_1=b_1=1$
$a_{n+1}=a_n+4b_n$
$b_{n+1}=a_n+b_n$を求めよ.
埼玉大過去問
神戸大 ３次関数の最大最小
単元：
#大学入試過去問(数学)#式と証明#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$t\gt 0$とし,
$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$
$-1\leqq x \leqq 2$ における最大値と最小値を求めよ.
神戸大過去問
この動画を見る
$t\gt 0$とし,
$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$
$-1\leqq x \leqq 2$ における最大値と最小値を求めよ.
神戸大過去問
シンガポール数学オリンピック整数問題の基本
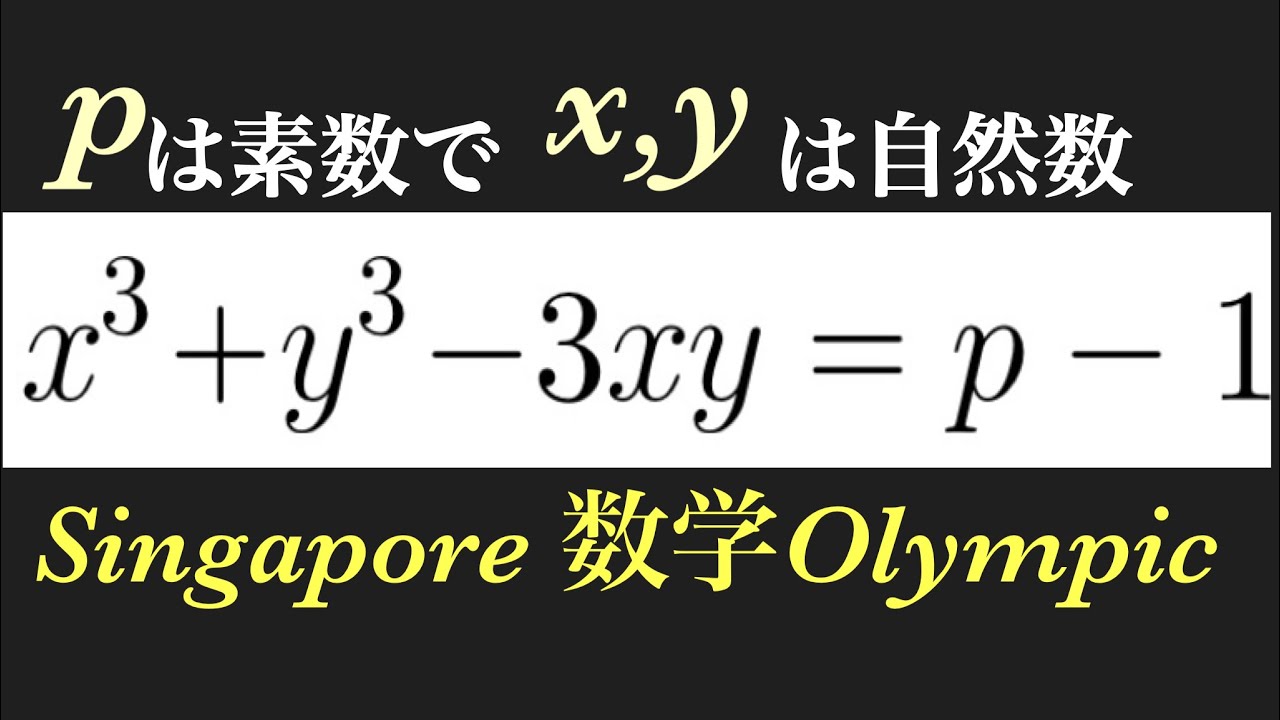
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$P$は素数であり,$x,y$を自然数としたとき,
$x^3+y^3-3xy=p-1$をみたす$(x,y)$をすべて求めよ.
シンガポール数学オリンピック過去問
この動画を見る
$P$は素数であり,$x,y$を自然数としたとき,
$x^3+y^3-3xy=p-1$をみたす$(x,y)$をすべて求めよ.
シンガポール数学オリンピック過去問
対数と不等式
単元：
#数Ⅰ#数Ⅱ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\dfrac{k-1}{k}\lt \log_{10}7 \lt \dfrac{k}{k+1}$
自然数kを求めよ.
この動画を見る
$\dfrac{k-1}{k}\lt \log_{10}7 \lt \dfrac{k}{k+1}$
自然数kを求めよ.
相加相乗平均のエレガントな証明２通り
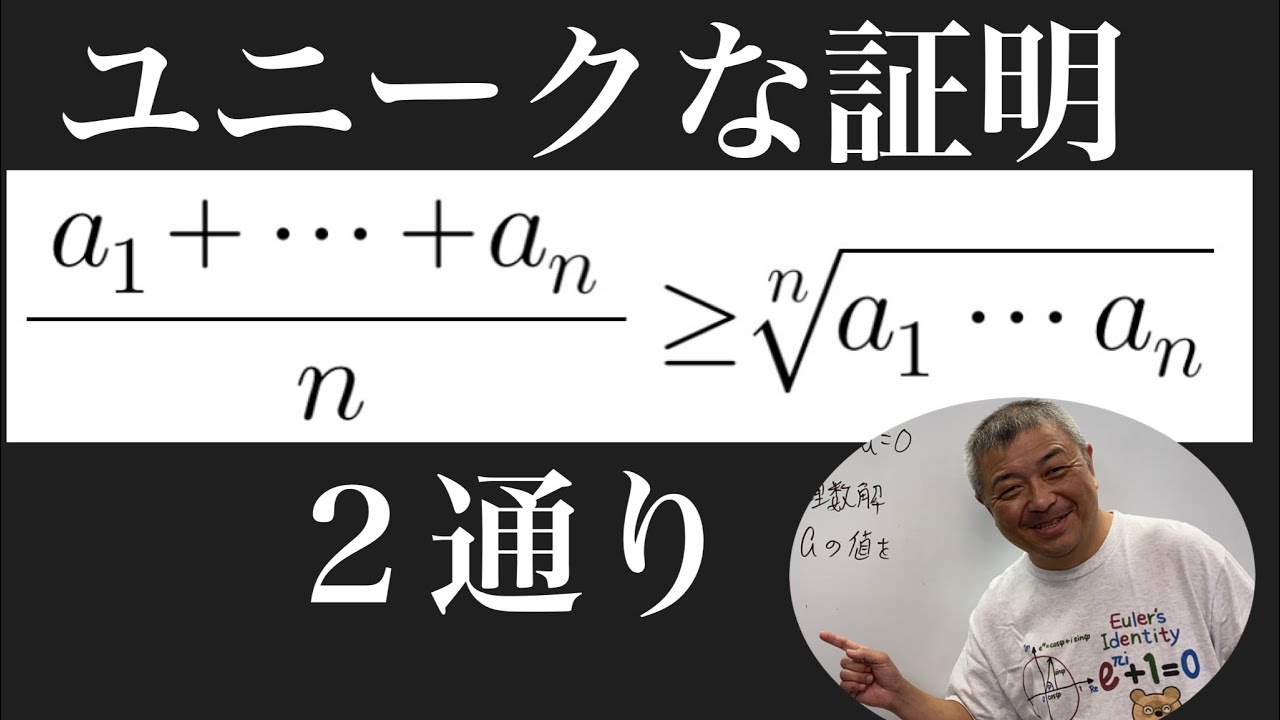
単元：
#数Ⅱ#式と証明#指数関数と対数関数#指数関数
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ \dfrac{a_1+a_2+････+a_n}{n}\geqq \sqrt[n]{a_1,a_2････a_n}$
これを求めよ.
この動画を見る
$ \dfrac{a_1+a_2+････+a_n}{n}\geqq \sqrt[n]{a_1,a_2････a_n}$
これを求めよ.
神戸大 不等式の証明
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#一次不等式（不等式・絶対値のある方程式・不等式）#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1････a_n\left(a_1+･･･a_n\right)\left(\dfrac{1}{a_1}+････+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
この動画を見る
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1････a_n\left(a_1+･･･a_n\right)\left(\dfrac{1}{a_1}+････+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
ただの因数分解だよ
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
次の式は整数の範囲で因数分解できることが分かっています.
$2x^2-2519376x-3^10$
$(2^{\Box}x-3^{\Box})(2^{\Box}x+3^{\Box})
\Box$ に0以上の整数を入れなさい.
この動画を見る
次の式は整数の範囲で因数分解できることが分かっています.
$2x^2-2519376x-3^10$
$(2^{\Box}x-3^{\Box})(2^{\Box}x+3^{\Box})
\Box$ に0以上の整数を入れなさい.
愛が１番！
i=1⁉️からくりは通常動画で❗️ #short
因数分解
単元：
#数Ⅰ#数Ⅱ#数と式#式の計算（整式・展開・因数分解）#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
因数分解せよ.
$9x^2+4168x+2^{15}$
この動画を見る
因数分解せよ.
$9x^2+4168x+2^{15}$
指数方程式 解は見えちゃうんだよね
一工夫必要な不定方程式
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
自然数(a,b)の組は何組あるか？
$3ab+4a-b=684$
この動画を見る
自然数(a,b)の組は何組あるか？
$3ab+4a-b=684$