 規則性(周期算・方陣算・数列・日暦算・N進法)
規則性(周期算・方陣算・数列・日暦算・N進法)
 規則性(周期算・方陣算・数列・日暦算・N進法)
規則性(周期算・方陣算・数列・日暦算・N進法)
【受験算数】下のように、あるきまりにしたがって左から順に分数が並んでいます。25番目の分数は何番目ですか。1/1, 1/2, 2/2, 1/3, 2/3, 3/3, 1/4, 2/4, 3/4, …

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1問
下のように、あるきまりにしたがって左から順に分数が並んでいます。25番目の分数は何番目ですか。
1/1, 1/2, 2/2, 1/3, 2/3, 3/3, 1/4, 2/4, 3/4, 4/4, 1/5, 2/5, …
第2問
下のように、あるきまりにしたがって左から順に分数が並んでいます。60番目の分数は何番目ですか。
1/1, 2/2, 1/2, 3/3, 2/3, 1/3, 4/4, 3/4, 2/4, 1/4, 5/5, 4/5, …
第3問
下のように、あるきまりにしたがって左から順に分数が並んでいます。
1/2, 1/3, 2/3, 1/4, 2/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 2/6, …
(1)60番目の分数は何ですか。
(2)1番目から60番目までの60個の分数の和を求めなさい。
この動画を見る
第1問
下のように、あるきまりにしたがって左から順に分数が並んでいます。25番目の分数は何番目ですか。
1/1, 1/2, 2/2, 1/3, 2/3, 3/3, 1/4, 2/4, 3/4, 4/4, 1/5, 2/5, …
第2問
下のように、あるきまりにしたがって左から順に分数が並んでいます。60番目の分数は何番目ですか。
1/1, 2/2, 1/2, 3/3, 2/3, 1/3, 4/4, 3/4, 2/4, 1/4, 5/5, 4/5, …
第3問
下のように、あるきまりにしたがって左から順に分数が並んでいます。
1/2, 1/3, 2/3, 1/4, 2/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 2/6, …
(1)60番目の分数は何ですか。
(2)1番目から60番目までの60個の分数の和を求めなさい。
【受験算数】三角数とは何か
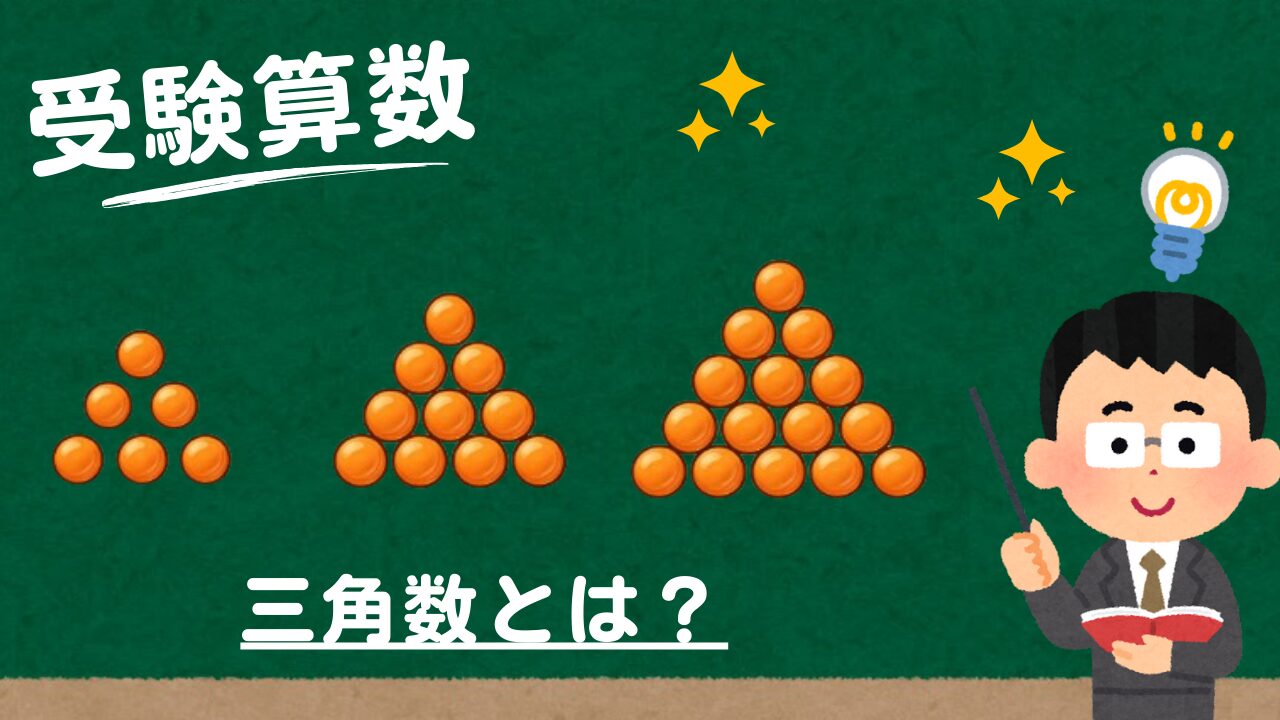
単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角数とは何かを説明する動画です。
この動画を見る
三角数とは何かを説明する動画です。
【受験算数】 (1) 12個の連続した整数の和が210になるとき、はじめの数はいくつか。 (2) 25個の連続した整数の和が2000になるとき、最後の数はいくつか。

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の問いに答えよ。
(1) 12個の連続した整数の和が210になるとき、はじめの数はいくつか。
(2) 25個の連続した整数の和が2000になるとき、最後の数はいくつか。
この動画を見る
次の問いに答えよ。
(1) 12個の連続した整数の和が210になるとき、はじめの数はいくつか。
(2) 25個の連続した整数の和が2000になるとき、最後の数はいくつか。
【受験算数】 (1) 7個の連続した整数の和が140になるとき、はじめの数はいくつか。 (2) 16個の連続した整数の和が1000になるとき、最後の数はいくつか。

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の問いに答えよ。
(1) 7個の連続した整数の和が140になるとき、はじめの数はいくつか。
(2) 16個の連続した整数の和が1000になるとき、最後の数はいくつか。
この動画を見る
次の問いに答えよ。
(1) 7個の連続した整数の和が140になるとき、はじめの数はいくつか。
(2) 16個の連続した整数の和が1000になるとき、最後の数はいくつか。
4年に一度?うるう年はどれ?

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
重吉
問題文全文(内容文):
次のうち、うるう年はどれですか?
ア:2000年
イ:2050年
ウ:2100年
この動画を見る
次のうち、うるう年はどれですか?
ア:2000年
イ:2050年
ウ:2100年
7秒で答えよ!31日まである月part2

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
重吉
問題文全文(内容文):
次のうち、31日まである月を7秒以内に答えなさい。
June, July, August, September, October, November, December, January, February, March, April, May
この動画を見る
次のうち、31日まである月を7秒以内に答えなさい。
June, July, August, September, October, November, December, January, February, March, April, May
7秒で答えよ!31日まである月


単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
重吉
問題文全文(内容文):
重要問題11
(1)
3で割ると2あまる数はあまりの▭から▭ずつ増えていく。
同様に、5で割ると1あまる数は、あまりの▭から▭ずつ増えていく。
この両方の数列に現れる最初の数字は▭であり、その後は3と5の最小公倍数である15増えるごとに同じ数字が両方の数列に現れる。
よって、両方の数列に現れる5番目の数字は、1番最初の11に15を4回足せば良いので▭である。
(2)
(1)の▭番目の数字を求める式は、▭である。
この式の答えは3桁の最大の整数999になると考えると、▭に当てはまる数字は次のように計算できる。
▭は整数であり、上の式の答えは▭よりも小さな整数なので、▭を上の式に当てはめると以下のように計算できる。
重要問題12
6で割ると2あまる数は、あまりの▭から▭ずつ増えていく。
同様に、14で割ると10あまる数は、あまりの▭から▭ずつ増えていく。
この両方の数列に現れる最初の数字は38であり、
その後は6と14の最小公倍数である▭増えるごとに同じ数字が両方の数列に現れる。
よって、▭番目の数字を求める式は、▭である。
この式の答えが900になると考えると、▭にあてはまる数を求められる。
▭は整数なので、▭と▭を上の式に当てはめると、
よって、900に近いのは、▭である。
この動画を見る
重要問題11
(1)
3で割ると2あまる数はあまりの▭から▭ずつ増えていく。
同様に、5で割ると1あまる数は、あまりの▭から▭ずつ増えていく。
この両方の数列に現れる最初の数字は▭であり、その後は3と5の最小公倍数である15増えるごとに同じ数字が両方の数列に現れる。
よって、両方の数列に現れる5番目の数字は、1番最初の11に15を4回足せば良いので▭である。
(2)
(1)の▭番目の数字を求める式は、▭である。
この式の答えは3桁の最大の整数999になると考えると、▭に当てはまる数字は次のように計算できる。
▭は整数であり、上の式の答えは▭よりも小さな整数なので、▭を上の式に当てはめると以下のように計算できる。
重要問題12
6で割ると2あまる数は、あまりの▭から▭ずつ増えていく。
同様に、14で割ると10あまる数は、あまりの▭から▭ずつ増えていく。
この両方の数列に現れる最初の数字は38であり、
その後は6と14の最小公倍数である▭増えるごとに同じ数字が両方の数列に現れる。
よって、▭番目の数字を求める式は、▭である。
この式の答えが900になると考えると、▭にあてはまる数を求められる。
▭は整数なので、▭と▭を上の式に当てはめると、
よって、900に近いのは、▭である。
予習シリーズ算数6年上 第13回数と規則性(2)重要問題5,6

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
重吉
問題文全文(内容文):
予習シリーズ算数6年上 第13回数と規則性(2)重要問題5,6
5. 次の整数の組の最小公倍数を求めなさい。
(1)(18,48)
(2)(28,42,63)
6. 1から100までの整数について、次の問いに答えなさい。ただし、「わり切れる」とは、商が整数であまりが0になることをさすものとします。
(1)6でも8でもわり切れる整数は何個ありますか。
(2)6でも8でもわり切れない整数は何個ありますか。
この動画を見る
予習シリーズ算数6年上 第13回数と規則性(2)重要問題5,6
5. 次の整数の組の最小公倍数を求めなさい。
(1)(18,48)
(2)(28,42,63)
6. 1から100までの整数について、次の問いに答えなさい。ただし、「わり切れる」とは、商が整数であまりが0になることをさすものとします。
(1)6でも8でもわり切れる整数は何個ありますか。
(2)6でも8でもわり切れない整数は何個ありますか。
予習シリーズ算数6年上 第13回数と規則性(2)重要問題1,2

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
重吉
問題文全文(内容文):
数と規則性(2)
1 60をわると6あまる整数をすべて答えなさい。
2 次の整数の組の最大公約数を求めなさい。
(1)(30,48)
(2)(112,196,252)
この動画を見る
数と規則性(2)
1 60をわると6あまる整数をすべて答えなさい。
2 次の整数の組の最大公約数を求めなさい。
(1)(30,48)
(2)(112,196,252)
【小6算数手元解説】青と赤の玉が同時に光る場所【問題文は概要欄】

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#約数・倍数を利用する問題#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#マスターテキスト#中学受験教材#小6 サマーサポート
指導講師:
理数個別チャンネル
問題文全文(内容文):
中心が同じ2つの円があって、図のように、そのまわりにはそれぞれ48個の電球がかざりつけてあり、外側では青い電球が0,1,2,3,.... 46, 47, 0,1,2,3, の順に5秒ごとにひとつずつパッ、パッ、パッ、・・・・・・と発光していきます。内側では赤い電球が同じように、13秒ごとに順に発光していきます。さて、出発点で青と赤の電球が同時に発光しました。次の問いに答えなさい。
(1) 出発してからはじめて赤い電球が番号8のところで発光しました。このすぐあとで青い電球はどこで発光しますか。番号を答えなさい。
(2) 青と赤の電球が出発点0以外の同じ番号のところで同時に発光することがあるとすればそれはどこですか。番号を全部書きなさい。
この動画を見る
中心が同じ2つの円があって、図のように、そのまわりにはそれぞれ48個の電球がかざりつけてあり、外側では青い電球が0,1,2,3,.... 46, 47, 0,1,2,3, の順に5秒ごとにひとつずつパッ、パッ、パッ、・・・・・・と発光していきます。内側では赤い電球が同じように、13秒ごとに順に発光していきます。さて、出発点で青と赤の電球が同時に発光しました。次の問いに答えなさい。
(1) 出発してからはじめて赤い電球が番号8のところで発光しました。このすぐあとで青い電球はどこで発光しますか。番号を答えなさい。
(2) 青と赤の電球が出発点0以外の同じ番号のところで同時に発光することがあるとすればそれはどこですか。番号を全部書きなさい。
【小6算数手元解説】受験算数 2輪車、4輪車、6輪車が全部で10台あって、車輪の合計が46個?【問題文は概要欄】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#文章題その他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
2輪車、4輪車、6輪車の合わせて10台の車があります。そして車輪は合計46個あります。このとき、2輪車、4輪車、6輪車はそれぞれ何台ずつありますか。考えられる場合をすべて書きなさい。ただし、どの場合にも各1台はあるものとします。
この動画を見る
2輪車、4輪車、6輪車の合わせて10台の車があります。そして車輪は合計46個あります。このとき、2輪車、4輪車、6輪車はそれぞれ何台ずつありますか。考えられる場合をすべて書きなさい。ただし、どの場合にも各1台はあるものとします。
【小6算数手元解説】受験算数 1個48円、36円、24円の商品をすべて買ってちょうど240円になるようにする 【問題文は概要欄】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#文章題その他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
A、B、Cの3種類の品物があります。Aは1個48円、Bは1個36円、Cは1個24円です。博子さんは240円の所持金を、ちょうど全部使って、3種類とも買うつもりです。A、B、Cをそれぞれ何個ずつ買うことができますか。すべての場合を書きなさい。
この動画を見る
A、B、Cの3種類の品物があります。Aは1個48円、Bは1個36円、Cは1個24円です。博子さんは240円の所持金を、ちょうど全部使って、3種類とも買うつもりです。A、B、Cをそれぞれ何個ずつ買うことができますか。すべての場合を書きなさい。
福田のおもしろ数学409〜7進法と2025番目の数

単元:
#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
福田次郎
問題文全文(内容文):
$A=\{0,1,2,3,4,5,6\}$
$M=$
$\left\{\dfrac{a_1}{7}+\dfrac{a_2}{7^2}+\dfrac{a_3}{7^3}+\dfrac{a_4}{7^4} \vert a_i \in A,i=1,2,3,4 \right\}$
$M$のすべての要素を降順に並べる。
$2025$番目の要素を求めて下さい。
この動画を見る
$A=\{0,1,2,3,4,5,6\}$
$M=$
$\left\{\dfrac{a_1}{7}+\dfrac{a_2}{7^2}+\dfrac{a_3}{7^3}+\dfrac{a_4}{7^4} \vert a_i \in A,i=1,2,3,4 \right\}$
$M$のすべての要素を降順に並べる。
$2025$番目の要素を求めて下さい。
【小6算数手元解説】受験算数 階段の上り方【問題文は概要欄】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図のような階段を、1歩で1段か2段ずつ上っていく方法を考えます。例えば、3段目まで上るとき、 1段→1段→1段,1段→2段,2段→1段 以上の3通りの上り方があります。次の問いに答えなさい。
(1) 4段目,5段目、6段目まで上るとき、それぞれ何通りの上り方がありますか。
(2) 9段目まで上るとき、何通りの上り方がありますか。
この動画を見る
下の図のような階段を、1歩で1段か2段ずつ上っていく方法を考えます。例えば、3段目まで上るとき、 1段→1段→1段,1段→2段,2段→1段 以上の3通りの上り方があります。次の問いに答えなさい。
(1) 4段目,5段目、6段目まで上るとき、それぞれ何通りの上り方がありますか。
(2) 9段目まで上るとき、何通りの上り方がありますか。
2025年早稲田中入試算数大問① 中学受験指導歴20年プロ塾講師のじっくり解説

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#文章題その他#早稲田中学
指導講師:
重吉
問題文全文(内容文):
(1) 次のように、ある規則にしたがって数が並んでいます。並べられた数の和を答えなさい。
1, 2, 3, 4, 3, 4, 5, 6, 5, 6, 7, 8, 7, 8, 9, 10,.....75, 76, 77, 78, 77, 78, 79, 80
(2) バス停からバス停Bまで5kmあり、途中に体育館があります。バス停 A もどから体育館まで行くのに、自転車で行く場合と、バスに乗ってバス停Bまで行き、体育館まで歩いて戻る場合では同じ時間かかります。バスは分速800m,自転車は分速180mで進み、歩く速さは分速45mです。バス停Aから体育館までの道のりは何mですか。
(3) みかん、りんご、ももの1個あたりの値段はそれぞれ100円,150円,173円 。これらの果物を3403円分おつりがないように買います。個数の合計が最も多くなるように買うには、みかん、りんご、ももをそれぞれ何個ずつ買えばよいですか。ただし、どの果物も1個以上は買うものとします。
この動画を見る
(1) 次のように、ある規則にしたがって数が並んでいます。並べられた数の和を答えなさい。
1, 2, 3, 4, 3, 4, 5, 6, 5, 6, 7, 8, 7, 8, 9, 10,.....75, 76, 77, 78, 77, 78, 79, 80
(2) バス停からバス停Bまで5kmあり、途中に体育館があります。バス停 A もどから体育館まで行くのに、自転車で行く場合と、バスに乗ってバス停Bまで行き、体育館まで歩いて戻る場合では同じ時間かかります。バスは分速800m,自転車は分速180mで進み、歩く速さは分速45mです。バス停Aから体育館までの道のりは何mですか。
(3) みかん、りんご、ももの1個あたりの値段はそれぞれ100円,150円,173円 。これらの果物を3403円分おつりがないように買います。個数の合計が最も多くなるように買うには、みかん、りんご、ももをそれぞれ何個ずつ買えばよいですか。ただし、どの果物も1個以上は買うものとします。
【受験算数】小数・分数:⑦循環小数応用

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
受験算数の森
問題文全文(内容文):
大問1
$\displaystyle \frac{1}{9}=(1÷9)=0.1111…、\frac{1}{99}=(1÷99)=0.010101…、\frac{1}{999} =(1÷999)=0.001001001…$です。次の問いに答えなさい。
(1) 次の小数を分数で表しなさい。
① 0.36363636…
② 0.040740740740…
③ 0.481818181
(2) 次の計算の結果を小数で表しなさい。
① $\displaystyle \frac{1}{9}+\frac{23}{99}$
② $\displaystyle \frac{2}{90}+\frac{34}{99}$
(3)$\displaystyle \frac{150}{1111}$を小数て表したとき、小数第30位の数は何ですか。
大問2
$\displaystyle \frac{1}{9}=(1÷9)=0.1111…、\frac{1}{99}=(1÷99)=0.010101…、\frac{1}{999} =(1÷999)=0.001001001…$です。次の問いに答えなさい。
(1) 次の小数を分数で表しなさい。
① 0.25252525…
② 0.518518518…
③ 0.216161616…
(2) 次の計算の結果を小数で表しなさい。
① $\displaystyle \frac{2}{9}+\frac{35}{99}$
② $\displaystyle \frac{5}{90}+\frac{21}{999}$
(3) $\displaystyle \frac{13}{37}$を小数で表したとき、小数第二位の数は何ですか。
この動画を見る
大問1
$\displaystyle \frac{1}{9}=(1÷9)=0.1111…、\frac{1}{99}=(1÷99)=0.010101…、\frac{1}{999} =(1÷999)=0.001001001…$です。次の問いに答えなさい。
(1) 次の小数を分数で表しなさい。
① 0.36363636…
② 0.040740740740…
③ 0.481818181
(2) 次の計算の結果を小数で表しなさい。
① $\displaystyle \frac{1}{9}+\frac{23}{99}$
② $\displaystyle \frac{2}{90}+\frac{34}{99}$
(3)$\displaystyle \frac{150}{1111}$を小数て表したとき、小数第30位の数は何ですか。
大問2
$\displaystyle \frac{1}{9}=(1÷9)=0.1111…、\frac{1}{99}=(1÷99)=0.010101…、\frac{1}{999} =(1÷999)=0.001001001…$です。次の問いに答えなさい。
(1) 次の小数を分数で表しなさい。
① 0.25252525…
② 0.518518518…
③ 0.216161616…
(2) 次の計算の結果を小数で表しなさい。
① $\displaystyle \frac{2}{9}+\frac{35}{99}$
② $\displaystyle \frac{5}{90}+\frac{21}{999}$
(3) $\displaystyle \frac{13}{37}$を小数で表したとき、小数第二位の数は何ですか。
2024年栄東中(A)算数大問②、③中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)#速さ#旅人算・通過算・流水算#麻布中学
指導講師:
重吉
問題文全文(内容文):
2
マラソン大会で栄くん、東さん、中さんの三人が同時にスタートして走り出し、栄くん、東さん、中さんの順にゴールしました。図1は三人がスタートしてからの時間と栄くんと東さんの道のりの差、東さんと中さんんお道のりの差を表したものです。このとき次の問いに答えなさい。ただし、三人は一定の速さで走るものとします。
※図は動画内参照
(1) 栄くんと中さんの走る速さの比を最も簡単な整数の比で表しなさい
(2) マラソン大会のコースは全長何mありますか。
(3) 東さんがゴールするのはスタートしてから何分何秒後になりますか。
3
一つの整数に対し、ある規則に従って約数を配置した図形をつくります。約数を配置した点を頂点と呼ぶことにします。例えば、4に対しては4=2×2だから、図1のような頂点の個数が3個の直線がつくれます。18に対しては18=2×3×3だから、図2にような頂点の個数が12個の直方体がつくれます。このとき次の問いに答えなさい。
(1) 図4のアに入る数を答えなさい。
(2) 2024に対して作れる図形の頂点の個数は全部で何個になりますか。
(3) ある整数に対し頂点の個数が8個になる図形がつくれるとき、その整数として考えられる150以下の数は全部で何通りありますか。
この動画を見る
2
マラソン大会で栄くん、東さん、中さんの三人が同時にスタートして走り出し、栄くん、東さん、中さんの順にゴールしました。図1は三人がスタートしてからの時間と栄くんと東さんの道のりの差、東さんと中さんんお道のりの差を表したものです。このとき次の問いに答えなさい。ただし、三人は一定の速さで走るものとします。
※図は動画内参照
(1) 栄くんと中さんの走る速さの比を最も簡単な整数の比で表しなさい
(2) マラソン大会のコースは全長何mありますか。
(3) 東さんがゴールするのはスタートしてから何分何秒後になりますか。
3
一つの整数に対し、ある規則に従って約数を配置した図形をつくります。約数を配置した点を頂点と呼ぶことにします。例えば、4に対しては4=2×2だから、図1のような頂点の個数が3個の直線がつくれます。18に対しては18=2×3×3だから、図2にような頂点の個数が12個の直方体がつくれます。このとき次の問いに答えなさい。
(1) 図4のアに入る数を答えなさい。
(2) 2024に対して作れる図形の頂点の個数は全部で何個になりますか。
(3) ある整数に対し頂点の個数が8個になる図形がつくれるとき、その整数として考えられる150以下の数は全部で何通りありますか。
2024年久留米附設中算数大問②、③中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#久留米大学附設中学
指導講師:
重吉
問題文全文(内容文):
2.今日は西暦2024年1月20日土曜日です。西暦2024年は閏年(うるうどし)で、2月は29日あり、1年は366日あります。閏年でない年を平年といい、1年は365日あります。地球が太陽の周りをまわる時間は365日より少しだけ長いので、閏年が次のように定められております。
「西暦が4で割り切れる年を閏年とするが、この中で西暦が100で割り切れて、400で割り切れない年は平年とする。」
これをもとに、次の問いに答えなさい。
(1) 西暦2100年は閏年と平年のどちらですか。理由をつけて答えなさい。
(2) 今年を含めて、今年から西暦2101年までに閏年は何回ありますか。
(3) 西暦2101年1月20日は今日から何日後の何曜日ですか。
3. 右の表(表は動画内参照)のように、1行1列から規則的に1,2,3,4,と整数を書き込みます。例えば2行3列に書かれている整数は8です。次の問いに答えなさい。
(1) 10行1列に書かれている整数は何ですか。
(2) 11行2列に書かれている整数は何ですか。
(3) 表の太枠のように、縦横二個ずつ、合計4個の整数を囲み、その和を考えます。表の太枠では4個の整数の和は35です。
(ア) 11行1列の整数が太枠の左上となるように4個の整数を囲んだ時、4個の整数の和はいくつになりますか
(イ) 太枠の中の4個の整数の和が999の時に、解答用紙の太枠の中に、規則にしたがって4個の整数を書き込みなさい。
この動画を見る
2.今日は西暦2024年1月20日土曜日です。西暦2024年は閏年(うるうどし)で、2月は29日あり、1年は366日あります。閏年でない年を平年といい、1年は365日あります。地球が太陽の周りをまわる時間は365日より少しだけ長いので、閏年が次のように定められております。
「西暦が4で割り切れる年を閏年とするが、この中で西暦が100で割り切れて、400で割り切れない年は平年とする。」
これをもとに、次の問いに答えなさい。
(1) 西暦2100年は閏年と平年のどちらですか。理由をつけて答えなさい。
(2) 今年を含めて、今年から西暦2101年までに閏年は何回ありますか。
(3) 西暦2101年1月20日は今日から何日後の何曜日ですか。
3. 右の表(表は動画内参照)のように、1行1列から規則的に1,2,3,4,と整数を書き込みます。例えば2行3列に書かれている整数は8です。次の問いに答えなさい。
(1) 10行1列に書かれている整数は何ですか。
(2) 11行2列に書かれている整数は何ですか。
(3) 表の太枠のように、縦横二個ずつ、合計4個の整数を囲み、その和を考えます。表の太枠では4個の整数の和は35です。
(ア) 11行1列の整数が太枠の左上となるように4個の整数を囲んだ時、4個の整数の和はいくつになりますか
(イ) 太枠の中の4個の整数の和が999の時に、解答用紙の太枠の中に、規則にしたがって4個の整数を書き込みなさい。
2024年久留米附設中算数大問②、③中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#久留米大学附設中学
指導講師:
重吉
問題文全文(内容文):
2
今日は西暦2024年1月20日土曜日です。西暦2024年は閏年で、2月は29日あり、1年は366日あります。閏年ではない年を平年といい、一年は365日あります。地球が太陽の周りをまわる時間は365日よりも少しだけ長いので、閏年が次のように定められております。
西暦が4で割り切れる年を閏年とするが、この中で西暦が100で割り切れて、400で割り切れない年は平年とする。
これをもとに、次の問いに答えなさい。
(1) 西暦2100年は閏年と平年のどちらですか。理由をつけて答えなさい。
(2) 今年を含めて、今年から西暦2101年までに閏年は何回ありますか。
(3) 西暦2101年1月20日は居から何日後の何曜日ですか。
3
右の表のように、1列1行から規則的に、1,2,3,4と整数を書き込みます。例えば、2行3列に書かれている整数は8です。次の問いに答えなさい。
(1) 10行1列に書かれている整数は何ですか
(2) 11行2列に書かれている整数は何ですか
(3) 表の太枠のように、縦横二個ずつ、合計四個の整数を囲み、その和を考えます。表の太枠では、4個の整数の和は35です。
(ア) 11行1列の整数が太枠の左上となるように4個の整数を囲んだ時、4個の整数の和はいくつになりますか。
(イ) 太枠の中の四個の整数の和が999の時、解答用紙の太枠の中に、規則に従って四個の整数整数を書き込みなさい。
この動画を見る
2
今日は西暦2024年1月20日土曜日です。西暦2024年は閏年で、2月は29日あり、1年は366日あります。閏年ではない年を平年といい、一年は365日あります。地球が太陽の周りをまわる時間は365日よりも少しだけ長いので、閏年が次のように定められております。
西暦が4で割り切れる年を閏年とするが、この中で西暦が100で割り切れて、400で割り切れない年は平年とする。
これをもとに、次の問いに答えなさい。
(1) 西暦2100年は閏年と平年のどちらですか。理由をつけて答えなさい。
(2) 今年を含めて、今年から西暦2101年までに閏年は何回ありますか。
(3) 西暦2101年1月20日は居から何日後の何曜日ですか。
3
右の表のように、1列1行から規則的に、1,2,3,4と整数を書き込みます。例えば、2行3列に書かれている整数は8です。次の問いに答えなさい。
(1) 10行1列に書かれている整数は何ですか
(2) 11行2列に書かれている整数は何ですか
(3) 表の太枠のように、縦横二個ずつ、合計四個の整数を囲み、その和を考えます。表の太枠では、4個の整数の和は35です。
(ア) 11行1列の整数が太枠の左上となるように4個の整数を囲んだ時、4個の整数の和はいくつになりますか。
(イ) 太枠の中の四個の整数の和が999の時、解答用紙の太枠の中に、規則に従って四個の整数整数を書き込みなさい。
2024年聖光学院中算数大問②中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#平面図形#平面図形その他#聖光学院中学
指導講師:
重吉
問題文全文(内容文):
【操作】
長方形abcdの縦の辺ABとCDの真ん中の点をそれぞれE,Fとします。下の図のように、E,Fを通る直線で長方形ABCDを切って二つに分けて、辺AEを辺FCに重ねて新たな長方形EBFDをつくります。
例えば、縦4 cm、横5 cmの長方形にこの操作を行うと、縦2cm,横10 cmの長方形になります。
縦ア cm、横イ cmの長方形Rにこの操作を何回か行うことを考えます。ア、イは整数であるもののとして、次の問いに答えなさい。
(1) 長方形Rにこの操作を7回続けて行ったところ、正方形ができました。ア、イを最も簡単な整数比で答えなさい。
(2) 長方形Rにこの操作を行うごとにできた長方形の周の長さを計算したところ8回目の操作後に初めて周の長さが奇数になりました。アとして考えられる整数のうち、三桁のものは何個ありますか。
(3) 長方形Rにこの操作を行うごとにできた長方形の周の長さを計算し、操作前と操作後の周の長さを比べて増加しているか減少しているかを調べたところ、四回目までの操作の前後ではすべて減少し、五回目の捜査では増加しました。ア÷イの商として考えられる整数は何個ありますか。
この動画を見る
【操作】
長方形abcdの縦の辺ABとCDの真ん中の点をそれぞれE,Fとします。下の図のように、E,Fを通る直線で長方形ABCDを切って二つに分けて、辺AEを辺FCに重ねて新たな長方形EBFDをつくります。
例えば、縦4 cm、横5 cmの長方形にこの操作を行うと、縦2cm,横10 cmの長方形になります。
縦ア cm、横イ cmの長方形Rにこの操作を何回か行うことを考えます。ア、イは整数であるもののとして、次の問いに答えなさい。
(1) 長方形Rにこの操作を7回続けて行ったところ、正方形ができました。ア、イを最も簡単な整数比で答えなさい。
(2) 長方形Rにこの操作を行うごとにできた長方形の周の長さを計算したところ8回目の操作後に初めて周の長さが奇数になりました。アとして考えられる整数のうち、三桁のものは何個ありますか。
(3) 長方形Rにこの操作を行うごとにできた長方形の周の長さを計算し、操作前と操作後の周の長さを比べて増加しているか減少しているかを調べたところ、四回目までの操作の前後ではすべて減少し、五回目の捜査では増加しました。ア÷イの商として考えられる整数は何個ありますか。
2024年市川中算数大問②、③中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#平面図形#角度と面積#市川中学
指導講師:
重吉
問題文全文(内容文):
2
【操作】
○の中に書き入れた整数を3で割ったとき
・余りが0であれば右に1つ進み、進んだ先の〇に商を書き入れる。
・余りが1であれば、右斜め上に進み、進んだ先の〇に商を書き入れる
・余りが2であれば、上に1進み、進んだ先の〇に商を書き入れる
最初、Aに整数を書き入れて操作を繰り返し、D,E,F,G,Hのいずれかに整数を書き入れると終了します。例えば、Aに15を書き入れたとき、15は3で割ると余りが0なのでBに進み、Bに商の5を書き入れます。次に5は3で割ると余りが2なので、Fに進み、Fの商に1を書き入れて終了します。このとき、次の問いに答えなさい。
(1) Aに111を書き入れたとき、最後にD,E,F,G,Hのどこの場所にどんな整数が書き入れられて終了するか答えなさい。
(2) Aに書き入れたとき、最後にDに進んで終了する整数は1から2024までに何個あるか求めなさい。
(3) Aに書き入れたとき、最後にGに進んで終了する整数は、1から2024までに何個あるか求めなさい。
3
円に対して、次の図のような規則で円を書き加えていく操作を繰り返していきます。操作を一回行った後の図を1番目の図、操作を二回行った後の図を2番目の図としていくとき、次の問いに答えなさい。
(1)次の図に、コンパスと定規を用いて円を書き加えて一番目の図を完成させなさい。ただし、作図に用いた線は消さないこと。
白く塗られている半径2 cmの円に対して、奇数回目の操作で書き加える円は灰色でぬり、偶数回目の操作操作で書き加える円は白色で塗ることを繰り返します。
(2) 3番目の図の灰色の部分の面積を引くと求めなさい。
(3) 5番目の図の白色の部分と灰色の部分の面積の比を求めなさい。
この動画を見る
2
【操作】
○の中に書き入れた整数を3で割ったとき
・余りが0であれば右に1つ進み、進んだ先の〇に商を書き入れる。
・余りが1であれば、右斜め上に進み、進んだ先の〇に商を書き入れる
・余りが2であれば、上に1進み、進んだ先の〇に商を書き入れる
最初、Aに整数を書き入れて操作を繰り返し、D,E,F,G,Hのいずれかに整数を書き入れると終了します。例えば、Aに15を書き入れたとき、15は3で割ると余りが0なのでBに進み、Bに商の5を書き入れます。次に5は3で割ると余りが2なので、Fに進み、Fの商に1を書き入れて終了します。このとき、次の問いに答えなさい。
(1) Aに111を書き入れたとき、最後にD,E,F,G,Hのどこの場所にどんな整数が書き入れられて終了するか答えなさい。
(2) Aに書き入れたとき、最後にDに進んで終了する整数は1から2024までに何個あるか求めなさい。
(3) Aに書き入れたとき、最後にGに進んで終了する整数は、1から2024までに何個あるか求めなさい。
3
円に対して、次の図のような規則で円を書き加えていく操作を繰り返していきます。操作を一回行った後の図を1番目の図、操作を二回行った後の図を2番目の図としていくとき、次の問いに答えなさい。
(1)次の図に、コンパスと定規を用いて円を書き加えて一番目の図を完成させなさい。ただし、作図に用いた線は消さないこと。
白く塗られている半径2 cmの円に対して、奇数回目の操作で書き加える円は灰色でぬり、偶数回目の操作操作で書き加える円は白色で塗ることを繰り返します。
(2) 3番目の図の灰色の部分の面積を引くと求めなさい。
(3) 5番目の図の白色の部分と灰色の部分の面積の比を求めなさい。
2024年ラ・サール中算数大問①、②中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#売買損益と食塩水#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平面図形#角度と面積#ラ・サール中学
指導講師:
重吉
この動画を見る
2024年慶應義塾湘南藤沢中算数大問③、④中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#平面図形#図形の移動#慶應義塾湘南藤沢中等部
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
3
図のようにマス目の中には「たての番号」×10+「よこの番号」を計算した数が書かれている。そして、「たての番号」と「よこの番号」の和をマス目の「番号和」と呼ぶことにする
例
➀「たての番号」が11、「よこの番号」が3のマス目には113が書かれ、このマスの「番号和」は14である。
②「たての番号」が3、「よこの番号」が11のマス目には41が書かれ、このマスの「番号和」は14である。
(1) 「番号和」が13になるマス目すべてに書かれている数のうち、最も大きいものと最も小さいものの和はいくつですか。
(2) 「番号和」が8になるマス目すべてに書かれている数の合計はいくつですか。
(3) 「番号和」がアになるマス目すべてに書かれている数の合計は1320である。アに入る数を求めなさい。
4
図1,2は1辺の長さが6 cmの正方形を一枚又は二枚使った図形である。これらの図形の周りを半径1 cmの円が転がりながら一周する。円周率は3.14として以下の問いに答えなさい。
(1) 図1において、円の中心が動く道のりを求めなさい。
(2) 図2において、円の中心が動く道のりを求めなさい。
(3) 図2において、円が通った後にできる部分の面積を求めなさい。
この動画を見る
※図は動画内参照
3
図のようにマス目の中には「たての番号」×10+「よこの番号」を計算した数が書かれている。そして、「たての番号」と「よこの番号」の和をマス目の「番号和」と呼ぶことにする
例
➀「たての番号」が11、「よこの番号」が3のマス目には113が書かれ、このマスの「番号和」は14である。
②「たての番号」が3、「よこの番号」が11のマス目には41が書かれ、このマスの「番号和」は14である。
(1) 「番号和」が13になるマス目すべてに書かれている数のうち、最も大きいものと最も小さいものの和はいくつですか。
(2) 「番号和」が8になるマス目すべてに書かれている数の合計はいくつですか。
(3) 「番号和」がアになるマス目すべてに書かれている数の合計は1320である。アに入る数を求めなさい。
4
図1,2は1辺の長さが6 cmの正方形を一枚又は二枚使った図形である。これらの図形の周りを半径1 cmの円が転がりながら一周する。円周率は3.14として以下の問いに答えなさい。
(1) 図1において、円の中心が動く道のりを求めなさい。
(2) 図2において、円の中心が動く道のりを求めなさい。
(3) 図2において、円が通った後にできる部分の面積を求めなさい。
2024年筑波大附属中算数大問①(5)~(7)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
重吉
問題文全文(内容文):
問題文
(5)縦の長さが200mm、横の長さが300mmの用紙がある、その重さは36gです。
この用紙1m²の重さは何gですか。
(6)下の図のように、半径3cmの円を規則的にならべて、そのまわりの長さがもっとも短くなるように囲んだ図形を考えます。図形の周りの長さ(図の太線部分)が初めて5mより大きくなるのは、何番目の図形ですか。ただし、円周率は3.14とします。
(7)1から1000mでの整数のうち、数字の4を使っていない整数は全部でいくつありますか。
この動画を見る
問題文
(5)縦の長さが200mm、横の長さが300mmの用紙がある、その重さは36gです。
この用紙1m²の重さは何gですか。
(6)下の図のように、半径3cmの円を規則的にならべて、そのまわりの長さがもっとも短くなるように囲んだ図形を考えます。図形の周りの長さ(図の太線部分)が初めて5mより大きくなるのは、何番目の図形ですか。ただし、円周率は3.14とします。
(7)1から1000mでの整数のうち、数字の4を使っていない整数は全部でいくつありますか。
2024年筑波大附属中算数大問①(5)~(7)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#単位・比と割合・比例・反比例#筑波大学附属中学
指導講師:
重吉
問題文全文(内容文):
(5) 縦の長さが200mm、横の長さが300mmの用紙があり、その重さは3.6gです。
この用紙1m²の重さは何gですか。
(6) 下の図のように、半径3cmの円を規則的にならべて、そのまわりの長さがもっとも短くなるように囲んだ図形を考えます。図形のまわりの長さ(図の太線部分)が初めて 5mより大きくなるのは、何番目の図形ですか。ただし、円周率は3.14とします。
※図は動画内参照
(7) 1から1000までの整数のうち、数字の4を使っていない整数は全部でいくつありますか。
この動画を見る
(5) 縦の長さが200mm、横の長さが300mmの用紙があり、その重さは3.6gです。
この用紙1m²の重さは何gですか。
(6) 下の図のように、半径3cmの円を規則的にならべて、そのまわりの長さがもっとも短くなるように囲んだ図形を考えます。図形のまわりの長さ(図の太線部分)が初めて 5mより大きくなるのは、何番目の図形ですか。ただし、円周率は3.14とします。
※図は動画内参照
(7) 1から1000までの整数のうち、数字の4を使っていない整数は全部でいくつありますか。
2024年筑波大学附属中算数大問①(1)~(4)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他#約数・倍数を利用する問題#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#筑波大学附属中学
指導講師:
重吉
問題文全文(内容文):
(1)
$4\dfrac{3}{16}\div\dfrac{13}{16}\div3\dfrac{1}{4}-3$を計算しなさい。
(2)
整数Aを5で割り、その商の小数第一位を四捨五入すると27になります。また、整数Aを8で割り、その商の小数第一位を切り捨てると16になります。このとき、Aに当てはまる整数は全部でいくつありますか。
(3)
えんぴつ136本、消しゴム187個、ノート343冊があります。これらを何人かの子どもにそれぞれ同じ数分けると、えんぴつは8本不足し、消しゴムは7個あまり、ノートは19冊あまりました。分けるときは、子どもの人数よりも多く余りが出ないように分けています。このとき子どもの人数は何人ですか。
(4)
下の図は、正方形ABCDの紙をAEを折り目として折ったものです。直線BDとBCによってできる角の大きさが12°のとき、図の㋐の角度を求めなさい。
この動画を見る
(1)
$4\dfrac{3}{16}\div\dfrac{13}{16}\div3\dfrac{1}{4}-3$を計算しなさい。
(2)
整数Aを5で割り、その商の小数第一位を四捨五入すると27になります。また、整数Aを8で割り、その商の小数第一位を切り捨てると16になります。このとき、Aに当てはまる整数は全部でいくつありますか。
(3)
えんぴつ136本、消しゴム187個、ノート343冊があります。これらを何人かの子どもにそれぞれ同じ数分けると、えんぴつは8本不足し、消しゴムは7個あまり、ノートは19冊あまりました。分けるときは、子どもの人数よりも多く余りが出ないように分けています。このとき子どもの人数は何人ですか。
(4)
下の図は、正方形ABCDの紙をAEを折り目として折ったものです。直線BDとBCによってできる角の大きさが12°のとき、図の㋐の角度を求めなさい。
2024年女子学院中算数大問①(1)~(5)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#平均算・過不足算・差集め算・消去算#平面図形#角度と面積#相似と相似を利用した問題#女子学院中学
指導講師:
重吉
問題文全文(内容文):
1. にあてはまる数を入れなさい。
(1)18.7+ {13.4× (1/20 +▭) -2(1/3)} ÷2(6/11) =20.24
(2)図(動画内参照)のように、円周を10等分する点をとりました。
点0は円の中心、三角形ABCは正三角形です。
角㋐▭度、角㋑▭度、角㋒▭度
(3) 図(動画内参照)のように、長方形の紙を対角線を折り目として折りました。
斜線部の部分の面積は▭cm²です。
(4) 図(動画内参照)のように、棒を使って正三角形と正方形を作ります。
① 100個目の正方形を作り終えたとき、使った棒は▭本です。
② 棒が1000本あるとき、正三角形は▭個,正方形は▭個まで作ることができます。
(5) クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、 消しゴムは9個余りました。 I
クラスの人数は▭人,消しゴムは全部で▭個です。
この動画を見る
1. にあてはまる数を入れなさい。
(1)18.7+ {13.4× (1/20 +▭) -2(1/3)} ÷2(6/11) =20.24
(2)図(動画内参照)のように、円周を10等分する点をとりました。
点0は円の中心、三角形ABCは正三角形です。
角㋐▭度、角㋑▭度、角㋒▭度
(3) 図(動画内参照)のように、長方形の紙を対角線を折り目として折りました。
斜線部の部分の面積は▭cm²です。
(4) 図(動画内参照)のように、棒を使って正三角形と正方形を作ります。
① 100個目の正方形を作り終えたとき、使った棒は▭本です。
② 棒が1000本あるとき、正三角形は▭個,正方形は▭個まで作ることができます。
(5) クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、 消しゴムは9個余りました。 I
クラスの人数は▭人,消しゴムは全部で▭個です。
2024年女子学院中算数大問①(1)~(5)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#平均算・過不足算・差集め算・消去算#平面図形#角度と面積#相似と相似を利用した問題#女子学院中学
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
(1)
$\Box$に当てはまる数を入れなさい。
$18.7+\{ 13.4\times(\dfrac{1}{20}+\Box)-2\dfrac{1}{3} \}\div2\dfrac{6}{11}=20.24$
(2)
図のように、円周を10等分する点を取りました。点Oは円の中心、三角形ABCは正三角形です。
角アは$\Box$度、角イは$\Box$度、角ウは$\Box$度
(3)
図のように、長方形の紙を対角線を折り目としておりました。
斜線部分の面積は$\Box$㎠です。
(4)
図のように、棒を使って正三角形と正方形を作ります。
➀100個目の正方形を作り終えたとき、使った棒は$\Box$本です。
②棒が1000本ある時、正三角形は$\Box$個、正方形は$\Box$個まで作ることができます。
(5)
クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、消しゴムは9個あまりました。
クラスの人数は$\Box$人、消しゴムは全部で$\Box$個です。
この動画を見る
※図は動画内参照
(1)
$\Box$に当てはまる数を入れなさい。
$18.7+\{ 13.4\times(\dfrac{1}{20}+\Box)-2\dfrac{1}{3} \}\div2\dfrac{6}{11}=20.24$
(2)
図のように、円周を10等分する点を取りました。点Oは円の中心、三角形ABCは正三角形です。
角アは$\Box$度、角イは$\Box$度、角ウは$\Box$度
(3)
図のように、長方形の紙を対角線を折り目としておりました。
斜線部分の面積は$\Box$㎠です。
(4)
図のように、棒を使って正三角形と正方形を作ります。
➀100個目の正方形を作り終えたとき、使った棒は$\Box$本です。
②棒が1000本ある時、正三角形は$\Box$個、正方形は$\Box$個まで作ることができます。
(5)
クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、消しゴムは9個あまりました。
クラスの人数は$\Box$人、消しゴムは全部で$\Box$個です。
2進法のかけ算

