相似と相似を利用した問題
相似と相似を利用した問題
 相似と相似を利用した問題
相似と相似を利用した問題
【算数練習】179(”大人”は頭の体操)
【算数練習】175(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
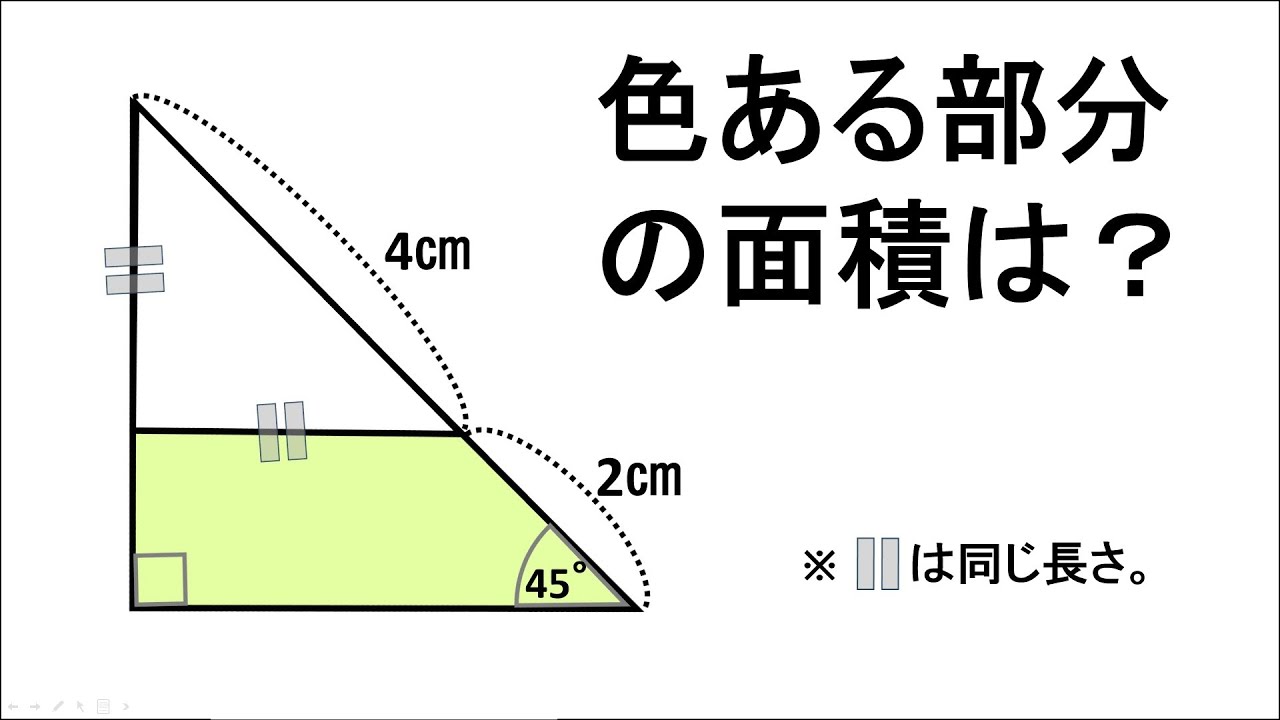
色ある部分の面積は?
※□□は同じ長さ
※図は動画内参照
この動画を見る
色ある部分の面積は?
※□□は同じ長さ
※図は動画内参照
【算数練習】176(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
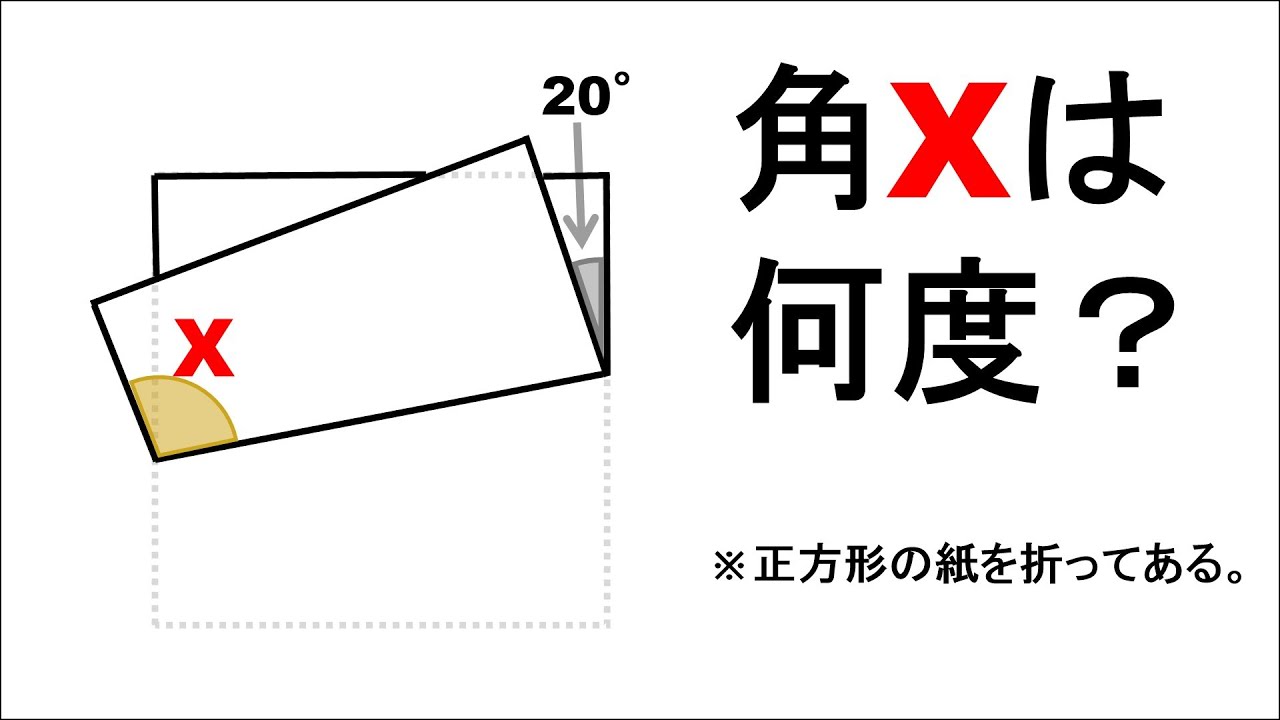
角Xは何度?
※正方形の紙を折っている
※図は動画内参照
この動画を見る
角Xは何度?
※正方形の紙を折っている
※図は動画内参照
【算数練習】174(”大人”は頭の体操)三角形と四角形の考察
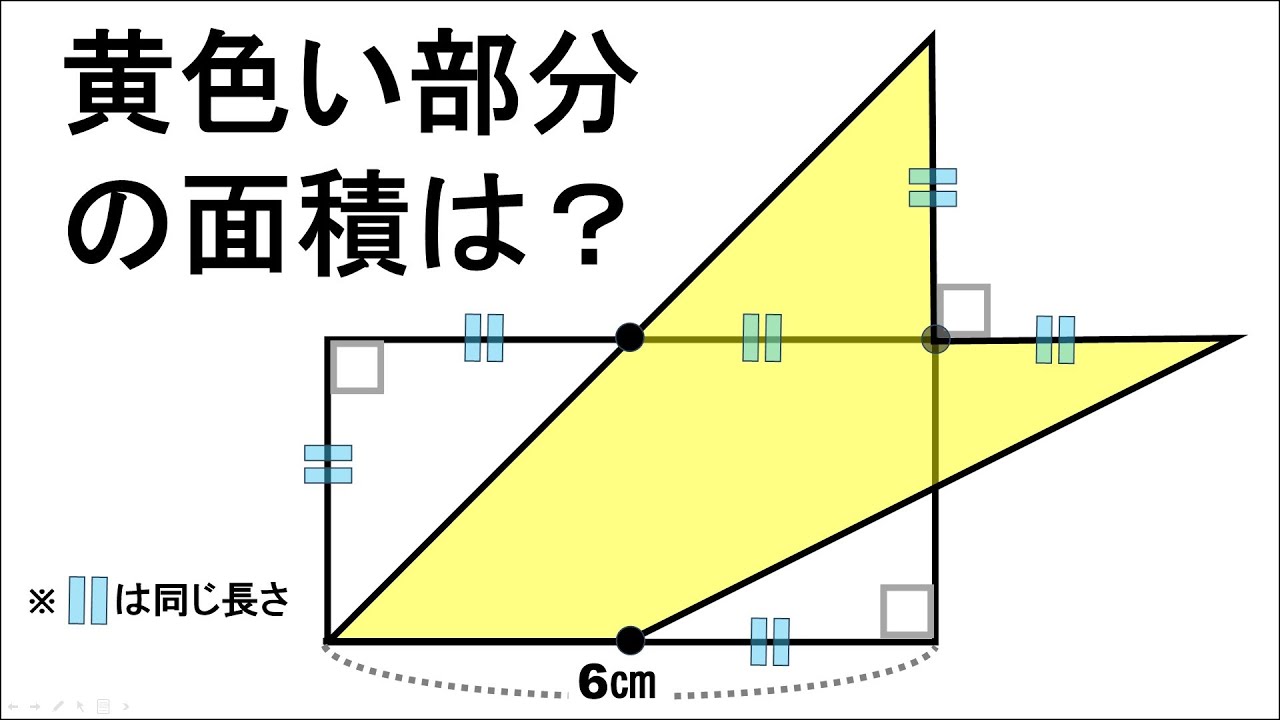
【中学受験問題に挑戦】143(”大人”は頭の体操)三角形の考察
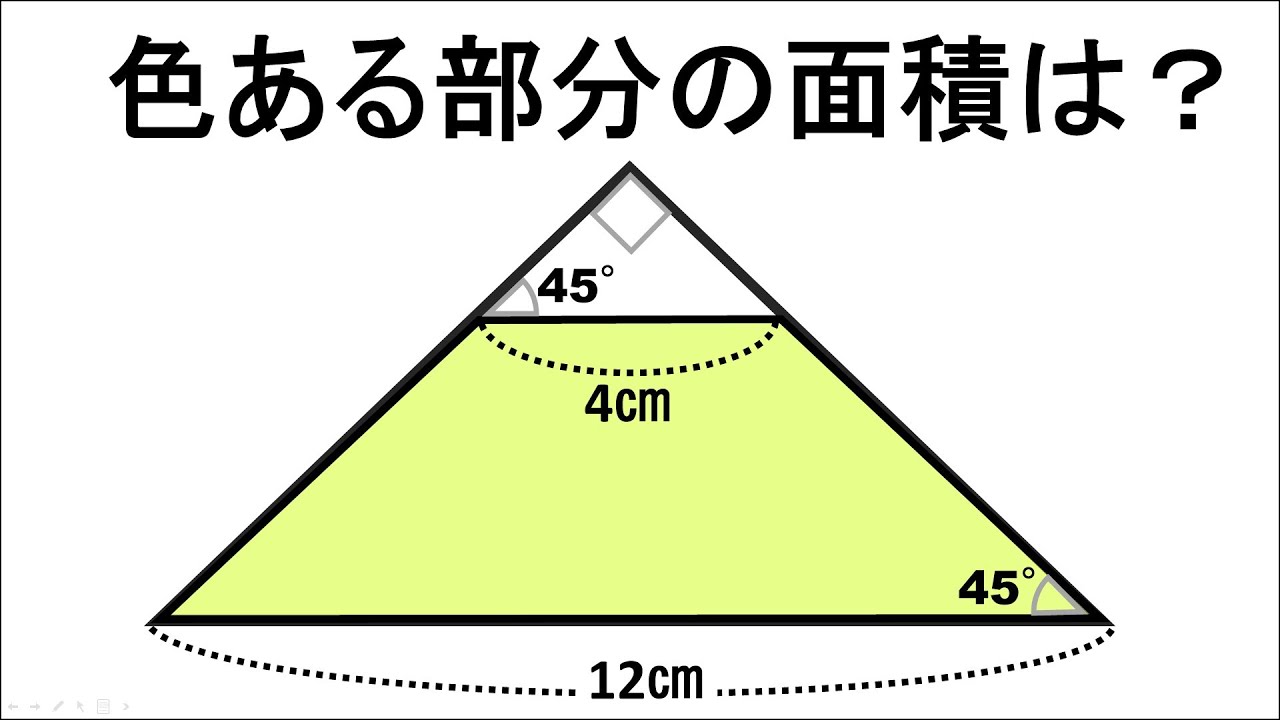
単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
問題文
図は、大きい三角形の中に小さい三角形が存在している
※図は動画内参照
色のある部分の面積は?
この動画を見る
問題文
図は、大きい三角形の中に小さい三角形が存在している
※図は動画内参照
色のある部分の面積は?
【中学受験問題に挑戦】138(”大人”は頭の体操) 三角形の考察
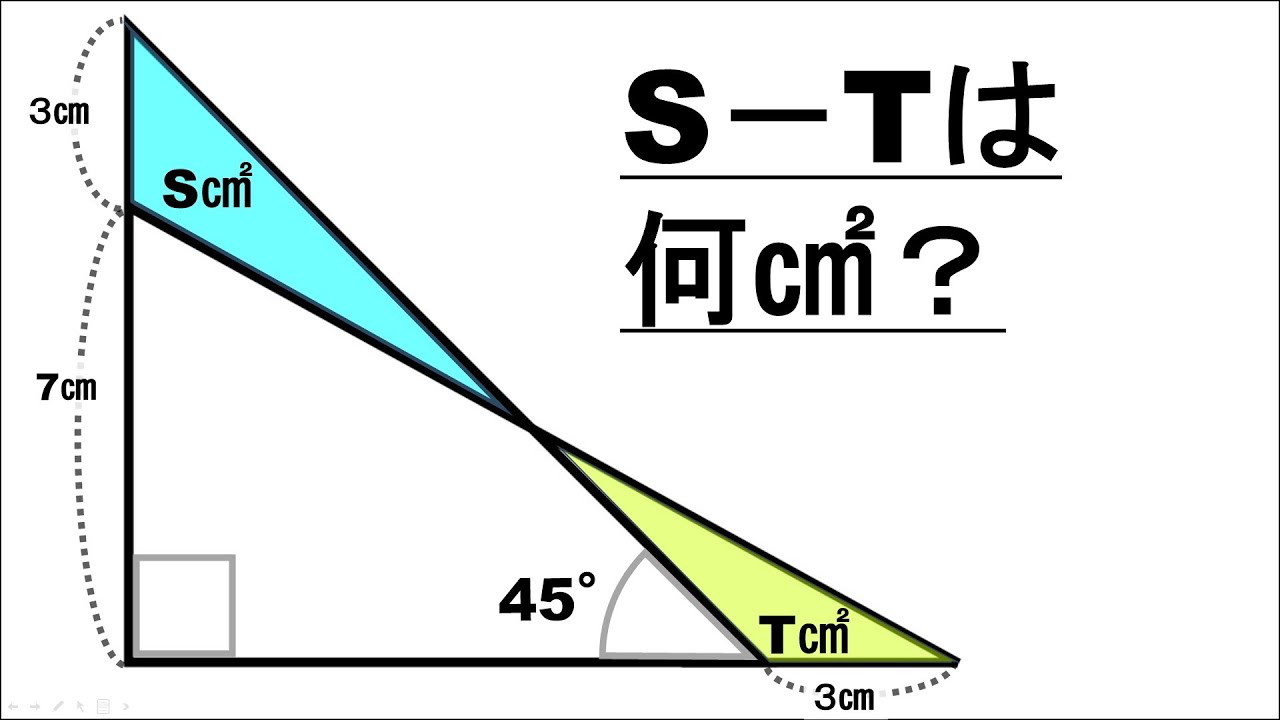
【算数練習】143(”大人”は頭の体操)
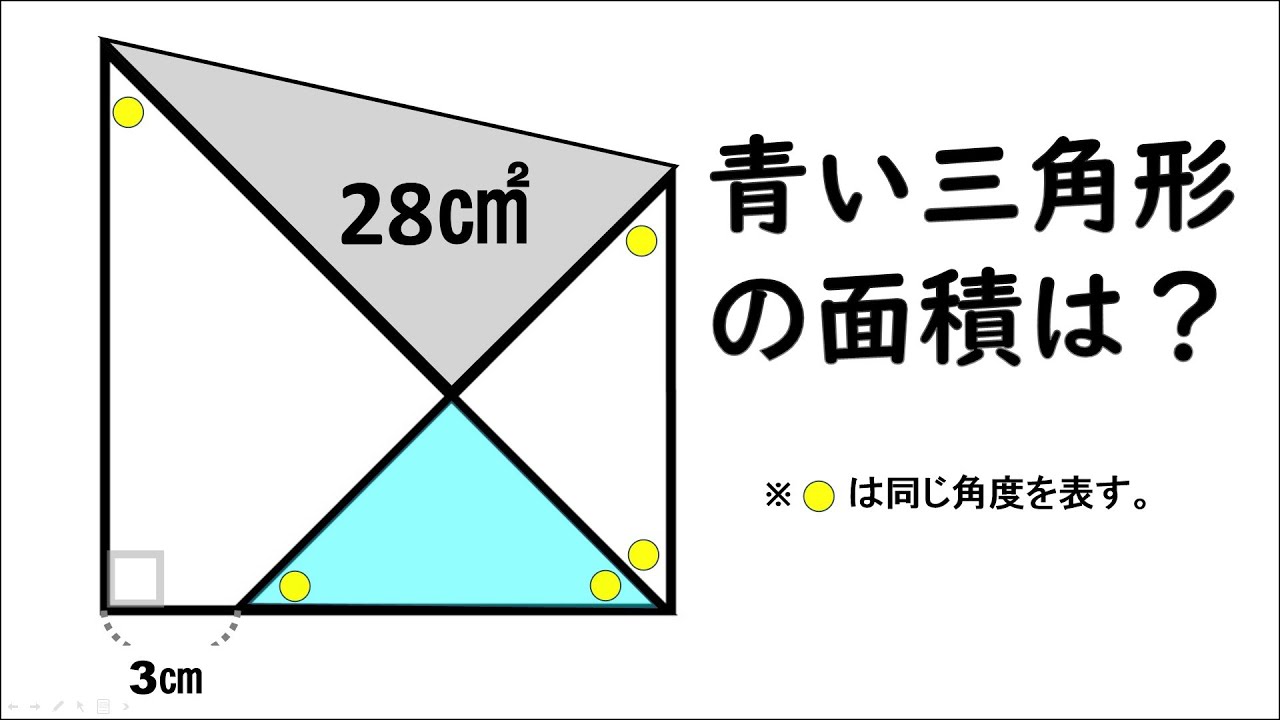
【算数練習】137(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
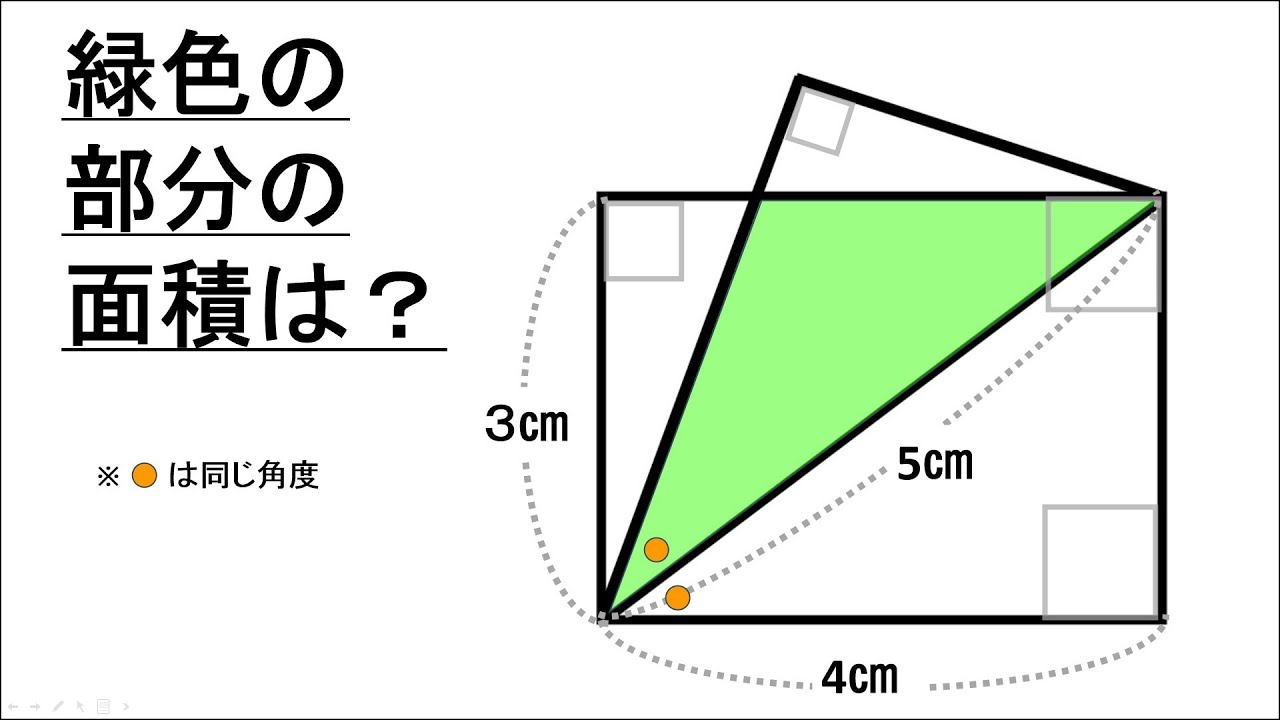
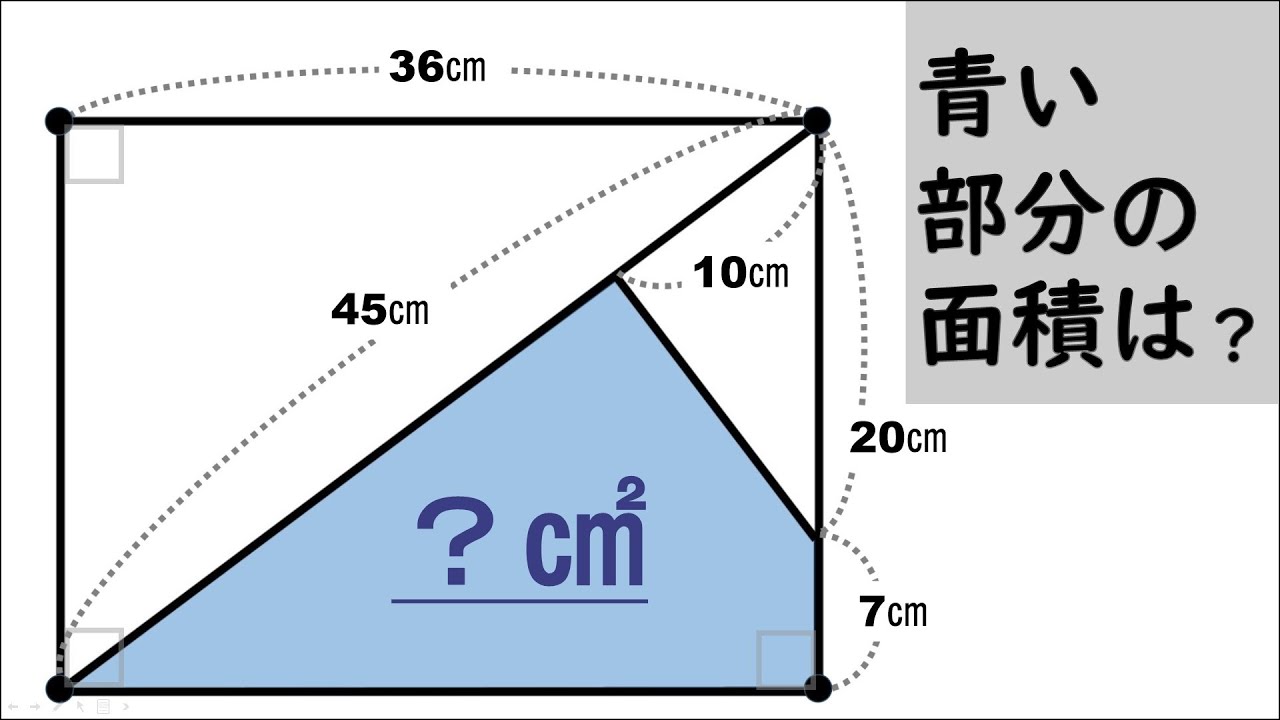
図は長方形の中に三角形が入っている。
*図は動画内参照
緑色の部分の面積は?
この動画を見る
図は長方形の中に三角形が入っている。
*図は動画内参照
緑色の部分の面積は?
【受験算数】拡大・縮小:⑧2つの台形の面積比
単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
受験算数の森
問題文全文(内容文):
大問1
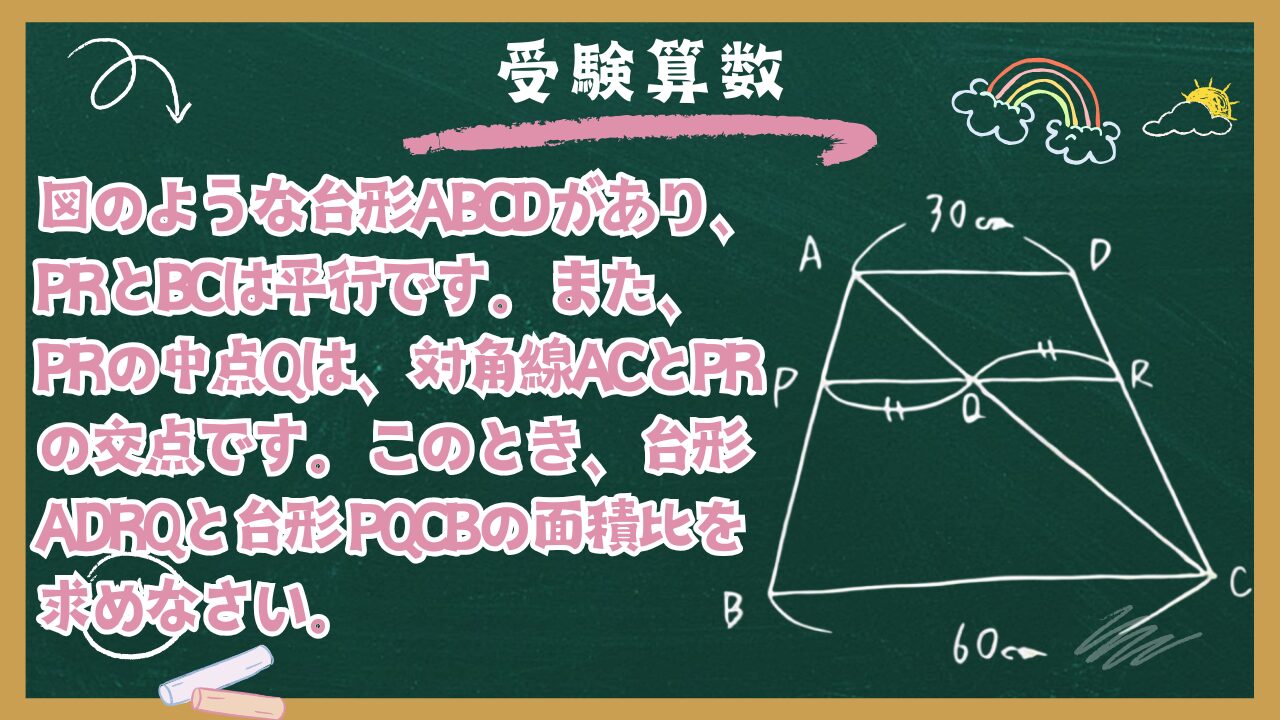
図のような台形ABCDがあり、PRとBCは平行です。また、PRの中点Qは、対角線ACとPRの交点です。このとき、台形ADRQと台形 PQCBの面積比を求めなさい。
大問2
図のような台形ABCDがあり、PRとBCは平行です。また、PRの中点Qは、対角線ACとPRの交点です。このとき、台形ADRQと台形 PQCBの面積比を求めなさい。
この動画を見る
大問1
図のような台形ABCDがあり、PRとBCは平行です。また、PRの中点Qは、対角線ACとPRの交点です。このとき、台形ADRQと台形 PQCBの面積比を求めなさい。
大問2
図のような台形ABCDがあり、PRとBCは平行です。また、PRの中点Qは、対角線ACとPRの交点です。このとき、台形ADRQと台形 PQCBの面積比を求めなさい。
【受験算数】拡大・縮小:⑧正方形で作る図形
単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
受験算数の森
問題文全文(内容文):
大問1
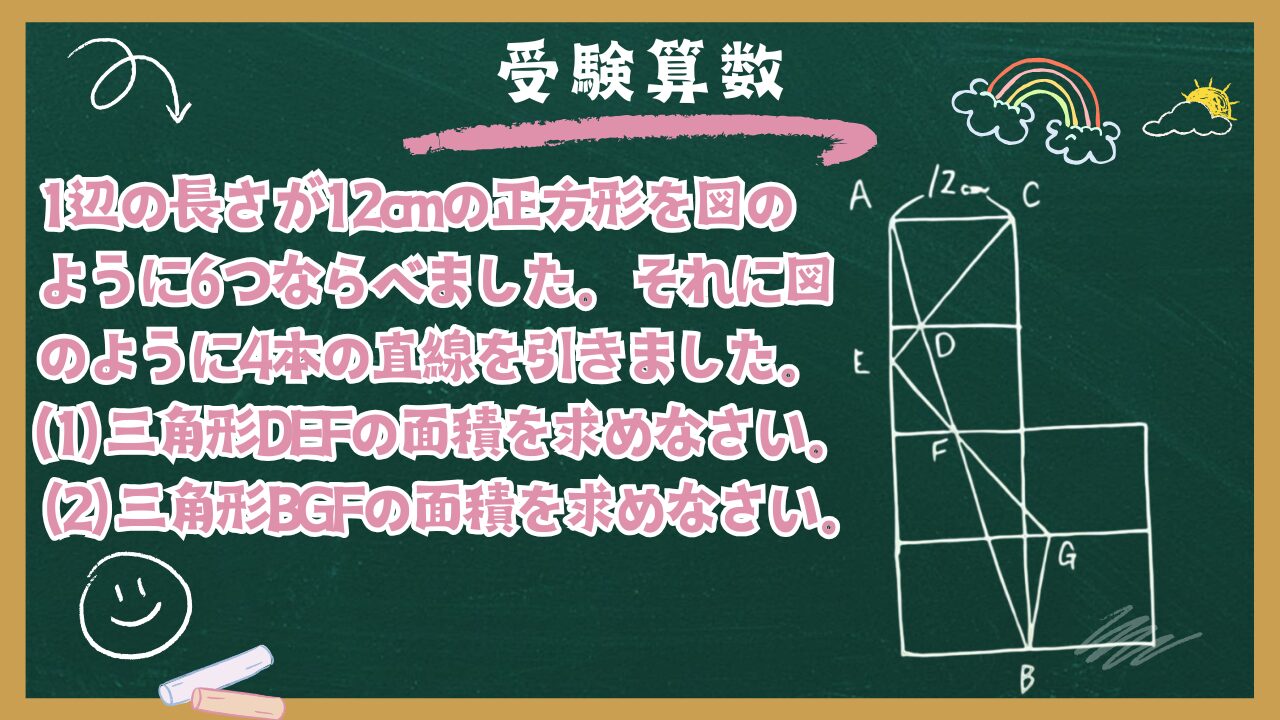
1辺の長さが12cmの正方形を図のように6つならべました。それに図のように4本の直線を引きました。このとき次の問いに答えなさい。
(1) 三角形DEFの面積を求めなさい。
(2) 三角形BGFの面積を求めなさい。
大問2
1辺の長さが12cmの正方形を図のように6つならべました。それに図のように5本の直線を引きました。このとき次の問いに答えなさい。
(1) 三角形DEFの面積を求めなさい。
(2) 三角形BGFの面積を求めなさい。
この動画を見る
大問1
1辺の長さが12cmの正方形を図のように6つならべました。それに図のように4本の直線を引きました。このとき次の問いに答えなさい。
(1) 三角形DEFの面積を求めなさい。
(2) 三角形BGFの面積を求めなさい。
大問2
1辺の長さが12cmの正方形を図のように6つならべました。それに図のように5本の直線を引きました。このとき次の問いに答えなさい。
(1) 三角形DEFの面積を求めなさい。
(2) 三角形BGFの面積を求めなさい。
【受験算数】拡大・縮小:⑦平行線と相似4
単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
受験算数の森
問題文全文(内容文):
大問1
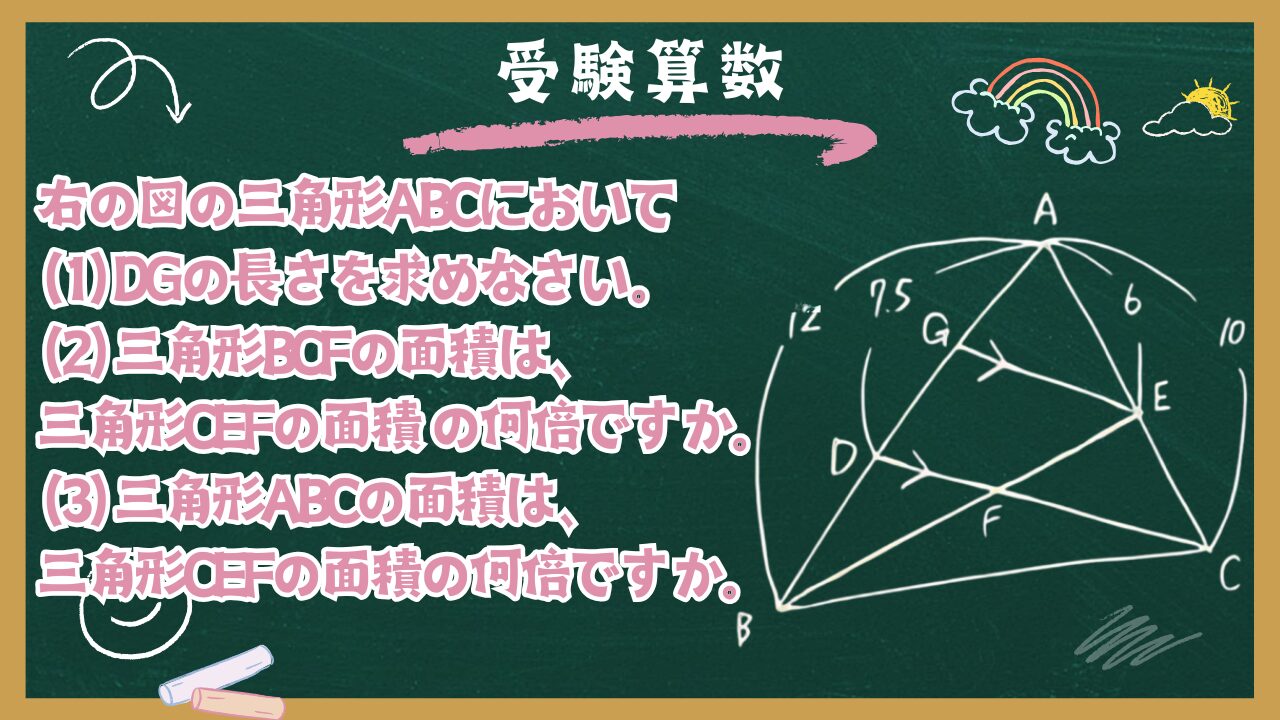
右の図の三角形ABCにおいて、AB=12cm, AC=10cmです。AB、AC上に点D、Eをそれぞれ AD=7.5cm、AE=6cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、 BEとCDの交点をFとします。次の問いに答えなさい。
(1) DGの長さを求めなさい。
(2) 三角形BCFの面積は、三角形CEFの面積 の何倍ですか。
(3) 三角形ABCの面積は、三角形CEFの面積の何倍ですか。
大問2
右の図の三角形ABCにおいて、AB=10cm, AC=8です。AB、AC上に点D、Eをそれぞれ AD=6.4cm、 AE=5cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、 BEとCDの交点をFとします。次の問いに答えなさい。
(1) DGの長さを求めなさい。
(2) 三角形BCFの面積は、三角形CEFの面積 の何倍ですか。
(3) 三角形ABCの面積は、三角形CEFの面積の何倍ですか。
この動画を見る
大問1
右の図の三角形ABCにおいて、AB=12cm, AC=10cmです。AB、AC上に点D、Eをそれぞれ AD=7.5cm、AE=6cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、 BEとCDの交点をFとします。次の問いに答えなさい。
(1) DGの長さを求めなさい。
(2) 三角形BCFの面積は、三角形CEFの面積 の何倍ですか。
(3) 三角形ABCの面積は、三角形CEFの面積の何倍ですか。
大問2
右の図の三角形ABCにおいて、AB=10cm, AC=8です。AB、AC上に点D、Eをそれぞれ AD=6.4cm、 AE=5cmとなるようにとり、EからCDに平行な線を引き、ABとの交点をGとし、 BEとCDの交点をFとします。次の問いに答えなさい。
(1) DGの長さを求めなさい。
(2) 三角形BCFの面積は、三角形CEFの面積 の何倍ですか。
(3) 三角形ABCの面積は、三角形CEFの面積の何倍ですか。
【受験算数】拡大・縮小:⑦平行線と相似3
単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
受験算数の森
問題文全文(内容文):
大問1
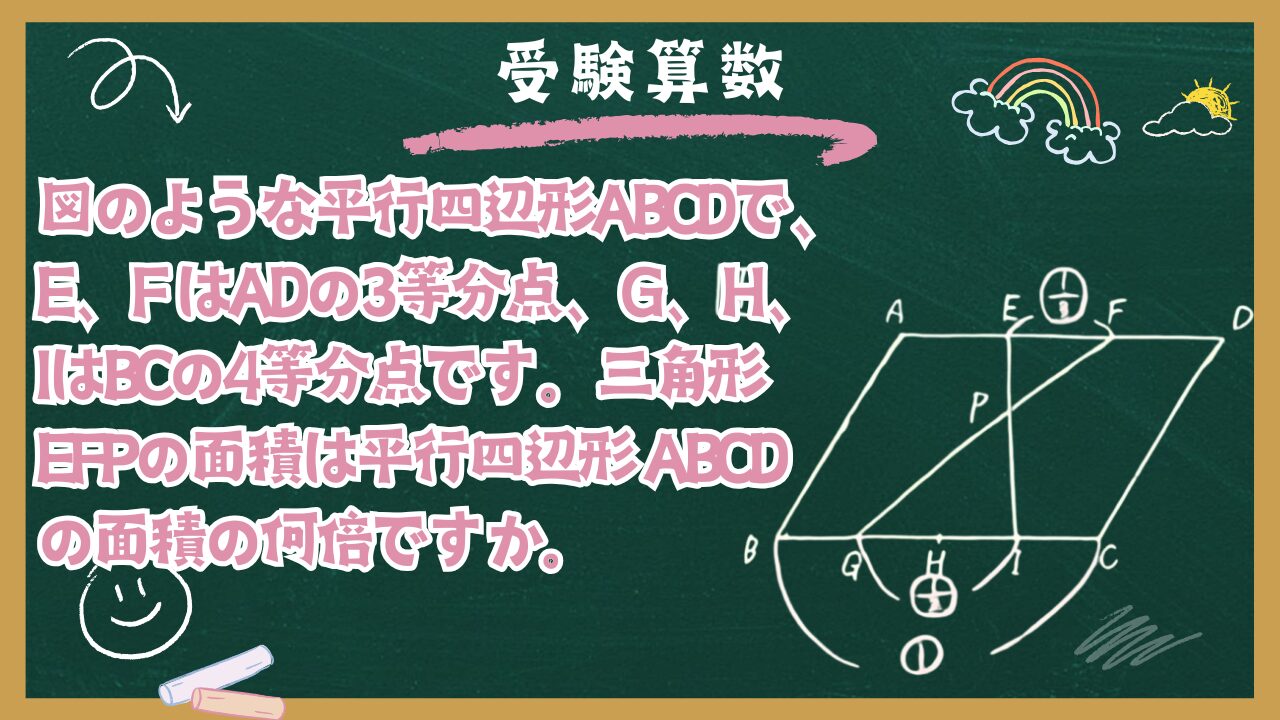
図のような平行四辺形ABCDで、E、F はADの3等分点、G、H、IはBCの4等分点です。三角形EFPの面積は平行四辺形 ABCDの面積の何倍ですか。
大問2
図のような平行四辺形ABCDで、E、F、GはADの4等分点、H、I、J、KはBCの5等分点です。三角形PEGの面積は平行四辺形ABCDの面積の何倍ですか。
この動画を見る
大問1
図のような平行四辺形ABCDで、E、F はADの3等分点、G、H、IはBCの4等分点です。三角形EFPの面積は平行四辺形 ABCDの面積の何倍ですか。
大問2
図のような平行四辺形ABCDで、E、F、GはADの4等分点、H、I、J、KはBCの5等分点です。三角形PEGの面積は平行四辺形ABCDの面積の何倍ですか。
【中学受験問題に挑戦】132(”大人”は頭の体操) 三角形と四角形の考察
算数練習125
単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
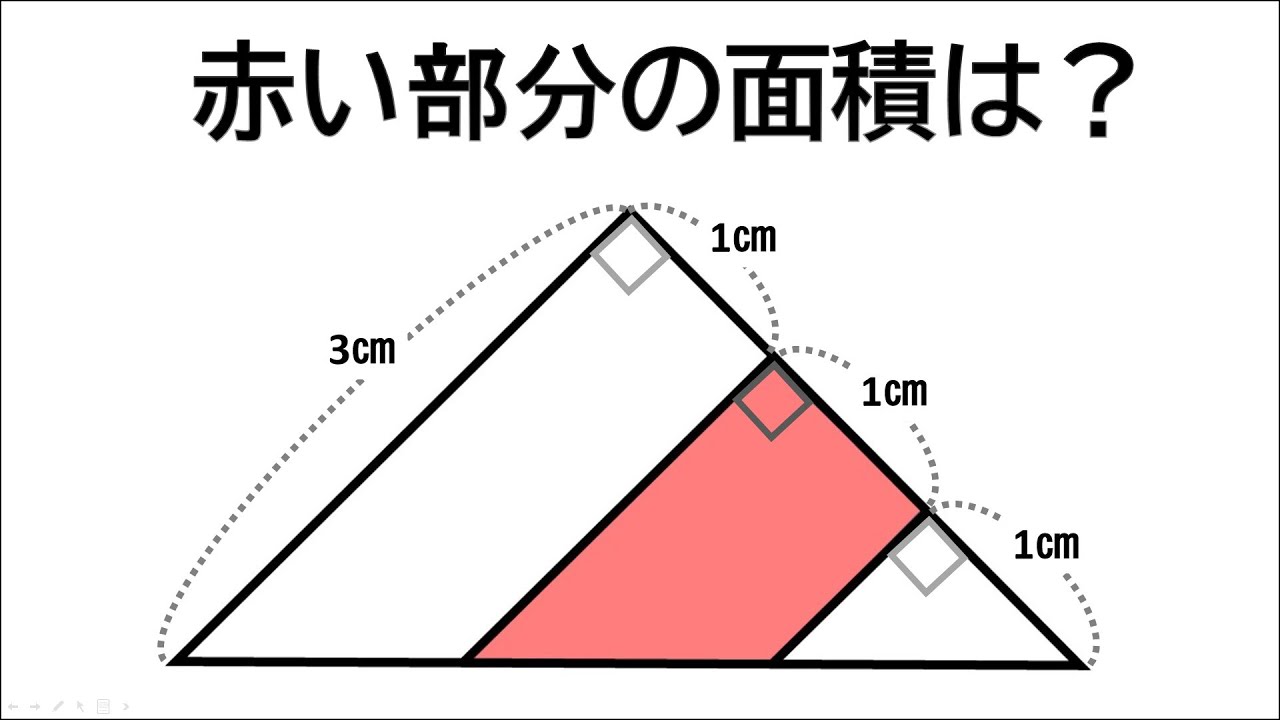
一辺3㎝の直角三角形がある。
赤い部分の面積は?
※図は動画内参照
この動画を見る
一辺3㎝の直角三角形がある。
赤い部分の面積は?
※図は動画内参照
【算数練習】124(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
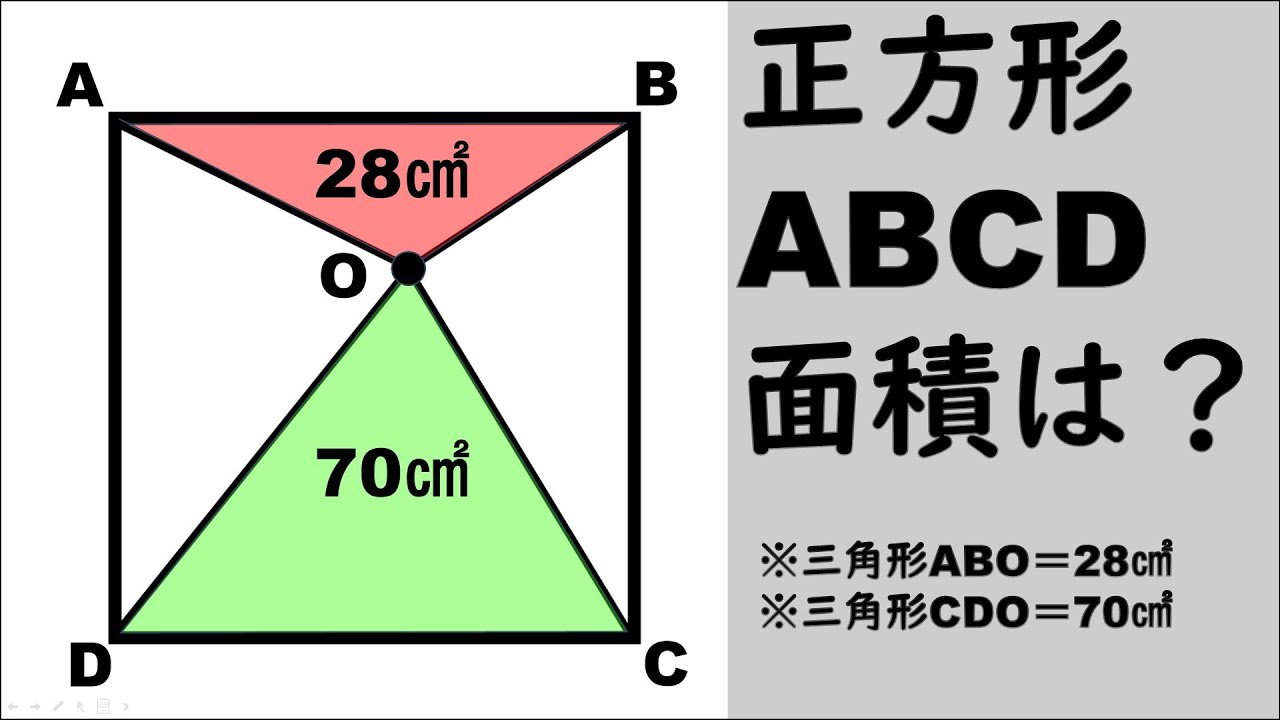
正方形ABCDの面積は?
※三角形ABO=28㎝
※三角形CDO=70㎝
※図は動画内参照
この動画を見る
正方形ABCDの面積は?
※三角形ABO=28㎝
※三角形CDO=70㎝
※図は動画内参照
2024年豊島岡女子学園中算数大問②(1)~(4)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#仕事算とニュートン算#平均算・過不足算・差集め算・消去算#平面図形#角度と面積#相似と相似を利用した問題#場合の数#場合の数#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
(1)
ある水槽には管A、管B、管Cの三つの水を入れる管がついています。空の状態から、管Aのみを20分間用いると水槽がいっぱいになり、管Aを5分間、管Bと管Cを18分間用いると水槽がいっぱいになります。また、管Aを8分間、管Bを17分間、管Cを12分間用いると水槽がいっぱいになります。管Bからは毎分1Lの水が出るとき、水槽の容積は何Lですか。
(2)
バスケットボールの試合では、シュートの種類によって1点、2点、3点の得点を取ることができます。豊子さんはある試合で10点を取りました。シュートの種類の組み合わせは全部で何通りありますか。ただし、得点の順番は考えないものとします。
(3)
正三角形ABCDEFGHIJがあります。図のように点Bを中心とし、点Dを通る円の弧DJと点Jを中心とし、点Bを通る円の弧BHの交わる点をKとします。このとき、角CDKの大きさは何度ですか。
※図は動画内参照
(4)
図のようにAB = AC = 3 cm, BC = 2cm の二等辺三角形ABCとDE = DF = 3 cm, EF = 2 cm の二等辺三角形DEFがあります。点Eは辺BCの真ん中の点であり、点Gは辺EFの真ん中のt点で、辺AC上にあります。辺ABと辺DFの交わる点をHとするとき、DHの長さは何cmですか。
※図は動画内参照
この動画を見る
(1)
ある水槽には管A、管B、管Cの三つの水を入れる管がついています。空の状態から、管Aのみを20分間用いると水槽がいっぱいになり、管Aを5分間、管Bと管Cを18分間用いると水槽がいっぱいになります。また、管Aを8分間、管Bを17分間、管Cを12分間用いると水槽がいっぱいになります。管Bからは毎分1Lの水が出るとき、水槽の容積は何Lですか。
(2)
バスケットボールの試合では、シュートの種類によって1点、2点、3点の得点を取ることができます。豊子さんはある試合で10点を取りました。シュートの種類の組み合わせは全部で何通りありますか。ただし、得点の順番は考えないものとします。
(3)
正三角形ABCDEFGHIJがあります。図のように点Bを中心とし、点Dを通る円の弧DJと点Jを中心とし、点Bを通る円の弧BHの交わる点をKとします。このとき、角CDKの大きさは何度ですか。
※図は動画内参照
(4)
図のようにAB = AC = 3 cm, BC = 2cm の二等辺三角形ABCとDE = DF = 3 cm, EF = 2 cm の二等辺三角形DEFがあります。点Eは辺BCの真ん中の点であり、点Gは辺EFの真ん中のt点で、辺AC上にあります。辺ABと辺DFの交わる点をHとするとき、DHの長さは何cmですか。
※図は動画内参照
2024年芝中学校算数大問①~③中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#文章題#単位・比と割合・比例・反比例#平均算・過不足算・差集め算・消去算#平面図形#角度と面積#相似と相似を利用した問題#芝中学
指導講師:
重吉
問題文全文(内容文):
1
次の計算をしなさい。
(1)
5.3 × 1.25 + 96 × 0,125 + 125 × 0.152 + 0.83 × 12.5 = □
(2)
{2×4/5×2 - 1.75×(1.85-□)÷1/3}÷(1×1/3-3/4)=6
2
今年のS中学校の学園祭に小学五年生と小学六年生合わせて4200人が参加しました。この参加人数は昨年より12 % 増え、小学五年生は昨年より16 %増えて、小学六年生は昨年より8 %減りました。
(1)
昨年の学園祭に参加した小学五年生は□人です。
(2)
今年の学園祭に参加した小学六年生は□人です。
(3)
毎年、学園祭では焼きそばとカレーライスを販売しています。今年の学園祭に参加した小学六年生全員にアンケートを取ったところ、焼きそばを買った人は210 人、カレーライスを買った人は180人、焼きそばもカレーライスも買わなかった人は200人でした。焼きそばとカレーライスのい両方を買った人は□人です。
※図は動画内参照
3
四角形ABCDはAB =6 cm, AD = 8 cmの長方形で、点E, F, Gは辺BCを四等分する点、点H, Iは辺CDを三等分する点とします。また、BDとAE, AIとの交わる点をそれぞれJ,Kとします。
(1)
BJ : KD を最も簡単な整数の比で表すと□:□です。
(2)
三角形AJKの面積は□㎠です。
この動画を見る
1
次の計算をしなさい。
(1)
5.3 × 1.25 + 96 × 0,125 + 125 × 0.152 + 0.83 × 12.5 = □
(2)
{2×4/5×2 - 1.75×(1.85-□)÷1/3}÷(1×1/3-3/4)=6
2
今年のS中学校の学園祭に小学五年生と小学六年生合わせて4200人が参加しました。この参加人数は昨年より12 % 増え、小学五年生は昨年より16 %増えて、小学六年生は昨年より8 %減りました。
(1)
昨年の学園祭に参加した小学五年生は□人です。
(2)
今年の学園祭に参加した小学六年生は□人です。
(3)
毎年、学園祭では焼きそばとカレーライスを販売しています。今年の学園祭に参加した小学六年生全員にアンケートを取ったところ、焼きそばを買った人は210 人、カレーライスを買った人は180人、焼きそばもカレーライスも買わなかった人は200人でした。焼きそばとカレーライスのい両方を買った人は□人です。
※図は動画内参照
3
四角形ABCDはAB =6 cm, AD = 8 cmの長方形で、点E, F, Gは辺BCを四等分する点、点H, Iは辺CDを三等分する点とします。また、BDとAE, AIとの交わる点をそれぞれJ,Kとします。
(1)
BJ : KD を最も簡単な整数の比で表すと□:□です。
(2)
三角形AJKの面積は□㎠です。
2024年洗足学園中算数大問①②中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平面図形#相似と相似を利用した問題#場合の数#場合の数#洗足学園中学
指導講師:
重吉
問題文全文(内容文):
(1) 次の計算をしなさい。
(23-0.5) × (2.8+3×5+1) + 3.14
(2) ▭にあてはまる数を答えなさい。
0.84 x (0.75-1 28 + ▭×9+14+(1.02-) = 76
2
次の問いに答えなさい。
(1) Aさんが買い物をしました。最初の店では所持金の今より200円多く使い。 2番目の店では残った所持金の方よりも400円多く使いました。3番目の店で残った所持金の一よりも600円多く使ったところ、所持金をすべて使いきりました。Aさんは、はじめに何円持っていましたか。
(2) 1. 2. 3. 4.5.6.7が1つずつ書いてある7枚のカードから4枚を選び、2枚ずつ並べて2桁の奇数を2つ作ります。大きい方の数が小さい方の数の倍数になるとき、考えることができる奇数の組をすべて求めなさい。なお、答えは(13.25) のように書きなさい。
(3) 高さが同じで底面積が異なる直方体の形をした2つの容器A.Bがあります。 この2つの容器に空の状態から毎分1Lの割合で同時に水を入れ、容器Aの高さの半分まで水を入れたところで、容器Aについている毎分200mLの水を排出する排水口を開けました。その後、容器AとBが同時に満水になりました。 このとき、容器AとBの底面積の比をもっとも簡単な整数で答えなさい。
(4)四角形ABCDは長方形です。 直線BEと直線FDが平行のとき、 三角形ABGと三角形FDHの面積の比をもっとも簡単な整数で答えなさい。 (図は動画内参照)
この動画を見る
(1) 次の計算をしなさい。
(23-0.5) × (2.8+3×5+1) + 3.14
(2) ▭にあてはまる数を答えなさい。
0.84 x (0.75-1 28 + ▭×9+14+(1.02-) = 76
2
次の問いに答えなさい。
(1) Aさんが買い物をしました。最初の店では所持金の今より200円多く使い。 2番目の店では残った所持金の方よりも400円多く使いました。3番目の店で残った所持金の一よりも600円多く使ったところ、所持金をすべて使いきりました。Aさんは、はじめに何円持っていましたか。
(2) 1. 2. 3. 4.5.6.7が1つずつ書いてある7枚のカードから4枚を選び、2枚ずつ並べて2桁の奇数を2つ作ります。大きい方の数が小さい方の数の倍数になるとき、考えることができる奇数の組をすべて求めなさい。なお、答えは(13.25) のように書きなさい。
(3) 高さが同じで底面積が異なる直方体の形をした2つの容器A.Bがあります。 この2つの容器に空の状態から毎分1Lの割合で同時に水を入れ、容器Aの高さの半分まで水を入れたところで、容器Aについている毎分200mLの水を排出する排水口を開けました。その後、容器AとBが同時に満水になりました。 このとき、容器AとBの底面積の比をもっとも簡単な整数で答えなさい。
(4)四角形ABCDは長方形です。 直線BEと直線FDが平行のとき、 三角形ABGと三角形FDHの面積の比をもっとも簡単な整数で答えなさい。 (図は動画内参照)
【算数練習】115(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
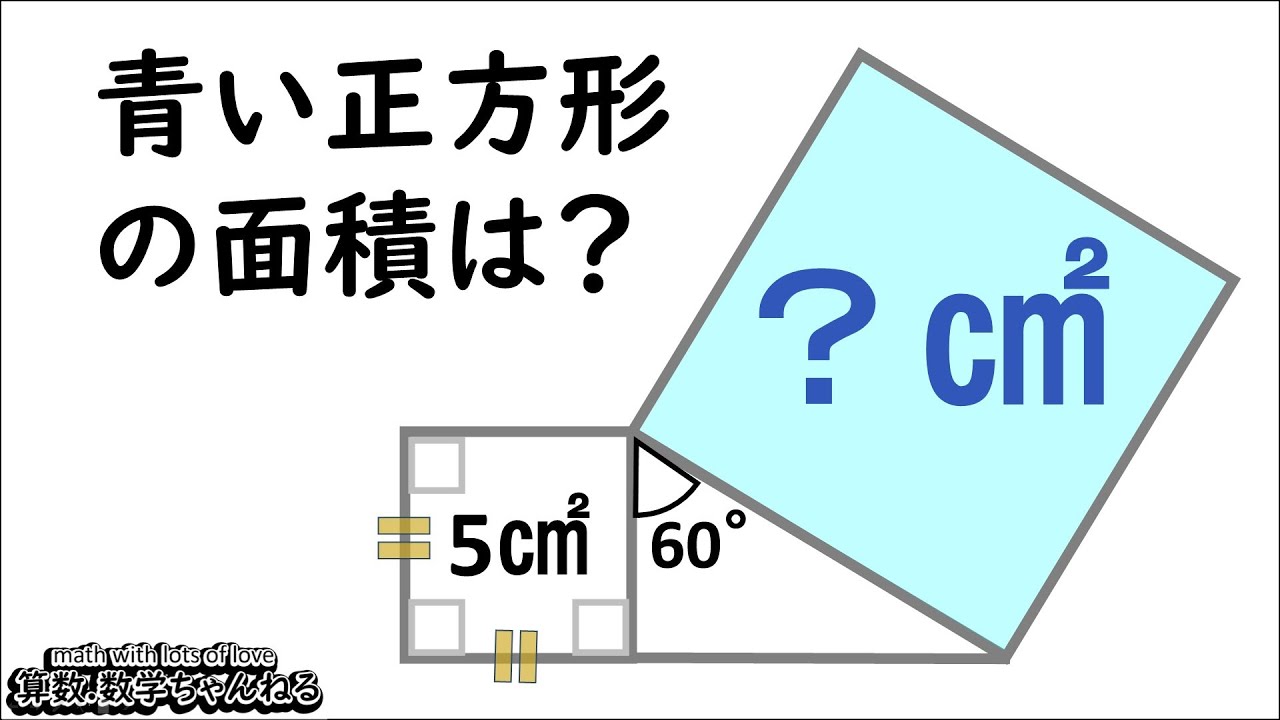
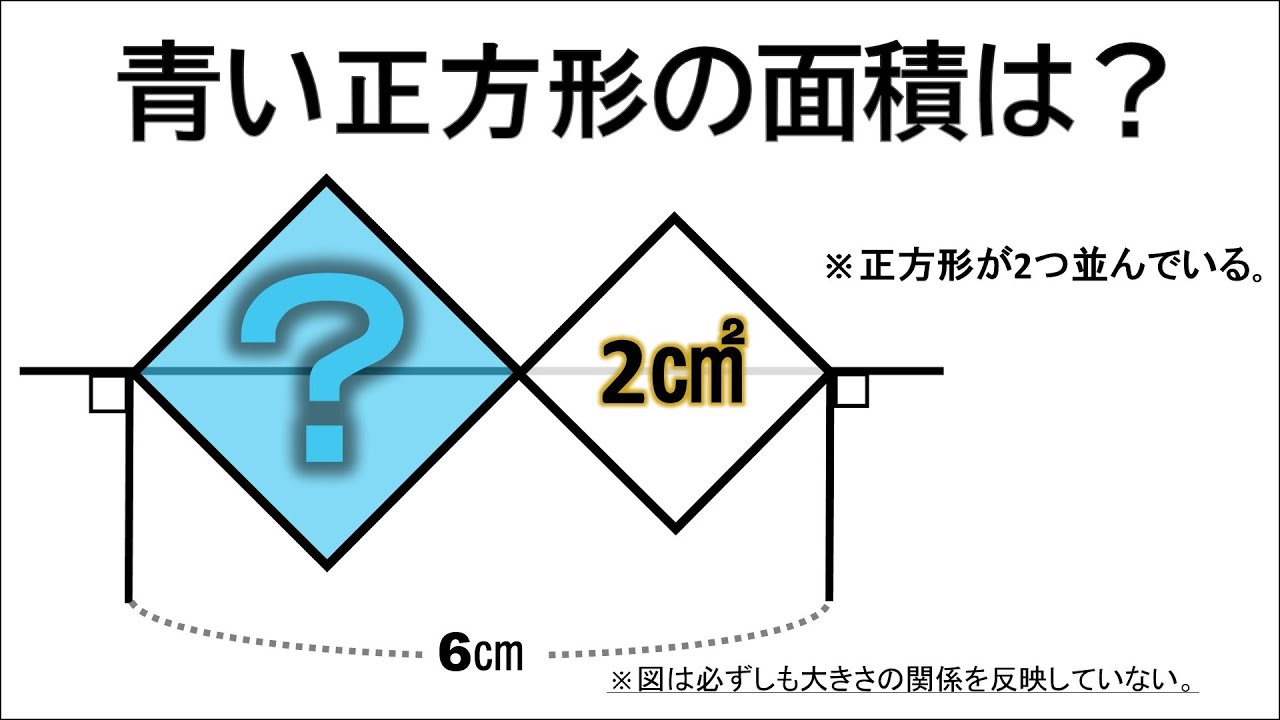
正方形が2つ並んでいる。
*図は動画内参照
青い正方形の面積は?
この動画を見る
正方形が2つ並んでいる。
*図は動画内参照
青い正方形の面積は?
2024年女子学院中算数大問①(1)~(5)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#平均算・過不足算・差集め算・消去算#平面図形#角度と面積#相似と相似を利用した問題#女子学院中学
指導講師:
重吉
問題文全文(内容文):
1. にあてはまる数を入れなさい。
(1)18.7+ {13.4× (1/20 +▭) -2(1/3)} ÷2(6/11) =20.24
(2)図(動画内参照)のように、円周を10等分する点をとりました。
点0は円の中心、三角形ABCは正三角形です。
角㋐▭度、角㋑▭度、角㋒▭度
(3) 図(動画内参照)のように、長方形の紙を対角線を折り目として折りました。
斜線部の部分の面積は▭cm²です。
(4) 図(動画内参照)のように、棒を使って正三角形と正方形を作ります。
① 100個目の正方形を作り終えたとき、使った棒は▭本です。
② 棒が1000本あるとき、正三角形は▭個,正方形は▭個まで作ることができます。
(5) クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、 消しゴムは9個余りました。 I
クラスの人数は▭人,消しゴムは全部で▭個です。
この動画を見る
1. にあてはまる数を入れなさい。
(1)18.7+ {13.4× (1/20 +▭) -2(1/3)} ÷2(6/11) =20.24
(2)図(動画内参照)のように、円周を10等分する点をとりました。
点0は円の中心、三角形ABCは正三角形です。
角㋐▭度、角㋑▭度、角㋒▭度
(3) 図(動画内参照)のように、長方形の紙を対角線を折り目として折りました。
斜線部の部分の面積は▭cm²です。
(4) 図(動画内参照)のように、棒を使って正三角形と正方形を作ります。
① 100個目の正方形を作り終えたとき、使った棒は▭本です。
② 棒が1000本あるとき、正三角形は▭個,正方形は▭個まで作ることができます。
(5) クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、 消しゴムは9個余りました。 I
クラスの人数は▭人,消しゴムは全部で▭個です。
2024年女子学院中算数大問①(1)~(5)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#平均算・過不足算・差集め算・消去算#平面図形#角度と面積#相似と相似を利用した問題#女子学院中学
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
(1)
$\Box$に当てはまる数を入れなさい。
$18.7+\{ 13.4\times(\dfrac{1}{20}+\Box)-2\dfrac{1}{3} \}\div2\dfrac{6}{11}=20.24$
(2)
図のように、円周を10等分する点を取りました。点Oは円の中心、三角形ABCは正三角形です。
角アは$\Box$度、角イは$\Box$度、角ウは$\Box$度
(3)
図のように、長方形の紙を対角線を折り目としておりました。
斜線部分の面積は$\Box$㎠です。
(4)
図のように、棒を使って正三角形と正方形を作ります。
➀100個目の正方形を作り終えたとき、使った棒は$\Box$本です。
②棒が1000本ある時、正三角形は$\Box$個、正方形は$\Box$個まで作ることができます。
(5)
クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、消しゴムは9個あまりました。
クラスの人数は$\Box$人、消しゴムは全部で$\Box$個です。
この動画を見る
※図は動画内参照
(1)
$\Box$に当てはまる数を入れなさい。
$18.7+\{ 13.4\times(\dfrac{1}{20}+\Box)-2\dfrac{1}{3} \}\div2\dfrac{6}{11}=20.24$
(2)
図のように、円周を10等分する点を取りました。点Oは円の中心、三角形ABCは正三角形です。
角アは$\Box$度、角イは$\Box$度、角ウは$\Box$度
(3)
図のように、長方形の紙を対角線を折り目としておりました。
斜線部分の面積は$\Box$㎠です。
(4)
図のように、棒を使って正三角形と正方形を作ります。
➀100個目の正方形を作り終えたとき、使った棒は$\Box$本です。
②棒が1000本ある時、正三角形は$\Box$個、正方形は$\Box$個まで作ることができます。
(5)
クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、消しゴムは9個あまりました。
クラスの人数は$\Box$人、消しゴムは全部で$\Box$個です。
2024年吉祥女子中算数大問①(5)~(7)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#平面図形#角度と面積#相似と相似を利用した問題#吉祥女子中学
指導講師:
重吉
問題文全文(内容文):
(5)
下の図の4本の直線AE,BF,CG,DHはすべて平行です。
AB:BC:CD=3:2:4, BF:CG=5:6のとき、AE:DHwp最も簡単な整数の比で答えなさい。
※図は動画内参照図
(6)
整数Aがあり、283をAで割った余りは、356をAで割った余りよりも4だけ小さく、463をAで割った余りより4だけ大きいです。整数Aを答えなさい。
(7)
下の図の三角形ABCと三角形ADEは正三角形です。正三角形ABCの一辺の長さは12 cmで、BDの長さは4 cmです。三角形ADFの面積は正三角形ABCの面積の何倍ですか。
※図は動画内参照図
この動画を見る
(5)
下の図の4本の直線AE,BF,CG,DHはすべて平行です。
AB:BC:CD=3:2:4, BF:CG=5:6のとき、AE:DHwp最も簡単な整数の比で答えなさい。
※図は動画内参照図
(6)
整数Aがあり、283をAで割った余りは、356をAで割った余りよりも4だけ小さく、463をAで割った余りより4だけ大きいです。整数Aを答えなさい。
(7)
下の図の三角形ABCと三角形ADEは正三角形です。正三角形ABCの一辺の長さは12 cmで、BDの長さは4 cmです。三角形ADFの面積は正三角形ABCの面積の何倍ですか。
※図は動画内参照図
2024年吉祥女子中算数大問①(5)~(7)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#平面図形#角度と面積#相似と相似を利用した問題#吉祥女子中学
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
(5)
下の図の四本の直線AE,BF,CG,DHはすべて平行です。AB:BC:CD = 3:2:4, BF:CG = 5:6 のとき、AE:DH = を最も簡単な整数の比で答えなさい。
(6)
整数Aがあり、283をAで割った余りは、356をAで割った余りよりも4だけ小さく、463をAで割った余りよりも4だけ大きいです。整数Aを答えなさい。
(7)
下の図の三角形ABCと三角形ADEは正三角形です。正三角形ABCの一辺の長さは12 cmで、BDの長さは4 cmです。三角形ADFの面積は正三角形の面積の何倍ですか。
この動画を見る
※図は動画内参照
(5)
下の図の四本の直線AE,BF,CG,DHはすべて平行です。AB:BC:CD = 3:2:4, BF:CG = 5:6 のとき、AE:DH = を最も簡単な整数の比で答えなさい。
(6)
整数Aがあり、283をAで割った余りは、356をAで割った余りよりも4だけ小さく、463をAで割った余りよりも4だけ大きいです。整数Aを答えなさい。
(7)
下の図の三角形ABCと三角形ADEは正三角形です。正三角形ABCの一辺の長さは12 cmで、BDの長さは4 cmです。三角形ADFの面積は正三角形の面積の何倍ですか。
2024年渋谷教育学園渋谷中算数大問①(4)~(6)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#売買損益と食塩水#平面図形#角度と面積#相似と相似を利用した問題#立体図形#体積・表面積・回転体・水量・変化のグラフ#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
(4)
下の図は二つの直角三角形からできています。影のついた部分を直線Lを軸として一回転させてできる立体の体積は何㎠ですか。
(5)
下の図は、円と正六角形と正十角形からできています。点Oは円の中心です。このとき、アの角の大きさは何度ですか。
(6)
容器Aには3 %の食塩水が600 g、容器Bには5 %の食塩水が300 g、容器Cには4 %の食塩水が入っています。A,B,Cから重さの比が1:2:2となるように食塩水を取り出し、空の容器Dに入れてよく混ぜ合わせました。Dの食塩水を3等分してA,B,Cにそれぞれ戻すと、Aの食塩水に溶けている食塩が22 gになりました。このときBの食塩水の濃さは何%になりますか。
この動画を見る
※図は動画内参照
(4)
下の図は二つの直角三角形からできています。影のついた部分を直線Lを軸として一回転させてできる立体の体積は何㎠ですか。
(5)
下の図は、円と正六角形と正十角形からできています。点Oは円の中心です。このとき、アの角の大きさは何度ですか。
(6)
容器Aには3 %の食塩水が600 g、容器Bには5 %の食塩水が300 g、容器Cには4 %の食塩水が入っています。A,B,Cから重さの比が1:2:2となるように食塩水を取り出し、空の容器Dに入れてよく混ぜ合わせました。Dの食塩水を3等分してA,B,Cにそれぞれ戻すと、Aの食塩水に溶けている食塩が22 gになりました。このときBの食塩水の濃さは何%になりますか。
2024年栄東中(A)算数大問①(5)~(8)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#仕事算とニュートン算#平面図形#角度と面積#相似と相似を利用した問題#立体図形#体積・表面積・回転体・水量・変化のグラフ#栄東中学
指導講師:
重吉
問題文全文(内容文):
(5) ある仕事をするのに、赤いロボット1体では24時間かかります。また、紫のロボットは赤いロボットの10倍の仕事ができます。合わせて18台のロボットがこの仕事をしたところ、20分でおわりました。このとき、赤いロボットは▭体でした。
(6) 右の図のように三角形をABCの辺AC上に点Dがあり、ABとADの長さは等しく、イの角度はアの角度の2倍で、ウの角度はアの角度の6倍です。このとき、エの角度は▭度です。
※図は動画内参照
(7) 右の図のように直角三角形ABCの紙をADを折り目として折り返したところ、点BがAC上の点Eに重なりました。このとき、三角形ABCの面積は▭㎠です。
※図は動画内参照
(8) 右の図のようにAB = BC = 3 cmの直角二等辺三角形二等辺三角形ABCを直線DEを軸に一回転させたときにできる立体の体積は▭㎤です。ただし、円周率は3.14とします。必要であれば、円錐の体積は「(底面積)×(高さ)÷3」で求められることを使っても構いません。
この動画を見る
(5) ある仕事をするのに、赤いロボット1体では24時間かかります。また、紫のロボットは赤いロボットの10倍の仕事ができます。合わせて18台のロボットがこの仕事をしたところ、20分でおわりました。このとき、赤いロボットは▭体でした。
(6) 右の図のように三角形をABCの辺AC上に点Dがあり、ABとADの長さは等しく、イの角度はアの角度の2倍で、ウの角度はアの角度の6倍です。このとき、エの角度は▭度です。
※図は動画内参照
(7) 右の図のように直角三角形ABCの紙をADを折り目として折り返したところ、点BがAC上の点Eに重なりました。このとき、三角形ABCの面積は▭㎠です。
※図は動画内参照
(8) 右の図のようにAB = BC = 3 cmの直角二等辺三角形二等辺三角形ABCを直線DEを軸に一回転させたときにできる立体の体積は▭㎤です。ただし、円周率は3.14とします。必要であれば、円錐の体積は「(底面積)×(高さ)÷3」で求められることを使っても構いません。
2024年吉祥女子中算数「相似」中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
指導講師:
重吉
問題文全文(内容文):
下の図の三角形ABCと三角形ADEは正三角形です。正三角形ABCの一辺の長さは12cmで、BDの長さは4cmです。三角形ADFの面積は正三角形ABCの面積の何倍ですか。
(図は動画内参照)
この動画を見る
下の図の三角形ABCと三角形ADEは正三角形です。正三角形ABCの一辺の長さは12cmで、BDの長さは4cmです。三角形ADFの面積は正三角形ABCの面積の何倍ですか。
(図は動画内参照)
2024年吉祥女子中算数「相似」中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#相似と相似を利用した問題#吉祥女子中学
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
$\triangle ADF$は$\triangle ABC$の何倍?
この動画を見る
※図は動画内参照
$\triangle ADF$は$\triangle ABC$の何倍?
中学受験解き方は高校受験の解き方より難しい
中学受験解き方は高校受験の解き方より難しい

単元:
#算数(中学受験)#数学(中学生)#中3数学#三平方の定理#平面図形#角度と面積#相似と相似を利用した問題
指導講師:
数学を数楽に
問題文全文(内容文):
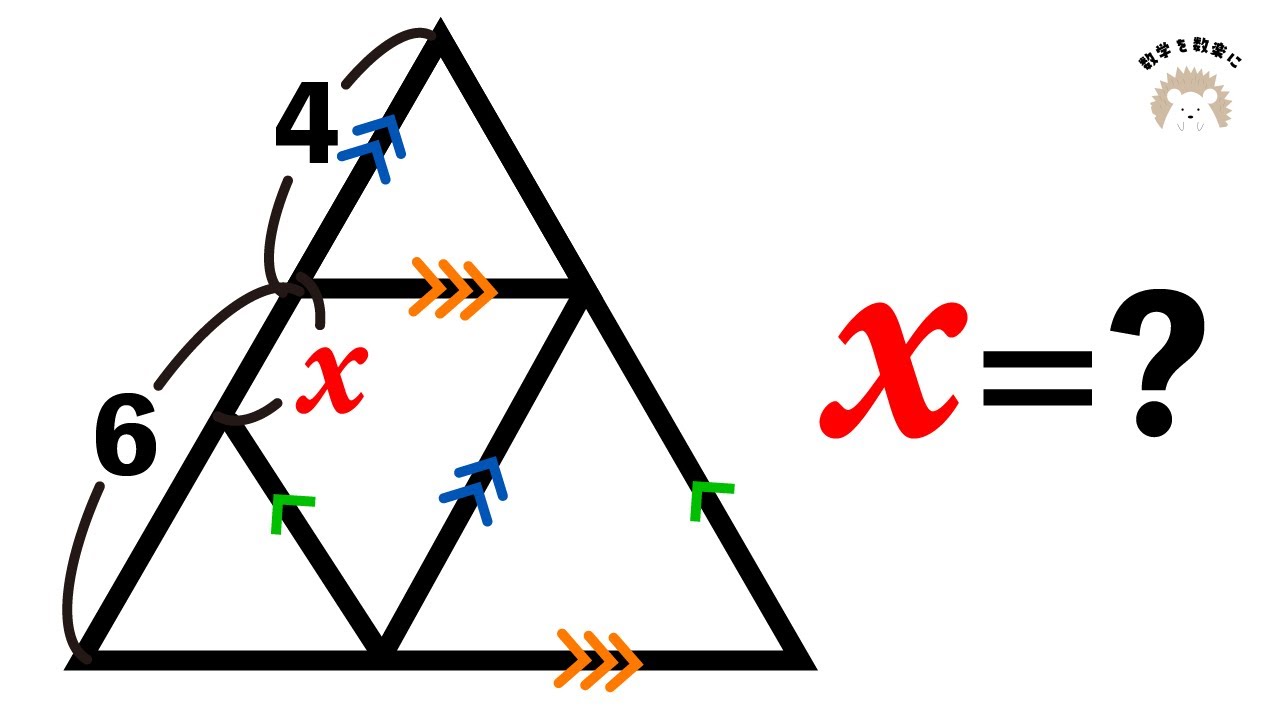
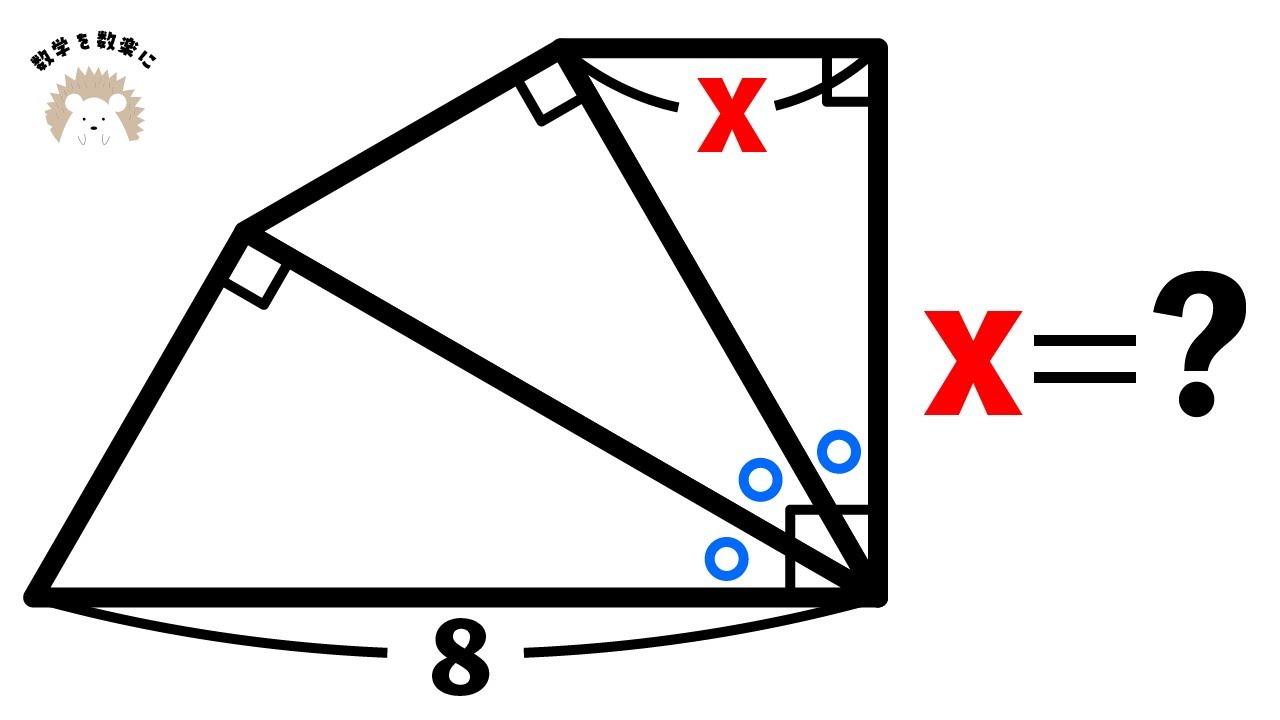
$x=?$
図は動画内を参照
この動画を見る
$x=?$
図は動画内を参照
平行線と比