 立体図形
立体図形
 立体図形
立体図形
2024年広尾学園中算数大問①(1)~(6)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#単位・比と割合・比例・反比例#平面図形#角度と面積#立体図形#立体切断#体積・表面積・回転体・水量・変化のグラフ
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
(1) 次の計算をしなさい。
$253\div8+25.3\times3.25+11\times2.3\times5.5$
(2) $\dfrac{1}{1+\dfrac{1}{\boxed{ ア }+\dfrac{1}{\boxed{ イ }}}}=\dfrac{3}{5}$ となるように、$\boxed{ ア }$、$\boxed{ イ }$に当てはまる整数を求めなさい。
(3) 広尾小学校のある学年で、算数と国語についてそれぞれ「好きか、好きではないか」のどちらかについて調査をしました。調査の結果、算数が好きな児童の数は学年全体の人数の$\dfrac{1}{3}$、国語が好きな児童の数は学年全体の人数の$\dfrac{2}{5}$、算数も国語も好きな児童の数は算数の好きな児童の数の$\dfrac{3}{10}$であり、算数も国語も好きではない児童の数は44人でした。算数も国語も好きな児童の数を求めなさい。
(4) 時計の長針と短針について、4時と5時の間で長針と短針が反対向きに一直線になるときの時刻は4時何分か求めなさい。
(5) 右の図は、正方形の図の中に同じ大きさの四分円を4つ描いた図です。斜線部分の面積を求めなさい。ただし円周率は3.14とします。
(6) 図1のような長方形があり、上、正面、横の面をそれぞれ面ア、面イ、面ウとします。面ア、面イにそれぞれ平行な面でこの直方体を切断すると、できた4つの直方体の表面積の合計は、もとの直方体の表面積よりも1400 ㎠大きくなります(図2)。同様に面イと面ウにそれぞれ平行な面で切断すると、できた4つの直方体の表面積の表面積の合計は、もとの直方体の表面積よりも1000 ㎠大きくなり、面アと面ウにそれぞれ平行な面で切断すると、もとの直方体の表面積よりも1200 ㎠大きくなります。もとの直方体の表面積を求めなさい。
この動画を見る
※図は動画内参照
(1) 次の計算をしなさい。
$253\div8+25.3\times3.25+11\times2.3\times5.5$
(2) $\dfrac{1}{1+\dfrac{1}{\boxed{ ア }+\dfrac{1}{\boxed{ イ }}}}=\dfrac{3}{5}$ となるように、$\boxed{ ア }$、$\boxed{ イ }$に当てはまる整数を求めなさい。
(3) 広尾小学校のある学年で、算数と国語についてそれぞれ「好きか、好きではないか」のどちらかについて調査をしました。調査の結果、算数が好きな児童の数は学年全体の人数の$\dfrac{1}{3}$、国語が好きな児童の数は学年全体の人数の$\dfrac{2}{5}$、算数も国語も好きな児童の数は算数の好きな児童の数の$\dfrac{3}{10}$であり、算数も国語も好きではない児童の数は44人でした。算数も国語も好きな児童の数を求めなさい。
(4) 時計の長針と短針について、4時と5時の間で長針と短針が反対向きに一直線になるときの時刻は4時何分か求めなさい。
(5) 右の図は、正方形の図の中に同じ大きさの四分円を4つ描いた図です。斜線部分の面積を求めなさい。ただし円周率は3.14とします。
(6) 図1のような長方形があり、上、正面、横の面をそれぞれ面ア、面イ、面ウとします。面ア、面イにそれぞれ平行な面でこの直方体を切断すると、できた4つの直方体の表面積の合計は、もとの直方体の表面積よりも1400 ㎠大きくなります(図2)。同様に面イと面ウにそれぞれ平行な面で切断すると、できた4つの直方体の表面積の表面積の合計は、もとの直方体の表面積よりも1000 ㎠大きくなり、面アと面ウにそれぞれ平行な面で切断すると、もとの直方体の表面積よりも1200 ㎠大きくなります。もとの直方体の表面積を求めなさい。
2024年栄東中(A)算数大問①(5)~(8)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#仕事算とニュートン算#平面図形#角度と面積#立体図形#体積・表面積・回転体・水量・変化のグラフ#栄東中学
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
(5)
ある仕事をするのに、赤いロボット一体では24時間かかります。また、紫のロボットは赤い仕事の10倍の仕事ができます。合わせて18台のロボットがこの仕事をしたところ、20分でおわりました。このとき、赤いロボットは□体でした。
(6)
右の図のように、三角形ABCの辺AC上に点Dがあり、ABとADの長さは等しく、イの角度はアの角度の2倍で、ウの角度はアの角度の6倍です。このとき、エの角度は□度です。
(7)
右の図のように、直角三角形ABCの紙をADを折り目として折り返したところ、点BがAC上の点Eに重なりました。このとき、三角形ABCの面積は□㎠です。
(8)
右の図のようにAB=BC=3 cmの直角二等辺三角形ABCを直線DEを軸に一回転させたときにできる立体の体積は▭㎤です。ただし、円周率は3.14とします。必要であれば、円錐の体積は「(底面積)×(高さ)÷3」で求められることを使っても構いません。
この動画を見る
※図は動画内参照
(5)
ある仕事をするのに、赤いロボット一体では24時間かかります。また、紫のロボットは赤い仕事の10倍の仕事ができます。合わせて18台のロボットがこの仕事をしたところ、20分でおわりました。このとき、赤いロボットは□体でした。
(6)
右の図のように、三角形ABCの辺AC上に点Dがあり、ABとADの長さは等しく、イの角度はアの角度の2倍で、ウの角度はアの角度の6倍です。このとき、エの角度は□度です。
(7)
右の図のように、直角三角形ABCの紙をADを折り目として折り返したところ、点BがAC上の点Eに重なりました。このとき、三角形ABCの面積は□㎠です。
(8)
右の図のようにAB=BC=3 cmの直角二等辺三角形ABCを直線DEを軸に一回転させたときにできる立体の体積は▭㎤です。ただし、円周率は3.14とします。必要であれば、円錐の体積は「(底面積)×(高さ)÷3」で求められることを使っても構いません。
重吉の母校!久留米附設中2024年算数大問①(1)~(4)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#過去問解説(学校別)#平面図形#角度と面積#立体図形#体積・表面積・回転体・水量・変化のグラフ#久留米大学附設中学
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
(1)
次の計算の答えを小数で書きなさい。
$5\times\{ 0.3-0.25\times(0.3+0.4\div25) \}+0.03\div5$
(2)
右の図で、同じ記号は同じ大きさの角を表しています。角アの大きさは何度ですか。
(3)
100をある整数で割ると商と余りが等しくなりました。このような整数をすべて答えなさい。
(4)
右の図のように、一辺の長さが1 cmの正方形を4個組み合わせた図形を、直線Lの周りに一回転させてできる立体について、
(ア)この立体の体積は何㎤ですか
(イ)この立体の表面積は何㎠ですか
この動画を見る
※図は動画内参照
(1)
次の計算の答えを小数で書きなさい。
$5\times\{ 0.3-0.25\times(0.3+0.4\div25) \}+0.03\div5$
(2)
右の図で、同じ記号は同じ大きさの角を表しています。角アの大きさは何度ですか。
(3)
100をある整数で割ると商と余りが等しくなりました。このような整数をすべて答えなさい。
(4)
右の図のように、一辺の長さが1 cmの正方形を4個組み合わせた図形を、直線Lの周りに一回転させてできる立体について、
(ア)この立体の体積は何㎤ですか
(イ)この立体の表面積は何㎠ですか
重吉の母校!久留米附設中2024年算数大問①(1)~(4)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他#過去問解説(学校別)#平面図形#角度と面積#立体図形#体積・表面積・回転体・水量・変化のグラフ#久留米大学附設中学
指導講師:
問題文全文(内容文):
(1)次の計算の答えを小数で答えなさい。
$5\times\{ 0.3-0.25\times(0.3+0.4\div25) \}+0.03\div5$
(2) 右の図で、同じ記号は同じ大きさの角を表しています。角アの大きさは何度ですか。
※図は動画内参照
(3) 100をある整数で割ると商と余りが等しくなりました。このような整数をすべて答えなさい。
(4) 右の図のように、一辺の長さが1 cmの正方形を4個組み合わせた図形を直線Lの周りに1回転させてできる立体について
(ア)この立体の体積は何㎤ですか。
(イ)この立体の表面積は何㎠ですか。
※図は動画内参照
この動画を見る
(1)次の計算の答えを小数で答えなさい。
$5\times\{ 0.3-0.25\times(0.3+0.4\div25) \}+0.03\div5$
(2) 右の図で、同じ記号は同じ大きさの角を表しています。角アの大きさは何度ですか。
※図は動画内参照
(3) 100をある整数で割ると商と余りが等しくなりました。このような整数をすべて答えなさい。
(4) 右の図のように、一辺の長さが1 cmの正方形を4個組み合わせた図形を直線Lの周りに1回転させてできる立体について
(ア)この立体の体積は何㎤ですか。
(イ)この立体の表面積は何㎠ですか。
※図は動画内参照
この出し方知ってる?

単元:
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
底面の半径が3、母線の長さが12である円錐の表面積を求めよ
この動画を見る
底面の半径が3、母線の長さが12である円錐の表面積を求めよ
2024年栄東中(A)算数大問①(5)~(8)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#仕事算とニュートン算#平面図形#角度と面積#相似と相似を利用した問題#立体図形#体積・表面積・回転体・水量・変化のグラフ#栄東中学
指導講師:
重吉
問題文全文(内容文):
(5) ある仕事をするのに、赤いロボット1体では24時間かかります。また、紫のロボットは赤いロボットの10倍の仕事ができます。合わせて18台のロボットがこの仕事をしたところ、20分でおわりました。このとき、赤いロボットは▭体でした。
(6) 右の図のように三角形をABCの辺AC上に点Dがあり、ABとADの長さは等しく、イの角度はアの角度の2倍で、ウの角度はアの角度の6倍です。このとき、エの角度は▭度です。
※図は動画内参照
(7) 右の図のように直角三角形ABCの紙をADを折り目として折り返したところ、点BがAC上の点Eに重なりました。このとき、三角形ABCの面積は▭㎠です。
※図は動画内参照
(8) 右の図のようにAB = BC = 3 cmの直角二等辺三角形二等辺三角形ABCを直線DEを軸に一回転させたときにできる立体の体積は▭㎤です。ただし、円周率は3.14とします。必要であれば、円錐の体積は「(底面積)×(高さ)÷3」で求められることを使っても構いません。
この動画を見る
(5) ある仕事をするのに、赤いロボット1体では24時間かかります。また、紫のロボットは赤いロボットの10倍の仕事ができます。合わせて18台のロボットがこの仕事をしたところ、20分でおわりました。このとき、赤いロボットは▭体でした。
(6) 右の図のように三角形をABCの辺AC上に点Dがあり、ABとADの長さは等しく、イの角度はアの角度の2倍で、ウの角度はアの角度の6倍です。このとき、エの角度は▭度です。
※図は動画内参照
(7) 右の図のように直角三角形ABCの紙をADを折り目として折り返したところ、点BがAC上の点Eに重なりました。このとき、三角形ABCの面積は▭㎠です。
※図は動画内参照
(8) 右の図のようにAB = BC = 3 cmの直角二等辺三角形二等辺三角形ABCを直線DEを軸に一回転させたときにできる立体の体積は▭㎤です。ただし、円周率は3.14とします。必要であれば、円錐の体積は「(底面積)×(高さ)÷3」で求められることを使っても構いません。
2024年青山学院中等部算数「底面積と体積の比」中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#単位・比と割合・比例・反比例#仕事算とニュートン算#立体図形#体積・表面積・回転体・水量・変化のグラフ#青山学院中等部
指導講師:
重吉
問題文全文(内容文):
円柱の形をした2つの容器A,Bがあります。
A,Bともに同じ一定の割合で水を入れると、入れ始めてからAは28分で、Bは36分でいっぱいになります。
今、両方の容器をいっぱいにしてから、入れるときと同じ水量で底から同時に水を出したところ12分後に2つの容器の水面の高さは等しくなりました。
AとBの底面の面積の比は$\Box:\Box$で、高さの比は$\Box:\Box$です。
この動画を見る
円柱の形をした2つの容器A,Bがあります。
A,Bともに同じ一定の割合で水を入れると、入れ始めてからAは28分で、Bは36分でいっぱいになります。
今、両方の容器をいっぱいにしてから、入れるときと同じ水量で底から同時に水を出したところ12分後に2つの容器の水面の高さは等しくなりました。
AとBの底面の面積の比は$\Box:\Box$で、高さの比は$\Box:\Box$です。
2024年青山学院中等部算数「底面積と体積の比」中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師:
重吉
問題文全文(内容文):
円柱の形をした2つの容器A、Bがあります。
A、Bともに同じ一定の割合で水を入れると、入れ始めてからAは28分で、Bは36分でいっぱいになります。
今、両方の容器をいっぱいにしてから、入れるときと同じ水量で底から同時に水を出したところ12分後に2つの容器の水面の高さは等しくなりました。
AとBの底面の面積の比は何対何で、高さの比は何対何です。
この動画を見る
円柱の形をした2つの容器A、Bがあります。
A、Bともに同じ一定の割合で水を入れると、入れ始めてからAは28分で、Bは36分でいっぱいになります。
今、両方の容器をいっぱいにしてから、入れるときと同じ水量で底から同時に水を出したところ12分後に2つの容器の水面の高さは等しくなりました。
AとBの底面の面積の比は何対何で、高さの比は何対何です。
自由研究のネタになる立体の展開図

単元:
#平面図形#立体図形#平面図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
自由研究のネタになる「正十二面体の展開図」について解説しています。
※展開図は動画内参照
この動画を見る
自由研究のネタになる「正十二面体の展開図」について解説しています。
※展開図は動画内参照
【改良版】立体の展開図のイメージ

これの作り方教えて

【中学数学】回転体と投影図~どこよりも丁寧に~【中1数学】

単元:
#算数(中学受験)#数学(中学生)#中1数学#空間図形#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【中学数学】回転体と投影図解説動画です
この動画を見る
【中学数学】回転体と投影図解説動画です
福田の中学入試の算数007〜ラサール中学校2006年〜立体の平面による切り口の面積
単元:
#算数(中学受験)#過去問解説(学校別)#立体図形#立体切断#ラ・サール中学
指導講師:
福田次郎
問題文全文(内容文):
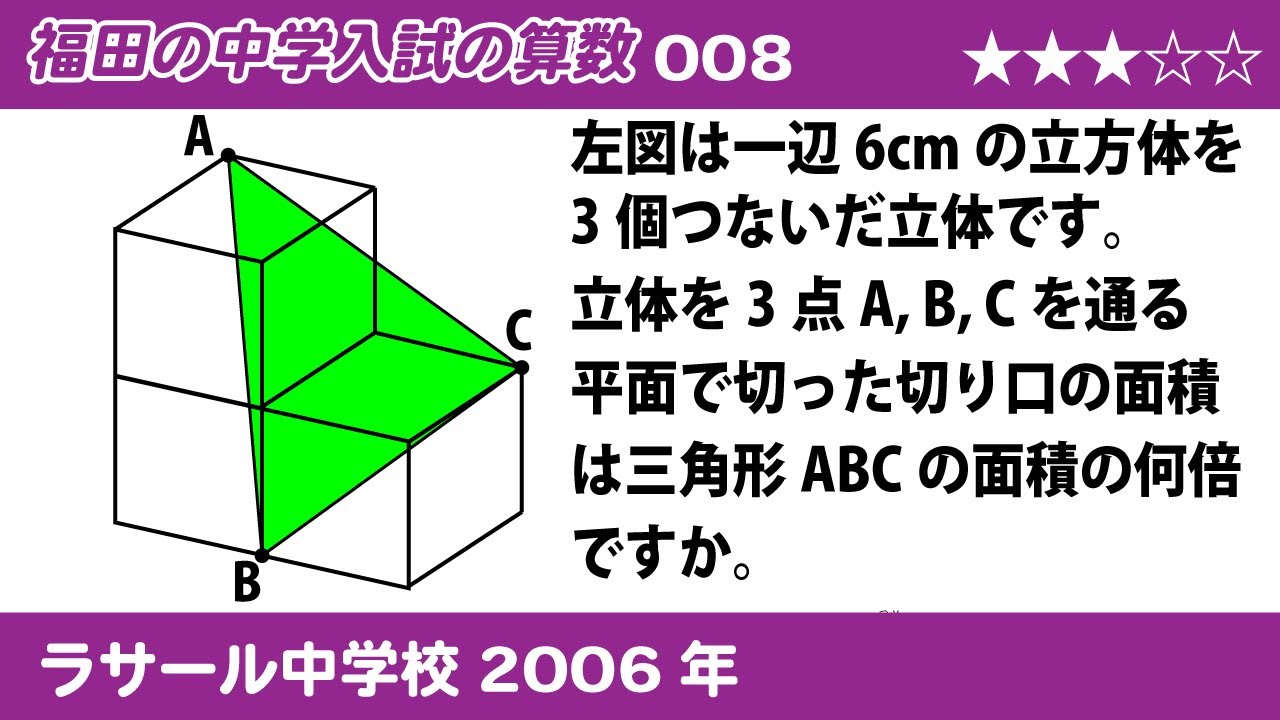
左図(動画参照)は一辺6cmの立方体を3個つないだ立体です。
立体を3点A,B,Cを通る平面で切った切り口の面積は三角形ABCの面積の何倍ですか。
この動画を見る
左図(動画参照)は一辺6cmの立方体を3個つないだ立体です。
立体を3点A,B,Cを通る平面で切った切り口の面積は三角形ABCの面積の何倍ですか。
福田の中学入試の算数005〜灘中学校2017年〜展開図から体積を求める
単元:
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師:
福田次郎
問題文全文(内容文):
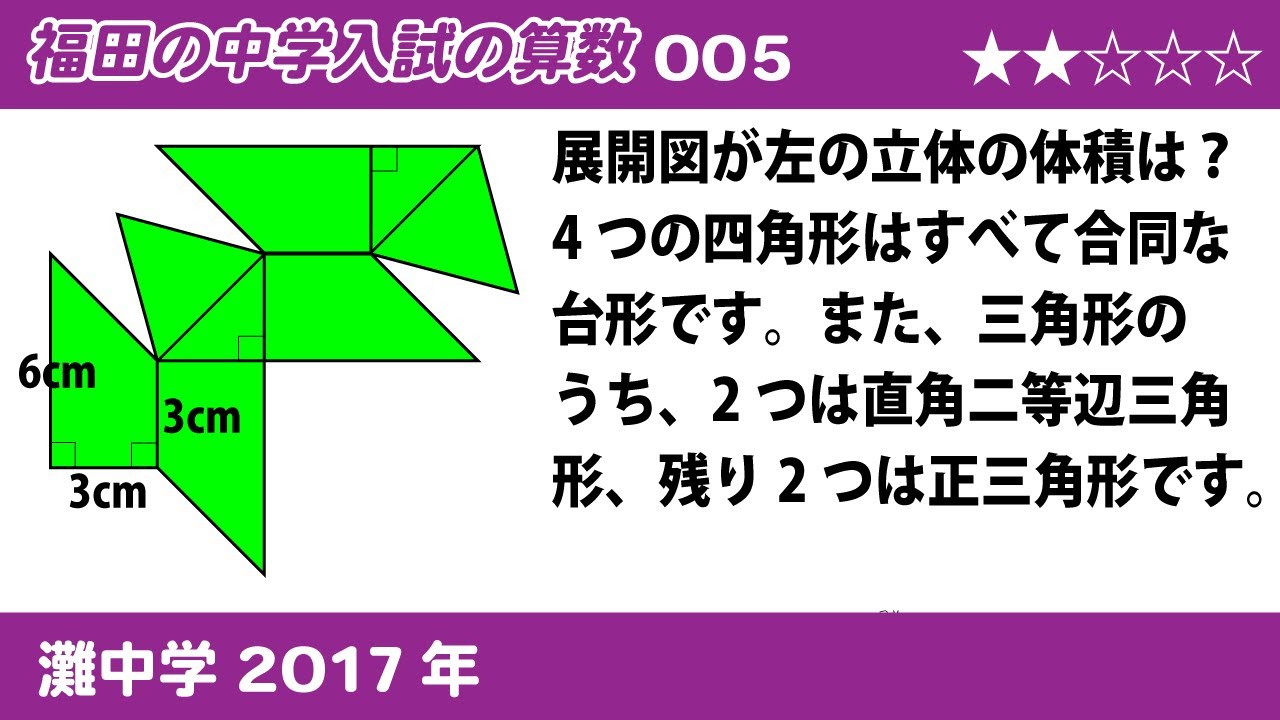
展開図(※動画参照)が左の立体の体積は?
4つの四角形はすべて合同な台形です。また、三角形のうち、
2つは直角二等辺三角形、残り2つは正三角形です。
この動画を見る
展開図(※動画参照)が左の立体の体積は?
4つの四角形はすべて合同な台形です。また、三角形のうち、
2つは直角二等辺三角形、残り2つは正三角形です。
【SPX小6算数手元解説】多面体を切る③【D-支援解説】

単元:
#算数(中学受験)#立体図形#立体切断#体積・表面積・回転体・水量・変化のグラフ#立体図形その他
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
受験算数の森
問題文全文(内容文):
次の(ア)~(カ)に当てはまる数を求めなさい。
図1の立体は、20個の同じ大きさの正三角形で囲まれていて、どの頂点のまわりにも5個の正三角形が集まってできています。この立体は正二十面体と呼ばれています。正二十面体の頂点の個数は(ア)個、辺の本数は(イ)本あります。
次に正二十面体の各頂点から出ている5本の辺を図2のように、その1/3の長さのところで切り落としていくと、図3のような立体ができます。この立体には正六角形の面は(ウ)面、正五角形の面は(エ)面ありますから、この立体の辺の本数は(オ)本です。また、この立体の頂点の個数は(カ)個です。
この動画を見る
次の(ア)~(カ)に当てはまる数を求めなさい。
図1の立体は、20個の同じ大きさの正三角形で囲まれていて、どの頂点のまわりにも5個の正三角形が集まってできています。この立体は正二十面体と呼ばれています。正二十面体の頂点の個数は(ア)個、辺の本数は(イ)本あります。
次に正二十面体の各頂点から出ている5本の辺を図2のように、その1/3の長さのところで切り落としていくと、図3のような立体ができます。この立体には正六角形の面は(ウ)面、正五角形の面は(エ)面ありますから、この立体の辺の本数は(オ)本です。また、この立体の頂点の個数は(カ)個です。
【SPX小6算数手元解説】多面体を切る②【D-支援解説】

単元:
#算数(中学受験)#立体図形#立体切断#体積・表面積・回転体・水量・変化のグラフ#立体図形その他
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
受験算数の森
問題文全文(内容文):
下図のように正八面体から各頂点に集まる4つの辺の真ん中の点を通る平面で、かどを切り取って1つの立体を作ります。この立体について、次の問いに答えなさい。
(1)この立体の面、辺、頂点の数はそれぞれいくつありますか
(2)この立体の体積もとの正八面体の何分のいくつになりますか。
この動画を見る
下図のように正八面体から各頂点に集まる4つの辺の真ん中の点を通る平面で、かどを切り取って1つの立体を作ります。この立体について、次の問いに答えなさい。
(1)この立体の面、辺、頂点の数はそれぞれいくつありますか
(2)この立体の体積もとの正八面体の何分のいくつになりますか。
【SPX小6算数手元解説】多面体を切る➀【D-支援解説】

単元:
#算数(中学受験)#立体図形#立体切断#体積・表面積・回転体・水量・変化のグラフ#立体図形その他
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
受験算数の森
問題文全文(内容文):
下図のように立方体から各頂点に集まる3つの辺の真ん中を通る平面で、かどを切り取って1つの立方体を作ります。この立体について、次の問いに答えなさい。
この動画を見る
下図のように立方体から各頂点に集まる3つの辺の真ん中を通る平面で、かどを切り取って1つの立方体を作ります。この立体について、次の問いに答えなさい。
【小6算数手元解説】容器に容器を入れる問題【問題文は概要欄】
単元:
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
底面が正方形の角柱の容器A、Bがあります。Aは底面の一辺の長さが20cmで高さが50cm、Bは底面の一辺の長さ10cmで高さが30cmです。Aに高さ46cmまで水を入れます。次に、水の入っていないBをAの水面に垂直に、静かに沈めていくとき、次の(1)、(2)、(3)に答えなさい。ただし、Bの厚さはないものとします。
(1)Aから水が外にこぼれはじめるのは、Bの底面がAの底面から何cmのときですか。
(2)さらにBを沈めていきます。その途中で止めたら、Bに深さ24cmまで水が入っていきました。このとき、Bの底面はAの底面から何cmのところにありますか。
(3)さらにBを沈めていって、Aの底面についたとき、Aの水の深さは何cmになっていますか。
この動画を見る
底面が正方形の角柱の容器A、Bがあります。Aは底面の一辺の長さが20cmで高さが50cm、Bは底面の一辺の長さ10cmで高さが30cmです。Aに高さ46cmまで水を入れます。次に、水の入っていないBをAの水面に垂直に、静かに沈めていくとき、次の(1)、(2)、(3)に答えなさい。ただし、Bの厚さはないものとします。
(1)Aから水が外にこぼれはじめるのは、Bの底面がAの底面から何cmのときですか。
(2)さらにBを沈めていきます。その途中で止めたら、Bに深さ24cmまで水が入っていきました。このとき、Bの底面はAの底面から何cmのところにありますか。
(3)さらにBを沈めていって、Aの底面についたとき、Aの水の深さは何cmになっていますか。
【SPX小6算数手元解説】穴のあき方【D-支援解説】※「受験算数の森」チャンネル始動特別企画
単元:
#算数(中学受験)#立体図形#立体図形その他
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
受験算数の森
問題文全文(内容文):
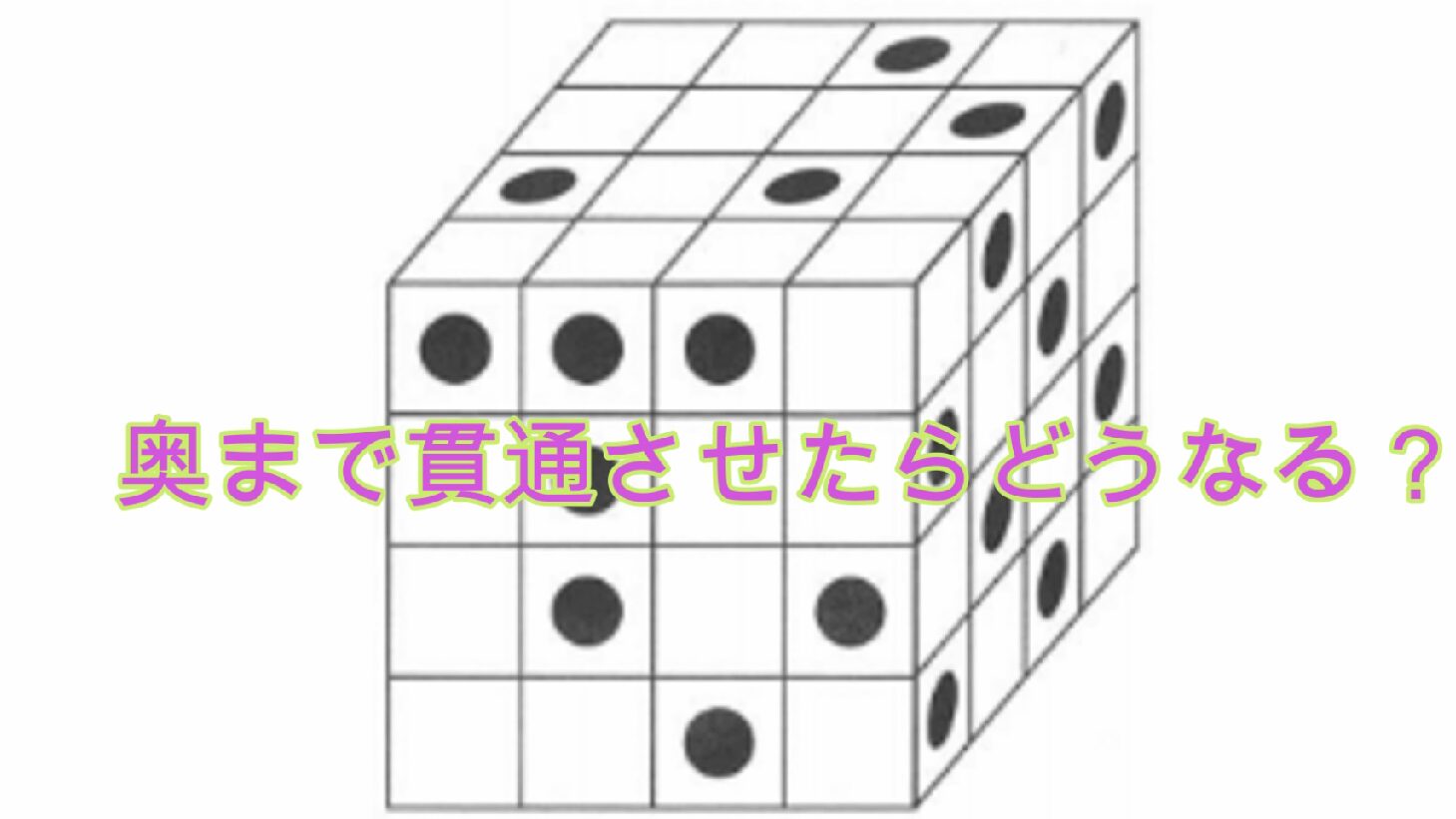
64個の小さな立方体を積み重ねて、右図のような大きな立方体を作ります。次に、この大きな立方体の上の面から垂直に、下の面までつきぬける穴を、右図の上の面の4つの黒丸の位置からあけます。他の面からも同じようにして、向かい側の面につきぬける穴を、それぞれ右図の黒丸の位置から開けます。このとき、おのおのの小さな立方体について考えると、1つも穴の開いていない立方体、1方向にだけ穴の開いている立方体、2方向に穴の開いている立方体、3方向に穴の開いている立方体の4種類に分けられます。
これらの個数をそれぞれ求めなさい。
この動画を見る
64個の小さな立方体を積み重ねて、右図のような大きな立方体を作ります。次に、この大きな立方体の上の面から垂直に、下の面までつきぬける穴を、右図の上の面の4つの黒丸の位置からあけます。他の面からも同じようにして、向かい側の面につきぬける穴を、それぞれ右図の黒丸の位置から開けます。このとき、おのおのの小さな立方体について考えると、1つも穴の開いていない立方体、1方向にだけ穴の開いている立方体、2方向に穴の開いている立方体、3方向に穴の開いている立方体の4種類に分けられます。
これらの個数をそれぞれ求めなさい。
【SPX小6算数手元解説】玉はどこにある?【D-支援解説】※「受験算数の森」チャンネル始動特別企画
単元:
#算数(中学受験)#立体図形#立体図形その他
教材:
#SPX#4年算数D-SPX#6年算数W-支援#中学受験教材
指導講師:
受験算数の森
問題文全文(内容文):
透明な立方体の小箱27個を3段に重ねて作った立方体があります。何個かの小箱には赤い球が入っていて、外から見えます。右図は、この立方体を真上、正面、真横の3つの方向から見て、玉が見える場所に〇印をつけたものです。
(1)図1の場合、上から1段目、2段目、3段目の小箱で、玉が入っている場所はそれぞれどこですか。
(2)図2の場合、玉が入った小箱の数は、何個以上何個以下と考えられますか。
この動画を見る
透明な立方体の小箱27個を3段に重ねて作った立方体があります。何個かの小箱には赤い球が入っていて、外から見えます。右図は、この立方体を真上、正面、真横の3つの方向から見て、玉が見える場所に〇印をつけたものです。
(1)図1の場合、上から1段目、2段目、3段目の小箱で、玉が入っている場所はそれぞれどこですか。
(2)図2の場合、玉が入った小箱の数は、何個以上何個以下と考えられますか。
【SPX小6算数手元解説】接する面の数【D-支援解説】※「受験算数の森」チャンネル始動特別企画
単元:
#算数(中学受験)#立体図形#立体図形その他
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
受験算数の森
問題文全文(内容文):
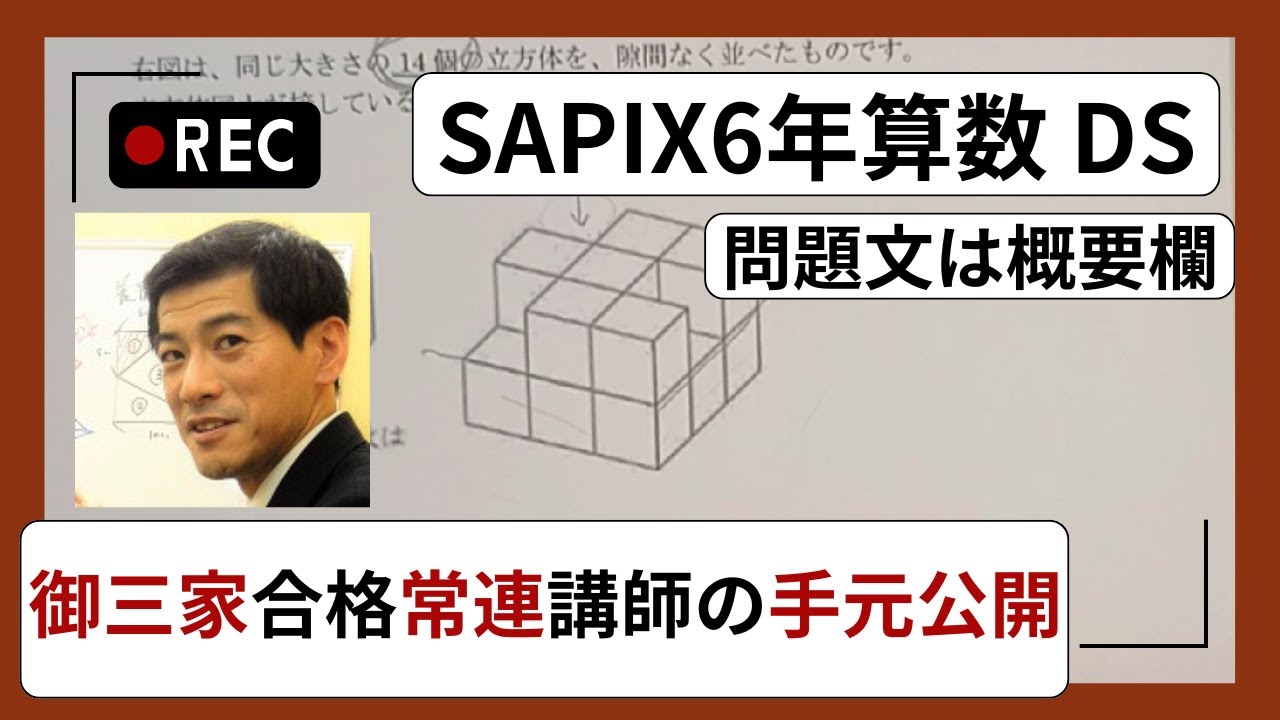
右図は、同じ大きさの14個の立方体を、隙間なく並べたものです。
立方体同士が接している面の数は何個ですか。
この動画を見る
右図は、同じ大きさの14個の立方体を、隙間なく並べたものです。
立方体同士が接している面の数は何個ですか。
福田の中学入試の算数003〜灘中学校2006年〜展開図から立体の体積を求める
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#図形の移動#立体図形#立体図形その他#灘中学校
指導講師:
福田次郎
問題文全文(内容文):
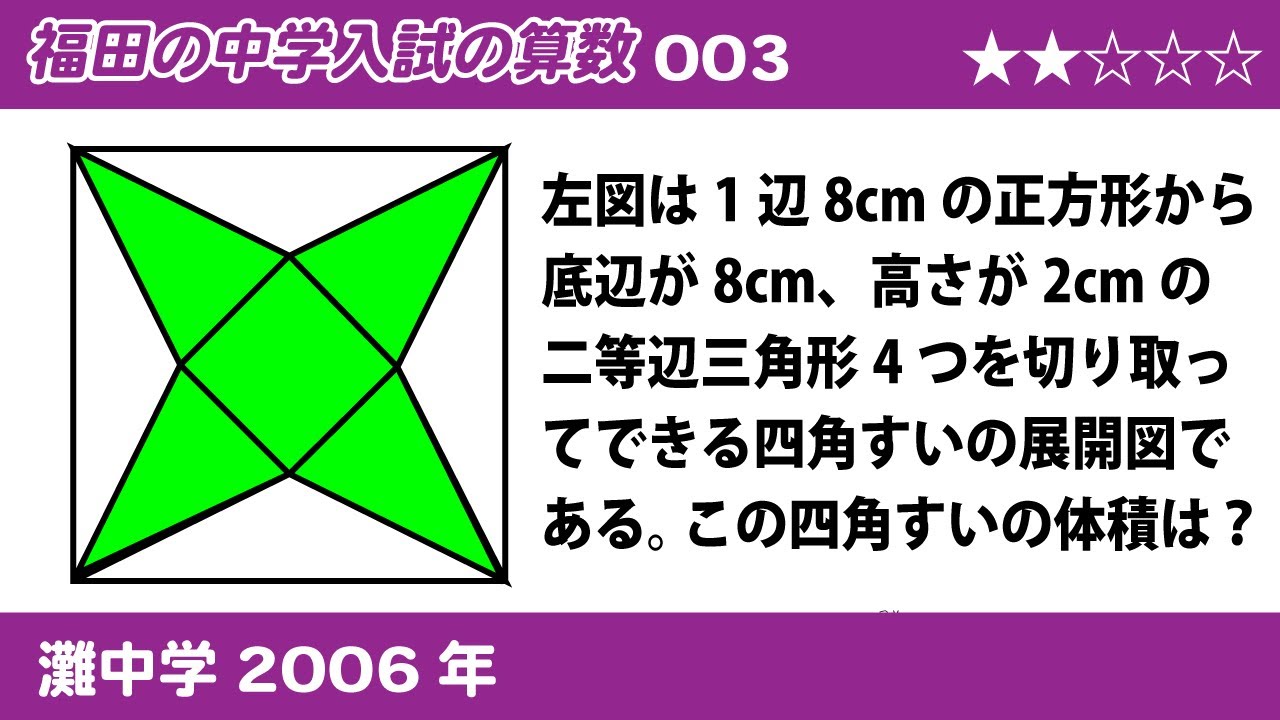
左図(※動画参照)は一辺8 cmの正方形から底辺が8 cm、高さ2 cmの二等辺三角形を4つ切り取ってできる四角すいの展開図である。この四角すいの体積を求めよ。
この動画を見る
左図(※動画参照)は一辺8 cmの正方形から底辺が8 cm、高さ2 cmの二等辺三角形を4つ切り取ってできる四角すいの展開図である。この四角すいの体積を求めよ。
福田の中学入試の算数001〜桜蔭中学校2005年〜立体の断面
単元:
#算数(中学受験)#立体図形#立体切断
指導講師:
福田次郎
問題文全文(内容文):
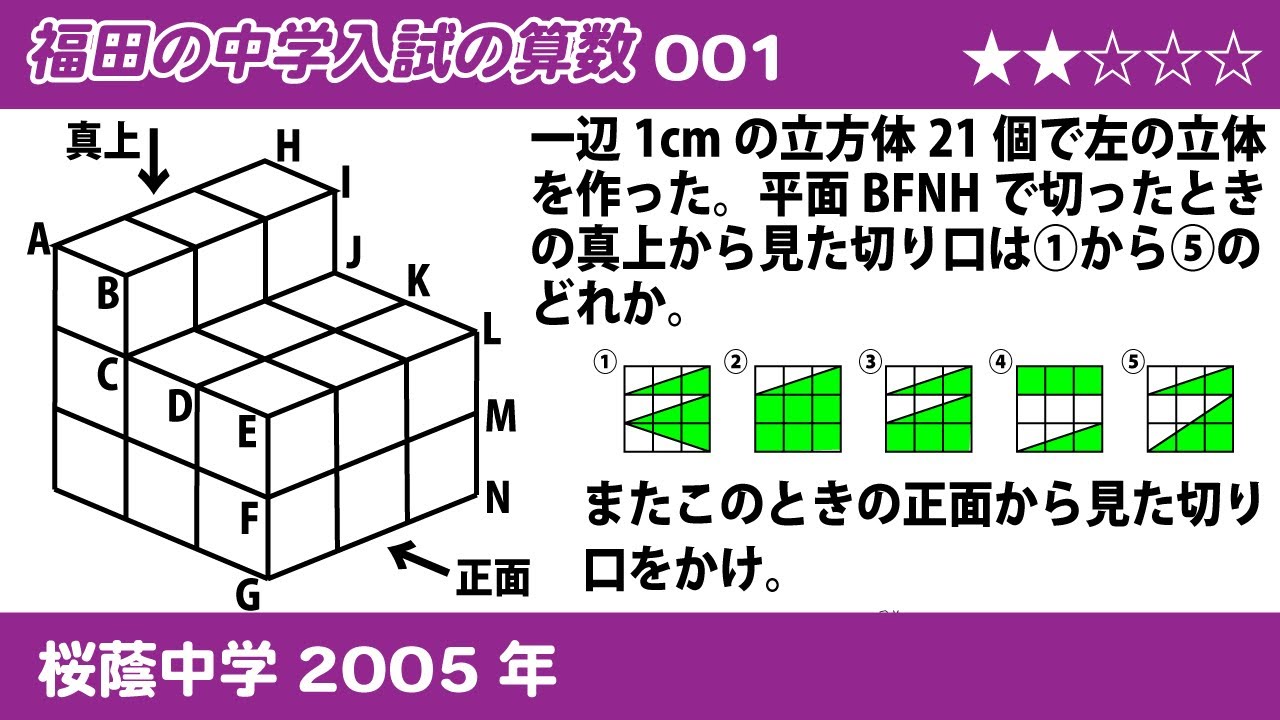
1辺が1 cmの立方体を21個使って下のような立体を作った。平面BFNHで切ったときの真上から見た切り口を①~⑤から選びなさい。またこのときの正面から見た切り口を図示してください。(※動画参照)
この動画を見る
1辺が1 cmの立方体を21個使って下のような立体を作った。平面BFNHで切ったときの真上から見た切り口を①~⑤から選びなさい。またこのときの正面から見た切り口を図示してください。(※動画参照)
4つの立方体
量の2倍は見た目何倍か知ってる?

単元:
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
見た目が倍のご飯の量は何倍なのか?解説動画です
この動画を見る
見た目が倍のご飯の量は何倍なのか?解説動画です
福田のおもしろ数学128〜灘中学の問題〜展開図から元の立体の体積を求める
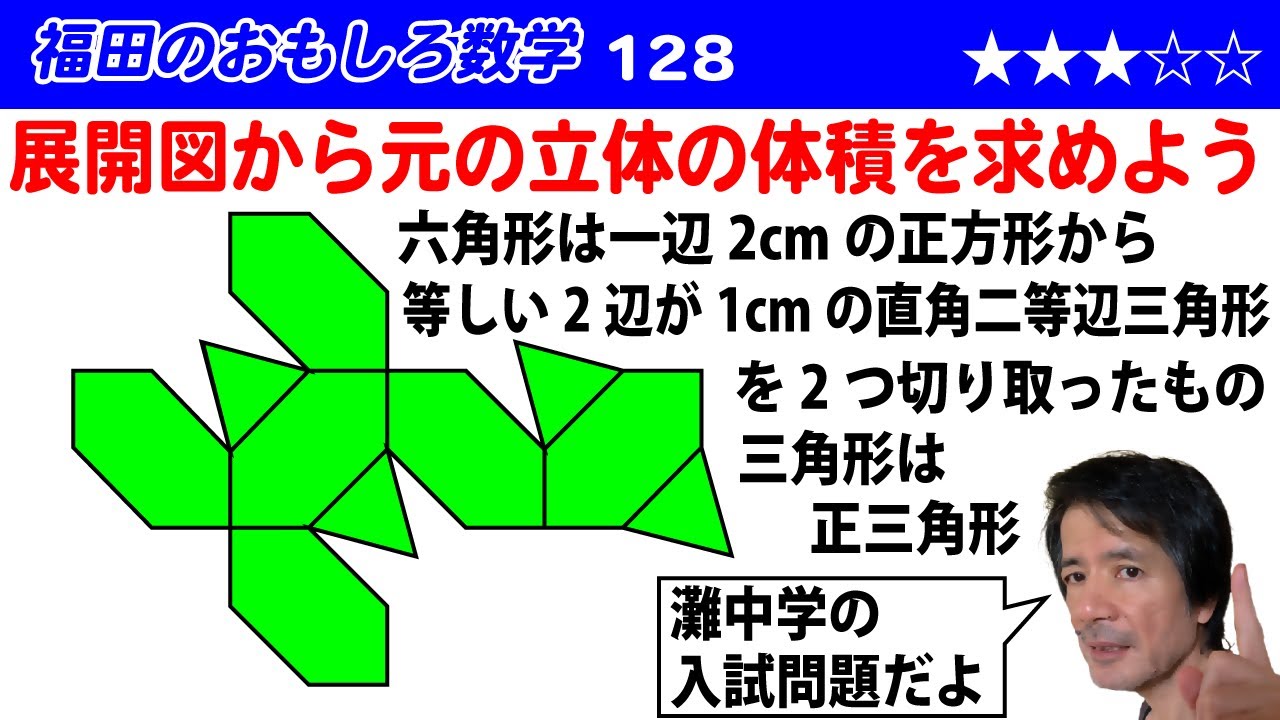
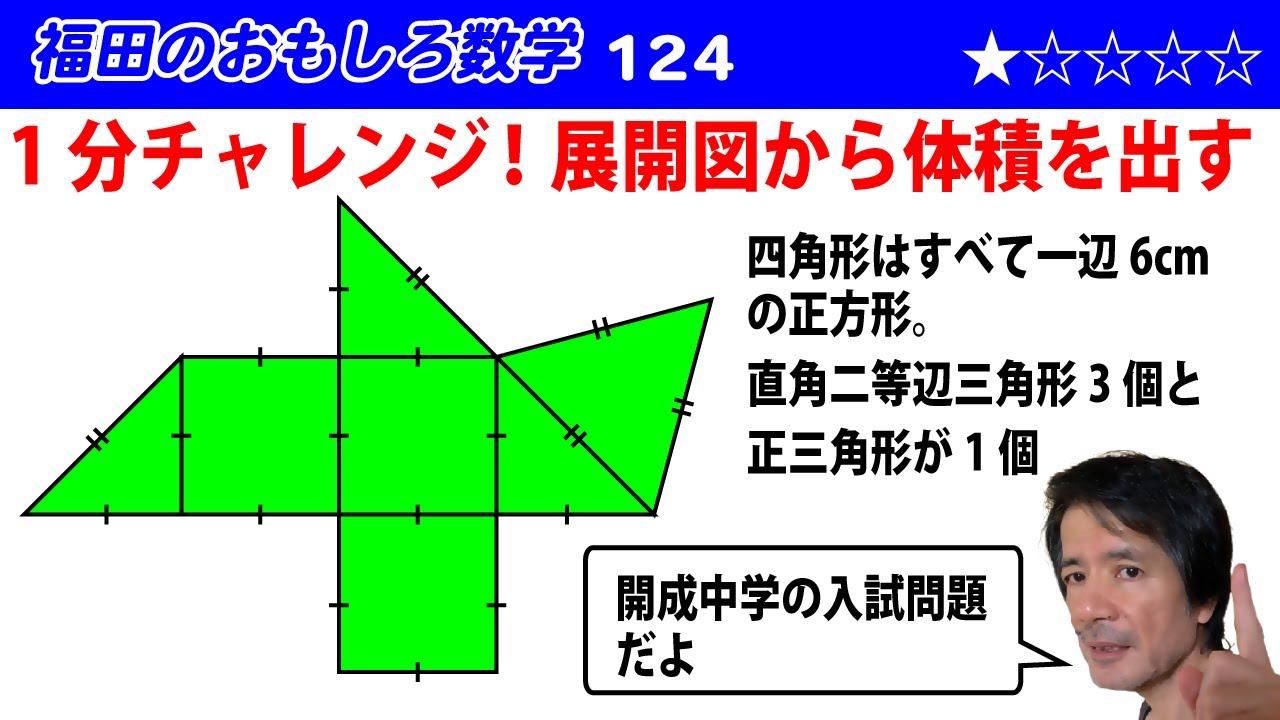
福田のおもしろ数学124〜展開図から立体の体積を求める
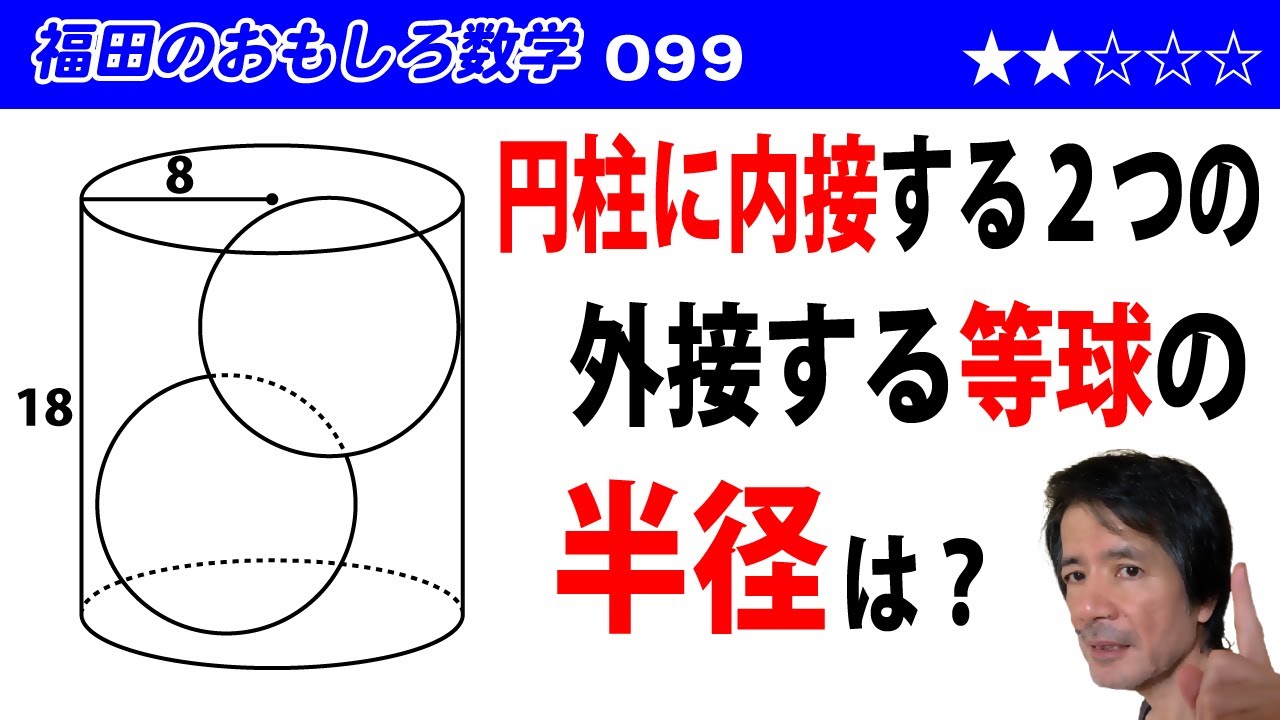
福田のおもしろ数学099〜円柱に内接する2つの球の半径
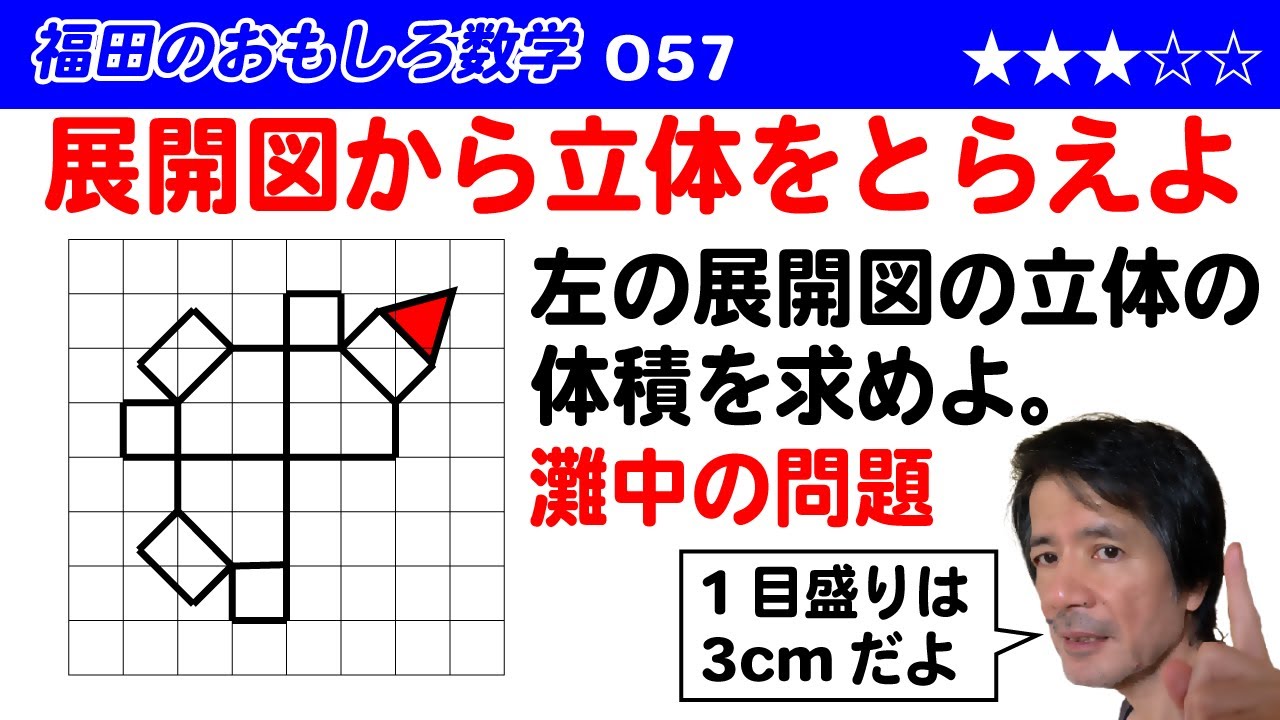
福田のおもしろ数学057〜灘中学の問題〜展開図を見て体積を求めよう
単元:
#算数(中学受験)#過去問解説(学校別)#立体図形#体積・表面積・回転体・水量・変化のグラフ#立体図形その他#灘中学校
指導講師:
福田次郎
問題文全文(内容文):
ある立体の展開図を、幅が 3cm の方眼紙にかくと、次の図のようになった。斜線をつけた三角形は正三角形である。また正方形でない四角形の面はすべて長方形である。この立体の体積を求めよ。
※図は動画内参照
この動画を見る
ある立体の展開図を、幅が 3cm の方眼紙にかくと、次の図のようになった。斜線をつけた三角形は正三角形である。また正方形でない四角形の面はすべて長方形である。この立体の体積を求めよ。
※図は動画内参照
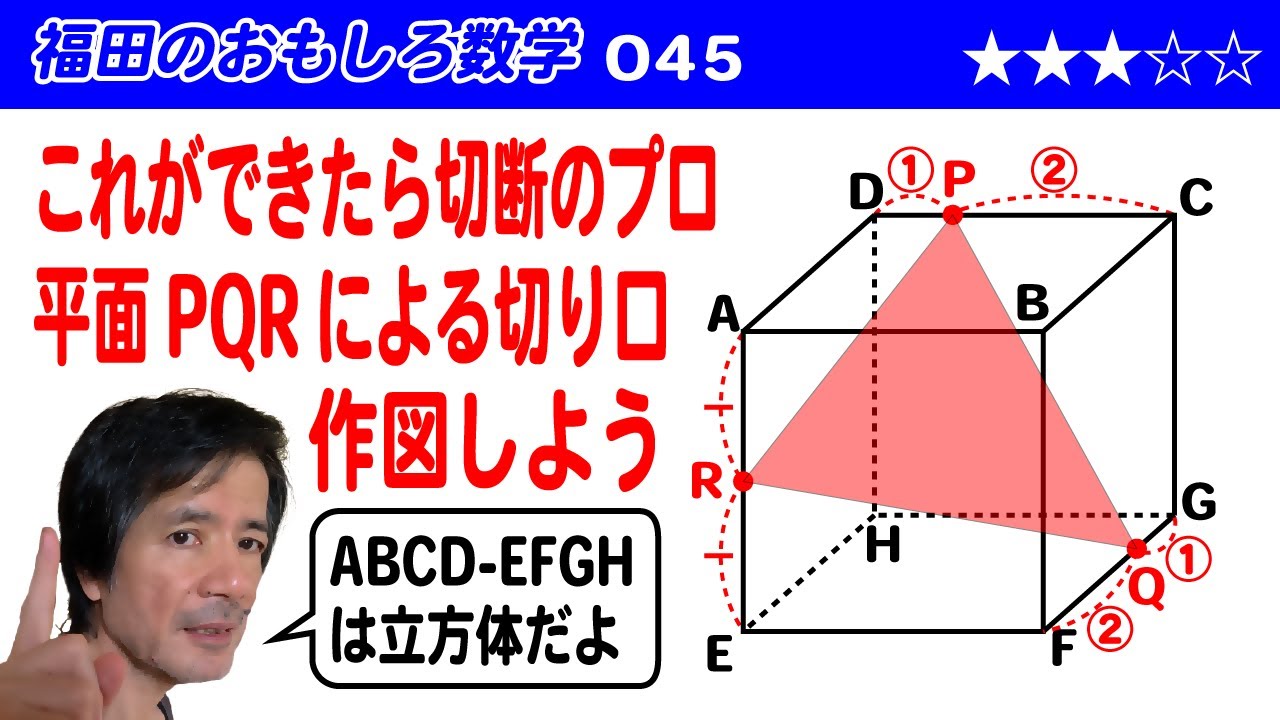
福田のおもしろ数学045〜これができたら切断のプロ〜立方体の切断
単元:
#算数(中学受験)#数学(中学生)#中1数学#空間図形#立体図形#立体切断
指導講師:
福田次郎
問題文全文(内容文):
立方体 ABCD ー EFGH を 3 点 P , Q , R を通る平面で切ったときの切り口を作図せよ。
※図は動画内参照
この動画を見る
立方体 ABCD ー EFGH を 3 点 P , Q , R を通る平面で切ったときの切り口を作図せよ。
※図は動画内参照
