電気通信大学
電気通信大学
大学入試問題#845「気持ち応用か！？」 #電気通信大学(2020) #区分求積法
単元：
#大学入試過去問(数学)#積分とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
出典：2020年電気通信大学
この動画を見る
出典：2020年電気通信大学
大学入試問題#844「まあ基本・・・」 #電気通信大学(2015) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
出典：2015年電気通信大学 入試問題
この動画を見る
出典：2015年電気通信大学 入試問題
大学入試問題#842「公式は使っていません」 #電気通信大学(2018) ＃定積分
#電気通信大学(2013) #極限 #Shorts
#電気通信大学(2014) #定積分 #Shorts
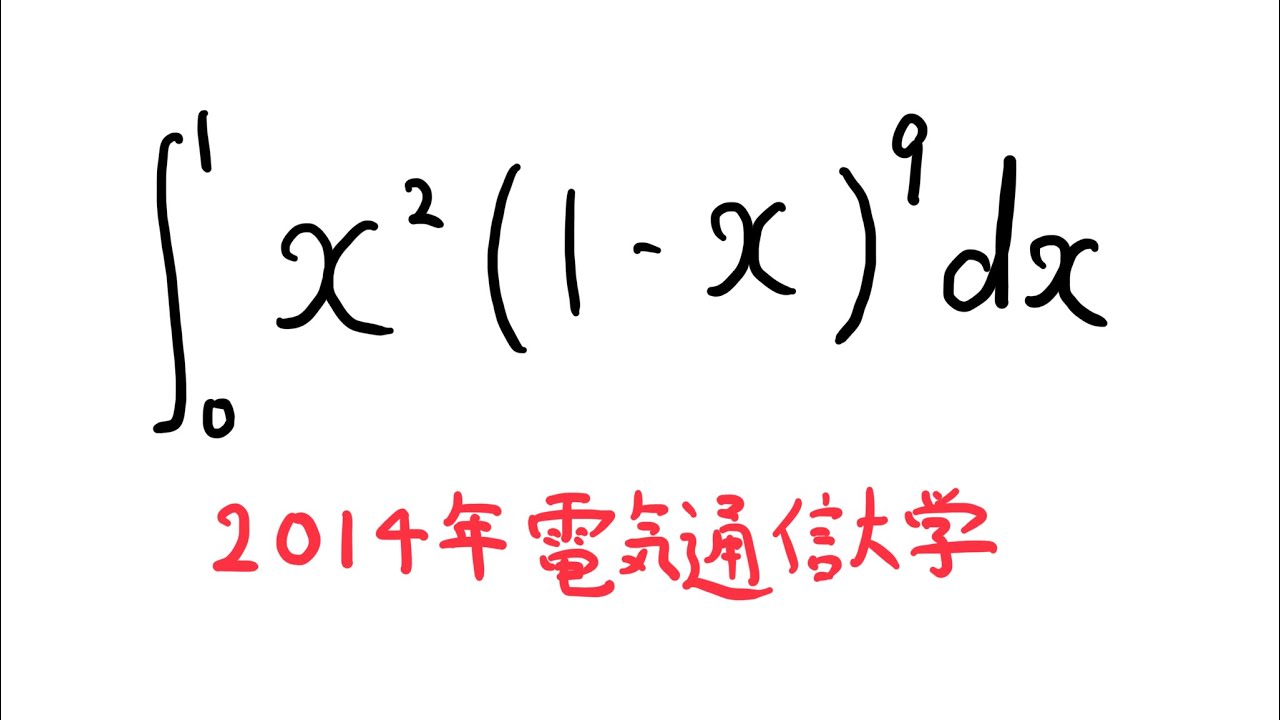
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
出典：2014年電気通信大学
この動画を見る
出典：2014年電気通信大学
#電気通信大学(2023) #不定積分 #Shorts
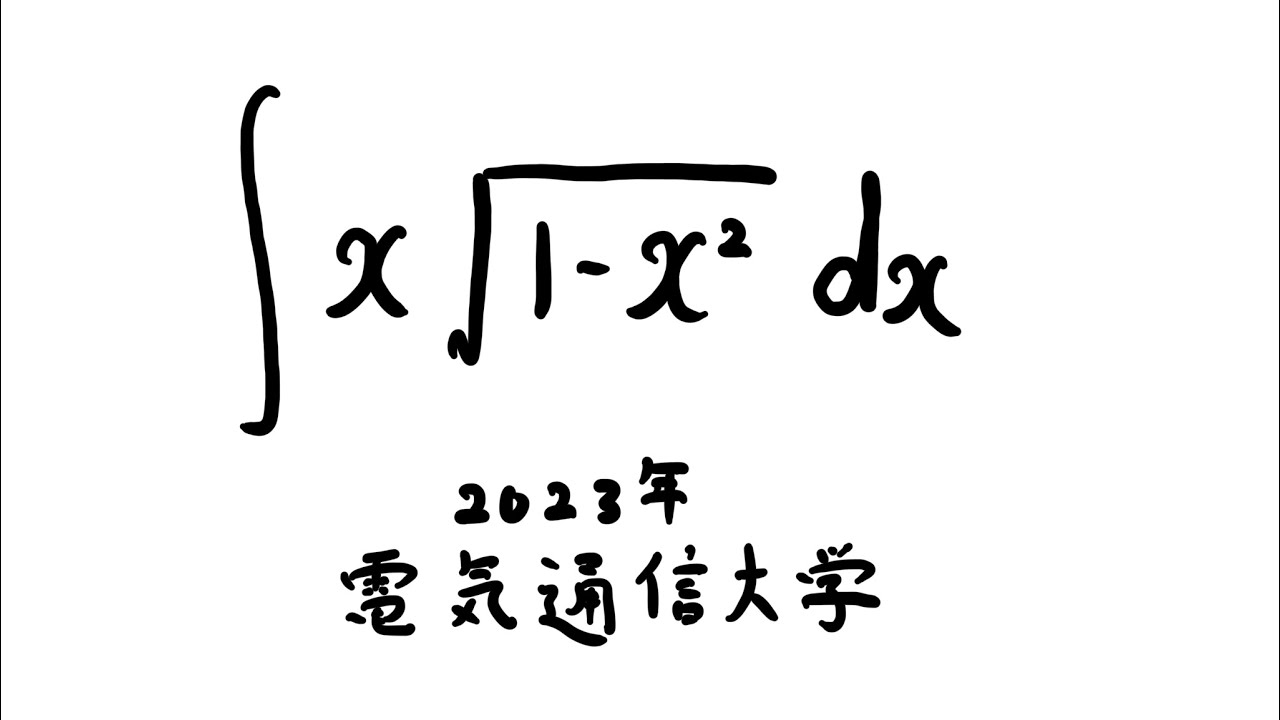
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
以下の不定積分を解け。
出典：2023年電気通信大学
この動画を見る
以下の不定積分を解け。
出典：2023年電気通信大学
#電気通信大学(2023) #定積分 #Shorts
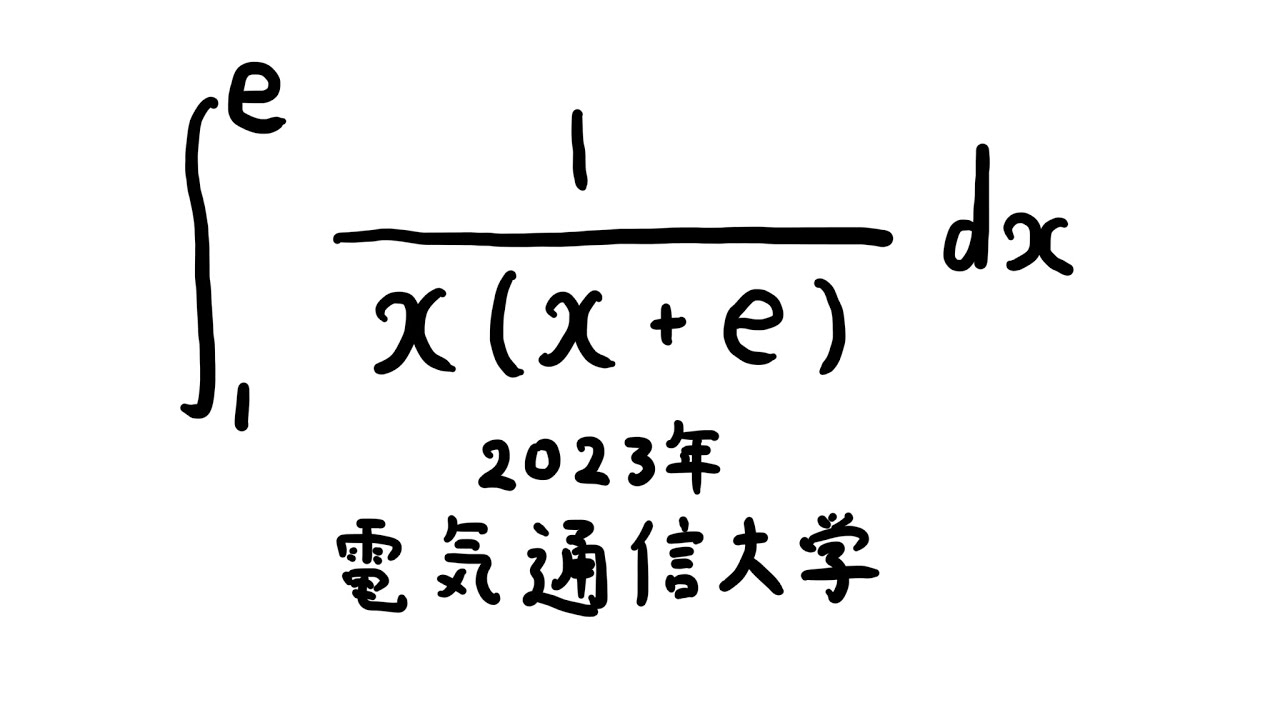
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
以下の定積分を解け。
出典：2023年電気通信大学
この動画を見る
以下の定積分を解け。
出典：2023年電気通信大学
#電気通信大学(2023) #不定積分 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
以下の不定積分を解け。
出典：2023年電気通信大学
この動画を見る
以下の不定積分を解け。
出典：2023年電気通信大学
大学入試問題#752「初見だと少し焦る」 電気通信大学後期(2023) #区分求積法
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
出典：2023年電子通信大学後期 入試問題
この動画を見る
出典：2023年電子通信大学後期 入試問題
電気通信大学2014年 #定積分 #Shorts
電気通信大学2014年 #極限 #Shorts
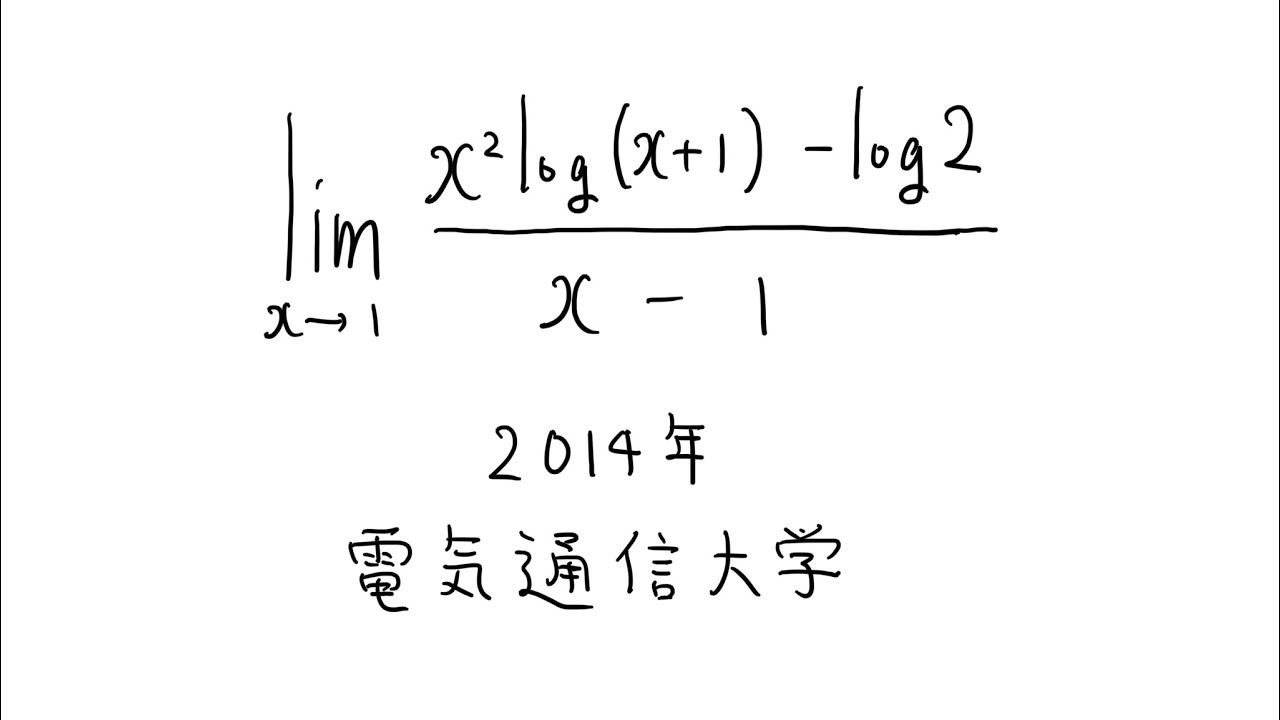
単元：
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
出典：2014年電気通信大学
この動画を見る
出典：2014年電気通信大学
大学入試問題#500「基本に沿って」 電気通信大学後期(2022) #区分求積法
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
出典：2022年電気通信大学後期 入試問題
この動画を見る
出典：2022年電気通信大学後期 入試問題
大学入試問題#467「基本すぎる極限問題」 電気通信大学(2013) #極限
単元：
#大学入試過去問(数学)#三角関数#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
出典：2013年電気通信大学 入試問題
この動画を見る
出典：2013年電気通信大学 入試問題
大学入試問題#466「絶対に知っておくべき解き方」 電気通信大学(2014) #極限
単元：
#大学入試過去問(数学)#三角関数#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
出典：2014年電気通信大学 入試問題
この動画を見る
出典：2014年電気通信大学 入試問題
大学入試問題#465「よくある極限問題」 電気通信大学2009 #極限
単元：
#大学入試過去問(数学)#三角関数#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
出典：2009年電気通信大学 入試問題
この動画を見る
出典：2009年電気通信大学 入試問題
大学入試問題#351「積分できて満足できない問題」 電気通信大学(2013) #定積分 #極限
単元：
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
出典：2013年電気通信大学 入試問題
この動画を見る
出典：2013年電気通信大学 入試問題
大学入試問題#346「2種類の解法の紹介」 電気通信大学(2013) #定積分 #キングプロパティ
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
出典：2013年電気通信大学 入試問題
この動画を見る
出典：2013年電気通信大学 入試問題
大学入試問題#319 電気通信大学(2010) #定積分 #極限
単元：
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
出典：2010年電気通信大学 入試問題
この動画を見る
出典：2010年電気通信大学 入試問題
大学入試問題#296 電気通信大学(2012) #定積分
大学入試問題#279 電気通信大学(2012) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
出典：2012年電気通信大学後期 入試問題
この動画を見る
出典：2012年電気通信大学後期 入試問題
大学入試問題#231 電気通信大学(2012) #不定積分
単元：
#大学入試過去問(数学)#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
出典：2012年電気通信大学 入試問題
この動画を見る
出典：2012年電気通信大学 入試問題
【合格体験記】宅浪で電通大に合格したFくん＆シノハラの戦略立案の話【篠原好】
単元：
#その他#勉強法#その他#電気通信大学
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
「宅浪で電通大に合格したFくんの合格体験記と篠原先生の戦略立案」についてお話しています。
この動画を見る
「宅浪で電通大に合格したFくんの合格体験記と篠原先生の戦略立案」についてお話しています。