 神戸大学
神戸大学
 神戸大学
神戸大学
福田の数学〜神戸大学2025文系第3問〜単位円周上の2点と確率

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#場合の数#三角関数#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$1$個のさいころを$2$回続けて投げるとき、
出た目の数を順に$a,b$とおく。
座標平面上の$2$点$A,B$を
$A\left(\cos \dfrac{a}{6}\pi,\sin\dfrac{a}{6}\pi\right),\quad B\left(\cos \dfrac{b+6}{6}\pi,\sin\dfrac{b+6}{6}\pi\right)$
とし、原点を$O$とする。
以下の問いに答えよ。
(1)$3$点$O,A,B$が一直線上にある確率を求めよ。
(2)$3$点$O,A,B$が一直線上になく、かつ
三角形$OAB$の面積が$\dfrac{1}{4}$以下である
確率を求めよ。
(3)$2$点$A,B$間の距離が$1$より
大きい確率を求めよ。
$2025$年神戸大学文系過去問題
この動画を見る
$\boxed{3}$
$1$個のさいころを$2$回続けて投げるとき、
出た目の数を順に$a,b$とおく。
座標平面上の$2$点$A,B$を
$A\left(\cos \dfrac{a}{6}\pi,\sin\dfrac{a}{6}\pi\right),\quad B\left(\cos \dfrac{b+6}{6}\pi,\sin\dfrac{b+6}{6}\pi\right)$
とし、原点を$O$とする。
以下の問いに答えよ。
(1)$3$点$O,A,B$が一直線上にある確率を求めよ。
(2)$3$点$O,A,B$が一直線上になく、かつ
三角形$OAB$の面積が$\dfrac{1}{4}$以下である
確率を求めよ。
(3)$2$点$A,B$間の距離が$1$より
大きい確率を求めよ。
$2025$年神戸大学文系過去問題
福田の数学〜神戸大学2025文系第2問〜小数部分と命題の証明

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
実数$a$に対して、
$a$を超えない最大の整数を$k$とするとき、
$a-k$を$a$の小数部分という。
$n$を自然数とし、$a_n=\sqrt{n^2+1}$とおく。
以下の問いに答えよ。
(1)$a_n \lt n+1$が成り立つことを示せ。
(2)$b_n$を$a_n$の小数部分とする。
$b_n$を$n$を用いて表せ。
(3)$b_n$を(2)で定めたものとする。
$m,n$を異なる$2$つの自然数とするとき、
$b_m \neq b_n$であることを示せ。
$2025$年神戸大学文系過去問題
この動画を見る
$\boxed{2}$
実数$a$に対して、
$a$を超えない最大の整数を$k$とするとき、
$a-k$を$a$の小数部分という。
$n$を自然数とし、$a_n=\sqrt{n^2+1}$とおく。
以下の問いに答えよ。
(1)$a_n \lt n+1$が成り立つことを示せ。
(2)$b_n$を$a_n$の小数部分とする。
$b_n$を$n$を用いて表せ。
(3)$b_n$を(2)で定めたものとする。
$m,n$を異なる$2$つの自然数とするとき、
$b_m \neq b_n$であることを示せ。
$2025$年神戸大学文系過去問題
福田の数学〜神戸大学2025文系第1問〜3次方程式が異なる3個の実数解をもつ条件

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
$a$を実数とする。
$f(x)=2x^3+ax^2-1$とおくとき、以下の問いに答えよ。
(1)方程式$f(x)=0$は$x=-1$に解にもつとする。
このとき、$a$の値を求め、
方程式$f(x)=0$の解をすべて求めよ。
(2)$a$の値を(1)で求めたものとする。
関数$f(x)$の極限を求めよ。
(3)方程式$f(x)=0$が異なる$3$つの実数解を
もつような$a$の値の範囲を求めよ。
$2025$年神戸大学文系過去問題
この動画を見る
$\boxed{1}$
$a$を実数とする。
$f(x)=2x^3+ax^2-1$とおくとき、以下の問いに答えよ。
(1)方程式$f(x)=0$は$x=-1$に解にもつとする。
このとき、$a$の値を求め、
方程式$f(x)=0$の解をすべて求めよ。
(2)$a$の値を(1)で求めたものとする。
関数$f(x)$の極限を求めよ。
(3)方程式$f(x)=0$が異なる$3$つの実数解を
もつような$a$の値の範囲を求めよ。
$2025$年神戸大学文系過去問題
福田の数学〜神戸大学2025理系第5問〜連続と微分可能と曲線の長さ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
連続関数$f(x)$は$x \geqq 0$で$f(x) \geqq 0$を満たし、
$x \gt 0$で微分可能であり、その導関数$f'(x)$は
連続であるとする。
$t \geqq 1$を満たす$t$に対して、
$y=f(x) \ (1\leqq x \leqq t)$で表される曲線の長さを
$h(t)$とし、$t=1$のときは$h(1)=0$とする。
以下の問いに答えよ。
(1)$t\gt 1$とする。
開区間$(1,t)$で常に$f(x)-xf'(x)=0$が成り立つならば、
閉区間$[1,t]$で$\dfrac{f(x)}{x}$は定数であることを示せ。
(2)$t\geqq 1$を満たす任意の$t$に対して、
$g(t)=h(t)+2$が成り立つとする。
このとき、$f(1)$の値を求めよ。
また、$t\geqq 1$のとき$f(t)$を$t$を用いて表せ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{5}$
連続関数$f(x)$は$x \geqq 0$で$f(x) \geqq 0$を満たし、
$x \gt 0$で微分可能であり、その導関数$f'(x)$は
連続であるとする。
$t \geqq 1$を満たす$t$に対して、
$y=f(x) \ (1\leqq x \leqq t)$で表される曲線の長さを
$h(t)$とし、$t=1$のときは$h(1)=0$とする。
以下の問いに答えよ。
(1)$t\gt 1$とする。
開区間$(1,t)$で常に$f(x)-xf'(x)=0$が成り立つならば、
閉区間$[1,t]$で$\dfrac{f(x)}{x}$は定数であることを示せ。
(2)$t\geqq 1$を満たす任意の$t$に対して、
$g(t)=h(t)+2$が成り立つとする。
このとき、$f(1)$の値を求めよ。
また、$t\geqq 1$のとき$f(t)$を$t$を用いて表せ。
$2025$年神戸大学理系過去問題
福田の数学〜神戸大学2025理系第4問〜空間ベクトルと三角形の面積の最小

単元:
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#三角形の辺の比(内分・外分・二等分線)#空間ベクトル#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$s,t$を実数とする。座標空間に$3$点
$A(-4,-1,0),B(-3,0,-1),P(s,t,-2s+t-1)$がある。
以下の問いに答えよ。
(1)$3$点$A,B,P$は一直線上にないことを示せ。
(2)点$P$から直線$AB$に下ろした垂線を$PH$とする。
点$H$の座標を$s$を用いて表せ。
(3)$s,t$が変化するとき、
三角形$ABP$の面積の最小値を求めよ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{4}$
$s,t$を実数とする。座標空間に$3$点
$A(-4,-1,0),B(-3,0,-1),P(s,t,-2s+t-1)$がある。
以下の問いに答えよ。
(1)$3$点$A,B,P$は一直線上にないことを示せ。
(2)点$P$から直線$AB$に下ろした垂線を$PH$とする。
点$H$の座標を$s$を用いて表せ。
(3)$s,t$が変化するとき、
三角形$ABP$の面積の最小値を求めよ。
$2025$年神戸大学理系過去問題
福田の数学〜神戸大学2025理系第3問〜媒介変数表示で表された曲線

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#微分法と積分法#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#神戸大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
媒介変数$\theta$を用いて
$x=\sin\theta,y=\cos\theta + \vert \sin\theta \vert \quad (0\leqq \theta \leqq 2\pi)$
で表される曲線を$C$とする。以下の問いに答えよ。
(1)曲線$C$の概形をかけ。
(2)曲線$C$で囲まれた部分の面積を求めよ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{3}$
媒介変数$\theta$を用いて
$x=\sin\theta,y=\cos\theta + \vert \sin\theta \vert \quad (0\leqq \theta \leqq 2\pi)$
で表される曲線を$C$とする。以下の問いに答えよ。
(1)曲線$C$の概形をかけ。
(2)曲線$C$で囲まれた部分の面積を求めよ。
$2025$年神戸大学理系過去問題
福田の数学〜神戸大学2025理系第1問〜曲線と直線の共有点の個数

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
$k$を実数とする。
$f(x)$と$g(x)$を
$f(x) = \vert x^3-x \vert,\quad g(x)=k(x+1)$
とおき、曲線$y=f(x)$を$C$、
直線$y=g(x)$を$\ell$とする。以下の問いに答えよ。
(1)曲線$C$の概形をかけ。
ただし、関数$f(x)$の極大値を調べる必要はない。
(2)曲線$C$と直線$\ell$がちょうど$4$つの
共有点をもつような$k$の値を求めよ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{1}$
$k$を実数とする。
$f(x)$と$g(x)$を
$f(x) = \vert x^3-x \vert,\quad g(x)=k(x+1)$
とおき、曲線$y=f(x)$を$C$、
直線$y=g(x)$を$\ell$とする。以下の問いに答えよ。
(1)曲線$C$の概形をかけ。
ただし、関数$f(x)$の極大値を調べる必要はない。
(2)曲線$C$と直線$\ell$がちょうど$4$つの
共有点をもつような$k$の値を求めよ。
$2025$年神戸大学理系過去問題
福田の数学〜神戸大学2024年文系第2問〜さいころの目と約数に関する確率

単元:
#数A#場合の数と確率#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#神戸大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $n$を自然数とする。以下の問いに答えよ。
(1)1個のサイコロを投げて出た目が必ず$n$の約数となるような$n$で最小のものを求めよ。
(2)1個のサイコロを投げて出た目が$n$の約数となる確率が$\displaystyle\frac{5}{6}$であるような$n$で最小のものを求めよ。
(3)1個のサイコロを3回投げて出た目の積が20の約数となる確率を求めよ。
この動画を見る
$\Large\boxed{2}$ $n$を自然数とする。以下の問いに答えよ。
(1)1個のサイコロを投げて出た目が必ず$n$の約数となるような$n$で最小のものを求めよ。
(2)1個のサイコロを投げて出た目が$n$の約数となる確率が$\displaystyle\frac{5}{6}$であるような$n$で最小のものを求めよ。
(3)1個のサイコロを3回投げて出た目の積が20の約数となる確率を求めよ。
福田の数学〜神戸大学2024年文系第1問〜3次関数で定義された数列

単元:
#数列#漸化式#神戸大学#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 各項が正である数列$\left\{a_n\right\}$を次のように定める。$a_1$は関数
$y$=$\displaystyle\frac{1}{3}x^3$-10$x$ ($x$≧0)
が最小値をとるときの$x$の値とする。$a_{n+1}$は関数
$y$=$\displaystyle\frac{1}{3}x^3$-100$a_nx$ ($x$≧0)
が最小値をとるときの$x$の値とする。数列$\left\{b_n\right\}$を$b_n$=$\log_{10}a_n$ で定める。以下の問いに答えよ。
(1)$a_1$と$b_1$を求めよ。 (2)$a_{n+1}$を$a_n$を用いて表せ。
(3)$b_{n+1}$を$b_n$を用いて表せ。
(4)数列$\left\{b_n\right\}$の一般項を求めよ。
(5)$\displaystyle\frac{a_1a_2a_3}{100}$ の値を求めよ。
この動画を見る
$\Large\boxed{1}$ 各項が正である数列$\left\{a_n\right\}$を次のように定める。$a_1$は関数
$y$=$\displaystyle\frac{1}{3}x^3$-10$x$ ($x$≧0)
が最小値をとるときの$x$の値とする。$a_{n+1}$は関数
$y$=$\displaystyle\frac{1}{3}x^3$-100$a_nx$ ($x$≧0)
が最小値をとるときの$x$の値とする。数列$\left\{b_n\right\}$を$b_n$=$\log_{10}a_n$ で定める。以下の問いに答えよ。
(1)$a_1$と$b_1$を求めよ。 (2)$a_{n+1}$を$a_n$を用いて表せ。
(3)$b_{n+1}$を$b_n$を用いて表せ。
(4)数列$\left\{b_n\right\}$の一般項を求めよ。
(5)$\displaystyle\frac{a_1a_2a_3}{100}$ の値を求めよ。
福田の数学〜神戸大学2024年理系第5問〜定積分で表された関数と不等式

単元:
#積分とその応用#定積分#神戸大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 0以上の実数$x$に対して、
$f(x)$=$\displaystyle\frac{1}{2}\int_{-x}^x\frac{1}{1+u^2}du$
と定める。以下の問いに答えよ。
(1)0≦$\alpha$<$\displaystyle\frac{\pi}{2}$ を満たす実数$\alpha$に対して、$f(\tan\alpha)$を求めよ。
(2)$xy$平面上で、次の連立不等式の表す領域を図示せよ。
0≦$x$≦1, 0≦$y$≦1, $f(x)$+$f(y)$≦$f(1)$
またその領域の面積を求めよ。
この動画を見る
$\Large\boxed{5}$ 0以上の実数$x$に対して、
$f(x)$=$\displaystyle\frac{1}{2}\int_{-x}^x\frac{1}{1+u^2}du$
と定める。以下の問いに答えよ。
(1)0≦$\alpha$<$\displaystyle\frac{\pi}{2}$ を満たす実数$\alpha$に対して、$f(\tan\alpha)$を求めよ。
(2)$xy$平面上で、次の連立不等式の表す領域を図示せよ。
0≦$x$≦1, 0≦$y$≦1, $f(x)$+$f(y)$≦$f(1)$
またその領域の面積を求めよ。
福田の数学〜神戸大学2024年理系第4問〜回転体の体積

単元:
#積分とその応用#面積・体積・長さ・速度#神戸大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 1辺の長さが$\sqrt 2$の正方形ABCDを底面にもち、高さが1である直方体ABCD-EFGHを、頂点の座標がそれぞれ
A(1,0,0), B(0,1,0), C(-1,0,0), D(0,-1,0),
E(1,0,1), F(0,1,1), G(-1,0,1), H(0,-1,1)
になるように$xyz$空間におく。以下の問いに答えよ。
(1)直方体ABCD-EFGHを直線AEのまわりに1回転してできる回転体を$X_1$とし、また直線ABのまわりに1回転してできる回転体を$X_2$とする。$X_1$の体積$V_1$と$X_2$の体積$V_2$を求めよ。
(2)0≦$t$≦1 とする。平面$x$=$t$と線分EFの共有点の座標を求めよ。
(3)直方体ABCD-EFGHを$x$軸のまわりに1回転してできる回転体を$X_3$とする。
$X_3$の体積$V_3$を求めよ。
この動画を見る
$\Large\boxed{4}$ 1辺の長さが$\sqrt 2$の正方形ABCDを底面にもち、高さが1である直方体ABCD-EFGHを、頂点の座標がそれぞれ
A(1,0,0), B(0,1,0), C(-1,0,0), D(0,-1,0),
E(1,0,1), F(0,1,1), G(-1,0,1), H(0,-1,1)
になるように$xyz$空間におく。以下の問いに答えよ。
(1)直方体ABCD-EFGHを直線AEのまわりに1回転してできる回転体を$X_1$とし、また直線ABのまわりに1回転してできる回転体を$X_2$とする。$X_1$の体積$V_1$と$X_2$の体積$V_2$を求めよ。
(2)0≦$t$≦1 とする。平面$x$=$t$と線分EFの共有点の座標を求めよ。
(3)直方体ABCD-EFGHを$x$軸のまわりに1回転してできる回転体を$X_3$とする。
$X_3$の体積$V_3$を求めよ。
福田の数学〜神戸大学2024年理系第3問〜さいころの目と約数に関する確率

単元:
#数A#場合の数と確率#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $n$を自然数とする。以下の問いに答えよ。
(1)1個のサイコロを投げて出た目が必ず$n$の約数となるような$n$を小さい順に3つ求めよ。
(2)1個のサイコロを投げて出た目が$n$の約数となる確率が$\displaystyle\frac{5}{6}$であるような$n$を小さい順に3つ求めよ。
(3)1個のサイコロを3回投げて出た目の積が160の約数となる確率を求めよ。
この動画を見る
$\Large\boxed{3}$ $n$を自然数とする。以下の問いに答えよ。
(1)1個のサイコロを投げて出た目が必ず$n$の約数となるような$n$を小さい順に3つ求めよ。
(2)1個のサイコロを投げて出た目が$n$の約数となる確率が$\displaystyle\frac{5}{6}$であるような$n$を小さい順に3つ求めよ。
(3)1個のサイコロを3回投げて出た目の積が160の約数となる確率を求めよ。
福田の数学〜神戸大学2024年理系第1問〜無理関数を利用して定義された数列の一般項

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#神戸大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ $c$を正の実数とする。各項が正である数列$\left\{a_n\right\}$を次のように定める。$a_1$は関数
$y$=$x$+$\sqrt{c-x^2}$ (0≦$x$≦$\sqrt c$)
が最大値をとるときの$x$の値とする。$a_{n+1}$は関数
$y$=$x$+$\sqrt{a_n-x^2}$ (0≦$x$≦$\sqrt{a_n}$)
が最大値をとるときの$x$の値とする。数列$\left\{b_n\right\}$を$b_n$=$\log_2a_n$ で定める。以下の問いに答えよ。
(1)$a_1$を$c$を用いて表せ。
(2)$b_{n+1}$を$b_n$を用いて表せ。
(3)数列$\left\{b_n\right\}$の一般項を$n$と$c$を用いて表せ。
この動画を見る
$\Large\boxed{1}$ $c$を正の実数とする。各項が正である数列$\left\{a_n\right\}$を次のように定める。$a_1$は関数
$y$=$x$+$\sqrt{c-x^2}$ (0≦$x$≦$\sqrt c$)
が最大値をとるときの$x$の値とする。$a_{n+1}$は関数
$y$=$x$+$\sqrt{a_n-x^2}$ (0≦$x$≦$\sqrt{a_n}$)
が最大値をとるときの$x$の値とする。数列$\left\{b_n\right\}$を$b_n$=$\log_2a_n$ で定める。以下の問いに答えよ。
(1)$a_1$を$c$を用いて表せ。
(2)$b_{n+1}$を$b_n$を用いて表せ。
(3)数列$\left\{b_n\right\}$の一般項を$n$と$c$を用いて表せ。
【高校数学】毎日積分75日目~47都道府県制覇への道~【⑱兵庫】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
【神戸大学 2023】
媒介変数表示
$\displaystyle x=sint, y=cos(t-\frac{π}{6})sint (0≦t≦π)$
で表される曲線を$C$とする。以下の問に答えよ。
(1) $\displaystyle \frac{dx}{dt}=0$ または $\displaystyle \frac{dy}{dt}=0$となる$t$の値を求めよ。
(2) $C$の概形を$xy$平面上に描け。
(3) $C$の$y≦0$の部分と$x$軸で囲まれた図形の面積を求めよ。
この動画を見る
【神戸大学 2023】
媒介変数表示
$\displaystyle x=sint, y=cos(t-\frac{π}{6})sint (0≦t≦π)$
で表される曲線を$C$とする。以下の問に答えよ。
(1) $\displaystyle \frac{dx}{dt}=0$ または $\displaystyle \frac{dy}{dt}=0$となる$t$の値を求めよ。
(2) $C$の概形を$xy$平面上に描け。
(3) $C$の$y≦0$の部分と$x$軸で囲まれた図形の面積を求めよ。
福田の数学〜神戸大学2023年文系第3問〜2つの円の位置関係と共通弦

単元:
#大学入試過去問(数学)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ aを正の実数とする。2つの円
$C_1$:$x^2$+$y^2$=$a$, $C_2$:$x^2$+$y^2$-$6x$-$4y$+3=0
が異なる2点A, Bで交わっているとする。直線ABが$x$軸および$y$軸と交わる点をそれぞれ($p$, 0), (0, $q$)とするとき、以下の問いに答えよ。
(1)$a$のとりうる値の範囲を求めよ。
(2)$p$, $q$の値を$a$を用いて表せ。
(3)$p$, $q$の値が共に整数となるような$a$の値をすべて求めよ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{3}$ aを正の実数とする。2つの円
$C_1$:$x^2$+$y^2$=$a$, $C_2$:$x^2$+$y^2$-$6x$-$4y$+3=0
が異なる2点A, Bで交わっているとする。直線ABが$x$軸および$y$軸と交わる点をそれぞれ($p$, 0), (0, $q$)とするとき、以下の問いに答えよ。
(1)$a$のとりうる値の範囲を求めよ。
(2)$p$, $q$の値を$a$を用いて表せ。
(3)$p$, $q$の値が共に整数となるような$a$の値をすべて求めよ。
2023筑波大学理系過去問
福田の数学〜神戸大学2023年文系第2問〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ A, Bの2人が、はじめに、Aは2枚の硬貨を、Bは1枚の硬貨を持っている。
2人は次の操作(P)を繰り返すゲームを行う。
(P)2人は持っている硬貨すべてを同時に投げる。それぞれが投げた硬貨のうち表がでた硬貨の枚数を数え、その枚数が少ない方が相手に1枚の硬貨を渡す。
操作(P)を繰り返し、2人のどちらかが持っている硬貨の枚数が3枚となった時点でこのゲームは終了する。操作(P)をn回繰り返し行ったとき、Aが持っている硬貨の枚数が3枚となってゲームが終了する確率を$p_n$とする。ただし、どの硬貨も1回投げたとき、表の出る確率は$\frac{1}{2}$とする。以下の問いに答えよ。
(1)$p_1$の値を求めよ。
(2)$p_2$の値を求めよ。
(3)$p_3$の値を求めよ。
2023神戸大学文系過去問
この動画を見る
$\Large\boxed{2}$ A, Bの2人が、はじめに、Aは2枚の硬貨を、Bは1枚の硬貨を持っている。
2人は次の操作(P)を繰り返すゲームを行う。
(P)2人は持っている硬貨すべてを同時に投げる。それぞれが投げた硬貨のうち表がでた硬貨の枚数を数え、その枚数が少ない方が相手に1枚の硬貨を渡す。
操作(P)を繰り返し、2人のどちらかが持っている硬貨の枚数が3枚となった時点でこのゲームは終了する。操作(P)をn回繰り返し行ったとき、Aが持っている硬貨の枚数が3枚となってゲームが終了する確率を$p_n$とする。ただし、どの硬貨も1回投げたとき、表の出る確率は$\frac{1}{2}$とする。以下の問いに答えよ。
(1)$p_1$の値を求めよ。
(2)$p_2$の値を求めよ。
(3)$p_3$の値を求めよ。
2023神戸大学文系過去問
福田の数学〜神戸大学2023年文系第1問〜2次方程式の解の存在範囲

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ $a$, $b$を実数とする。整式$f(x)$を$f(x)$=$x^2$+$ax$+$b$で定める。以下の問いに答えよ。
(1)2次方程式$f(x)$=0 が異なる2つの正の解をもつための$a$と$b$が満たすべき必要十分条件を求めよ。
(2)2次方程式$f(x)$=0 が異なる2つの実数解をもち、それらが共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲を$ab$平面上に図示せよ。
(3)2次方程式$f(x)$=0 の2つの解の実部が共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲を$ab$平面上に図示せよ。ただし、2次方程式の重解は2つと数える。
2023神戸大学文系過去問
この動画を見る
$\Large\boxed{1}$ $a$, $b$を実数とする。整式$f(x)$を$f(x)$=$x^2$+$ax$+$b$で定める。以下の問いに答えよ。
(1)2次方程式$f(x)$=0 が異なる2つの正の解をもつための$a$と$b$が満たすべき必要十分条件を求めよ。
(2)2次方程式$f(x)$=0 が異なる2つの実数解をもち、それらが共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲を$ab$平面上に図示せよ。
(3)2次方程式$f(x)$=0 の2つの解の実部が共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲を$ab$平面上に図示せよ。ただし、2次方程式の重解は2つと数える。
2023神戸大学文系過去問
福田の数学〜神戸大学2023年理系第5問〜媒介変数表示で表された曲線と面積

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#積分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#神戸大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 媒介変数表示
$x$=$\sin t$, $y$=$\cos(t-\frac{\pi}{6})\sin t$ (0≦$t$≦$\pi$)
で表される曲線をCとする。以下の問いに答えよ。
(1)$\frac{dx}{dt}$=0 または $\frac{dy}{dt}$=0 となる$t$の値を求めよ。
(2)Cの概形を$xy$平面上に描け。
(3)Cの$y$≦0 の部分と$x$軸で囲まれた図形の面積を求めよ。
2023神戸大学理系過去問
この動画を見る
$\Large\boxed{5}$ 媒介変数表示
$x$=$\sin t$, $y$=$\cos(t-\frac{\pi}{6})\sin t$ (0≦$t$≦$\pi$)
で表される曲線をCとする。以下の問いに答えよ。
(1)$\frac{dx}{dt}$=0 または $\frac{dy}{dt}$=0 となる$t$の値を求めよ。
(2)Cの概形を$xy$平面上に描け。
(3)Cの$y$≦0 の部分と$x$軸で囲まれた図形の面積を求めよ。
2023神戸大学理系過去問
福田の数学〜神戸大学2023年理系第4問〜平面に下ろした垂線ベクトルと四面体の体積
単元:
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#神戸大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
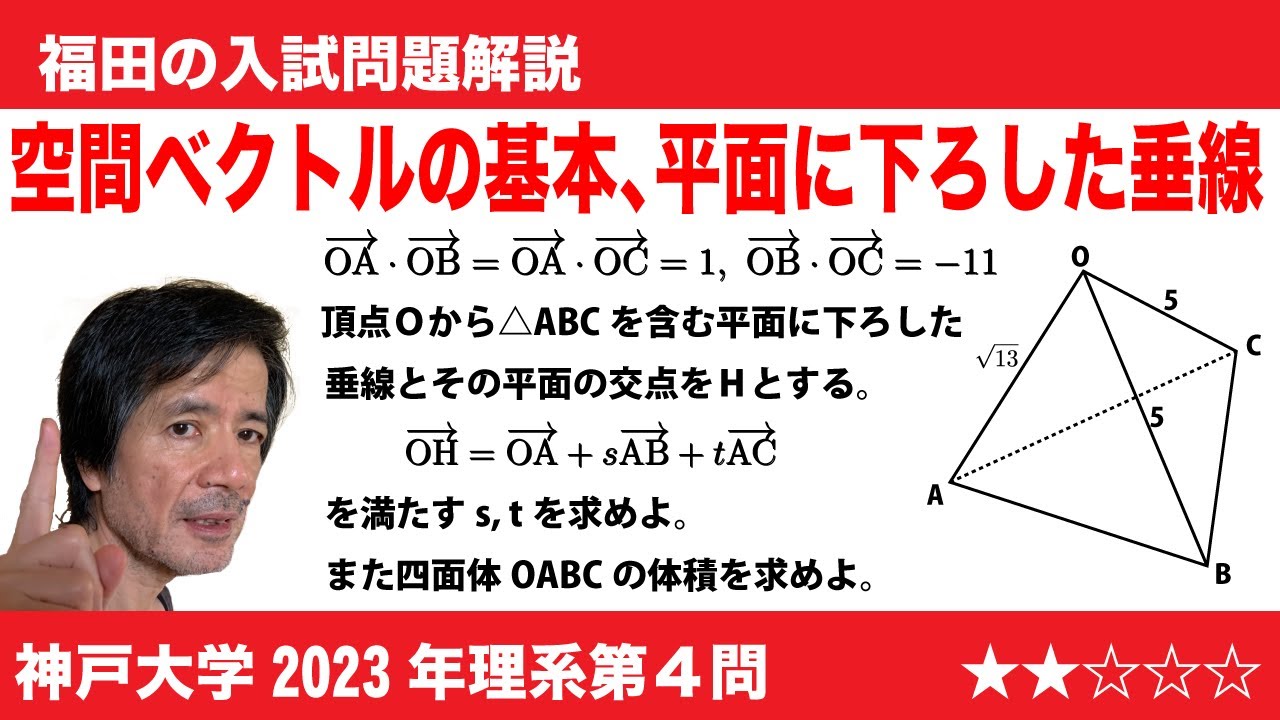
$\Large\boxed{4}$ 四面体OABCがあり、辺OA, OB, OCの長さはそれぞれ$\sqrt{13}$, 5, 5である。
$\overrightarrow{OA}$・$\overrightarrow{OB}$=$\overrightarrow{OA}$・$\overrightarrow{OC}$=1, $\overrightarrow{OB}$・$\overrightarrow{OC}$=-11 とする。頂点Oから$\triangle$ABCを含む平面に下ろした垂線とその平面の交点をHとする。以下の問いに答えよ。
(1)線分ABの長さを求めよ。
(2)実数$s$, $t$を$\overrightarrow{OH}$=$\overrightarrow{OA}$+$s\overrightarrow{AB}$+$t\overrightarrow{AC}$ を満たすように定めるとき、$s$と$t$の値を求めよ。
(3)四面体OABCの体積を求めよ。
2023神戸大学理系過去問
この動画を見る
$\Large\boxed{4}$ 四面体OABCがあり、辺OA, OB, OCの長さはそれぞれ$\sqrt{13}$, 5, 5である。
$\overrightarrow{OA}$・$\overrightarrow{OB}$=$\overrightarrow{OA}$・$\overrightarrow{OC}$=1, $\overrightarrow{OB}$・$\overrightarrow{OC}$=-11 とする。頂点Oから$\triangle$ABCを含む平面に下ろした垂線とその平面の交点をHとする。以下の問いに答えよ。
(1)線分ABの長さを求めよ。
(2)実数$s$, $t$を$\overrightarrow{OH}$=$\overrightarrow{OA}$+$s\overrightarrow{AB}$+$t\overrightarrow{AC}$ を満たすように定めるとき、$s$と$t$の値を求めよ。
(3)四面体OABCの体積を求めよ。
2023神戸大学理系過去問
福田の数学〜神戸大学2023年理系第3問〜確率の基本性質と数え上げ

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ nを2以上の整数とする。袋の中には1から2nまでの整数が1つずつ書いてある2n枚のカードが入っている。以下の問いに答えよ。
(1)この袋から同時に2枚のカードを取り出したとき、そのカードに書かれている数の和が偶数である確率を求めよ。
(2)この袋から同時に3枚のカードを取り出したとき、そのカードに書かれている数の和が偶数である確率を求めよ。
(3)この袋から同時に2枚のカードを取り出したとき、そのカードに書かれている数の和が2n+1以上である確率を求めよ。
2023神戸大学理系過去問
この動画を見る
$\Large\boxed{3}$ nを2以上の整数とする。袋の中には1から2nまでの整数が1つずつ書いてある2n枚のカードが入っている。以下の問いに答えよ。
(1)この袋から同時に2枚のカードを取り出したとき、そのカードに書かれている数の和が偶数である確率を求めよ。
(2)この袋から同時に3枚のカードを取り出したとき、そのカードに書かれている数の和が偶数である確率を求めよ。
(3)この袋から同時に2枚のカードを取り出したとき、そのカードに書かれている数の和が2n+1以上である確率を求めよ。
2023神戸大学理系過去問
福田の数学〜神戸大学2023年理系第2問〜2次方程式の解の存在範囲

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#複素数と方程式#2次方程式と2次不等式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ a,bを実数とする。整式$f(x)$=$x^2$+$ax$+$b$ で定める。以下の問いに答えよ。ただし、2次方程式の重解は2つと数える。
(1)2次方程式$f(x)$=0が異なる2つの正の解をもつためのaとbが満たすべき必要十分条件を求めよ。
(2)2次方程式$f(x)$=0の2つの解の実部が共に0より小さくなるような点(a, b)の存在する範囲をab平面上に図示せよ。
(3)2次方程式$f(x)$=0の2つの解の実部が共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲をab平面上に図示せよ。
2023神戸大学理系過去問
この動画を見る
$\Large\boxed{2}$ a,bを実数とする。整式$f(x)$=$x^2$+$ax$+$b$ で定める。以下の問いに答えよ。ただし、2次方程式の重解は2つと数える。
(1)2次方程式$f(x)$=0が異なる2つの正の解をもつためのaとbが満たすべき必要十分条件を求めよ。
(2)2次方程式$f(x)$=0の2つの解の実部が共に0より小さくなるような点(a, b)の存在する範囲をab平面上に図示せよ。
(3)2次方程式$f(x)$=0の2つの解の実部が共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲をab平面上に図示せよ。
2023神戸大学理系過去問
福田の数学〜神戸大学2023年理系第1問〜漸化式の解法

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 関数$f(x)$を
$f(x)$=$\left\{\begin{array} \\
\frac{1}{2}x+\frac{1}{2} (x≦ 1)\\
2x-1 (x \gt 1)\\
\end{array}\right.$
で定める。aを実数とし、数列$\left\{a_n\right\}$を
$a_1$=a, $a_{n+1}$=$f(a_n)$ (n=1,2,3,...)
で定める。以下の問いに答えよ。
(1)すべての実数xについて$f(x)$≧x が成り立つことを示せ。
(2)a≦1のとき、すべての正の整数nについて$a_n$≦1が成り立つことを示せ。
(3)数列$\left\{a_n\right\}$の一般項をnとaを用いて表せ。
2023神戸大学理系過去問
この動画を見る
$\Large\boxed{1}$ 関数$f(x)$を
$f(x)$=$\left\{\begin{array} \\
\frac{1}{2}x+\frac{1}{2} (x≦ 1)\\
2x-1 (x \gt 1)\\
\end{array}\right.$
で定める。aを実数とし、数列$\left\{a_n\right\}$を
$a_1$=a, $a_{n+1}$=$f(a_n)$ (n=1,2,3,...)
で定める。以下の問いに答えよ。
(1)すべての実数xについて$f(x)$≧x が成り立つことを示せ。
(2)a≦1のとき、すべての正の整数nについて$a_n$≦1が成り立つことを示せ。
(3)数列$\left\{a_n\right\}$の一般項をnとaを用いて表せ。
2023神戸大学理系過去問
神戸大 3次関数の最大最小

単元:
#大学入試過去問(数学)#式と証明#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$t\gt 0$とし,
$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$
$-1\leqq x \leqq 2$ における最大値と最小値を求めよ.
神戸大過去問
この動画を見る
$t\gt 0$とし,
$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$
$-1\leqq x \leqq 2$ における最大値と最小値を求めよ.
神戸大過去問
神戸大 不等式の証明

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1・・・・a_n\left(a_1+・・・a_n\right)\left(\dfrac{1}{a_1}+・・・・+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
この動画を見る
(1)$\dfrac{y}{x}+\dfrac{x}{y}\geqq 2$を示せ.等号成立するか?
(2)n個の正実数$a_1・・・・a_n\left(a_1+・・・a_n\right)\left(\dfrac{1}{a_1}+・・・・+\dfrac{1}{a_n}\right)\geqq n^2$
を示せ。等号成立はするか?
大学入試問題#505「綺麗な数列の問題」 #神戸大学 (2022) #数列 #極限
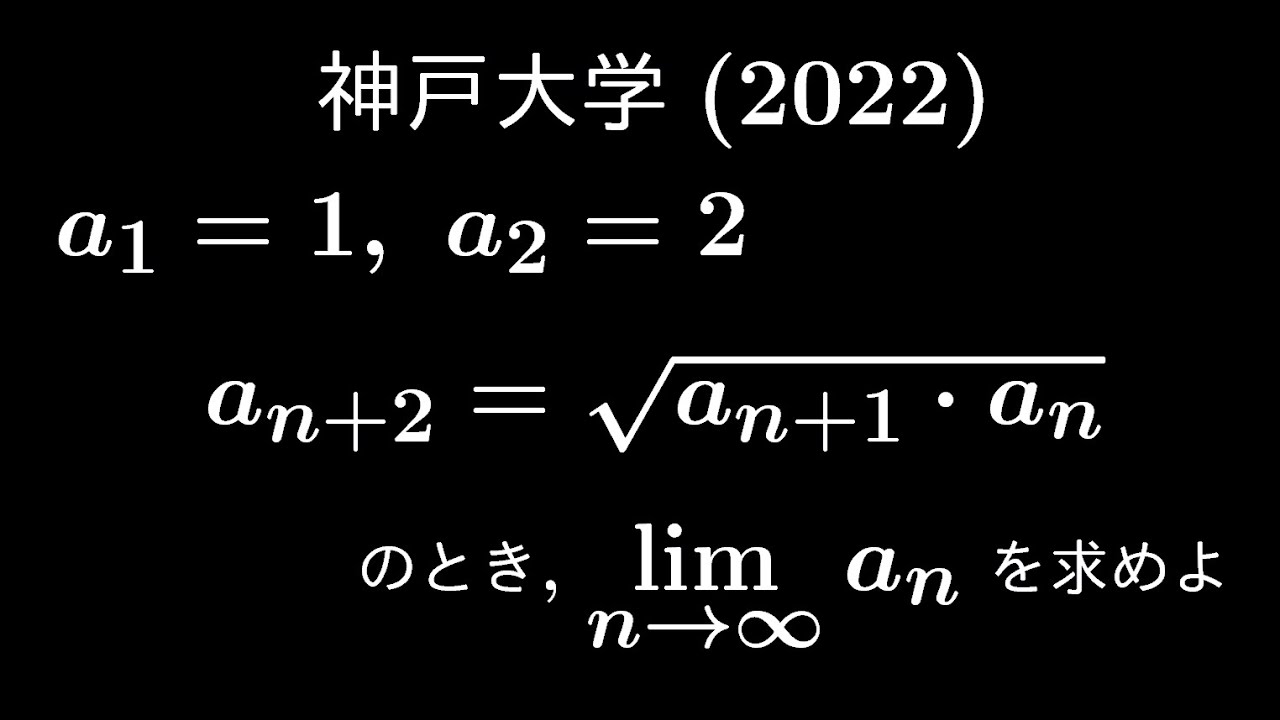
単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,\ a_2=2$
$a_{n+2}=\sqrt{ a_{n+1}・a_n }$のとき
$\displaystyle \lim_{ n \to \infty } a_n$を求めよ
出典:2022年神戸大学 入試問題
この動画を見る
$a_1=1,\ a_2=2$
$a_{n+2}=\sqrt{ a_{n+1}・a_n }$のとき
$\displaystyle \lim_{ n \to \infty } a_n$を求めよ
出典:2022年神戸大学 入試問題
大学入試問題#464「誘導の力は偉大」 神戸大学(2000) #不定積分 #積分の応用

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \frac{1}{x^3(1-x)}$
(1)
$f(x)=\displaystyle \frac{a_1}{x}+\displaystyle \frac{a_2}{x^2}+\displaystyle \frac{a_3}{x^3}+\displaystyle \frac{b}{1-x}$
とおくとき、定数$a_1,a_2,a_3,b$を求めよ
(2)
$\displaystyle \int f(x) dx$
(3)
$\displaystyle \int \displaystyle \frac{dx}{x^P(1-x)}(P=1,2,3,・・・)$
出典:2000年神戸大学 入試問題
この動画を見る
$f(x)=\displaystyle \frac{1}{x^3(1-x)}$
(1)
$f(x)=\displaystyle \frac{a_1}{x}+\displaystyle \frac{a_2}{x^2}+\displaystyle \frac{a_3}{x^3}+\displaystyle \frac{b}{1-x}$
とおくとき、定数$a_1,a_2,a_3,b$を求めよ
(2)
$\displaystyle \int f(x) dx$
(3)
$\displaystyle \int \displaystyle \frac{dx}{x^P(1-x)}(P=1,2,3,・・・)$
出典:2000年神戸大学 入試問題
福田の1.5倍速演習〜合格する重要問題092〜神戸大学2018年度理系第5問〜回転体の体積

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 座標空間において、Oを原点とし、A(2,0,0), B(0,2,0), C(1,1,0)とする。$\triangle$OABを直線OCの周りに1回転してできる回転体をLとする。
(1)直線OC上にない点P(x,y,z)から直線OCにおろした垂線をPHとする。
$\overrightarrow{OH}$と$\overrightarrow{HP}$をx,y,zの式で表せ。
(2)点P(x,y,z)がLの点であるための条件は
$z^2≦2xy$ かつ $0≦x+y≦2$
であることを示せ。
(3)$1≦a≦2$とする。Lを平面x=aで切った切り口の面積S(a)を求めよ。
(4)立体${(x,y,z)|(x,y,z)\in L, 1≦x≦2}$の体積を求めよ。
2018神戸大学理系過去問
この動画を見る
$\Large\boxed{5}$ 座標空間において、Oを原点とし、A(2,0,0), B(0,2,0), C(1,1,0)とする。$\triangle$OABを直線OCの周りに1回転してできる回転体をLとする。
(1)直線OC上にない点P(x,y,z)から直線OCにおろした垂線をPHとする。
$\overrightarrow{OH}$と$\overrightarrow{HP}$をx,y,zの式で表せ。
(2)点P(x,y,z)がLの点であるための条件は
$z^2≦2xy$ かつ $0≦x+y≦2$
であることを示せ。
(3)$1≦a≦2$とする。Lを平面x=aで切った切り口の面積S(a)を求めよ。
(4)立体${(x,y,z)|(x,y,z)\in L, 1≦x≦2}$の体積を求めよ。
2018神戸大学理系過去問
大学入試問題#444「複素数の王道手筋」 神戸大学(1998) 文系 #複素数

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$z$:虚数
(1)
$z+\displaystyle \frac{1}{z}$が実数の時
$|z|$の値$a$を求めよ。
(2)
$|z|=a$のとき
$\omega=(z+\sqrt{ 2 }+\sqrt{ 2 }i)^4$において$|\omega|,\ argw$の範囲を求めよ。
出典:1998年神戸大学 入試問題
この動画を見る
$z$:虚数
(1)
$z+\displaystyle \frac{1}{z}$が実数の時
$|z|$の値$a$を求めよ。
(2)
$|z|=a$のとき
$\omega=(z+\sqrt{ 2 }+\sqrt{ 2 }i)^4$において$|\omega|,\ argw$の範囲を求めよ。
出典:1998年神戸大学 入試問題
二次関数の難問!大事な考え方【神戸大学】【数学 入試問題】

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$a$を実数とし,$f(x)=-x^2-2x+2,g(x)=-x^2+ax+a$とする。以下の問いに答えよ。
(1)すべての実数$s,t$に対して$f(x)≧g(t)$が成り立つような,$a$の値の範囲を求めよ。
(2)$0≦x≦1を満たすすべての$x$に対して,$f(x)≧g(x)が成り立つような$a$の範囲を求めよ。
神戸大過去問
この動画を見る
$a$を実数とし,$f(x)=-x^2-2x+2,g(x)=-x^2+ax+a$とする。以下の問いに答えよ。
(1)すべての実数$s,t$に対して$f(x)≧g(t)$が成り立つような,$a$の値の範囲を求めよ。
(2)$0≦x≦1を満たすすべての$x$に対して,$f(x)≧g(x)が成り立つような$a$の範囲を求めよ。
神戸大過去問
福田の1.5倍速演習〜合格する重要問題056〜神戸大学2017年度文系第1問〜3次関数の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ tを正の実数とする。$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$とおく。
以下の問いに答えよ。
(1)2t^3-3t^2+1 を因数分解せよ。
(2)$f(x)$が極小値0をもつことを示せ。
(3)$-1 \leqq x \leqq 2$における$f(x)$の最小値$m$と最大値$M$をtの式で表せ。
2017神戸大学文系過去問
この動画を見る
$\Large{\boxed{1}}$ tを正の実数とする。$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$とおく。
以下の問いに答えよ。
(1)2t^3-3t^2+1 を因数分解せよ。
(2)$f(x)$が極小値0をもつことを示せ。
(3)$-1 \leqq x \leqq 2$における$f(x)$の最小値$m$と最大値$M$をtの式で表せ。
2017神戸大学文系過去問
