 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
福田の数学〜慶應義塾大学2022年看護医療学部第1問(5)〜解と係数の関係と式の値の計算

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(5)iを虚数単位とし、$\alpha=\frac{1-\sqrt3i}{4}$とする。このとき、
$a,b$を実数とする2次方程式$x^2+ax+b=0$の解の1つが$\alpha$であるならば、
$a=\boxed{\ \ ア\ \ },\ b=\boxed{\ \ イ\ \ }$である。
また、$f(x)=4x^4-3x^3+2x^2$とするとき、$f(\alpha)$の値は$\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{1}}$(5)iを虚数単位とし、$\alpha=\frac{1-\sqrt3i}{4}$とする。このとき、
$a,b$を実数とする2次方程式$x^2+ax+b=0$の解の1つが$\alpha$であるならば、
$a=\boxed{\ \ ア\ \ },\ b=\boxed{\ \ イ\ \ }$である。
また、$f(x)=4x^4-3x^3+2x^2$とするとき、$f(\alpha)$の値は$\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
大学入試問題#257 東京理科大学(2011) #極限 #区分求積法

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{k}{n^2}log(\displaystyle \frac{n+k}{n})$を求めよ。
出典:2011年東京理科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{k}{n^2}log(\displaystyle \frac{n+k}{n})$を求めよ。
出典:2011年東京理科大学 入試問題
福田の数学〜慶應義塾大学2022年看護医療学部第1問(4)〜サイコロの目の最小値が2である確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(4)3個のさいころを同時に投げるとき、出た目の最小値が2以上となる確率は
$\boxed{\ \ ア\ \ }$であり、最小値がちょうど2となる確率は$\boxed{\ \ イ\ \ }$である。また、
出た目の最小値が2であったとき、どの2つの目も互いに素である条件付き確率は
$\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{1}}$(4)3個のさいころを同時に投げるとき、出た目の最小値が2以上となる確率は
$\boxed{\ \ ア\ \ }$であり、最小値がちょうど2となる確率は$\boxed{\ \ イ\ \ }$である。また、
出た目の最小値が2であったとき、どの2つの目も互いに素である条件付き確率は
$\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
【誘導あり:概要欄】大学入試問題#256 神戸大学2012 #極限 #はさみうちの定理

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$2 \leqq n$自然数
$S_n=\displaystyle \sum_{k=1}^{n^3-1}\displaystyle \frac{1}{k\ log\ k}$
(1)
$2 \leqq k$:自然数
$\displaystyle \frac{1}{(k+1)log(k+1)} \lt \displaystyle \int_{k}^{k+1}\displaystyle \frac{dx}{x\ log\ x} \lt \displaystyle \frac{1}{k\ log\ k}$
(2)
$\displaystyle \lim_{ n \to \infty }S_n$を求めよ。
出典:2012年神戸大学 入試問題
この動画を見る
$2 \leqq n$自然数
$S_n=\displaystyle \sum_{k=1}^{n^3-1}\displaystyle \frac{1}{k\ log\ k}$
(1)
$2 \leqq k$:自然数
$\displaystyle \frac{1}{(k+1)log(k+1)} \lt \displaystyle \int_{k}^{k+1}\displaystyle \frac{dx}{x\ log\ x} \lt \displaystyle \frac{1}{k\ log\ k}$
(2)
$\displaystyle \lim_{ n \to \infty }S_n$を求めよ。
出典:2012年神戸大学 入試問題
福田の数学〜慶應義塾大学2022年看護医療学部第1問(3)〜三角関数の最大最小の種類

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(3)関数$f(\theta)=\cos2\theta+2\cos\theta$が
$0 \leqq \theta \leqq \pi$ の範囲で最小値をとるのは$\theta=\boxed{\ \ ア\ \ }$
のときであり、最大値を取るのは$\theta=\boxed{\ \ イ\ \ }$のときである。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{1}}$(3)関数$f(\theta)=\cos2\theta+2\cos\theta$が
$0 \leqq \theta \leqq \pi$ の範囲で最小値をとるのは$\theta=\boxed{\ \ ア\ \ }$
のときであり、最大値を取るのは$\theta=\boxed{\ \ イ\ \ }$のときである。
2022慶應義塾大学看護医療学科過去問
山形大 ナイスな問題

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#山形大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \alpha=\cos36°+i\sin36°$とする.
(1)$(x-1)(x-\alpha)(x-\alpha^2)・・・・・・(x-\alpha^9)$を計算せよ.
(2)$(x-1)(x-\alpha^2)(x-\alpha^4)(x-\alpha^6)(x-\alpha^8)$を計算せよ.
(3)$(x-\alpha)(x-\alpha^3)(x-\alpha^7)(x-\alpha^9)$を計算せよ.
(4)(3)を用いて\alpha+\dfrac{1}{\alpha}を計算せよ.
山形大過去問
この動画を見る
$ \alpha=\cos36°+i\sin36°$とする.
(1)$(x-1)(x-\alpha)(x-\alpha^2)・・・・・・(x-\alpha^9)$を計算せよ.
(2)$(x-1)(x-\alpha^2)(x-\alpha^4)(x-\alpha^6)(x-\alpha^8)$を計算せよ.
(3)$(x-\alpha)(x-\alpha^3)(x-\alpha^7)(x-\alpha^9)$を計算せよ.
(4)(3)を用いて\alpha+\dfrac{1}{\alpha}を計算せよ.
山形大過去問
福田の数学〜慶應義塾大学2022年看護医療学部第1問(2)〜指数計算

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
問題文全文(内容文):
${\large\boxed{1}}$(2)aを正の実数、pを実数とする。$a^{2p}=3$のとき、
$\frac{a^{2p}-a^{-2p}}{a^p-a^{-p}}$の値は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{1}}$(2)aを正の実数、pを実数とする。$a^{2p}=3$のとき、
$\frac{a^{2p}-a^{-2p}}{a^p-a^{-p}}$の値は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
実数とは? 法政大学

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a,b,cの値を求めよ(a,b,c:実数)
$a^2+b^2+c^2=2(-a+c-1)$
法政大学
この動画を見る
a,b,cの値を求めよ(a,b,c:実数)
$a^2+b^2+c^2=2(-a+c-1)$
法政大学
福田の数学〜慶應義塾大学2022年看護医療学部第1問(1)〜対数計算

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(1)$\log_3\sqrt6\ -\log_3\frac{2}{3}+\log_3\sqrt2\ $を有理数で表すと$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{1}}$(1)$\log_3\sqrt6\ -\log_3\frac{2}{3}+\log_3\sqrt2\ $を有理数で表すと$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
大学入試問題#254 神戸大学2012 #定積分
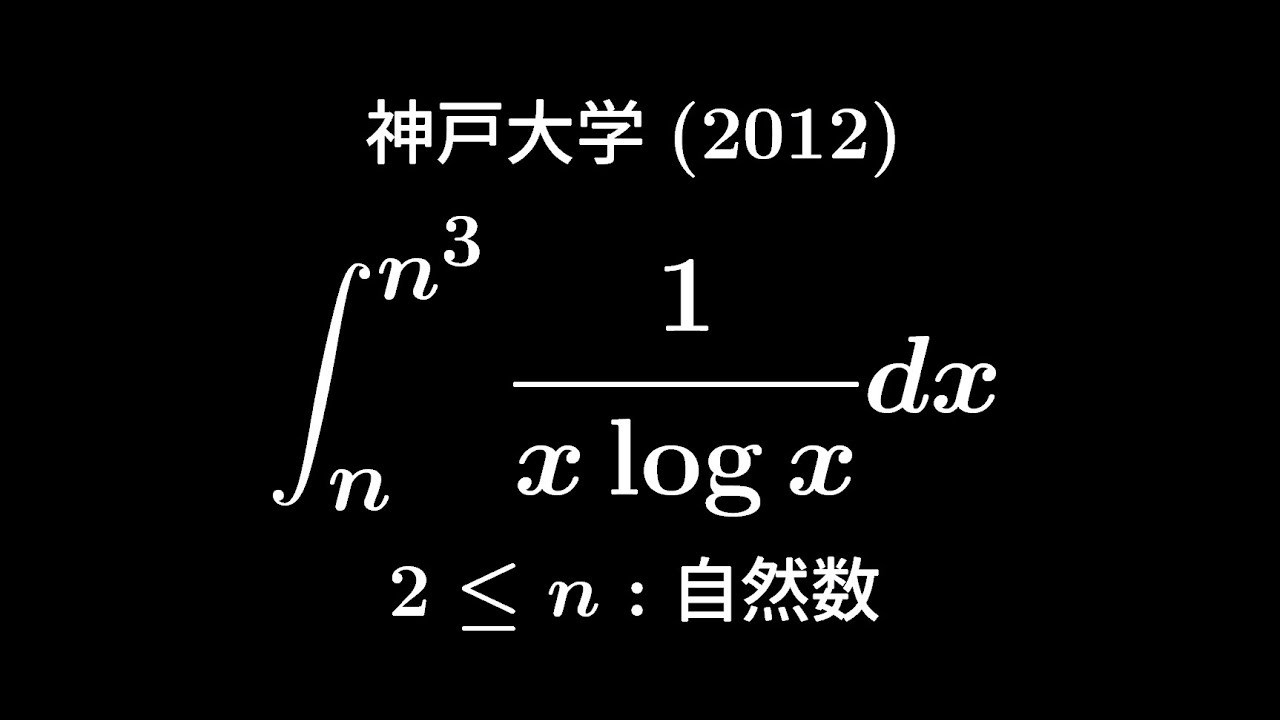
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$2 \leqq n$自然数
$\displaystyle \int_{n}^{n^3}\displaystyle \frac{dx}{x\ log\ x}$を計算せよ。
出典:2012年神戸大学 入試問題
この動画を見る
$2 \leqq n$自然数
$\displaystyle \int_{n}^{n^3}\displaystyle \frac{dx}{x\ log\ x}$を計算せよ。
出典:2012年神戸大学 入試問題
確率×整数問題!さいころの目の最小公倍数や最大公約数【数学 入試問題】【北海道大学】

単元:
#数Ⅰ#数A#場合の数と確率#場合の数#確率#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を2以上の自然数とする。1個のさいころを続けて$n$回投げる試行を行い,出た目を順に$X_1,X_2,・・・,X_n$とする。
(1)$X_1,X_2,・・・,X_n$の最大公約数が3となる確率を$n$の式で表せ。
北海道大過去問
この動画を見る
$n$を2以上の自然数とする。1個のさいころを続けて$n$回投げる試行を行い,出た目を順に$X_1,X_2,・・・,X_n$とする。
(1)$X_1,X_2,・・・,X_n$の最大公約数が3となる確率を$n$の式で表せ。
北海道大過去問
福田の数学〜慶應義塾大学2022年環境情報学部第6問〜新型ウィルス感染拡大による大学の授業形態の決定

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#図形と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{6}}$ある大学で来学期の授業の形式をどうするかを検討している。
授業形式の選択としては、通常の対面形式(授業形式uと呼ぶことにする)、
$\textrm{Web}$上で試料を閲覧できたり課題を行ったりできるオンデマンド形式(授業形式vと呼ぶことにする)
$\textrm{Web}$会議システムを使用するオンライン配信形式(授業形式wと呼ぶことにする)
の3つがあるとする。
また、来学期の新型ウイルスの感染状況については、
急激に拡大している状況(感染状況xと呼ぶことにする)、
ピークは過ぎたが十分な収束にはいたっていない状況(感染状況yとよぶことにする)、
ある程度収束した状況(感染状況zとよぶことにする)の3つが考えられるとする。
いま、この大学は授業形式と新型ウイルスの感染状況の組み合わせについて、
次の表(※動画参照)に示す評論値(値が高いほど評価も高い)を定めているものとする。
来学期の感染状況について、感染状況xである確率を$p_x$、
感染状況yである確率をp_y、感染状況zである確率を$p_z$とすると、
xyz空間において点$p=(p_x,p_y,p_z)は(1,0,0),(0,1,0),(0,0,1)$を頂点とする正三角形上の
点としてあらわすことができる。この正三角形上において、点pから各辺に垂線を下ろしたとき、
(1,0,0)と向かいの辺に下ろした垂線の長さをl_x、(0,1,0)と向かいの辺に下した垂線の長さを$l_y$、
(0,0,1)と向かいの辺に下した垂線の長さを$l_z$とする。
(1)このとき$p_x=\frac{\sqrt{\boxed{\ \ アイ\ \ }}}{\boxed{\ \ ウエ\ \ }}\ l_x,\ \ \ \,$
$p_y=\frac{\sqrt{\boxed{\ \ オカ\ \ }}}{\boxed{\ \ キク\ \ }}\ l_y,\ \ \ \ p_z=\frac{\sqrt{\boxed{\ \ ケコ\ \ }}}{\boxed{\ \ サシ\ \ }}\ l_z$が成り立つ。
いま、正三角形上の点$p=(p_x,p_y,p_z)$に対して、上記の評価の期待値を最大にする
授業形式のラベルをつけることにする。ただし、pによっては評価値を最大にする選択が
複数ある場合もあり、その場合にはpに複数のラベルをつけることにする。
さらに、原点と(0,1,0),(0,0,1)を原点とするyz平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にxという感染状況のラベルをつけ、
原点と(1,0,0),(0,0,1)を原点とするxz平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にyという感染状況のラベルをつけ、
原点と(1,0,0),(0,1,0)を原点とするxy平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にzという感染状況のラベルをつけることにする。
すると、正三角形と3つの直角二等辺三角形からなる四面体の面上(頂点、辺も含む)
のそれぞれの点には、1つもしくは複数のラベルがつくことになる。例えば、
原点には$\left\{x,y,z\right\}$の3つのラベルがつく。
(2)このとき、正三角形の面上(頂点、辺も含む)の各点pにつけられるラベルの
可能性を列挙すると、以下の通りとなる。ただし、複数のラベルがつけられる場合には、
それぞれの中括弧内では、アルファベット順に書くものとする。空欄に入る
ラベルについて下記の選択肢から選びなさい。
単一のラベルがつく場合:$\left\{\boxed{\ \ ス\ \ }\right\},\left\{w\right\}$
2つのラベルがつく場合:$\left\{\boxed{\ \ セ\ \ },w\right\},\left\{u,\boxed{\ \ ソ\ \ }\right\},$
$\left\{\boxed{\ \ タ\ \ },y\right\},\left\{w,y\right\},\left\{\boxed{\ \ チ\ \ },z\right\}$
3つのラベルがつく場合:$\left\{\boxed{\ \ ツ\ \ },w,\boxed{\ \ テ\ \ }\right\},\left\{\boxed{\ \ ト\ \ },\boxed{\ \ ナ\ \ },\boxed{\ \ ニ\ \ }\right\}$
4つのラベルがつく場合:$\left\{u,\boxed{\ \ ヌ\ \ },\boxed{\ \ ネ\ \ },\boxed{\ \ ノ\ \ }\right\},\left\{\boxed{\ \ ハ\ \ },\boxed{\ \ ヒ\ \ },\boxed{\ \ フ\ \ },\boxed{\ \ ヘ\ \ }\right\}$
選択肢:$(1)\ \ \ u\ \ \ (2)\ \ \ v\ \ \ (3)\ \ \ w\ \ \ (4)\ \ \ x\ \ \ (5)\ \ \ y\ \ \ (6)\ \ \ z$
2022慶應義塾大学環境情報学部過去問
この動画を見る
${\large\boxed{6}}$ある大学で来学期の授業の形式をどうするかを検討している。
授業形式の選択としては、通常の対面形式(授業形式uと呼ぶことにする)、
$\textrm{Web}$上で試料を閲覧できたり課題を行ったりできるオンデマンド形式(授業形式vと呼ぶことにする)
$\textrm{Web}$会議システムを使用するオンライン配信形式(授業形式wと呼ぶことにする)
の3つがあるとする。
また、来学期の新型ウイルスの感染状況については、
急激に拡大している状況(感染状況xと呼ぶことにする)、
ピークは過ぎたが十分な収束にはいたっていない状況(感染状況yとよぶことにする)、
ある程度収束した状況(感染状況zとよぶことにする)の3つが考えられるとする。
いま、この大学は授業形式と新型ウイルスの感染状況の組み合わせについて、
次の表(※動画参照)に示す評論値(値が高いほど評価も高い)を定めているものとする。
来学期の感染状況について、感染状況xである確率を$p_x$、
感染状況yである確率をp_y、感染状況zである確率を$p_z$とすると、
xyz空間において点$p=(p_x,p_y,p_z)は(1,0,0),(0,1,0),(0,0,1)$を頂点とする正三角形上の
点としてあらわすことができる。この正三角形上において、点pから各辺に垂線を下ろしたとき、
(1,0,0)と向かいの辺に下ろした垂線の長さをl_x、(0,1,0)と向かいの辺に下した垂線の長さを$l_y$、
(0,0,1)と向かいの辺に下した垂線の長さを$l_z$とする。
(1)このとき$p_x=\frac{\sqrt{\boxed{\ \ アイ\ \ }}}{\boxed{\ \ ウエ\ \ }}\ l_x,\ \ \ \,$
$p_y=\frac{\sqrt{\boxed{\ \ オカ\ \ }}}{\boxed{\ \ キク\ \ }}\ l_y,\ \ \ \ p_z=\frac{\sqrt{\boxed{\ \ ケコ\ \ }}}{\boxed{\ \ サシ\ \ }}\ l_z$が成り立つ。
いま、正三角形上の点$p=(p_x,p_y,p_z)$に対して、上記の評価の期待値を最大にする
授業形式のラベルをつけることにする。ただし、pによっては評価値を最大にする選択が
複数ある場合もあり、その場合にはpに複数のラベルをつけることにする。
さらに、原点と(0,1,0),(0,0,1)を原点とするyz平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にxという感染状況のラベルをつけ、
原点と(1,0,0),(0,0,1)を原点とするxz平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にyという感染状況のラベルをつけ、
原点と(1,0,0),(0,1,0)を原点とするxy平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にzという感染状況のラベルをつけることにする。
すると、正三角形と3つの直角二等辺三角形からなる四面体の面上(頂点、辺も含む)
のそれぞれの点には、1つもしくは複数のラベルがつくことになる。例えば、
原点には$\left\{x,y,z\right\}$の3つのラベルがつく。
(2)このとき、正三角形の面上(頂点、辺も含む)の各点pにつけられるラベルの
可能性を列挙すると、以下の通りとなる。ただし、複数のラベルがつけられる場合には、
それぞれの中括弧内では、アルファベット順に書くものとする。空欄に入る
ラベルについて下記の選択肢から選びなさい。
単一のラベルがつく場合:$\left\{\boxed{\ \ ス\ \ }\right\},\left\{w\right\}$
2つのラベルがつく場合:$\left\{\boxed{\ \ セ\ \ },w\right\},\left\{u,\boxed{\ \ ソ\ \ }\right\},$
$\left\{\boxed{\ \ タ\ \ },y\right\},\left\{w,y\right\},\left\{\boxed{\ \ チ\ \ },z\right\}$
3つのラベルがつく場合:$\left\{\boxed{\ \ ツ\ \ },w,\boxed{\ \ テ\ \ }\right\},\left\{\boxed{\ \ ト\ \ },\boxed{\ \ ナ\ \ },\boxed{\ \ ニ\ \ }\right\}$
4つのラベルがつく場合:$\left\{u,\boxed{\ \ ヌ\ \ },\boxed{\ \ ネ\ \ },\boxed{\ \ ノ\ \ }\right\},\left\{\boxed{\ \ ハ\ \ },\boxed{\ \ ヒ\ \ },\boxed{\ \ フ\ \ },\boxed{\ \ ヘ\ \ }\right\}$
選択肢:$(1)\ \ \ u\ \ \ (2)\ \ \ v\ \ \ (3)\ \ \ w\ \ \ (4)\ \ \ x\ \ \ (5)\ \ \ y\ \ \ (6)\ \ \ z$
2022慶應義塾大学環境情報学部過去問
大学入試問題#253 青山学院大学(2011) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi}x(\sin\ x+\cos\ 2x)dx$を計算せよ。
出典:2011年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2\pi}x(\sin\ x+\cos\ 2x)dx$を計算せよ。
出典:2011年青山学院大学 入試問題
福田の数学〜慶應義塾大学2022年環境情報学部第5問〜ジャンケンで勝者1人を決める確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{5}}$複数人でじゃんけんを何回か行い勝ち残った1人を決めることを考える。
最初は全員がじゃんけんに参加して始める。それぞれのじゃんけんでは、
そのじゃんけんの参加者がそれぞれグー、チョキ、パーのどれかを出し、
もし誰か1人が他の全員に買った場合にはその1人が商社となりじゃんけん
はそこで終了する。そうでない場合、全員が同じ手を出したか、グー、チョキ、
パーのそれぞれを誰かが出した場合には'あいこ'となり、そのじゃんけんの参加者全員が
次のじゃんけんに進む。上記以外で、2つの手に分かれた場合には、
負けた手を出した人を除いて勝った手を出した人だけが次のじゃんけんに進む。
このように、じゃんけんを繰り返し行い、1人の勝者が決まるまで続けるものとする。
ただし、じゃんけんの参加者全員、グー、チョキ、パーのどれかを等しい確率
で毎回ランダムに出すものとする。また通常のじゃんけんのように
グーはチョキに勝ち、チョキはパーに勝ち、パーはグーに勝つものとする。
(1)3人でじゃんけんを複数回行い1人の勝者を決める場合、1回目のじゃんけんで
勝者が決まる確率は$\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}$であり、
ちょうど2回目のじゃんけんで勝者が決まる確率は$\frac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }}$であり、
ちょうど3回目のじゃんけんで勝者が決まる確率は$\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}$である。
(2)4人でじゃんけんを複数回行い1人の勝者を決める場合、1回目のじゃんけんで
勝者が決まる確率は$\frac{\boxed{\ \ スセソ\ \ }}{\boxed{\ \ タチツ\ \ }}$であり、
ちょうど2回目のじゃんけんで勝者が決まる確率は$\frac{\boxed{\ \ テトナ\ \ }}{\boxed{\ \ ニヌネ\ \ }}$である。
2022慶應義塾大学環境情報学部過去問
この動画を見る
${\large\boxed{5}}$複数人でじゃんけんを何回か行い勝ち残った1人を決めることを考える。
最初は全員がじゃんけんに参加して始める。それぞれのじゃんけんでは、
そのじゃんけんの参加者がそれぞれグー、チョキ、パーのどれかを出し、
もし誰か1人が他の全員に買った場合にはその1人が商社となりじゃんけん
はそこで終了する。そうでない場合、全員が同じ手を出したか、グー、チョキ、
パーのそれぞれを誰かが出した場合には'あいこ'となり、そのじゃんけんの参加者全員が
次のじゃんけんに進む。上記以外で、2つの手に分かれた場合には、
負けた手を出した人を除いて勝った手を出した人だけが次のじゃんけんに進む。
このように、じゃんけんを繰り返し行い、1人の勝者が決まるまで続けるものとする。
ただし、じゃんけんの参加者全員、グー、チョキ、パーのどれかを等しい確率
で毎回ランダムに出すものとする。また通常のじゃんけんのように
グーはチョキに勝ち、チョキはパーに勝ち、パーはグーに勝つものとする。
(1)3人でじゃんけんを複数回行い1人の勝者を決める場合、1回目のじゃんけんで
勝者が決まる確率は$\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}$であり、
ちょうど2回目のじゃんけんで勝者が決まる確率は$\frac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }}$であり、
ちょうど3回目のじゃんけんで勝者が決まる確率は$\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}$である。
(2)4人でじゃんけんを複数回行い1人の勝者を決める場合、1回目のじゃんけんで
勝者が決まる確率は$\frac{\boxed{\ \ スセソ\ \ }}{\boxed{\ \ タチツ\ \ }}$であり、
ちょうど2回目のじゃんけんで勝者が決まる確率は$\frac{\boxed{\ \ テトナ\ \ }}{\boxed{\ \ ニヌネ\ \ }}$である。
2022慶應義塾大学環境情報学部過去問
大学入試問題#252 茨城大学(2012) #定積分

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
注意ポイントあり!定数分離の良問です【数学 入試問題】【北海道大学】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
関数 $f(\theta)=\dfrac{1}{\sqrt 2}sin2 \theta-sin \theta+cos\theta$ ($0≦\theta≦\pi)$を考える。
(3)$a$を実数の定数とする。
$f(\theta)=a$となる$\theta$がちょうど2個であるような$a$のい範囲を求めよ。
北海道大過去問
この動画を見る
関数 $f(\theta)=\dfrac{1}{\sqrt 2}sin2 \theta-sin \theta+cos\theta$ ($0≦\theta≦\pi)$を考える。
(3)$a$を実数の定数とする。
$f(\theta)=a$となる$\theta$がちょうど2個であるような$a$のい範囲を求めよ。
北海道大過去問
二重根号にビビるな! 東京電機大学

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt x = \sqrt {17 + \sqrt {253}} - \sqrt {17 - \sqrt {253}}$
整数xを求めよ
東京電機大学
この動画を見る
$\sqrt x = \sqrt {17 + \sqrt {253}} - \sqrt {17 - \sqrt {253}}$
整数xを求めよ
東京電機大学
福田の数学〜慶應義塾大学2022年環境情報学部第4問〜ピラミッドを切って体積を求める

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{4}}$(1)$xyz$空間において$|x|+|y|+|z| \leqq 1$を満たす立体の体積は$\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}$である。
(2)aを実数としたとき、xyz空間において
$|x-a|+|y-a|+|z| \leqq 1,\ \ \ x \geqq 0,\ \ \ y \geqq 0,\ \ \ z \geqq 0$
を満たす立体の体積V(a)は
$(\textrm{a})a \lt \frac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }}$のとき、$V(a)=0$,
$(\textrm{b})\frac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }} \leqq a \lt 0$のとき、
$V(a)=\frac{\boxed{\ \ ケコ\ \ }a^3+\boxed{\ \ サシ\ \ }a^2+\boxed{\ \ スセ\ \ }a+\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }},$
$(\textrm{c})0 \leqq a \lt \frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニ\ \ }}$のとき、
$V(a)=\frac{\boxed{\ \ ヌネ\ \ }a^3+\boxed{\ \ ノハ\ \ }a+\boxed{\ \ ヒフ\ \ }}{\boxed{\ \ ヘホ\ \ }},$
$(\textrm{d})\frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニ\ \ }} \leqq a \lt \frac{\boxed{\ \ マミ\ \ }}{\boxe$d{\ \ ムメ\ \ }}$のとき、
$V(a)=\frac{\boxed{\ \ モヤ\ \ }a^3+\boxed{\ \ ユヨ\ \ }a^2+\boxed{\ \ ラリ\ \ }a}{\boxed{\ \ ルレ\ \ }},$
$(\textrm{e})\frac{\boxed{\ \ マミ\ \ }}{\boxed{\ \ ムメ\ \ }} \leqq a$のとき、
$V(a)=\frac{\boxed{\ \ ロワ\ \ }}{\boxed{\ \ ヲン\ \ }}$
2022慶應義塾大学環境情報学部過去問
この動画を見る
${\large\boxed{4}}$(1)$xyz$空間において$|x|+|y|+|z| \leqq 1$を満たす立体の体積は$\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}$である。
(2)aを実数としたとき、xyz空間において
$|x-a|+|y-a|+|z| \leqq 1,\ \ \ x \geqq 0,\ \ \ y \geqq 0,\ \ \ z \geqq 0$
を満たす立体の体積V(a)は
$(\textrm{a})a \lt \frac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }}$のとき、$V(a)=0$,
$(\textrm{b})\frac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }} \leqq a \lt 0$のとき、
$V(a)=\frac{\boxed{\ \ ケコ\ \ }a^3+\boxed{\ \ サシ\ \ }a^2+\boxed{\ \ スセ\ \ }a+\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }},$
$(\textrm{c})0 \leqq a \lt \frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニ\ \ }}$のとき、
$V(a)=\frac{\boxed{\ \ ヌネ\ \ }a^3+\boxed{\ \ ノハ\ \ }a+\boxed{\ \ ヒフ\ \ }}{\boxed{\ \ ヘホ\ \ }},$
$(\textrm{d})\frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニ\ \ }} \leqq a \lt \frac{\boxed{\ \ マミ\ \ }}{\boxe$d{\ \ ムメ\ \ }}$のとき、
$V(a)=\frac{\boxed{\ \ モヤ\ \ }a^3+\boxed{\ \ ユヨ\ \ }a^2+\boxed{\ \ ラリ\ \ }a}{\boxed{\ \ ルレ\ \ }},$
$(\textrm{e})\frac{\boxed{\ \ マミ\ \ }}{\boxed{\ \ ムメ\ \ }} \leqq a$のとき、
$V(a)=\frac{\boxed{\ \ ロワ\ \ }}{\boxed{\ \ ヲン\ \ }}$
2022慶應義塾大学環境情報学部過去問
大学入試問題#251 新潟大学(2012) #相加相乗平均

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学
指導講師:
ますただ
問題文全文(内容文):
$a,b,c,d$:正の実数
$\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[ 4 ]{ abcd }$を示せ
出典:2012年新潟大学 入試問題
この動画を見る
$a,b,c,d$:正の実数
$\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[ 4 ]{ abcd }$を示せ
出典:2012年新潟大学 入試問題
福田の数学〜慶應義塾大学2022年環境情報学部第3問〜4次関数のグラフの接線と囲まれた面積

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{3}}$xy平面上の曲線Cを$y=x^2(x-1)(x+2)$とする。
(1)Cに2点で下から接する直線Lの方程式は
$y=\frac{\boxed{\ \ アイウ\ \ }}{\boxed{\ \ エオカ\ \ }}\ x+\frac{\boxed{\ \ キクケ\ \ }}{\boxed{\ \ コサシ\ \ }}$である。
(2)CとLが囲む図の斜線部分の面積(※動画参照)は
$\frac{\boxed{\ \ スセソ\ \ }\sqrt{\boxed{\ \ タチツ\ \ }}}{\boxed{\ \ テトナ\ \ }}$となる。
ただし、次の公式を使ってもかまわない(m,nは正の整数)
$\int_{\alpha}^{\beta}(x-\alpha)^m(x-\beta)^ndx=\frac{(-1)^nm!n!}{(m+n+1)!}(\beta-\alpha)^{m+n+1}$
2022慶應義塾大学環境情報学部過去問
この動画を見る
${\large\boxed{3}}$xy平面上の曲線Cを$y=x^2(x-1)(x+2)$とする。
(1)Cに2点で下から接する直線Lの方程式は
$y=\frac{\boxed{\ \ アイウ\ \ }}{\boxed{\ \ エオカ\ \ }}\ x+\frac{\boxed{\ \ キクケ\ \ }}{\boxed{\ \ コサシ\ \ }}$である。
(2)CとLが囲む図の斜線部分の面積(※動画参照)は
$\frac{\boxed{\ \ スセソ\ \ }\sqrt{\boxed{\ \ タチツ\ \ }}}{\boxed{\ \ テトナ\ \ }}$となる。
ただし、次の公式を使ってもかまわない(m,nは正の整数)
$\int_{\alpha}^{\beta}(x-\alpha)^m(x-\beta)^ndx=\frac{(-1)^nm!n!}{(m+n+1)!}(\beta-\alpha)^{m+n+1}$
2022慶應義塾大学環境情報学部過去問
大学入試問題#250 福井大学(2012) #定積分
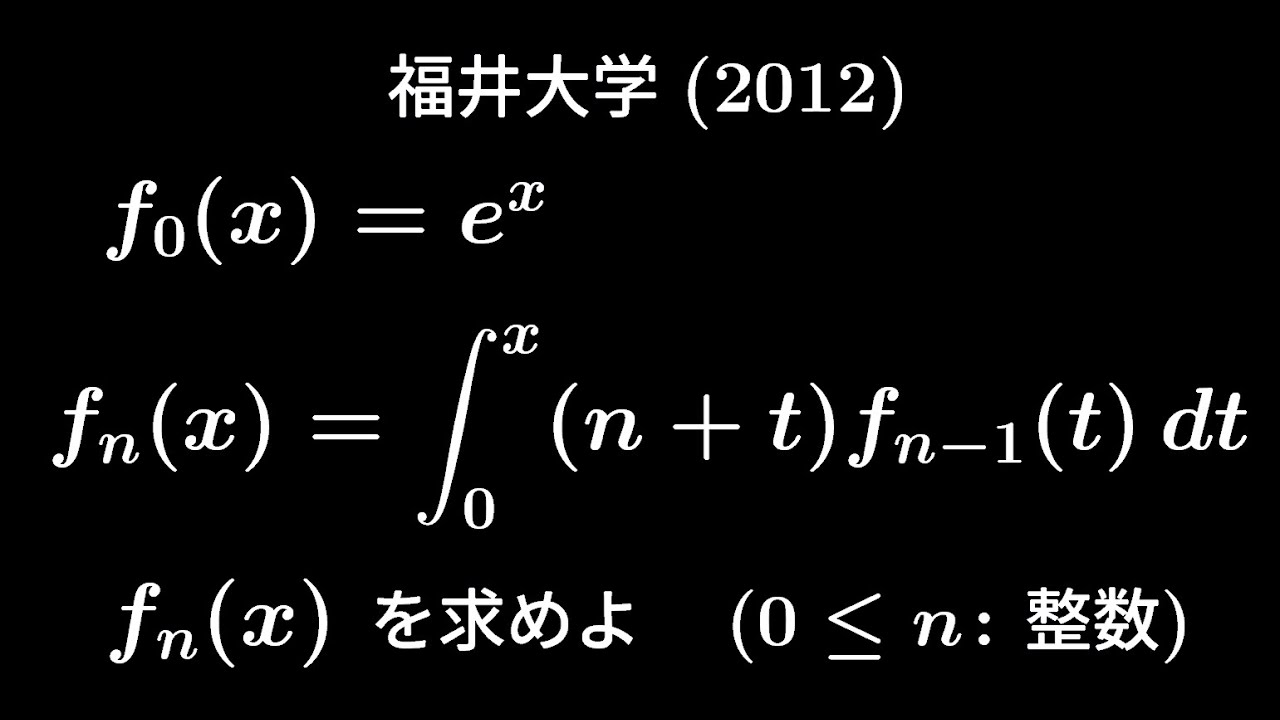
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#数列#漸化式#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$n$を0以上の整数とする。
次の2つの条件をみたす関数$f_n(x)$を求めよ。
(ⅰ)$f_0(x)=e^x$
(ⅱ)$f_n(x)=\displaystyle \int_{0}^{x}(n+t)f_{n-1}(t)dt$
出典:2012年福井大学 入試問題
この動画を見る
$n$を0以上の整数とする。
次の2つの条件をみたす関数$f_n(x)$を求めよ。
(ⅰ)$f_0(x)=e^x$
(ⅱ)$f_n(x)=\displaystyle \int_{0}^{x}(n+t)f_{n-1}(t)dt$
出典:2012年福井大学 入試問題
福田の数学〜慶應義塾大学2022年環境情報学部第2問〜三角関数の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}\ 0 \leqq \theta \leqq \pi $のとき、関数$y=\sin3\theta-3\cos(\theta-\frac{\pi}{6})$の最大値と最小値を求めたい。
(1)$x=\cos(\theta-\frac{\pi}{6})$とおくと、もとの関数は
$y=\boxed{\ \ アイ\ \ }\ x^3+\boxed{\ \ ウエ\ \ }\ x^2+\boxed{\ \ オカ\ \ }\ x+\boxed{\ \ キク\ \ }$
と書き直すことができる。
(2)このことから、もとの関数の最大値は$\theta=\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}\ \pi$のときに
$\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }}$
であり、最小値は$\theta=\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テト\ \ }}\ \pi$のときに
$\boxed{\ \ ナニ\ \ }\sqrt{\boxed{\ \ ヌネ\ \ }}$であることがわかる。
2022慶應義塾大学環境情報学部過去問
この動画を見る
${\large\boxed{2}}\ 0 \leqq \theta \leqq \pi $のとき、関数$y=\sin3\theta-3\cos(\theta-\frac{\pi}{6})$の最大値と最小値を求めたい。
(1)$x=\cos(\theta-\frac{\pi}{6})$とおくと、もとの関数は
$y=\boxed{\ \ アイ\ \ }\ x^3+\boxed{\ \ ウエ\ \ }\ x^2+\boxed{\ \ オカ\ \ }\ x+\boxed{\ \ キク\ \ }$
と書き直すことができる。
(2)このことから、もとの関数の最大値は$\theta=\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}\ \pi$のときに
$\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }}$
であり、最小値は$\theta=\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テト\ \ }}\ \pi$のときに
$\boxed{\ \ ナニ\ \ }\sqrt{\boxed{\ \ ヌネ\ \ }}$であることがわかる。
2022慶應義塾大学環境情報学部過去問
九州大のナイスな問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=\sqrt5-1+\sqrt{10+2\sqrt5}i$
$\beta=-\sqrt5-1+\sqrt{10-2\sqrt5}i$
(1)$\alpha$を解にもつ実数係数の2次方程式を1つ例示せよ.
(2)$\alpha,\beta$を解にもつ実数係数の4次方程式を1つ例示せよ.
(3)$\beta^5$の値を求めよ.
九州大(類)過去問
この動画を見る
$\alpha=\sqrt5-1+\sqrt{10+2\sqrt5}i$
$\beta=-\sqrt5-1+\sqrt{10-2\sqrt5}i$
(1)$\alpha$を解にもつ実数係数の2次方程式を1つ例示せよ.
(2)$\alpha,\beta$を解にもつ実数係数の4次方程式を1つ例示せよ.
(3)$\beta^5$の値を求めよ.
九州大(類)過去問
福田の数学〜慶應義塾大学2022年環境情報学部第1問〜4つの音で作るチャイムの種類

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$ある学校では、ドミソシの4つの音を4つ組み合わせてチャイムを作り、
授業の開始・終了などを知らせるために鳴らしている。
チャイムは、図1(※動画参照)のように4×4の格子状に並んだ16個のボタン
を押すことによって作ることができる。縦方向は音の種類を表し、横方向は時間
を表している。例えば、ドミソシという音を1つずつ、
順番に鳴らすチャイムを作るには、図2(※動画参照)のようにボタンを押せばよい。
ただし、鳴らすことのできる音の数は縦1列あたり1つだけであり、
音を鳴らさない無音は許されず、それぞれの例で必ず1つの音を選ばなければならないとする。
(1)4つの音を1回ずつ鳴らすことを考えた場合、チャイムの種類は$\boxed{\ \ アイウ\ \ }$通り。
(2)(1)に加えて、同じ音を連続して2回繰り返すことを1度だけしてもかまわない(例:ドミミソ)
とした場合、
チャイムの種類は合わせて$\boxed{\ \ エオカ\ \ }$通りになる。
ただし、連続する音以外は高々1回までしか鳴らすことはできず、
それらは連続する音とは異ならなければならないものとする。
(3)(1)と(2)に加えて、同じ音を連続して4回繰り返すチャイムを許すと、
可能なチャイムの種類は合わせて$\boxed{\ \ キクケ\ \ }$通りになる。
2022慶應義塾大学環境情報学部過去問
この動画を見る
${\large\boxed{1}}$ある学校では、ドミソシの4つの音を4つ組み合わせてチャイムを作り、
授業の開始・終了などを知らせるために鳴らしている。
チャイムは、図1(※動画参照)のように4×4の格子状に並んだ16個のボタン
を押すことによって作ることができる。縦方向は音の種類を表し、横方向は時間
を表している。例えば、ドミソシという音を1つずつ、
順番に鳴らすチャイムを作るには、図2(※動画参照)のようにボタンを押せばよい。
ただし、鳴らすことのできる音の数は縦1列あたり1つだけであり、
音を鳴らさない無音は許されず、それぞれの例で必ず1つの音を選ばなければならないとする。
(1)4つの音を1回ずつ鳴らすことを考えた場合、チャイムの種類は$\boxed{\ \ アイウ\ \ }$通り。
(2)(1)に加えて、同じ音を連続して2回繰り返すことを1度だけしてもかまわない(例:ドミミソ)
とした場合、
チャイムの種類は合わせて$\boxed{\ \ エオカ\ \ }$通りになる。
ただし、連続する音以外は高々1回までしか鳴らすことはできず、
それらは連続する音とは異ならなければならないものとする。
(3)(1)と(2)に加えて、同じ音を連続して4回繰り返すチャイムを許すと、
可能なチャイムの種類は合わせて$\boxed{\ \ キクケ\ \ }$通りになる。
2022慶應義塾大学環境情報学部過去問
大学入試問題#249 早稲田大学(2014) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a,b$を正の定数
$\displaystyle \int_{0}^{2\pi}|a\ \sin\ x+b\ \cos\ x|dx$を求めよ。
出典:2014年早稲田大学 入試問題
この動画を見る
$a,b$を正の定数
$\displaystyle \int_{0}^{2\pi}|a\ \sin\ x+b\ \cos\ x|dx$を求めよ。
出典:2014年早稲田大学 入試問題
どっちがでかい?2通りの解法で

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
a,b,cは正の実数で$a^2+b^2=c^2$を満たす次の大小を比較せよ.
(1)$a^3+b^3,c^3$
(2)$\sqrt a+\sqrt b.\sqrt c$
この動画を見る
a,b,cは正の実数で$a^2+b^2=c^2$を満たす次の大小を比較せよ.
(1)$a^3+b^3,c^3$
(2)$\sqrt a+\sqrt b.\sqrt c$
福田の数学〜慶應義塾大学2022年総合政策学部第6問〜新型ウィルス感染拡大による休業要請と補償金の期待値

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{6}}$新型ウイルスの感染拡大にともなって、ある国の自治体がある飲食店に1ヵ月間
の休業要請を行い、もし飲食店が要請に応じた場合、自治体は飲食店に補償金を
払うことになったものとする。いま、この飲食店は補償金が90万円以上であれば
要請に応じ、90万円未満なら要請に応じないものとする。補償金の額をC万円で
したとき、(C-90)万円を飲食店の超過利益と呼ぶことにする。もし$C \lt 90$
であれば、飲食店は要請に応じず、超過利益は0万円とする。
また、この自治体は支払うことのできる補償金の上限が定まっていて、それがD万円
$(D \geqq C)$であったとき、飲食店がC万円で要請に応じた場合、(D-C)万円は
補償金の節約分となる。ただし、飲食店が要請に応じなかった場合には、補償金の
節約分は0万円とする。
(1)まず、自治体が飲食店に休業要請する場合の補償金の額C万円を提示する場合
について考える。いま、自治体の補償金の上限が125万円であったとき、自治体
の補償金の節約分が最も大きくなるのは$C=\boxed{\ \ アイウ\ \ }$万円の場合である。
(2)次に、飲食店が自治体に休業要請し、自治体が申請を受理した場合に、飲食店
は休業と引き替えに補償金を受け取ることができる場合について考える。なお、
飲食店は休業申請をする際に90万円以上の補償金の額を自治体に提示するもの
とする。また、ここでは自治体が支払うことができる補償金の上限については、
125万円か150万円か175万円のどれかに定まっているが公表されておらず、
飲食店は125万円である確率が\frac{2}{5}、150万円である確率が\frac{1}{5}、175万円である
確率が\frac{2}{5}であると予想しているものとする。
ただし、飲食店が提示した補償金の額が、実際に自治体が支払うことができる上限
を超えていた場合、自治体は申請を受理せず、そのときの補償金の節約分は0万円
になり、申請が受理されなければ、飲食店は休業せず、超過利益は0万円になる。
たとえば、飲食店が休業申請をする際にC=160万円を提示した場合、飲食店
の超過利益(の期待値)は$\boxed{\ \ エオカ\ \ }$万円となる。
そこで、飲食店が超過利益(の期待値)を最も大きくする補償金の額を休業申請
の際に自治体に提示したとすると
$(\textrm{a})$飲食店の超過利益(の期待値)は$\boxed{\ \ キクケ\ \ }$万円であり、
$(\textrm{b})$自治体の補償金の上限が実際は125万円であった場合、補償金の節約分は
$\boxed{\ \ コサシ\ \ }$万円。
$(\textrm{c})$自治体の補償金の上限が実際は175万円であった場合、補償金の節約分は
$\boxed{\ \ スセソ\ \ }$万円。
2022慶應義塾大学総合政策学部過去問
この動画を見る
${\large\boxed{6}}$新型ウイルスの感染拡大にともなって、ある国の自治体がある飲食店に1ヵ月間
の休業要請を行い、もし飲食店が要請に応じた場合、自治体は飲食店に補償金を
払うことになったものとする。いま、この飲食店は補償金が90万円以上であれば
要請に応じ、90万円未満なら要請に応じないものとする。補償金の額をC万円で
したとき、(C-90)万円を飲食店の超過利益と呼ぶことにする。もし$C \lt 90$
であれば、飲食店は要請に応じず、超過利益は0万円とする。
また、この自治体は支払うことのできる補償金の上限が定まっていて、それがD万円
$(D \geqq C)$であったとき、飲食店がC万円で要請に応じた場合、(D-C)万円は
補償金の節約分となる。ただし、飲食店が要請に応じなかった場合には、補償金の
節約分は0万円とする。
(1)まず、自治体が飲食店に休業要請する場合の補償金の額C万円を提示する場合
について考える。いま、自治体の補償金の上限が125万円であったとき、自治体
の補償金の節約分が最も大きくなるのは$C=\boxed{\ \ アイウ\ \ }$万円の場合である。
(2)次に、飲食店が自治体に休業要請し、自治体が申請を受理した場合に、飲食店
は休業と引き替えに補償金を受け取ることができる場合について考える。なお、
飲食店は休業申請をする際に90万円以上の補償金の額を自治体に提示するもの
とする。また、ここでは自治体が支払うことができる補償金の上限については、
125万円か150万円か175万円のどれかに定まっているが公表されておらず、
飲食店は125万円である確率が\frac{2}{5}、150万円である確率が\frac{1}{5}、175万円である
確率が\frac{2}{5}であると予想しているものとする。
ただし、飲食店が提示した補償金の額が、実際に自治体が支払うことができる上限
を超えていた場合、自治体は申請を受理せず、そのときの補償金の節約分は0万円
になり、申請が受理されなければ、飲食店は休業せず、超過利益は0万円になる。
たとえば、飲食店が休業申請をする際にC=160万円を提示した場合、飲食店
の超過利益(の期待値)は$\boxed{\ \ エオカ\ \ }$万円となる。
そこで、飲食店が超過利益(の期待値)を最も大きくする補償金の額を休業申請
の際に自治体に提示したとすると
$(\textrm{a})$飲食店の超過利益(の期待値)は$\boxed{\ \ キクケ\ \ }$万円であり、
$(\textrm{b})$自治体の補償金の上限が実際は125万円であった場合、補償金の節約分は
$\boxed{\ \ コサシ\ \ }$万円。
$(\textrm{c})$自治体の補償金の上限が実際は175万円であった場合、補償金の節約分は
$\boxed{\ \ スセソ\ \ }$万円。
2022慶應義塾大学総合政策学部過去問
大学入試問題#248 慶應義塾大学(2014) #方程式

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x,y,z:0$でない整数
$\displaystyle \frac{1}{xy}+\displaystyle \frac{1}{yz}+\displaystyle \frac{1}{zx}=\displaystyle \frac{1}{xy+yz+zx}$
$2^{x+1}=\displaystyle \frac{5^{2y}}{10^{z+1}}$
をみたすとき$x,y,z$の値を求めよ。
出典:2014年慶應義塾大学 入試問題
この動画を見る
$x,y,z:0$でない整数
$\displaystyle \frac{1}{xy}+\displaystyle \frac{1}{yz}+\displaystyle \frac{1}{zx}=\displaystyle \frac{1}{xy+yz+zx}$
$2^{x+1}=\displaystyle \frac{5^{2y}}{10^{z+1}}$
をみたすとき$x,y,z$の値を求めよ。
出典:2014年慶應義塾大学 入試問題
【数学】入試問題(国公立):一橋大学2018年(前期)第1問の解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
自然数nの各位の和をS(n)とする。n≧10000のとき、
n>30S(n)+2018が成り立つことを示せ。
この動画を見る
自然数nの各位の和をS(n)とする。n≧10000のとき、
n>30S(n)+2018が成り立つことを示せ。
【理数個別の過去問解説】2018年度一橋大学(前期) 数学 大問1解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
自然数nの各位の和を$S(n)$とする。$n\geqq 10000$のとき、
$n\gt 30S(n)+2018$が成り立つことを示せ。
この動画を見る
自然数nの各位の和を$S(n)$とする。$n\geqq 10000$のとき、
$n\gt 30S(n)+2018$が成り立つことを示せ。
