 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
大学入試問題#128 東京理科大学(2020) 定積分
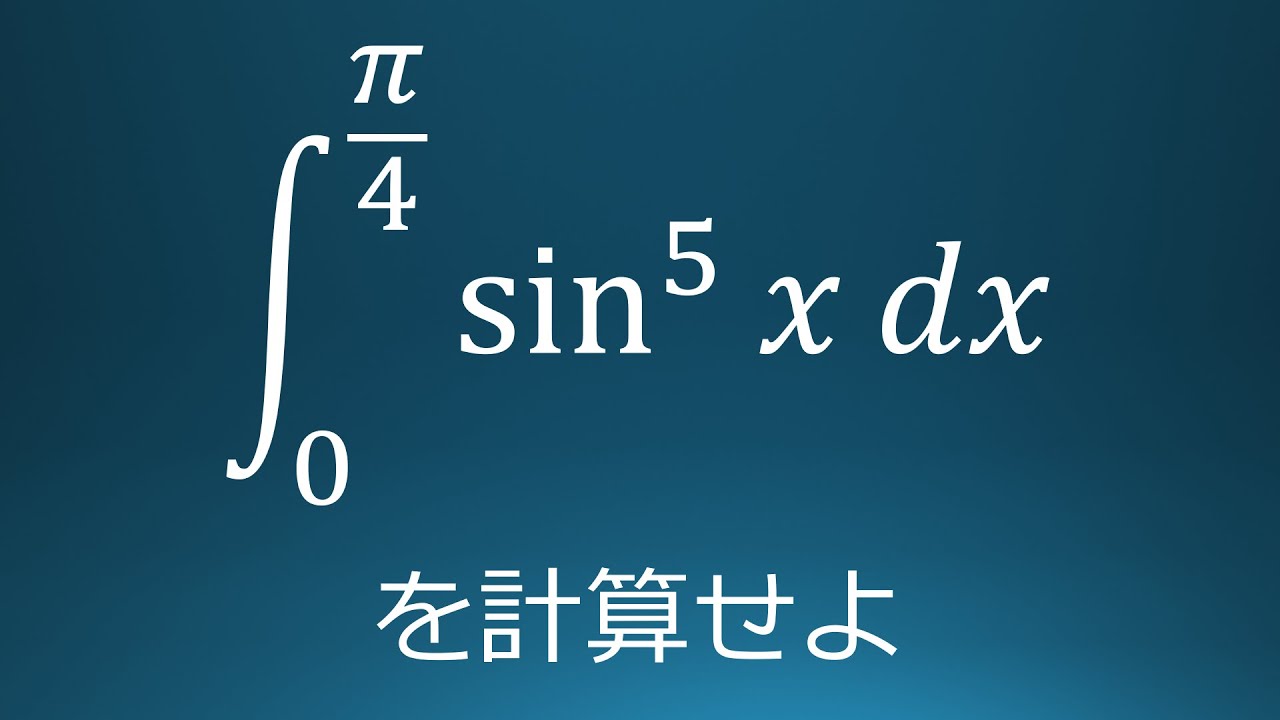
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#東京理科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\sin^5x\ dx$を計算せよ。
出典:2020年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\sin^5x\ dx$を計算せよ。
出典:2020年東京理科大学 入試問題
福田の入試問題解説〜東京大学2022年理系第3問〜点の存在する条件と領域の面積

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
Oを原点とする座標平面上で考える。座標平面上の2点$S(x_1,y_1),T(x_2,y_2)$
に対し、点Sが点Tから十分離れているとは、
$|x_1-x_2| \geqq 1$ または $|y_1-y_2| \geqq 1$
が成り立つことと定義する。
不等式
$0 \leqq x \leqq 3, 0 \leqq y \leqq 3$
が表す正方形の領域をDとし、その2つの頂点A(3,0), B(3,3)を考える。
さらに、次の条件$(\textrm{i}),(\textrm{ii})$を共に満たす点Pをとる。
$(\textrm{i})$点Pは領域Dの点であり、かつ、放物線$y=x^2$上にある。
$(\textrm{ii})$点Pは、3点O,A,Bのいずれからも十分離れている。
点Pのx座標をaとする。
(1)aのとりうる値の範囲を求めよ。
(2)次の条件$(\textrm{iii}),(\textrm{iv})$をともに満たす点Qが存在しうる範囲の面積f(a)を求めよ。
$(\textrm{iii})$点Qは領域Dの点である。
$(\textrm{iv})$点Qは、4点O,A,B,Pのいずれからも十分離れている。
(3)aは(1)で求めた範囲を動くとする。(2)のf(a)を最小にするaの値を求めよ。
2022東京大学理系過去問
この動画を見る
Oを原点とする座標平面上で考える。座標平面上の2点$S(x_1,y_1),T(x_2,y_2)$
に対し、点Sが点Tから十分離れているとは、
$|x_1-x_2| \geqq 1$ または $|y_1-y_2| \geqq 1$
が成り立つことと定義する。
不等式
$0 \leqq x \leqq 3, 0 \leqq y \leqq 3$
が表す正方形の領域をDとし、その2つの頂点A(3,0), B(3,3)を考える。
さらに、次の条件$(\textrm{i}),(\textrm{ii})$を共に満たす点Pをとる。
$(\textrm{i})$点Pは領域Dの点であり、かつ、放物線$y=x^2$上にある。
$(\textrm{ii})$点Pは、3点O,A,Bのいずれからも十分離れている。
点Pのx座標をaとする。
(1)aのとりうる値の範囲を求めよ。
(2)次の条件$(\textrm{iii}),(\textrm{iv})$をともに満たす点Qが存在しうる範囲の面積f(a)を求めよ。
$(\textrm{iii})$点Qは領域Dの点である。
$(\textrm{iv})$点Qは、4点O,A,B,Pのいずれからも十分離れている。
(3)aは(1)で求めた範囲を動くとする。(2)のf(a)を最小にするaの値を求めよ。
2022東京大学理系過去問
福田の数学〜慶應義塾大学2022年薬学部第1問(1)〜複素数の計算とド・モアブルの定理

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
(1)整数a,bは等式$(a+bi)^3=-16+16i$を満たす。ただし、iは虚数単位とする。
$(\textrm{i})a=\boxed{\ \ ア\ \ }, b=\boxed{\ \ イ\ \ }$である。
$(\textrm{ii})\frac{i}{a+bi}-\frac{1+5i}{4}$を計算すると$\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
(1)整数a,bは等式$(a+bi)^3=-16+16i$を満たす。ただし、iは虚数単位とする。
$(\textrm{i})a=\boxed{\ \ ア\ \ }, b=\boxed{\ \ イ\ \ }$である。
$(\textrm{ii})\frac{i}{a+bi}-\frac{1+5i}{4}$を計算すると$\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学薬学部過去問
大学入試問題#127 関西大学(1991) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$l,m,n$:正の整数
$l^2mn=64$を満たす組($l,m,n$)の個数を求めよ。
出典:1991年関西大学 入試問題
この動画を見る
$l,m,n$:正の整数
$l^2mn=64$を満たす組($l,m,n$)の個数を求めよ。
出典:1991年関西大学 入試問題
一橋大学2022整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 2^a3^b+2^c3^d=2022$を満たす$0$以上の整数$(a,b,c,d)$を求めよ.
2022一橋大過去問
この動画を見る
$ 2^a3^b+2^c3^d=2022$を満たす$0$以上の整数$(a,b,c,d)$を求めよ.
2022一橋大過去問
福田の入試問題解説〜東京大学2022年理系第2問〜約数と倍数と最大公約数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数列$\left\{a_n\right\}$を次のように定める。
$a_1=1, a_{n+1}=a_n^2+1 (n=1,2,3,\ldots)$
(1)正の整数nが3の倍数のとき、$a_n$は5の倍数となることを示せ。
(2)k,nを正の整数とする。$a_n$が$a_k$の倍数となるための必要十分条件をk,nを
用いて表せ。
(3)$a_{2022}$と$(a_{8091})^2$の最大公約数を求めよ。
2022東京大学理系過去問
この動画を見る
数列$\left\{a_n\right\}$を次のように定める。
$a_1=1, a_{n+1}=a_n^2+1 (n=1,2,3,\ldots)$
(1)正の整数nが3の倍数のとき、$a_n$は5の倍数となることを示せ。
(2)k,nを正の整数とする。$a_n$が$a_k$の倍数となるための必要十分条件をk,nを
用いて表せ。
(3)$a_{2022}$と$(a_{8091})^2$の最大公約数を求めよ。
2022東京大学理系過去問
福田の入試問題解説〜東京大学2022年理系第1問〜最小値の存在と定積分の計算

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
次の関数f(x)を考える。
$f(x)=(\cos x)\log(\cos x)-\cos x+\int_0^x(\cos t)\log(\cos t)dt (0 \leqq x \lt \frac{\pi}{2})$
(1)f(x)は区間$0 \leqq x \lt \frac{\pi}{2}$において最小値を持つことを示せ。
(2)f(x)は区間$0 \leqq x \lt \frac{\pi}{2}$における最小値を求めよ。
2022東京大学理系過去問
この動画を見る
次の関数f(x)を考える。
$f(x)=(\cos x)\log(\cos x)-\cos x+\int_0^x(\cos t)\log(\cos t)dt (0 \leqq x \lt \frac{\pi}{2})$
(1)f(x)は区間$0 \leqq x \lt \frac{\pi}{2}$において最小値を持つことを示せ。
(2)f(x)は区間$0 \leqq x \lt \frac{\pi}{2}$における最小値を求めよ。
2022東京大学理系過去問
福田の数学〜東京慈恵会医科大学2022年医学部第4問〜複素数平面と図形

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#平面上の曲線#複素数平面#方べきの定理と2つの円の関係#図形と方程式#点と直線#2次曲線#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
複素数平面上の点zが原点を中心とする半径1の円周上を動くとき、$w=z+\frac{2}{z}$
で表される点wの描く図形をCとする。Cで囲まれた部分の内部(ただし、
境界線は含まない)に定点$\alpha$をとり、$\alpha$を通る直線lがCと交わる2点を$\beta_1,\beta_2$とする。
(1)$w=u+vi$(u,vは実数)とするとき、uとvの間に成り立つ関係式を求めよ。
(2)点$\alpha$を固定したままlを動かすとき、積$|\beta_1-\alpha|・|\beta_2-\alpha|$が最大となる
ようなlはどのような直線のときか調べよ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
複素数平面上の点zが原点を中心とする半径1の円周上を動くとき、$w=z+\frac{2}{z}$
で表される点wの描く図形をCとする。Cで囲まれた部分の内部(ただし、
境界線は含まない)に定点$\alpha$をとり、$\alpha$を通る直線lがCと交わる2点を$\beta_1,\beta_2$とする。
(1)$w=u+vi$(u,vは実数)とするとき、uとvの間に成り立つ関係式を求めよ。
(2)点$\alpha$を固定したままlを動かすとき、積$|\beta_1-\alpha|・|\beta_2-\alpha|$が最大となる
ようなlはどのような直線のときか調べよ。
2022東京慈恵会医科大学医学部過去問
大学入試問題#126 慶應大学医学部(2005) 不定積分
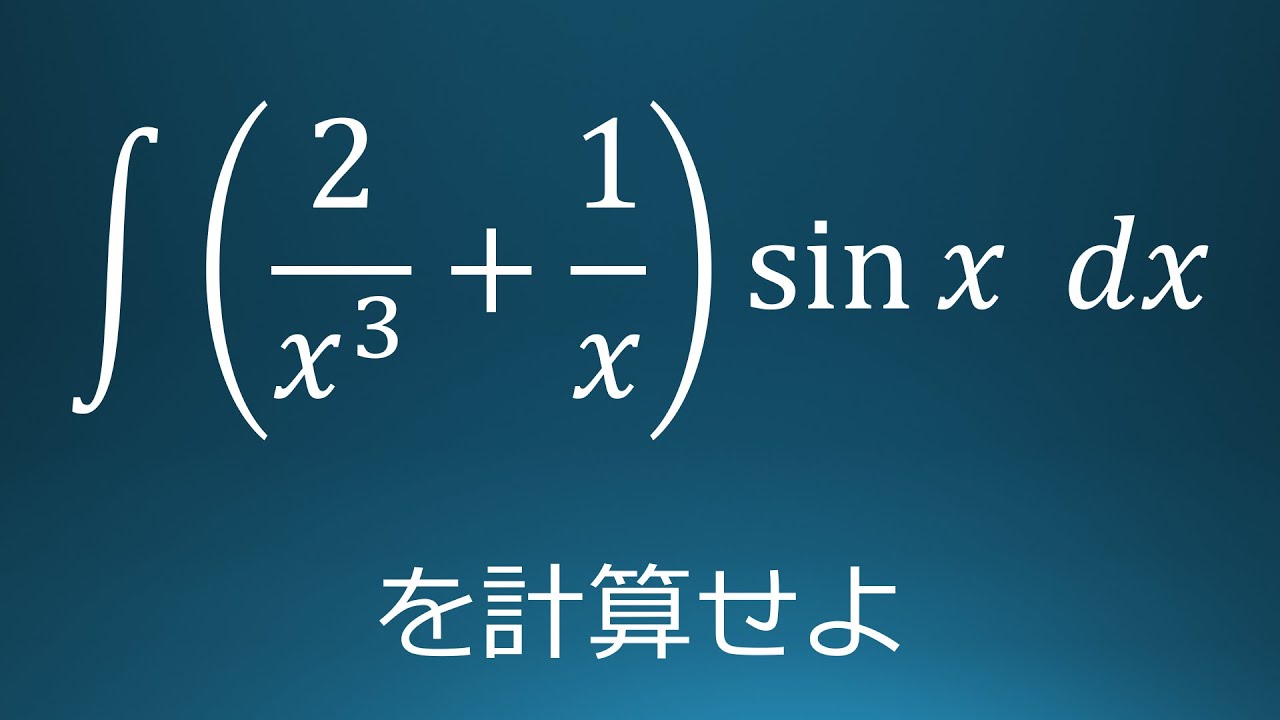
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (\displaystyle \frac{2}{x^3}+\displaystyle \frac{1}{x})\sin\ x\ dx$を計算せよ。
出典:2005年慶應義塾大学 入試問題
この動画を見る
$\displaystyle \int (\displaystyle \frac{2}{x^3}+\displaystyle \frac{1}{x})\sin\ x\ dx$を計算せよ。
出典:2005年慶應義塾大学 入試問題
【理数個別の過去問解説】2021年度 神奈川大学給費生入試 文系数学 第3問解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
座標平面上に3点О(0,0),A(0,4),B(8,0)がある。次の問いに答えよ。
(1) 3点A,B,Oを通る円Cの中心の座標を求めよ。
(2) 点Oを回転の中心として,円Cを反時計回りに60°回転させた円をC'とする。CとC'の共有点のうちOと異なる点の座標を求めよ。
この動画を見る
座標平面上に3点О(0,0),A(0,4),B(8,0)がある。次の問いに答えよ。
(1) 3点A,B,Oを通る円Cの中心の座標を求めよ。
(2) 点Oを回転の中心として,円Cを反時計回りに60°回転させた円をC'とする。CとC'の共有点のうちOと異なる点の座標を求めよ。
福田の数学〜東京慈恵会医科大学2022年医学部第3問〜約数と倍数の性質

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
mは3以上の奇数とし、mの全ての正の約数を$a_1,a_2,\ldots,a_k$と並べる。
ただし、$a_1 \lt a_2 \lt \ldots \lt a_k$とする。
以下の2つの条件$(\textrm{i}),(\textrm{ii})$を満たすmについて考える。
$(\textrm{i})m$は素数ではない。
$(\textrm{ii})i \leqq j,1 \lt i \lt k ,1 \lt j \lt k$を満たす全ての整数i,jについて$a_j-a_i \leqq 3$が
成り立つ。
このとき、次の問いに答えよ。
(1)kは3または4であることを示し、mを$a_2$を用いて表せ。
(2)$k=3$となるとき、全ての正の整数nについて$(a_2n+1)^{a_2}-1$は
mの倍数であることを示せ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
mは3以上の奇数とし、mの全ての正の約数を$a_1,a_2,\ldots,a_k$と並べる。
ただし、$a_1 \lt a_2 \lt \ldots \lt a_k$とする。
以下の2つの条件$(\textrm{i}),(\textrm{ii})$を満たすmについて考える。
$(\textrm{i})m$は素数ではない。
$(\textrm{ii})i \leqq j,1 \lt i \lt k ,1 \lt j \lt k$を満たす全ての整数i,jについて$a_j-a_i \leqq 3$が
成り立つ。
このとき、次の問いに答えよ。
(1)kは3または4であることを示し、mを$a_2$を用いて表せ。
(2)$k=3$となるとき、全ての正の整数nについて$(a_2n+1)^{a_2}-1$は
mの倍数であることを示せ。
2022東京慈恵会医科大学医学部過去問
大学入試問題#125 広島修道大学(2015) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$n$:自然数
$2n-1$と$2n+1$は互いに素であることを示せ
出典:2015年広島修道大学 入試問題
この動画を見る
$n$:自然数
$2n-1$と$2n+1$は互いに素であることを示せ
出典:2015年広島修道大学 入試問題
福田の数学〜東京慈恵会医科大学2022年医学部第2問〜微分可能性と最大値と体積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
実数aは正の定数とする。実数全体で定義された関数$f(x)=\frac{|x+a|}{\sqrt{x^2+1}}$について、
次の問いに答えよ。
(1)$f(x)$が$x=-a$で微分可能であるかどうか調べよ。
(2)$f(x)$の最大値が$\sqrt2$となるように、定数aの値を定めよ。
(3)定数aは(2)で定めた値とする。$y=f(x)$のグラフとx軸およびy軸で囲まれた部分
をx軸の周りに1回転させてできる立体の体積Vを求めよ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
実数aは正の定数とする。実数全体で定義された関数$f(x)=\frac{|x+a|}{\sqrt{x^2+1}}$について、
次の問いに答えよ。
(1)$f(x)$が$x=-a$で微分可能であるかどうか調べよ。
(2)$f(x)$の最大値が$\sqrt2$となるように、定数aの値を定めよ。
(3)定数aは(2)で定めた値とする。$y=f(x)$のグラフとx軸およびy軸で囲まれた部分
をx軸の周りに1回転させてできる立体の体積Vを求めよ。
2022東京慈恵会医科大学医学部過去問
大学入試問題#124 高知大学(2020) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{7}{2}}^{\frac{9}{2}}\displaystyle \frac{2^x}{2^x+\sqrt{ 2 }}\ dx$を計算せよ。
出典:2020年高知大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{7}{2}}^{\frac{9}{2}}\displaystyle \frac{2^x}{2^x+\sqrt{ 2 }}\ dx$を計算せよ。
出典:2020年高知大学 入試問題
福田の数学〜東京慈恵会医科大学2022年医学部第1問〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
袋Aには白玉2個、赤玉1個、袋Bには白玉1個、赤玉2個が入っている。
この状態から始めて、次の操作を繰り返し行う。
操作
① 袋A、袋Bから玉を1個ずつ取り出す。
② $(\textrm{i})$取り出した2個の玉の色が同じである場合は、取り出した玉を2個とも
袋Aに入れる。
$(\textrm{ii})$取り出した2個の玉の色が異なる場合は、袋Aから取り出した玉は袋B
に入れ、袋Bから取り出した玉は袋Aに入れる。
このとき、
・操作を2回繰り返した後に袋Aに入っている赤玉の個数が1個である確率は$\boxed{\ \ (ア)\ \ }$
・操作を3回繰り返した後に袋Aに入っている赤玉の個数が0個である確率は$\boxed{\ \ (イ)\ \ }$
である。
2022東京慈恵会医科大学医学部過去問
この動画を見る
袋Aには白玉2個、赤玉1個、袋Bには白玉1個、赤玉2個が入っている。
この状態から始めて、次の操作を繰り返し行う。
操作
① 袋A、袋Bから玉を1個ずつ取り出す。
② $(\textrm{i})$取り出した2個の玉の色が同じである場合は、取り出した玉を2個とも
袋Aに入れる。
$(\textrm{ii})$取り出した2個の玉の色が異なる場合は、袋Aから取り出した玉は袋B
に入れ、袋Bから取り出した玉は袋Aに入れる。
このとき、
・操作を2回繰り返した後に袋Aに入っている赤玉の個数が1個である確率は$\boxed{\ \ (ア)\ \ }$
・操作を3回繰り返した後に袋Aに入っている赤玉の個数が0個である確率は$\boxed{\ \ (イ)\ \ }$
である。
2022東京慈恵会医科大学医学部過去問
大学入試問題#123 鳥取大学 改 (2020) Σの計算

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#鳥取大学#数B
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \sum_{k=1}^n k^2 2^k$を計算せよ。
出典:2020年鳥取大学 入試問題
この動画を見る
$\displaystyle \sum_{k=1}^n k^2 2^k$を計算せよ。
出典:2020年鳥取大学 入試問題
【数学】横浜国立大2018年度(理系前期)第5問の解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大(理系)2018年度前期入試
第5問
xy平面上に双曲線$C1:y=\dfrac{1}{x}$がある。C1上の点P$(t,\dfrac{1}{t})$(ただし$t>0$)におけるC1の接線をlとする。
放物線$C2:y=x^2+ax+b$(a,bは実数)は点Pを通りC1と第3象限において共有点をただ一つ持つ。C2とlで囲まれた部分の面積をSとする。
(1) lの方程式を求めよ。
(2) a,bをそれぞれtの式で表せ。
(3) Sをtの式で表せ。
(4) tが正の実数全体を動くとき、Sの最小値を求めよ。
この動画を見る
横浜国立大(理系)2018年度前期入試
第5問
xy平面上に双曲線$C1:y=\dfrac{1}{x}$がある。C1上の点P$(t,\dfrac{1}{t})$(ただし$t>0$)におけるC1の接線をlとする。
放物線$C2:y=x^2+ax+b$(a,bは実数)は点Pを通りC1と第3象限において共有点をただ一つ持つ。C2とlで囲まれた部分の面積をSとする。
(1) lの方程式を求めよ。
(2) a,bをそれぞれtの式で表せ。
(3) Sをtの式で表せ。
(4) tが正の実数全体を動くとき、Sの最小値を求めよ。
大学入試問題#122 愛知県立大学(2020) 極限
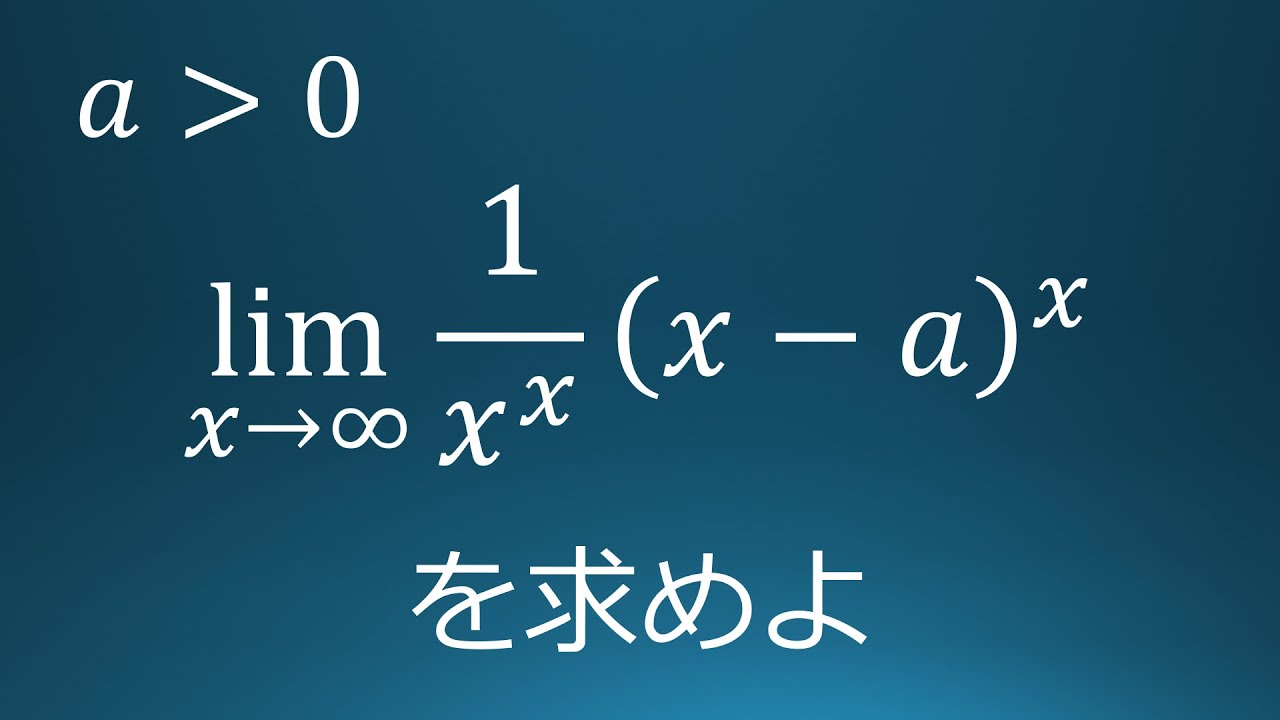
単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0$
$\displaystyle \lim_{ x \to \infty }\displaystyle \frac{1}{x^x}(x-a)^x$を求めよ。
出典:2020年愛知県立大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \lim_{ x \to \infty }\displaystyle \frac{1}{x^x}(x-a)^x$を求めよ。
出典:2020年愛知県立大学 入試問題
【数学】横浜国立大2018年度(理系前期)第1問の解説

単元:
#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大(理系)2018年度前期入試
第1問
(1) 定積分$\displaystyle \int_{0}^{\frac{\pi}{3}}\dfrac{x}{\cos(x)^2} dx$を求めよ。
(2) $\dfrac{-\pi}{2}\lt x\lt \dfrac{\pi}{2}$で定義された関数f(x)が
$f(x)\cos(x)^2 =\pi-\dfrac{x}{\log2}\displaystyle \int_{0}^{\frac{\pi}{3}f(t)dt$
をみたすとき、f(x)を求めよ。
この動画を見る
横浜国立大(理系)2018年度前期入試
第1問
(1) 定積分$\displaystyle \int_{0}^{\frac{\pi}{3}}\dfrac{x}{\cos(x)^2} dx$を求めよ。
(2) $\dfrac{-\pi}{2}\lt x\lt \dfrac{\pi}{2}$で定義された関数f(x)が
$f(x)\cos(x)^2 =\pi-\dfrac{x}{\log2}\displaystyle \int_{0}^{\frac{\pi}{3}f(t)dt$
をみたすとき、f(x)を求めよ。
大学入試問題#121 横浜国立大学(2004) 定積分
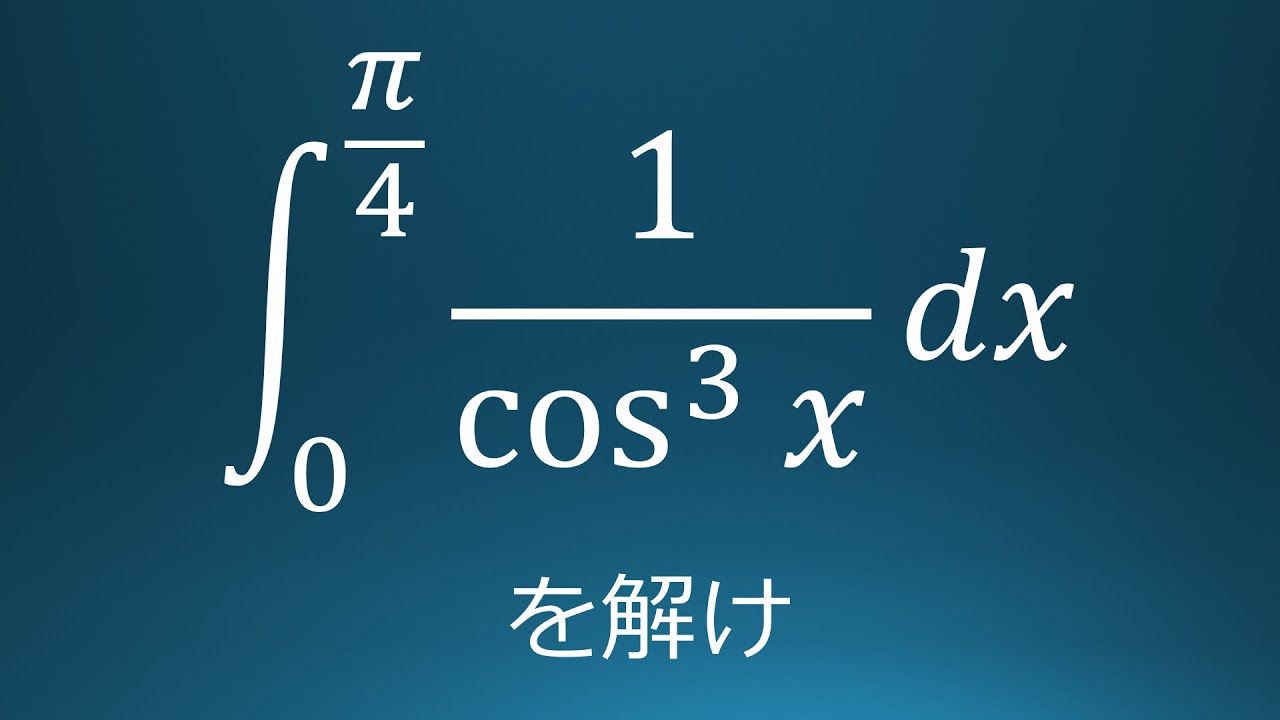
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{1}{\cos^3\ x}\ dx$を計算せよ。
出典:2004年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{1}{\cos^3\ x}\ dx$を計算せよ。
出典:2004年横浜国立大学 入試問題
大学入試問題#120 早稲田大学(2003) 対数の不等式
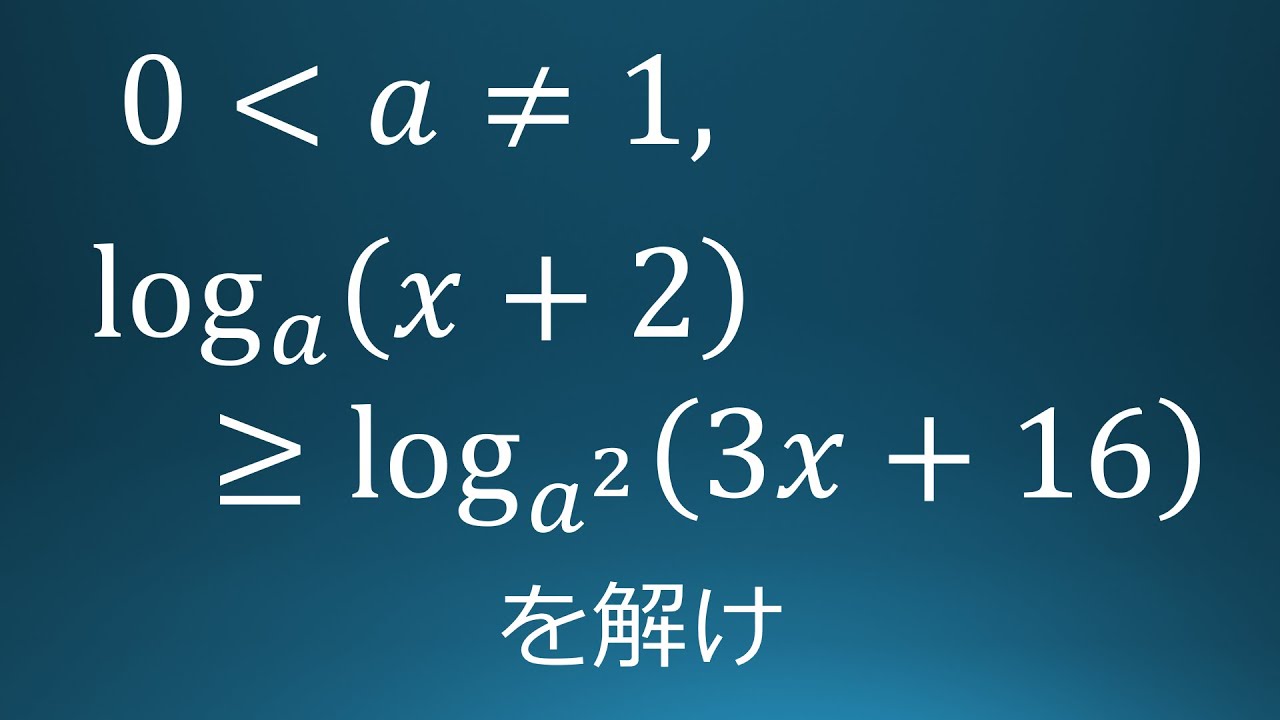
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0,\ a \neq 1$
$log\ a(x+2) \geqq log\ a^2(3x+16)$を解け
出典:2003年早稲田大学 入試問題
この動画を見る
$a \gt 0,\ a \neq 1$
$log\ a(x+2) \geqq log\ a^2(3x+16)$を解け
出典:2003年早稲田大学 入試問題
大学入試問題#119 横浜国立大学(2020) 定積分
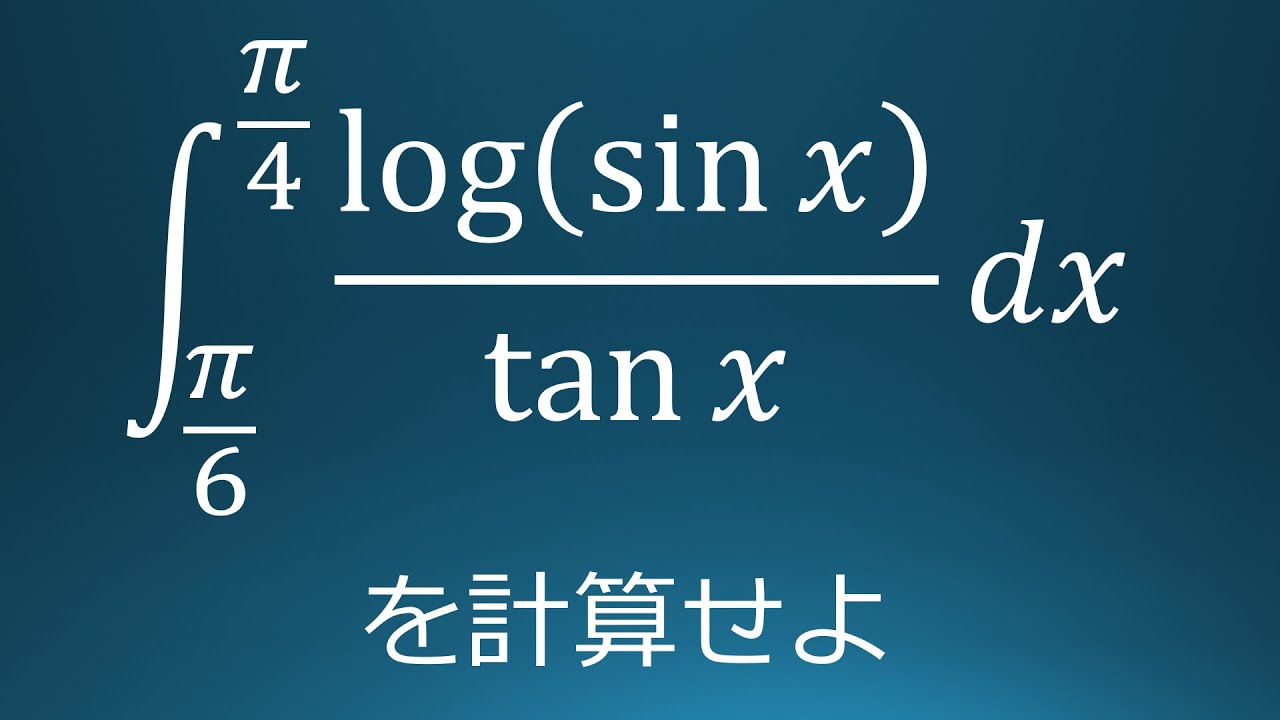
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\displaystyle \frac{log(\sin\ x)}{\tan\ x}\ dx$を計算せよ。
出典:2020年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\displaystyle \frac{log(\sin\ x)}{\tan\ x}\ dx$を計算せよ。
出典:2020年横浜国立大学 入試問題
3次方程式の解の公式 順天堂大(医)

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#順天堂大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$ x^3+9x+6=0$
*誘導あり
解には$ \omega^3=1$の$\omega$を用いる$(\omega\neq 1)$
順天堂大(医)過去問
この動画を見る
これを解け.
$ x^3+9x+6=0$
*誘導あり
解には$ \omega^3=1$の$\omega$を用いる$(\omega\neq 1)$
順天堂大(医)過去問
大学入試問題#118 防衛医科大学(2012) 区分求積法

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ \displaystyle \frac{(4n)!}{(3n)!} }$を求めよ。
出典:2012年防衛医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ \displaystyle \frac{(4n)!}{(3n)!} }$を求めよ。
出典:2012年防衛医科大学 入試問題
2022東海大(医)ドモアブルの定理の基本

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(\sqrt{2+\sqrt2}+\sqrt{2-\sqrt2i})^8$を解け.
2022東海大(医)過去問
この動画を見る
$(\sqrt{2+\sqrt2}+\sqrt{2-\sqrt2i})^8$を解け.
2022東海大(医)過去問
2022東海大(医)ドモアブルの定理の基本

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東海大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ (\sqrt{2+\sqrt2}+\sqrt{2-\sqrt2i})^8$
これを解け.
2022東海大(医)過去問
この動画を見る
$ (\sqrt{2+\sqrt2}+\sqrt{2-\sqrt2i})^8$
これを解け.
2022東海大(医)過去問
結局2021年東大理系第1問はどう解くのがよかったのか?~東京大学入試問題研究〜福田の数学

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
東京大学2021年理系大問1
$C:s^2+ax+b$は放物線$y=x^2$と2つの共有点を持ち、一方の共有点のx座標は
$-1 \lt x \lt 0$を満たし、他方の共有点のx座標は$0 \lt x \lt 1$を満たす。
(1)点$(a,b)$のとりうる範囲を座標平面上に図示せよ。
(2)放物線Cの通りうる範囲を座標平面上に図示せよ。
2022東京大学理系過去問
この動画を見る
東京大学2021年理系大問1
$C:s^2+ax+b$は放物線$y=x^2$と2つの共有点を持ち、一方の共有点のx座標は
$-1 \lt x \lt 0$を満たし、他方の共有点のx座標は$0 \lt x \lt 1$を満たす。
(1)点$(a,b)$のとりうる範囲を座標平面上に図示せよ。
(2)放物線Cの通りうる範囲を座標平面上に図示せよ。
2022東京大学理系過去問
大学入試問題#117 大分大学(2007) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#大分大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x,y,z$:自然数
$x \leqq y \leqq z$
$7(x+y+z)=2(xy+yz+zx)$をみたす組$(x,y,z)$をすべて求めよ。
出典:2007年大分大学 入試問題
この動画を見る
$x,y,z$:自然数
$x \leqq y \leqq z$
$7(x+y+z)=2(xy+yz+zx)$をみたす組$(x,y,z)$をすべて求めよ。
出典:2007年大分大学 入試問題
大学入試問題#116 岡山県立大学(2009) 定積分②
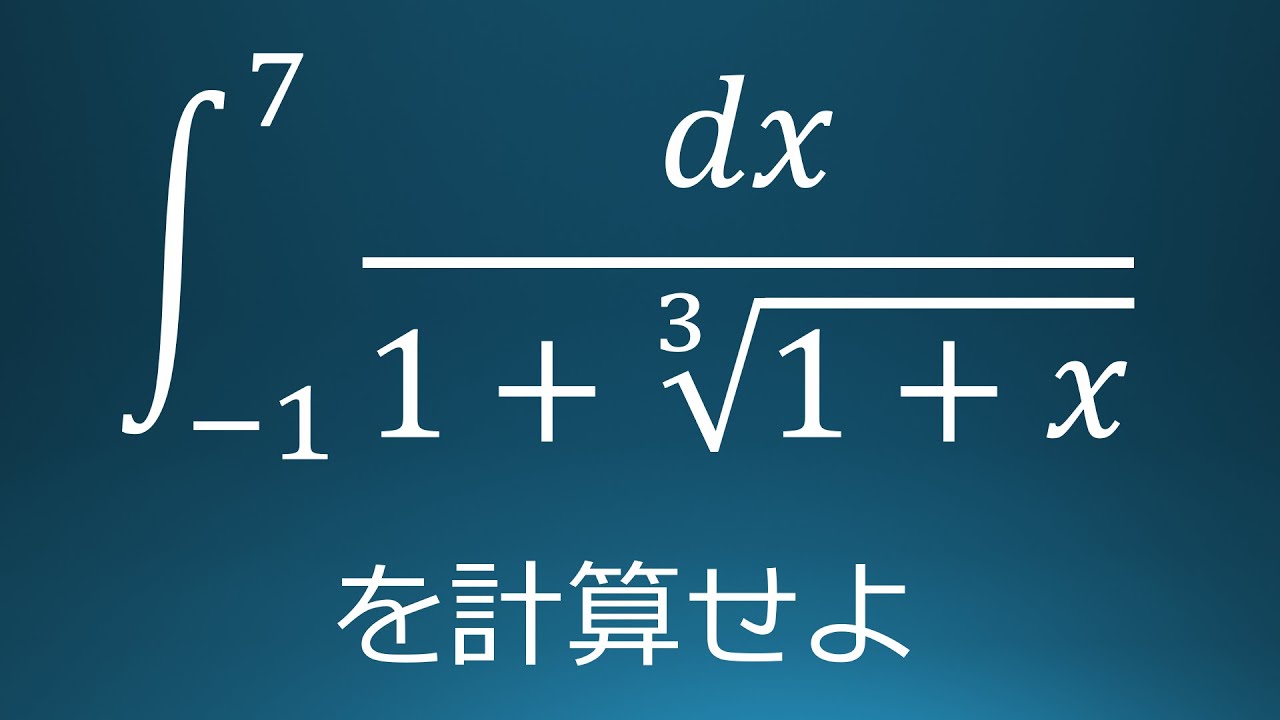
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{7}\displaystyle \frac{dx}{1+\sqrt[ 3 ]{ 1+x }}$を計算せよ。
出典:2009年岡山県立大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{7}\displaystyle \frac{dx}{1+\sqrt[ 3 ]{ 1+x }}$を計算せよ。
出典:2009年岡山県立大学 入試問題
【概要欄に誘導あり】大学入試問題#115 京都大学(2002) 曲線の長さ(極方程式)

単元:
#大学入試過去問(数学)#平面上の曲線#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
(1)
$x \geqq 0$
$f(x)=log(x+\sqrt{ 1+x^2 })$を微分せよ。
(2)
極方程式
$r=\theta(0 \leqq \theta \leqq \pi)$で定まる曲線の長さ$L$を求めよ。
出典:2002年京都大学 入試問題
この動画を見る
(1)
$x \geqq 0$
$f(x)=log(x+\sqrt{ 1+x^2 })$を微分せよ。
(2)
極方程式
$r=\theta(0 \leqq \theta \leqq \pi)$で定まる曲線の長さ$L$を求めよ。
出典:2002年京都大学 入試問題
