 大学入試過去問(数学)
大学入試過去問(数学)
 大学入試過去問(数学)
大学入試過去問(数学)
大学入試問題#227 琉球大学(2012) 方程式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学
指導講師:
ますただ
問題文全文(内容文):
方程式
$log_5(1-4・5^x)=2x+1$を解け
出典:2012年琉球大学 入試問題
この動画を見る
方程式
$log_5(1-4・5^x)=2x+1$を解け
出典:2012年琉球大学 入試問題
福島大 3数の相加相乗平均の応用

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
${\left(\dfrac{1}{3}(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}) \right)}^{-1} \leqq \dfrac{a+b+c}{3},$
a,b,cは正の実数である.これを証明せよ.
この動画を見る
${\left(\dfrac{1}{3}(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}) \right)}^{-1} \leqq \dfrac{a+b+c}{3},$
a,b,cは正の実数である.これを証明せよ.
6次式の最大値と最小値!?【数学 入試問題】【自治医科大学】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$sin^6x+cos^6x$の最小値が$A$となるとき、$\dfrac{1}{A}$の値を求めよ。
自治医科大過去問
この動画を見る
$sin^6x+cos^6x$の最小値が$A$となるとき、$\dfrac{1}{A}$の値を求めよ。
自治医科大過去問
大学入試問題#226 信州大学(2012) #不定積分
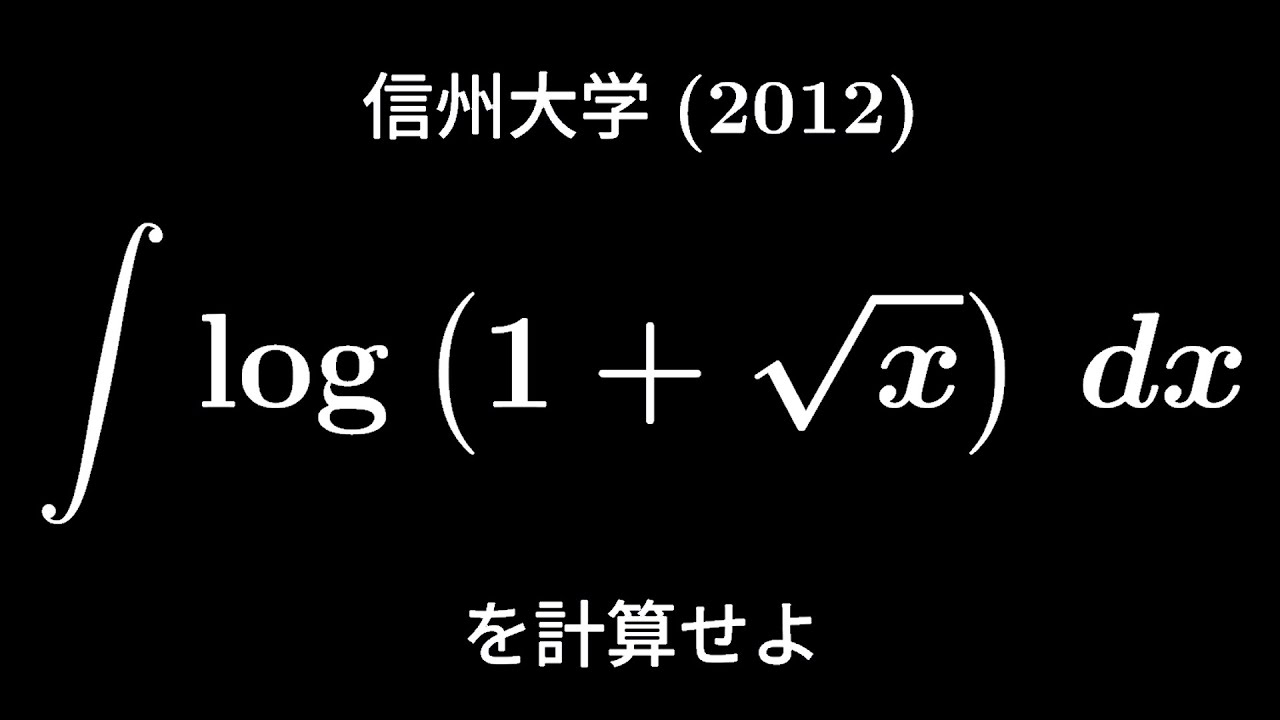
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int log(1+\sqrt{ x })dx$を計算せよ
出典:2012年信州大学 入試問題
この動画を見る
$\displaystyle \int log(1+\sqrt{ x })dx$を計算せよ
出典:2012年信州大学 入試問題
福田の入試問題解説〜慶應義塾大学2022年理工学部第5問〜三角比と空間図形の計量

単元:
#数Ⅰ#大学入試過去問(数学)#空間図形#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
半径$4\sqrt2$の球面S上に3点A,B,Cがあり、線分AB,BC,CAの長さはそれぞれ$AB=4\sqrt6,BC=10,C=6$とする。
(1)$\cos\angle ABC=\boxed{\ \ テ\ \ }$である。平面ABCで球面Sを切った切り口の円をTとする。
Tの半径は$\boxed{\ \ ト\ \ }$である。点Dが円T上を動くとき、$\triangle DAB$の面積の最大値は
$\boxed{\ \ ナ\ \ }$である。
(2)球面Sの中心Oから平面ABCに下ろした垂線OHの長さは$\boxed{\ \ ニ\ \ }$である。
(3)点Eは球面S上を動くとき、三角錐EABCの体積の最大値は$\boxed{\ \ ヌ\ \ }$である。
2022慶應義塾大学理工学部過去問
この動画を見る
半径$4\sqrt2$の球面S上に3点A,B,Cがあり、線分AB,BC,CAの長さはそれぞれ$AB=4\sqrt6,BC=10,C=6$とする。
(1)$\cos\angle ABC=\boxed{\ \ テ\ \ }$である。平面ABCで球面Sを切った切り口の円をTとする。
Tの半径は$\boxed{\ \ ト\ \ }$である。点Dが円T上を動くとき、$\triangle DAB$の面積の最大値は
$\boxed{\ \ ナ\ \ }$である。
(2)球面Sの中心Oから平面ABCに下ろした垂線OHの長さは$\boxed{\ \ ニ\ \ }$である。
(3)点Eは球面S上を動くとき、三角錐EABCの体積の最大値は$\boxed{\ \ ヌ\ \ }$である。
2022慶應義塾大学理工学部過去問
分数式の計算(数II)

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{x+2}{x^2-4} - \frac{1}{x-1}$
札幌学院大学
この動画を見る
$\frac{x+2}{x^2-4} - \frac{1}{x-1}$
札幌学院大学
【良問】京大の整数問題!2つの解法で解きます!【数学 入試問題】【京都大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n^3-7n+9$が素数となるような整数$n$を全て求めよ。
京都大過去問
この動画を見る
$n^3-7n+9$が素数となるような整数$n$を全て求めよ。
京都大過去問
式の値 最後に落とし穴!? 福岡大学
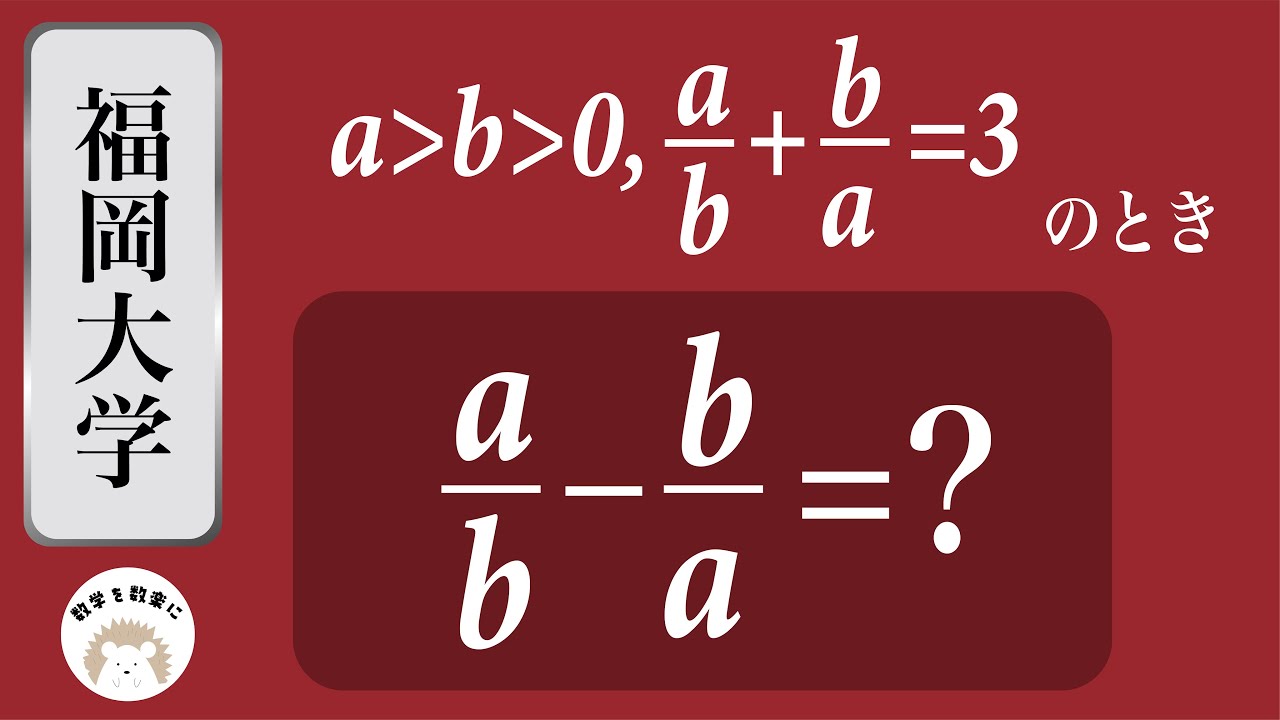
単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a>b>0$ , $\frac{a}{b}+\frac{b}{a} = 3$のとき
$\frac{a}{b} - \frac{b}{a} =?$
福岡大学
この動画を見る
$a>b>0$ , $\frac{a}{b}+\frac{b}{a} = 3$のとき
$\frac{a}{b} - \frac{b}{a} =?$
福岡大学
福田の入試問題解説〜慶應義塾大学2022年理工学部第4問〜指数関数と直線の位置関係と極限

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#関数と極限#微分とその応用#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
曲線$C:y=e^x$を考える。
(1)$a,b$を実数とし、$a \geqq 0$とする。曲線Cと直線$y=ax+b$が共有点をもつため
のaとbの条件を求めよ。
(2)正の実数tに対し、C上の点$A(t,e^t)$を中心とし、直線$y=x$に接する円Dを
考える。直線$y=x$と円Dの接点Bのx座標は$\boxed{\ \ タ\ \ }$であり、
円Dの半径は$\boxed{\ \ チ\ \ }$である。線分ABを3:2に内分する点をPとし、Pのx座標、y座標
をそれぞれX(t),Y(t)とする。このとき、等式
$\lim_{t \to \infty}\frac{Y(t)-kX(t)}{\sqrt{\left\{X(t)\right\}^2+\left\{Y(t)\right\}^2}}=0$
が成り立つような実数kを定めると$k=\boxed{\ \ ツ\ \ }$である。
ただし、$\lim_{t \to \infty}te^{-t}=0$である。
2022慶應義塾大学理工学部過去問
この動画を見る
曲線$C:y=e^x$を考える。
(1)$a,b$を実数とし、$a \geqq 0$とする。曲線Cと直線$y=ax+b$が共有点をもつため
のaとbの条件を求めよ。
(2)正の実数tに対し、C上の点$A(t,e^t)$を中心とし、直線$y=x$に接する円Dを
考える。直線$y=x$と円Dの接点Bのx座標は$\boxed{\ \ タ\ \ }$であり、
円Dの半径は$\boxed{\ \ チ\ \ }$である。線分ABを3:2に内分する点をPとし、Pのx座標、y座標
をそれぞれX(t),Y(t)とする。このとき、等式
$\lim_{t \to \infty}\frac{Y(t)-kX(t)}{\sqrt{\left\{X(t)\right\}^2+\left\{Y(t)\right\}^2}}=0$
が成り立つような実数kを定めると$k=\boxed{\ \ ツ\ \ }$である。
ただし、$\lim_{t \to \infty}te^{-t}=0$である。
2022慶應義塾大学理工学部過去問
大学入試問題#225 埼玉大学 #定積分
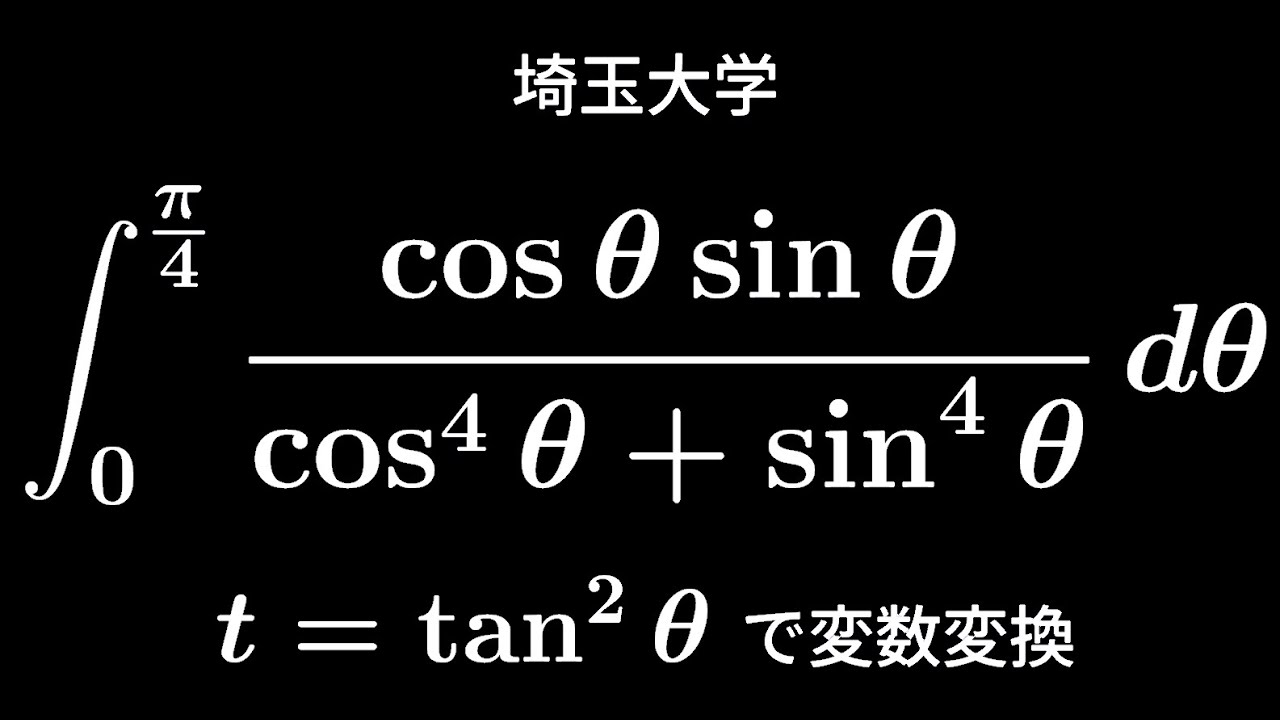
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{\cos\theta\sin\theta}{\cos^4\theta+\sin^4\theta}d\theta$
$t=\tan^2\theta$で変数変換
出典:埼玉大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{\cos\theta\sin\theta}{\cos^4\theta+\sin^4\theta}d\theta$
$t=\tan^2\theta$で変数変換
出典:埼玉大学 入試問題
整数問題 × 確率!京大の取りたい問題【数学 入試問題】【京都大学】

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
1から5までの自然数を1列に並べる。どの並べ方も同様の確からしさで起こるものとする。このとき1番目と2番目と3番目の数の和と、3番目と4番目と5番目の数の和が等しくなる確率を求めよ。ただし、各並べ方において、それぞれの数字は重複なく1度ずつ用いるものとする。
京都大過去問
この動画を見る
1から5までの自然数を1列に並べる。どの並べ方も同様の確からしさで起こるものとする。このとき1番目と2番目と3番目の数の和と、3番目と4番目と5番目の数の和が等しくなる確率を求めよ。ただし、各並べ方において、それぞれの数字は重複なく1度ずつ用いるものとする。
京都大過去問
福田の入試問題解説〜慶應義塾大学2022年理工学部第3問〜複雑な反復試行と条件付き確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
最初に袋の中に白玉が1個入っている。次の規則に従って、1回の操作につき
白玉または赤玉を1個ずつ加えていく。
・1回目の操作では、コインを投げ、表が出たときには赤玉を袋の中に1個加
え、裏が出たときには白玉を袋の中に1個加える。
・2回目以降の操作では、コインを投げ、表が出たときには赤玉を袋の中に1個
加え、裏が出たときには袋から玉を1個無作為に取り出し、その色を見てから
袋に戻し、さらに同じ色の玉を袋の中に1個加える。
(1) 2回目の操作を終えたとき、袋の中に白玉がちょうど2個入っている確率は
$\boxed{\ \ サ\ \ }$である。
(2) 3回目の操作を終えたとき、コインの表が2回、裏が1回出ていたという条件
の下で、袋の中に白玉がちょうど2個入っている条件つき確率は$\boxed{\ \ シ\ \ }$である。
以下、kは2以上の整数とし、k回目の操作を終えたときを考える。
(3)袋の中に白玉のみが入っている確率は$\boxed{\ \ ス\ \ }$である。
(4)1回目の操作で赤玉を加えたという条件の下で、袋の中に白玉がちょうどk個
入っている条件つき確率は$\boxed{\ \ セ\ \ }$である。
(5)袋の中に白玉がちょうどk個入っている確率は$\boxed{\ \ ソ\ \ }$である。
2022慶應義塾大学理工学部過去問
この動画を見る
最初に袋の中に白玉が1個入っている。次の規則に従って、1回の操作につき
白玉または赤玉を1個ずつ加えていく。
・1回目の操作では、コインを投げ、表が出たときには赤玉を袋の中に1個加
え、裏が出たときには白玉を袋の中に1個加える。
・2回目以降の操作では、コインを投げ、表が出たときには赤玉を袋の中に1個
加え、裏が出たときには袋から玉を1個無作為に取り出し、その色を見てから
袋に戻し、さらに同じ色の玉を袋の中に1個加える。
(1) 2回目の操作を終えたとき、袋の中に白玉がちょうど2個入っている確率は
$\boxed{\ \ サ\ \ }$である。
(2) 3回目の操作を終えたとき、コインの表が2回、裏が1回出ていたという条件
の下で、袋の中に白玉がちょうど2個入っている条件つき確率は$\boxed{\ \ シ\ \ }$である。
以下、kは2以上の整数とし、k回目の操作を終えたときを考える。
(3)袋の中に白玉のみが入っている確率は$\boxed{\ \ ス\ \ }$である。
(4)1回目の操作で赤玉を加えたという条件の下で、袋の中に白玉がちょうどk個
入っている条件つき確率は$\boxed{\ \ セ\ \ }$である。
(5)袋の中に白玉がちょうどk個入っている確率は$\boxed{\ \ ソ\ \ }$である。
2022慶應義塾大学理工学部過去問
大学入試問題#224 防衛医科大学(2015) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x^2+x+1}$を計算せよ
出典:2015年防衛医科大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x^2+x+1}$を計算せよ
出典:2015年防衛医科大学 入試問題
簡単すぎる京大の入試問題!解けますか?【数学】【京都大学】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\triangle ABC$において、$AB=2,AC=1$とする。$\angle BAC$の二等分線と辺$BC$の交点を$D$とする。$AD=BD$となるとき、$\triangle ABC$の面積を求めよ。
京都大過去問
この動画を見る
$\triangle ABC$において、$AB=2,AC=1$とする。$\angle BAC$の二等分線と辺$BC$の交点を$D$とする。$AD=BD$となるとき、$\triangle ABC$の面積を求めよ。
京都大過去問
福田の入試問題解説〜慶應義塾大学2022年理工学部第2問〜連立不等式の表す領域の面積と回転体の体積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$r$を正の実数とし、円$C_1:(x-2)^2+y^2=r^2$、楕円$C_2:\frac{x^2}{9}+y^2=1$を考える。
(1)円$C_1$と楕円$C_2$の共有点が存在するようなrの値の範囲は$\boxed{\ \ カ\ \ } \leqq r \leqq \boxed{\ \ キ\ \ }$である。
(2)$r=1$のとき、$C_1$と$C_2$の共有点の座標を全て求めると$\boxed{\ \ ク\ \ }$である。
これらの共有点のうちy座標が正となる点のy座標を$y_0$とする。連立不等式
$\left\{\begin{array}{1}
(x-2)^2+y^2 \leqq 1\\
0 \leqq y \leqq y_0\\
\end{array}\right.$
の表す領域の面積は$\boxed{\ \ ケ\ \ }$である。
(3)連立不等式
$\left\{\begin{array}{1}
(x-2)^2+y^2 \leqq 1\\
\displaystyle\frac{x^2}{9}+y^2 \geqq 1\\
y \geqq 0\\
\end{array}\right.$
の表す領域をDとする。Dをy軸のまわりに
1回転させてできる立体の体積は$\boxed{\ \ コ\ \ }$である。
2022慶應義塾大学理工学部過去問
この動画を見る
$r$を正の実数とし、円$C_1:(x-2)^2+y^2=r^2$、楕円$C_2:\frac{x^2}{9}+y^2=1$を考える。
(1)円$C_1$と楕円$C_2$の共有点が存在するようなrの値の範囲は$\boxed{\ \ カ\ \ } \leqq r \leqq \boxed{\ \ キ\ \ }$である。
(2)$r=1$のとき、$C_1$と$C_2$の共有点の座標を全て求めると$\boxed{\ \ ク\ \ }$である。
これらの共有点のうちy座標が正となる点のy座標を$y_0$とする。連立不等式
$\left\{\begin{array}{1}
(x-2)^2+y^2 \leqq 1\\
0 \leqq y \leqq y_0\\
\end{array}\right.$
の表す領域の面積は$\boxed{\ \ ケ\ \ }$である。
(3)連立不等式
$\left\{\begin{array}{1}
(x-2)^2+y^2 \leqq 1\\
\displaystyle\frac{x^2}{9}+y^2 \geqq 1\\
y \geqq 0\\
\end{array}\right.$
の表す領域をDとする。Dをy軸のまわりに
1回転させてできる立体の体積は$\boxed{\ \ コ\ \ }$である。
2022慶應義塾大学理工学部過去問
大学入試問題#223 宮崎大学(2015) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3+3x^2}{x^2+3x+2}\ dx$
出典:2015年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3+3x^2}{x^2+3x+2}\ dx$
出典:2015年宮崎大学 入試問題
絶対に取りたい問題!京大の確率の問題!【数学 入試問題】【京都大学】

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
正四角形$ABCD$を考える。点$P$は時刻0では頂点$A$に位置し、1秒毎にある頂点から他の3頂点のいずれかに、等しい確率で動くとする。このとき、時刻0から時刻$n$までの間に、4頂点$A,B,C,D$のすべてに点$P$が現れる確率を求めよ。
ただし、$n$は1以上の整数とする。
京都大過去問
この動画を見る
正四角形$ABCD$を考える。点$P$は時刻0では頂点$A$に位置し、1秒毎にある頂点から他の3頂点のいずれかに、等しい確率で動くとする。このとき、時刻0から時刻$n$までの間に、4頂点$A,B,C,D$のすべてに点$P$が現れる確率を求めよ。
ただし、$n$は1以上の整数とする。
京都大過去問
福田の入試問題解説〜慶應義塾大学2022年理工学部第1問(2)〜ガウス記号と倍数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)$n$を奇数とする。nと$[\frac{3n+2}{2}]$の積が6の倍数であるための必要十分条件は、
nを$\boxed{\ \ エ\ \ }$で割った時の余りが$\boxed{\ \ オ\ \ }$となるときである。ただし、
実数xに対しxを超えない最大の整数を[x]と表す。
また、$\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ }$は$0 \leqq \boxed{\ \ オ\ \ } \lt \boxed{\ \ エ\ \ }$
を満たす整数である。$\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ }$を求める過程を解答欄に記述しなさい。
2022慶應義塾大学理工学部過去問
この動画を見る
(2)$n$を奇数とする。nと$[\frac{3n+2}{2}]$の積が6の倍数であるための必要十分条件は、
nを$\boxed{\ \ エ\ \ }$で割った時の余りが$\boxed{\ \ オ\ \ }$となるときである。ただし、
実数xに対しxを超えない最大の整数を[x]と表す。
また、$\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ }$は$0 \leqq \boxed{\ \ オ\ \ } \lt \boxed{\ \ エ\ \ }$
を満たす整数である。$\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ }$を求める過程を解答欄に記述しなさい。
2022慶應義塾大学理工学部過去問
大学入試問題#222 広島市立大学2015 #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\cos\ x}{\cos^2x+2\sin\ x-2}dx$を計算せよ
出典:2015年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\cos\ x}{\cos^2x+2\sin\ x-2}dx$を計算せよ
出典:2015年広島市立大学 入試問題
京大の確率の問題!解けますか?【数学 入試問題】【京都大学】

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
さいころを$n$個同時に投げるとき、出た目の数の和が$n+3$になる確率を求めよ。
京都大過去問
この動画を見る
さいころを$n$個同時に投げるとき、出た目の数の和が$n+3$になる確率を求めよ。
京都大過去問
福田の入試問題解説〜慶應義塾大学2022年理工学部第1問(1)〜空間のベクトル方程式

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
(1)$\overrightarrow{ a }=(\sqrt3,0,1)$とする。
空間ベクトル$\overrightarrow{ b }, \overrightarrow{ c }$はともに大きさが1であり、
$\overrightarrow{ a }∟\overrightarrow{ b }, \overrightarrow{ b }∟\overrightarrow{ c }, \overrightarrow{ c }∟\overrightarrow{ a }$とする。
$(\textrm{i})p,q,r$を実数とし、$\overrightarrow{ x }=p\overrightarrow{ a }+q\overrightarrow{ b }+r\overrightarrow{ c }$とするとき、
内積$\overrightarrow{ x }・\overrightarrow{ a }$と$\overrightarrow{ x }$の大きさ$|\overrightarrow{ x }|$をp,q,rを用いて表すと、
$\overrightarrow{ x }・\overrightarrow{ a }=\boxed{\ \ ア\ \ },|\ \overrightarrow{ x } \ |=\boxed{\ \ イ\ \ }$である。
$(\textrm{ii})(5,0,z)=s\overrightarrow{ a }+(\cos\theta)\overrightarrow{ b }+(\sin\theta)\overrightarrow{ c }$を満たす実数$s,\theta$が存在するような
実数zは2個あるが、それらを全て求めると$z=\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学理工学部過去問
この動画を見る
(1)$\overrightarrow{ a }=(\sqrt3,0,1)$とする。
空間ベクトル$\overrightarrow{ b }, \overrightarrow{ c }$はともに大きさが1であり、
$\overrightarrow{ a }∟\overrightarrow{ b }, \overrightarrow{ b }∟\overrightarrow{ c }, \overrightarrow{ c }∟\overrightarrow{ a }$とする。
$(\textrm{i})p,q,r$を実数とし、$\overrightarrow{ x }=p\overrightarrow{ a }+q\overrightarrow{ b }+r\overrightarrow{ c }$とするとき、
内積$\overrightarrow{ x }・\overrightarrow{ a }$と$\overrightarrow{ x }$の大きさ$|\overrightarrow{ x }|$をp,q,rを用いて表すと、
$\overrightarrow{ x }・\overrightarrow{ a }=\boxed{\ \ ア\ \ },|\ \overrightarrow{ x } \ |=\boxed{\ \ イ\ \ }$である。
$(\textrm{ii})(5,0,z)=s\overrightarrow{ a }+(\cos\theta)\overrightarrow{ b }+(\sin\theta)\overrightarrow{ c }$を満たす実数$s,\theta$が存在するような
実数zは2個あるが、それらを全て求めると$z=\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学理工学部過去問
大学入試問題#221 横浜国立大学(2015) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt{ \frac{\pi}{2} }}x^3\cos(x^2)dx$を計算せよ
出典:2015年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ \frac{\pi}{2} }}x^3\cos(x^2)dx$を計算せよ
出典:2015年横浜国立大学 入試問題
中学生でも解ける京大の入試問題!解けますか?【数学 入試問題】【京都大学】

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
1歩で1段または2段のいずれかで階段を昇るとき、1歩で2段昇ることは連続しないものとする。15段の階段を昇る昇り方は何通りあるか。
京都大過去問
この動画を見る
1歩で1段または2段のいずれかで階段を昇るとき、1歩で2段昇ることは連続しないものとする。15段の階段を昇る昇り方は何通りあるか。
京都大過去問
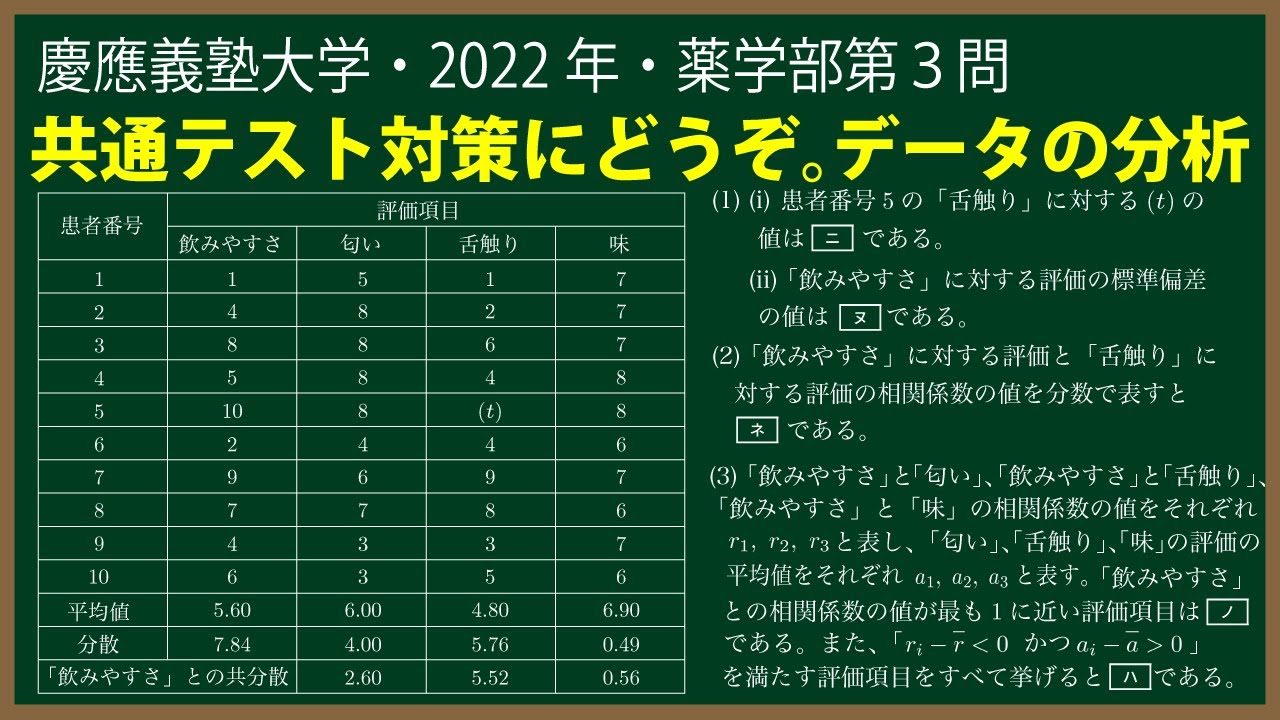
福田の数学〜慶應義塾大学2022年薬学部第3問〜データの分析・平均・標準偏差・共分散・相関係数
単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
ある病院の入院患者10人に対して、病院内で作っている粉薬の評価を調査した。
調査の評価項目は、粉薬の「飲みやすさ」と、「飲みやすさ」の要因と考えられる
「匂い」「舌触り」、「味」の計4項目についてである。
10人の患者が、評価項目について最も満足な場合は10、最も不安な場合は1として、
1以上10以下の整数で評価した。表内の平均値、分散、共分散の数値は四捨五入
されていない正確な値である。(※動画参照)
「飲みやすさ」との共分散は、「飲みやすさ」に対する評価の偏差と、各評価項目
に対する評価の偏差の積の平均値である。
(1)$(\textrm{i})$患者番号5の「舌触り」に対する(t)の値は$\boxed{\ \ ニ\ \ }$である。
$(\textrm{ii})$「飲みやすさ」に対する評価の標準偏差の値は$\boxed{\ \ ヌ\ \ }$である。
(2)「飲みやすさ」に対する評価と「舌触り」に対する評価の相関係数の値を
分数で表すと$\boxed{\ \ ネ\ \ }$である。
(3)「飲みやすさ」と「匂い」、「飲みやすさ」と「舌触り」、「飲みやすさ」と「味」
の相関係数の値をそれぞれ$r_1,r_2,r_3$と表し、「匂い」、「舌触り」、「味」の評価の
平均値をそれぞれ$a_1,a_2,a_3$と表す。$a_i,r_i (1 \leqq i \leqq 3)$に対し、$\bar{ r }$と$\bar{ a }$は以下の式で定める。
$\bar{ r }=\frac{r_1+r_2+r_3}{3},\bar{ a }=\frac{a_1+a_2+a_3}{3}$
「飲みやすさ」との相関係数の値が最も1に近い評価項目は$\boxed{\ \ ノ\ \ }$である。
また、「$r_i-\bar{ r } \lt0$かつ$a_i-\bar{ a } \gt0$」を満たす評価項目をすべて挙げると$\boxed{\ \ ノ\ \ }$である。
(4)「匂い」、「舌触り」、「味」のうち、$\boxed{\ \ ハ\ \ }$にあてはまらない評価項目
(以降、この評価項目をXと表す)に関して改良を行った。改良後の紛薬に対して、同じ10人の
患者がXと「飲みやすさ」について再び評価した。
改良後の調査結果では、Xの評価は10人全員の評価が改良前に比べてそれぞれ1上がっていた。
改良後のXの評価の平均値を求めると$\boxed{\ \ ヒ\ \ }$であり、標準偏差は改良前調査における値と
比べて$\boxed{\ \ フ\ \ }$。また、「飲みやすさ」の評価については、改良前の調査において評価が
1以上4以下の場合は2上がり、5以上9以下の場合は1上がり、10の場合は評価が変わらず
10であった。よって改良後の「飲みやすさ」に対する評価の平均値を求めると$\boxed{\ \ ヘ\ \ }$であり、
標準偏差は改良前の調査における値と比べて$\boxed{\ \ ホ\ \ }$。
2022慶應義塾大学薬学部過去問
この動画を見る
ある病院の入院患者10人に対して、病院内で作っている粉薬の評価を調査した。
調査の評価項目は、粉薬の「飲みやすさ」と、「飲みやすさ」の要因と考えられる
「匂い」「舌触り」、「味」の計4項目についてである。
10人の患者が、評価項目について最も満足な場合は10、最も不安な場合は1として、
1以上10以下の整数で評価した。表内の平均値、分散、共分散の数値は四捨五入
されていない正確な値である。(※動画参照)
「飲みやすさ」との共分散は、「飲みやすさ」に対する評価の偏差と、各評価項目
に対する評価の偏差の積の平均値である。
(1)$(\textrm{i})$患者番号5の「舌触り」に対する(t)の値は$\boxed{\ \ ニ\ \ }$である。
$(\textrm{ii})$「飲みやすさ」に対する評価の標準偏差の値は$\boxed{\ \ ヌ\ \ }$である。
(2)「飲みやすさ」に対する評価と「舌触り」に対する評価の相関係数の値を
分数で表すと$\boxed{\ \ ネ\ \ }$である。
(3)「飲みやすさ」と「匂い」、「飲みやすさ」と「舌触り」、「飲みやすさ」と「味」
の相関係数の値をそれぞれ$r_1,r_2,r_3$と表し、「匂い」、「舌触り」、「味」の評価の
平均値をそれぞれ$a_1,a_2,a_3$と表す。$a_i,r_i (1 \leqq i \leqq 3)$に対し、$\bar{ r }$と$\bar{ a }$は以下の式で定める。
$\bar{ r }=\frac{r_1+r_2+r_3}{3},\bar{ a }=\frac{a_1+a_2+a_3}{3}$
「飲みやすさ」との相関係数の値が最も1に近い評価項目は$\boxed{\ \ ノ\ \ }$である。
また、「$r_i-\bar{ r } \lt0$かつ$a_i-\bar{ a } \gt0$」を満たす評価項目をすべて挙げると$\boxed{\ \ ノ\ \ }$である。
(4)「匂い」、「舌触り」、「味」のうち、$\boxed{\ \ ハ\ \ }$にあてはまらない評価項目
(以降、この評価項目をXと表す)に関して改良を行った。改良後の紛薬に対して、同じ10人の
患者がXと「飲みやすさ」について再び評価した。
改良後の調査結果では、Xの評価は10人全員の評価が改良前に比べてそれぞれ1上がっていた。
改良後のXの評価の平均値を求めると$\boxed{\ \ ヒ\ \ }$であり、標準偏差は改良前調査における値と
比べて$\boxed{\ \ フ\ \ }$。また、「飲みやすさ」の評価については、改良前の調査において評価が
1以上4以下の場合は2上がり、5以上9以下の場合は1上がり、10の場合は評価が変わらず
10であった。よって改良後の「飲みやすさ」に対する評価の平均値を求めると$\boxed{\ \ ヘ\ \ }$であり、
標準偏差は改良前の調査における値と比べて$\boxed{\ \ ホ\ \ }$。
2022慶應義塾大学薬学部過去問
大学入試問題#220 東海大学医学部【再投稿】 #定積分 #King property

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東海大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi}x(\cos^2x)(\sin\ x)dx$
出典:東海大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi}x(\cos^2x)(\sin\ x)dx$
出典:東海大学医学部 入試問題
京大の整数問題!落としてはいけない問題です!【数学 入試問題】【京都大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
2以上の自然数$n$に対し、$n$と$n^2+2$がともに素数になるのは、$n=3$の場合に限ることを示せ。
京都大過去問
この動画を見る
2以上の自然数$n$に対し、$n$と$n^2+2$がともに素数になるのは、$n=3$の場合に限ることを示せ。
京都大過去問
難関国立大学入試問題解説2022年度版がリリースされたので紹介するよ

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
難関国立大学入試問題解説2022年度版がリリースされたので紹介していきます.
この動画を見る
難関国立大学入試問題解説2022年度版がリリースされたので紹介していきます.
大学入試問題#219 京都大学? (2016) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_n=\displaystyle \int_{\sqrt{ 3 }}^{2\sqrt{ 2 }}\displaystyle \frac{x^{2n-1}}{\sqrt{ x^2+1 }}\ dx$
$a_1,\ a_2$を求めよ。
出典:2016年京都大学 入試問題
この動画を見る
$a_n=\displaystyle \int_{\sqrt{ 3 }}^{2\sqrt{ 2 }}\displaystyle \frac{x^{2n-1}}{\sqrt{ x^2+1 }}\ dx$
$a_1,\ a_2$を求めよ。
出典:2016年京都大学 入試問題
京大の標準的な問題!三角関数の知識だけで解けます【数学 入試問題】【京都大学】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ f(\theta)=cos4\theta-4sin^2\theta$とする。$0≦\theta≦\dfrac{3\pi}{4}$における$f(\theta)$の最大値および最小値を求めよ。
京都大過去問
この動画を見る
$ f(\theta)=cos4\theta-4sin^2\theta$とする。$0≦\theta≦\dfrac{3\pi}{4}$における$f(\theta)$の最大値および最小値を求めよ。
京都大過去問
福田の数学〜九州大学2022年文系第4問〜定義に従って定積分の性質を証明する

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#微分法と積分法#恒等式・等式・不等式の証明#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
定積分について述べた次の文章を読んで、後の問いに答えよ。
$f(x)$を整式とする。$F'(x)=f(x)$となる$F(x)$を1つ選び、
$f(x)$のaからbまでの定積分を
$#\int_a^bf(x)dx=F(b)-F(a)\ldots①$
で定義する。定積分の値はF(x)の選び方によらずに定まる。
定積分は次の性質(A),(B),(C)をもつ。
(A)$\int_a^b\left\{kf(x)+lg(x)\right\}dx=k\int_a^bf(x)dx+l\int_a^bg(x)dx$
(B)$a \leqq c \leqq b$のとき、$\int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx$
(C)区間$a \leqq x \leqq b$において$g(x) \geqq h(x)$ならば、$\int_a^bg(x)dx \geqq \int_a^bh(x)dx$
ただし、f(x),g(x),h(x)は整式、k,lは定数である。
以下、$f(x)$が区間$0 \leqq x \leqq 1$上で増加関数になる場合を考える。
$n$を自然数とする。定積分の性質$\boxed{\ \ ア\ \ }$を用い、定数関数に対する定積分の計算を行うと、
$\frac{1}{n}f(\frac{i-1}{n}) \leqq \int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx \leqq \frac{1}{n}f(\frac{i}{n}) (i = 1,2,\ldots,n) \ldots②$
が成り立つことがわかる。$S_n=\frac{1}{n}\sum_{i=1}^nf(\frac{i-1}{n})$とおくと、
不等式②と定積分の性質$\boxed{\ \ イ\ \ }$より次の不等式が成り立つ。
$0 \leqq \int_0^1f(x)dx-S_n \leqq \frac{f(1)-f(0)}{n} \ldots③$
よって、$n$を限りなく大きくすると$S_n$は$\int_0^1f(x)dx$に限りなく近づく。
(1)関数F(x),G(x)が微分可能であるとき、$\left\{F(x)+G(x)\right\}'=F'(x)+G'(x)$が
成り立つことと定積分の定義①を用いて、性質(A)で$k=l=1$とした場合の等式
$\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx$ を示せ。
(2)定積分の定義①と関数の増減と導関数の関係を用いて、次を示せ。
$a \lt b$のとき、区間$a \leqq x \leqq b$において$g(x) \gt 0$ならば、$\int_a^bg(x)dx \gt 0$
(3)(A),(B),(C)のうち、空欄$\boxed{\ \ ア\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、文章中の下線部の内容を詳しく説明することで、
不等式②を示せ。
(4)(A),(B),(C)のうち、空欄$\boxed{\ \ イ\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、不等式③を示せ。
2022九州大学文系過去問
この動画を見る
定積分について述べた次の文章を読んで、後の問いに答えよ。
$f(x)$を整式とする。$F'(x)=f(x)$となる$F(x)$を1つ選び、
$f(x)$のaからbまでの定積分を
$#\int_a^bf(x)dx=F(b)-F(a)\ldots①$
で定義する。定積分の値はF(x)の選び方によらずに定まる。
定積分は次の性質(A),(B),(C)をもつ。
(A)$\int_a^b\left\{kf(x)+lg(x)\right\}dx=k\int_a^bf(x)dx+l\int_a^bg(x)dx$
(B)$a \leqq c \leqq b$のとき、$\int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx$
(C)区間$a \leqq x \leqq b$において$g(x) \geqq h(x)$ならば、$\int_a^bg(x)dx \geqq \int_a^bh(x)dx$
ただし、f(x),g(x),h(x)は整式、k,lは定数である。
以下、$f(x)$が区間$0 \leqq x \leqq 1$上で増加関数になる場合を考える。
$n$を自然数とする。定積分の性質$\boxed{\ \ ア\ \ }$を用い、定数関数に対する定積分の計算を行うと、
$\frac{1}{n}f(\frac{i-1}{n}) \leqq \int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx \leqq \frac{1}{n}f(\frac{i}{n}) (i = 1,2,\ldots,n) \ldots②$
が成り立つことがわかる。$S_n=\frac{1}{n}\sum_{i=1}^nf(\frac{i-1}{n})$とおくと、
不等式②と定積分の性質$\boxed{\ \ イ\ \ }$より次の不等式が成り立つ。
$0 \leqq \int_0^1f(x)dx-S_n \leqq \frac{f(1)-f(0)}{n} \ldots③$
よって、$n$を限りなく大きくすると$S_n$は$\int_0^1f(x)dx$に限りなく近づく。
(1)関数F(x),G(x)が微分可能であるとき、$\left\{F(x)+G(x)\right\}'=F'(x)+G'(x)$が
成り立つことと定積分の定義①を用いて、性質(A)で$k=l=1$とした場合の等式
$\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx$ を示せ。
(2)定積分の定義①と関数の増減と導関数の関係を用いて、次を示せ。
$a \lt b$のとき、区間$a \leqq x \leqq b$において$g(x) \gt 0$ならば、$\int_a^bg(x)dx \gt 0$
(3)(A),(B),(C)のうち、空欄$\boxed{\ \ ア\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、文章中の下線部の内容を詳しく説明することで、
不等式②を示せ。
(4)(A),(B),(C)のうち、空欄$\boxed{\ \ イ\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、不等式③を示せ。
2022九州大学文系過去問
