 大学入試過去問(数学)
大学入試過去問(数学)
 大学入試過去問(数学)
大学入試過去問(数学)
【整数問題の超難問】素数の中のあの数字を使え!一橋大学で実際に出された入試問題【数学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ a-b-8$と$b-c-8$が素数となるような素数の組$(a,b,c)$をすべて求めよ。
一橋大過去問
この動画を見る
$ a-b-8$と$b-c-8$が素数となるような素数の組$(a,b,c)$をすべて求めよ。
一橋大過去問
福田の数学〜筑波大学2022年理系第1問〜円と放物線の接線と面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
$t,\ p$を実数とし、$t \gt 0$とする。xy平面において、原点Oを中心とし点A(1,t)
を通る円を$C_1$とする。また、点Aにおける$C_1$の接線をlとする。直線$x=p$
を軸とする2次関数のグラフC_2は、x軸と接し、点Aにおいて直線lとも接するとする。
(1)直線$l$の方程式をtを用いて表せ。
(2)pをtを用いて表せ。
(3)$C_2$とx軸の接点をMとし、$C_2$とy軸の交点をNとする。tが正の実数全体を動くとき、
三角形OMNの面積の最小値を求めよ。
2022筑波大学理系過去問
この動画を見る
$t,\ p$を実数とし、$t \gt 0$とする。xy平面において、原点Oを中心とし点A(1,t)
を通る円を$C_1$とする。また、点Aにおける$C_1$の接線をlとする。直線$x=p$
を軸とする2次関数のグラフC_2は、x軸と接し、点Aにおいて直線lとも接するとする。
(1)直線$l$の方程式をtを用いて表せ。
(2)pをtを用いて表せ。
(3)$C_2$とx軸の接点をMとし、$C_2$とy軸の交点をNとする。tが正の実数全体を動くとき、
三角形OMNの面積の最小値を求めよ。
2022筑波大学理系過去問
大学入試問題#208 信州大学(2021) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\pi}^{\pi}\displaystyle \frac{\sin^2x}{1+e^{-x}}\ dx$を計算せよ。
出典:2021年信州大学 入試問題
この動画を見る
$\displaystyle \int_{-\pi}^{\pi}\displaystyle \frac{\sin^2x}{1+e^{-x}}\ dx$を計算せよ。
出典:2021年信州大学 入試問題
頻出の整数問題!難関大学でよく出る重要な性質【一橋大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ m $を整数とする。3次方程式$ x^3+mx^2+(m+8)x+1=0$は有理数の解$a$を持つ。
(1)$a$は整数であることを示せ。
(2)$m$の値を求めよ
一橋大過去問
この動画を見る
$ m $を整数とする。3次方程式$ x^3+mx^2+(m+8)x+1=0$は有理数の解$a$を持つ。
(1)$a$は整数であることを示せ。
(2)$m$の値を求めよ
一橋大過去問
福田の数学〜東京医科歯科大学2022年理系第3問〜定積分と面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#積分とその応用#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
曲線$C:y=f(x) (0 \leqq x \lt 1)$が次の条件を満たすとする。
・$f(0)=0$
・$0 \lt x \lt 1$のとき$f'(x) \gt 0$
・$0 \lt a \lt 1$を満たすすべての実数aについて、曲線C上の点$(a, f(a))$
における接線と直線$x=1$との交点をQとするとき、$PQ=1$
この時以下の問いに答えよ。
(1)$f'(x)$を求めよ。
(2)$\int_0^{\frac{1}{2}}(1-x)f'(x)dx$の値を求めよ。
(3)曲線Cとx軸、直線$x=1$、直線$y=f(\frac{1}{2})$で囲まれた部分の面積を求めよ。
2022東京医科歯科大学理系過去問
この動画を見る
曲線$C:y=f(x) (0 \leqq x \lt 1)$が次の条件を満たすとする。
・$f(0)=0$
・$0 \lt x \lt 1$のとき$f'(x) \gt 0$
・$0 \lt a \lt 1$を満たすすべての実数aについて、曲線C上の点$(a, f(a))$
における接線と直線$x=1$との交点をQとするとき、$PQ=1$
この時以下の問いに答えよ。
(1)$f'(x)$を求めよ。
(2)$\int_0^{\frac{1}{2}}(1-x)f'(x)dx$の値を求めよ。
(3)曲線Cとx軸、直線$x=1$、直線$y=f(\frac{1}{2})$で囲まれた部分の面積を求めよ。
2022東京医科歯科大学理系過去問
大学入試問題#207 埼玉大学(2006) 不定積分
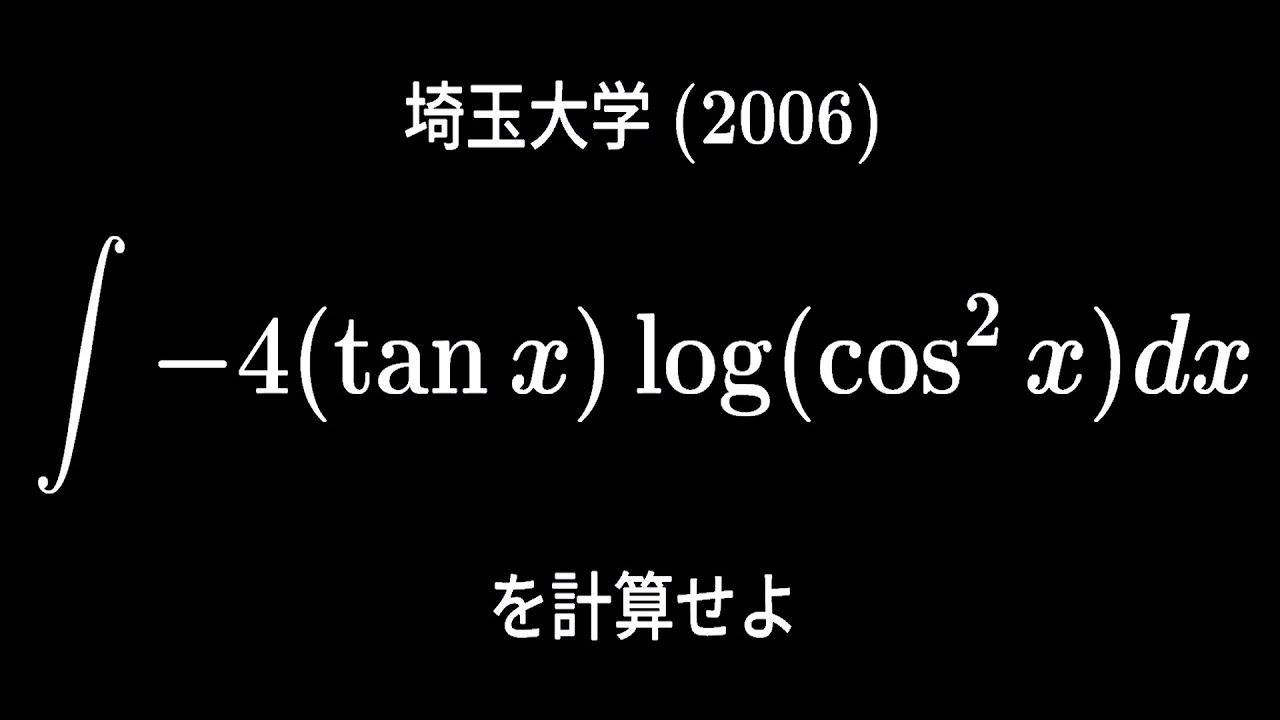
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int -4\tan\ x\ log(\cos^2x)dx$を計算せよ。
出典:2006年埼玉大学 入試問題
この動画を見る
$\displaystyle \int -4\tan\ x\ log(\cos^2x)dx$を計算せよ。
出典:2006年埼玉大学 入試問題
難問整数問題!大事なのは指数の感覚!?【一橋大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ 6・3^{3x}+1=7・5^{2x}$を満たす$0$以上の整数$x$をすべて求めよ。
一橋大過去問
この動画を見る
$ 6・3^{3x}+1=7・5^{2x}$を満たす$0$以上の整数$x$をすべて求めよ。
一橋大過去問
福田の数学〜東京医科歯科大学2022年理系第2問〜放物線に反射する直線の方程式と面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#微分法と積分法#点と直線#円と方程式#微分とその応用#積分とその応用#接線と法線・平均値の定理#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$xy$平面上の放物線$P:y^2=4x$上に異なる2点A,Bをとり、A,Bそれぞれに
おいてPへの接線と直交する直線を$n_A,\ n_B$とする。aを正の数として、点Aの座標
を$(a,\ \sqrt{4a})$とするとき、以下の各問いに答えよ。
(1)$\ n_A$の方程式を求めよ。
(2)直線ABと直線$y=\sqrt{4a}$とがなす角の2等分線の一つが、$n_A$に一致する
とき、直線ABの方程式をaを用いて表せ。
(3)(2)のとき、点Bを通る直線$r_B$を考える。$r_B$と直線ABとがなす角の
2等分線の一つが、$n_B$に一致するとき、$r_B$の方程式をaを用いて表せ。
(4)(3)のとき、直線ABと放物線Pで囲まれた図形の面積をS_1とし、Pと直線\\
$y=\sqrt{4a}$、直線$x=-1$および(3)の$r_B$で囲まれた図形の面積を$S_2$とする。
aを変化させたとき、$\frac{S_1}{S_2}$の最大値を求めよ。
2022東京医科歯科大学理系過去問
この動画を見る
$xy$平面上の放物線$P:y^2=4x$上に異なる2点A,Bをとり、A,Bそれぞれに
おいてPへの接線と直交する直線を$n_A,\ n_B$とする。aを正の数として、点Aの座標
を$(a,\ \sqrt{4a})$とするとき、以下の各問いに答えよ。
(1)$\ n_A$の方程式を求めよ。
(2)直線ABと直線$y=\sqrt{4a}$とがなす角の2等分線の一つが、$n_A$に一致する
とき、直線ABの方程式をaを用いて表せ。
(3)(2)のとき、点Bを通る直線$r_B$を考える。$r_B$と直線ABとがなす角の
2等分線の一つが、$n_B$に一致するとき、$r_B$の方程式をaを用いて表せ。
(4)(3)のとき、直線ABと放物線Pで囲まれた図形の面積をS_1とし、Pと直線\\
$y=\sqrt{4a}$、直線$x=-1$および(3)の$r_B$で囲まれた図形の面積を$S_2$とする。
aを変化させたとき、$\frac{S_1}{S_2}$の最大値を求めよ。
2022東京医科歯科大学理系過去問
大学入試問題#206 東京農工大学(2020) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京農工大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1}{e^x+2}\ dx$
出典:2020年東京農業工業大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{e^x+2}\ dx$
出典:2020年東京農業工業大学 入試問題
整数問題の難問!君は解けるか!?【一橋大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ a^4=b^2+2^c$を満たす正の整数の組$(a,b,c)$で$a$が奇数であるものを求めよ。
一橋大過去問
この動画を見る
$ a^4=b^2+2^c$を満たす正の整数の組$(a,b,c)$で$a$が奇数であるものを求めよ。
一橋大過去問
福田の数学〜東京医科歯科大学2022年理系第1問〜2つのベクトルで生成される異なる点の個数

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#平面上のベクトル#場合の数#三角関数#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
nを自然数とする。整数i,jに対し、xy平面上の点$P_{i,j}$の座標を
$(\cos\frac{2\pi}{n}i+\cos\frac{2\pi}{n}j, \sin\frac{2\pi}{n}i+\sin\frac{2\pi}{n}j)$
で与える。さらに、i,jを動かしたとき、$P_{i,j}$の取り得る異なる座標の
個数を$S_n$とする。このとき、以下の問いに答えよ。
(1)$n=3$のとき、$\triangle P_{0,0}P_{0,1}P_{0,2}$および$\triangle P_{1,0}P_{1,1}P_{1,2}$を同一平面上
に図示せよ。
(2)$S_4$を求めよ。
(3)平面上の異なる2点A,Bに対して、$AQ=BQ=1$であるような
同一平面上の点Qはいくつあるか。AB=dの値で場合分けして答えよ。
(4)$S_n$をnを用いて表せ。
2022東京医科歯科大学理系過去問
この動画を見る
nを自然数とする。整数i,jに対し、xy平面上の点$P_{i,j}$の座標を
$(\cos\frac{2\pi}{n}i+\cos\frac{2\pi}{n}j, \sin\frac{2\pi}{n}i+\sin\frac{2\pi}{n}j)$
で与える。さらに、i,jを動かしたとき、$P_{i,j}$の取り得る異なる座標の
個数を$S_n$とする。このとき、以下の問いに答えよ。
(1)$n=3$のとき、$\triangle P_{0,0}P_{0,1}P_{0,2}$および$\triangle P_{1,0}P_{1,1}P_{1,2}$を同一平面上
に図示せよ。
(2)$S_4$を求めよ。
(3)平面上の異なる2点A,Bに対して、$AQ=BQ=1$であるような
同一平面上の点Qはいくつあるか。AB=dの値で場合分けして答えよ。
(4)$S_n$をnを用いて表せ。
2022東京医科歯科大学理系過去問
【誘導:概要欄】大学入試問題#205 大阪教育大学(2022) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#大阪教育大学
指導講師:
ますただ
問題文全文(内容文):
(1)
$\displaystyle \int e^x(f(x)+f'(x))dx=e^xf(x)+c$を示せ
(2)
$\displaystyle \int_{0}^{\frac{\pi}{4}}e^x\displaystyle \frac{\sqrt{ 1+\sin\ 2x }}{1+\cos\ 2x}\ dx$を計算せよ。
出典:2022年大阪教育大学 入試問題
この動画を見る
(1)
$\displaystyle \int e^x(f(x)+f'(x))dx=e^xf(x)+c$を示せ
(2)
$\displaystyle \int_{0}^{\frac{\pi}{4}}e^x\displaystyle \frac{\sqrt{ 1+\sin\ 2x }}{1+\cos\ 2x}\ dx$を計算せよ。
出典:2022年大阪教育大学 入試問題
分数式の値 京都産業大学

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{y+z}{x} = \frac{z+x}{y} = \frac{x+y}{z} = k$
$x+y+z \neq 0$ のときk=▢
$x+y+z = 0$ のときk=▢
京都産業大学
この動画を見る
$\frac{y+z}{x} = \frac{z+x}{y} = \frac{x+y}{z} = k$
$x+y+z \neq 0$ のときk=▢
$x+y+z = 0$ のときk=▢
京都産業大学
整数問題の難問!2つの解法を紹介【一橋大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2=yz+7 \\
y^2=zx+7 \\
z^2=xy+7
\end{array}
\right.
\end{eqnarray}$
整数$(x,y,z)$を求めよ.
一橋大過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2=yz+7 \\
y^2=zx+7 \\
z^2=xy+7
\end{array}
\right.
\end{eqnarray}$
整数$(x,y,z)$を求めよ.
一橋大過去問
福田の数学〜千葉大学2022年理系第9問〜関数が常に増加する条件

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
rを正の実数とし、関数
$f(x)=x+\frac{r}{\sqrt{1+\sin^2x}}$
を考える。
(1)$r=1$のとき、f$(x)$は常に増加することを示せ。
(2)次の条件を満たす最大の正の実数cを求めよ。
条件:$0 \lt r \lt c$のときは$f(x)$が常に増加する。
2022千葉大学理系過去問
この動画を見る
rを正の実数とし、関数
$f(x)=x+\frac{r}{\sqrt{1+\sin^2x}}$
を考える。
(1)$r=1$のとき、f$(x)$は常に増加することを示せ。
(2)次の条件を満たす最大の正の実数cを求めよ。
条件:$0 \lt r \lt c$のときは$f(x)$が常に増加する。
2022千葉大学理系過去問
大学入試問題#204 東京大学(改) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{\sqrt{ 3 }}\sqrt{ 1+\displaystyle \frac{1}{x^2} }\ dx$
出典:東京大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{\sqrt{ 3 }}\sqrt{ 1+\displaystyle \frac{1}{x^2} }\ dx$
出典:東京大学 入試問題
微分でも解けるけど・・・【数学 入試問題】【慶應義塾大学 改題】

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
関数$ f(x)=x(x-1)(x-3)(x-4)$の$0≦x≦4$の範囲における最大値と最小値、およびそれらの値を取るときの$x$の値を求めよ。
慶應義塾大改題過去問
この動画を見る
関数$ f(x)=x(x-1)(x-3)(x-4)$の$0≦x≦4$の範囲における最大値と最小値、およびそれらの値を取るときの$x$の値を求めよ。
慶應義塾大改題過去問
福田の数学〜千葉大学2022年理系第8問〜定積分で著された式の極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
正の整数$m,n$に対して、
$A(m,n)=(m+1)n^{m+1}\int_o^{\frac{1}{n}}x^me^{-x}dx$
とおく。
(1)$e^{-\frac{1}{n}} \leqq A(m,n) \leqq 1$ を証明せよ。
(2)各$m$に対して、$b_m=\lim_{n \to \infty}A(m,n)$ を求めよ。
(3)各$n$に対して、$c_n=\lim_{m \to \infty}A(m,n)$ を求めよ。
2022千葉大学理系過去問
この動画を見る
正の整数$m,n$に対して、
$A(m,n)=(m+1)n^{m+1}\int_o^{\frac{1}{n}}x^me^{-x}dx$
とおく。
(1)$e^{-\frac{1}{n}} \leqq A(m,n) \leqq 1$ を証明せよ。
(2)各$m$に対して、$b_m=\lim_{n \to \infty}A(m,n)$ を求めよ。
(3)各$n$に対して、$c_n=\lim_{m \to \infty}A(m,n)$ を求めよ。
2022千葉大学理系過去問
大学入試問題#203 琉球大学(2020) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{log2}^{log3}\displaystyle \frac{xe^x}{(e^x-1)^2}dx$を計算せよ
出典:2020年琉球大学 入試問題
この動画を見る
$\displaystyle \int_{log2}^{log3}\displaystyle \frac{xe^x}{(e^x-1)^2}dx$を計算せよ
出典:2020年琉球大学 入試問題
あの慶應(経済)の過去問

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#微分法と積分法#慶應義塾大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ f(x)=-2(x-1)^3+ax^2+bx+c$は$(x-1)$を因数にもち,
$x=1$における接線の傾きは2で,この接線とf(x)はx=2で交わる.a,b,cを求めよ.
慶應(経済)過去問
この動画を見る
$ f(x)=-2(x-1)^3+ax^2+bx+c$は$(x-1)$を因数にもち,
$x=1$における接線の傾きは2で,この接線とf(x)はx=2で交わる.a,b,cを求めよ.
慶應(経済)過去問
対数とみせて様々な知識を使う良問【数学 入試問題】【奈良県立医大】

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$x$の関数$ f(x)=(\log_{10}\dfrac{x}{a})(\log_{10}\dfrac{x}{b})$の最小値が$-\dfrac{1}{4}$であるとき、$a,b$mの値を求めよ。
ただし、$a,b$は$ab=100,a>b$を満たす正の実数とする。
奈良県立医大過去問
この動画を見る
$x$の関数$ f(x)=(\log_{10}\dfrac{x}{a})(\log_{10}\dfrac{x}{b})$の最小値が$-\dfrac{1}{4}$であるとき、$a,b$mの値を求めよ。
ただし、$a,b$は$ab=100,a>b$を満たす正の実数とする。
奈良県立医大過去問
福田の数学〜千葉大学2022年理系第7問〜不定方程式の自然数解と漸化式で与えられた数列

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$x,y$についての方程式
$x^2-6xy+y^2=9 \ldots\ldots(*)$
に関する次の問いに答えよ。
(1)$x,y$がともに正の整数であるような(*)の解のうち、yが最小であるものを
求めよ。
(2)数列$a_1,a_2,a_3,\ldots$が漸化式
$a_{n+2}-6a_{n+1}+a_n=0 (n=1,2,3,\ldots)$
を満たすとする。このとき、$(x,y)=(a_{n+1},a_n)$が(*)を満たすならば、
$(x,y)=(a_{n+2},a_{n+1})$も(*)を満たすことを示せ。
(3)(*)の整数解(x,y)は無数に存在することを示せ。
2022千葉大学理系過去問
この動画を見る
$x,y$についての方程式
$x^2-6xy+y^2=9 \ldots\ldots(*)$
に関する次の問いに答えよ。
(1)$x,y$がともに正の整数であるような(*)の解のうち、yが最小であるものを
求めよ。
(2)数列$a_1,a_2,a_3,\ldots$が漸化式
$a_{n+2}-6a_{n+1}+a_n=0 (n=1,2,3,\ldots)$
を満たすとする。このとき、$(x,y)=(a_{n+1},a_n)$が(*)を満たすならば、
$(x,y)=(a_{n+2},a_{n+1})$も(*)を満たすことを示せ。
(3)(*)の整数解(x,y)は無数に存在することを示せ。
2022千葉大学理系過去問
大学入試問題#202 横浜国立大学 定積分
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
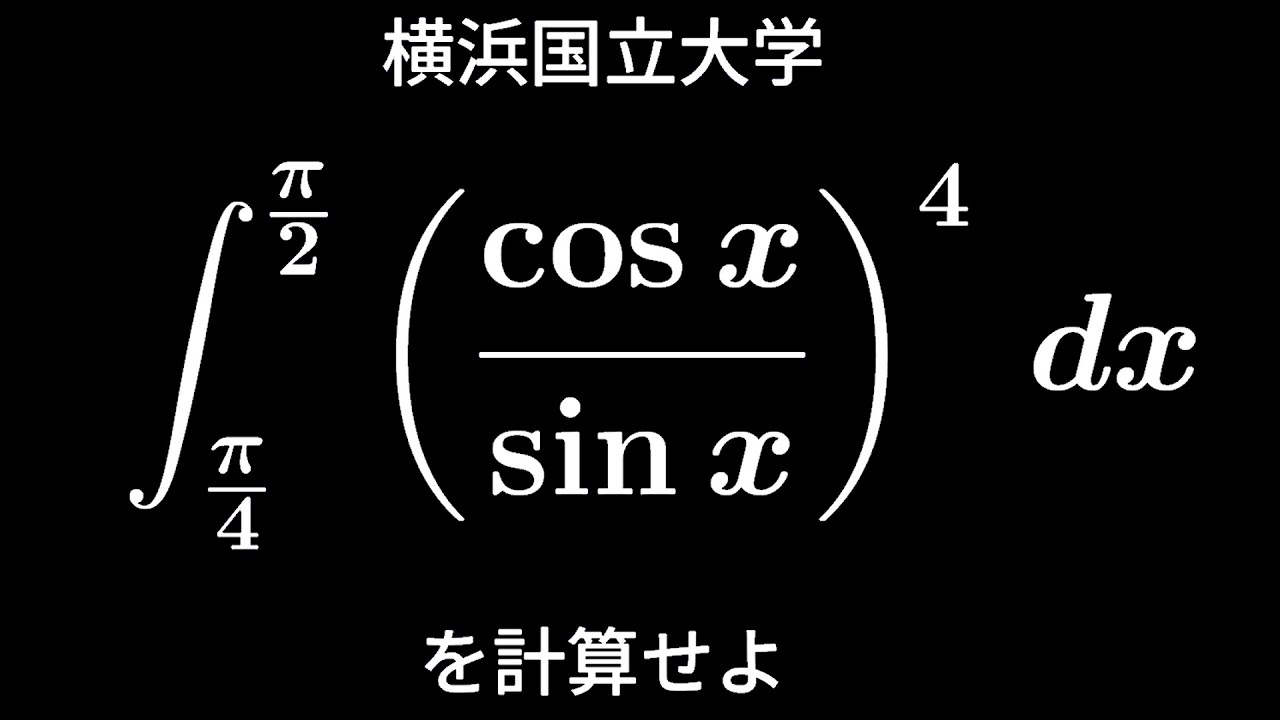
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}}(\displaystyle \frac{\cos\ x}{\sin\ x})^4dx$
出典:横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}}(\displaystyle \frac{\cos\ x}{\sin\ x})^4dx$
出典:横浜国立大学 入試問題
ずばずば約分できる問題【数学 入試問題】【奈良県立医大】

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$abc=n$のとき、
$\dfrac{3a}{ab+a+1}+\dfrac{3nb}{bc+nb+n}+\dfrac{3c}{ca+c+n}$の値を求めよ。
ただし、$a,b,c$はすべて正の実数。
奈良県立医大過去問
この動画を見る
$abc=n$のとき、
$\dfrac{3a}{ab+a+1}+\dfrac{3nb}{bc+nb+n}+\dfrac{3c}{ca+c+n}$の値を求めよ。
ただし、$a,b,c$はすべて正の実数。
奈良県立医大過去問
中学生でも理解可能。ルートの中の二乗 奈良大
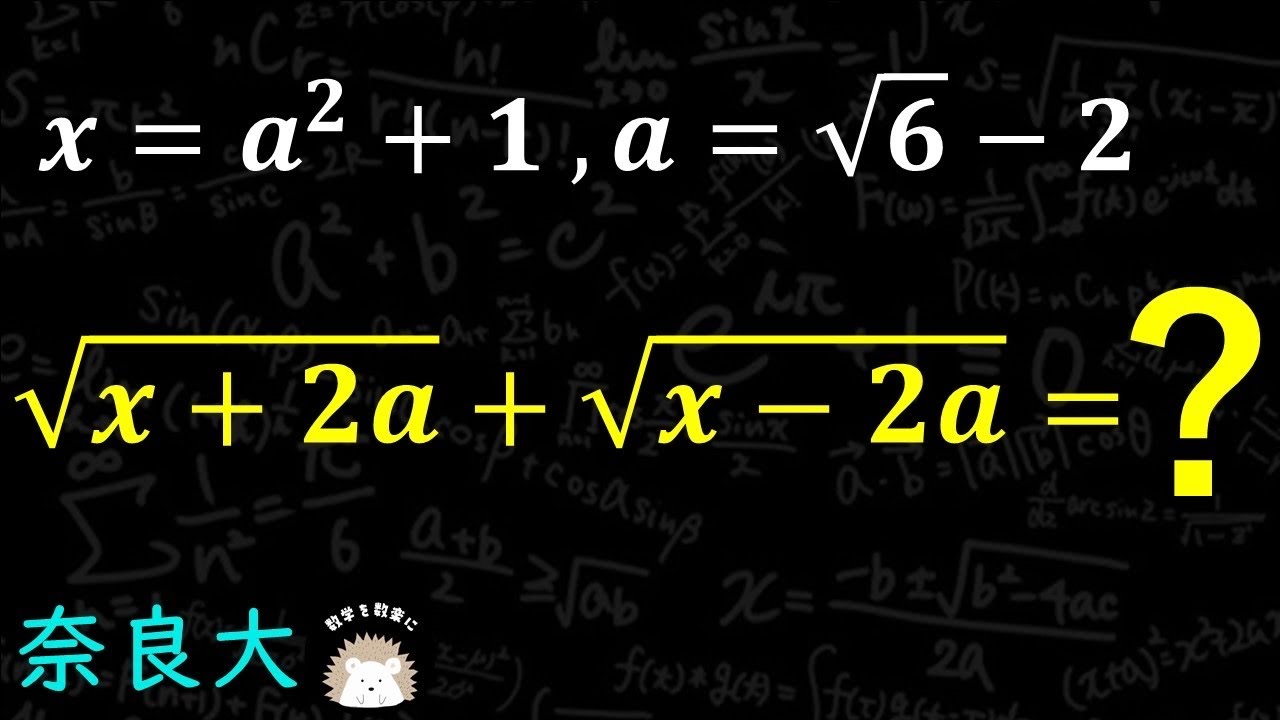
単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=a^2+1$ , $a=\sqrt 6 -2$
$\sqrt {x+2a} + \sqrt {x-2a} =?$
奈良大学
この動画を見る
$x=a^2+1$ , $a=\sqrt 6 -2$
$\sqrt {x+2a} + \sqrt {x-2a} =?$
奈良大学
福田の数学〜千葉大学2022年理系第6問〜独立に動く空間上の2点の距離の最小

単元:
#大学入試過去問(数学)#空間ベクトル#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標空間において、原点Oと点A(1,0,-1)と点B(0,5,0)がある。
実数$t$を用いて$t\ \overrightarrow{ OA }+\overrightarrow{ OB }$と表される点全体をlとする。また、平面xy平面上
の$y=x^2$を満たす点全体からなる曲線をCとする。
(1)曲線$C$上の点$P(a,a^2,0)$を固定する。l上の点Qを、$\overrightarrow{ OA }$と$\overrightarrow{ PQ }$
が垂直であるようにとる。このとき、点Qの座標をaを用いて表せ。
(2)曲線C上の点Rとl上の点Sのうち、$|\overrightarrow{ RS }|$を最小にする点Rと点Sの
組み合わせを全て求めよ。また、そのときの$|\overrightarrow{ RS }|$の値を求めよ。
2022千葉大学理系過去問
この動画を見る
座標空間において、原点Oと点A(1,0,-1)と点B(0,5,0)がある。
実数$t$を用いて$t\ \overrightarrow{ OA }+\overrightarrow{ OB }$と表される点全体をlとする。また、平面xy平面上
の$y=x^2$を満たす点全体からなる曲線をCとする。
(1)曲線$C$上の点$P(a,a^2,0)$を固定する。l上の点Qを、$\overrightarrow{ OA }$と$\overrightarrow{ PQ }$
が垂直であるようにとる。このとき、点Qの座標をaを用いて表せ。
(2)曲線C上の点Rとl上の点Sのうち、$|\overrightarrow{ RS }|$を最小にする点Rと点Sの
組み合わせを全て求めよ。また、そのときの$|\overrightarrow{ RS }|$の値を求めよ。
2022千葉大学理系過去問
大学入試問題#201 山梨大学(2021) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}\cos(\sin\ x)\sin2x\ dx$を計算せよ
出典:2021年山梨大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\cos(\sin\ x)\sin2x\ dx$を計算せよ
出典:2021年山梨大学 入試問題
早稲田(教育)見た目は数2か数3 中身は中学入試
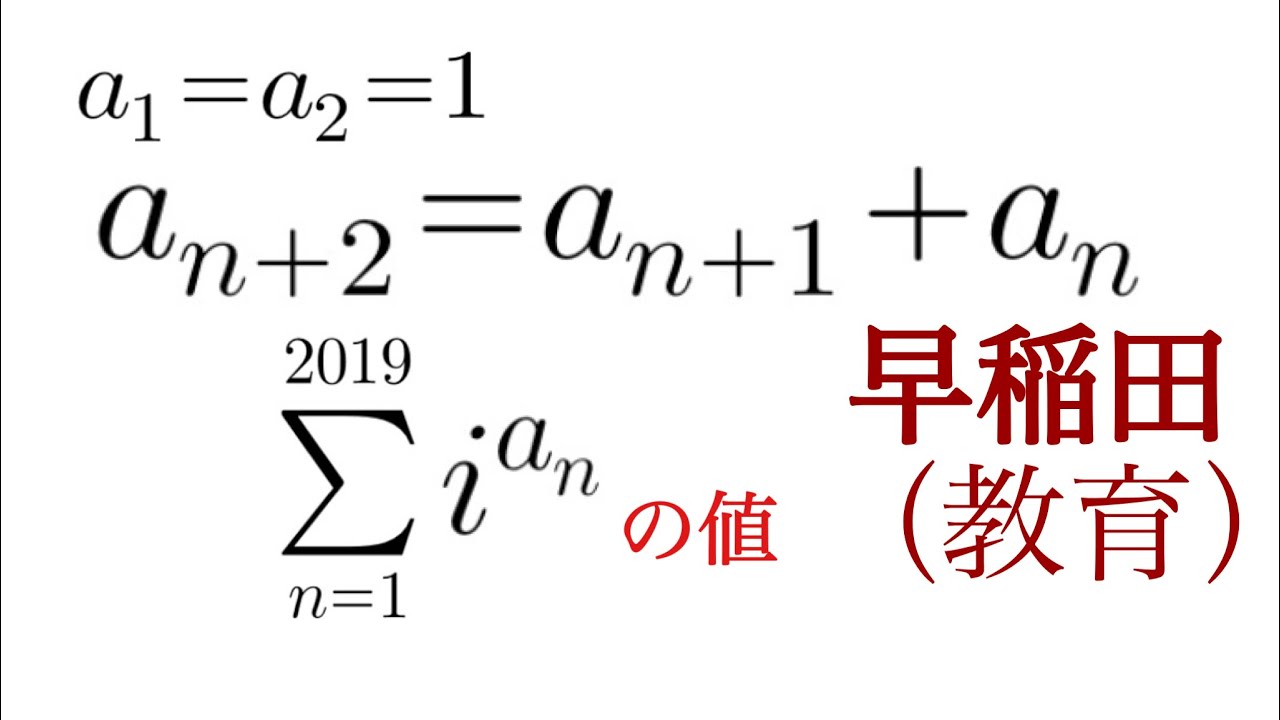
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#数列#早稲田大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1=a_2=1,a_{n+2}=a_{n+1}+a_n,\displaystyle \sum_{n=1}^{2019} ia_n,$
$i$は虚数単位である.これを解け.
早稲田大(教育)過去問
この動画を見る
$ a_1=a_2=1,a_{n+2}=a_{n+1}+a_n,\displaystyle \sum_{n=1}^{2019} ia_n,$
$i$は虚数単位である.これを解け.
早稲田大(教育)過去問
三角関数の重要ポイントが詰まった問題【数学 入試問題】【奈良県立医大】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$0<\theta<\pi,\theta \neq \dfrac{\pi}{2}$のとき、
$ tan\theta-\dfrac{1}{tan\theta}=\dfrac{1}{sin\theta}-\dfrac{1}{cos\theta}$を満たす$\theta$の値を求めよ。
奈良県立医大過去問
この動画を見る
$0<\theta<\pi,\theta \neq \dfrac{\pi}{2}$のとき、
$ tan\theta-\dfrac{1}{tan\theta}=\dfrac{1}{sin\theta}-\dfrac{1}{cos\theta}$を満たす$\theta$の値を求めよ。
奈良県立医大過去問
福田の数学〜千葉大学2022年理系第5問〜n個のサイコロの目の積の確率

単元:
#計算と数の性質#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
nを自然数とする。n個のサイコロを同時に投げ、出た目の積をMとおく。
(1)Mが2でも3でも割り切れない確率を求めよ。
(2)Mが2で割り切れるが、3でも4でも割り切れない確率を求めよ。
(3)Mが4では割り切れるが、3では割り切れない確率を求めよ。
2022千葉大学理系過去問
この動画を見る
nを自然数とする。n個のサイコロを同時に投げ、出た目の積をMとおく。
(1)Mが2でも3でも割り切れない確率を求めよ。
(2)Mが2で割り切れるが、3でも4でも割り切れない確率を求めよ。
(3)Mが4では割り切れるが、3では割り切れない確率を求めよ。
2022千葉大学理系過去問
