 式の計算(整式・展開・因数分解)
式の計算(整式・展開・因数分解)
 式の計算(整式・展開・因数分解)
式の計算(整式・展開・因数分解)
消えるのが気持ち良い
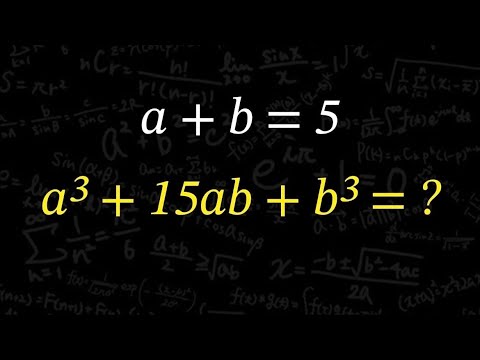
因数分解

素因数分解せよ

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
12317
素因数分解せよ
この動画を見る
12317
素因数分解せよ
秋だけど因数分解

因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$
\begin{eqnarray}
因数分解(整数係数)\\
x^4-2x^2-20x-24
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
因数分解(整数係数)\\
x^4-2x^2-20x-24
\end{eqnarray}
$
因数分解できない因数分解

福田の数学〜中央大学2023年経済学部第1問(1)〜整式の割り算

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)整式$x^3$+$ax^2$+$bx$-3 が$x^2$+$x$-6 で割り切れるとき、定数$a$, $b$の値を求めよ。
この動画を見る
$\Large\boxed{1}$ (1)整式$x^3$+$ax^2$+$bx$-3 が$x^2$+$x$-6 で割り切れるとき、定数$a$, $b$の値を求めよ。
2通りで解説!!因数分解 朋優学院

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$(a+1)^2+a-b-(b+1)^2$
朋優学院高等学校
この動画を見る
因数分解せよ
$(a+1)^2+a-b-(b+1)^2$
朋優学院高等学校
因数分解せよ 昭和学院秀英

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^3y^3+18-9xy-2x^2y^2$
昭和学院秀英高等学校
この動画を見る
因数分解せよ
$x^3y^3+18-9xy-2x^2y^2$
昭和学院秀英高等学校
まさかそのまま代入しないよね?因数分解はできないよ。式の値 早稲田実業

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=1+\sqrt 2 + \sqrt 3$のとき
$x^2-2x-4=?$
早稲田実業学校
この動画を見る
$x=1+\sqrt 2 + \sqrt 3$のとき
$x^2-2x-4=?$
早稲田実業学校
かかってしまいました。因数分解せよ。履正社(大阪府)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
2x(4x-1)-y(2y+1)
履正社高等学校
この動画を見る
因数分解せよ
2x(4x-1)-y(2y+1)
履正社高等学校
手強い計算 慶應義塾(神奈川県)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(30^2+37^2+44^2+ \cdots + 79^2) - (1^2+8^2+15^2+ \cdots +50^2)$
2023慶應義塾高等学校(改)
この動画を見る
$(30^2+37^2+44^2+ \cdots + 79^2) - (1^2+8^2+15^2+ \cdots +50^2)$
2023慶應義塾高等学校(改)
因数分解 大垣日大 (岐阜)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$(x+y)(x+y+2)-8$
大垣日本大学高等学校
この動画を見る
因数分解せよ
$(x+y)(x+y+2)-8$
大垣日本大学高等学校
連立二元二次方程式
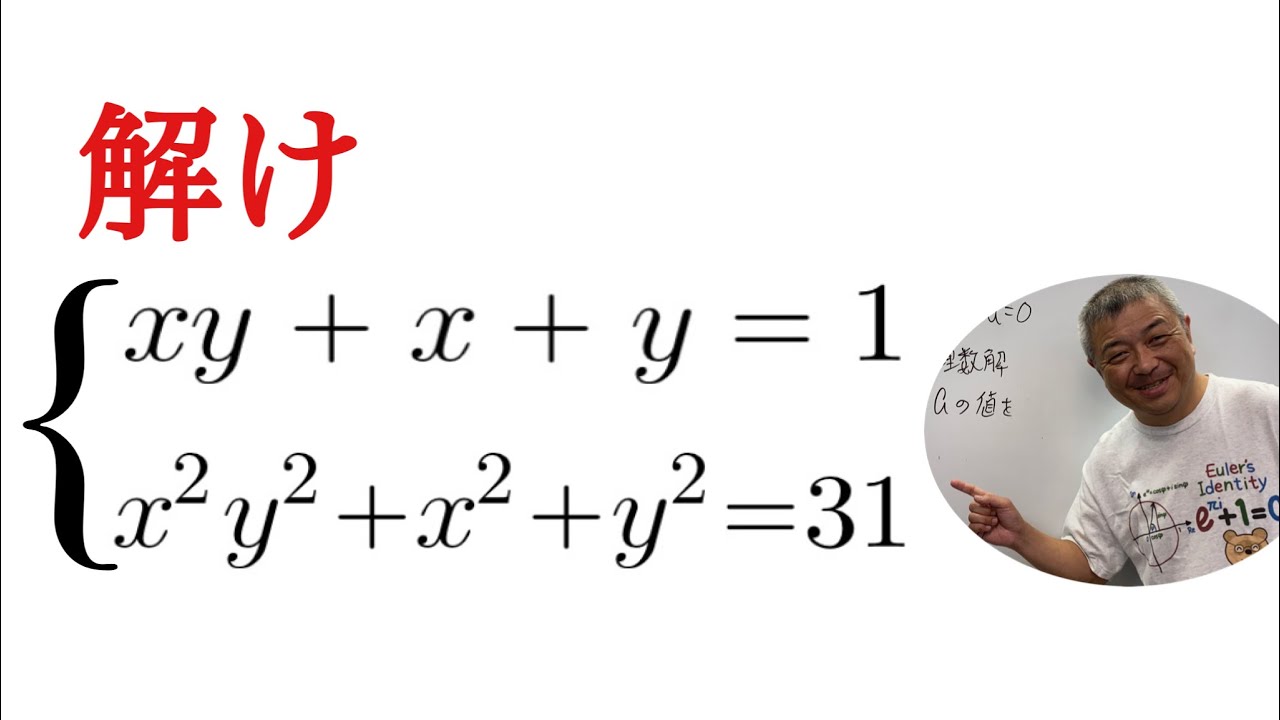
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
解け
\begin{eqnarray}
\left\{
\begin{array}{l}
xy + x + y = 1 \\
x^2y^2 + x^2 + y^2 = 31
\end{array}
\right.
\end{eqnarray}
この動画を見る
解け
\begin{eqnarray}
\left\{
\begin{array}{l}
xy + x + y = 1 \\
x^2y^2 + x^2 + y^2 = 31
\end{array}
\right.
\end{eqnarray}
因数分解は試してなんぼ。立命館宇治(京都)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$a^2-4ab-3a+4b^2+6b$
立命館宇治高等学校
この動画を見る
因数分解せよ
$a^2-4ab-3a+4b^2+6b$
立命館宇治高等学校
正負を答えよ 大垣日大(改)(岐阜)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a>0 , b<0 , |a| < |b|のとき式の正負答えよ
(1)$a+b$
(2)$b^2-a^2$
(3)$\sqrt a - \sqrt{-b}$
大垣日本大学高等学校
この動画を見る
a>0 , b<0 , |a| < |b|のとき式の正負答えよ
(1)$a+b$
(2)$b^2-a^2$
(3)$\sqrt a - \sqrt{-b}$
大垣日本大学高等学校
式の値 中学生の解き方 高校生の解き方
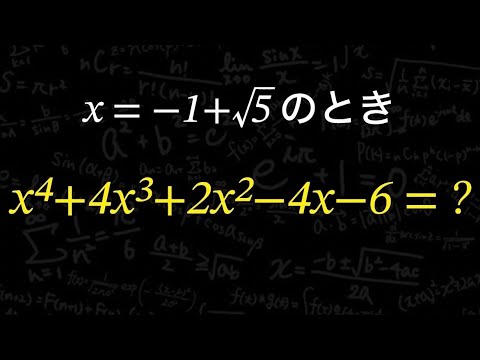
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=-1+\sqrt 5$のとき
$x^4+4x^3+2x^2-4x-6=?$
この動画を見る
$x=-1+\sqrt 5$のとき
$x^4+4x^3+2x^2-4x-6=?$
【数学】2022年度 第2回 K塾記述高2模試 全問解説(ベクトルはおまけ)、※修正箇所:問1(1)(概要欄へ)

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#複素数と方程式#図形と計量#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#2次方程式と2次不等式#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#確率#図形と方程式#三角関数#複素数#三角関数とグラフ#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
2022年度第2回全統記述高2模試全問解説動画です!
この動画を見る
2022年度第2回全統記述高2模試全問解説動画です!
頭の体操に。因数分解せよ
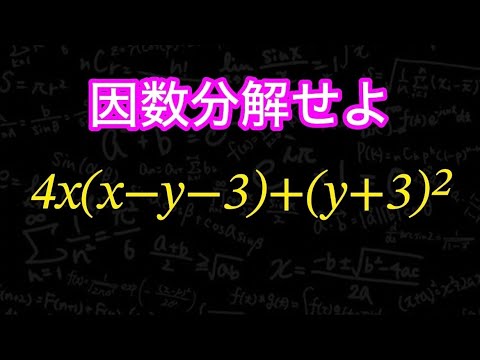
式の値
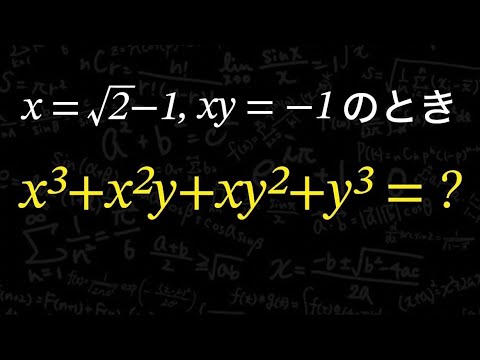
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=\sqrt 2 -1$ , $xy= -1$のとき
$x^3+x^2y+xy^2+y^3=?$
この動画を見る
$x=\sqrt 2 -1$ , $xy= -1$のとき
$x^3+x^2y+xy^2+y^3=?$
一工夫必要なBBB
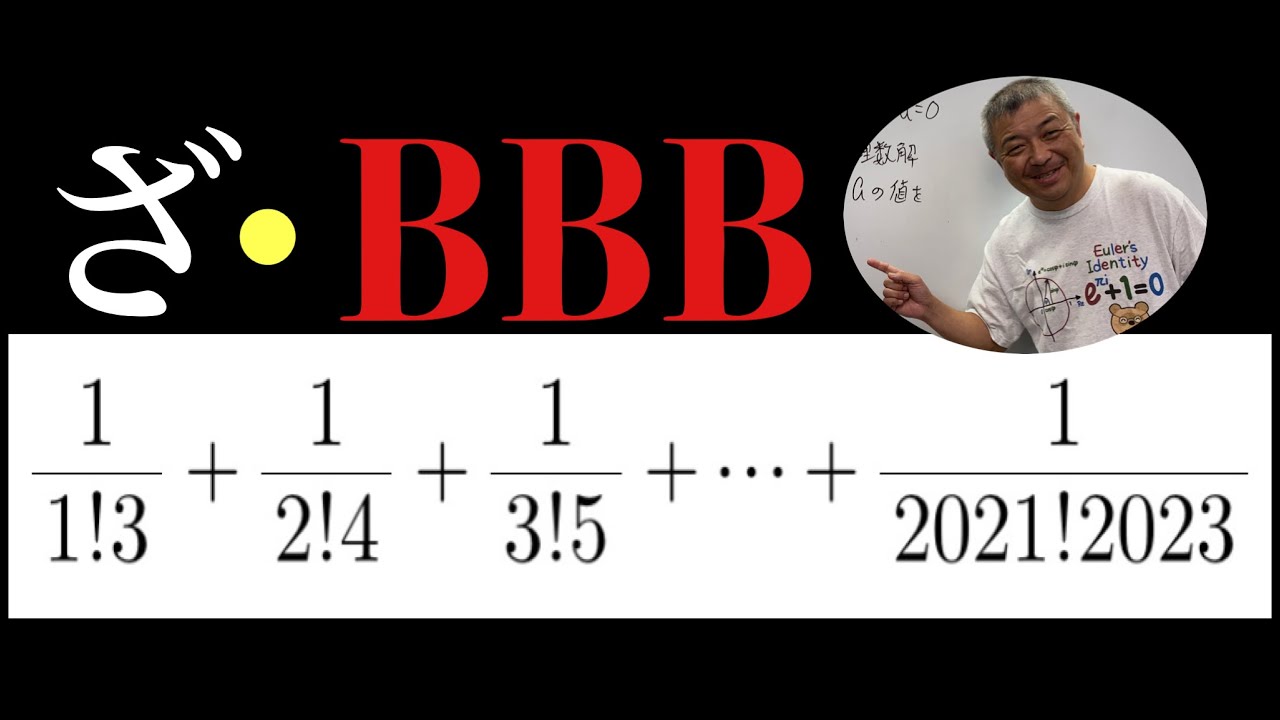
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{1}{1!3}+\dfrac{1}{2!4}+\dfrac{1}{3!5}+・・・+\dfrac{1}{2021!2023}$
この動画を見る
$\dfrac{1}{1!3}+\dfrac{1}{2!4}+\dfrac{1}{3!5}+・・・+\dfrac{1}{2021!2023}$
米国選抜数学試験

単元:
#数学検定・数学甲子園・数学オリンピック等#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
1990米国選抜数学試験
a,b,x,yは実数
$ax+by=3$
$ax^2+by^2=7$
$ax^3+by^3=16$
$ax^4+by^4=42$
$ax^5+by^5=?$
この動画を見る
1990米国選抜数学試験
a,b,x,yは実数
$ax+by=3$
$ax^2+by^2=7$
$ax^3+by^3=16$
$ax^4+by^4=42$
$ax^5+by^5=?$
因数分解 昭和秀英

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^3y^3+18-9xy -2x^2 y^2$
昭和学院秀英高等学校
この動画を見る
因数分解せよ
$x^3y^3+18-9xy -2x^2 y^2$
昭和学院秀英高等学校
ただの連立二元三次方程式

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yは実数
\begin{eqnarray}
\left\{
\begin{array}{l}
(x + y)(x^2+y^2) = 520 \\
(x-y)(x^2-y^2) = 40
\end{array}
\right.
\end{eqnarray}
この動画を見る
x,yは実数
\begin{eqnarray}
\left\{
\begin{array}{l}
(x + y)(x^2+y^2) = 520 \\
(x-y)(x^2-y^2) = 40
\end{array}
\right.
\end{eqnarray}
2024を素因数分解

誘導にのれ!!(堀川高校)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)$a^4+4b^4$を因数分解せよ
(2)$10004$を素因数分解せよ
堀川高等学校(改)
この動画を見る
(1)$a^4+4b^4$を因数分解せよ
(2)$10004$を素因数分解せよ
堀川高等学校(改)
東大寺学園の因数分解 おかげさまでYouTubeチャンネル登録10万人達成しました。ありがとうございます。

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^4+6x^3+9x^2-8(x^2+3x)-20$
東大寺学園高等学校
この動画を見る
因数分解せよ
$x^4+6x^3+9x^2-8(x^2+3x)-20$
東大寺学園高等学校
3乗➖3乗の因数分解

分数が入っている因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^2- \frac{5}{3}x - \frac{2}{3}$
この動画を見る
因数分解せよ
$x^2- \frac{5}{3}x - \frac{2}{3}$
式の値 高校数学

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
abc=1のとき
$\frac{1}{ab+a+1} +\frac{1}{bc+b+1} + \frac{1}{ca+c+1}$
の値を求めよ
この動画を見る
abc=1のとき
$\frac{1}{ab+a+1} +\frac{1}{bc+b+1} + \frac{1}{ca+c+1}$
の値を求めよ
