 数と式
数と式
 数と式
数と式
福田の共通テスト解答速報〜2022年共通テスト数学IA問題1[1]。式の値の計算問題。

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
第1問\ [1] 実数a,b,cが$a+b+c=1\ldots①$および$a^2+b^2+c^2=13\ldots②$を満たしているとする。
(1)$(a+b+c)^2$を展開した式において、①と②を用いると$ab+bc+ca=\boxed{アイ}$
であることが分かる。
よって、$(a-b)^2+(b-c)^2+(c-a)^2=\boxed{ウエ}$である。
(2)$a-b=2\sqrt5$の場合に、$(a-b)(b-c)(c-a)$の値を求めてみよう。
$b-c=x, c-a=y$とおくと、$x+y=\boxed{オカ}\sqrt5$である。また(1)の計算から
$x^2+y^2=\boxed{キク}$が成り立つ。これらより
$(a-b)(b-c)(c-a)=\boxed{ケ}\sqrt5$ である。
2022共通テスト数学過去問
この動画を見る
第1問\ [1] 実数a,b,cが$a+b+c=1\ldots①$および$a^2+b^2+c^2=13\ldots②$を満たしているとする。
(1)$(a+b+c)^2$を展開した式において、①と②を用いると$ab+bc+ca=\boxed{アイ}$
であることが分かる。
よって、$(a-b)^2+(b-c)^2+(c-a)^2=\boxed{ウエ}$である。
(2)$a-b=2\sqrt5$の場合に、$(a-b)(b-c)(c-a)$の値を求めてみよう。
$b-c=x, c-a=y$とおくと、$x+y=\boxed{オカ}\sqrt5$である。また(1)の計算から
$x^2+y^2=\boxed{キク}$が成り立つ。これらより
$(a-b)(b-c)(c-a)=\boxed{ケ}\sqrt5$ である。
2022共通テスト数学過去問
数学ゴールデン【漫画】で紹介された数オリの問題の解答がなかったから作成してみた。

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#式の計算(整式・展開・因数分解)#数学オリンピック#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \lt x$:実数
$x+\sqrt{ x(x+1) }+\sqrt{ x(x+2) }+\sqrt{ (x+1)(x+2) }=2$を解け。
出典:数学ゴールデン 数学オリンピック
この動画を見る
$0 \lt x$:実数
$x+\sqrt{ x(x+1) }+\sqrt{ x(x+2) }+\sqrt{ (x+1)(x+2) }=2$を解け。
出典:数学ゴールデン 数学オリンピック
整数問題

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$(a,b)$を求めよ.
$a^2+b^2=(ab-7)^2$
この動画を見る
整数$(a,b)$を求めよ.
$a^2+b^2=(ab-7)^2$
無理数の2022乗の1の位の数

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(2+\sqrt5)^{2022}$の1の位の数を求めよ.
この動画を見る
$(2+\sqrt5)^{2022}$の1の位の数を求めよ.
基本問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt{2022+a^2+2a}$が整数となる自然数$a$を求めよ.
この動画を見る
$\sqrt{2022+a^2+2a}$が整数となる自然数$a$を求めよ.
π=3はやばい?

二重根号の方程式

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解$\sqrt{2-\sqrt{x+2}}=x$を求めよ.
この動画を見る
実数解$\sqrt{2-\sqrt{x+2}}=x$を求めよ.
ただ二重根号を外すだけ

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt{2065+180\sqrt{10}}$
これを求めよ.
この動画を見る
$\sqrt{2065+180\sqrt{10}}$
これを求めよ.
こう見えても慶應義塾

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数A#数と式#場合の数と確率#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
絶対値が2になる数と49の平方根の和は何通り?
慶應義塾高等学校
この動画を見る
絶対値が2になる数と49の平方根の和は何通り?
慶應義塾高等学校
4乗根の分母の有理化

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
分母の有理化をせよ.
$\dfrac{1}{\sqrt[4]{8}+\sqrt2+\sqrt[4]{2}+1}$
この動画を見る
分母の有理化をせよ.
$\dfrac{1}{\sqrt[4]{8}+\sqrt2+\sqrt[4]{2}+1}$
単位円周上には無限の有理点

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
単位円周上に$x$座標,$y$座標ともに有理数である点は無限に存在することを示せ.
この動画を見る
単位円周上に$x$座標,$y$座標ともに有理数である点は無限に存在することを示せ.
平方根 小数部分 成城学園

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2 \sqrt 3$の小数部分をaとするとき
$a^2+6a-16=?$
成城学園高等学校
この動画を見る
$2 \sqrt 3$の小数部分をaとするとき
$a^2+6a-16=?$
成城学園高等学校
#49 数検1級1次 過去問 根号を外す

単元:
#数Ⅰ#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#数と式#2次関数#複素数と方程式#式の計算(整式・展開・因数分解)#2次方程式と2次不等式#2次関数とグラフ#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\sqrt[ 3 ]{ -5+2\sqrt{ 13 } }\ $の二重根号をはずせ
この動画を見る
$\sqrt[ 3 ]{ -5+2\sqrt{ 13 } }\ $の二重根号をはずせ
高校入試だけど二重根号
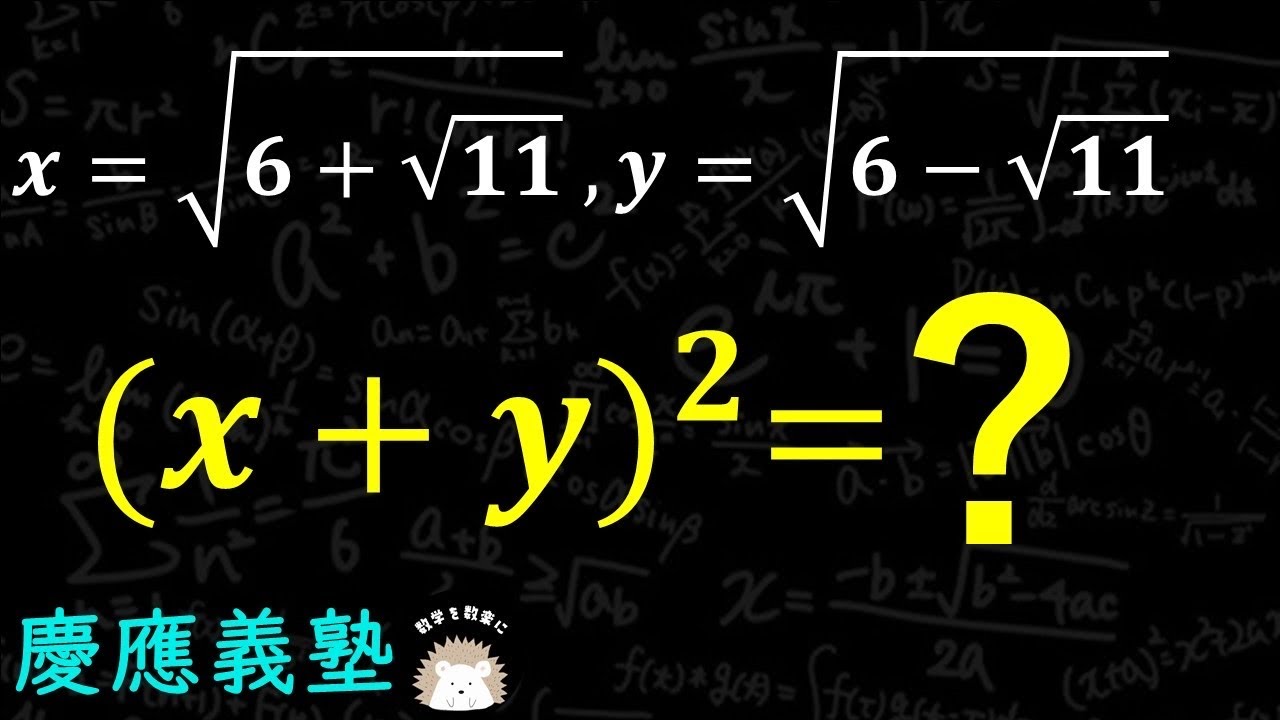
単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=\sqrt{6+\sqrt{11}} , y=\sqrt{6-\sqrt{11}} $
$(x+y)^2 = ?$
慶應義塾高等学校
この動画を見る
$x=\sqrt{6+\sqrt{11}} , y=\sqrt{6-\sqrt{11}} $
$(x+y)^2 = ?$
慶應義塾高等学校
【数学】平方根:暗算で根号の中身を変形できない生徒がまずするべき考え方

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
平方根:暗算で根号の中身を変形できない生徒がまずするべき考え方に関して解説していきます.
この動画を見る
平方根:暗算で根号の中身を変形できない生徒がまずするべき考え方に関して解説していきます.
無限に続く3乗根
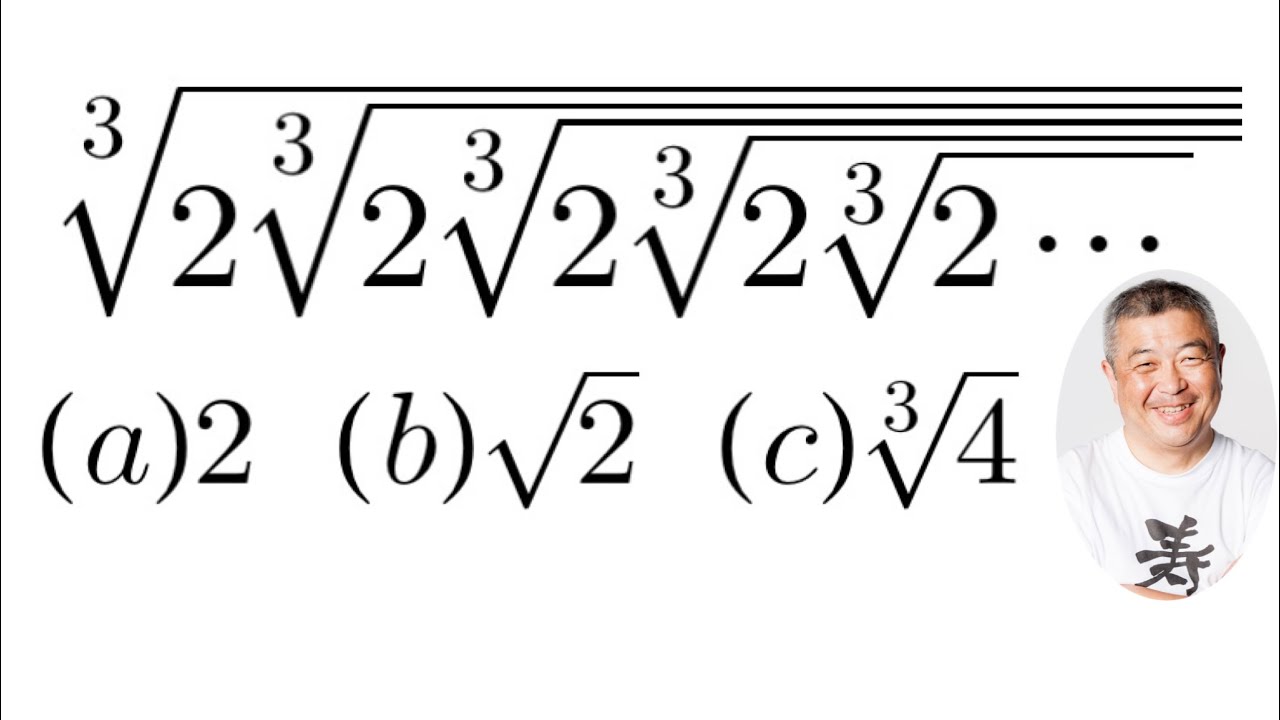
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3\sqrt{2\sqrt[3]{2\sqrt[3]{2\sqrt[3]{2\sqrt[3]{2・・・・・・}}}}}$
$(a)2$
$(b)\sqrt2$
$(c)\sqrt[3]{4}$
これを解け.
この動画を見る
$3\sqrt{2\sqrt[3]{2\sqrt[3]{2\sqrt[3]{2\sqrt[3]{2・・・・・・}}}}}$
$(a)2$
$(b)\sqrt2$
$(c)\sqrt[3]{4}$
これを解け.
【高校数学】摂南大学の過去問演習~代入の問題~【大学受験】

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
摂南大学の過去問演習
この動画を見る
摂南大学の過去問演習
この因数分解できる?

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
因数分解してください
$a^2-b^2-c^2+4a-2bc+4$
この動画を見る
因数分解してください
$a^2-b^2-c^2+4a-2bc+4$
福田のわかった数学〜高校3年生理系105〜絶対不等式(3)

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 絶対不等式(3)
$0 \leqq x \lt \frac{\pi}{2}$であるすべてのxについて
$\sin x\cos x \leqq kk(\sin^2x+3\cos^2x)$
が成り立つような実数kの最小値を求めよ。
この動画を見る
数学$\textrm{III}$ 絶対不等式(3)
$0 \leqq x \lt \frac{\pi}{2}$であるすべてのxについて
$\sin x\cos x \leqq kk(\sin^2x+3\cos^2x)$
が成り立つような実数kの最小値を求めよ。
福田のわかった数学〜高校3年生理系104〜絶対不等式(2)

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 絶対不等式(2)
$\sqrt x+\sqrt y \leqq k\sqrt{2x+y}$
が任意の正の実数x,yに対して成り立つような実数$k$
の値の範囲を求めよ。
この動画を見る
数学$\textrm{III}$ 絶対不等式(2)
$\sqrt x+\sqrt y \leqq k\sqrt{2x+y}$
が任意の正の実数x,yに対して成り立つような実数$k$
の値の範囲を求めよ。
方程式
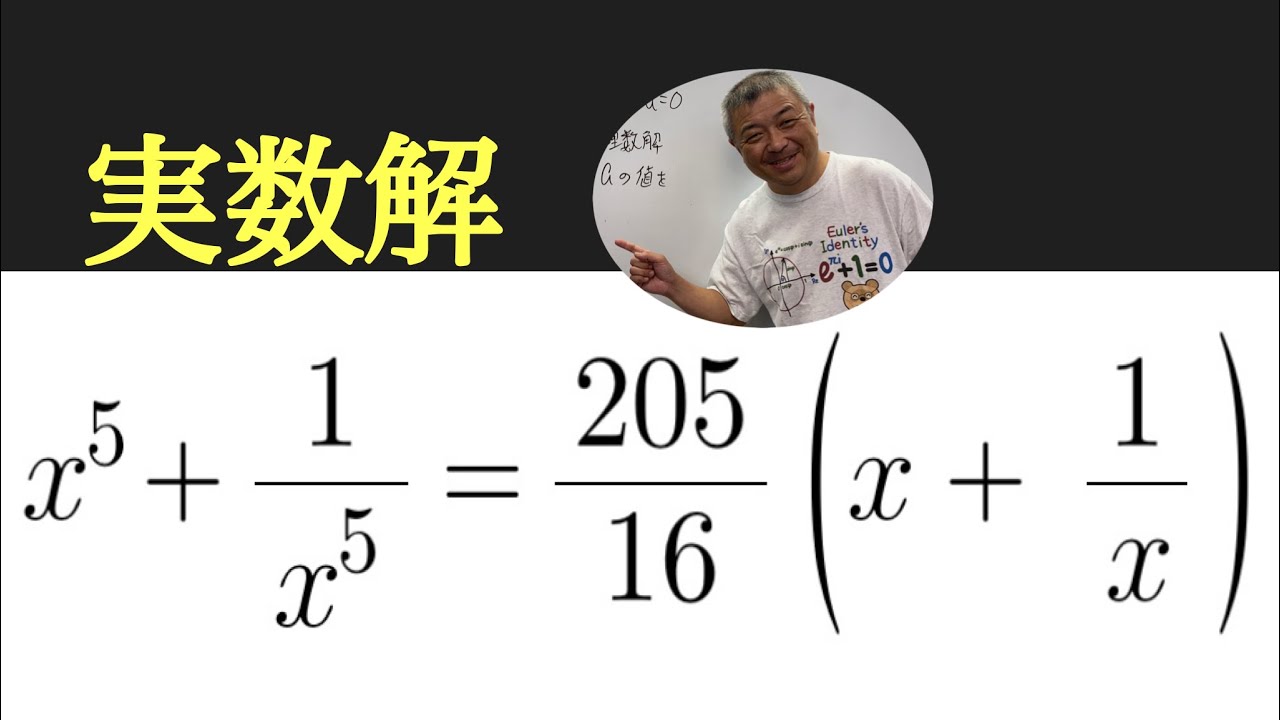
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$x^5+\dfrac{1}{x^5}=\dfrac{205}{16}\left(x+\dfrac{1}{x}\right)$
この動画を見る
実数解を求めよ.
$x^5+\dfrac{1}{x^5}=\dfrac{205}{16}\left(x+\dfrac{1}{x}\right)$
福田のわかった数学〜高校3年生理系103〜絶対不等式(1)

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 絶対不等式(1)
$a^x \geqq x$
が任意の正の実数xに対して成り立つような
正の定数aの値の範囲を求めよ。
この動画を見る
数学$\textrm{III}$ 絶対不等式(1)
$a^x \geqq x$
が任意の正の実数xに対して成り立つような
正の定数aの値の範囲を求めよ。
#46 数検1級1次 過去問 複雑な方程式

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$2\sqrt[ 3 ]{ 2x-1 }=x^3+1$をみたす実数解を求めよ。
この動画を見る
$2\sqrt[ 3 ]{ 2x-1 }=x^3+1$をみたす実数解を求めよ。
超絶良問 どっちがでかい?その差僅か0.0005

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$\sqrt{2022}+\sqrt{2052}$ vs $\sqrt{2032}+\sqrt{2042}$
この動画を見る
どちらが大きいか?
$\sqrt{2022}+\sqrt{2052}$ vs $\sqrt{2032}+\sqrt{2042}$
単なる計算問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt{99910000+\dfrac{81}{4}}$
これを解け.
この動画を見る
$\sqrt{99910000+\dfrac{81}{4}}$
これを解け.
工夫して簡単に!
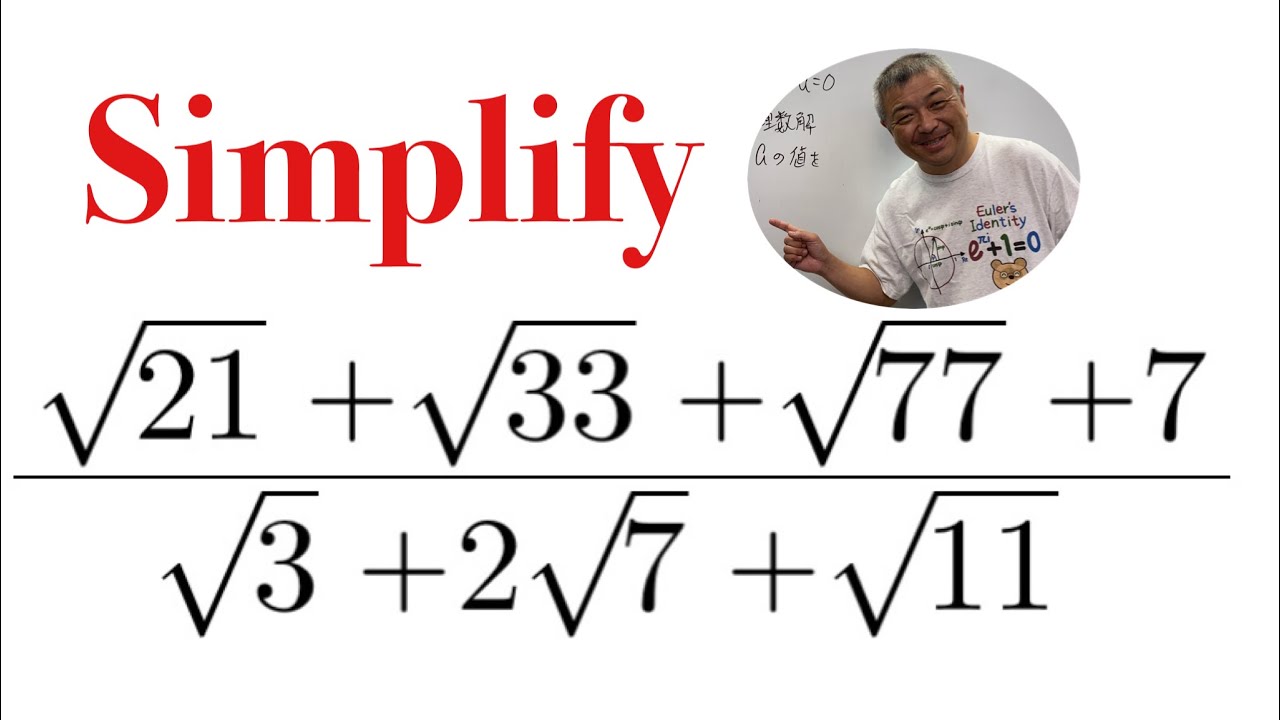
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを簡単にせよ.
$\dfrac{\sqrt{21}+\sqrt{33}+\sqrt{77}+7}{\sqrt3+2\sqrt 7+\sqrt{11}}$
この動画を見る
これを簡単にせよ.
$\dfrac{\sqrt{21}+\sqrt{33}+\sqrt{77}+7}{\sqrt3+2\sqrt 7+\sqrt{11}}$
長方形といえる? ひし形といえる?

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
○か✖か?
・2本の対角線の長さが等しい四角形は長方形である。
・2本の対角線が垂直に交わっている四角形はひし形である。
この動画を見る
○か✖か?
・2本の対角線の長さが等しい四角形は長方形である。
・2本の対角線が垂直に交わっている四角形はひし形である。
全ての角が等しい六角形は正六角形?

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
○か✖か?
・3つの角がすべて等しい三角形は正三角形
・6つの角がすべて等しい六角形は正六角形
この動画を見る
○か✖か?
・3つの角がすべて等しい三角形は正三角形
・6つの角がすべて等しい六角形は正六角形
失敗しないたすきがけ因数分解

負の数の三乗根
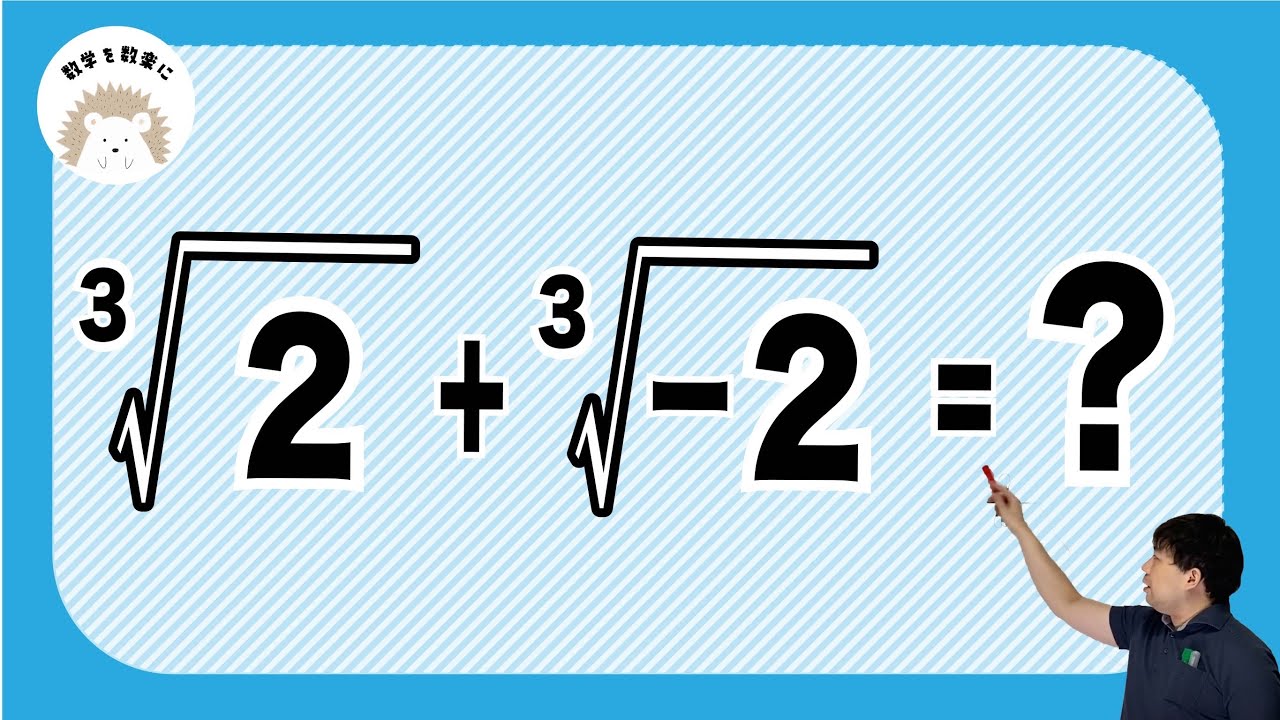
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
${}^3 \sqrt 2 + {}^3 \sqrt {-2}$
この動画を見る
${}^3 \sqrt 2 + {}^3 \sqrt {-2}$
