図形と計量
図形と計量
 図形と計量
図形と計量
福田の数学〜浜松医科大学2023年医学部第4問〜三角形と整数問題

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#整数の性質#三角形の辺の比(内分・外分・二等分線)#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $\triangle$ABCにおいて、BC=3, AC=$b$, AB=$c$, $\angle$ACB=$\theta$とする。$b$と$c$を素数とするとき、以下の問いに答えよ。
(1)$b$=3,$c$=5 のとき、$\cos\theta$の値を求めよ。
(2)$\cos\theta$<0 のとき、$c$=$b$+2 が成り立つことを示せ。
(3)$-\displaystyle\frac{5}{8}$<$\cos\theta$<$-\displaystyle\frac{7}{12}$ のとき、$b$と$c$の値の組をすべて求めよ。
この動画を見る
$\Large\boxed{4}$ $\triangle$ABCにおいて、BC=3, AC=$b$, AB=$c$, $\angle$ACB=$\theta$とする。$b$と$c$を素数とするとき、以下の問いに答えよ。
(1)$b$=3,$c$=5 のとき、$\cos\theta$の値を求めよ。
(2)$\cos\theta$<0 のとき、$c$=$b$+2 が成り立つことを示せ。
(3)$-\displaystyle\frac{5}{8}$<$\cos\theta$<$-\displaystyle\frac{7}{12}$ のとき、$b$と$c$の値の組をすべて求めよ。
座標平面上の三角形の面積 文星芸術大附(改)
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
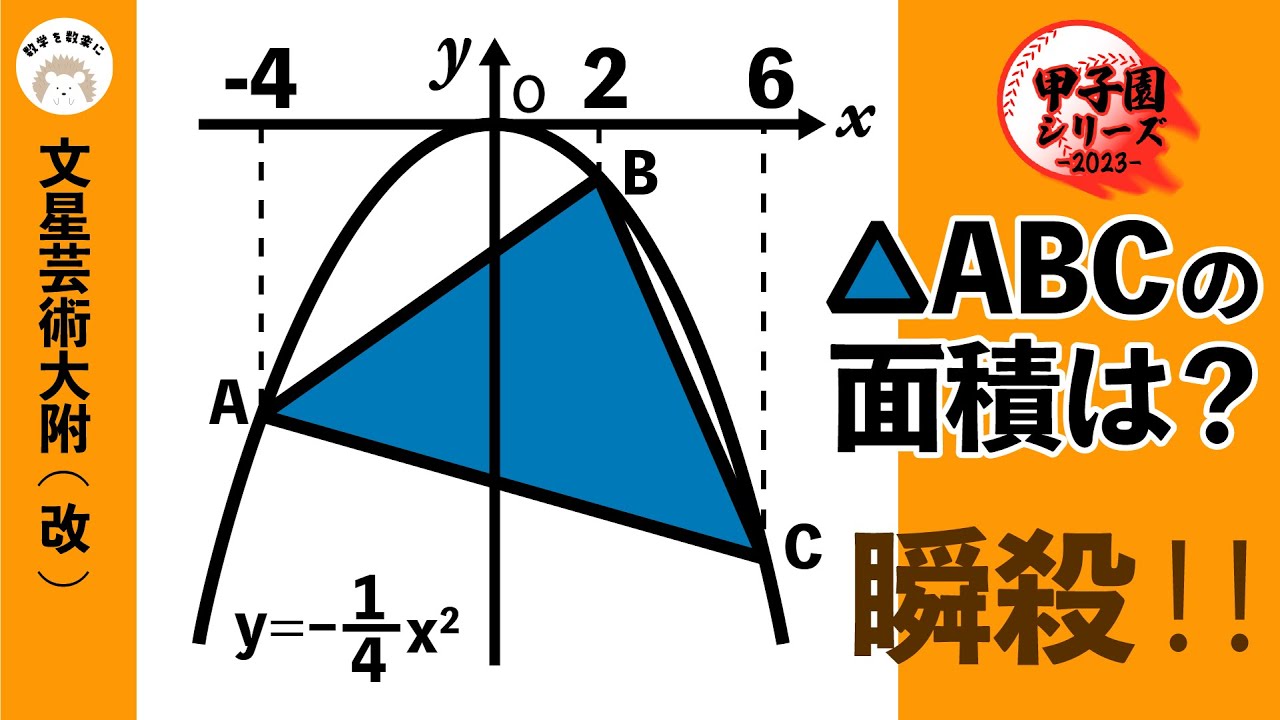
△ABCの面積は?
*図は動画内参照
文星芸術大学附属高等学校(改)
この動画を見る
△ABCの面積は?
*図は動画内参照
文星芸術大学附属高等学校(改)
座標平面上の三角形 日大山形 (山形)
cosの和を求める

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
次の値
$
\cos{\frac{\pi}{7}}-\cos{\frac{2\pi}{7}}+\cos{\frac{3\pi}{7}}
$を求めよ.
この動画を見る
次の値
$
\cos{\frac{\pi}{7}}-\cos{\frac{2\pi}{7}}+\cos{\frac{3\pi}{7}}
$を求めよ.
円とブーメランの角 浦和学院(埼玉)
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
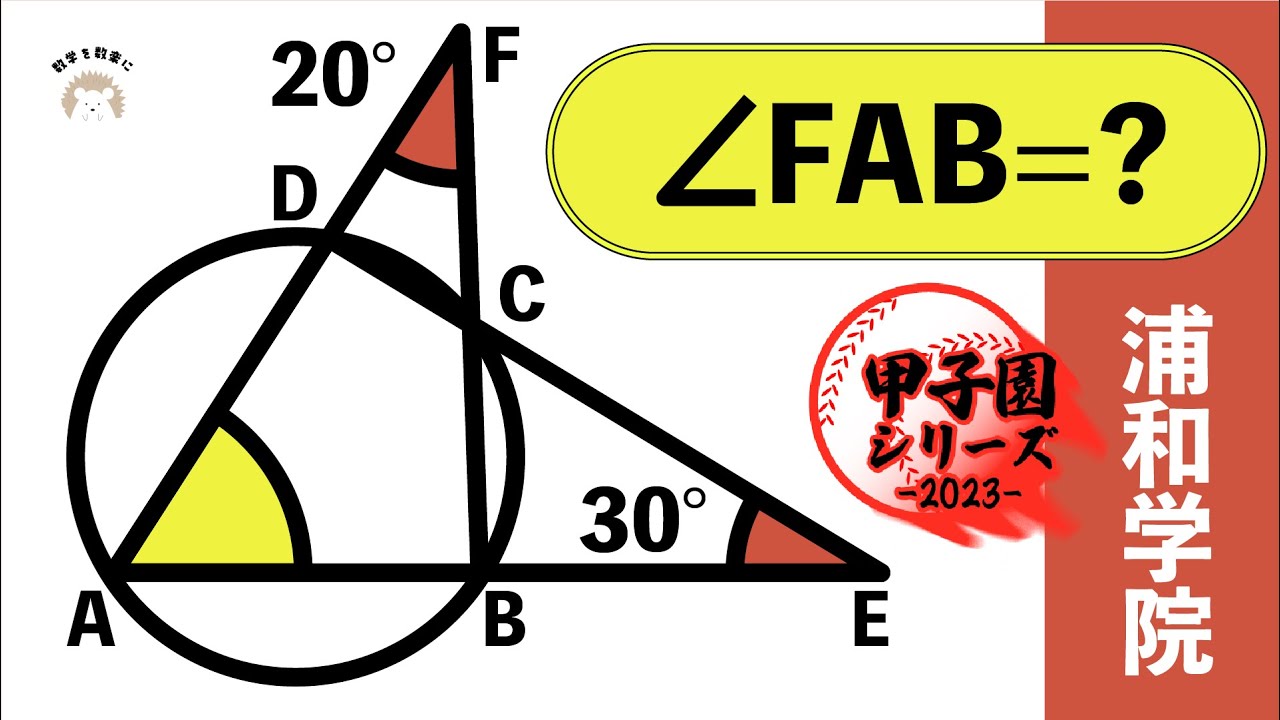
$\angle FAB =?$
*図は動画内参照
浦和学院高等学校
この動画を見る
$\angle FAB =?$
*図は動画内参照
浦和学院高等学校
気付けば一瞬!!正方形と円

単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△BODの面積は?
*図は動画内参照
この動画を見る
△BODの面積は?
*図は動画内参照
三角比の相互関係と符号の決め方について解説(数学Ⅰ)

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$90^{ \circ } \lt \alpha \lt 180^{ \circ }$で$\sin\alpha=\displaystyle \frac{2}{5}$のとき、$\cos\alpha,\tan\alpha$の値を求めよ。
この動画を見る
$90^{ \circ } \lt \alpha \lt 180^{ \circ }$で$\sin\alpha=\displaystyle \frac{2}{5}$のとき、$\cos\alpha,\tan\alpha$の値を求めよ。
小学生向け問題
【数学】2022年度 第2回 K塾記述高2模試 全問解説(ベクトルはおまけ)、※修正箇所:問1(1)(概要欄へ)

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#複素数と方程式#図形と計量#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#2次方程式と2次不等式#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#確率#図形と方程式#三角関数#複素数#三角関数とグラフ#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
2022年度第2回全統記述高2模試全問解説動画です!
この動画を見る
2022年度第2回全統記述高2模試全問解説動画です!
【三角比の基本】三角比の値の求め方を解説(数学Ⅰ)

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の三角比の表を完成させよ。
この動画を見る
次の三角比の表を完成させよ。
【テスト対策】三角比の相互関係をわかりやすく解説!

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$A$は鋭角とする。
$\sin A=\displaystyle \frac{2}{3}$のとき、$\cos A,\tan A$の値を求めよ。
この動画を見る
$A$は鋭角とする。
$\sin A=\displaystyle \frac{2}{3}$のとき、$\cos A,\tan A$の値を求めよ。
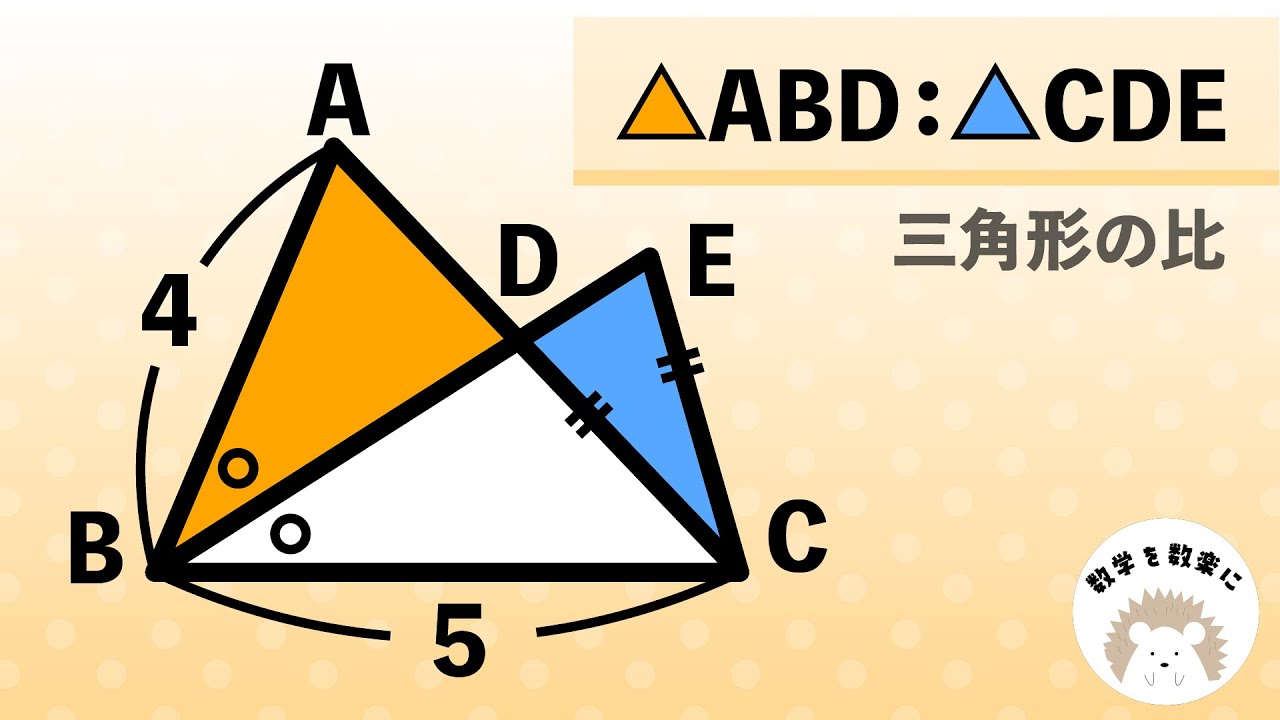
気付ける男は一味違う。面積比
三角比の不等式

単元:
#数Ⅰ#数と式#図形と計量#一次不等式(不等式・絶対値のある方程式・不等式)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
不等式を解け
$sinθ \leqq cosθ$
$(0° \leqq θ < 360°)$
この動画を見る
不等式を解け
$sinθ \leqq cosθ$
$(0° \leqq θ < 360°)$
2つの円 土佐高校
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
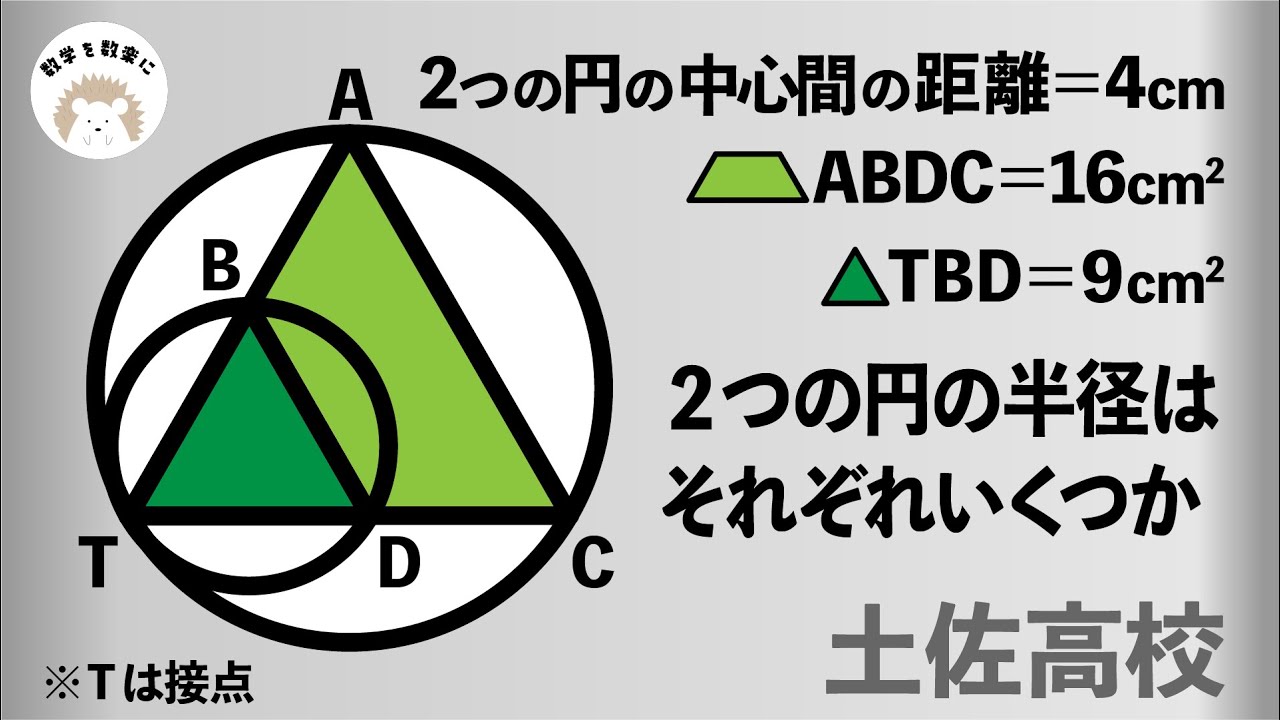
2つの円の中心間の距離=4㎝
台形ABCD=16㎠
△TBD=9㎠
2つの円の半径はそれぞれ何㎝?
*図は動画内参照
土佐高等学校
この動画を見る
2つの円の中心間の距離=4㎝
台形ABCD=16㎠
△TBD=9㎠
2つの円の半径はそれぞれ何㎝?
*図は動画内参照
土佐高等学校
小学生にも解ける?

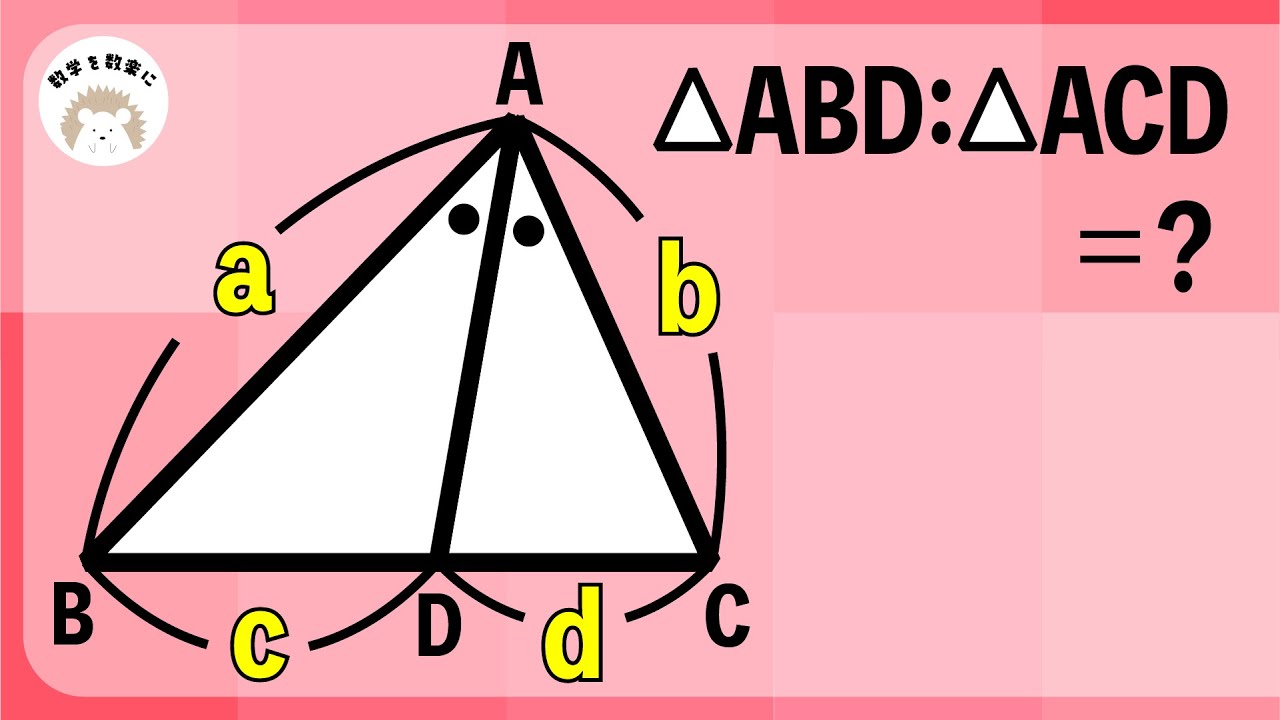
角の二等分線と面積比
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABD:△ACD=?
*図は動画内参照
この動画を見る
△ABD:△ACD=?
*図は動画内参照
受験テクニックを学べ!!座標平面上の平行四辺形 鎌倉学園 (改)
【数Ⅰ】図形と計量:三角比:【超重要】斜辺と角から線分の長さを求める!

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
【超重要】直角三角形の「斜辺」と「角」を用いて他の辺を表せ!
この動画を見る
【超重要】直角三角形の「斜辺」と「角」を用いて他の辺を表せ!
福田の数学〜立教大学2023年経済学部第1問(3)〜三角形を解く
単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
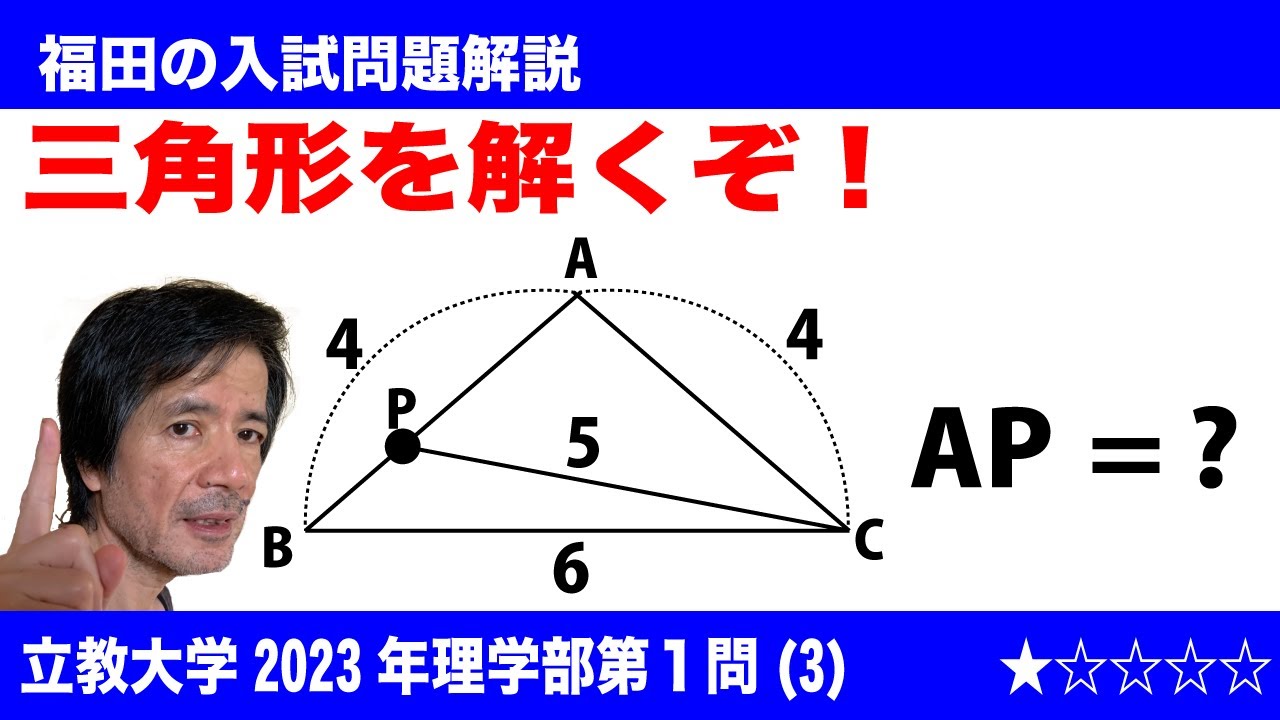
$\Large\boxed{1}$ (3)三角形ABCにおいてAB=AC=4, BC=6とする。AB上の点PがCP=5を満たすとき、AP=$\boxed{\ \ ウ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (3)三角形ABCにおいてAB=AC=4, BC=6とする。AB上の点PがCP=5を満たすとき、AP=$\boxed{\ \ ウ\ \ }$である。
久しぶりのロニー先生の問題

図形と計量空間の基本1 【烈's study!がていねいに解説】
単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
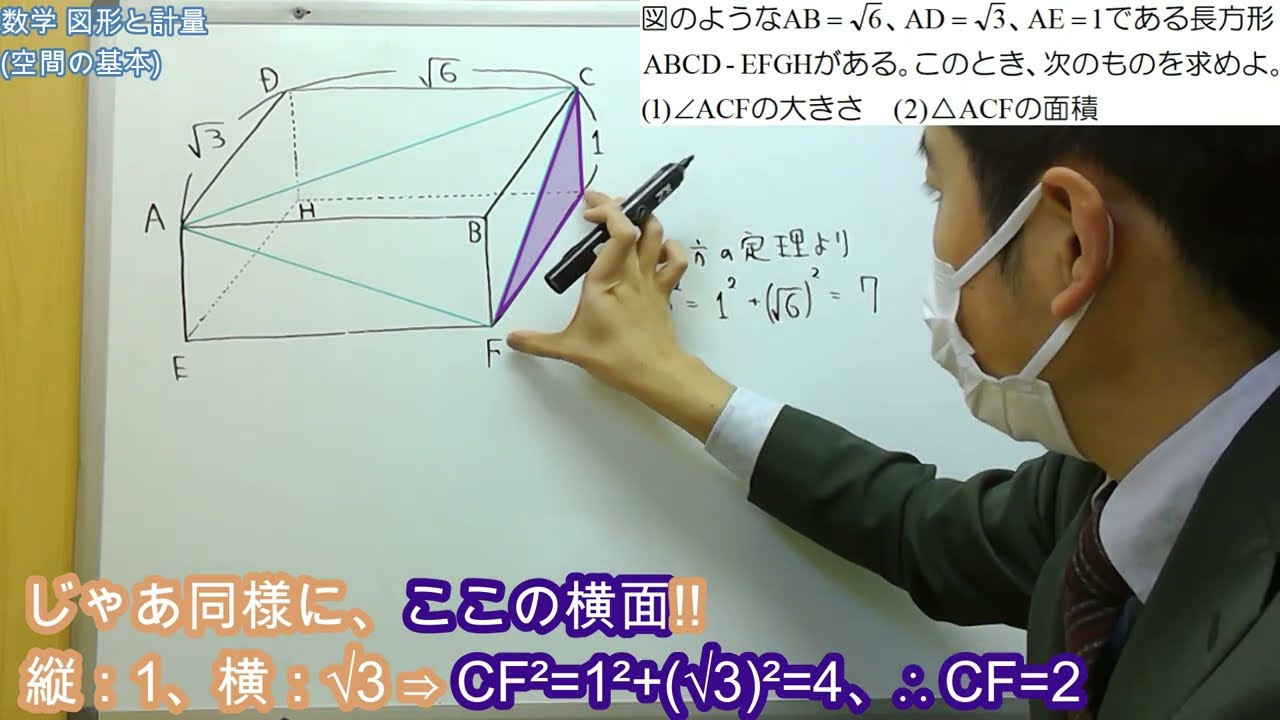
右の図のような$AB=\sqrt6、AD=\sqrt3、AE=1$である直方体$ABCD-EFGH$がある。このとき、次のものを求めよ。
(1)$\angle ACF$の大きさ
(2)$△ACF$の面積
この動画を見る
右の図のような$AB=\sqrt6、AD=\sqrt3、AE=1$である直方体$ABCD-EFGH$がある。このとき、次のものを求めよ。
(1)$\angle ACF$の大きさ
(2)$△ACF$の面積
図形と計量 余弦定理応用2【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
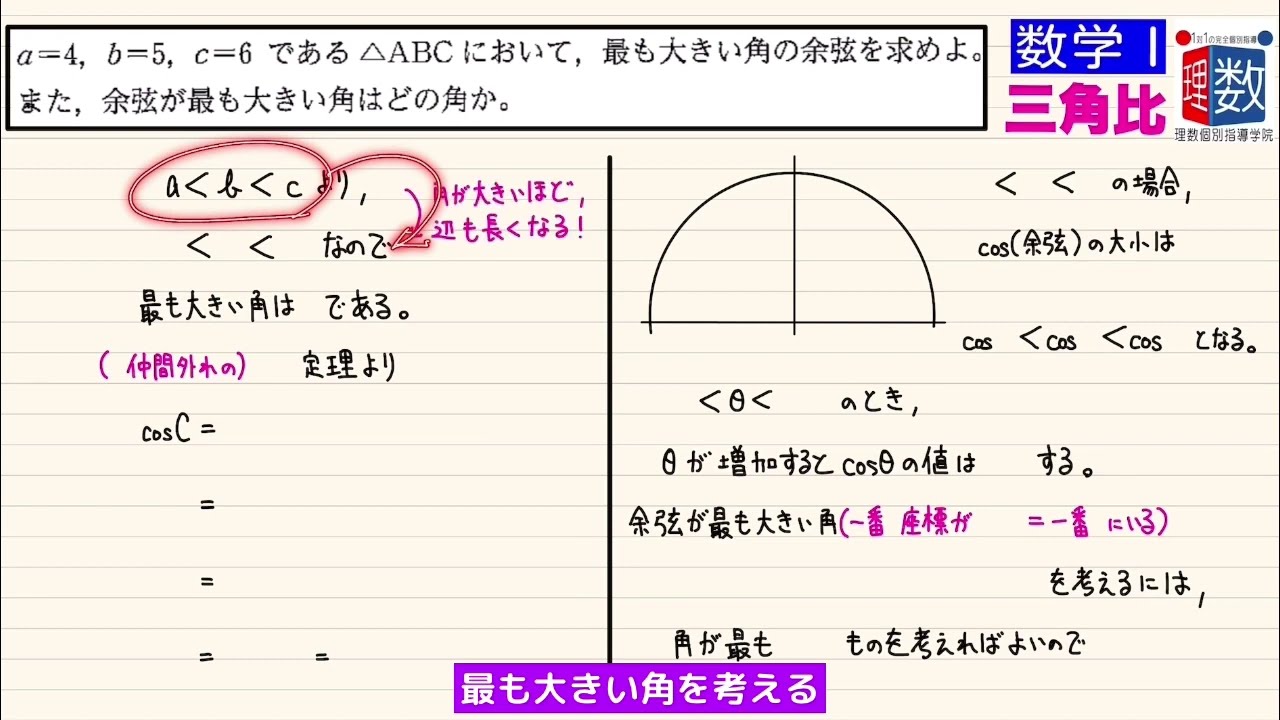
$a=4,b=5,c=6$ である$△ABC$において,最も大きい角の余弦を求めよ。また,余弦が最も大きい角はどの角か。
この動画を見る
$a=4,b=5,c=6$ である$△ABC$において,最も大きい角の余弦を求めよ。また,余弦が最も大きい角はどの角か。
図形と計量 余弦定理応用1【NI・SHI・NOがていねいに解説】

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の各場合について,$△ABC$ の残りの辺の長さと角の大きさを求めよ。
(1) $b=3,c=\sqrt3,B=60°$
(2) $b=2\sqrt3,c=2,C=30°$
この動画を見る
次の各場合について,$△ABC$ の残りの辺の長さと角の大きさを求めよ。
(1) $b=3,c=\sqrt3,B=60°$
(2) $b=2\sqrt3,c=2,C=30°$
気付けば一瞬!!円と角の和

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x + \angle y = ?$
*図は動画内参照
この動画を見る
$\angle x + \angle y = ?$
*図は動画内参照
ルートの計算だけど図形

単元:
#数Ⅰ#数と式#図形と計量#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt {33^2 + 44^2} = $
この動画を見る
$\sqrt {33^2 + 44^2} = $
円 灘高校(改)
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BD=CDのとき△ABCはどんな三角形か?
*図は動画内参照
灘高等学校
この動画を見る
BD=CDのとき△ABCはどんな三角形か?
*図は動画内参照
灘高等学校
工夫して計算!!甲陽学院
2通りで解説 気付けば一瞬!!円の半径は?

青山学院大 放物線の中の四角形

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#図形の性質#図形と計量#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=-x^2+4x$
原点$O,A(4,0),P(p,f_{(p)}),Q(q,f_{(q)})$ $(0\lt p\lt q\lt 4)$
四角形$OAQP$の面積の最大値を求めよ.
青山学院大過去問
この動画を見る
$f(x)=-x^2+4x$
原点$O,A(4,0),P(p,f_{(p)}),Q(q,f_{(q)})$ $(0\lt p\lt q\lt 4)$
四角形$OAQP$の面積の最大値を求めよ.
青山学院大過去問
半円とおうぎ形と正方形