数Ⅰ
数Ⅰ
東京大学の整数問題！5つの文字を求める！？どう解く？
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#式の計算（整式・展開・因数分解）#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
n,a,b,c,dは0または正の整数であって、
a^2+b^2+c^2+d^2=n^2-6
a+b+c+d≦n
a≧b≧c≧d
を満たすものとする。このような整数の組(n,a,b,c,d)をすべて求めよ。
この動画を見る
n,a,b,c,dは0または正の整数であって、
a^2+b^2+c^2+d^2=n^2-6
a+b+c+d≦n
a≧b≧c≧d
を満たすものとする。このような整数の組(n,a,b,c,d)をすべて求めよ。
この覚え方はあり？なし？
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
三角比の有名角の覚え方を紹介する動画です
この動画を見る
三角比の有名角の覚え方を紹介する動画です
福田の数学〜早稲田大学2024商学部第1問(4)〜放物線と2本の接線で囲まれた図形の面積
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#２次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
座標平面において、放物線$y=x^2$を$C$とする。点$P(s,t)$から放物線$C$に異なる2本の接線が引け、その接点をそれぞれ$A,B$とする。線分$PA,PB$と放物線$C$で囲まれた図形の面積が$\displaystyle\frac{144}{125}$であるとき$s,t$の満たす方程式は？
この動画を見る
座標平面において、放物線$y=x^2$を$C$とする。点$P(s,t)$から放物線$C$に異なる2本の接線が引け、その接点をそれぞれ$A,B$とする。線分$PA,PB$と放物線$C$で囲まれた図形の面積が$\displaystyle\frac{144}{125}$であるとき$s,t$の満たす方程式は？
これなにしてるん？
単元：
#算数(中学受験)#数学(中学生)#中１数学#数Ⅰ#図形と計量#平面図形#図形の移動#平面図形その他#平面図形#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
円に内接する正多角形
この動画を見る
円に内接する正多角形
福田のおもしろ数学305〜四角形に内接する円の半径
単元：
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用（正弦・余弦・面積）#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
図は動画参照
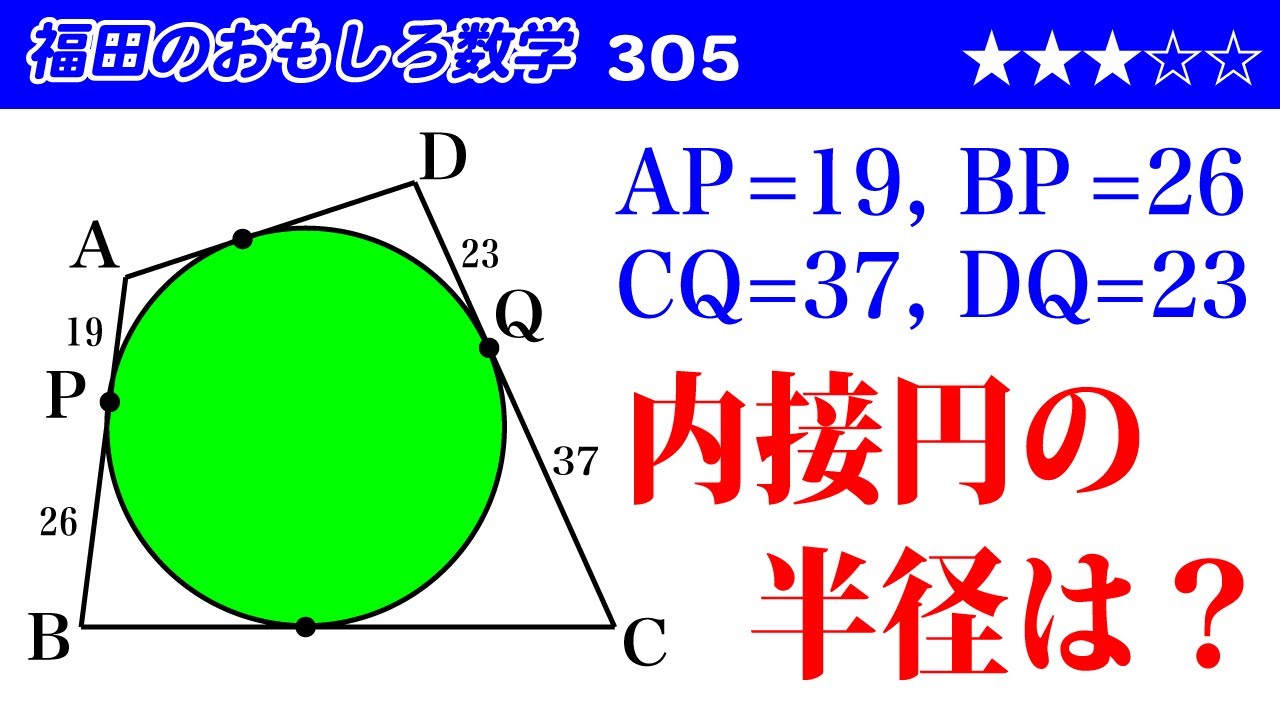
$AP=19,BP=26,CQ=37,DQ=23$
内接円の半径は？
この動画を見る
図は動画参照
$AP=19,BP=26,CQ=37,DQ=23$
内接円の半径は？
福田の数学〜早稲田大学2024商学部第1問(1)〜絶対値の付いた式の不等式を解く
単元：
#数Ⅰ#数と式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
不等式 $\displaystyle |\frac{2024n}{1 - 46n} + 44| < \frac{1}{2025}$ を満たす正の整数 $n$ の最小値を求めよ。
この動画を見る
不等式 $\displaystyle |\frac{2024n}{1 - 46n} + 44| < \frac{1}{2025}$ を満たす正の整数 $n$ の最小値を求めよ。
福田の数学〜早稲田大学2024教育学部第1問(4)〜領域と奇跡
単元：
#数Ⅰ#数Ⅱ#２次関数#図形と方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$
\begin{eqnarray}
\fcolorbox{#000}{ #fff }{$1$} \ (4) \\
\end{eqnarray}
$
$xy$平面上に3点$O(0,0),A(1,0),B(1,1)$をとる。点$(x,y)$が三角形$OAB$の周および内部を動くときに点$(x+y,xy)$が動く範囲の面積を求めよ。
この動画を見る
$
\begin{eqnarray}
\fcolorbox{#000}{ #fff }{$1$} \ (4) \\
\end{eqnarray}
$
$xy$平面上に3点$O(0,0),A(1,0),B(1,1)$をとる。点$(x,y)$が三角形$OAB$の周および内部を動くときに点$(x+y,xy)$が動く範囲の面積を求めよ。
この出し方知ってる？
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
二次関数$y=\frac{1}{2}x^2$上の2点A(-4, 8), B(2, 2)と原点Oを結んでできる三角形の面積を求めよ
この動画を見る
二次関数$y=\frac{1}{2}x^2$上の2点A(-4, 8), B(2, 2)と原点Oを結んでできる三角形の面積を求めよ
意外と差がつく！互いに素の証明！できるようになっておきたい【一橋大学】【数学 入試問題】
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
nは正の整数とする。n^2と2n+1は互いに素であることを示せ。
この動画を見る
nは正の整数とする。n^2と2n+1は互いに素であることを示せ。
#関西大学2024 #方程式_70
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次方程式と2次不等式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$x^2+x-\dfrac{2}{x}+\dfrac{4}{x^2}-6=0$
の解のうち最小のものを求めよ.
2024関西大学過去問題
この動画を見る
$x^2+x-\dfrac{2}{x}+\dfrac{4}{x^2}-6=0$
の解のうち最小のものを求めよ.
2024関西大学過去問題
#関西学院大学2011#方程式_69
単元：
#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$(x+1)(x-2)(x+3)(x-4)=-24$を解け.
2011関西学院大学過去問題
この動画を見る
$(x+1)(x-2)(x+3)(x-4)=-24$を解け.
2011関西学院大学過去問題
福田のおもしろ数学293〜三角方程式を満たす正の整数xの最小値
単元：
#図形と計量#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#整数の性質#約数・倍数・整数の割り算と余り・合同式#三角関数とグラフ#加法定理とその応用
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \tan 19x^{\circ}\ =\ \frac{\cos 96^{\circ}+\sin 96^{\circ}}{\cos 96^{\circ}-\sin 96^{\circ}}\ $を満たす最小の正の整数$\ x\ $を求めよ。
この動画を見る
$\displaystyle \tan 19x^{\circ}\ =\ \frac{\cos 96^{\circ}+\sin 96^{\circ}}{\cos 96^{\circ}-\sin 96^{\circ}}\ $を満たす最小の正の整数$\ x\ $を求めよ。
福田のおもしろ数学292〜実数と実数の間に必ず有理数が存在する証明
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
異なる2つの実数の間に有理数が存在することを証明して下さい。
この動画を見る
異なる2つの実数の間に有理数が存在することを証明して下さい。
これ因数分解できる？
#北海道大学1957#方程式_65
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#２次関数#一次不等式（不等式・絶対値のある方程式・不等式）#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
ますただ
問題文全文(内容文)：
$\dfrac{10x-10^{-x}}{10x+10^{-x}}=a \ (\vert a \vert \gt 1)$
$x$について解け.
1957北海道大学過去問題
この動画を見る
$\dfrac{10x-10^{-x}}{10x+10^{-x}}=a \ (\vert a \vert \gt 1)$
$x$について解け.
1957北海道大学過去問題
福田の数学〜東京理科大学2024創域理工学部第1問(3)〜条件を満たす点の個数
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b$を正の実数とする。座標平面上に点$\textrm{A}(a,1)$をとり、自然数$n=1,2,3,\cdots$に対して点$\textrm{P}_n(n,0)$をとる。集合$U$を次で定める。
$U=\{n|n$は自然数かつ2点$\textrm{A}, \textrm{P}_n$間の距離は$b$以下$\}$
(a) $a=2$とする。$b=1$のとき、$U$の要素の個数は？また、$b=\sqrt{3}$のとき、$U$の要素の個数は？
(b) $a=\dfrac72$とする。$b=\sqrt2$のとき、$U$の要素の個数は？また、$b=2\sqrt2$のとき、$U$の要素の個数は？
(c) $b=2$のとき、$U$の要素の個数が2個となる正の整数$a$は？また、$b=5$のとき、$U$の要素の個数が9個となる最小の正の整数$a$は？
この動画を見る
$a,b$を正の実数とする。座標平面上に点$\textrm{A}(a,1)$をとり、自然数$n=1,2,3,\cdots$に対して点$\textrm{P}_n(n,0)$をとる。集合$U$を次で定める。
$U=\{n|n$は自然数かつ2点$\textrm{A}, \textrm{P}_n$間の距離は$b$以下$\}$
(a) $a=2$とする。$b=1$のとき、$U$の要素の個数は？また、$b=\sqrt{3}$のとき、$U$の要素の個数は？
(b) $a=\dfrac72$とする。$b=\sqrt2$のとき、$U$の要素の個数は？また、$b=2\sqrt2$のとき、$U$の要素の個数は？
(c) $b=2$のとき、$U$の要素の個数が2個となる正の整数$a$は？また、$b=5$のとき、$U$の要素の個数が9個となる最小の正の整数$a$は？
花巻東高校の平均年収4000万円なん？
単元：
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
大谷翔平選手のおかげで花巻東高校の卒業生の年収が上がっているみたいなので計算しました
この動画を見る
大谷翔平選手のおかげで花巻東高校の卒業生の年収が上がっているみたいなので計算しました
福田のおもしろ数学273〜命題の真偽を確認するにはどのカードを裏返すか
単元：
#数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
表にアルファベット、裏に数字が書かれた5枚のカード $\rm P,Q,1,3,6$が机に置かれている。命題「表が$\rm P$ならば裏は素数である」の真偽を確認するにはどれを裏返せばいい？
この動画を見る
表にアルファベット、裏に数字が書かれた5枚のカード $\rm P,Q,1,3,6$が机に置かれている。命題「表が$\rm P$ならば裏は素数である」の真偽を確認するにはどれを裏返せばいい？
福田のおもしろ数学272〜複雑な分数計算どうやって約分するか
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\dfrac{(10^4+324)(22^4+324)(34^4+324)(46^4+324)(58^4+324)}{(4^4+324)(16^4+324)(28^4+324)(40^4+324)(52^4+324)}$
を計算してください。
この動画を見る
$\dfrac{(10^4+324)(22^4+324)(34^4+324)(46^4+324)(58^4+324)}{(4^4+324)(16^4+324)(28^4+324)(40^4+324)(52^4+324)}$
を計算してください。
福田のおもしろ数学269〜三角形における三角関数の性質の証明その2
単元：
#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\triangle \mathrm{ABC}$ において、$ \cos A \cos B \cos C \leqq $$\displaystyle \frac{1}{8} \cdots ①$ が成り立つことを証明して下さい。
この動画を見る
$\triangle \mathrm{ABC}$ において、$ \cos A \cos B \cos C \leqq $$\displaystyle \frac{1}{8} \cdots ①$ が成り立つことを証明して下さい。
福田のおもしろ数学265〜直交する2つの円柱の共通部分の体積
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$
x軸、y軸を軸とする半径1の円柱T_1 , \ T_2の共通部分の体積を求めよ。$（図は動画参照）
この動画を見る
$
x軸、y軸を軸とする半径1の円柱T_1 , \ T_2の共通部分の体積を求めよ。$（図は動画参照）
福田の数学〜上智大学2024TEAP利用型文系第3問(2)〜角の二等分線の長さを求める
単元：
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
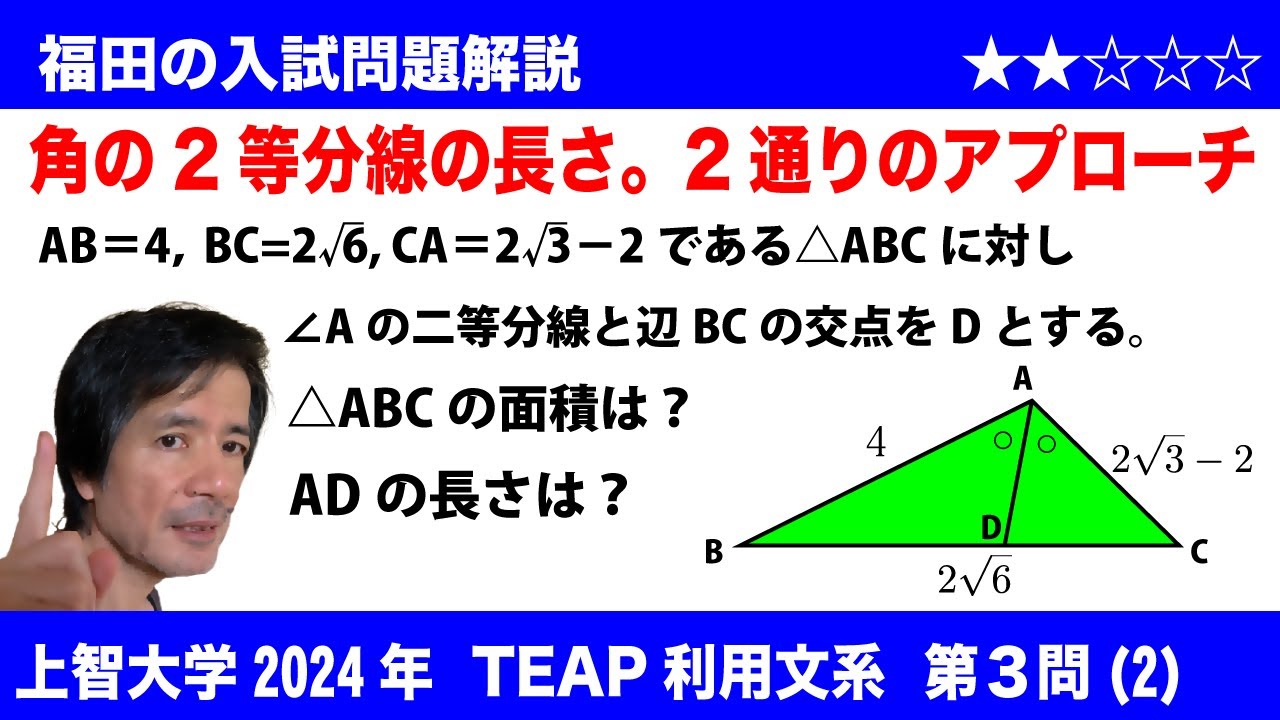
$\boxed{3}(2)AB=4,BC=2\sqrt{6},CA=2\sqrt{3}-2$の$\triangle ABC$がある。$\angle A$の二等分線と辺BCの交点をDとする。このとき、$\triangle ABC$の面積は$\boxed{フ}+\boxed{ヘ}\sqrt{\boxed{ホ}}$であり、$AD=\boxed{マ}+\boxed{ミ}\sqrt{\boxed{ム}}$である。
この動画を見る
$\boxed{3}(2)AB=4,BC=2\sqrt{6},CA=2\sqrt{3}-2$の$\triangle ABC$がある。$\angle A$の二等分線と辺BCの交点をDとする。このとき、$\triangle ABC$の面積は$\boxed{フ}+\boxed{ヘ}\sqrt{\boxed{ホ}}$であり、$AD=\boxed{マ}+\boxed{ミ}\sqrt{\boxed{ム}}$である。
ルートが入っている二次方程式 広尾学園
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
広尾学園
方程式を解け
$x^{2}-\sqrt{ 2 }(1+\sqrt{ 5 })x+2\sqrt{ 5 }=0$
この動画を見る
広尾学園
方程式を解け
$x^{2}-\sqrt{ 2 }(1+\sqrt{ 5 })x+2\sqrt{ 5 }=0$
二次方程式の応用 三田学園
単元：
#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
次の2つの二次方程式の共通な解が$x=-2$だけになるときa,bの値を求めよ
$x^{2}-(b+2)x-b^{2}=0$
$x^{2}+ax+2b=0$
この動画を見る
次の2つの二次方程式の共通な解が$x=-2$だけになるときa,bの値を求めよ
$x^{2}-(b+2)x-b^{2}=0$
$x^{2}+ax+2b=0$
1089になる証明ついてこれた？フルは↑
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
任意の3桁の数とそれを逆から読んだ数のうち大きい方から小さい方を引いた3桁の数と、これを逆から読んだ3桁の数の和が1089になることを証明する動画です
この動画を見る
任意の3桁の数とそれを逆から読んだ数のうち大きい方から小さい方を引いた3桁の数と、これを逆から読んだ3桁の数の和が1089になることを証明する動画です
3桁の数字が1089になる証明
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
任意の3桁の数とそれを逆から読んだ数のうち大きい方から小さい方を引いた3桁の数と、これを逆から読んだ3桁の数の和が1089になることを証明する動画です
この動画を見る
任意の3桁の数とそれを逆から読んだ数のうち大きい方から小さい方を引いた3桁の数と、これを逆から読んだ3桁の数の和が1089になることを証明する動画です
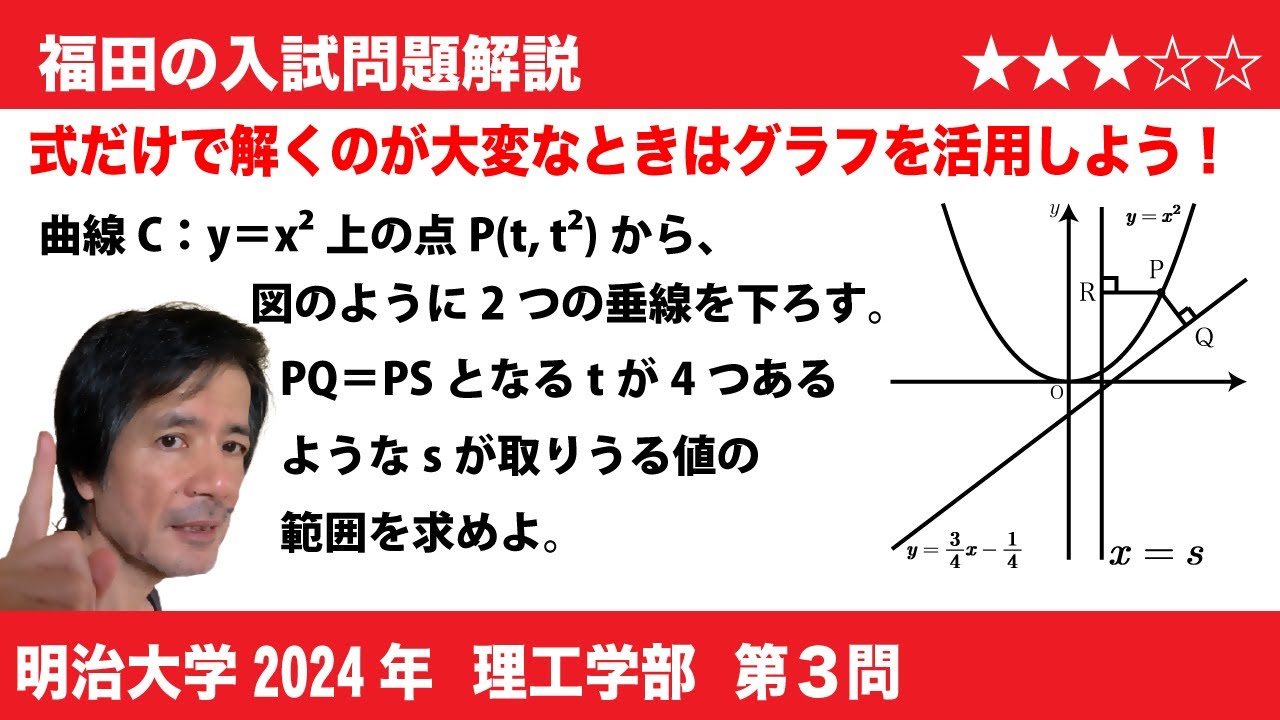
福田の数学〜明治大学2024理工学部第3問〜放物線と折れ線の位置関係
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#2次関数とグラフ#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$座標平面上も曲線$y=x^2$を$C$、直線$y=\frac{3}{4}x-\frac{1}{4}$を$l$とする。$s$を実数とし、直線$x=s$を$m$とする。曲線$C$上の点$P(t,t^2)$に対し、$P$から直線$l$との交点$Q$とする。また、$P$から直線$m$に下ろした垂線と$m$との交点を$R$とする。
$(1)$点$P$と点$Q$の距離$PQ$を$l$の式で表すと、$PQ=\boxed{け}$である。
$(2)$点$P$と点$R$の距離$PR$を$s$と$l$の式で表すと、$PR=\boxed{こ}$である。
$(3)PQ$は$t=\boxed{さ}$のとき、最小値$\boxed{し}$をとる。
$(4)s=\frac{2}{5}$のとき、$PQ=PR$となる点$P$をすべて求め、その$x$座標を小さい順に並べると$\boxed{す}$となる。
$(5)$実数$s$を固定したとき、$PQ=PR$となるような点$P$の個数を$N_s$とする。$N_s=4$となる$s$の範囲は$\boxed{せ}$
この動画を見る
$\boxed{3}$座標平面上も曲線$y=x^2$を$C$、直線$y=\frac{3}{4}x-\frac{1}{4}$を$l$とする。$s$を実数とし、直線$x=s$を$m$とする。曲線$C$上の点$P(t,t^2)$に対し、$P$から直線$l$との交点$Q$とする。また、$P$から直線$m$に下ろした垂線と$m$との交点を$R$とする。
$(1)$点$P$と点$Q$の距離$PQ$を$l$の式で表すと、$PQ=\boxed{け}$である。
$(2)$点$P$と点$R$の距離$PR$を$s$と$l$の式で表すと、$PR=\boxed{こ}$である。
$(3)PQ$は$t=\boxed{さ}$のとき、最小値$\boxed{し}$をとる。
$(4)s=\frac{2}{5}$のとき、$PQ=PR$となる点$P$をすべて求め、その$x$座標を小さい順に並べると$\boxed{す}$となる。
$(5)$実数$s$を固定したとき、$PQ=PR$となるような点$P$の個数を$N_s$とする。$N_s=4$となる$s$の範囲は$\boxed{せ}$
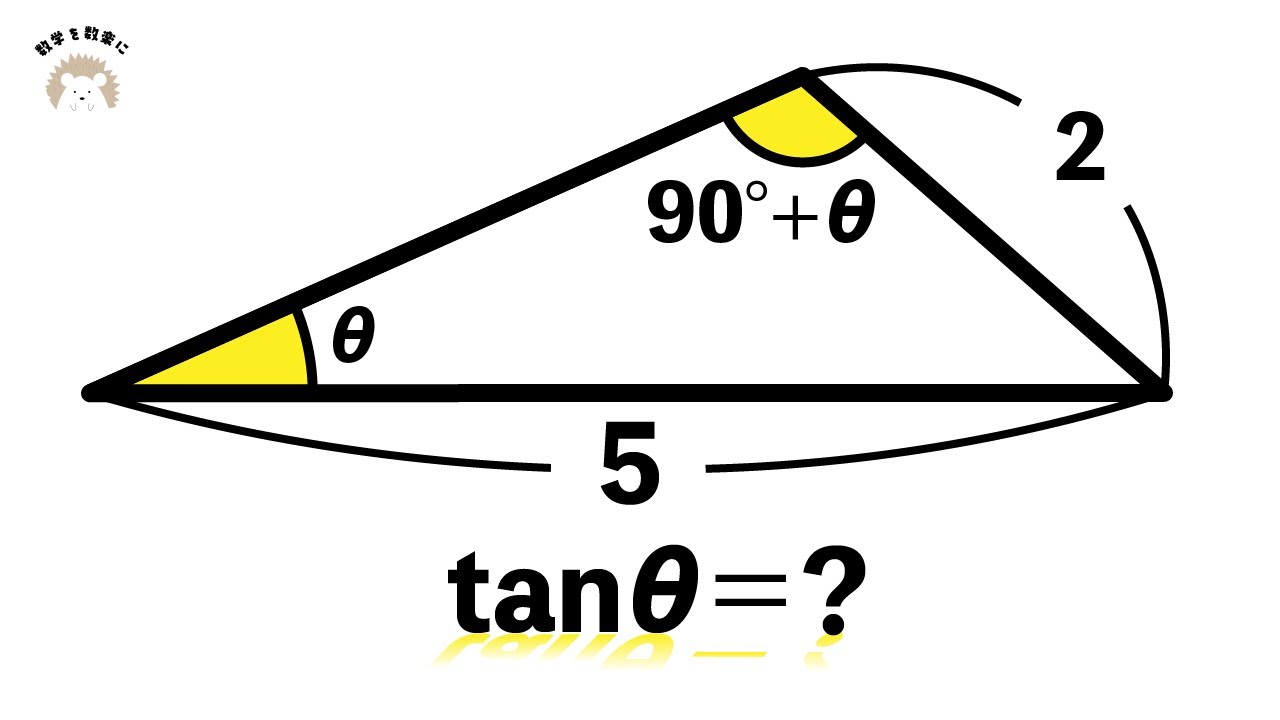
tanθ＝❓
単元：
#数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
次の図の$\tan {\theta}$を求めよ（図は動画参照）
この動画を見る
次の図の$\tan {\theta}$を求めよ（図は動画参照）
福田のおもしろ数学244〜1次不等式が常に成り立つ条件
単元：
#数Ⅰ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$0\lt m\lt3$であるすべての$m$に対して$2x-1\lt m(x-2)$が成り立つような$x$の範囲を求めよ。
この動画を見る
$0\lt m\lt3$であるすべての$m$に対して$2x-1\lt m(x-2)$が成り立つような$x$の範囲を求めよ。
sin cos
