場合の数
場合の数
福田のわかった数学〜高校１年生077〜場合の数(16)道順(3)
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
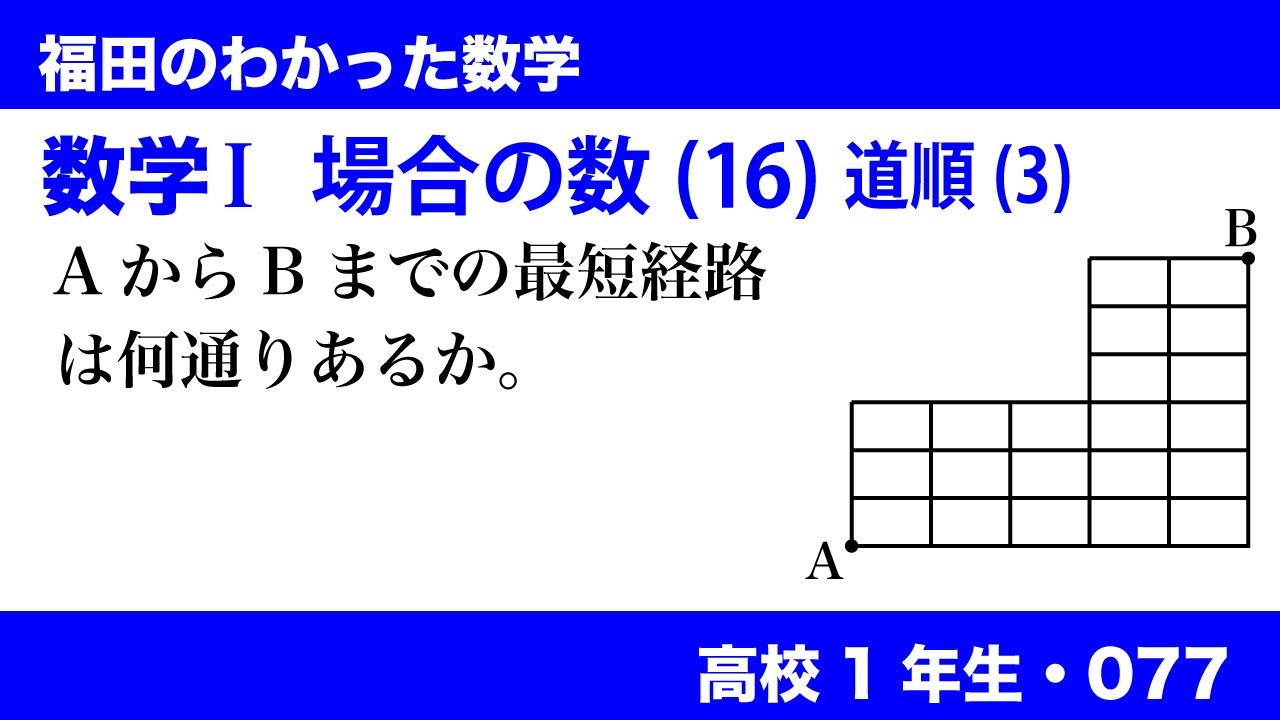
数学$\textrm{I}$ 場合の数(16) 道順(3)
AからBまでの最短経路は何通りあるか。(※図は動画参照)
この動画を見る
数学$\textrm{I}$ 場合の数(16) 道順(3)
AからBまでの最短経路は何通りあるか。(※図は動画参照)
福田のわかった数学〜高校１年生076〜場合の数(15)道順(2)
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
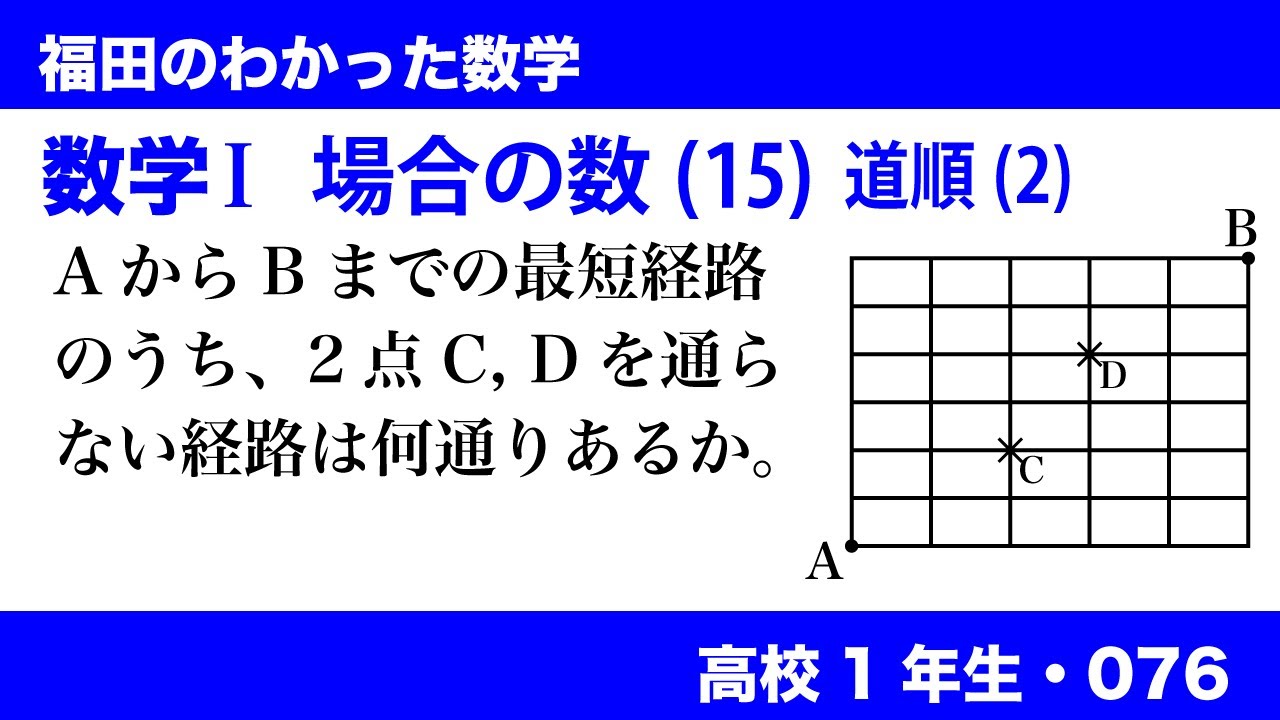
数学$\textrm{I}$ 場合の数(15) 道順(2)
AからBへの最短経路のうち2点C,Dを通らない経路は何通りあるか。
(※図は動画参照)
この動画を見る
数学$\textrm{I}$ 場合の数(15) 道順(2)
AからBへの最短経路のうち2点C,Dを通らない経路は何通りあるか。
(※図は動画参照)
福田のわかった数学〜高校１年生075〜場合の数(14)道順(1)
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 場合の数(14) 道順(1)
右の街路図(※動画参照)を点Aから出発して3回だけ曲がってBへ
到達する最短経路は何通りあるか。
この動画を見る
数学$\textrm{I}$ 場合の数(14) 道順(1)
右の街路図(※動画参照)を点Aから出発して3回だけ曲がってBへ
到達する最短経路は何通りあるか。
福田のわかった数学〜高校１年生074〜場合の数(13)整数解の個数
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 場合の数(13) 整数解の個数
次の条件を満たす整数の組(x,y,z,u)は何個あるか。
(1)$x+y+z+u=10, x \geqq 0, y \geqq 0, z \geqq 0, u \geqq 0$
(2)$x+y+z+u=10, x \geqq 1, y \geqq 1, z \geqq 1, u \geqq 1$
(3)$x+y+z+u \leqq 10, x \geqq 0, y \geqq 0, z \geqq 0, u \geqq 0$
この動画を見る
数学$\textrm{I}$ 場合の数(13) 整数解の個数
次の条件を満たす整数の組(x,y,z,u)は何個あるか。
(1)$x+y+z+u=10, x \geqq 0, y \geqq 0, z \geqq 0, u \geqq 0$
(2)$x+y+z+u=10, x \geqq 1, y \geqq 1, z \geqq 1, u \geqq 1$
(3)$x+y+z+u \leqq 10, x \geqq 0, y \geqq 0, z \geqq 0, u \geqq 0$
福田のわかった数学〜高校１年生073〜場合の数(12)組み分け
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
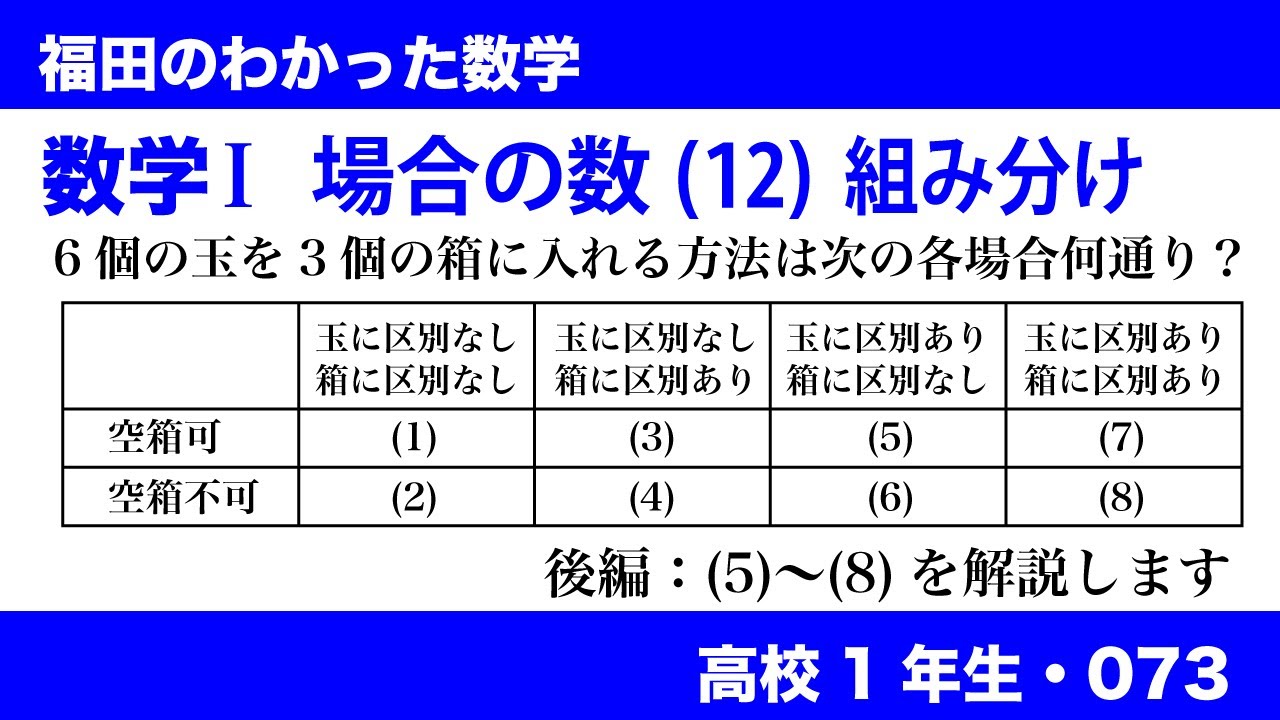
数学$\textrm{I}$ 場合の数(12) 組み分け
6個の玉を3個の箱に入れる方法は次の各場合に何通りあるか。
\begin{array}{|c|c|c|c|c|}
\hline
& 玉に区別なし & 玉に区別なし & 玉に区別あり &玉に区別あり\\
& 箱に区別なし & 箱に区別あり & 箱に区別なし &箱に区別あり\\
\hline
空箱可 & (1) & (3) & (5) & (7)\\
\hline
空箱不可 & (2) & (4) & (6) & (8)\\
\hline
\end{array}
\end{eqnarray}
この動画を見る
数学$\textrm{I}$ 場合の数(12) 組み分け
6個の玉を3個の箱に入れる方法は次の各場合に何通りあるか。
\begin{array}{|c|c|c|c|c|}
\hline
& 玉に区別なし & 玉に区別なし & 玉に区別あり &玉に区別あり\\
& 箱に区別なし & 箱に区別あり & 箱に区別なし &箱に区別あり\\
\hline
空箱可 & (1) & (3) & (5) & (7)\\
\hline
空箱不可 & (2) & (4) & (6) & (8)\\
\hline
\end{array}
\end{eqnarray}
福田のわかった数学〜高校１年生072〜場合の数(11)組み分け
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
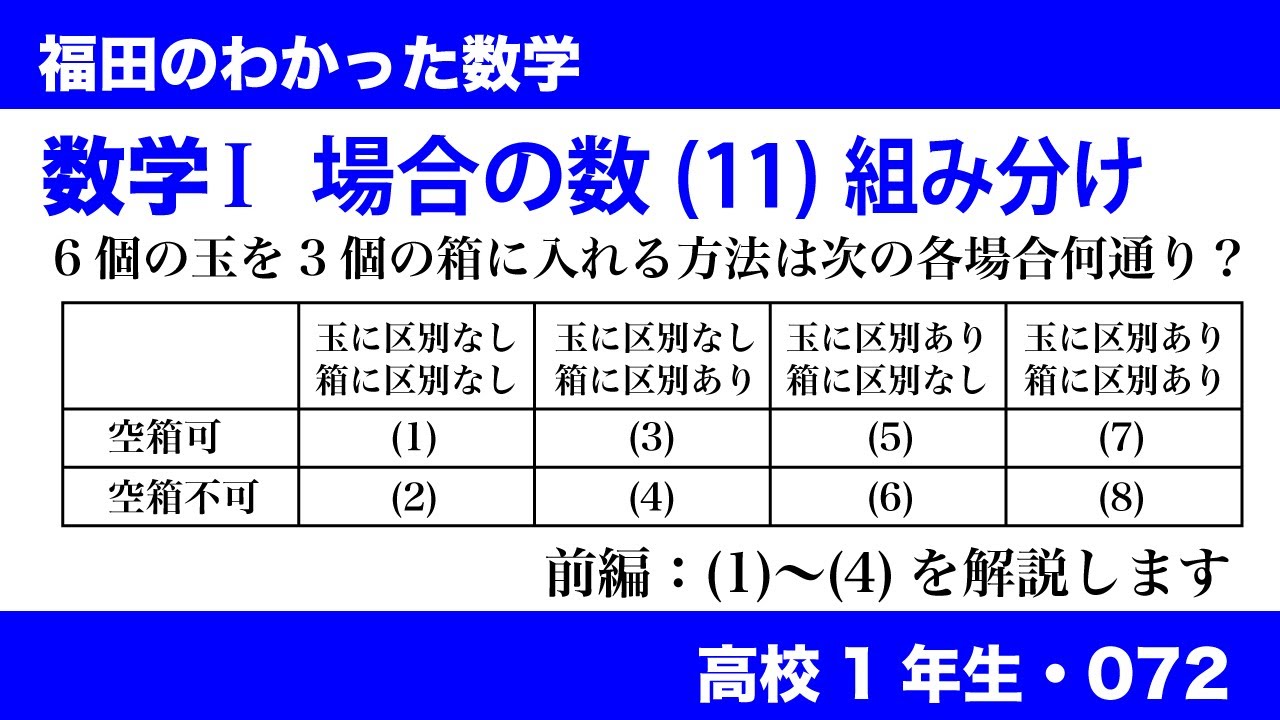
数学$\textrm{I}$ 場合の数(11) 組み分け
6個の玉を3個の箱に入れる方法は次の各場合に何通りあるか。
\begin{array}{|c|c|c|c|c|}
\hline
& 玉に区別なし & 玉に区別なし & 玉に区別あり &玉に区別あり\\
& 箱に区別なし & 箱に区別あり & 箱に区別なし &箱に区別あり\\
\hline
空箱可 & (1) & (3) & (5) & (7)\\
\hline
空箱不可 & (2) & (4) & (6) & (8)\\
\hline
\end{array}
\end{eqnarray}
この動画を見る
数学$\textrm{I}$ 場合の数(11) 組み分け
6個の玉を3個の箱に入れる方法は次の各場合に何通りあるか。
\begin{array}{|c|c|c|c|c|}
\hline
& 玉に区別なし & 玉に区別なし & 玉に区別あり &玉に区別あり\\
& 箱に区別なし & 箱に区別あり & 箱に区別なし &箱に区別あり\\
\hline
空箱可 & (1) & (3) & (5) & (7)\\
\hline
空箱不可 & (2) & (4) & (6) & (8)\\
\hline
\end{array}
\end{eqnarray}
福田のわかった数学〜高校１年生071〜場合の数(10)組み分け
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 場合の数(10) 組み分け
次のような分け方は何通りか。
(1)4人を2人ずつA,Bの2組に分けるとき
(2)4人を2人ずつの2組に分けるとき
(3)5人を3人、2人の2組に分けるとき
(4)6人を2人ずつの3組に分けるとき
(5)6人を3組に
(6)n人を3組に $(n \geqq 3)$
この動画を見る
数学$\textrm{I}$ 場合の数(10) 組み分け
次のような分け方は何通りか。
(1)4人を2人ずつA,Bの2組に分けるとき
(2)4人を2人ずつの2組に分けるとき
(3)5人を3人、2人の2組に分けるとき
(4)6人を2人ずつの3組に分けるとき
(5)6人を3組に
(6)n人を3組に $(n \geqq 3)$
福田のわかった数学〜高校１年生070〜場合の数(9)じゅず順列
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 場合の数(9) じゅず順列
次のような玉で数珠を作る方法は何通りか。
(1)白玉1個、黄玉2個、赤玉4個
(2)白玉2個、黄玉2個、赤玉4個
この動画を見る
数学$\textrm{I}$ 場合の数(9) じゅず順列
次のような玉で数珠を作る方法は何通りか。
(1)白玉1個、黄玉2個、赤玉4個
(2)白玉2個、黄玉2個、赤玉4個
福田のわかった数学〜高校１年生069〜場合の数(8)円順列その2
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 場合の数(8) 円順列(2)
次のような玉を円形に並べる方法は何通りか。
(1)白玉1個、黄玉2個、赤玉3個
(2)白玉2個、赤玉4個
(3)白玉2個、黄玉2個、赤玉2個
この動画を見る
数学$\textrm{I}$ 場合の数(8) 円順列(2)
次のような玉を円形に並べる方法は何通りか。
(1)白玉1個、黄玉2個、赤玉3個
(2)白玉2個、赤玉4個
(3)白玉2個、黄玉2個、赤玉2個
福田のわかった数学〜高校１年生068〜場合の数(7)円順列
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 場合の数(7) 円順列
8人を図のように(1)円形のテーブル (2)正方形のテーブル (3)長方形のテーブルに並べる方法は
それぞれ何通りあるか。
(※図は動画参照)
この動画を見る
数学$\textrm{I}$ 場合の数(7) 円順列
8人を図のように(1)円形のテーブル (2)正方形のテーブル (3)長方形のテーブルに並べる方法は
それぞれ何通りあるか。
(※図は動画参照)
福田のわかった数学〜高校１年生067〜場合の数(6)色々な順列
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 場合の数(6) 並べ方色々
さいころを4回投げたとき、出た目を順に$a,b,c,d$とする。
次のような目の出方は何通りあるか。
(1)全て異なる目が出る
(2)$a \lt b \lt c \lt d$
(3)$a \leqq b \leqq c \leqq d$
この動画を見る
数学$\textrm{I}$ 場合の数(6) 並べ方色々
さいころを4回投げたとき、出た目を順に$a,b,c,d$とする。
次のような目の出方は何通りあるか。
(1)全て異なる目が出る
(2)$a \lt b \lt c \lt d$
(3)$a \leqq b \leqq c \leqq d$
福田のわかった数学〜高校１年生066〜場合の数(5)色々な順列
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 場合の数(5) 並べ方色々
男子5人、女子3人(a,b,cとする)が次のように横一列に
並ぶ方法は何通りか。
(1)女子3人が隣り合う並び方
(2)どの女子2人も隣り合わない並び方
(3)aがbより左、bがcより左に現れる並び方
この動画を見る
数学$\textrm{I}$ 場合の数(5) 並べ方色々
男子5人、女子3人(a,b,cとする)が次のように横一列に
並ぶ方法は何通りか。
(1)女子3人が隣り合う並び方
(2)どの女子2人も隣り合わない並び方
(3)aがbより左、bがcより左に現れる並び方
福田のわかった数学〜高校１年生065〜場合の数(4)0を含む順列
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 場合の数(4) 0を含む順列
$0,1,2,3,4,5,6$から異なる4個を選んで
4桁の整数を作るとき、次の個数を求めよ。
(1)全部で (2)偶数 (3)奇数 (4)9の倍数 (5)4の倍数
この動画を見る
数学$\textrm{I}$ 場合の数(4) 0を含む順列
$0,1,2,3,4,5,6$から異なる4個を選んで
4桁の整数を作るとき、次の個数を求めよ。
(1)全部で (2)偶数 (3)奇数 (4)9の倍数 (5)4の倍数
福田のわかった数学〜高校１年生064〜場合の数(3)約数の個数と総和
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 場合の数(3) 約数の総和
600の正の約数の個数と総和を求めよ。
また、正の約数のうち、偶数であるものの
個数とその総和を求めよ。
この動画を見る
数学$\textrm{I}$ 場合の数(3) 約数の総和
600の正の約数の個数と総和を求めよ。
また、正の約数のうち、偶数であるものの
個数とその総和を求めよ。
福田のわかった数学〜高校１年生063〜場合の数(2)完全順列
単元：
#数A#場合の数と確率#場合の数#数列#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 場合の数(2) 完全順列
1,2,3,4を1列に並べたものを$a_1a_2a_3a_4$とする。
$a_1\neq 1,a_2\neq 2,a_3\neq 3,a_4\neq 4$を満たす並べ方は何通りあるか。
この動画を見る
数学$\textrm{I}$ 場合の数(2) 完全順列
1,2,3,4を1列に並べたものを$a_1a_2a_3a_4$とする。
$a_1\neq 1,a_2\neq 2,a_3\neq 3,a_4\neq 4$を満たす並べ方は何通りあるか。
福田のわかった数学〜高校１年生062〜場合の数(1)正n角形の対角線と三角形の個数
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{I}$ 場合の数(1) 正n角形
$正\ n\ 角形A_1A_2\ldots A_n (n \geqq 4)$について次を求めよ。
(1)対角線の本数
(2)頂点を結んでできる三角形で正n角形$A_1A_2\ldots A_n$
と辺を教習しないものの個数
この動画を見る
数学$\textrm{I}$ 場合の数(1) 正n角形
$正\ n\ 角形A_1A_2\ldots A_n (n \geqq 4)$について次を求めよ。
(1)対角線の本数
(2)頂点を結んでできる三角形で正n角形$A_1A_2\ldots A_n$
と辺を教習しないものの個数
【数A】中高一貫校用問題集(論理・確率編)場合の数と確率：反復試行の確率（ひっかけあり!!）：先に3勝する確率
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
教材：
#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
AとBが試合を行い、先に3勝した方を優勝者とする。各試合でAが勝つ確率は2/3で引き分けはないとする。このとき、Aが優勝する確率を求めよ。
この動画を見る
AとBが試合を行い、先に3勝した方を優勝者とする。各試合でAが勝つ確率は2/3で引き分けはないとする。このとき、Aが優勝する確率を求めよ。
福田の数学〜青山学院大学2021年理工学部第１問〜さいころの目の最大最小の確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#確率#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$1個のさいころを4回投げるとき、出た目の最小値をm、最大値をMとする。
(1)$m \geqq 2$となる確率は$\frac{\boxed{\ \ アイウ\ \ }}{\boxed{\ \ エオカキ\ \ }}$であり、
$m=1$となる確率は$\frac{\boxed{\ \ クケコ\ \ }}{\boxed{\ \ サシスセ\ \ }}$である。
(2)$m \geqq 2$かつ$M \leqq 5$となる確率は$\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}$であり、$m \geqq 2$かつ$M=6$となる確率は
$\frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニヌ\ \ }}$である。
(3)$m=1$かつ$M=6$となる確率は$\frac{\boxed{\ \ ネノハ\ \ }}{\boxed{\ \ ヒフヘ\ \ }}$である。
2021青山学院大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$1個のさいころを4回投げるとき、出た目の最小値をm、最大値をMとする。
(1)$m \geqq 2$となる確率は$\frac{\boxed{\ \ アイウ\ \ }}{\boxed{\ \ エオカキ\ \ }}$であり、
$m=1$となる確率は$\frac{\boxed{\ \ クケコ\ \ }}{\boxed{\ \ サシスセ\ \ }}$である。
(2)$m \geqq 2$かつ$M \leqq 5$となる確率は$\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}$であり、$m \geqq 2$かつ$M=6$となる確率は
$\frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニヌ\ \ }}$である。
(3)$m=1$かつ$M=6$となる確率は$\frac{\boxed{\ \ ネノハ\ \ }}{\boxed{\ \ ヒフヘ\ \ }}$である。
2021青山学院大学理工学部過去問
【数学】中高一貫校用問題集場合の数と確率：重複順列：9人を2つのグループに分ける。考え方は格付けチェック！？
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
教材：
#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
9人を次のように分ける方法は通りあるか。
(1)2つのグループA、Bに分ける。ただし、各グループには少なくとも1人は入るものとする。
(2)2つのグループに分ける。
この動画を見る
9人を次のように分ける方法は通りあるか。
(1)2つのグループA、Bに分ける。ただし、各グループには少なくとも1人は入るものとする。
(2)2つのグループに分ける。
【数A】中高一貫校問題集3(論理・確率編)86：場合の数と確率：重複順列：9人を2つのグループに分ける。考え方は格付けチェック！？
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
教材：
#TK数学#TK数学問題集3(論理・確率編)#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
9人を次のように分ける方法は通りあるか。
(1)2つのグループA、Bに分ける。ただし、各グループには少なくとも1人は入るものとする。
(2)2つのグループに分ける。
この動画を見る
9人を次のように分ける方法は通りあるか。
(1)2つのグループA、Bに分ける。ただし、各グループには少なくとも1人は入るものとする。
(2)2つのグループに分ける。
PとCの違い分かる？
【全パターンこの一本でOK！】場合の数の全手法まとめ！！(順列、組み合わせ、重複順列、円順列、樹形図)【高校数学 数学】
福田の数学〜慶應義塾大学2021年環境情報学部第２問〜ポーカーの役が揃う場合の数
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{2}}$
ジョーカーを除いた52枚のトランプでポーカーを行う。トランプには♠♧♦♡の4つのスートのそれぞれに1から13までの数が書かれた13枚のカードがある。(1,11,12,13の代わりに、A,J,Q,Kの記号を用いることが多い)
「10,J,Q,K,A」の組合せはストレートやストレートフラッシュとして認めるが、Aを超えて「J,Q,K,A,2」のように2まで含めるものは認めない。52枚のカードから5枚を抜き出す組合せの数は${}_{52}\textrm{C}_5=2598960$通りあるが、それがストレートフラッシュとなる組合せの数を求めてみよう。ストレートフラッシュの5枚のカードの最小の数は$1,2,\ldots,\boxed{\ \ アイ\ \ }$のどれかであるから、それぞれのスートごとに$\boxed{\ \ アイ\ \ }$通り考えられる。よって、$4\times \boxed{\ \ アイ\ \ }=\boxed{\ \ ウエ\ \ }$通りのストレートフラッシュの組合せがある。また、ストレートについては、数は順番に並んでいるが、スートがそろっていない組合せの数なので$\boxed{\ \ オカキクケ\ \ }$通りある。
次に、フルハウスとなる組合せの数を求めてみよう。同じ数のカードが3枚と2枚のふたつの組があり、3枚の組を選ぶ組合せ$\boxed{\ \ コサ\ \ }\times {}_4\textrm{C}_3$、残り2枚のカードを選ぶ組合せは$\boxed{\ \ シス\ \ }\times {}_4\textrm{C}_2$であるから、フルハウスとなる組合せの数は$\boxed{\ \ コサ\ \ }\times{}_4\textrm{C}_3\times$$\boxed{\ \ シス\ \ }\times$${}_4\textrm{C}_2=\boxed{\ \ セソタチ\ \ }$ 通りである。
2021慶應義塾大学環境情報学部過去問
この動画を見る
${\Large\boxed{2}}$
ジョーカーを除いた52枚のトランプでポーカーを行う。トランプには♠♧♦♡の4つのスートのそれぞれに1から13までの数が書かれた13枚のカードがある。(1,11,12,13の代わりに、A,J,Q,Kの記号を用いることが多い)
「10,J,Q,K,A」の組合せはストレートやストレートフラッシュとして認めるが、Aを超えて「J,Q,K,A,2」のように2まで含めるものは認めない。52枚のカードから5枚を抜き出す組合せの数は${}_{52}\textrm{C}_5=2598960$通りあるが、それがストレートフラッシュとなる組合せの数を求めてみよう。ストレートフラッシュの5枚のカードの最小の数は$1,2,\ldots,\boxed{\ \ アイ\ \ }$のどれかであるから、それぞれのスートごとに$\boxed{\ \ アイ\ \ }$通り考えられる。よって、$4\times \boxed{\ \ アイ\ \ }=\boxed{\ \ ウエ\ \ }$通りのストレートフラッシュの組合せがある。また、ストレートについては、数は順番に並んでいるが、スートがそろっていない組合せの数なので$\boxed{\ \ オカキクケ\ \ }$通りある。
次に、フルハウスとなる組合せの数を求めてみよう。同じ数のカードが3枚と2枚のふたつの組があり、3枚の組を選ぶ組合せ$\boxed{\ \ コサ\ \ }\times {}_4\textrm{C}_3$、残り2枚のカードを選ぶ組合せは$\boxed{\ \ シス\ \ }\times {}_4\textrm{C}_2$であるから、フルハウスとなる組合せの数は$\boxed{\ \ コサ\ \ }\times{}_4\textrm{C}_3\times$$\boxed{\ \ シス\ \ }\times$${}_4\textrm{C}_2=\boxed{\ \ セソタチ\ \ }$ 通りである。
2021慶應義塾大学環境情報学部過去問
【数A】場合の数：2021年高3第1回K塾記述模試
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#全統模試(河合塾)#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
白玉6個、赤玉2個、青玉2個の計10個の玉を横一列に並べる。ただし、同じ色の玉は区別しない。
(1)並べ方は全部で何通りあるか。
(2)白赤白赤白と連続して並ぶ箇所があるような並べ方は何通りあるか。
(3)次の、赤玉についての条件A、青玉についての条件Bを考える。
A：「同じ色の玉が両隣にある」
B：「異なる色の玉が 両隣にある」
ただし、列の両端の玉は、AもBも満たさないものとする。例えば、 白赤白白白青赤青白白は、2個の赤玉はともにAを満たし、2個の青玉もともにBを 満たす。また、白赤赤白白青青白白白は、2個の青玉はともにBを満たすが、2個 の赤玉はともにAを満たさない。
(i)2個の赤玉がともにAを満たすような並べ方は 何通りあるか。
(ii)2個の赤玉がともにAを満たし、かつ、2個の青玉がともにBを満たすような並べ方は何通りあるか。
この動画を見る
白玉6個、赤玉2個、青玉2個の計10個の玉を横一列に並べる。ただし、同じ色の玉は区別しない。
(1)並べ方は全部で何通りあるか。
(2)白赤白赤白と連続して並ぶ箇所があるような並べ方は何通りあるか。
(3)次の、赤玉についての条件A、青玉についての条件Bを考える。
A：「同じ色の玉が両隣にある」
B：「異なる色の玉が 両隣にある」
ただし、列の両端の玉は、AもBも満たさないものとする。例えば、 白赤白白白青赤青白白は、2個の赤玉はともにAを満たし、2個の青玉もともにBを 満たす。また、白赤赤白白青青白白白は、2個の青玉はともにBを満たすが、2個 の赤玉はともにAを満たさない。
(i)2個の赤玉がともにAを満たすような並べ方は 何通りあるか。
(ii)2個の赤玉がともにAを満たし、かつ、2個の青玉がともにBを満たすような並べ方は何通りあるか。
福田の数学〜早稲田大学2021年商学部第１問(4)〜空間内の点の移動の場合の数
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$
(4)座標空間において、各座標が整数である6個の点$\rm P_0,P_1,P_2,P_3,P_4,P_5$を、次の条件を満たすように重複を許して選ぶ。
$(\textrm{i}) \rm P_0=(0,0,0)$
$(\textrm{ii})$ ${\rm P}_k$と${\rm P}_{k+1}$との距離は$1$$ (k=0,1,2,3,4,5)$
$(\textrm{iii})$ ${\rm P}_0$と${\rm P}_5$との距離は$1$
このとき、選び方の総数は$\boxed{\ \ エ\ \ }$通りである。
2021早稲田大学商学部過去問
この動画を見る
${\Large\boxed{1}}$
(4)座標空間において、各座標が整数である6個の点$\rm P_0,P_1,P_2,P_3,P_4,P_5$を、次の条件を満たすように重複を許して選ぶ。
$(\textrm{i}) \rm P_0=(0,0,0)$
$(\textrm{ii})$ ${\rm P}_k$と${\rm P}_{k+1}$との距離は$1$$ (k=0,1,2,3,4,5)$
$(\textrm{iii})$ ${\rm P}_0$と${\rm P}_5$との距離は$1$
このとき、選び方の総数は$\boxed{\ \ エ\ \ }$通りである。
2021早稲田大学商学部過去問
福田の数学〜早稲田大学2021年教育学部第１問(4)〜箱に玉を入れる場合の数
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$
(4)箱が6個あり、1から6までの番号がついている。赤、黄、青それぞれ2個ずつ合計6個の玉があり、ひとつの箱にひとつずつ玉を入れるとする。ただし、隣り合う番号の箱には異なる色の玉が入るようにする。このような入れ方は全部で何通りあるかを求めよ。
2021早稲田大学教育学部過去問
この動画を見る
${\Large\boxed{1}}$
(4)箱が6個あり、1から6までの番号がついている。赤、黄、青それぞれ2個ずつ合計6個の玉があり、ひとつの箱にひとつずつ玉を入れるとする。ただし、隣り合う番号の箱には異なる色の玉が入るようにする。このような入れ方は全部で何通りあるかを求めよ。
2021早稲田大学教育学部過去問
【40分で総整理】基礎の基礎から『場合の数』(数学A)
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
1⃣
$A,B,C,D,E$の5人から3人を選んで並べるとき、その総数は？
2⃣
男子5人、女子3人の合計8人が1列に並ぶとき、次の並び方は何通りあるか。
（1）男子が両端に来る
（2）女子3人が隣り合う
3⃣
$a,b,c,d,e$を1つずつ使ってできる文字列を$abcde$から$edcba$までアルファベット順で並べるとき、$cbdea$は何番目か。
4⃣
5人を円形に並べたとき、その総数は何通り？
5⃣
1から5までの自然数を使ってできる3桁の整数は何通りあるか？
ただし同じ数字を繰り返し使ってもよい。
6⃣
$A,B,C,D,E$の5人から3人を選んで組をつくるとき、その総数は？
7⃣
生徒9人を3人ずつ、3つのグループ$A,B,C$に分ける分け方は何通りか。
8⃣
$a,a,a,b,b$の5文字を1列に並べる順列は何通りあるか。
この動画を見る
1⃣
$A,B,C,D,E$の5人から3人を選んで並べるとき、その総数は？
2⃣
男子5人、女子3人の合計8人が1列に並ぶとき、次の並び方は何通りあるか。
（1）男子が両端に来る
（2）女子3人が隣り合う
3⃣
$a,b,c,d,e$を1つずつ使ってできる文字列を$abcde$から$edcba$までアルファベット順で並べるとき、$cbdea$は何番目か。
4⃣
5人を円形に並べたとき、その総数は何通り？
5⃣
1から5までの自然数を使ってできる3桁の整数は何通りあるか？
ただし同じ数字を繰り返し使ってもよい。
6⃣
$A,B,C,D,E$の5人から3人を選んで組をつくるとき、その総数は？
7⃣
生徒9人を3人ずつ、3つのグループ$A,B,C$に分ける分け方は何通りか。
8⃣
$a,a,a,b,b$の5文字を1列に並べる順列は何通りあるか。
福田の数学〜早稲田大学2021年理工学部第４問〜場合の数と確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{4}}$ $n,k$を$2$以上の自然数とする。$n$個の箱の中に$k$個の玉を無作為に入れ、各箱に入った玉の
個数を数える。その最大値と最小値の差がlとなる確率を$P_l(0 \leqq l \leqq k)$とする。
(1)$n=2,$ $k=3$のとき、$P_0,P_1,P_2,P_3$を求めよ。
(2)$n \geqq 2,$ $k=2$のとき、$P_0,P_1,P_2$を求めよ。
(3)$n \geqq 3,$ $k=3$のとき、$P_0,P_1,P_2,P_3$を求めよ。
2021早稲田大学理工学部過去問
この動画を見る
${\Large\boxed{4}}$ $n,k$を$2$以上の自然数とする。$n$個の箱の中に$k$個の玉を無作為に入れ、各箱に入った玉の
個数を数える。その最大値と最小値の差がlとなる確率を$P_l(0 \leqq l \leqq k)$とする。
(1)$n=2,$ $k=3$のとき、$P_0,P_1,P_2,P_3$を求めよ。
(2)$n \geqq 2,$ $k=2$のとき、$P_0,P_1,P_2$を求めよ。
(3)$n \geqq 3,$ $k=3$のとき、$P_0,P_1,P_2,P_3$を求めよ。
2021早稲田大学理工学部過去問
部屋割り 組分け 他の問題もあり
単元：
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
部屋割り・グループ分け
(1)6人がAまたはBまたはCの3部屋に入る方法は何通り？
（1人も入らない部屋があってよい）
(2)6人を2つのグループに分ける方法は何通り？
（各グループは少なくとも2人以上）
(3)6人を3つのグループに分ける方法は何通り？
（各グループは少なくとも1人以上）
この動画を見る
部屋割り・グループ分け
(1)6人がAまたはBまたはCの3部屋に入る方法は何通り？
（1人も入らない部屋があってよい）
(2)6人を2つのグループに分ける方法は何通り？
（各グループは少なくとも2人以上）
(3)6人を3つのグループに分ける方法は何通り？
（各グループは少なくとも1人以上）
【数A】場合の数：岐阜大学2008年
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#岐阜大学#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
7個の文字FGGIIUUを横1列に並べる。次の問いに答えよ。
(1)『GIFU』という連続 した4文字が現れるように並べる方法は何通りあるか。
(2)『GI』と『FU』という 連続した2文字がともに現れ、少なくとも1つの『GI』が『FU』よりも左にあるよ うに並べる方法は何通りあるか。
この動画を見る
7個の文字FGGIIUUを横1列に並べる。次の問いに答えよ。
(1)『GIFU』という連続 した4文字が現れるように並べる方法は何通りあるか。
(2)『GI』と『FU』という 連続した2文字がともに現れ、少なくとも1つの『GI』が『FU』よりも左にあるよ うに並べる方法は何通りあるか。