 場合の数と確率
場合の数と確率
 場合の数と確率
場合の数と確率
中学生でも解ける京大の入試問題!解けますか?【数学 入試問題】【京都大学】

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
1歩で1段または2段のいずれかで階段を昇るとき、1歩で2段昇ることは連続しないものとする。15段の階段を昇る昇り方は何通りあるか。
京都大過去問
この動画を見る
1歩で1段または2段のいずれかで階段を昇るとき、1歩で2段昇ることは連続しないものとする。15段の階段を昇る昇り方は何通りあるか。
京都大過去問
解けるかな?

単元:
#算数(中学受験)#数A#場合の数と確率#場合の数#場合の数#場合の数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
机の上にたくさんのコインが置いてます。
そのうち10枚だけ表、残りは全部裏が上になっています。
目隠しをした状態で表が上になっているコインの枚数が同じような
2つのグループに分けるにはどうすればよいか?
ただし、触って表裏の判断はできないとする
この動画を見る
机の上にたくさんのコインが置いてます。
そのうち10枚だけ表、残りは全部裏が上になっています。
目隠しをした状態で表が上になっているコインの枚数が同じような
2つのグループに分けるにはどうすればよいか?
ただし、触って表裏の判断はできないとする
福田の数学〜浜松医科大学2022年医学部第4問〜確率漸化式と誤った答案に対する指摘

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の問題
問題
表面と裏面が出る確率がそれぞれであるコインを投げる試行を繰り返し、同
じ面が3回連続して出た時点で試行を終了する。n回投げ終えた段階で試行が
終了する確率 $p_n$を求めよ。
に対する次の答案Aについて以下の問いに答えよ。
(1) もし答案Aに誤りがあれば誤りを指摘し、その理由を述べよ。ただし、すでに
指摘してある誤った結論から論理的に導き出した結論を誤りとして指摘する必要
はない。誤りがないときは「誤りなし」と答えよ。
(2) 答案Aで導かれたp_nと正解の$p_n$とで値が異なるとき、値が異なる最小のnを
求め、そのnに対する正解のpnの値を答えよ。そのようなnがないときは
「すべて一致する」と答えよ。
答案A
自然数nに対して、コインをn回投げ終えた段階で、その後最短で試行が終了するために
必要な回数がk回($k \geqq 0$)である確率を$p_n(k)$とする。このとき、
kは0,1,2のいずれかであるから、確率の総和は
$p_n(0)+p_n(1)+p_n(2)=1$
である。また、$p_n(0)=p_n,p_{n+1}(0)=\frac{1}{2}p_n(1),p_{n+2}(0)=\frac{1}{4}p_n(2)$であるから漸化式
$p_n+2p_{n+1}+4p_{n+2}=1 (n \geqq 1)$
を得る。ここで$\frac{1}{7}+\frac{2}{7}+\frac{4}{7}=1$なので、$q_n=2^n(p_n-\frac{1}{7})$とすれば
$q_n+q_{n+1}+q_{n+2}=0$
である。よって$n \geqq 4$に対して
$q_n=-q_{n-1}-q_{n-2}=(q_{n-2}+q_{n-3})-q_{n-2}=q_{n-3}$
が成立する。以上より、
$Q(x)=
\left\{
\begin{array}{1}q_1 (nを3で割った時の余りが1のとき)\\
q_2 (nを3で割った時の余りが2のとき)\\
q_3 (nが3で割り切れるとき)\\
\end{array}
\right.$
とすれば求める確率は
$p_n=\frac{q_n}{2^n}+\frac{1}{7}=\frac{Q(n)}{2^n}+\frac{1}{7} (n \geqq 4)$
である。また最初の2項は定義より$p_1=p_2=0$であり$p_n$の漸化式で$n=1$とすれば
$p_1+2p_2+4p_3=1$ であるから$p_3=\frac{1}{4}$である。さらに
$q_1=-\frac{2}{7}, q_2=-\frac{4}{7}, q_3=\frac{6}{7}$
である。したがって
$p_1=p_2=0, p_3=\frac{1}{4}, p_n=\frac{Q(n)}{2^n}+\frac{1}{7} (n \geqq 4)$
となる。
2022浜松医科大学医学部過去問
この動画を見る
次の問題
問題
表面と裏面が出る確率がそれぞれであるコインを投げる試行を繰り返し、同
じ面が3回連続して出た時点で試行を終了する。n回投げ終えた段階で試行が
終了する確率 $p_n$を求めよ。
に対する次の答案Aについて以下の問いに答えよ。
(1) もし答案Aに誤りがあれば誤りを指摘し、その理由を述べよ。ただし、すでに
指摘してある誤った結論から論理的に導き出した結論を誤りとして指摘する必要
はない。誤りがないときは「誤りなし」と答えよ。
(2) 答案Aで導かれたp_nと正解の$p_n$とで値が異なるとき、値が異なる最小のnを
求め、そのnに対する正解のpnの値を答えよ。そのようなnがないときは
「すべて一致する」と答えよ。
答案A
自然数nに対して、コインをn回投げ終えた段階で、その後最短で試行が終了するために
必要な回数がk回($k \geqq 0$)である確率を$p_n(k)$とする。このとき、
kは0,1,2のいずれかであるから、確率の総和は
$p_n(0)+p_n(1)+p_n(2)=1$
である。また、$p_n(0)=p_n,p_{n+1}(0)=\frac{1}{2}p_n(1),p_{n+2}(0)=\frac{1}{4}p_n(2)$であるから漸化式
$p_n+2p_{n+1}+4p_{n+2}=1 (n \geqq 1)$
を得る。ここで$\frac{1}{7}+\frac{2}{7}+\frac{4}{7}=1$なので、$q_n=2^n(p_n-\frac{1}{7})$とすれば
$q_n+q_{n+1}+q_{n+2}=0$
である。よって$n \geqq 4$に対して
$q_n=-q_{n-1}-q_{n-2}=(q_{n-2}+q_{n-3})-q_{n-2}=q_{n-3}$
が成立する。以上より、
$Q(x)=
\left\{
\begin{array}{1}q_1 (nを3で割った時の余りが1のとき)\\
q_2 (nを3で割った時の余りが2のとき)\\
q_3 (nが3で割り切れるとき)\\
\end{array}
\right.$
とすれば求める確率は
$p_n=\frac{q_n}{2^n}+\frac{1}{7}=\frac{Q(n)}{2^n}+\frac{1}{7} (n \geqq 4)$
である。また最初の2項は定義より$p_1=p_2=0$であり$p_n$の漸化式で$n=1$とすれば
$p_1+2p_2+4p_3=1$ であるから$p_3=\frac{1}{4}$である。さらに
$q_1=-\frac{2}{7}, q_2=-\frac{4}{7}, q_3=\frac{6}{7}$
である。したがって
$p_1=p_2=0, p_3=\frac{1}{4}, p_n=\frac{Q(n)}{2^n}+\frac{1}{7} (n \geqq 4)$
となる。
2022浜松医科大学医学部過去問
【数A】確率:感覚でわかる最短経路

福田の数学〜筑波大学2022年理系第2問〜確率漸化式と常用対数

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数B
指導講師:
福田次郎
問題文全文(内容文):
整数$\ a_1,\ a_2,\ a_3,\ \ldots$を、さいころをくり返し投げることにより、以下のように
定めていく。まず$a_1=1$とする。そして、正の整数$n$に対し、$a_{n+1}$の値を、n回目に
出たさいころの目に応じて、次の規則で定める。
$(\ 規則\ )$ n回目に出た目が1,2,3,4なら$a_{n+1}=a_n、5,6$なら$a_{n+1}=-a_n$
例えば、さいころを3回投げ、その出た目が順に5,3,6であったとすると、
$a_1=1,a_2=-1,a_3=-1,a_4=1$となる。
$a_n=1$となる確率を$p_n$とする。ただし、$p_1=1$とし、さいころのどの目も、
出る確率は$\frac{1}{6}$であるとする。
(1)$p_2,p_3$を求めよ。
(2)$p_{n+1}$を$p_n$を用いて表せ。
(3)$p_n \leqq 0.5000005$を満たす最小の正の整数nを求めよ。
ただし、$0.47 \lt \log_{10}3 \lt 0.48$であることを用いてよい。
2022筑波大学理系過去問
この動画を見る
整数$\ a_1,\ a_2,\ a_3,\ \ldots$を、さいころをくり返し投げることにより、以下のように
定めていく。まず$a_1=1$とする。そして、正の整数$n$に対し、$a_{n+1}$の値を、n回目に
出たさいころの目に応じて、次の規則で定める。
$(\ 規則\ )$ n回目に出た目が1,2,3,4なら$a_{n+1}=a_n、5,6$なら$a_{n+1}=-a_n$
例えば、さいころを3回投げ、その出た目が順に5,3,6であったとすると、
$a_1=1,a_2=-1,a_3=-1,a_4=1$となる。
$a_n=1$となる確率を$p_n$とする。ただし、$p_1=1$とし、さいころのどの目も、
出る確率は$\frac{1}{6}$であるとする。
(1)$p_2,p_3$を求めよ。
(2)$p_{n+1}$を$p_n$を用いて表せ。
(3)$p_n \leqq 0.5000005$を満たす最小の正の整数nを求めよ。
ただし、$0.47 \lt \log_{10}3 \lt 0.48$であることを用いてよい。
2022筑波大学理系過去問
福田の数学〜東京医科歯科大学2022年理系第1問〜2つのベクトルで生成される異なる点の個数

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#平面上のベクトル#場合の数#三角関数#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
nを自然数とする。整数i,jに対し、xy平面上の点$P_{i,j}$の座標を
$(\cos\frac{2\pi}{n}i+\cos\frac{2\pi}{n}j, \sin\frac{2\pi}{n}i+\sin\frac{2\pi}{n}j)$
で与える。さらに、i,jを動かしたとき、$P_{i,j}$の取り得る異なる座標の
個数を$S_n$とする。このとき、以下の問いに答えよ。
(1)$n=3$のとき、$\triangle P_{0,0}P_{0,1}P_{0,2}$および$\triangle P_{1,0}P_{1,1}P_{1,2}$を同一平面上
に図示せよ。
(2)$S_4$を求めよ。
(3)平面上の異なる2点A,Bに対して、$AQ=BQ=1$であるような
同一平面上の点Qはいくつあるか。AB=dの値で場合分けして答えよ。
(4)$S_n$をnを用いて表せ。
2022東京医科歯科大学理系過去問
この動画を見る
nを自然数とする。整数i,jに対し、xy平面上の点$P_{i,j}$の座標を
$(\cos\frac{2\pi}{n}i+\cos\frac{2\pi}{n}j, \sin\frac{2\pi}{n}i+\sin\frac{2\pi}{n}j)$
で与える。さらに、i,jを動かしたとき、$P_{i,j}$の取り得る異なる座標の
個数を$S_n$とする。このとき、以下の問いに答えよ。
(1)$n=3$のとき、$\triangle P_{0,0}P_{0,1}P_{0,2}$および$\triangle P_{1,0}P_{1,1}P_{1,2}$を同一平面上
に図示せよ。
(2)$S_4$を求めよ。
(3)平面上の異なる2点A,Bに対して、$AQ=BQ=1$であるような
同一平面上の点Qはいくつあるか。AB=dの値で場合分けして答えよ。
(4)$S_n$をnを用いて表せ。
2022東京医科歯科大学理系過去問
福田の数学〜千葉大学2022年理系第5問〜n個のサイコロの目の積の確率

単元:
#計算と数の性質#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
nを自然数とする。n個のサイコロを同時に投げ、出た目の積をMとおく。
(1)Mが2でも3でも割り切れない確率を求めよ。
(2)Mが2で割り切れるが、3でも4でも割り切れない確率を求めよ。
(3)Mが4では割り切れるが、3では割り切れない確率を求めよ。
2022千葉大学理系過去問
この動画を見る
nを自然数とする。n個のサイコロを同時に投げ、出た目の積をMとおく。
(1)Mが2でも3でも割り切れない確率を求めよ。
(2)Mが2で割り切れるが、3でも4でも割り切れない確率を求めよ。
(3)Mが4では割り切れるが、3では割り切れない確率を求めよ。
2022千葉大学理系過去問
【数A】確率:条件付き確率の考え方

【数A】条件付き確率の考え方

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
1/3 の確率で肝心なものを忘れるAOIさん 坂田アキラの「確率」が面白いほどとける本
この動画を見る
1/3 の確率で肝心なものを忘れるAOIさん 坂田アキラの「確率」が面白いほどとける本
福田の数学〜千葉大学2022年理系第1問〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
円周を12等分するように点$A_1,A_2,A_3,\ldots,A_{12}$が時計回りに並んでいる。
また、白球2個と黒球4個が入った袋がある。点Pを、次の操作によって
12個の点上を移動させる。
操作:袋から球を一つ取り出した後にサイコロを投げる。白球ならば時計回りに、
黒球ならば反時計回りに、サイコロの目の数だけPを移動させる。
取り出した球は袋に戻さないこととする。
Pを最初に点 $A_1$に置く。操作を1回行い、Pが$A_1$から移動した点をQとおく。
続けて操作を1回行い、PがQから移動した点をRとおく。
もう一度操作を行い、 PがRから移動した点をSとおく。
(1) $R=A_1$となる確率を求めよ。
(2)3点Q, R, Sを結んでできる図形が正三角形となる確率を求めよ。
2022千葉大学理系過去問
この動画を見る
円周を12等分するように点$A_1,A_2,A_3,\ldots,A_{12}$が時計回りに並んでいる。
また、白球2個と黒球4個が入った袋がある。点Pを、次の操作によって
12個の点上を移動させる。
操作:袋から球を一つ取り出した後にサイコロを投げる。白球ならば時計回りに、
黒球ならば反時計回りに、サイコロの目の数だけPを移動させる。
取り出した球は袋に戻さないこととする。
Pを最初に点 $A_1$に置く。操作を1回行い、Pが$A_1$から移動した点をQとおく。
続けて操作を1回行い、PがQから移動した点をRとおく。
もう一度操作を行い、 PがRから移動した点をSとおく。
(1) $R=A_1$となる確率を求めよ。
(2)3点Q, R, Sを結んでできる図形が正三角形となる確率を求めよ。
2022千葉大学理系過去問
福田の数学〜大阪大学2022年文系第2問〜さいころの目と最大公約数、最小公倍数の確率(そのまま考えるか余事象で考えるかの判断基準を解説します)

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
nを2以上の自然数とし、1個のさいころをn回投げて出る目の数を順に
$X_1,X_2,\ldots\ldots,X_n$とする。$X_1,X_2,\ldots\ldots,X_n$の最小公倍数を$L_n$,
最大公約数を$G_n$とするとき、以下の問いに答えよ。
(1)$L_2=5$となる確率および$G_2=5$となる確率を求めよ。
(2)$L_n$が素数でない確率を求めよ。
(3)$G_n$が素数でない確率を求めよ。
2022大阪大学文系過去問
この動画を見る
nを2以上の自然数とし、1個のさいころをn回投げて出る目の数を順に
$X_1,X_2,\ldots\ldots,X_n$とする。$X_1,X_2,\ldots\ldots,X_n$の最小公倍数を$L_n$,
最大公約数を$G_n$とするとき、以下の問いに答えよ。
(1)$L_2=5$となる確率および$G_2=5$となる確率を求めよ。
(2)$L_n$が素数でない確率を求めよ。
(3)$G_n$が素数でない確率を求めよ。
2022大阪大学文系過去問
【数A】場合の数:PとCの違い

福田の数学〜一橋大学2022年文系第5問〜確率漸化式

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
中身の見えない2つの箱があり、1つの箱には赤玉2つと白玉1つが入っており、
もう1つの箱には赤玉1つと白玉2つが入っている。どちらかの箱を選び、選んだ
箱の中から玉を1つ取り出して元に戻す、という操作を繰り返す。
(1) 1回目は箱を無作為に選び、2回目以降は、前回取り出した玉が赤玉なら前回
と同じ箱、前回取り出した玉が白玉なら前回とは異なる箱を選ぶ。n回目に赤玉
を取り出す確率$p_n$を求めよ。
(2)1回目は箱を無作為に選び、2回目以降は、前回取り出した玉が赤玉なら前回
と同じ箱、前回取り出した玉が白玉なら箱を無作為に選ぶ。n回目に赤玉を取り
出す確率 $q_n$を求めよ。
2022一橋大学文系過去問
この動画を見る
中身の見えない2つの箱があり、1つの箱には赤玉2つと白玉1つが入っており、
もう1つの箱には赤玉1つと白玉2つが入っている。どちらかの箱を選び、選んだ
箱の中から玉を1つ取り出して元に戻す、という操作を繰り返す。
(1) 1回目は箱を無作為に選び、2回目以降は、前回取り出した玉が赤玉なら前回
と同じ箱、前回取り出した玉が白玉なら前回とは異なる箱を選ぶ。n回目に赤玉
を取り出す確率$p_n$を求めよ。
(2)1回目は箱を無作為に選び、2回目以降は、前回取り出した玉が赤玉なら前回
と同じ箱、前回取り出した玉が白玉なら箱を無作為に選ぶ。n回目に赤玉を取り
出す確率 $q_n$を求めよ。
2022一橋大学文系過去問
ポケモンで数学を使おう!

単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ポケモンでマヒ状態かつ混乱のとき攻撃できない確率はどれくらいですか?
この動画を見る
ポケモンでマヒ状態かつ混乱のとき攻撃できない確率はどれくらいですか?
福田の数学〜名古屋大学2022年理系第2問〜互いに素になるような確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
1つのサイコロを3回投げる。1回目に出る目をa、2回目に出る目をb、
3回目に出る目をcとする。なおサイコロは1から6までの目が等しい確率で出るもの
とする。
(1)$ab+2c \geqq abc$となる確率を求めよ。
(2)$ab+2cと2abc$が互いに素となる確率を求めよ。
2022名古屋大学理系過去問
この動画を見る
1つのサイコロを3回投げる。1回目に出る目をa、2回目に出る目をb、
3回目に出る目をcとする。なおサイコロは1から6までの目が等しい確率で出るもの
とする。
(1)$ab+2c \geqq abc$となる確率を求めよ。
(2)$ab+2cと2abc$が互いに素となる確率を求めよ。
2022名古屋大学理系過去問
福田の入試問題解説〜北海道大学2022年文系第4問〜復元抽出と非復元抽出の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
箱の中に1文字ずつ書かれたカードが10枚ある。そのうち5枚にはA、
3枚にはB、2枚にはCと書かれている。箱から1枚ずつ、3回カードを
取り出す試行を考える。
(1)カードを取り出すごとに箱に戻す場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(2)取り出したカードを箱に戻さない場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(3)取り出したカードを箱に戻さない場合、2回目に取り出したカードの文字が
Cであるとき、1回目と3回目に取り出したカードの文字が一致する
条件つき確率を求めよ。
2022北海道大学文系過去問
この動画を見る
箱の中に1文字ずつ書かれたカードが10枚ある。そのうち5枚にはA、
3枚にはB、2枚にはCと書かれている。箱から1枚ずつ、3回カードを
取り出す試行を考える。
(1)カードを取り出すごとに箱に戻す場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(2)取り出したカードを箱に戻さない場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(3)取り出したカードを箱に戻さない場合、2回目に取り出したカードの文字が
Cであるとき、1回目と3回目に取り出したカードの文字が一致する
条件つき確率を求めよ。
2022北海道大学文系過去問
福田の入試問題解説〜東京大学2022年文系第4問〜複雑な反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
{\Large{\boxed{4}}}\ Oを原点とする座標平面上で考える。0以上の整数kに対して、ベクトル\overrightarrow{ v_k }を\\
\overrightarrow{ v_k }=(\cos\frac{2k\pi}{3}, \sin\frac{2k\pi}{3})\\
と定める。投げたとき表と裏がどちらも\frac{1}{2}の確率で出るコインをN回投げて、\\
座標平面上に点X_0,X_1,X_2,\ldots,X_Nを以下の規則(\textrm{i}),(\textrm{ii})に従って定める。\\
(\textrm{i})X_0はOにある。\\
(\textrm{ii})nを1以上N以下の整数とする。X_{n-1}が定まったとし、\\
X_nを次のように定める。\\
・n回目のコイン投げで表が出た場合、\overrightarrow{ OX_n }=\overrightarrow{ OX_{n-1} }+\overrightarrow{ v_k }によりX_nを定める。\\
ただし、kは1回目からn回目までのコイン投げで裏が出た回数とする。\\
・n回目のコイン投げで裏が出た場合、X_nをX_{n-1}と定める。\\
(1)N=5とする。X_5がOにある確率を求めよ。\\
(2)N=98とする。X_{98}がOにあり、かつ、表が90回、裏が8回出る確率を求めよ。
\end{eqnarray}
2022東京大学文系過去問
この動画を見る
\begin{eqnarray}
{\Large{\boxed{4}}}\ Oを原点とする座標平面上で考える。0以上の整数kに対して、ベクトル\overrightarrow{ v_k }を\\
\overrightarrow{ v_k }=(\cos\frac{2k\pi}{3}, \sin\frac{2k\pi}{3})\\
と定める。投げたとき表と裏がどちらも\frac{1}{2}の確率で出るコインをN回投げて、\\
座標平面上に点X_0,X_1,X_2,\ldots,X_Nを以下の規則(\textrm{i}),(\textrm{ii})に従って定める。\\
(\textrm{i})X_0はOにある。\\
(\textrm{ii})nを1以上N以下の整数とする。X_{n-1}が定まったとし、\\
X_nを次のように定める。\\
・n回目のコイン投げで表が出た場合、\overrightarrow{ OX_n }=\overrightarrow{ OX_{n-1} }+\overrightarrow{ v_k }によりX_nを定める。\\
ただし、kは1回目からn回目までのコイン投げで裏が出た回数とする。\\
・n回目のコイン投げで裏が出た場合、X_nをX_{n-1}と定める。\\
(1)N=5とする。X_5がOにある確率を求めよ。\\
(2)N=98とする。X_{98}がOにあり、かつ、表が90回、裏が8回出る確率を求めよ。
\end{eqnarray}
2022東京大学文系過去問
みんなが間違う?コイントスの確率

単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
コイントスの確率
コインを10回投げて表がぴったり5回出る確率を求めよ
この動画を見る
コイントスの確率
コインを10回投げて表がぴったり5回出る確率を求めよ
これ解ける?

単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
コインを10回投げて表がぴったり5回出る確率は?
この動画を見る
コインを10回投げて表がぴったり5回出る確率は?
一橋大 漸化式
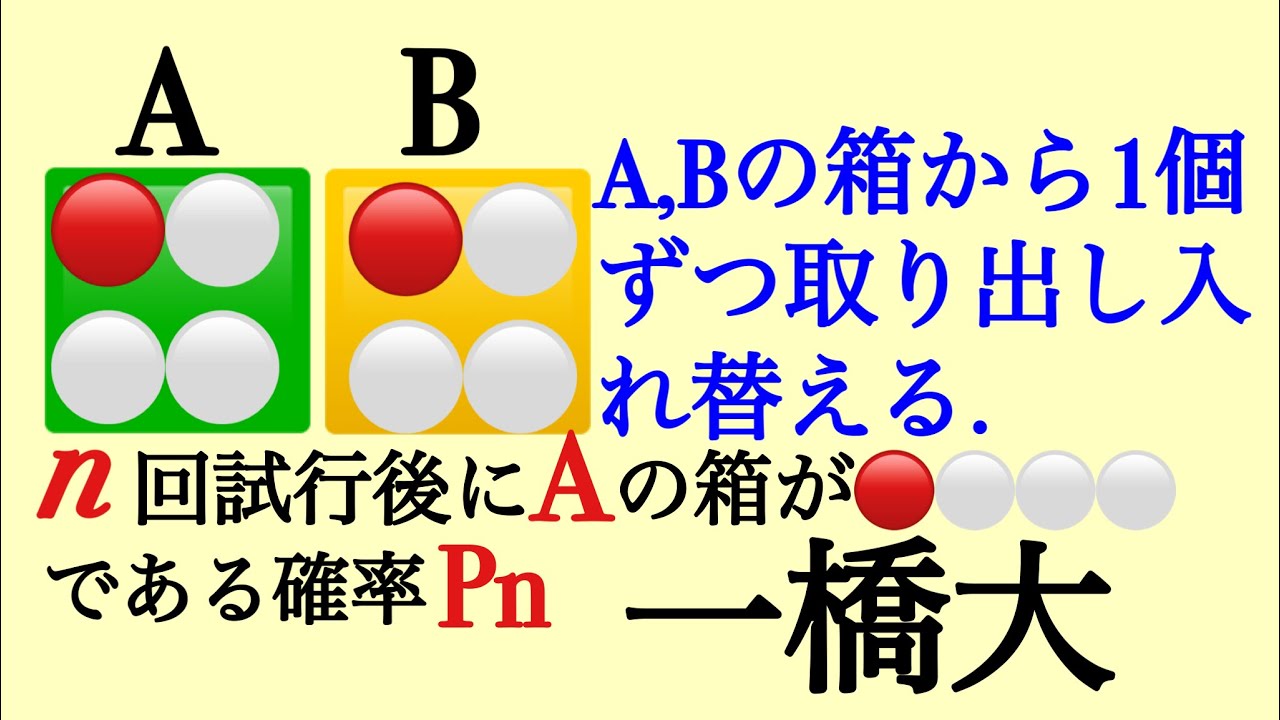
単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#漸化式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
同時に1個ずつ取り出して入れかえる.
n回後にAがA,Bである確率を求めよ.
2022一橋大過去問
この動画を見る
同時に1個ずつ取り出して入れかえる.
n回後にAがA,Bである確率を求めよ.
2022一橋大過去問
これ2通りで解ける?

福田の入試問題解説〜北海道大学2022年理系第4問〜円順列と確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
アルファベットのAと書かれた玉が1個、Dと書かれた玉が1個、Hと書かれ
た玉が1個、Iと書かれた玉が1個、Kと書かれた玉が2個、Oと書かれた玉が
2個ある。これら8個の玉を円形に並べる。
(1) 時計回りにHOKKAIDOと並ぶ確率を求めよ。
(2) 隣り合う子音が存在する確率を求めよ。ここで子音とは、D, H, K の3文字
(玉は4個)のことである。
(3) 隣り合う子音が存在するとき、それがKKだけである条件つき確率を求めよ。
2022北海道大学理系過去問
この動画を見る
アルファベットのAと書かれた玉が1個、Dと書かれた玉が1個、Hと書かれ
た玉が1個、Iと書かれた玉が1個、Kと書かれた玉が2個、Oと書かれた玉が
2個ある。これら8個の玉を円形に並べる。
(1) 時計回りにHOKKAIDOと並ぶ確率を求めよ。
(2) 隣り合う子音が存在する確率を求めよ。ここで子音とは、D, H, K の3文字
(玉は4個)のことである。
(3) 隣り合う子音が存在するとき、それがKKだけである条件つき確率を求めよ。
2022北海道大学理系過去問
福田の入試問題解説〜東京大学2022年理系第6問〜複雑な反復試行の確率と確率の最大

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
Oを原点とする座標平面上で考える。0以上の整数kに対して、ベクトル$\overrightarrow{ v_k }$を
$\overrightarrow{ v_k }=(\cos\frac{2k\pi}{3}, \sin\frac{2k\pi}{3})$
と定める。投げたとき表と裏がどちらも$\frac{1}{2}$の確率で出るコインをN回投げて、
座標平面上に点$X_0,X_1,X_2,\ldots,X_N$を以下の規則$(\textrm{i}),(\textrm{ii})$に従って定める。
$(\textrm{i})X_0$はOにある。
$(\textrm{ii})n$を1以上N以下の整数とする。$X_{n-1}$が定まったとし、$X_n$を次のように定める。
・n回目のコイン投げで表が出た場合、
$\overrightarrow{ OX_n }=\overrightarrow{ OX_{n-1} }+\overrightarrow{ v_k }$
により$X_n$を定める。ただし、kは1回目からn回目までの
コイン投げで裏が出た回数とする。
・n回目のコイン投げで裏が出た場合、$X_n$を$X_{n-1}$と定める。
(1)$N=8$とする。$X_8$がOにある確率を求めよ。
(2)$N=200$とする。$X_{200}$がOにあり、かつ、合計200回のコイン投げで表が
ちょうどr回出る確率を$p_r$とおく。ただし$0 \leqq r \leqq 200$である。$p_r$を求めよ。
また$p_r$が最大となるrの値を求めよ。
2022東京大学理系過去問
この動画を見る
Oを原点とする座標平面上で考える。0以上の整数kに対して、ベクトル$\overrightarrow{ v_k }$を
$\overrightarrow{ v_k }=(\cos\frac{2k\pi}{3}, \sin\frac{2k\pi}{3})$
と定める。投げたとき表と裏がどちらも$\frac{1}{2}$の確率で出るコインをN回投げて、
座標平面上に点$X_0,X_1,X_2,\ldots,X_N$を以下の規則$(\textrm{i}),(\textrm{ii})$に従って定める。
$(\textrm{i})X_0$はOにある。
$(\textrm{ii})n$を1以上N以下の整数とする。$X_{n-1}$が定まったとし、$X_n$を次のように定める。
・n回目のコイン投げで表が出た場合、
$\overrightarrow{ OX_n }=\overrightarrow{ OX_{n-1} }+\overrightarrow{ v_k }$
により$X_n$を定める。ただし、kは1回目からn回目までの
コイン投げで裏が出た回数とする。
・n回目のコイン投げで裏が出た場合、$X_n$を$X_{n-1}$と定める。
(1)$N=8$とする。$X_8$がOにある確率を求めよ。
(2)$N=200$とする。$X_{200}$がOにあり、かつ、合計200回のコイン投げで表が
ちょうどr回出る確率を$p_r$とおく。ただし$0 \leqq r \leqq 200$である。$p_r$を求めよ。
また$p_r$が最大となるrの値を求めよ。
2022東京大学理系過去問
みんな騙されるくない?

単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle \frac{1}{100}$の確率でレアが当たる。
100回引く。
レアは絶対当たる?
この動画を見る
$\displaystyle \frac{1}{100}$の確率でレアが当たる。
100回引く。
レアは絶対当たる?
福田の数学〜慶應義塾大学2022年薬学部第1問(4)〜2次関数と積分の確率

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(4)f(x)はxの2次関数である。$f(x)$は$x=-2$で極値をとり、$\int_{-3}^0f(x)dx=0$
を満たす。またxy平面上において、f(x)のグラフ$y=f(x)$はx軸と異なる2点で交わり、
$y=f(x)$とx軸で囲まれる部分の面積は$\frac{8}{3}$である。このとき$f(x)=\boxed{\ \ キ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
(4)f(x)はxの2次関数である。$f(x)$は$x=-2$で極値をとり、$\int_{-3}^0f(x)dx=0$
を満たす。またxy平面上において、f(x)のグラフ$y=f(x)$はx軸と異なる2点で交わり、
$y=f(x)$とx軸で囲まれる部分の面積は$\frac{8}{3}$である。このとき$f(x)=\boxed{\ \ キ\ \ }$である。
2022慶應義塾大学薬学部過去問
福田の数学〜京都大学2022年理系第2問〜連続しない自然数を選ぶ確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
箱の中に1からnまでの番号の付いたn枚の札がある。ただし、$n \geqq 5$とし、
同じ番号の札はないとする。この箱から3枚の札を同時に取り出し、札の番号を
小さい順に$X,Y,Z$とする。このとき、$Y-X \geqq 2$かつ$Z-Y \geqq 2$となる確率を
求めよ。
2022京都大学理系過去問
この動画を見る
箱の中に1からnまでの番号の付いたn枚の札がある。ただし、$n \geqq 5$とし、
同じ番号の札はないとする。この箱から3枚の札を同時に取り出し、札の番号を
小さい順に$X,Y,Z$とする。このとき、$Y-X \geqq 2$かつ$Z-Y \geqq 2$となる確率を
求めよ。
2022京都大学理系過去問
福田の数学〜慶應義塾大学2022年薬学部第1問(3)〜部屋わけ・グループ分けの確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(3)3つの部屋A,B,Cがある。この3つの部屋に対して、複数の生徒が以下の
試行(*)を繰り返し行うことを考える。
$(*)\left\{
\begin{array}{1}
・生徒それぞれが部屋を無作為に1つ選んで入る。\\
・生徒全員が部屋に入ったら、各部屋の生徒の人数を確認する。\\
・生徒全員が部屋を出る。\\
・1人の生徒しかいない部屋があった場合、その部屋に入った生徒は\\
次回以降の試行に参加しない。\\
\end{array}
\right.$
$(\textrm{i})$4人の生徒が試行(*)を1回行ったとき、2回目の試行に参加する生徒が
3人になる確率は$\boxed{\ \ オ\ \ }$である。
$(\textrm{ii})$5人の生徒が試行(*)を続けて2回行ったとき、3回目の試行に参加する
生徒が2人になる確率は$\boxed{\ \ カ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
(3)3つの部屋A,B,Cがある。この3つの部屋に対して、複数の生徒が以下の
試行(*)を繰り返し行うことを考える。
$(*)\left\{
\begin{array}{1}
・生徒それぞれが部屋を無作為に1つ選んで入る。\\
・生徒全員が部屋に入ったら、各部屋の生徒の人数を確認する。\\
・生徒全員が部屋を出る。\\
・1人の生徒しかいない部屋があった場合、その部屋に入った生徒は\\
次回以降の試行に参加しない。\\
\end{array}
\right.$
$(\textrm{i})$4人の生徒が試行(*)を1回行ったとき、2回目の試行に参加する生徒が
3人になる確率は$\boxed{\ \ オ\ \ }$である。
$(\textrm{ii})$5人の生徒が試行(*)を続けて2回行ったとき、3回目の試行に参加する
生徒が2人になる確率は$\boxed{\ \ カ\ \ }$である。
2022慶應義塾大学薬学部過去問
福田の数学〜東京慈恵会医科大学2022年医学部第1問〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
袋Aには白玉2個、赤玉1個、袋Bには白玉1個、赤玉2個が入っている。
この状態から始めて、次の操作を繰り返し行う。
操作
① 袋A、袋Bから玉を1個ずつ取り出す。
② $(\textrm{i})$取り出した2個の玉の色が同じである場合は、取り出した玉を2個とも
袋Aに入れる。
$(\textrm{ii})$取り出した2個の玉の色が異なる場合は、袋Aから取り出した玉は袋B
に入れ、袋Bから取り出した玉は袋Aに入れる。
このとき、
・操作を2回繰り返した後に袋Aに入っている赤玉の個数が1個である確率は$\boxed{\ \ (ア)\ \ }$
・操作を3回繰り返した後に袋Aに入っている赤玉の個数が0個である確率は$\boxed{\ \ (イ)\ \ }$
である。
2022東京慈恵会医科大学医学部過去問
この動画を見る
袋Aには白玉2個、赤玉1個、袋Bには白玉1個、赤玉2個が入っている。
この状態から始めて、次の操作を繰り返し行う。
操作
① 袋A、袋Bから玉を1個ずつ取り出す。
② $(\textrm{i})$取り出した2個の玉の色が同じである場合は、取り出した玉を2個とも
袋Aに入れる。
$(\textrm{ii})$取り出した2個の玉の色が異なる場合は、袋Aから取り出した玉は袋B
に入れ、袋Bから取り出した玉は袋Aに入れる。
このとき、
・操作を2回繰り返した後に袋Aに入っている赤玉の個数が1個である確率は$\boxed{\ \ (ア)\ \ }$
・操作を3回繰り返した後に袋Aに入っている赤玉の個数が0個である確率は$\boxed{\ \ (イ)\ \ }$
である。
2022東京慈恵会医科大学医学部過去問
順天堂(医)確率 基本
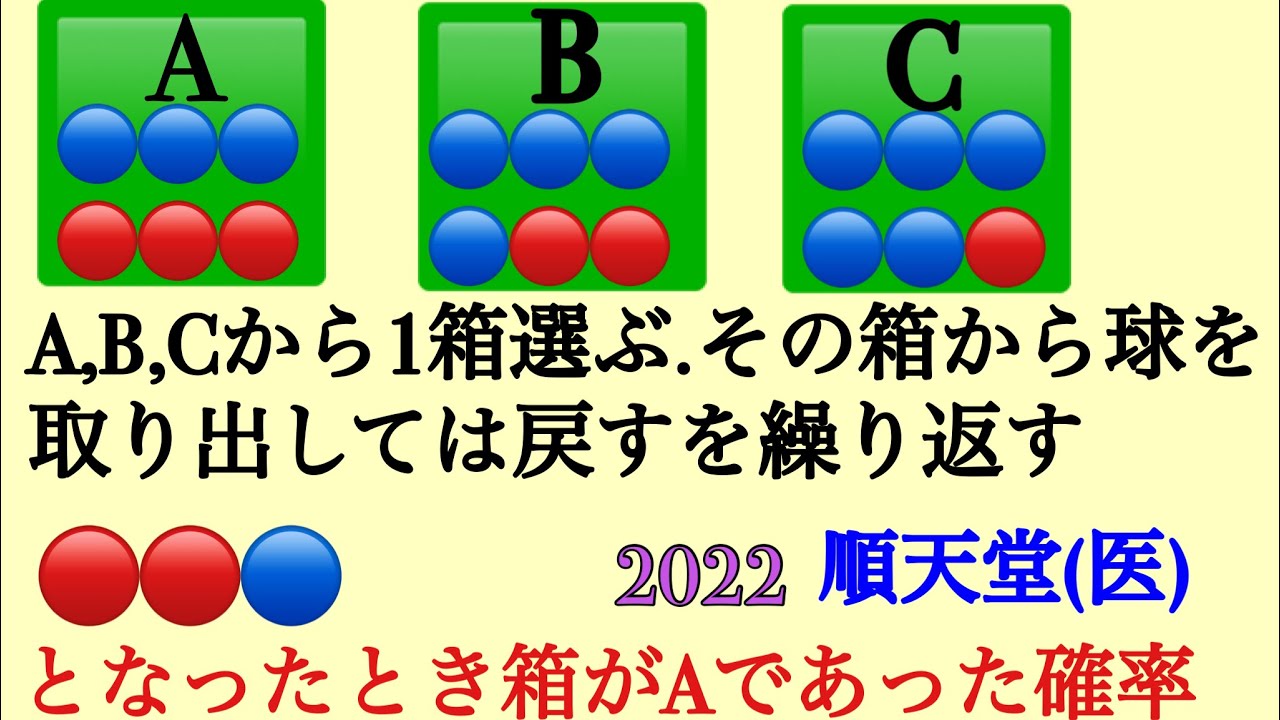
単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#順天堂大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
ある1つの箱から とり出して戻すを3回行ったら
●●○となった
箱がAである確率を求めよ
2022年順天堂医学大学 過去問
この動画を見る
ある1つの箱から とり出して戻すを3回行ったら
●●○となった
箱がAである確率を求めよ
2022年順天堂医学大学 過去問
2022近畿大(医)場合の数

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$人を区別のある 部屋に入れます。
0人部屋はダメ
(1)2部屋 (2)3部屋 (3)4部屋
何通りか求めよ。
2022年 近畿大学医学部 過去問
この動画を見る
$n$人を区別のある 部屋に入れます。
0人部屋はダメ
(1)2部屋 (2)3部屋 (3)4部屋
何通りか求めよ。
2022年 近畿大学医学部 過去問
