 数A
数A
 数A
数A
【数A】互除法 よりも mod ! ②演習編

福田の数学〜千葉大学2023年第2問〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 1個のさいころを投げて出た目によって得点を得るゲームを考える。出た目が1,2であれば得点は2、出た目が3であれば得点は1、出た目が4,5,6であれば得点は0とする。このゲームを$k$回繰り返すとき、得点の合計を$S_k$とする。
(1)$S_2$=3 となる確率を求めよ。
(2)$S_3$が奇数となる確率を求めよ。
(3)$S_4$≧$n$となる確率が$\frac{1}{9}$以下となる最小の整数$n$を求めよ。
この動画を見る
$\Large\boxed{2}$ 1個のさいころを投げて出た目によって得点を得るゲームを考える。出た目が1,2であれば得点は2、出た目が3であれば得点は1、出た目が4,5,6であれば得点は0とする。このゲームを$k$回繰り返すとき、得点の合計を$S_k$とする。
(1)$S_2$=3 となる確率を求めよ。
(2)$S_3$が奇数となる確率を求めよ。
(3)$S_4$≧$n$となる確率が$\frac{1}{9}$以下となる最小の整数$n$を求めよ。
【数A】互除法 よりも mod ! ①導入編

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$12x+7Y=1$ の特殊解を互除法とmodで計算していきます.
この動画を見る
$12x+7Y=1$ の特殊解を互除法とmodで計算していきます.
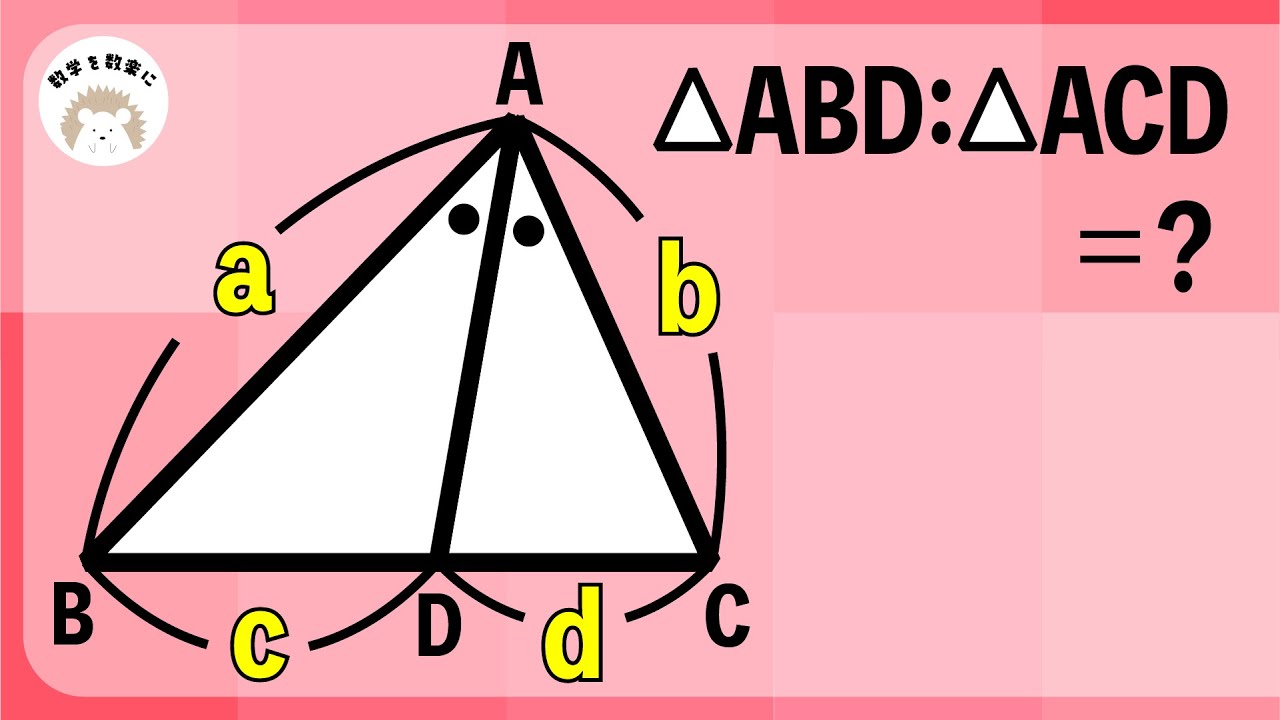
角の二等分線と面積比
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABD:△ACD=?
*図は動画内参照
この動画を見る
△ABD:△ACD=?
*図は動画内参照
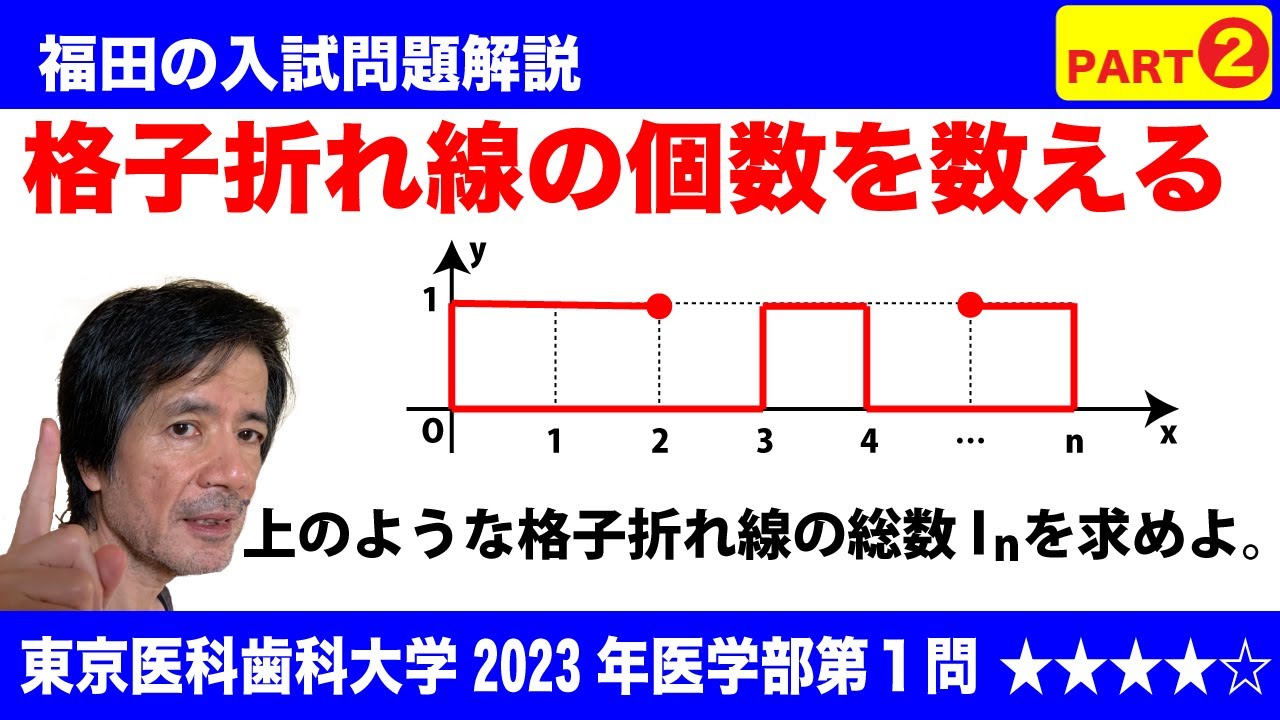
福田の数学〜東京医科歯科大学2023年医学部第1問PART2〜格子折れ線の個数を数える
単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ xy平面において、x座標およびy座標が共に整数であるような点を格子点と呼ぶ。xy平面上の相異なる2つの格子点を端点とする折れ線のうち、x座標またはy座標が等しい格子点どうしを結ぶ線分のみから構成され、かつ同じ点を2度通ることはないものを、格子折れ線と呼ぶ。ここで格子折れ線の向きは考慮せず、端点および通過する点がすべて等しい格子折れ線は同じものとする。また、自然数$n$に対し、
0≦$x$≦$n$ かつ 0≦$y$≦1
を満たす格子点全体の集合を$V_n$とする。さらに、$V_n$に属する格子点をすべて通り、かつ$V_n$に属さない格子点は通らない格子折れ線全体の集合を$L_n$とする。たとえば、7つの格子点(0,1),(0,0),(1,0),(1,1),(4,1),(4,0),(2,0)を順に結んだ折れ線は$L_4$に属する。このとき、以下の問いに答えよ。
(1)$L_1$および$L_2$に属する格子折れ線をすべて図示せよ。
(2)$L_4$に属する格子折れ線のうち、両端点の$x$座標の差が3以上となるものをすべて図示せよ。
(3)$n$≧3のとき、$L_n$に属する格子折れ線のうち、両端点の$x$座標の差が$n$-2となるものの個数を求めよ。
(4)$L_n$に属する格子折れ線の個数$l_n$を$n$を用いて表せ。
この動画を見る
$\Large\boxed{1}$ xy平面において、x座標およびy座標が共に整数であるような点を格子点と呼ぶ。xy平面上の相異なる2つの格子点を端点とする折れ線のうち、x座標またはy座標が等しい格子点どうしを結ぶ線分のみから構成され、かつ同じ点を2度通ることはないものを、格子折れ線と呼ぶ。ここで格子折れ線の向きは考慮せず、端点および通過する点がすべて等しい格子折れ線は同じものとする。また、自然数$n$に対し、
0≦$x$≦$n$ かつ 0≦$y$≦1
を満たす格子点全体の集合を$V_n$とする。さらに、$V_n$に属する格子点をすべて通り、かつ$V_n$に属さない格子点は通らない格子折れ線全体の集合を$L_n$とする。たとえば、7つの格子点(0,1),(0,0),(1,0),(1,1),(4,1),(4,0),(2,0)を順に結んだ折れ線は$L_4$に属する。このとき、以下の問いに答えよ。
(1)$L_1$および$L_2$に属する格子折れ線をすべて図示せよ。
(2)$L_4$に属する格子折れ線のうち、両端点の$x$座標の差が3以上となるものをすべて図示せよ。
(3)$n$≧3のとき、$L_n$に属する格子折れ線のうち、両端点の$x$座標の差が$n$-2となるものの個数を求めよ。
(4)$L_n$に属する格子折れ線の個数$l_n$を$n$を用いて表せ。
大阪公立大 フェルマーの小定理を利用した証明

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#大阪公立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023大阪公立大学過去問題
p素数 a,n自然数
$4n^2+4n-1=ap$なら
①2n+1とapは互いに素であることを示せ
②$2^{\frac{p-1}{2}}-1$はpで割り切れることを示せ
この動画を見る
2023大阪公立大学過去問題
p素数 a,n自然数
$4n^2+4n-1=ap$なら
①2n+1とapは互いに素であることを示せ
②$2^{\frac{p-1}{2}}-1$はpで割り切れることを示せ
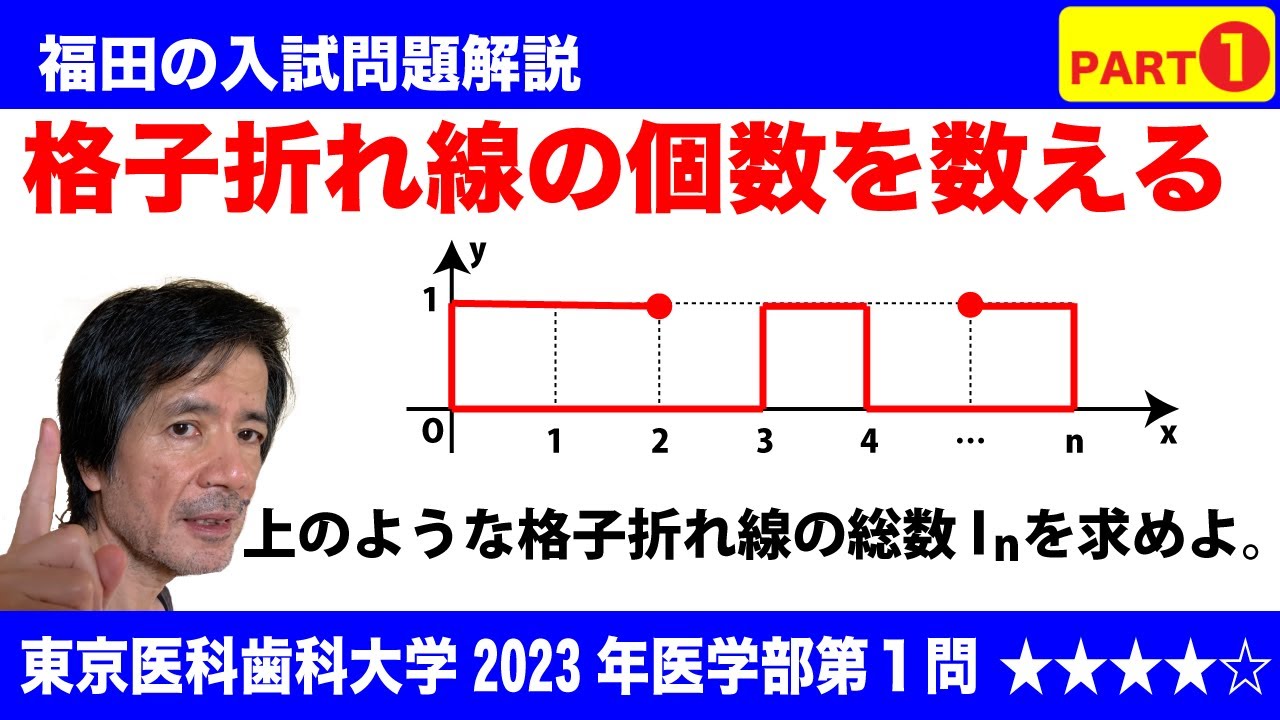
福田の数学〜東京医科歯科大学2023年医学部第1問PART1〜格子折れ線の個数を数える
単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ xy平面において、x座標およびy座標が共に整数であるような点を格子点と呼ぶ。xy平面上の相異なる2つの格子点を端点とする折れ線のうち、x座標またはy座標が等しい格子点どうしを結ぶ線分のみから構成され、かつ同じ点を2度通ることはないものを、格子折れ線と呼ぶ。ここで格子折れ線の向きは考慮せず、端点および通過する点がすべて等しい格子折れ線は同じものとする。また、自然数$n$に対し、
0≦$x$≦$n$ かつ 0≦$y$≦1
を満たす格子点全体の集合を$V_n$とする。さらに、$V_n$に属する格子点をすべて通り、かつ$V_n$に属さない格子点は通らない格子折れ線全体の集合を$L_n$とする。たとえば、7つの格子点(0,1),(0,0),(1,0),(1,1),(4,1),(4,0),(2,0)を順に結んだ折れ線は$L_4$に属する。このとき、以下の問いに答えよ。
(1)$L_1$および$L_2$に属する格子折れ線をすべて図示せよ。
(2)$L_4$に属する格子折れ線のうち、両端点の$x$座標の差が3以上となるものをすべて図示せよ。
(3)$n$≧3のとき、$L_n$に属する格子折れ線のうち、両端点の$x$座標の差が$n$-2となるものの個数を求めよ。
(4)$L_n$に属する格子折れ線の個数$l_n$を$n$を用いて表せ。
この動画を見る
$\Large\boxed{1}$ xy平面において、x座標およびy座標が共に整数であるような点を格子点と呼ぶ。xy平面上の相異なる2つの格子点を端点とする折れ線のうち、x座標またはy座標が等しい格子点どうしを結ぶ線分のみから構成され、かつ同じ点を2度通ることはないものを、格子折れ線と呼ぶ。ここで格子折れ線の向きは考慮せず、端点および通過する点がすべて等しい格子折れ線は同じものとする。また、自然数$n$に対し、
0≦$x$≦$n$ かつ 0≦$y$≦1
を満たす格子点全体の集合を$V_n$とする。さらに、$V_n$に属する格子点をすべて通り、かつ$V_n$に属さない格子点は通らない格子折れ線全体の集合を$L_n$とする。たとえば、7つの格子点(0,1),(0,0),(1,0),(1,1),(4,1),(4,0),(2,0)を順に結んだ折れ線は$L_4$に属する。このとき、以下の問いに答えよ。
(1)$L_1$および$L_2$に属する格子折れ線をすべて図示せよ。
(2)$L_4$に属する格子折れ線のうち、両端点の$x$座標の差が3以上となるものをすべて図示せよ。
(3)$n$≧3のとき、$L_n$に属する格子折れ線のうち、両端点の$x$座標の差が$n$-2となるものの個数を求めよ。
(4)$L_n$に属する格子折れ線の個数$l_n$を$n$を用いて表せ。
大阪公立大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#大阪公立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023大阪公立大学過去問題
n自然数
$a_n=\frac{5^{2^{n-1}}-1}{2^{n+1}}$
$b_n=\frac{a_{n+1}}{a_n}$
示せ
①$b_n$は整数
②$a_n$は整数
③$a_n$は奇数
この動画を見る
2023大阪公立大学過去問題
n自然数
$a_n=\frac{5^{2^{n-1}}-1}{2^{n+1}}$
$b_n=\frac{a_{n+1}}{a_n}$
示せ
①$b_n$は整数
②$a_n$は整数
③$a_n$は奇数
知っていれば一瞬だけど。。。法政大学高校

単元:
#数学(中学生)#数A#場合の数と確率#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
7個のみかんをA,B,Cの3人に分ける方法は何通り?
ただし、3人は少なくとも1個はもらえるものとする。
2023法政大学中学高等学校
この動画を見る
7個のみかんをA,B,Cの3人に分ける方法は何通り?
ただし、3人は少なくとも1個はもらえるものとする。
2023法政大学中学高等学校
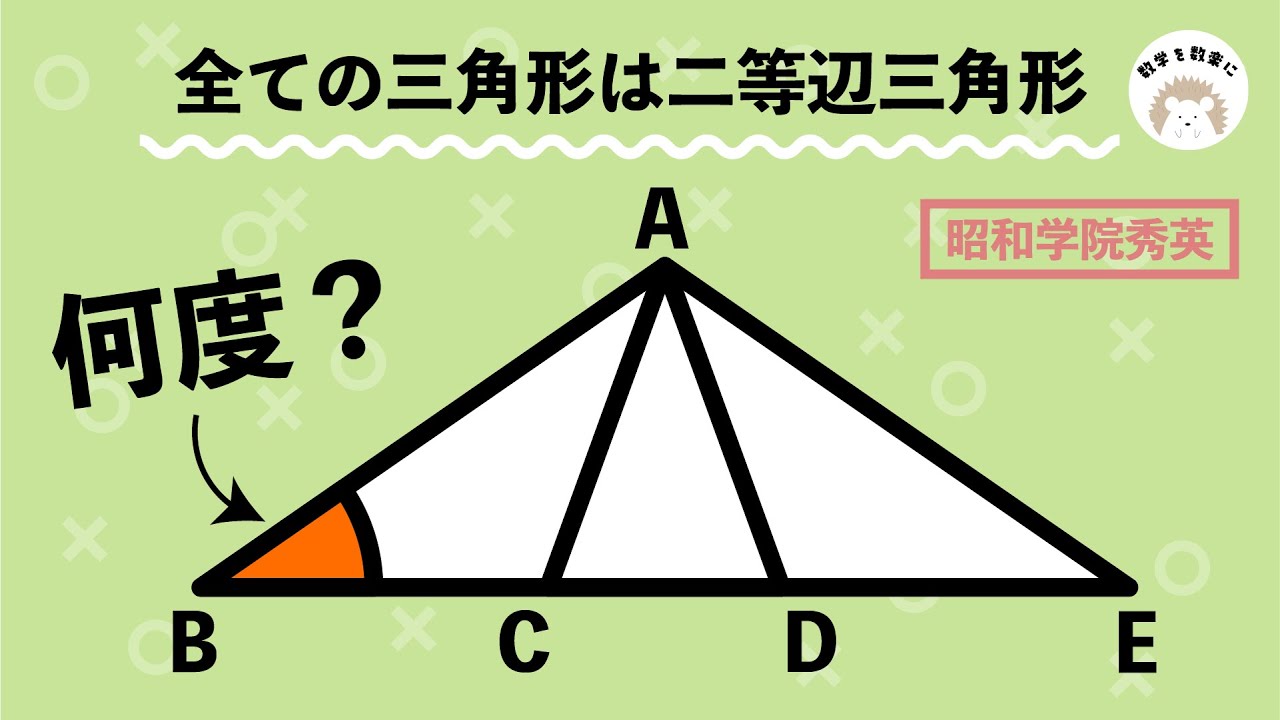
すべて二等辺三角形のときの角度 昭和学院秀英
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
全ての三角形は二等辺三角形
$\angle$B=?
*図は動画内参照
昭和学院秀英高等学校
この動画を見る
全ての三角形は二等辺三角形
$\angle$B=?
*図は動画内参照
昭和学院秀英高等学校
記数法の基本問題 京都府立大

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2020京都府立大学過去問題
$N = abc_{(5)}$
$= cba_{(6)}$
Nは十進法でいくつ?
この動画を見る
2020京都府立大学過去問題
$N = abc_{(5)}$
$= cba_{(6)}$
Nは十進法でいくつ?
補助線引けるかな?
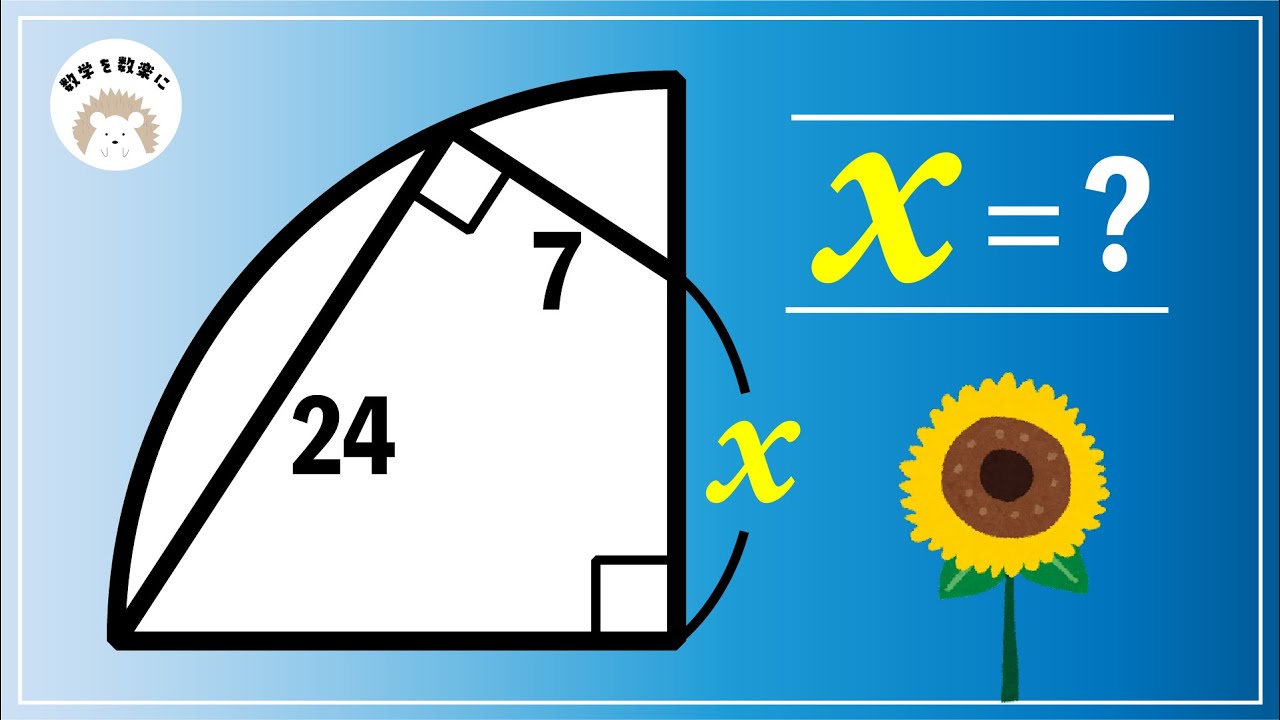
確率の基本問題 成蹊大

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023成蹊大学過去問題
5人で1回だけジャンケン、次の確率を求めよ.
①1人だけ勝つ確率
②2人だけ勝つ確率
③あいこの確率
この動画を見る
2023成蹊大学過去問題
5人で1回だけジャンケン、次の確率を求めよ.
①1人だけ勝つ確率
②2人だけ勝つ確率
③あいこの確率
高校入試だけど不定方程式 日大習志野

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$5x+3y=99$を満たす正の整数の組(x,y)は全部で何組ある?
日本大学習志野高等学校
この動画を見る
$5x+3y=99$を満たす正の整数の組(x,y)は全部で何組ある?
日本大学習志野高等学校
福田の数学〜立教大学2023年経済学部第1問(4)〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)大小2個のさいころを同時に投げる。大きいサイコロのでた目を$a$、小さいサイコロのでた目を$b$とするとき、$\displaystyle\frac{a}{b}$が整数になる確率は$\boxed{\ \ エ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (4)大小2個のさいころを同時に投げる。大きいサイコロのでた目を$a$、小さいサイコロのでた目を$b$とするとき、$\displaystyle\frac{a}{b}$が整数になる確率は$\boxed{\ \ エ\ \ }$である。
大阪市立大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#数B#大阪市立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
20216大阪市立大学過去問題
x,y整数 n自然数
$x^2+y^2$が$3^{2n-1}$の倍数ならx,yともに$3^n$の倍数であることを示せ
①n=1のとき
②n=2のとき
③すべての自然数n
この動画を見る
20216大阪市立大学過去問題
x,y整数 n自然数
$x^2+y^2$が$3^{2n-1}$の倍数ならx,yともに$3^n$の倍数であることを示せ
①n=1のとき
②n=2のとき
③すべての自然数n
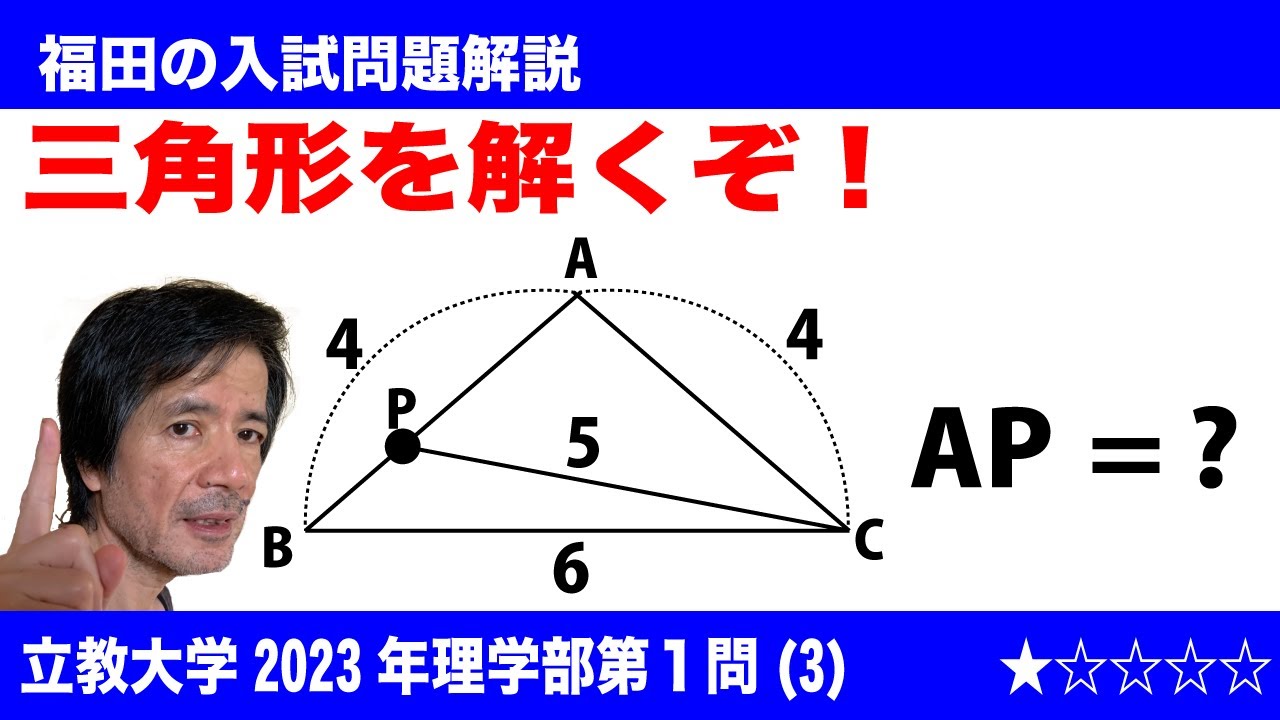
福田の数学〜立教大学2023年経済学部第1問(3)〜三角形を解く
単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)三角形ABCにおいてAB=AC=4, BC=6とする。AB上の点PがCP=5を満たすとき、AP=$\boxed{\ \ ウ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (3)三角形ABCにおいてAB=AC=4, BC=6とする。AB上の点PがCP=5を満たすとき、AP=$\boxed{\ \ ウ\ \ }$である。
難関中入試に出そうな問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
1×3×5×7・・・×999
=$3^nP(P\not\equiv 0 \mod 3)$
nの値を求めよ.
この動画を見る
1×3×5×7・・・×999
=$3^nP(P\not\equiv 0 \mod 3)$
nの値を求めよ.
ベン図おかしくね?

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ベン図に違和感を持つ人に対しての動画に関して解説していきます.
この動画を見る
ベン図に違和感を持つ人に対しての動画に関して解説していきます.
大阪市立大 奇数の平方の和

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B#大阪市立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2021大阪市立大学
nは奇数
$S_n=1+3+5+7+\cdots+n$
$T_n=1^2+3^2+5^2+7^2+\cdots+n^2$
①$S_n$,$T_n$をnの式で表せ
②$T_n$がnで割り切れるためのnの条件
この動画を見る
2021大阪市立大学
nは奇数
$S_n=1+3+5+7+\cdots+n$
$T_n=1^2+3^2+5^2+7^2+\cdots+n^2$
①$S_n$,$T_n$をnの式で表せ
②$T_n$がnで割り切れるためのnの条件
円錐の展開図から体積を求める(高校受験数学)

ナイスな整数問題 富山大

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023富山大学
z整数,n自然数
$z^{3^{n}}-z^{3^{n-1}}$は$3^n$の倍数である。を次の場合で示せ
①n=1
②n=2
③すべてのn
この動画を見る
2023富山大学
z整数,n自然数
$z^{3^{n}}-z^{3^{n-1}}$は$3^n$の倍数である。を次の場合で示せ
①n=1
②n=2
③すべてのn
2人だけ隣り合う並び方 京都産業大

単元:
#数A#大学入試過去問(数学)#場合の数と確率#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
男子3人、女子3人の合わせて6人が1列に並ぶとき、女子のうち2人だけが隣り合う並び方は何通り?
京都産業大学附属中学校・高等学校
この動画を見る
男子3人、女子3人の合わせて6人が1列に並ぶとき、女子のうち2人だけが隣り合う並び方は何通り?
京都産業大学附属中学校・高等学校
ダブル直角!!
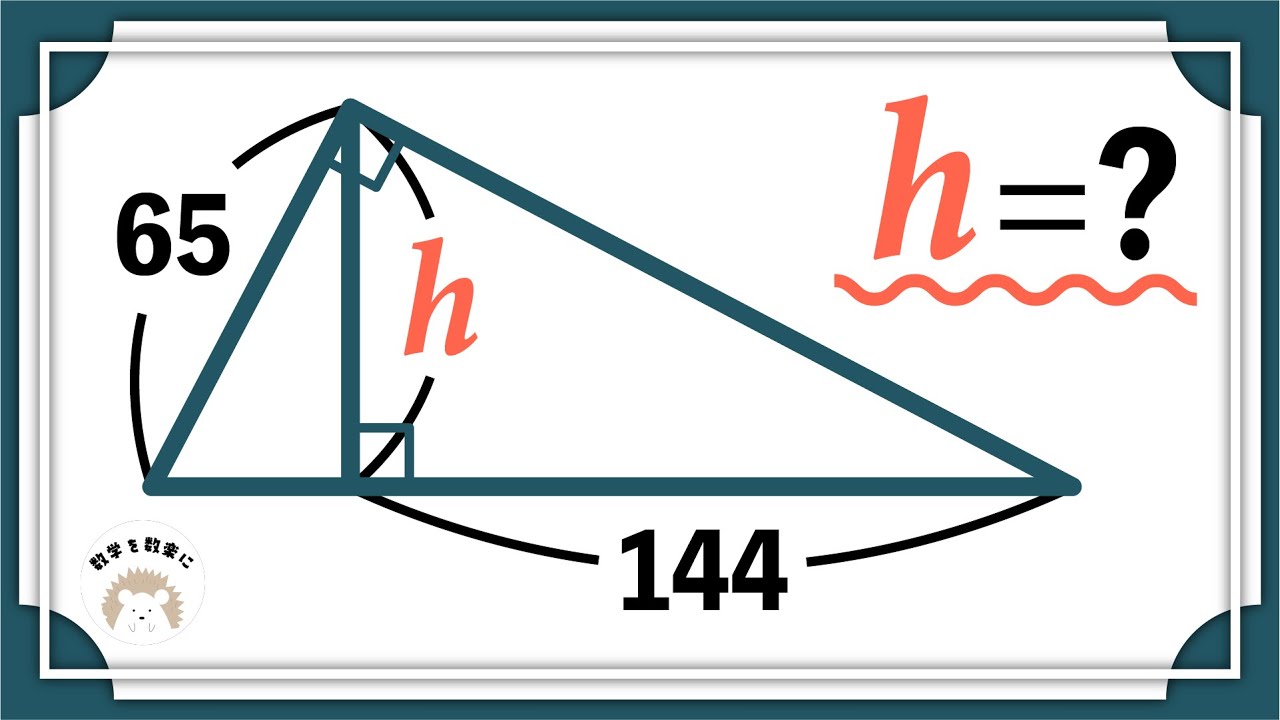
福田の数学〜立教大学2023年理学部第1問(5)〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (5)表の出る確率が$\frac{2}{3}$、裏の出る確率が$\frac{1}{3}$のコインを投げて、表が出たら+1点を加え、裏が出たら-1点を加える。というルールのゲームを行う。
0点から初めて5回コインを投げ終わった時、得点が3点以上となる確率は$\boxed{\ \ オ\ \ }$である。
2023立教大学理学部過去問
この動画を見る
$\Large\boxed{1}$ (5)表の出る確率が$\frac{2}{3}$、裏の出る確率が$\frac{1}{3}$のコインを投げて、表が出たら+1点を加え、裏が出たら-1点を加える。というルールのゲームを行う。
0点から初めて5回コインを投げ終わった時、得点が3点以上となる確率は$\boxed{\ \ オ\ \ }$である。
2023立教大学理学部過去問
補助線を引くか引かないか
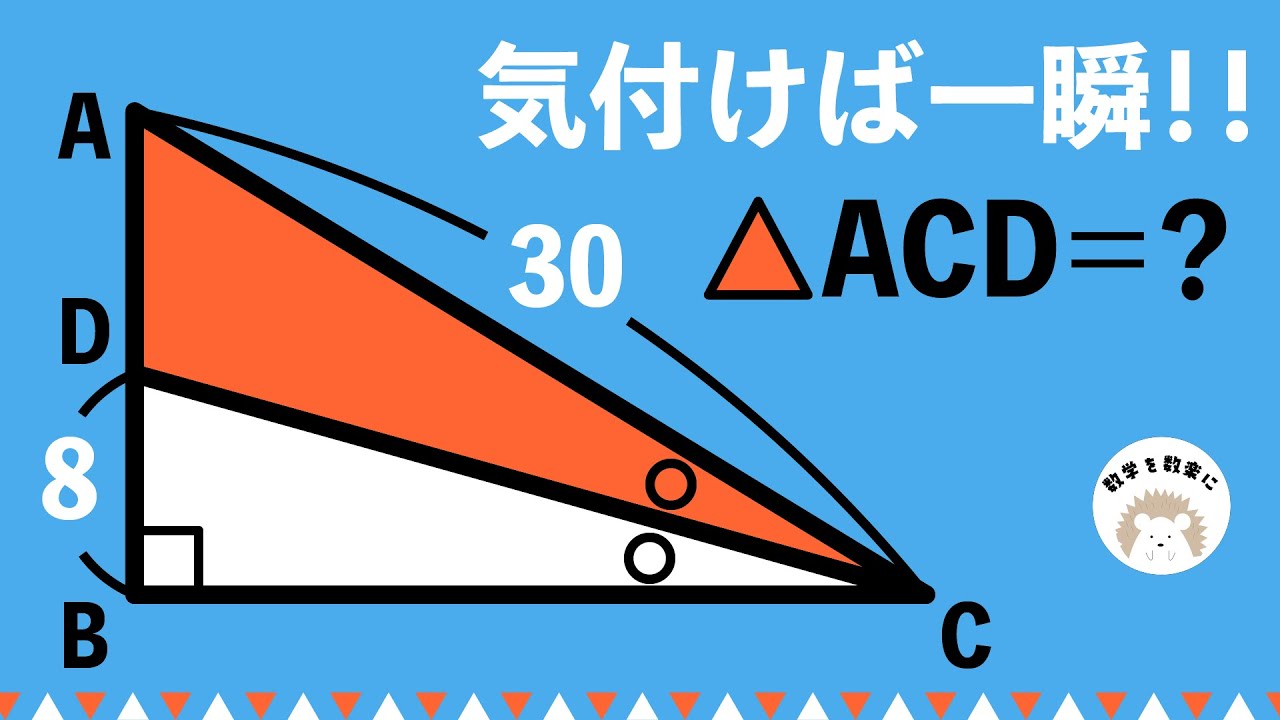
図形の折り返し
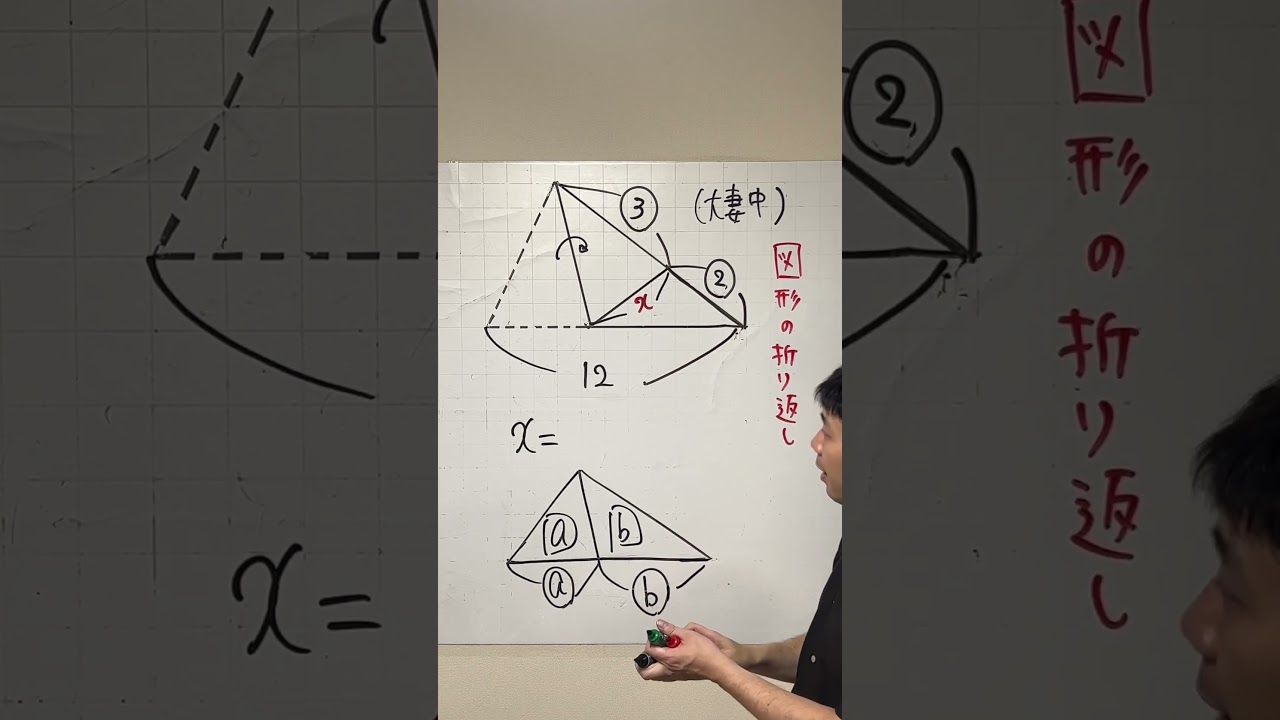
図形の折り返し 大妻中 中学受験算数
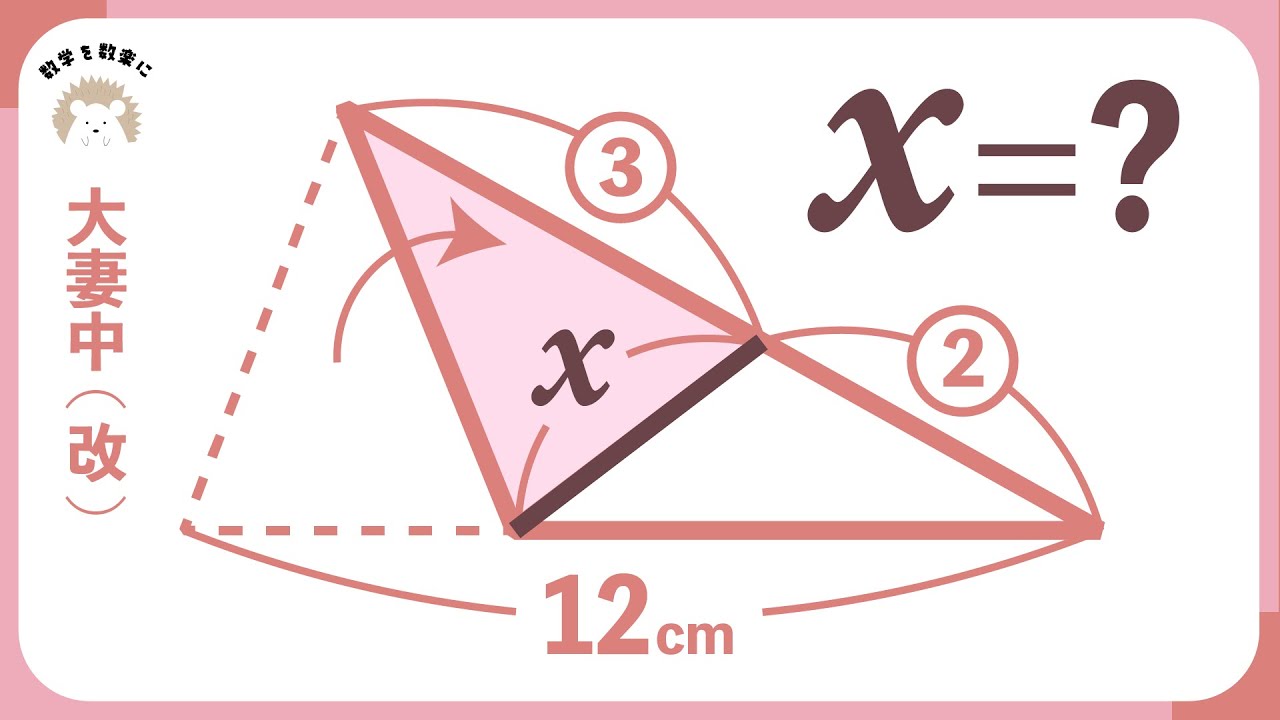
大学生が解けない小学生の問題
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
大学生が解けない小学生の問題を解説していきいます.
この動画を見る
大学生が解けない小学生の問題を解説していきいます.
福田の数学〜筑波大学2023年理系第3問〜球面に内接する四面体

単元:
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)#筑波大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標空間内の原点Oを中心とする半径$r$の球面S上に4つの頂点がある四面体ABCDが
$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$+$\overrightarrow{OD}$=$\overrightarrow{0}$
を満たしているとする。また三角形ABCの重心をGとする。
(1)$\overrightarrow{OG}$を$\overrightarrow{OD}$を用いて表せ。
(2)$\overrightarrow{OA}$・$\overrightarrow{OB}$+$\overrightarrow{OB}$・$\overrightarrow{OC}$+$\overrightarrow{OC}$・$\overrightarrow{OA}$を$r$を用いて表せ。
(3)点Pが球面S上を動くとき、$\overrightarrow{PA}$・$\overrightarrow{PB}$+$\overrightarrow{PB}$・$\overrightarrow{PC}$+$\overrightarrow{PC}$・$\overrightarrow{PA}$の最大値を$r$を用いて表せ。さらに、最大値をとるときの点Pに対して、|$\overrightarrow{PG}$|を$r$を用いて表せ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{3}$ 座標空間内の原点Oを中心とする半径$r$の球面S上に4つの頂点がある四面体ABCDが
$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$+$\overrightarrow{OD}$=$\overrightarrow{0}$
を満たしているとする。また三角形ABCの重心をGとする。
(1)$\overrightarrow{OG}$を$\overrightarrow{OD}$を用いて表せ。
(2)$\overrightarrow{OA}$・$\overrightarrow{OB}$+$\overrightarrow{OB}$・$\overrightarrow{OC}$+$\overrightarrow{OC}$・$\overrightarrow{OA}$を$r$を用いて表せ。
(3)点Pが球面S上を動くとき、$\overrightarrow{PA}$・$\overrightarrow{PB}$+$\overrightarrow{PB}$・$\overrightarrow{PC}$+$\overrightarrow{PC}$・$\overrightarrow{PA}$の最大値を$r$を用いて表せ。さらに、最大値をとるときの点Pに対して、|$\overrightarrow{PG}$|を$r$を用いて表せ。
2023筑波大学理系過去問
