 数A
数A
 数A
数A
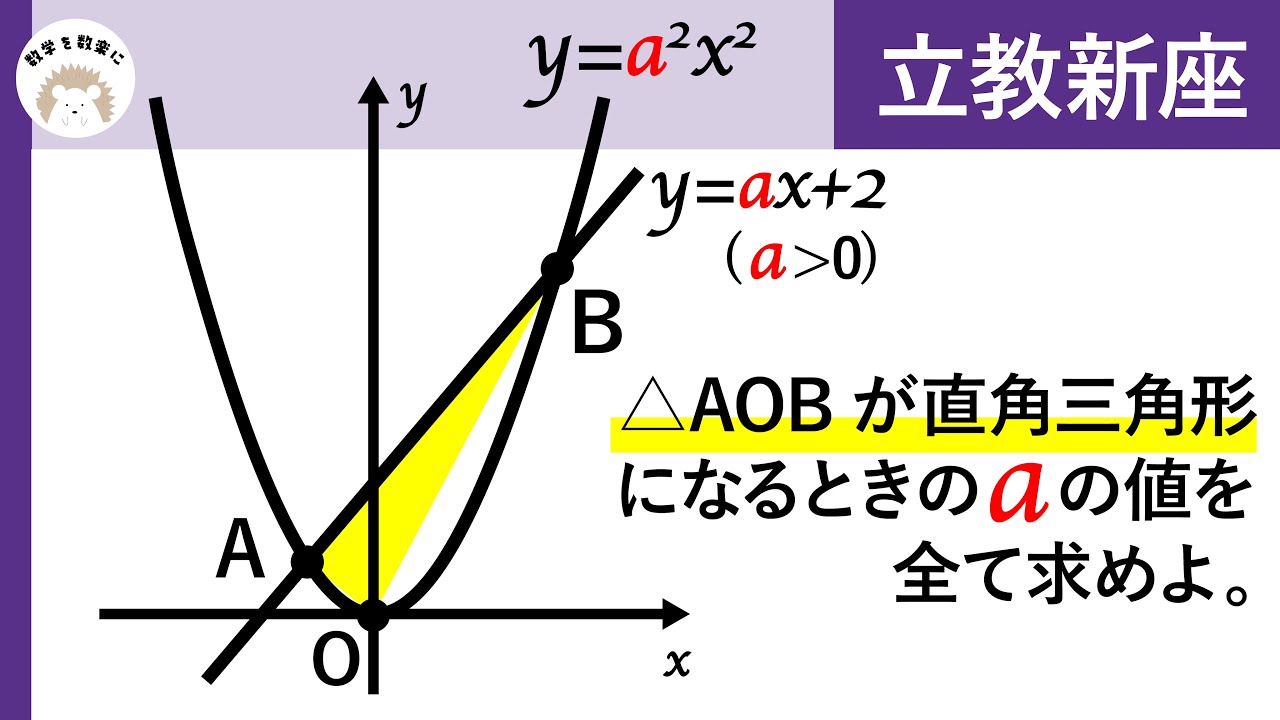
座標平面上の直角三角形 立教新座
単元:
#数学(中学生)#中3数学#数A#図形の性質#2次関数#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△AOBが直角三角形になるときのaの値を全て求めよ。
*図は動画内参照
立教新座高等学校
この動画を見る
△AOBが直角三角形になるときのaの値を全て求めよ。
*図は動画内参照
立教新座高等学校
整数問題!地味に難しいです【大阪医科薬科大学】【数学 入試問題】

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
自然数$x,y$に対する方程式$3^x-2^y=1$を考える。
(1)y≧2に対し解$x$が存在するならば,$x$は偶数であることを示せ。
(2)上の方程式を満たす自然数$x,y$の組をすべて求めよ。
大阪医科歯科大過去問
この動画を見る
自然数$x,y$に対する方程式$3^x-2^y=1$を考える。
(1)y≧2に対し解$x$が存在するならば,$x$は偶数であることを示せ。
(2)上の方程式を満たす自然数$x,y$の組をすべて求めよ。
大阪医科歯科大過去問
【高校数学あるある】よく見る問題!下4桁を求めよ! #Shorts

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$99^{99}$の下4桁を求めよ。
この動画を見る
$99^{99}$の下4桁を求めよ。
角の三等分
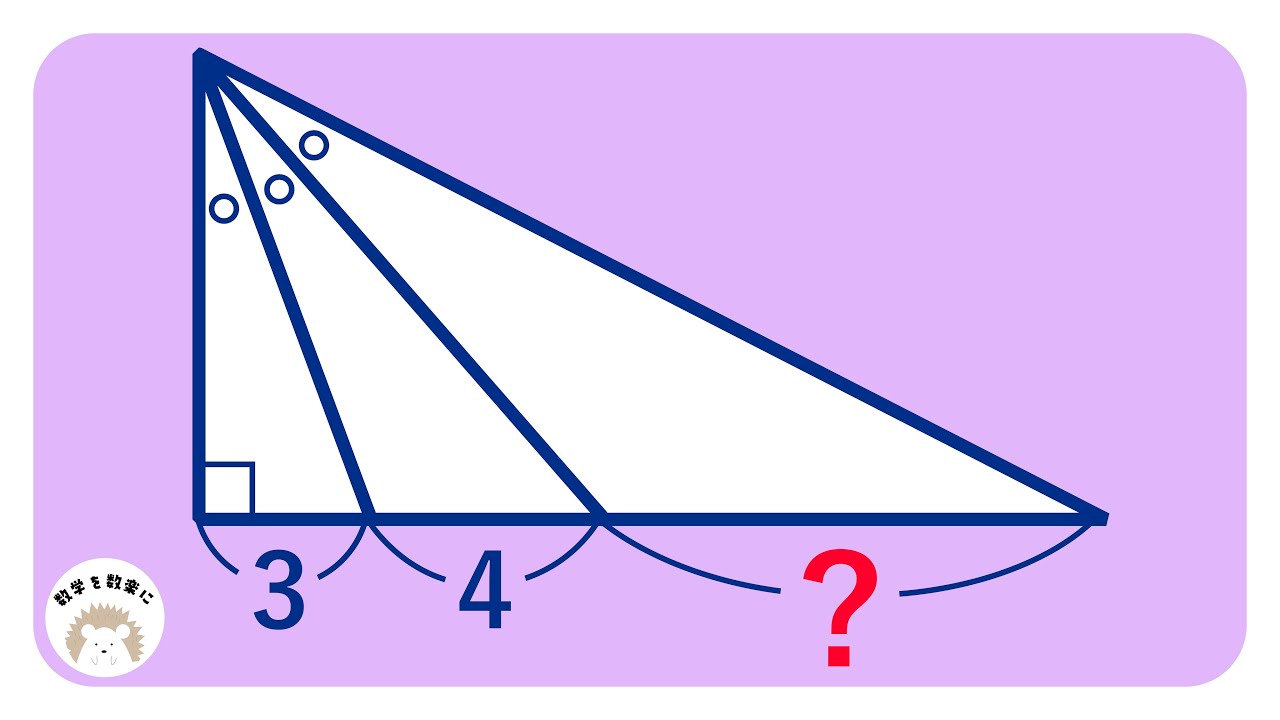
福田の数学〜明治大学2022年全学部統一入試12AB第1問(4)〜角の二等分線と辺の長さの軽量

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(4)三角形$ABC$の$\angle A$の二等分線と辺$BC$との交点をDとする。
$AB=8,\ AC=3,\ AD=4$とするとき、
$BD:CD=\boxed{\ \ ソ\ \ }:\boxed{\ \ タ\ \ }$であり、
$BC=\frac{\boxed{\ \ チツ\ \ }\sqrt{\boxed{\ \ テ\ \ }}}{\boxed{\ \ ト\ \ }}$である。
2022明治大学全統過去問
この動画を見る
(4)三角形$ABC$の$\angle A$の二等分線と辺$BC$との交点をDとする。
$AB=8,\ AC=3,\ AD=4$とするとき、
$BD:CD=\boxed{\ \ ソ\ \ }:\boxed{\ \ タ\ \ }$であり、
$BC=\frac{\boxed{\ \ チツ\ \ }\sqrt{\boxed{\ \ テ\ \ }}}{\boxed{\ \ ト\ \ }}$である。
2022明治大学全統過去問
【高校数学】n進法のかけ算割り算をどこよりも丁寧に 5-13【数学A】

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
かけ算
(1)$1011_{(2)}\times1101_{(2)}$ (2)$203_{(4)}\times12_{(4)}$
割り算
(1)$101001101_{(2)}\div1001_{(2)}$ (2)$1542_{(7)}\div36_{(7)}$
この動画を見る
かけ算
(1)$1011_{(2)}\times1101_{(2)}$ (2)$203_{(4)}\times12_{(4)}$
割り算
(1)$101001101_{(2)}\div1001_{(2)}$ (2)$1542_{(7)}\div36_{(7)}$
手強いよ。角度を求める問題。
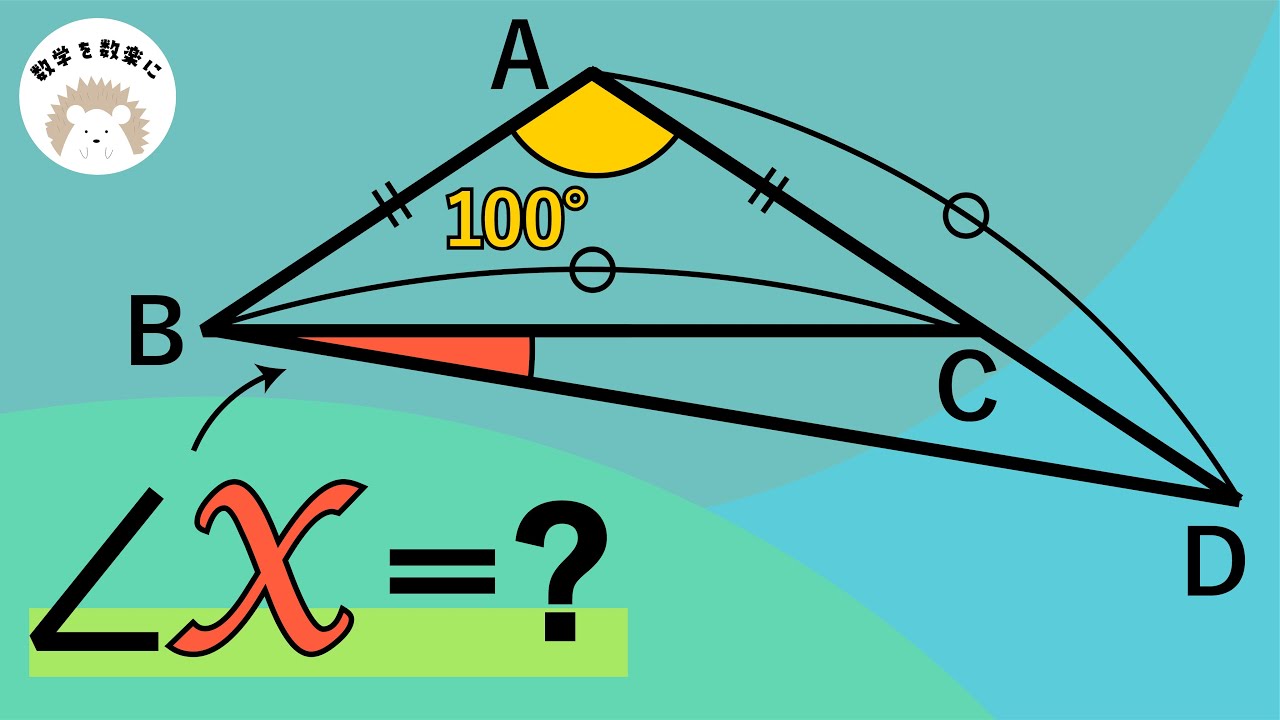
福田の数学〜明治大学2022年全学部統一入試12AB第1問(3)〜隣り合わない重複順列

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(3)4個の文字$A,B,C,D$から重複を許して5個取り出して1列に並べる。
このとき、AとBが隣り合わず、CとDが隣り合わないような並べ方は$\boxed{\ \ シスセ\ \ }$通りある。
2022明治大学全統過去問
この動画を見る
(3)4個の文字$A,B,C,D$から重複を許して5個取り出して1列に並べる。
このとき、AとBが隣り合わず、CとDが隣り合わないような並べ方は$\boxed{\ \ シスセ\ \ }$通りある。
2022明治大学全統過去問
見える人には〇〇が見える
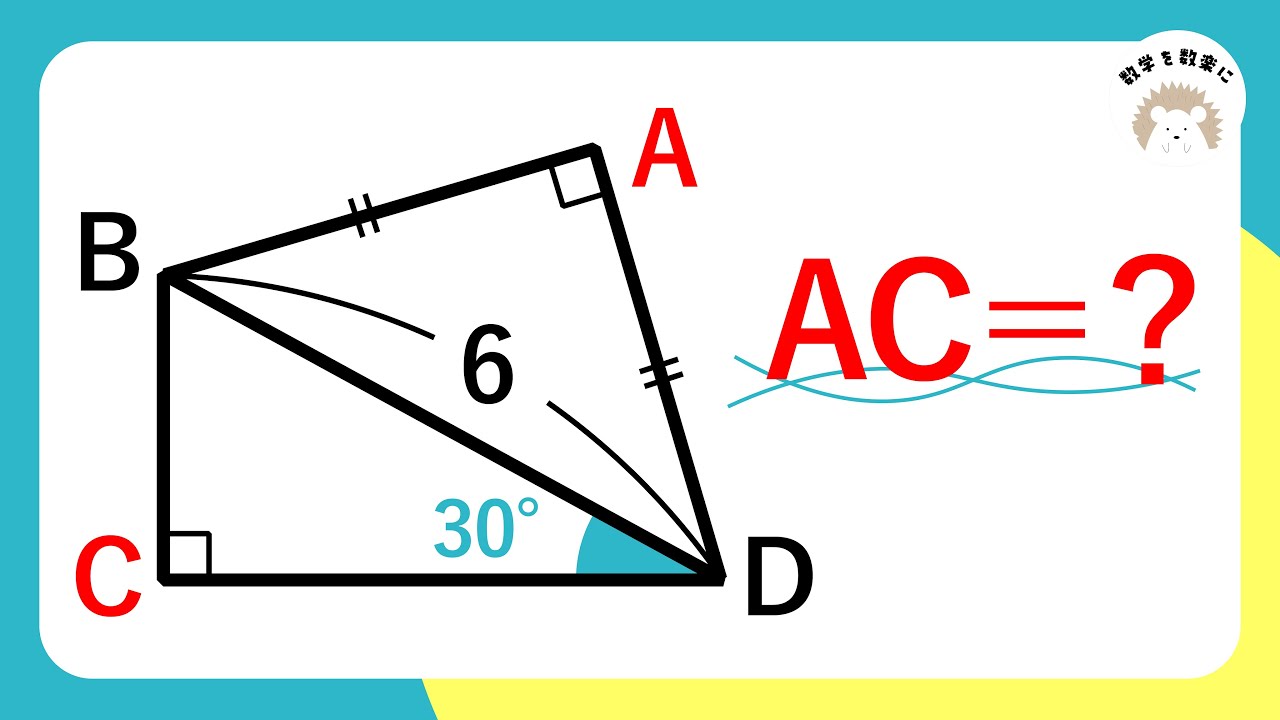
福田の数学〜早稲田大学2022年社会科学部第3問〜整式の割り算の余りの問題

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
整式$P(x)$を$x-1$で割ると1余り、$(x+1)^2$で割ると$3x+2$余る。
このとき、次の問いに答えよ。
(1)$P(x)$を$x+1$で割った時の余りを求めよ。
(2)$P(x)$を$(x-1)(x+1)$で割った時の余りを求めよ。
(3)$P(x)$を$(x-1)(x+1)^2$で割った時の余りを求めよ。
2022早稲田大学社会科学部過去問
この動画を見る
整式$P(x)$を$x-1$で割ると1余り、$(x+1)^2$で割ると$3x+2$余る。
このとき、次の問いに答えよ。
(1)$P(x)$を$x+1$で割った時の余りを求めよ。
(2)$P(x)$を$(x-1)(x+1)$で割った時の余りを求めよ。
(3)$P(x)$を$(x-1)(x+1)^2$で割った時の余りを求めよ。
2022早稲田大学社会科学部過去問
階乗の虫食い算

仙台育英 正四面体の内接球の半径

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
内接球の半径=?
*図は動画内参照
仙台育英学園高等学校
この動画を見る
内接球の半径=?
*図は動画内参照
仙台育英学園高等学校
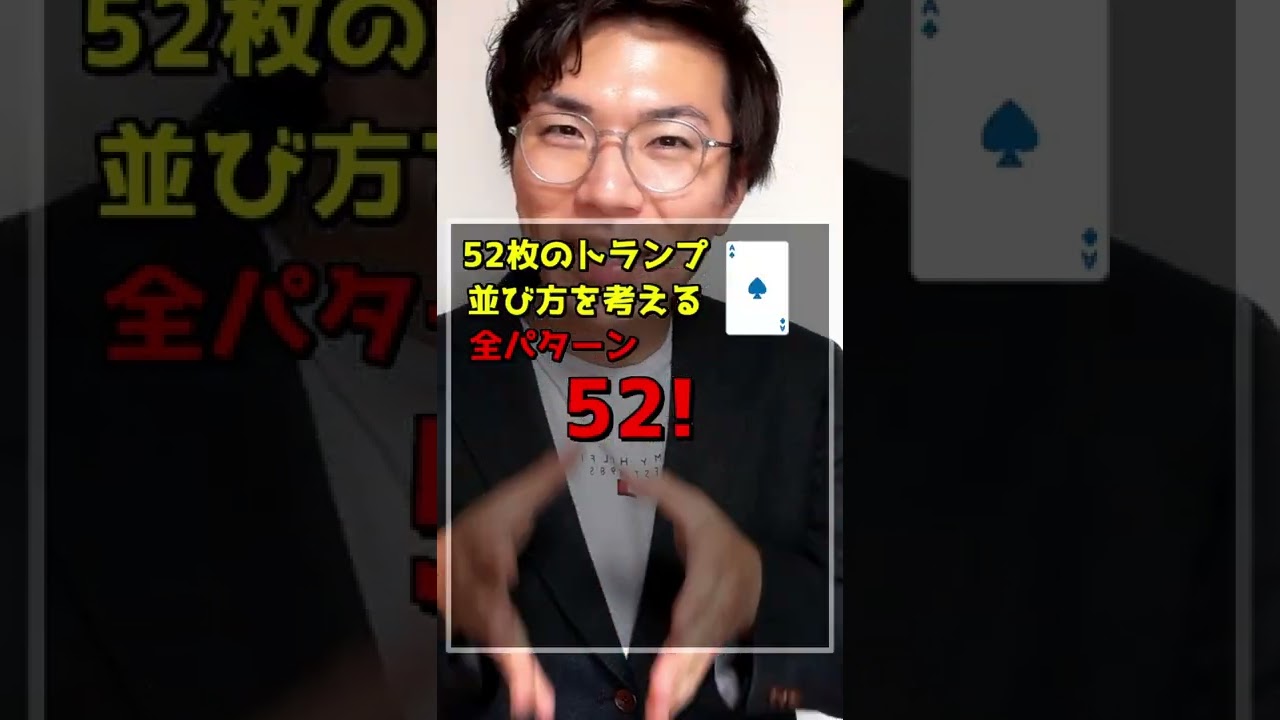
トランプシャッフルして,元に戻る確率は?
単元:
#数A#場合の数と確率#場合の数#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
トランプを適当にシャッフルしてA~Kまで52枚全部順番で揃う確率はどのくらいですか?
この動画を見る
下記質問の解説動画です
トランプを適当にシャッフルしてA~Kまで52枚全部順番で揃う確率はどのくらいですか?
福田の数学〜早稲田大学2022年社会科学部第2問〜平面幾何と3次関数の増減

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$AB=AC=1,\ BC=a$の二等辺三角形$ABC$の内接円を$I$、外接円を$O$とする。
ただし、$0 \lt a \lt \sqrt2$ である。また、三角形$ABC$と円$I$の3つの接点を頂点とする
三角形を$T$、3点$A,\ B,\ C$で円$O$に外接する三角形を$U$とする。次の問いに答えよ。
(1)三角形$T$の、$BC$に平行な辺の長さ$t$を$a$で表せ。
(2)三角形$U$の、$BC$に平行な辺の長さ$u$を$a$で表せ。
(3)$\frac{t}{u}=p$とする。$p$が最大となる$a$の値と、そのときの$p$の値を求めよ。
2022早稲田大学社会科学部過去問
この動画を見る
$AB=AC=1,\ BC=a$の二等辺三角形$ABC$の内接円を$I$、外接円を$O$とする。
ただし、$0 \lt a \lt \sqrt2$ である。また、三角形$ABC$と円$I$の3つの接点を頂点とする
三角形を$T$、3点$A,\ B,\ C$で円$O$に外接する三角形を$U$とする。次の問いに答えよ。
(1)三角形$T$の、$BC$に平行な辺の長さ$t$を$a$で表せ。
(2)三角形$U$の、$BC$に平行な辺の長さ$u$を$a$で表せ。
(3)$\frac{t}{u}=p$とする。$p$が最大となる$a$の値と、そのときの$p$の値を求めよ。
2022早稲田大学社会科学部過去問
整数問題 基本

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2P^4-P^2+16$が平方数となるような素数$P$をすべて求めよ.
この動画を見る
$2P^4-P^2+16$が平方数となるような素数$P$をすべて求めよ.
福田の数学〜早稲田大学2022年社会科学部第1問〜条件付き確率と大小比較

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
ある国の国民がある病気に罹患している確率を$p$とする。
その病気の検査において、罹患者が陽性と判定される確率を$q$,
非罹患者が陽性と判定される確率を$r$とする。ただし$0 \lt p \lt 1,\ 0 \lt r \lt q$である。
さらに、検査で陽性と判定された人が罹患している確率を$s$とする。次の問いに答えよ。
(1)$s$を$p,\ q,\ r$を用いて表せ。
(2)$k$回すべて陽性と判定されれば最終的に陽性と判断される場合、最終的に陽性
と判断された人が罹患している確率を$a_k$とする。$a_k$を$p,q,r,k$を用いて表せ。
(3)$k$回のうち1回でも陽性と判定されれば最終的に陽性と判断される場合、
最終的に陽性と判断された人が罹患している確率を$b_k$とする。$b_k$を$p,q,r,k$を用いて表せ。
(4)$s,\ a_2,\ b_2$の大小関係を示せ。
2022早稲田大学社会科学部過去問
この動画を見る
ある国の国民がある病気に罹患している確率を$p$とする。
その病気の検査において、罹患者が陽性と判定される確率を$q$,
非罹患者が陽性と判定される確率を$r$とする。ただし$0 \lt p \lt 1,\ 0 \lt r \lt q$である。
さらに、検査で陽性と判定された人が罹患している確率を$s$とする。次の問いに答えよ。
(1)$s$を$p,\ q,\ r$を用いて表せ。
(2)$k$回すべて陽性と判定されれば最終的に陽性と判断される場合、最終的に陽性
と判断された人が罹患している確率を$a_k$とする。$a_k$を$p,q,r,k$を用いて表せ。
(3)$k$回のうち1回でも陽性と判定されれば最終的に陽性と判断される場合、
最終的に陽性と判断された人が罹患している確率を$b_k$とする。$b_k$を$p,q,r,k$を用いて表せ。
(4)$s,\ a_2,\ b_2$の大小関係を示せ。
2022早稲田大学社会科学部過去問
福田の数学〜早稲田大学2022年商学部第3問〜空間図形の計量

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と方程式#三角関数#円と方程式#加法定理とその応用#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標空間において、2つの円$C_1,\ C_2$を
$C_1=\left\{(x,y,0)\ | \ x^2+y^2=1\right\},\ C_2=\left\{(0,y,z)\ | \ (y-1)^2+z^2=1\right\}$
とする。次の設問に答えよ。
(1)$C_1$上の2点と$C_2$上の点(0,1,1)を頂点とする正三角形を考える。
このような正三角形の一辺の長さをすべて求めよ。
(2)すべての頂点がC_1∪C_2上にある正四面体を考える。
このような正四面体の一辺の長さをすべて求めよ。
2022早稲田大学商学部過去問
この動画を見る
座標空間において、2つの円$C_1,\ C_2$を
$C_1=\left\{(x,y,0)\ | \ x^2+y^2=1\right\},\ C_2=\left\{(0,y,z)\ | \ (y-1)^2+z^2=1\right\}$
とする。次の設問に答えよ。
(1)$C_1$上の2点と$C_2$上の点(0,1,1)を頂点とする正三角形を考える。
このような正三角形の一辺の長さをすべて求めよ。
(2)すべての頂点がC_1∪C_2上にある正四面体を考える。
このような正四面体の一辺の長さをすべて求めよ。
2022早稲田大学商学部過去問
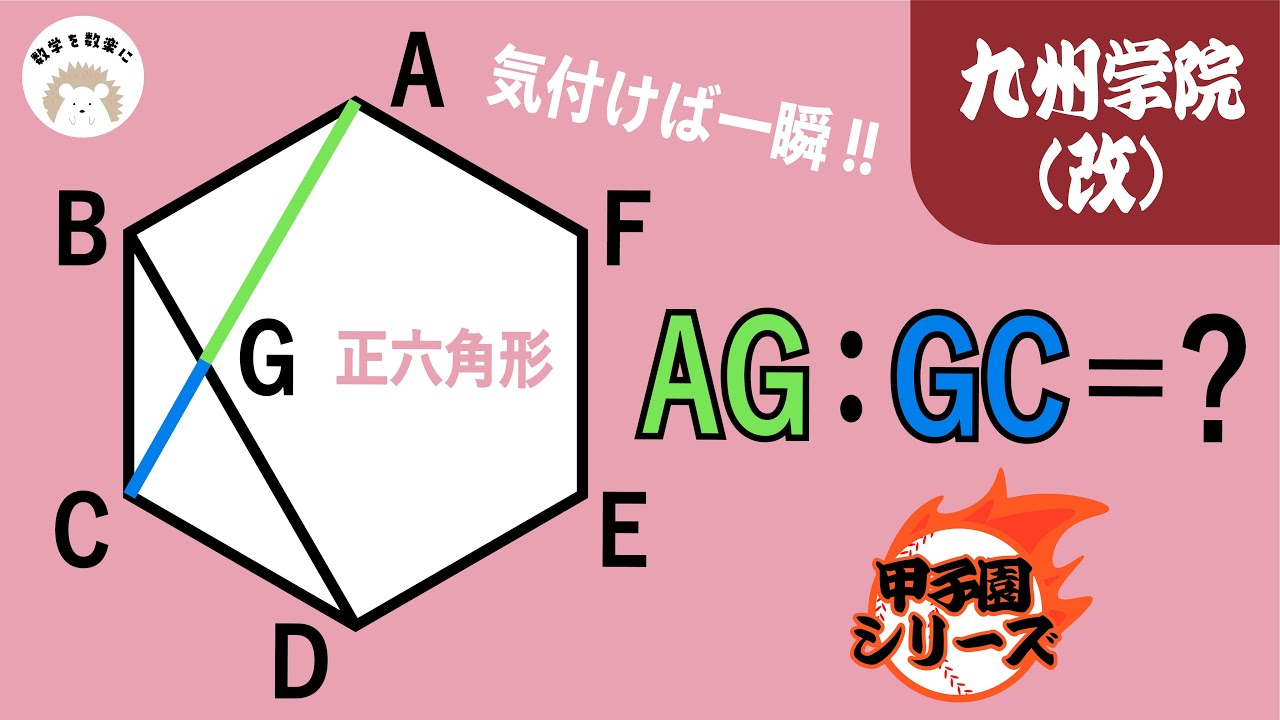
気付けば一瞬!! 正六角形 九州学院(熊本)
単元:
#数学(中学生)#数Ⅰ#数A#図形の性質#図形と計量#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AG:GC=?
*図は動画内参照
九州学院高等学校(改)
この動画を見る
AG:GC=?
*図は動画内参照
九州学院高等学校(改)
福田の数学〜早稲田大学2022年商学部第2問〜ベクトルに序列を定義して数える

単元:
#数A#大学入試過去問(数学)#場合の数と確率#空間ベクトル#場合の数#空間ベクトル#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
空間ベクトルに対し、次の関係を定める。
$\overrightarrow{ a }=(a_1,a_2,a_3)$と$\overrightarrow{ b }=(b_1,b_2,b_3)$が、
次の$(\textrm{i}),(\textrm{ii}),(\textrm{iii})$のいずれかを
満たしているとき$\overrightarrow{ a }$は$\overrightarrow{ b }$より前であるといい、
$\overrightarrow{ a }≺ \overrightarrow{ b }$と表す。
$(\textrm{i})a_1 \lt b_1\ \ \ (\textrm{ii})a_1=b_1$かつ
$a_2 \lt b_2\ \ \ (\textrm{iii})a_1=b_1$かつ$a_2=b_2$かつ$a_3 \lt b_3$
空間ベクトルの集合$P=\left{{(x,y,z) | x,y,zは0以上7以下の整数\right}$の要素を
前から順に$\overrightarrow{ p_1 },\overrightarrow{ p_2 },\ldots,\overrightarrow{ p_m }$とする。
ここで、mはPに含まれる要素の総数を表す。
つまり、$P=\left\{\overrightarrow{ p_1 },\overrightarrow{ p_2 },\ldots,\overrightarrow{ p_m }\right\}$であり、
$\overrightarrow{ p_n }≺ \overrightarrow{ p_{n+1} }(n=1,2,\ldots,m-1)$
を満たしている。次の各設問に答えよ。
(1)$\overrightarrow{ p_{67} }$を求めよ。
(2)集合$\left\{n\ \ \ | \ \overrightarrow{ p_n }∟(1,0,-2)\right\}$の要素のうちで最大のものを求めよ。
2022早稲田大学商学部過去問
この動画を見る
空間ベクトルに対し、次の関係を定める。
$\overrightarrow{ a }=(a_1,a_2,a_3)$と$\overrightarrow{ b }=(b_1,b_2,b_3)$が、
次の$(\textrm{i}),(\textrm{ii}),(\textrm{iii})$のいずれかを
満たしているとき$\overrightarrow{ a }$は$\overrightarrow{ b }$より前であるといい、
$\overrightarrow{ a }≺ \overrightarrow{ b }$と表す。
$(\textrm{i})a_1 \lt b_1\ \ \ (\textrm{ii})a_1=b_1$かつ
$a_2 \lt b_2\ \ \ (\textrm{iii})a_1=b_1$かつ$a_2=b_2$かつ$a_3 \lt b_3$
空間ベクトルの集合$P=\left{{(x,y,z) | x,y,zは0以上7以下の整数\right}$の要素を
前から順に$\overrightarrow{ p_1 },\overrightarrow{ p_2 },\ldots,\overrightarrow{ p_m }$とする。
ここで、mはPに含まれる要素の総数を表す。
つまり、$P=\left\{\overrightarrow{ p_1 },\overrightarrow{ p_2 },\ldots,\overrightarrow{ p_m }\right\}$であり、
$\overrightarrow{ p_n }≺ \overrightarrow{ p_{n+1} }(n=1,2,\ldots,m-1)$
を満たしている。次の各設問に答えよ。
(1)$\overrightarrow{ p_{67} }$を求めよ。
(2)集合$\left\{n\ \ \ | \ \overrightarrow{ p_n }∟(1,0,-2)\right\}$の要素のうちで最大のものを求めよ。
2022早稲田大学商学部過去問
特殊な方程式

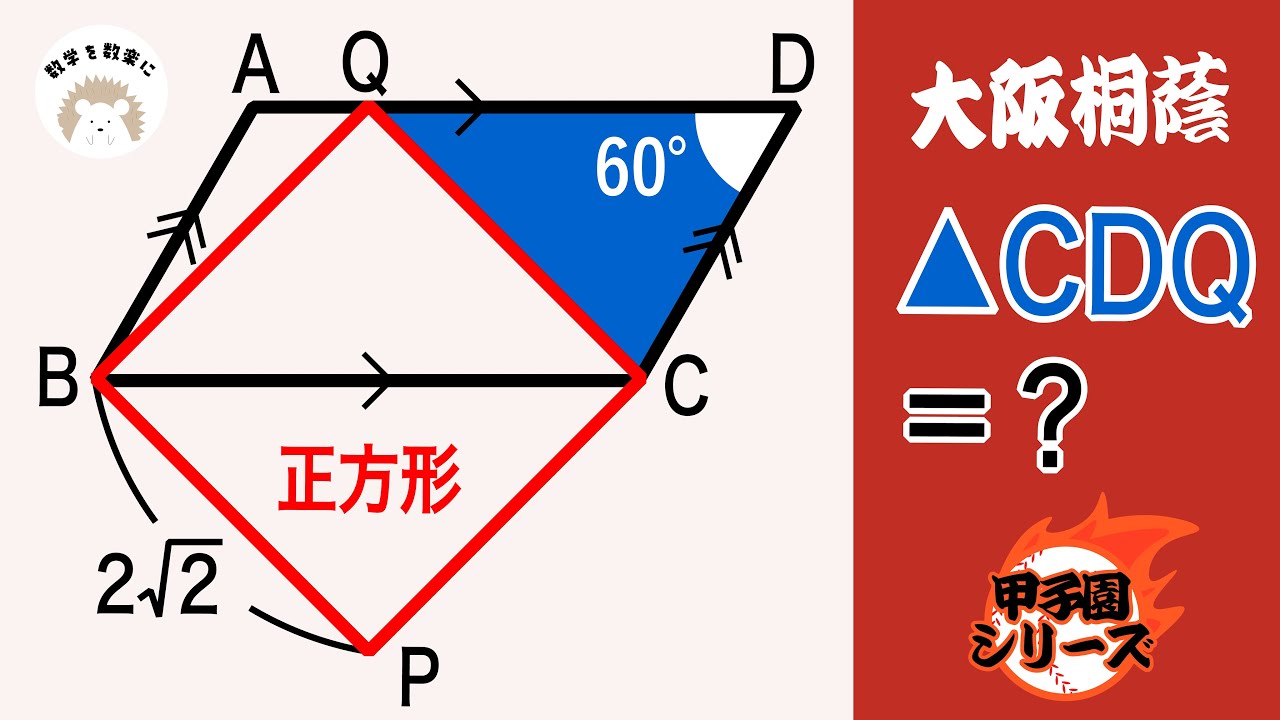
決め手は角度。大阪桐蔭
単元:
#数学(中学生)#数Ⅰ#数A#図形の性質#図形と計量#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△CDQ=?
*図は動画内参照
大阪桐蔭高等学校
この動画を見る
△CDQ=?
*図は動画内参照
大阪桐蔭高等学校
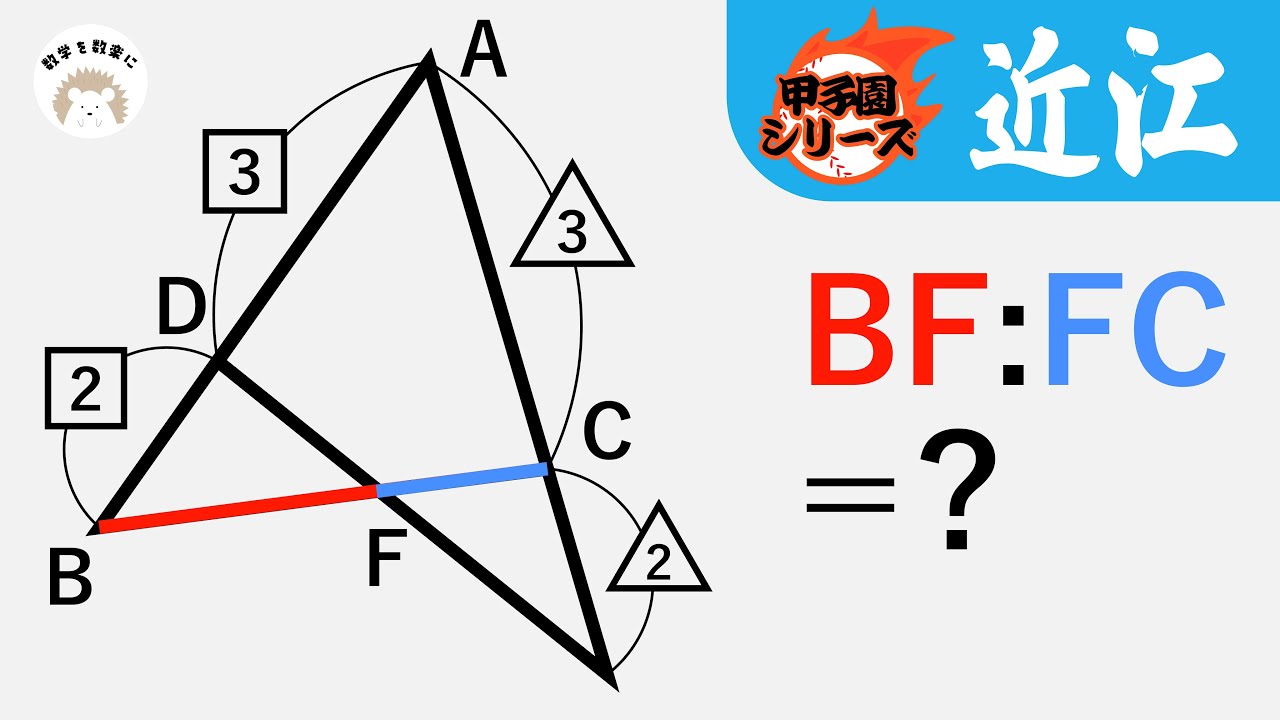
メネラウスの定理でも良いと思います。近江高校(滋賀)
単元:
#数学(中学生)#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BF:FC=?
*図は動画内参照
近江高等学校
この動画を見る
BF:FC=?
*図は動画内参照
近江高等学校
ロト7全パターン買ったらどうなるか?

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
ロト7を全パターン買ったらプラスですか?マイナスですか?
この動画を見る
下記質問の解説動画です
ロト7を全パターン買ったらプラスですか?マイナスですか?
【経験することが何よりも大切!】整数:和歌山県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sqrt{\dfrac{20}{n}}$の値が自然数となるような自然数$n$をすべて求めなさい.
和歌山県高校過去問
この動画を見る
$ \sqrt{\dfrac{20}{n}}$の値が自然数となるような自然数$n$をすべて求めなさい.
和歌山県高校過去問
ロト7全パターン買ったらプラス?

絶対に取りたい整数問題!分からない時はとにかく実験あるのみ【早稲田大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n^2+1,2n^2+3,6n^2+5$がすべて素数となる自然数$n$は$n=1,2$のみであることを示せ。
早稲田大過去問
この動画を見る
$n^2+1,2n^2+3,6n^2+5$がすべて素数となる自然数$n$は$n=1,2$のみであることを示せ。
早稲田大過去問
ハルハル様の作成問題④ #整数問題 【難】

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$(x^3+1)^3+(x^2+1)^2=2^y$を満たす整数の組$(x,y)$をすべて求めよ。
この動画を見る
$(x^3+1)^3+(x^2+1)^2=2^y$を満たす整数の組$(x,y)$をすべて求めよ。
絶対値 中1も解ける!! 海星高校

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
ある整数xの絶対値が4より小さいという。
xは全部でいくつの整数が考えられるか。
海星高校
この動画を見る
ある整数xの絶対値が4より小さいという。
xは全部でいくつの整数が考えられるか。
海星高校
福田の数学〜早稲田大学2022年教育学部第2問〜サイコロの目の積の約数の個数と確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}$サイコロをn回投げて出た目の積をSとする。Sの正の約数の個数がk個となる
確率を$P_k$とする。次の問いに答えよ。
(1)$P_3$を$n$の式で表せ。
(1)$P_4$を$n$の式で表せ。
2022早稲田大学教育学部過去問
この動画を見る
${\large\boxed{2}}$サイコロをn回投げて出た目の積をSとする。Sの正の約数の個数がk個となる
確率を$P_k$とする。次の問いに答えよ。
(1)$P_3$を$n$の式で表せ。
(1)$P_4$を$n$の式で表せ。
2022早稲田大学教育学部過去問
7で割ったあまり 札幌大谷

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$10^{2021}$を7で割った余りは?
札幌大谷高等学校(改)
この動画を見る
$10^{2021}$を7で割った余りは?
札幌大谷高等学校(改)
