 数A
数A
 数A
数A
雑問

単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 25^{63}\times 63^{25}$の下3桁を求めよ.
この動画を見る
$ 25^{63}\times 63^{25}$の下3桁を求めよ.
福田の入試問題解説〜東京大学2022年理系第6問〜複雑な反復試行の確率と確率の最大

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
Oを原点とする座標平面上で考える。0以上の整数kに対して、ベクトル$\overrightarrow{ v_k }$を
$\overrightarrow{ v_k }=(\cos\frac{2k\pi}{3}, \sin\frac{2k\pi}{3})$
と定める。投げたとき表と裏がどちらも$\frac{1}{2}$の確率で出るコインをN回投げて、
座標平面上に点$X_0,X_1,X_2,\ldots,X_N$を以下の規則$(\textrm{i}),(\textrm{ii})$に従って定める。
$(\textrm{i})X_0$はOにある。
$(\textrm{ii})n$を1以上N以下の整数とする。$X_{n-1}$が定まったとし、$X_n$を次のように定める。
・n回目のコイン投げで表が出た場合、
$\overrightarrow{ OX_n }=\overrightarrow{ OX_{n-1} }+\overrightarrow{ v_k }$
により$X_n$を定める。ただし、kは1回目からn回目までの
コイン投げで裏が出た回数とする。
・n回目のコイン投げで裏が出た場合、$X_n$を$X_{n-1}$と定める。
(1)$N=8$とする。$X_8$がOにある確率を求めよ。
(2)$N=200$とする。$X_{200}$がOにあり、かつ、合計200回のコイン投げで表が
ちょうどr回出る確率を$p_r$とおく。ただし$0 \leqq r \leqq 200$である。$p_r$を求めよ。
また$p_r$が最大となるrの値を求めよ。
2022東京大学理系過去問
この動画を見る
Oを原点とする座標平面上で考える。0以上の整数kに対して、ベクトル$\overrightarrow{ v_k }$を
$\overrightarrow{ v_k }=(\cos\frac{2k\pi}{3}, \sin\frac{2k\pi}{3})$
と定める。投げたとき表と裏がどちらも$\frac{1}{2}$の確率で出るコインをN回投げて、
座標平面上に点$X_0,X_1,X_2,\ldots,X_N$を以下の規則$(\textrm{i}),(\textrm{ii})$に従って定める。
$(\textrm{i})X_0$はOにある。
$(\textrm{ii})n$を1以上N以下の整数とする。$X_{n-1}$が定まったとし、$X_n$を次のように定める。
・n回目のコイン投げで表が出た場合、
$\overrightarrow{ OX_n }=\overrightarrow{ OX_{n-1} }+\overrightarrow{ v_k }$
により$X_n$を定める。ただし、kは1回目からn回目までの
コイン投げで裏が出た回数とする。
・n回目のコイン投げで裏が出た場合、$X_n$を$X_{n-1}$と定める。
(1)$N=8$とする。$X_8$がOにある確率を求めよ。
(2)$N=200$とする。$X_{200}$がOにあり、かつ、合計200回のコイン投げで表が
ちょうどr回出る確率を$p_r$とおく。ただし$0 \leqq r \leqq 200$である。$p_r$を求めよ。
また$p_r$が最大となるrの値を求めよ。
2022東京大学理系過去問
明治学院 令和4年度 2022 入試問題100題解説85問目!

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a,bは整数とする。
$ab^2+2ab+a=50$
a+bの最小値は?
2022明治学院高等学校
この動画を見る
a,bは整数とする。
$ab^2+2ab+a=50$
a+bの最小値は?
2022明治学院高等学校
みんな騙されるくない?

単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle \frac{1}{100}$の確率でレアが当たる。
100回引く。
レアは絶対当たる?
この動画を見る
$\displaystyle \frac{1}{100}$の確率でレアが当たる。
100回引く。
レアは絶対当たる?
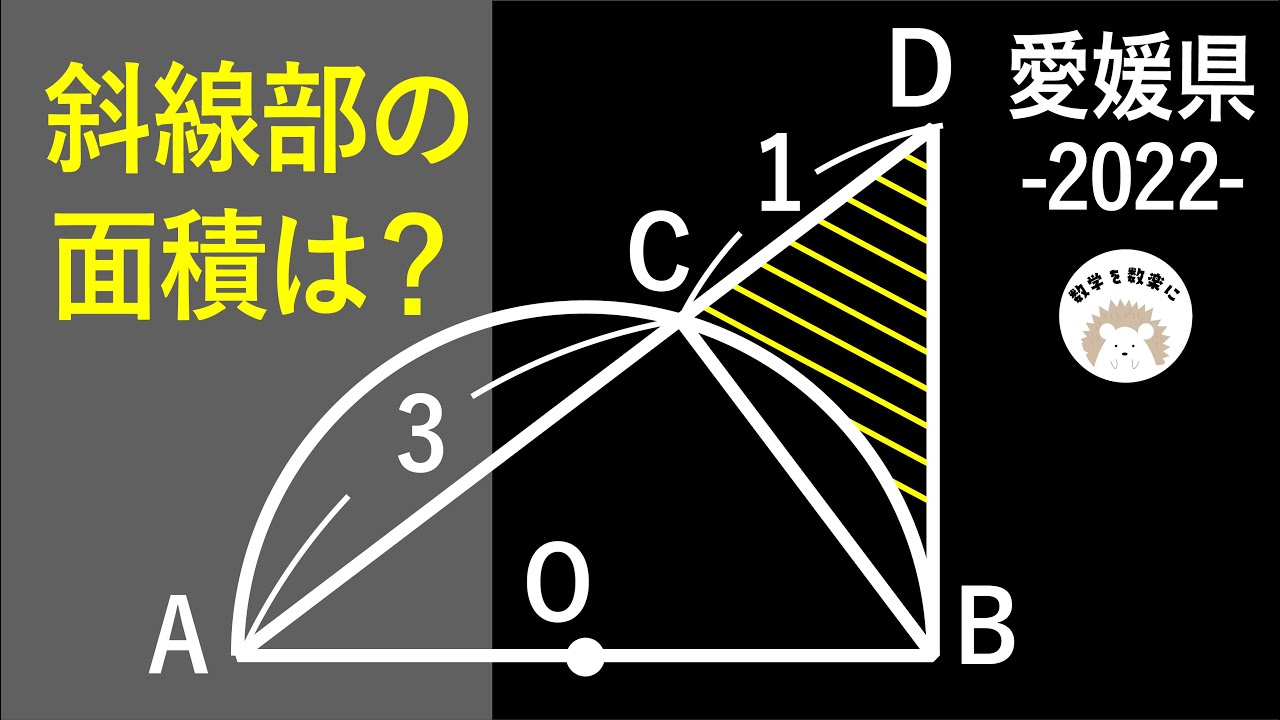
おうぎ形と正方形 令和4年度 愛媛県ラスト問題(改) 数学 2022 入試問題100題解説83問目!
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積は?
*図は動画内参照
2022愛媛県
この動画を見る
斜線部の面積は?
*図は動画内参照
2022愛媛県
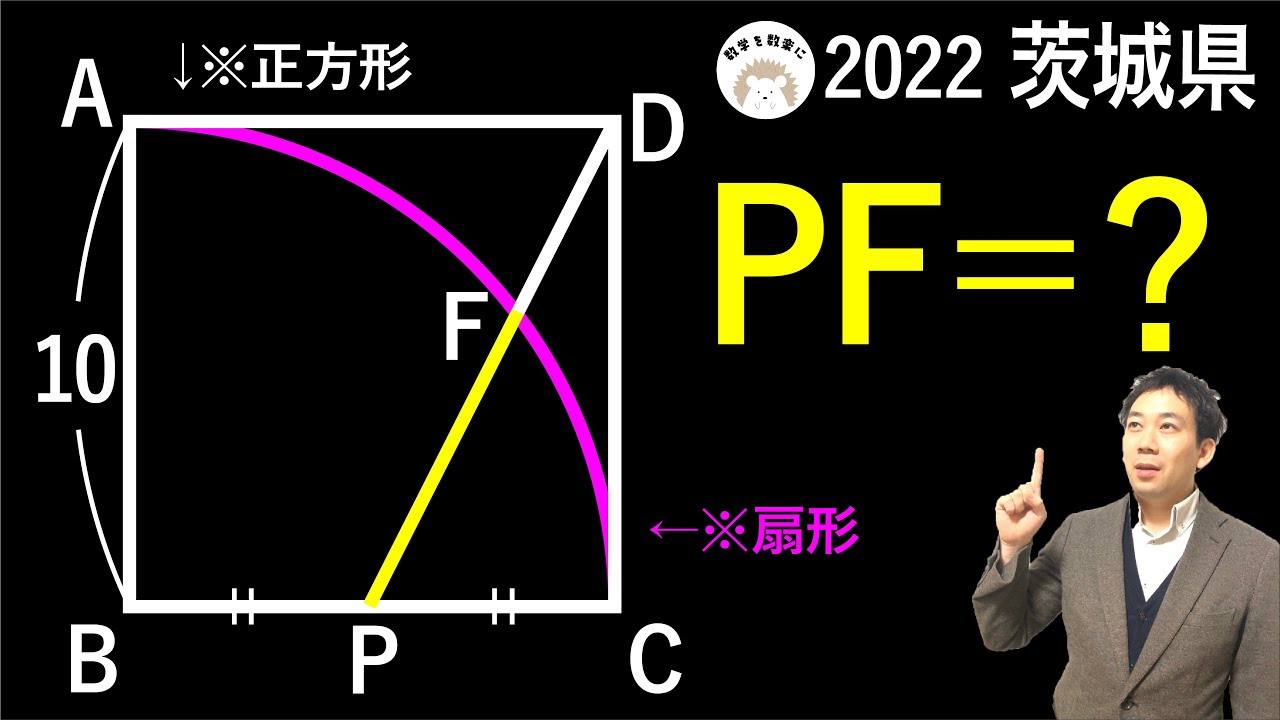
おうぎ形と正方形 2通りで解説!令和4年度 茨城県 数学 2022 入試問題100題解説81問目!
単元:
#数学(中学生)#中2数学#数Ⅰ#数A#図形の性質#図形と計量#三角形と四角形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点PはBCの中点
PF=?
*図は動画内参照
2022茨城県
この動画を見る
点PはBCの中点
PF=?
*図は動画内参照
2022茨城県
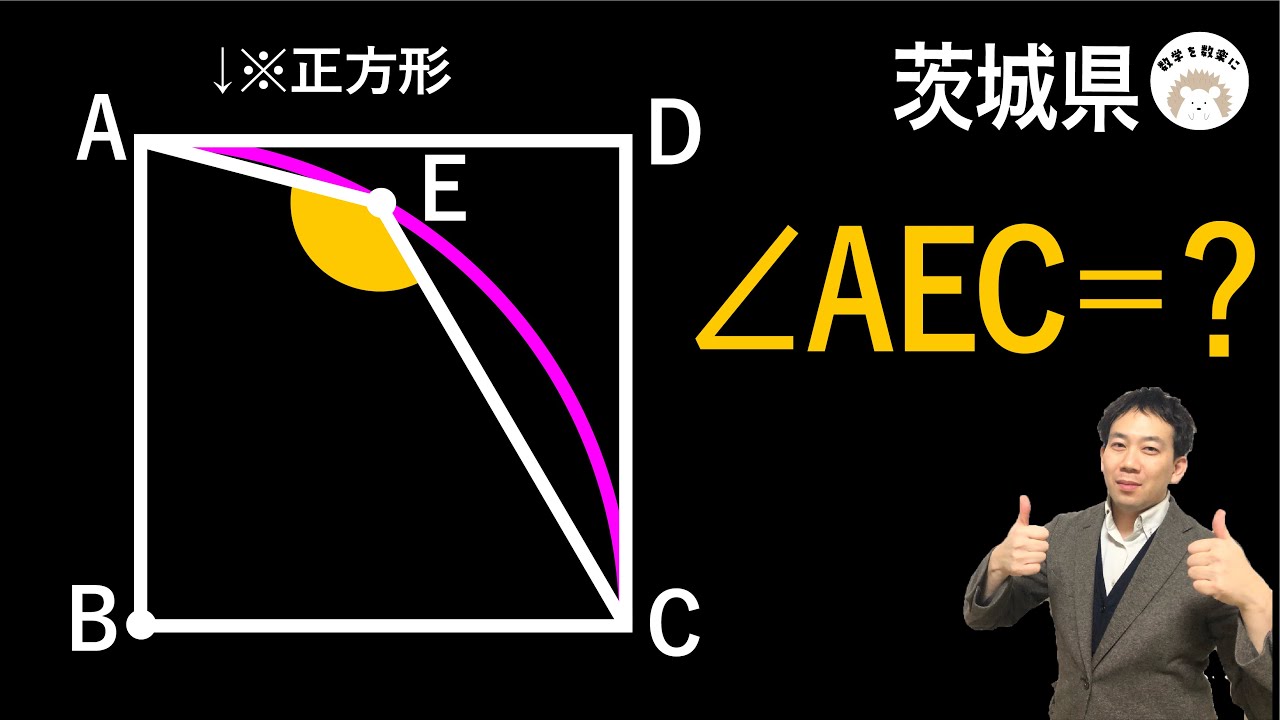
おうぎ形と正方形 令和4年度 茨城県 数学 2022 入試問題100題解説80問目!
福田の数学〜慶應義塾大学2022年薬学部第1問(7)〜直三角柱の切断面の面積の最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形の性質#微分法と積分法#学校別大学入試過去問解説(数学)#立体図形#立体切断#空間における垂直と平行と多面体(オイラーの法則)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(7)1辺の長さが$\sqrt2$の正三角形を底面とし、高さが4の直三角柱を考える。
この直三角柱を以下の条件①と条件②を共に満たす平面で切断するとき、切断面の
面積の最小値は$\boxed{\ \ シ\ \ }$である。ただし、直三角柱は底面と側面が垂直である三角柱
のことである。
条件① 切断面が直角三角形になる。
条件② 切断面の図形のすべての辺が直三角柱の側面上にある。
2022慶應義塾大学薬学部過去問
この動画を見る
(7)1辺の長さが$\sqrt2$の正三角形を底面とし、高さが4の直三角柱を考える。
この直三角柱を以下の条件①と条件②を共に満たす平面で切断するとき、切断面の
面積の最小値は$\boxed{\ \ シ\ \ }$である。ただし、直三角柱は底面と側面が垂直である三角柱
のことである。
条件① 切断面が直角三角形になる。
条件② 切断面の図形のすべての辺が直三角柱の側面上にある。
2022慶應義塾大学薬学部過去問
ニャンニャン問題2022

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 222.......22$のようにすべての桁の数が$2$である整数の中には
必ず$2022$の倍数があることを示せ.
この動画を見る
$ 222.......22$のようにすべての桁の数が$2$である整数の中には
必ず$2022$の倍数があることを示せ.
【糸口を探せ!】整数:同志社国際高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sqrt{24n}$と$\sqrt{n+27}$がともに整数になるような最小の自然数$n$の値を求めよ.
同志社国際高校過去問
この動画を見る
$\sqrt{24n}$と$\sqrt{n+27}$がともに整数になるような最小の自然数$n$の値を求めよ.
同志社国際高校過去問
福田の数学〜京都大学2022年理系第3問〜3つの数の最大公約数

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
nを自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
2022京都大学理系過去問
この動画を見る
nを自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
2022京都大学理系過去問
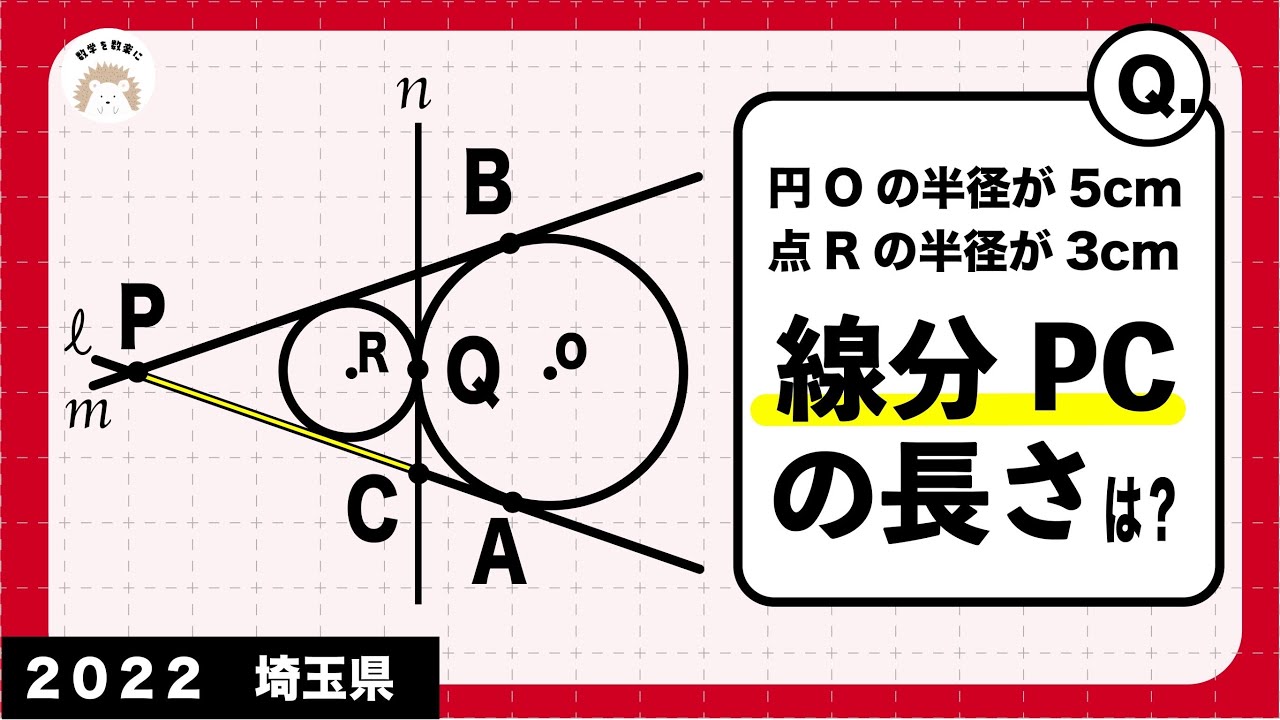
2つの円 埼玉県 令和4年度 数学 2022 入試問題100題解説77問目!
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円Oの半径が5㎝
点Rの半径が3㎝
線分PCの長さは?
*図は動画内参照
2022埼玉県
この動画を見る
円Oの半径が5㎝
点Rの半径が3㎝
線分PCの長さは?
*図は動画内参照
2022埼玉県
福田の数学〜慶應義塾大学2022年薬学部第1問(4)〜2次関数と積分の確率

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(4)f(x)はxの2次関数である。$f(x)$は$x=-2$で極値をとり、$\int_{-3}^0f(x)dx=0$
を満たす。またxy平面上において、f(x)のグラフ$y=f(x)$はx軸と異なる2点で交わり、
$y=f(x)$とx軸で囲まれる部分の面積は$\frac{8}{3}$である。このとき$f(x)=\boxed{\ \ キ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
(4)f(x)はxの2次関数である。$f(x)$は$x=-2$で極値をとり、$\int_{-3}^0f(x)dx=0$
を満たす。またxy平面上において、f(x)のグラフ$y=f(x)$はx軸と異なる2点で交わり、
$y=f(x)$とx軸で囲まれる部分の面積は$\frac{8}{3}$である。このとき$f(x)=\boxed{\ \ キ\ \ }$である。
2022慶應義塾大学薬学部過去問
福田の数学〜京都大学2022年理系第2問〜連続しない自然数を選ぶ確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
箱の中に1からnまでの番号の付いたn枚の札がある。ただし、$n \geqq 5$とし、
同じ番号の札はないとする。この箱から3枚の札を同時に取り出し、札の番号を
小さい順に$X,Y,Z$とする。このとき、$Y-X \geqq 2$かつ$Z-Y \geqq 2$となる確率を
求めよ。
2022京都大学理系過去問
この動画を見る
箱の中に1からnまでの番号の付いたn枚の札がある。ただし、$n \geqq 5$とし、
同じ番号の札はないとする。この箱から3枚の札を同時に取り出し、札の番号を
小さい順に$X,Y,Z$とする。このとき、$Y-X \geqq 2$かつ$Z-Y \geqq 2$となる確率を
求めよ。
2022京都大学理系過去問
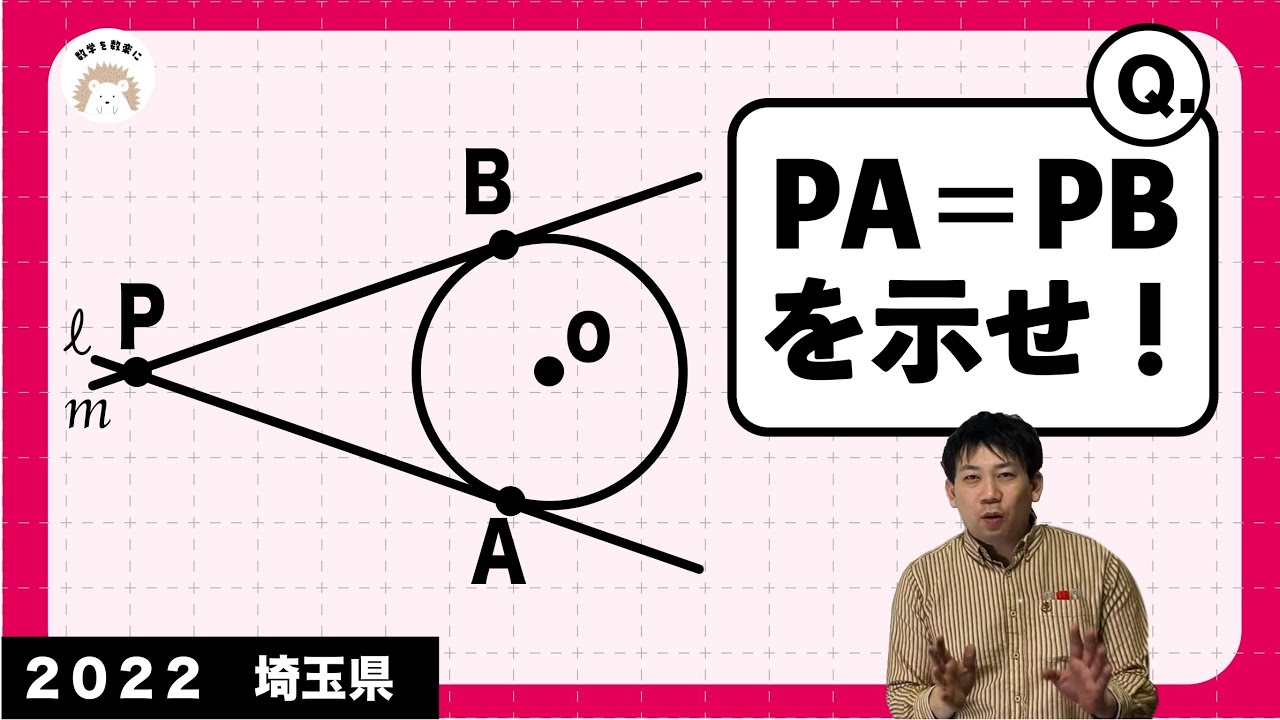
接線の長さが等しいことの証明 埼玉県 令和4年度 数学 2022 入試問題100題解説76問目!
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
PA=PBを示せ
*図は動画内参照
2022埼玉県
この動画を見る
PA=PBを示せ
*図は動画内参照
2022埼玉県
福田の数学〜慶應義塾大学2022年薬学部第1問(3)〜部屋わけ・グループ分けの確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(3)3つの部屋A,B,Cがある。この3つの部屋に対して、複数の生徒が以下の
試行(*)を繰り返し行うことを考える。
$(*)\left\{
\begin{array}{1}
・生徒それぞれが部屋を無作為に1つ選んで入る。\\
・生徒全員が部屋に入ったら、各部屋の生徒の人数を確認する。\\
・生徒全員が部屋を出る。\\
・1人の生徒しかいない部屋があった場合、その部屋に入った生徒は\\
次回以降の試行に参加しない。\\
\end{array}
\right.$
$(\textrm{i})$4人の生徒が試行(*)を1回行ったとき、2回目の試行に参加する生徒が
3人になる確率は$\boxed{\ \ オ\ \ }$である。
$(\textrm{ii})$5人の生徒が試行(*)を続けて2回行ったとき、3回目の試行に参加する
生徒が2人になる確率は$\boxed{\ \ カ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
(3)3つの部屋A,B,Cがある。この3つの部屋に対して、複数の生徒が以下の
試行(*)を繰り返し行うことを考える。
$(*)\left\{
\begin{array}{1}
・生徒それぞれが部屋を無作為に1つ選んで入る。\\
・生徒全員が部屋に入ったら、各部屋の生徒の人数を確認する。\\
・生徒全員が部屋を出る。\\
・1人の生徒しかいない部屋があった場合、その部屋に入った生徒は\\
次回以降の試行に参加しない。\\
\end{array}
\right.$
$(\textrm{i})$4人の生徒が試行(*)を1回行ったとき、2回目の試行に参加する生徒が
3人になる確率は$\boxed{\ \ オ\ \ }$である。
$(\textrm{ii})$5人の生徒が試行(*)を続けて2回行ったとき、3回目の試行に参加する
生徒が2人になる確率は$\boxed{\ \ カ\ \ }$である。
2022慶應義塾大学薬学部過去問
無題

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ n^2-331n-2022$が$101$の倍数となる
$ 2$桁の自然数$ n$を$1$つ見つけよ.
この動画を見る
$ n^2-331n-2022$が$101$の倍数となる
$ 2$桁の自然数$ n$を$1$つ見つけよ.
【数A】図形の性質:<これを見て思い出そう>三角形の重心の性質 ~何対何?~

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形の重心における、頂点→重心:重心→中点の線分の比を導出する動画になります。
この動画を見る
三角形の重心における、頂点→重心:重心→中点の線分の比を導出する動画になります。
大学入試問題#127 関西大学(1991) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$l,m,n$:正の整数
$l^2mn=64$を満たす組($l,m,n$)の個数を求めよ。
出典:1991年関西大学 入試問題
この動画を見る
$l,m,n$:正の整数
$l^2mn=64$を満たす組($l,m,n$)の個数を求めよ。
出典:1991年関西大学 入試問題
一橋大学2022整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 2^a3^b+2^c3^d=2022$を満たす$0$以上の整数$(a,b,c,d)$を求めよ.
2022一橋大過去問
この動画を見る
$ 2^a3^b+2^c3^d=2022$を満たす$0$以上の整数$(a,b,c,d)$を求めよ.
2022一橋大過去問
福田の入試問題解説〜東京大学2022年理系第2問〜約数と倍数と最大公約数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数列$\left\{a_n\right\}$を次のように定める。
$a_1=1, a_{n+1}=a_n^2+1 (n=1,2,3,\ldots)$
(1)正の整数nが3の倍数のとき、$a_n$は5の倍数となることを示せ。
(2)k,nを正の整数とする。$a_n$が$a_k$の倍数となるための必要十分条件をk,nを
用いて表せ。
(3)$a_{2022}$と$(a_{8091})^2$の最大公約数を求めよ。
2022東京大学理系過去問
この動画を見る
数列$\left\{a_n\right\}$を次のように定める。
$a_1=1, a_{n+1}=a_n^2+1 (n=1,2,3,\ldots)$
(1)正の整数nが3の倍数のとき、$a_n$は5の倍数となることを示せ。
(2)k,nを正の整数とする。$a_n$が$a_k$の倍数となるための必要十分条件をk,nを
用いて表せ。
(3)$a_{2022}$と$(a_{8091})^2$の最大公約数を求めよ。
2022東京大学理系過去問
福田の数学〜東京慈恵会医科大学2022年医学部第4問〜複素数平面と図形

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#平面上の曲線#複素数平面#方べきの定理と2つの円の関係#図形と方程式#点と直線#2次曲線#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
複素数平面上の点zが原点を中心とする半径1の円周上を動くとき、$w=z+\frac{2}{z}$
で表される点wの描く図形をCとする。Cで囲まれた部分の内部(ただし、
境界線は含まない)に定点$\alpha$をとり、$\alpha$を通る直線lがCと交わる2点を$\beta_1,\beta_2$とする。
(1)$w=u+vi$(u,vは実数)とするとき、uとvの間に成り立つ関係式を求めよ。
(2)点$\alpha$を固定したままlを動かすとき、積$|\beta_1-\alpha|・|\beta_2-\alpha|$が最大となる
ようなlはどのような直線のときか調べよ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
複素数平面上の点zが原点を中心とする半径1の円周上を動くとき、$w=z+\frac{2}{z}$
で表される点wの描く図形をCとする。Cで囲まれた部分の内部(ただし、
境界線は含まない)に定点$\alpha$をとり、$\alpha$を通る直線lがCと交わる2点を$\beta_1,\beta_2$とする。
(1)$w=u+vi$(u,vは実数)とするとき、uとvの間に成り立つ関係式を求めよ。
(2)点$\alpha$を固定したままlを動かすとき、積$|\beta_1-\alpha|・|\beta_2-\alpha|$が最大となる
ようなlはどのような直線のときか調べよ。
2022東京慈恵会医科大学医学部過去問
ざ・見掛け倒しだよ

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+……+\dfrac{32}{33}=\dfrac{a}{33!}$
$a$を$17$で割った余りを求めよ.
この動画を見る
$ \dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+……+\dfrac{32}{33}=\dfrac{a}{33!}$
$a$を$17$で割った余りを求めよ.
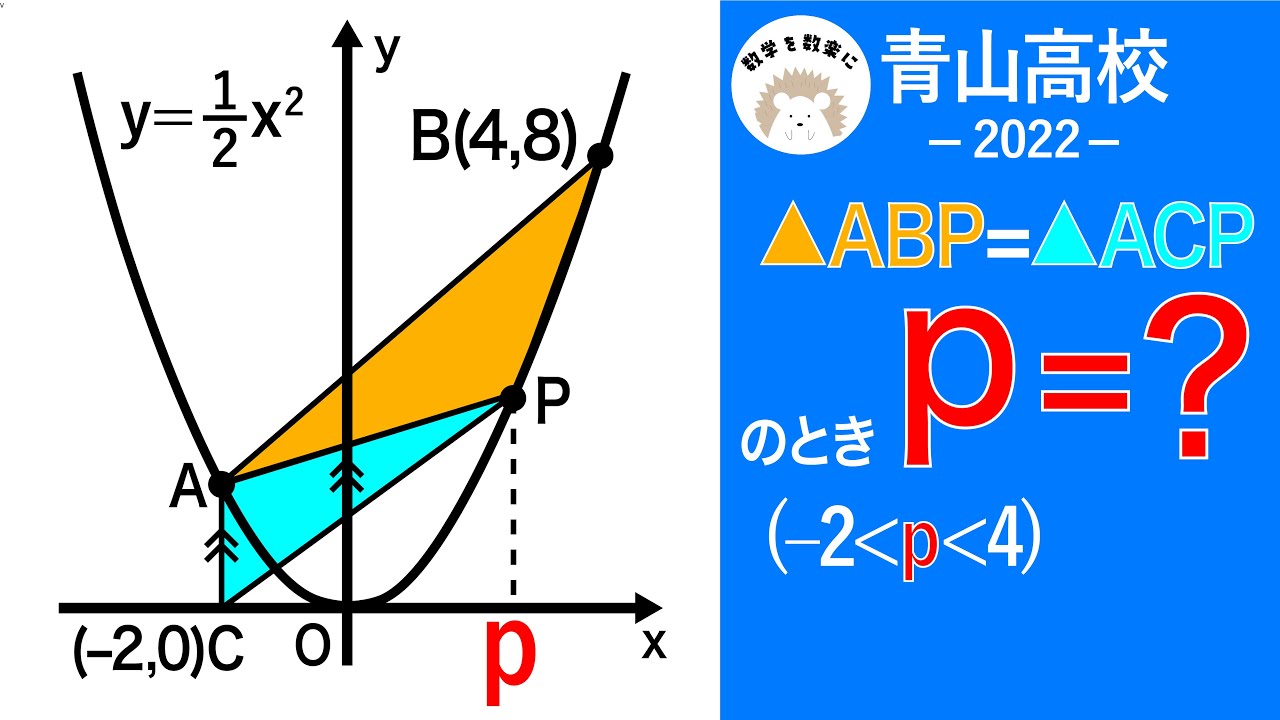
面積について方程式を立てず解くこともできます。青山高校 関数 2022 入試問題100題解説72問目!!
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABP=△ACPのとき
p=?(-2<p<4)
*図は動画内参照
2022青山高等学校
この動画を見る
△ABP=△ACPのとき
p=?(-2<p<4)
*図は動画内参照
2022青山高等学校
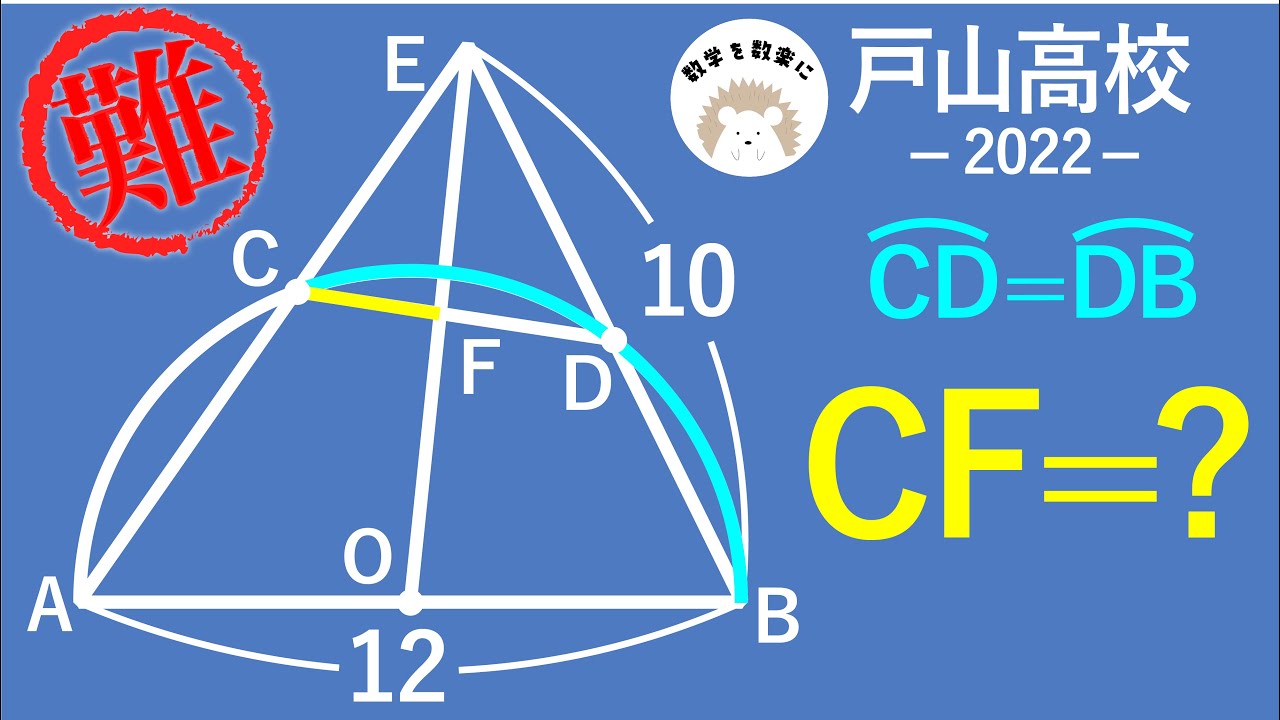
戸山高校 2022 入試問題100題解説71問目!!
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\stackrel{\huge\frown}{CD}$ = $\stackrel{\huge\frown}{DB}$
CF=?
*図は動画内参照
2022戸山高等学校
この動画を見る
$\stackrel{\huge\frown}{CD}$ = $\stackrel{\huge\frown}{DB}$
CF=?
*図は動画内参照
2022戸山高等学校
福田の数学〜東京慈恵会医科大学2022年医学部第3問〜約数と倍数の性質

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
mは3以上の奇数とし、mの全ての正の約数を$a_1,a_2,\ldots,a_k$と並べる。
ただし、$a_1 \lt a_2 \lt \ldots \lt a_k$とする。
以下の2つの条件$(\textrm{i}),(\textrm{ii})$を満たすmについて考える。
$(\textrm{i})m$は素数ではない。
$(\textrm{ii})i \leqq j,1 \lt i \lt k ,1 \lt j \lt k$を満たす全ての整数i,jについて$a_j-a_i \leqq 3$が
成り立つ。
このとき、次の問いに答えよ。
(1)kは3または4であることを示し、mを$a_2$を用いて表せ。
(2)$k=3$となるとき、全ての正の整数nについて$(a_2n+1)^{a_2}-1$は
mの倍数であることを示せ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
mは3以上の奇数とし、mの全ての正の約数を$a_1,a_2,\ldots,a_k$と並べる。
ただし、$a_1 \lt a_2 \lt \ldots \lt a_k$とする。
以下の2つの条件$(\textrm{i}),(\textrm{ii})$を満たすmについて考える。
$(\textrm{i})m$は素数ではない。
$(\textrm{ii})i \leqq j,1 \lt i \lt k ,1 \lt j \lt k$を満たす全ての整数i,jについて$a_j-a_i \leqq 3$が
成り立つ。
このとき、次の問いに答えよ。
(1)kは3または4であることを示し、mを$a_2$を用いて表せ。
(2)$k=3$となるとき、全ての正の整数nについて$(a_2n+1)^{a_2}-1$は
mの倍数であることを示せ。
2022東京慈恵会医科大学医学部過去問
大学入試問題#125 広島修道大学(2015) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$n$:自然数
$2n-1$と$2n+1$は互いに素であることを示せ
出典:2015年広島修道大学 入試問題
この動画を見る
$n$:自然数
$2n-1$と$2n+1$は互いに素であることを示せ
出典:2015年広島修道大学 入試問題
不定方程式
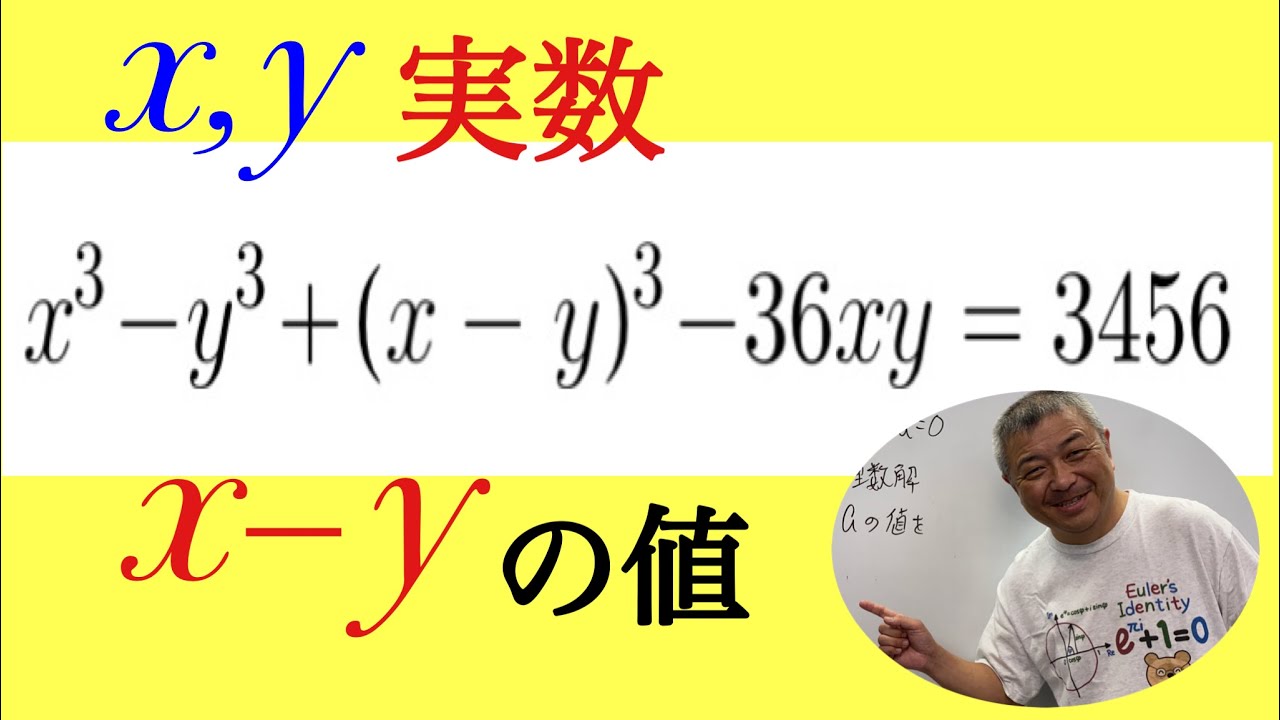
単元:
#数A#複素数と方程式#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y$を実数とする.
$ x^3-y^3+(x-y)^3-36xy=3456$のとき,$ x-y$の値を求めよ.
この動画を見る
$x,y$を実数とする.
$ x^3-y^3+(x-y)^3-36xy=3456$のとき,$ x-y$の値を求めよ.
福田の数学〜東京慈恵会医科大学2022年医学部第1問〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
袋Aには白玉2個、赤玉1個、袋Bには白玉1個、赤玉2個が入っている。
この状態から始めて、次の操作を繰り返し行う。
操作
① 袋A、袋Bから玉を1個ずつ取り出す。
② $(\textrm{i})$取り出した2個の玉の色が同じである場合は、取り出した玉を2個とも
袋Aに入れる。
$(\textrm{ii})$取り出した2個の玉の色が異なる場合は、袋Aから取り出した玉は袋B
に入れ、袋Bから取り出した玉は袋Aに入れる。
このとき、
・操作を2回繰り返した後に袋Aに入っている赤玉の個数が1個である確率は$\boxed{\ \ (ア)\ \ }$
・操作を3回繰り返した後に袋Aに入っている赤玉の個数が0個である確率は$\boxed{\ \ (イ)\ \ }$
である。
2022東京慈恵会医科大学医学部過去問
この動画を見る
袋Aには白玉2個、赤玉1個、袋Bには白玉1個、赤玉2個が入っている。
この状態から始めて、次の操作を繰り返し行う。
操作
① 袋A、袋Bから玉を1個ずつ取り出す。
② $(\textrm{i})$取り出した2個の玉の色が同じである場合は、取り出した玉を2個とも
袋Aに入れる。
$(\textrm{ii})$取り出した2個の玉の色が異なる場合は、袋Aから取り出した玉は袋B
に入れ、袋Bから取り出した玉は袋Aに入れる。
このとき、
・操作を2回繰り返した後に袋Aに入っている赤玉の個数が1個である確率は$\boxed{\ \ (ア)\ \ }$
・操作を3回繰り返した後に袋Aに入っている赤玉の個数が0個である確率は$\boxed{\ \ (イ)\ \ }$
である。
2022東京慈恵会医科大学医学部過去問
2022都立入試 整数問題証明(11の倍数)

単元:
#数学(中学生)#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数列#数列とその和(等差・等比・階差・Σ)#高校入試過去問(数学)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
2022都立入試 整数問題証明に関して解説していきます.
この動画を見る
2022都立入試 整数問題証明に関して解説していきます.
