 数A
数A
 数A
数A
比例式と整数

単元:
#数学(中学生)#中1数学#数A#比例・反比例#整数の性質#約数・倍数・整数の割り算と余り・合同式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y,z,n$は自然数である.
$2x=3y=5z,x+y+z=n$である.
$\sqrt{xyz}$が整数となる$n$の条件を求めよ.
この動画を見る
$x,y,z,n$は自然数である.
$2x=3y=5z,x+y+z=n$である.
$\sqrt{xyz}$が整数となる$n$の条件を求めよ.
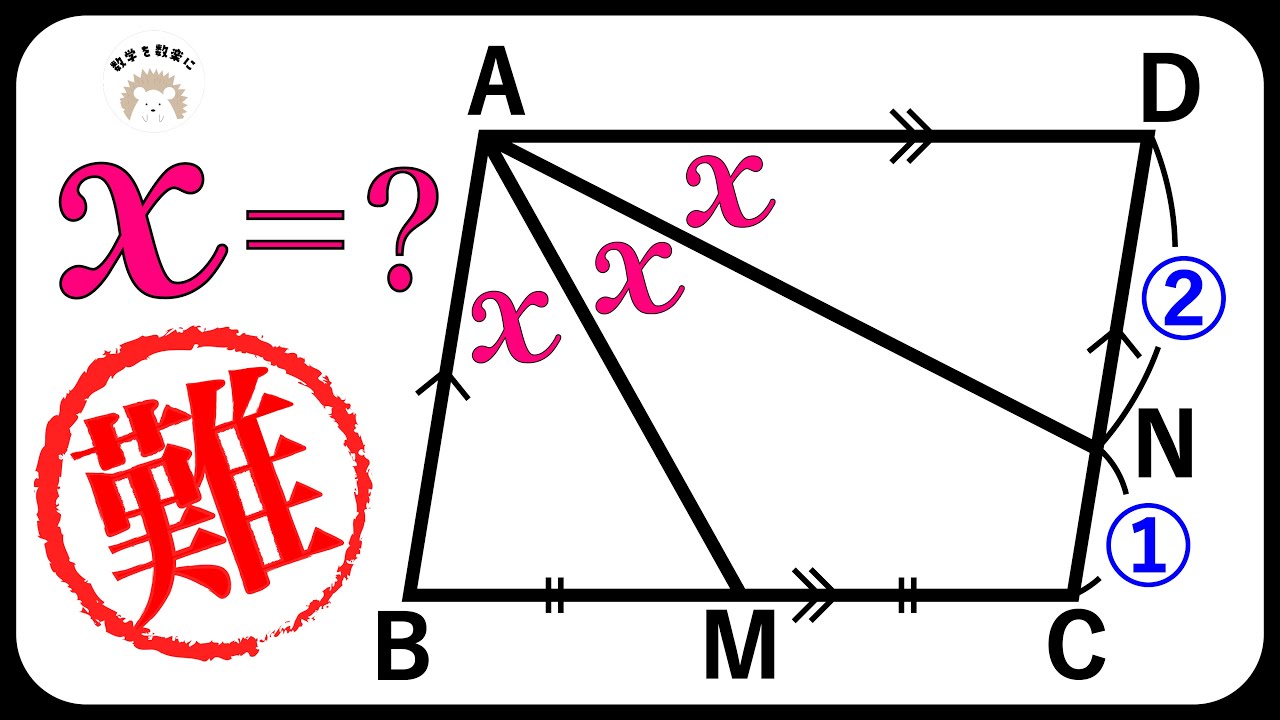
難問!?まさかの答え。
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x=?
*図は動画内参照
この動画を見る
x=?
*図は動画内参照
福田のわかった数学〜高校1年生084〜確率(4)さいころの目の最大と最小の確率

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{A}$ 確率(4) さいころの目(2)さいころをn回投げて出た目の最大値が5
で最小値が3である確率を求めよ。ただし、$n \geqq 2$とする。
この動画を見る
数学$\textrm{A}$ 確率(4) さいころの目(2)さいころをn回投げて出た目の最大値が5
で最小値が3である確率を求めよ。ただし、$n \geqq 2$とする。
千葉大(医)の類題 整数
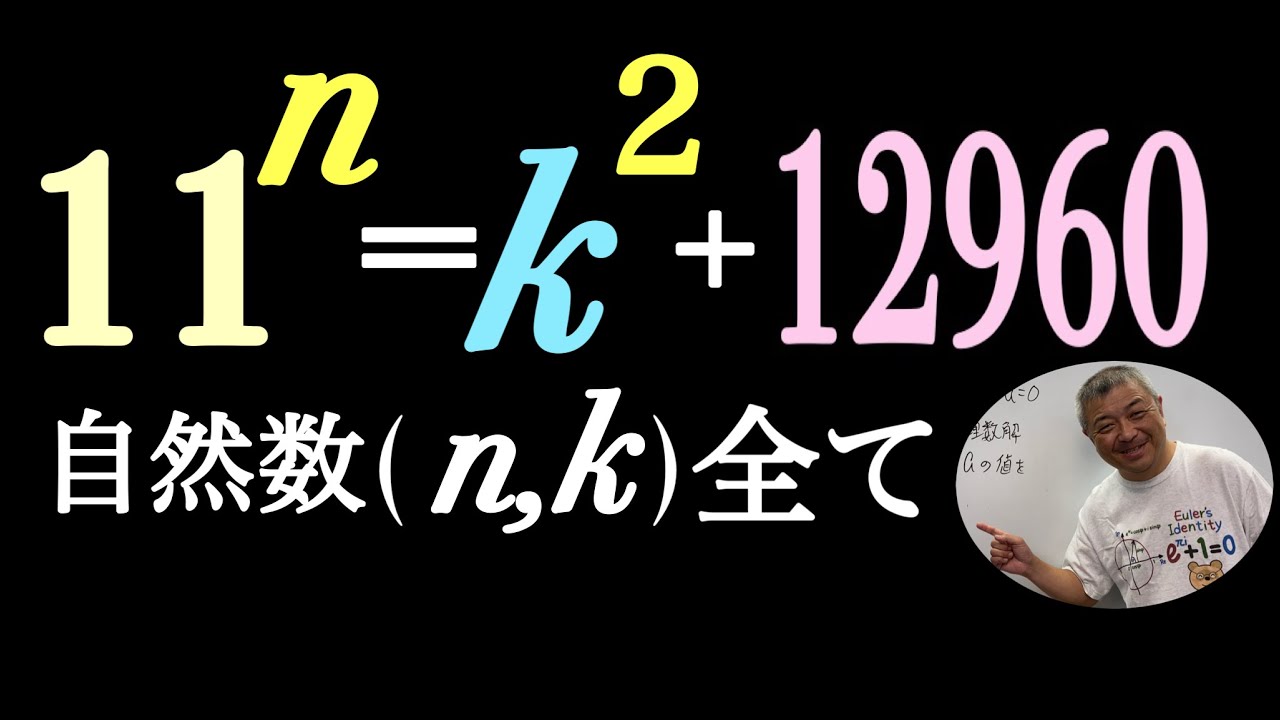
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$(n,k)$をすべて求めよ.
$11^n=k^2+12960$
千葉大(医)過去問
この動画を見る
自然数$(n,k)$をすべて求めよ.
$11^n=k^2+12960$
千葉大(医)過去問
コインを投げる 確率

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
○×問題 コインを投げる
(1)2枚投げた時、表1枚裏1枚になる確率は$\frac{1}{2}$
(2)4枚投げた時、表2枚裏2枚になる確率は$\frac{1}{2}$
この動画を見る
○×問題 コインを投げる
(1)2枚投げた時、表1枚裏1枚になる確率は$\frac{1}{2}$
(2)4枚投げた時、表2枚裏2枚になる確率は$\frac{1}{2}$
福田のわかった数学〜高校1年生083〜確率(3)さいころの目の積の確率

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{A}$確率(3)
さいころの目(1)
さいころをn回投げて出た目の積が6の倍数となる
確率を求めよ。ただし、nは2以上の自然数とする。
この動画を見る
数学$\textrm{A}$確率(3)
さいころの目(1)
さいころをn回投げて出た目の積が6の倍数となる
確率を求めよ。ただし、nは2以上の自然数とする。
【数A】確率:期待値の巧みな利用

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#場合の数と確率#確率#その他#その他#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
【高校数学 数学A 場合の数と確率 期待値】
無限に続く階段がある。さいころを振って出た目の数だけ登っては立ち止まるということを繰り返す。このとき十分上の方のとある段に立ち止まる確率を求めよ。
(出典 上級国家公務員試験より)
この動画を見る
【高校数学 数学A 場合の数と確率 期待値】
無限に続く階段がある。さいころを振って出た目の数だけ登っては立ち止まるということを繰り返す。このとき十分上の方のとある段に立ち止まる確率を求めよ。
(出典 上級国家公務員試験より)
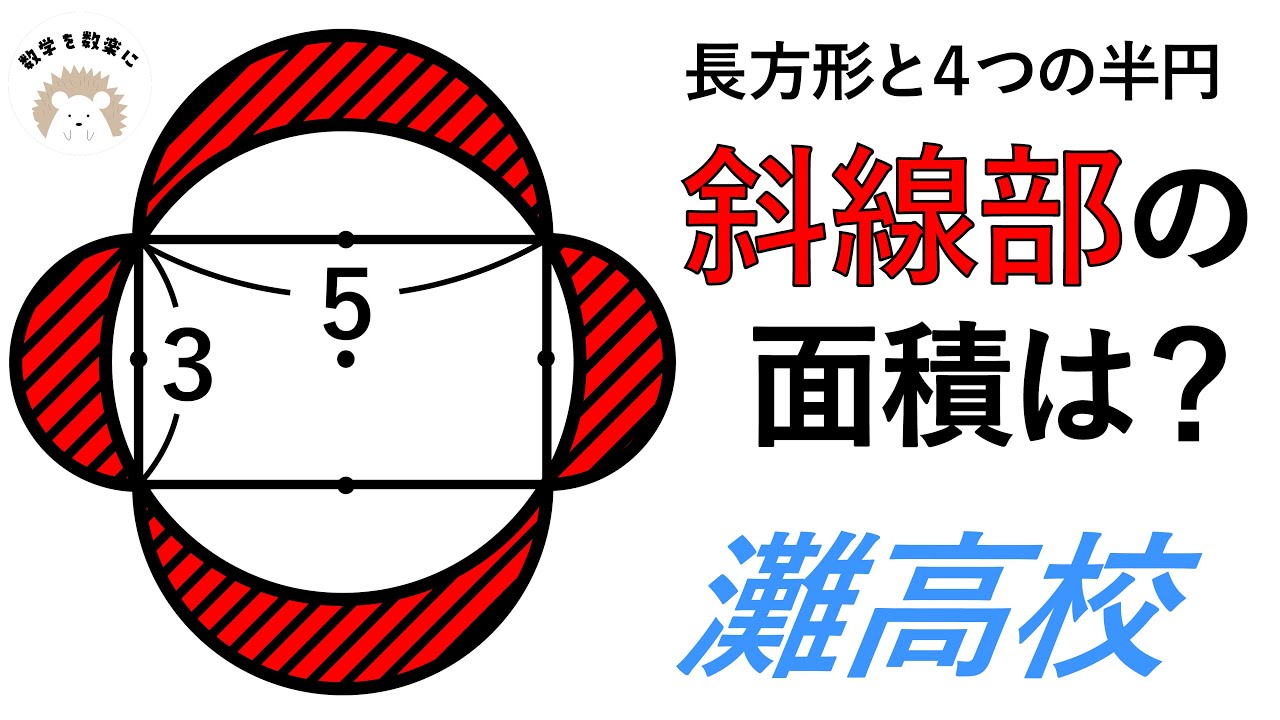
灘高校に受かるのは難だけど、この問題は難てこともない問題
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
長方形と4つの半円
斜線部の面積は?
*図は動画内参照
灘高等学校
この動画を見る
長方形と4つの半円
斜線部の面積は?
*図は動画内参照
灘高等学校
整数問題基本

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
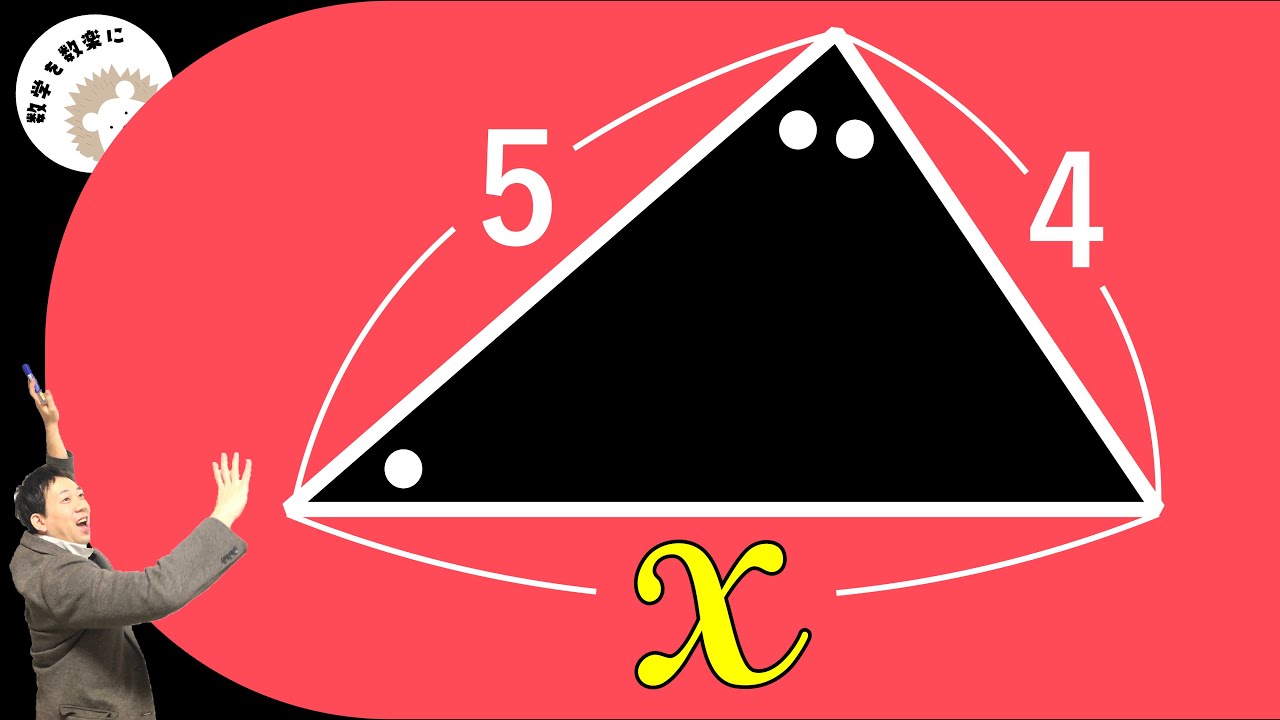
整数$m,n$をすべて求めよ.
$m^4+n^4-2mn=13$
この動画を見る
整数$m,n$をすべて求めよ.
$m^4+n^4-2mn=13$
補助線引けるかな??
中学レベル 倍数の見分け方の証明

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y,z$は1~9の整数である.
$XX+YY+ZZ=XYZ$
これを解け.
この動画を見る
$x,y,z$は1~9の整数である.
$XX+YY+ZZ=XYZ$
これを解け.
すべて選べ。高校の内容だけど、中学生も知っておいて損はない。

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$n(n+1)(n+5)$は何の倍数?(n:整数)
すべて選べ
(a)2の倍数
(b)3の倍数
(c)6の倍数
(d)12の倍数
この動画を見る
$n(n+1)(n+5)$は何の倍数?(n:整数)
すべて選べ
(a)2の倍数
(b)3の倍数
(c)6の倍数
(d)12の倍数
福田のわかった数学〜高校1年生082〜確率(2)くじ引き(2)

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{A}$確率(2) くじ引き(2)
10本中1等賞が2本、2等賞が3本入ったくじから
5人が順に1本ずつ引いていく。(元に戻さない)
4人目が1等賞、5人目が2等賞に当たる確率を
求めよ。
この動画を見る
数学$\textrm{A}$確率(2) くじ引き(2)
10本中1等賞が2本、2等賞が3本入ったくじから
5人が順に1本ずつ引いていく。(元に戻さない)
4人目が1等賞、5人目が2等賞に当たる確率を
求めよ。
変な方程式 指数タワー
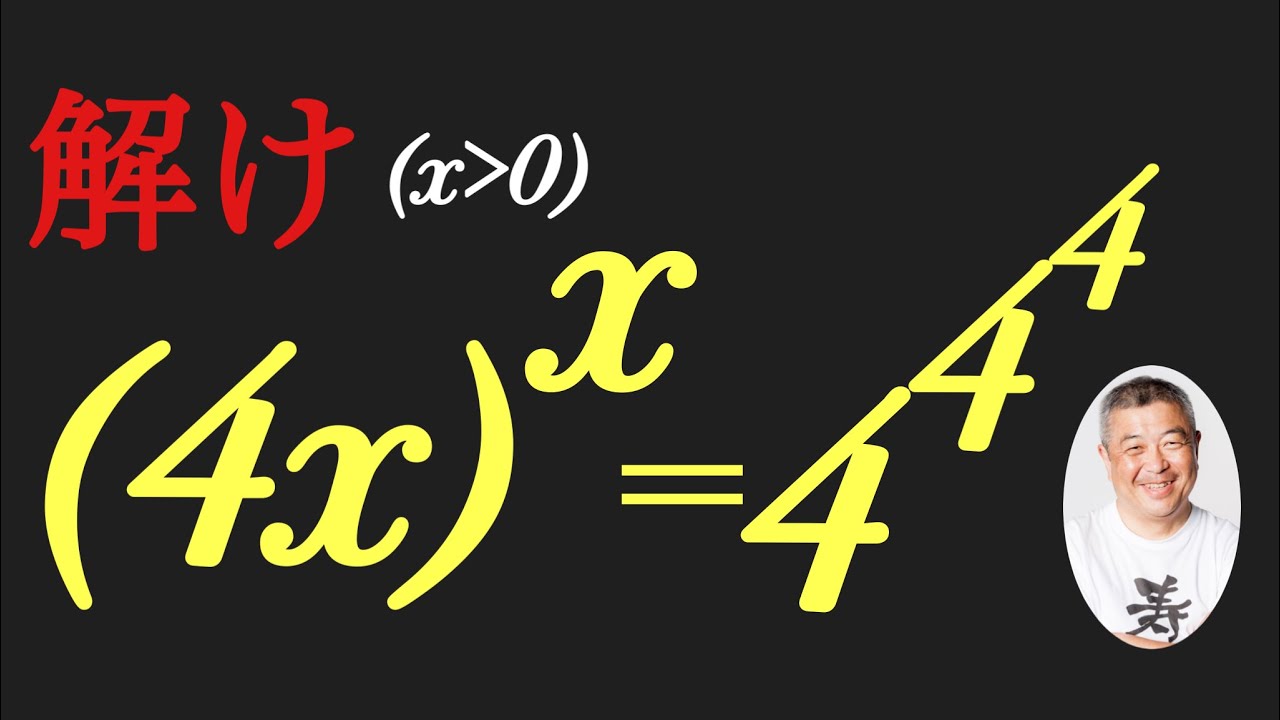
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け. $x\gt 0$
$(4x)^x=4^{4^4}$
この動画を見る
これを解け. $x\gt 0$
$(4x)^x=4^{4^4}$
変な指数方程式
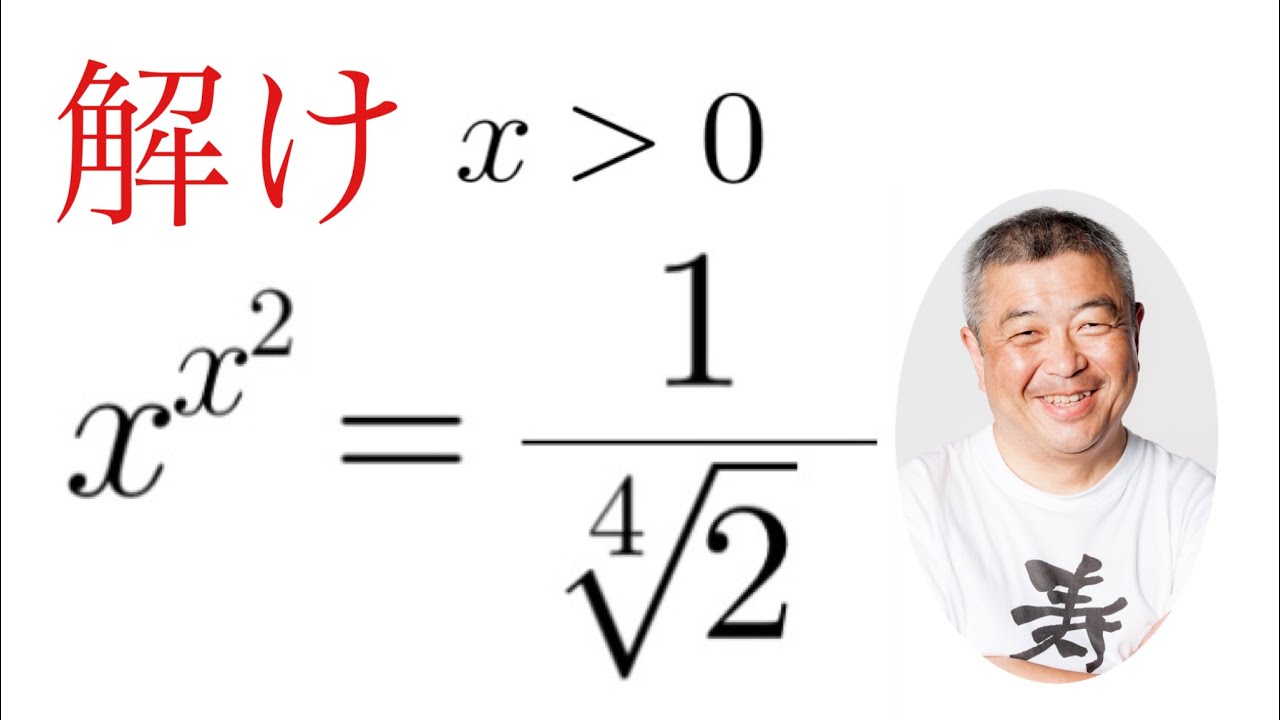
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x\gt 0$
$x^{x^2}=\dfrac{1}{\sqrt[4]{2}}$
この動画を見る
これを解け.$x\gt 0$
$x^{x^2}=\dfrac{1}{\sqrt[4]{2}}$
2021東京海洋大 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$P$は5以上の素数である.
$P^2-1$は$24$の倍数を示せ.
2021東京海洋大過去問
この動画を見る
$P$は5以上の素数である.
$P^2-1$は$24$の倍数を示せ.
2021東京海洋大過去問
福田のわかった数学〜高校1年生081〜確率(1)くじ引き(1)

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{A}$ 確率(1) くじ引き(1)
10本中3本当たりのくじから
(1)同時に3本のくじを引いたとき、1本だけ当たる確率を求めよ。
(2)A,B,Cの3人が順に1本ずつ引いたとき(元に戻さない)、
1人だけが当たる確率を求めよ。
この動画を見る
数学$\textrm{A}$ 確率(1) くじ引き(1)
10本中3本当たりのくじから
(1)同時に3本のくじを引いたとき、1本だけ当たる確率を求めよ。
(2)A,B,Cの3人が順に1本ずつ引いたとき(元に戻さない)、
1人だけが当たる確率を求めよ。
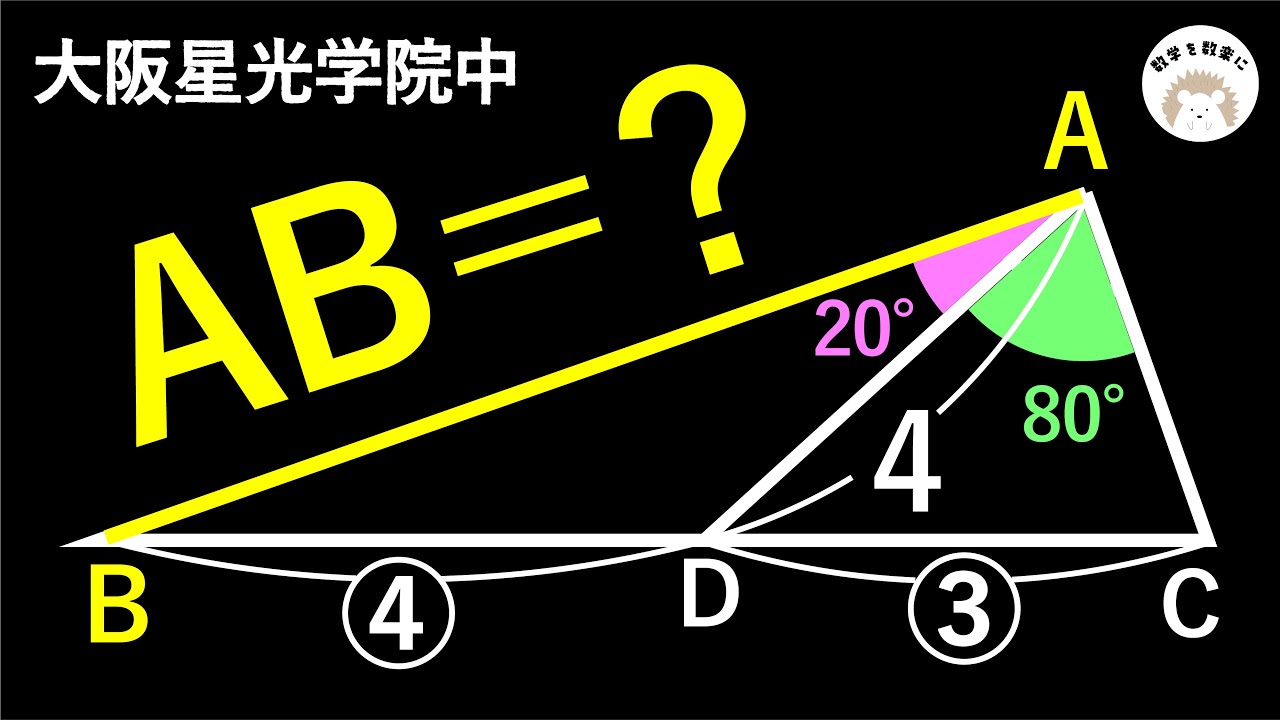
補助線どこ引く? 大阪星光学院中
単元:
#算数(中学受験)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#過去問解説(学校別)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AB=?
*図は動画内参照
大阪星光学院中学校
この動画を見る
AB=?
*図は動画内参照
大阪星光学院中学校
指数方程式 答えは1つじゃないよ

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
すべての解を求めよ.
$5^x・8^{\frac{x}{x+1}}=100$
この動画を見る
すべての解を求めよ.
$5^x・8^{\frac{x}{x+1}}=100$
福田のわかった数学〜高校1年生080〜場合の数(19)道順(5)

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(17) 道順(5)
図(※動画参照)のように立方体ABCD-EFGHの各面が3×3の正方形となるような
碁盤の目状に区切られた図形がある。点Aから点Gまで辺上を通って最短経路で行く
方法は何通りあるか。
この動画を見る
数学$\textrm{I}$ 場合の数(17) 道順(5)
図(※動画参照)のように立方体ABCD-EFGHの各面が3×3の正方形となるような
碁盤の目状に区切られた図形がある。点Aから点Gまで辺上を通って最短経路で行く
方法は何通りあるか。
気付けば一瞬!!の確率の問題 東奥義塾

単元:
#数学(中学生)#数A#場合の数と確率#確率#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1⃣ 2⃣ 3⃣ 4⃣ 5⃣
の5枚のカードから3枚のカードを並べてできる3ケタの整数で
奇数となる確率は?
東奥義塾高等学校
この動画を見る
1⃣ 2⃣ 3⃣ 4⃣ 5⃣
の5枚のカードから3枚のカードを並べてできる3ケタの整数で
奇数となる確率は?
東奥義塾高等学校
方程式
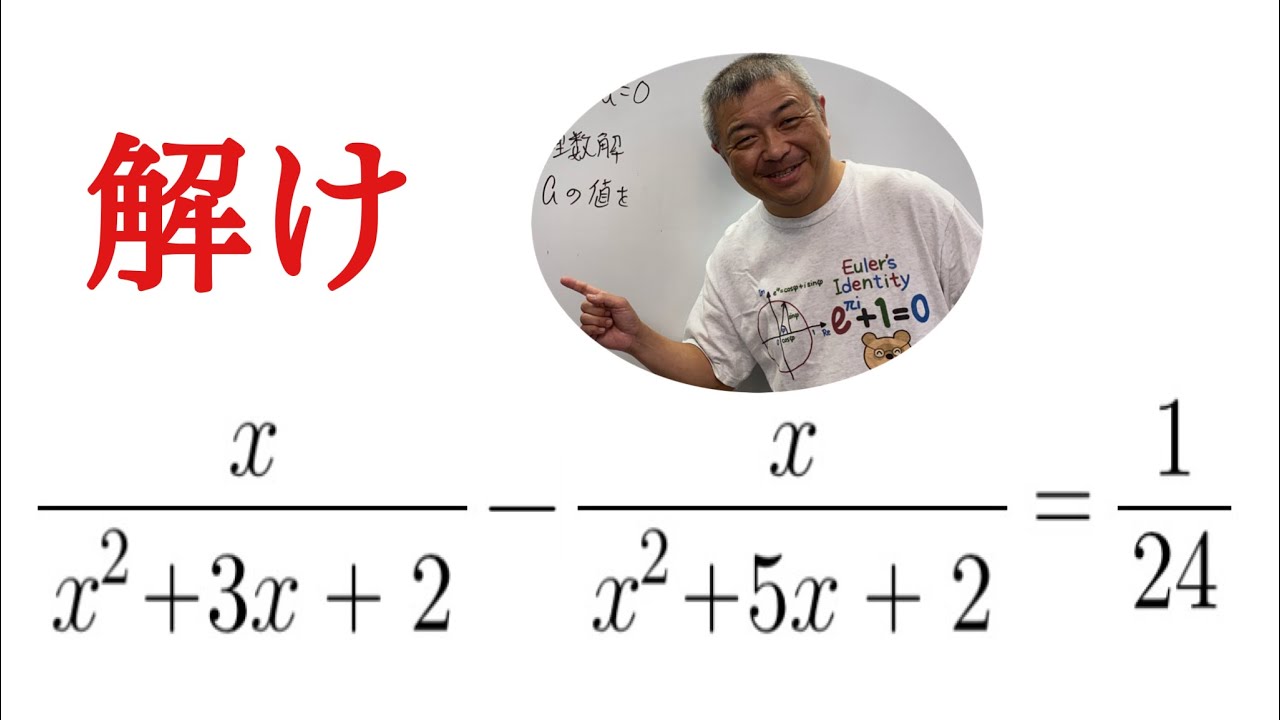
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\dfrac{x}{x^2+3x+2}-\dfrac{x}{x^2+5x+2}=\dfrac{1}{24}$
この動画を見る
これを解け.
$\dfrac{x}{x^2+3x+2}-\dfrac{x}{x^2+5x+2}=\dfrac{1}{24}$
福田のわかった数学〜高校1年生079〜場合の数(18)連続しない自然数の選び方

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(18) 連続しない整数
$1,2,3,\ldots,19,20$の20個の数字から、どの2つも連続しないような8個の数字を
選ぶ方法は何通りあるか。
この動画を見る
数学$\textrm{I}$ 場合の数(18) 連続しない整数
$1,2,3,\ldots,19,20$の20個の数字から、どの2つも連続しないような8個の数字を
選ぶ方法は何通りあるか。
未知数2で式1つの方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これの実数解を求めよ.
$x^2+y^2+15=\sqrt 6(x-3y)$
この動画を見る
これの実数解を求めよ.
$x^2+y^2+15=\sqrt 6(x-3y)$
#39 数検1級1次 過去問 解と係数の関係 整数問題

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$m,n:$正の整数
$x^3-mx^2+nx-n=0$のすべての解が正の整数であるような組$(m,n)$を求めよ。
この動画を見る
$m,n:$正の整数
$x^3-mx^2+nx-n=0$のすべての解が正の整数であるような組$(m,n)$を求めよ。
4乗根の方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$\sqrt[4]{97-x}+\sqrt[4]{x-15}=4$
この動画を見る
実数解を求めよ.
$\sqrt[4]{97-x}+\sqrt[4]{x-15}=4$
初見で解けたら認めよう。2通りで解説。
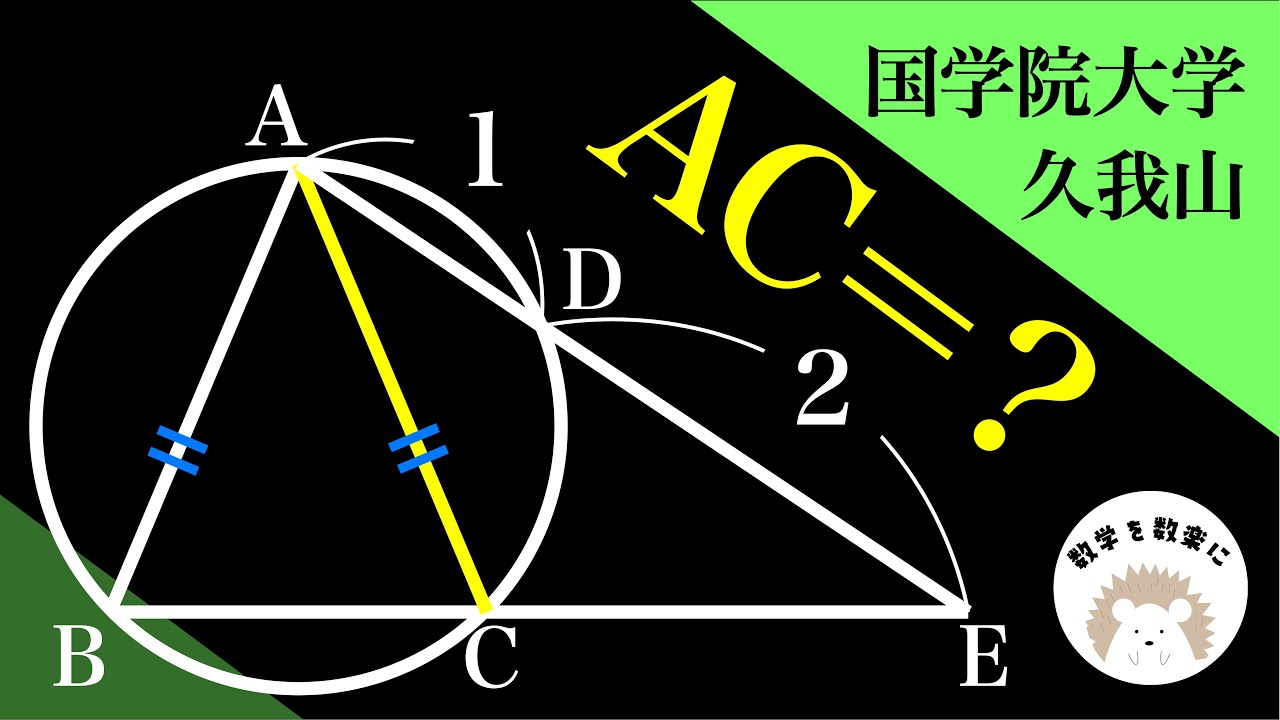
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#方べきの定理と2つの円の関係#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AC=?
*図は動画内参照
國學院大學久我山高等学校
この動画を見る
AC=?
*図は動画内参照
國學院大學久我山高等学校
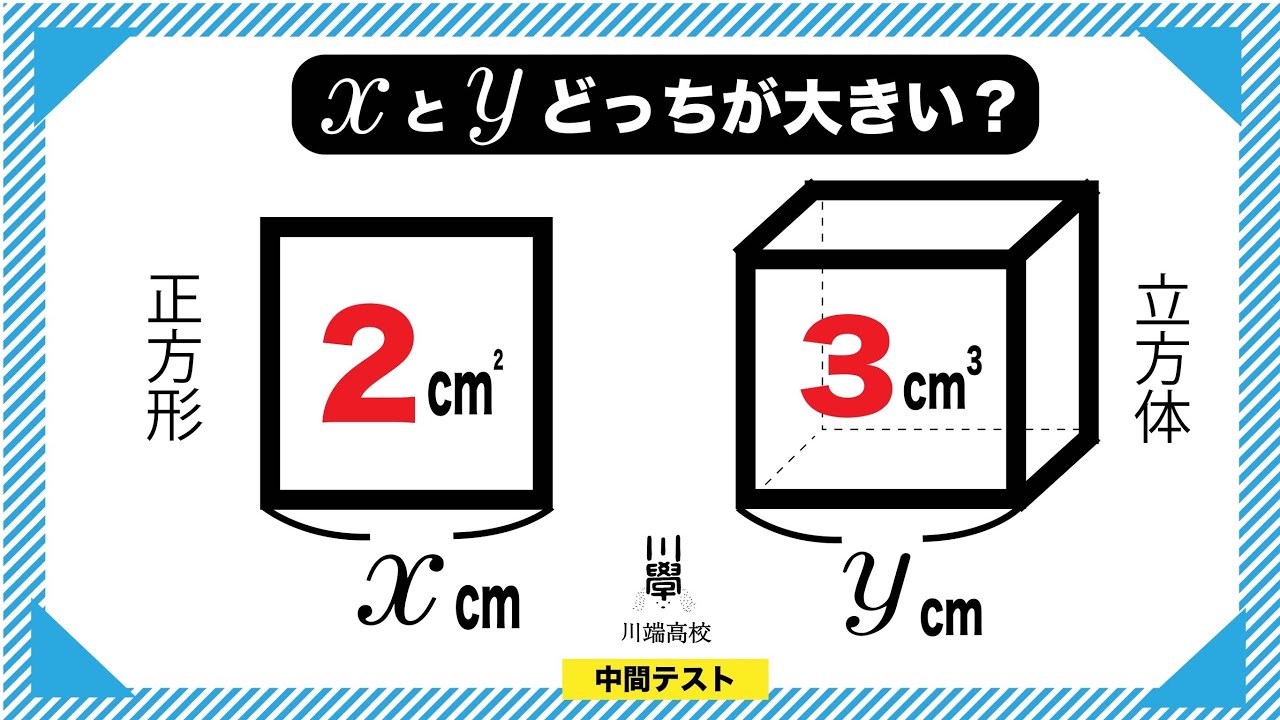
中3生も解けるし どっちが大きい?
福田のわかった数学〜高校1年生078〜場合の数(17)道順(4)

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(17) 道順(4)
赤玉6個、白玉6個が入った袋から、1個ずつ玉を取り出す。
(取り出した玉は元に戻さない)全部の玉を取り出すとき、
常に取り出した赤玉の個数が取り出した白玉の個数を下回らないような
取り出し方は何通りあるか。同じ色の玉には区別がないものとする。
この動画を見る
数学$\textrm{I}$ 場合の数(17) 道順(4)
赤玉6個、白玉6個が入った袋から、1個ずつ玉を取り出す。
(取り出した玉は元に戻さない)全部の玉を取り出すとき、
常に取り出した赤玉の個数が取り出した白玉の個数を下回らないような
取り出し方は何通りあるか。同じ色の玉には区別がないものとする。
2022年問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(45+\sqrt{2022})^{2022}$の1の位を求めよ.
この動画を見る
$(45+\sqrt{2022})^{2022}$の1の位を求めよ.
