 数A
数A
 数A
数A
九州大の過去問をパクって問題作ってみた

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^3+3b^3=7c^3$を満たす整数$(a,b,c)$の組をすべて求めよ.
この動画を見る
$a^3+3b^3=7c^3$を満たす整数$(a,b,c)$の組をすべて求めよ.
福田のわかった数学〜高校1年生069〜場合の数(8)円順列その2

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(8) 円順列(2)
次のような玉を円形に並べる方法は何通りか。
(1)白玉1個、黄玉2個、赤玉3個
(2)白玉2個、赤玉4個
(3)白玉2個、黄玉2個、赤玉2個
この動画を見る
数学$\textrm{I}$ 場合の数(8) 円順列(2)
次のような玉を円形に並べる方法は何通りか。
(1)白玉1個、黄玉2個、赤玉3個
(2)白玉2個、赤玉4個
(3)白玉2個、黄玉2個、赤玉2個
高校入試の軌跡の問題
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
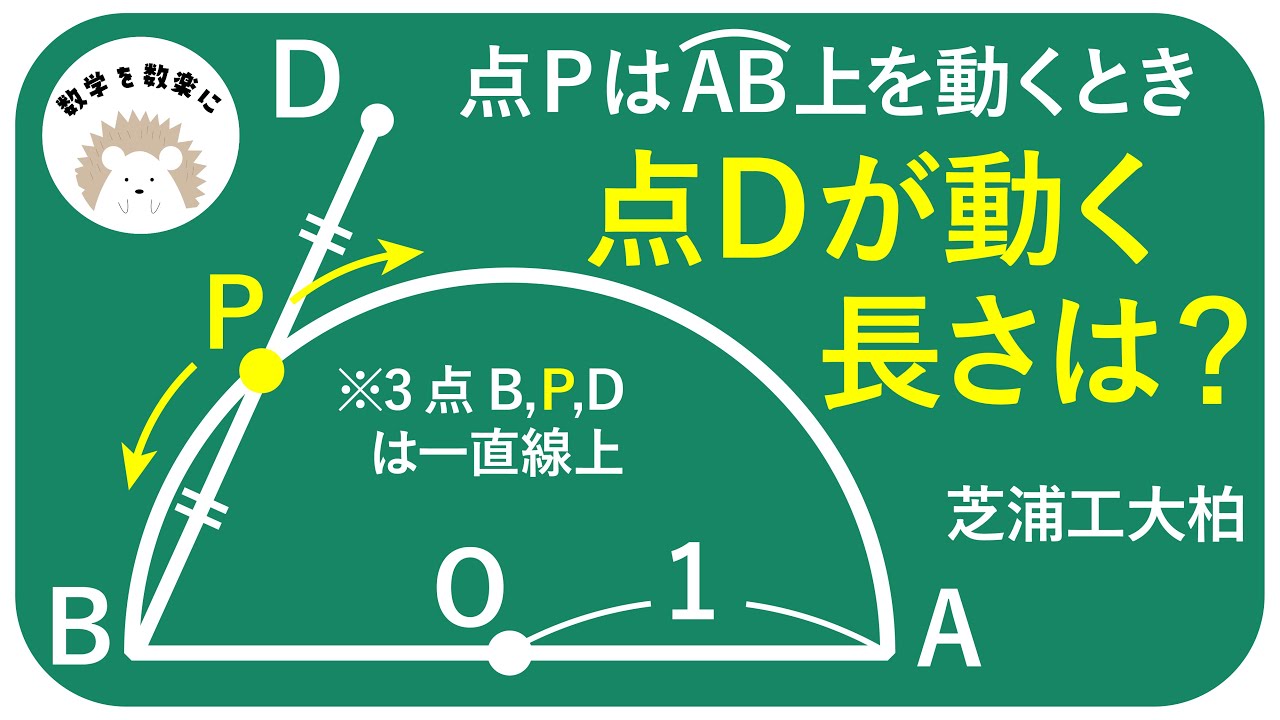
点Pは$\stackrel{\huge\frown}{AB}$上を動く。
BP=DPとなるように点Dを定めるとき点Dが動く長さは?
芝浦工業大学柏高等学校
この動画を見る
点Pは$\stackrel{\huge\frown}{AB}$上を動く。
BP=DPとなるように点Dを定めるとき点Dが動く長さは?
芝浦工業大学柏高等学校
指数方程式 解は1つではない

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^x・2^{\frac{6}{x}}=72$
この動画を見る
実数解を求めよ.
$3^x・2^{\frac{6}{x}}=72$
福田のわかった数学〜高校1年生068〜場合の数(7)円順列
単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(7) 円順列
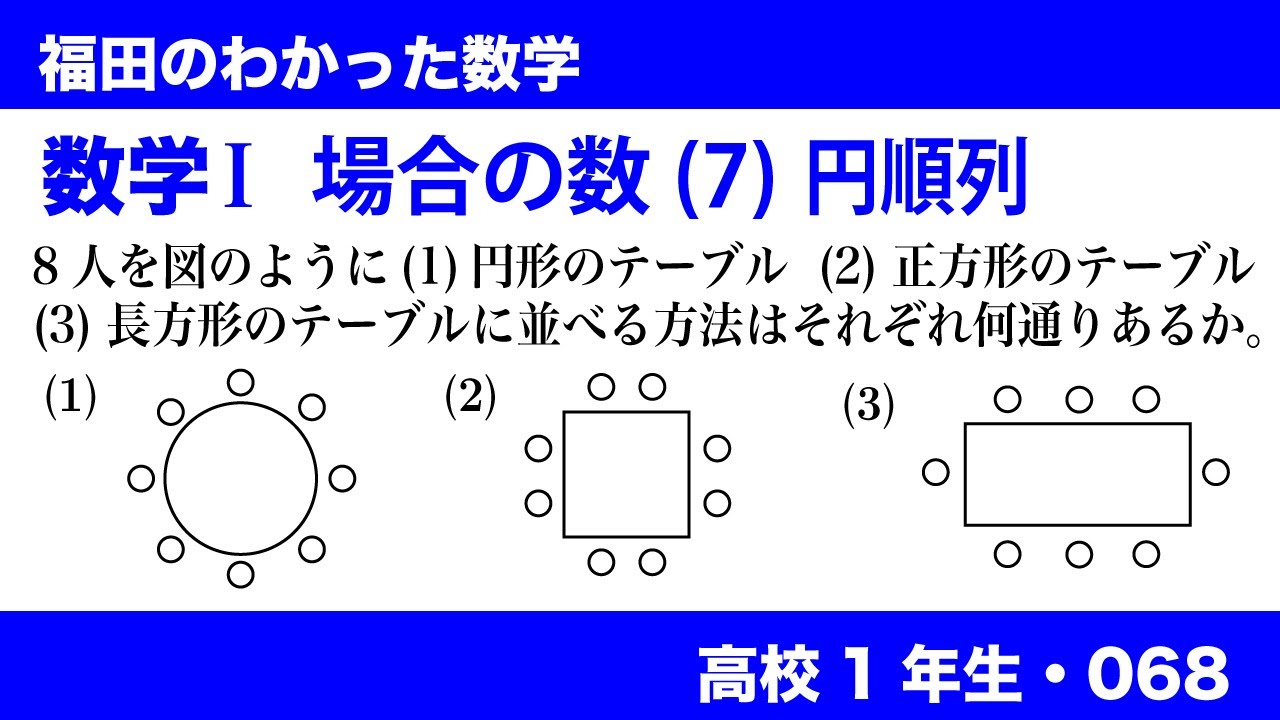
8人を図のように(1)円形のテーブル (2)正方形のテーブル (3)長方形のテーブルに並べる方法は
それぞれ何通りあるか。
(※図は動画参照)
この動画を見る
数学$\textrm{I}$ 場合の数(7) 円順列
8人を図のように(1)円形のテーブル (2)正方形のテーブル (3)長方形のテーブルに並べる方法は
それぞれ何通りあるか。
(※図は動画参照)
たった4という数字だけで。。。
単元:
#中1数学#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
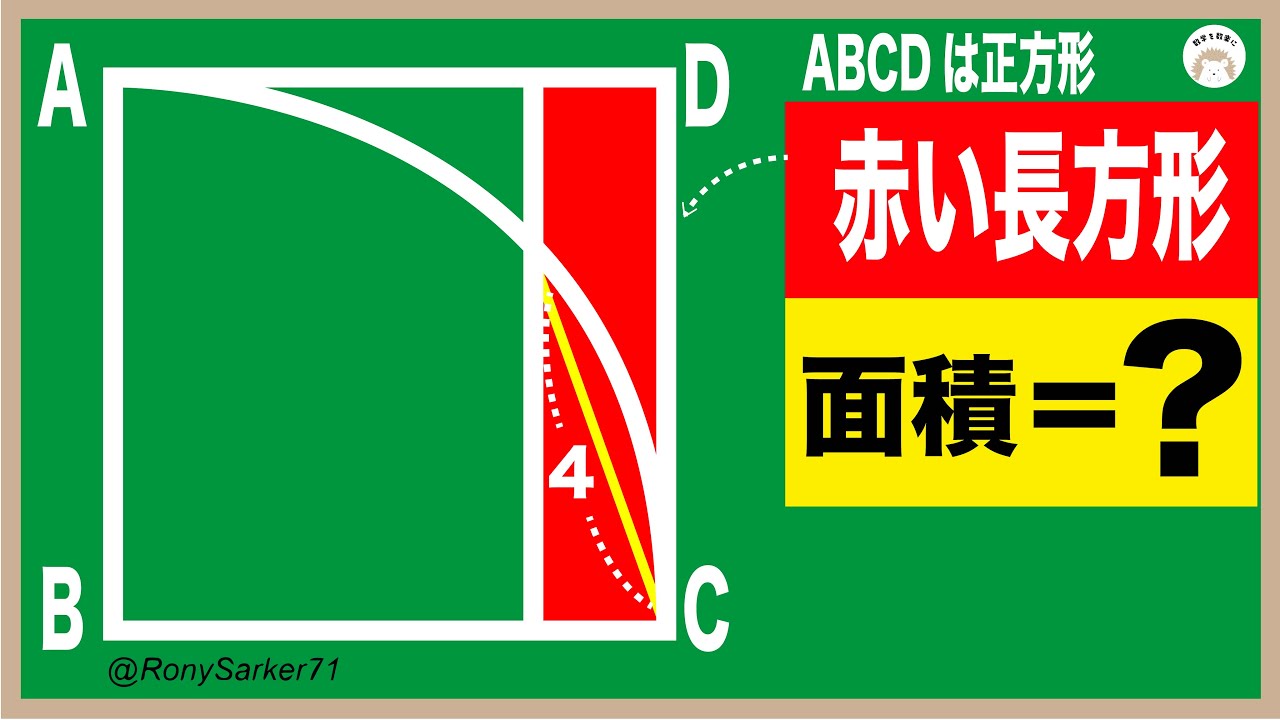
長方形の面積=?
*図は動画内参照
この動画を見る
長方形の面積=?
*図は動画内参照
京都と言ったら八つ橋くらい定番です
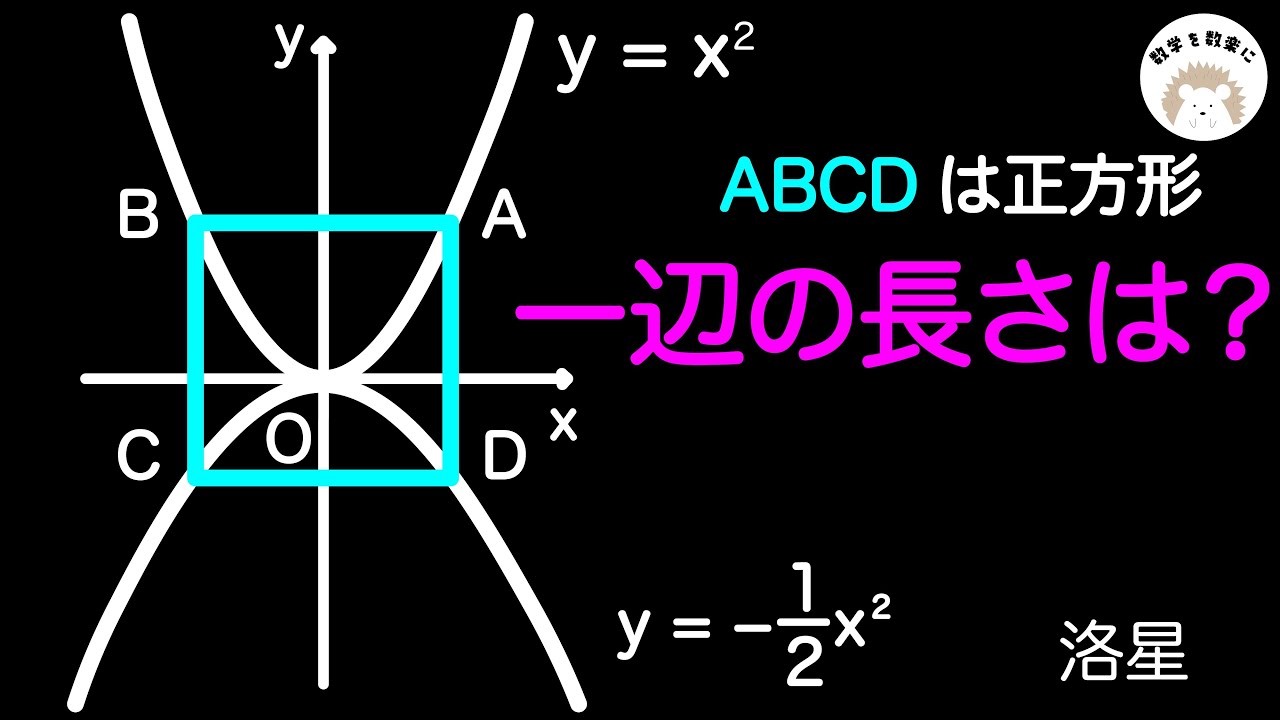
見掛け倒しの対数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\log_{\log_6(x-3)}81=4$
この動画を見る
これを解け.
$\log_{\log_6(x-3)}81=4$
福田のわかった数学〜高校1年生067〜場合の数(6)色々な順列

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(6) 並べ方色々
さいころを4回投げたとき、出た目を順に$a,b,c,d$とする。
次のような目の出方は何通りあるか。
(1)全て異なる目が出る
(2)$a \lt b \lt c \lt d$
(3)$a \leqq b \leqq c \leqq d$
この動画を見る
数学$\textrm{I}$ 場合の数(6) 並べ方色々
さいころを4回投げたとき、出た目を順に$a,b,c,d$とする。
次のような目の出方は何通りあるか。
(1)全て異なる目が出る
(2)$a \lt b \lt c \lt d$
(3)$a \leqq b \leqq c \leqq d$
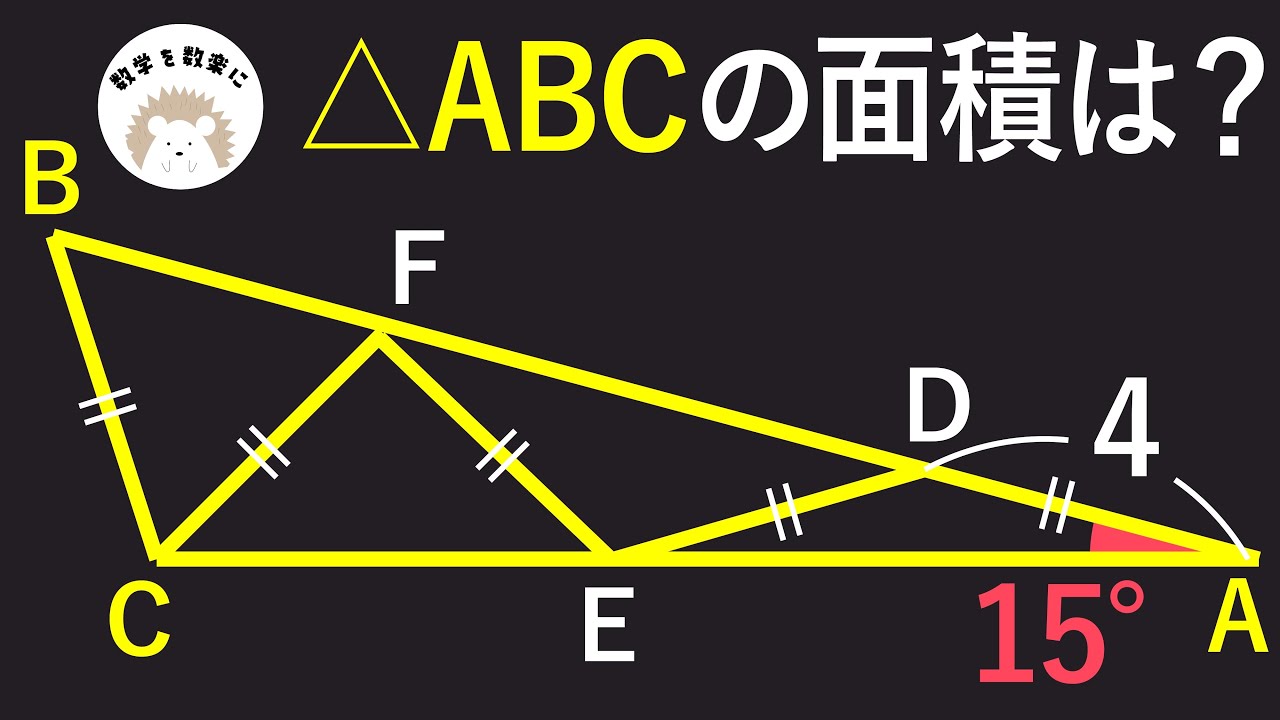
「長さ等しい」がいっぱい
【演習で復習・解説!】条件付き確率を5分で復習!〔数学 高校数学〕

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
大小のサイコロを1個ずつ投げた。このとき以下の2つの事象を定義する。
A: 大きいサイコロの目が4
B: サイコロの目の和が9
以下の問に答えよ。
(1)事象Aが起こる確率と事象Bが起こる確率をそれぞれ求めよ。
(2)事象Bが起こった時の事象Aが起こる条件付き確率を求めよ。
この動画を見る
大小のサイコロを1個ずつ投げた。このとき以下の2つの事象を定義する。
A: 大きいサイコロの目が4
B: サイコロの目の和が9
以下の問に答えよ。
(1)事象Aが起こる確率と事象Bが起こる確率をそれぞれ求めよ。
(2)事象Bが起こった時の事象Aが起こる条件付き確率を求めよ。
連続する五つの整数から一つ除く

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
連続する5つの整数がある。そのうち1つを除いた4つの整数の和は2017となる。
除いた数を求めよ。
明治大学付属明治高等学校
この動画を見る
連続する5つの整数がある。そのうち1つを除いた4つの整数の和は2017となる。
除いた数を求めよ。
明治大学付属明治高等学校
福田の数学〜立教大学2021年経済学部第1問(3)〜さいころの確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(3)3個のさいころを1回投げるとき、出た目の最大値が3となる確率は
$\boxed{エ}$であり、また、出た目の積が8となる確率は$\boxed{オ}$である。
2021立教大学経済学部過去問
この動画を見る
${\Large\boxed{1}}$(3)3個のさいころを1回投げるとき、出た目の最大値が3となる確率は
$\boxed{エ}$であり、また、出た目の積が8となる確率は$\boxed{オ}$である。
2021立教大学経済学部過去問
福田のわかった数学〜高校1年生066〜場合の数(5)色々な順列

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(5) 並べ方色々
男子5人、女子3人(a,b,cとする)が次のように横一列に
並ぶ方法は何通りか。
(1)女子3人が隣り合う並び方
(2)どの女子2人も隣り合わない並び方
(3)aがbより左、bがcより左に現れる並び方
この動画を見る
数学$\textrm{I}$ 場合の数(5) 並べ方色々
男子5人、女子3人(a,b,cとする)が次のように横一列に
並ぶ方法は何通りか。
(1)女子3人が隣り合う並び方
(2)どの女子2人も隣り合わない並び方
(3)aがbより左、bがcより左に現れる並び方
高校入試最上級レベル 球の断面積
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
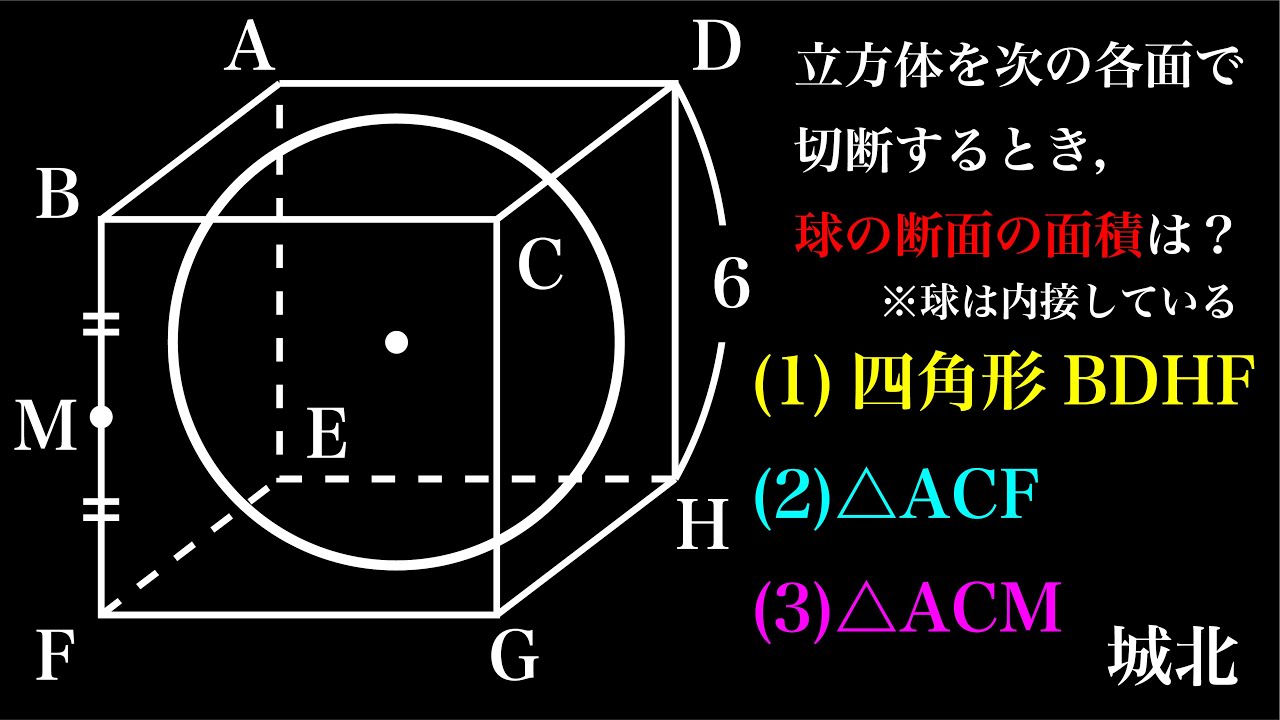
立方体を次の各面で切断したときの球の断面積=?
(1)四角形BDHF
(2)△ACF
(3)△ACH
*図は動画内参照
城北高等学校
この動画を見る
立方体を次の各面で切断したときの球の断面積=?
(1)四角形BDHF
(2)△ACF
(3)△ACH
*図は動画内参照
城北高等学校
福田の数学〜立教大学2021年経済学部第1問(2)〜円に内接する四角形

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)円Cに内接する四角形PQRSにおいて、対角線PRは円Cの中心Oを通る。
また、各辺の長さは、$PQ=1, QR=8, RS=4, SP=7$であり、
角Pの大きさを$\theta$とする。ただし、$0 \lt \theta \lt \pi$とする。
このとき円Cの直径は$\boxed{イ},\cos\theta=\boxed{ウ}$である。
2021立教大学経済学部過去問
この動画を見る
${\Large\boxed{1}}$(2)円Cに内接する四角形PQRSにおいて、対角線PRは円Cの中心Oを通る。
また、各辺の長さは、$PQ=1, QR=8, RS=4, SP=7$であり、
角Pの大きさを$\theta$とする。ただし、$0 \lt \theta \lt \pi$とする。
このとき円Cの直径は$\boxed{イ},\cos\theta=\boxed{ウ}$である。
2021立教大学経済学部過去問
いい問題
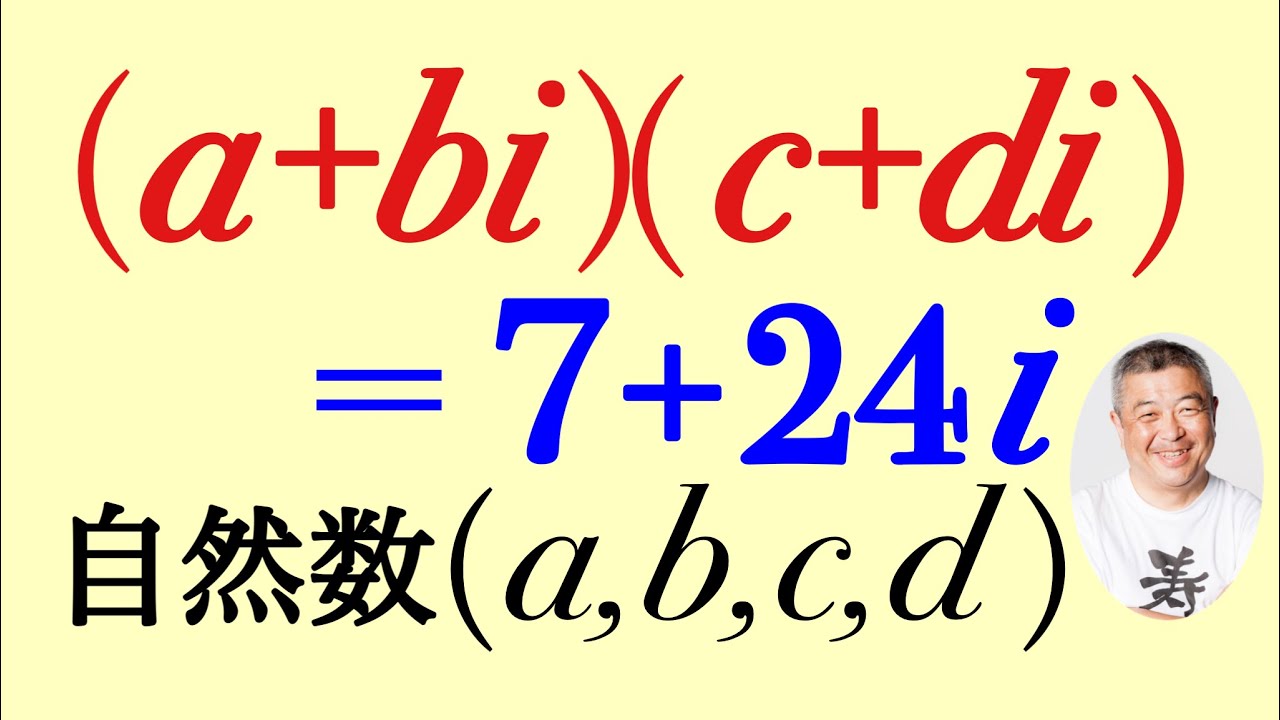
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$(a,b,c,d)$をすべて求めよ.
$(a+bi)(c+di)=7+24i$
この動画を見る
自然数$(a,b,c,d)$をすべて求めよ.
$(a+bi)(c+di)=7+24i$
福田のわかった数学〜高校1年生065〜場合の数(4)0を含む順列

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(4) 0を含む順列
$0,1,2,3,4,5,6$から異なる4個を選んで
4桁の整数を作るとき、次の個数を求めよ。
(1)全部で (2)偶数 (3)奇数 (4)9の倍数 (5)4の倍数
この動画を見る
数学$\textrm{I}$ 場合の数(4) 0を含む順列
$0,1,2,3,4,5,6$から異なる4個を選んで
4桁の整数を作るとき、次の個数を求めよ。
(1)全部で (2)偶数 (3)奇数 (4)9の倍数 (5)4の倍数
不思議な方程式。優秀な視聴者様!疑問に答えて!
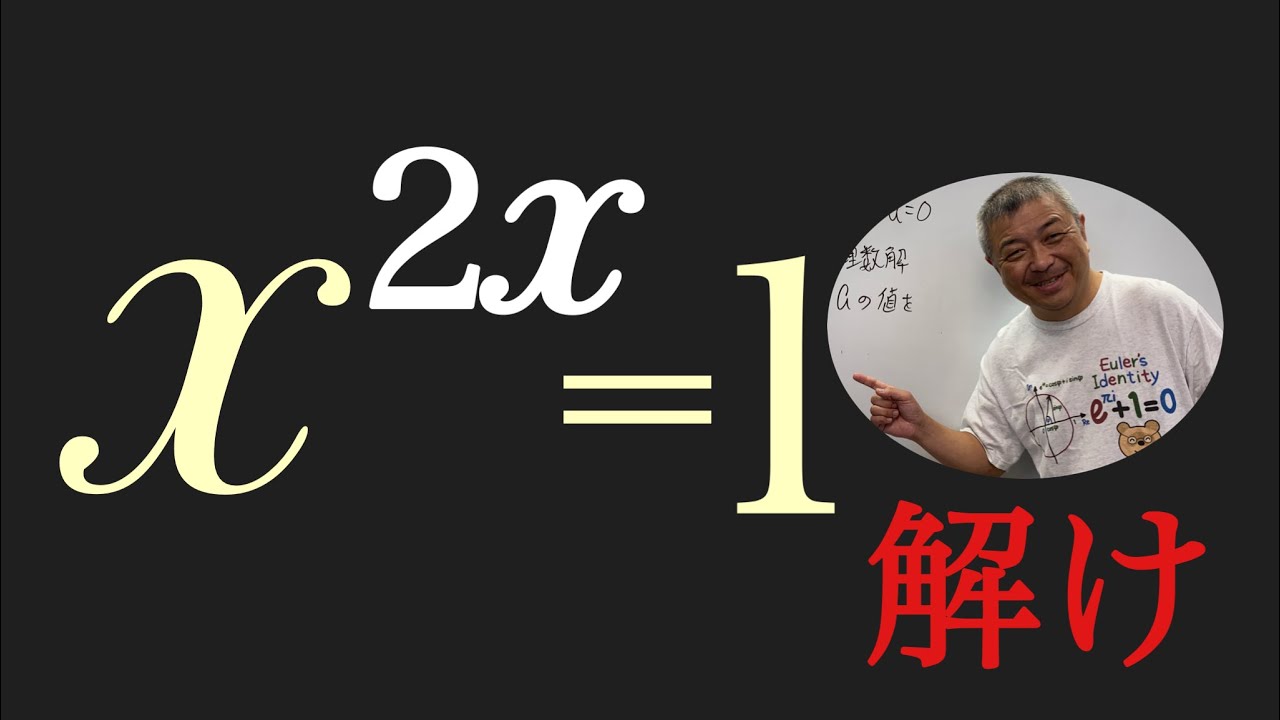
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x$は実数である.
$x^{2x}=1$
この動画を見る
これを解け.$x$は実数である.
$x^{2x}=1$
藤井聡太 三冠 竜王奪取の確率を計算する

福田のわかった数学〜高校1年生064〜場合の数(3)約数の個数と総和

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(3) 約数の総和
600の正の約数の個数と総和を求めよ。
また、正の約数のうち、偶数であるものの
個数とその総和を求めよ。
この動画を見る
数学$\textrm{I}$ 場合の数(3) 約数の総和
600の正の約数の個数と総和を求めよ。
また、正の約数のうち、偶数であるものの
個数とその総和を求めよ。
ウィルソンの定理

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$22!$を$23$で割った余りを求めよ.
$100!$を$101$で割った余りを求めよ.
この動画を見る
$22!$を$23$で割った余りを求めよ.
$100!$を$101$で割った余りを求めよ.
福田の数学〜立教大学2021年理学部第1問(3)〜じゃんけんの確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(3)4人でじゃんけんを1回するとき、ちょうど2人が勝つ確率は$\boxed{\ \ ウ\ \ }$であり、
また、だれも勝たない確率は$\boxed{\ \ エ\ \ }$である。
2021立教大学理学部過去問
この動画を見る
${\Large\boxed{1}}$(3)4人でじゃんけんを1回するとき、ちょうど2人が勝つ確率は$\boxed{\ \ ウ\ \ }$であり、
また、だれも勝たない確率は$\boxed{\ \ エ\ \ }$である。
2021立教大学理学部過去問
e^π>22 示せ
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$e^{\pi}\gt 22$を示せ.
$e \gt 2.71,\pi\gt 3.14$
この動画を見る
$e^{\pi}\gt 22$を示せ.
$e \gt 2.71,\pi\gt 3.14$
福田のわかった数学〜高校1年生063〜場合の数(2)完全順列

単元:
#数A#場合の数と確率#場合の数#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(2) 完全順列
1,2,3,4を1列に並べたものを$a_1a_2a_3a_4$とする。
$a_1\neq 1,a_2\neq 2,a_3\neq 3,a_4\neq 4$を満たす並べ方は何通りあるか。
この動画を見る
数学$\textrm{I}$ 場合の数(2) 完全順列
1,2,3,4を1列に並べたものを$a_1a_2a_3a_4$とする。
$a_1\neq 1,a_2\neq 2,a_3\neq 3,a_4\neq 4$を満たす並べ方は何通りあるか。
放物線と正三角形 成蹊
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
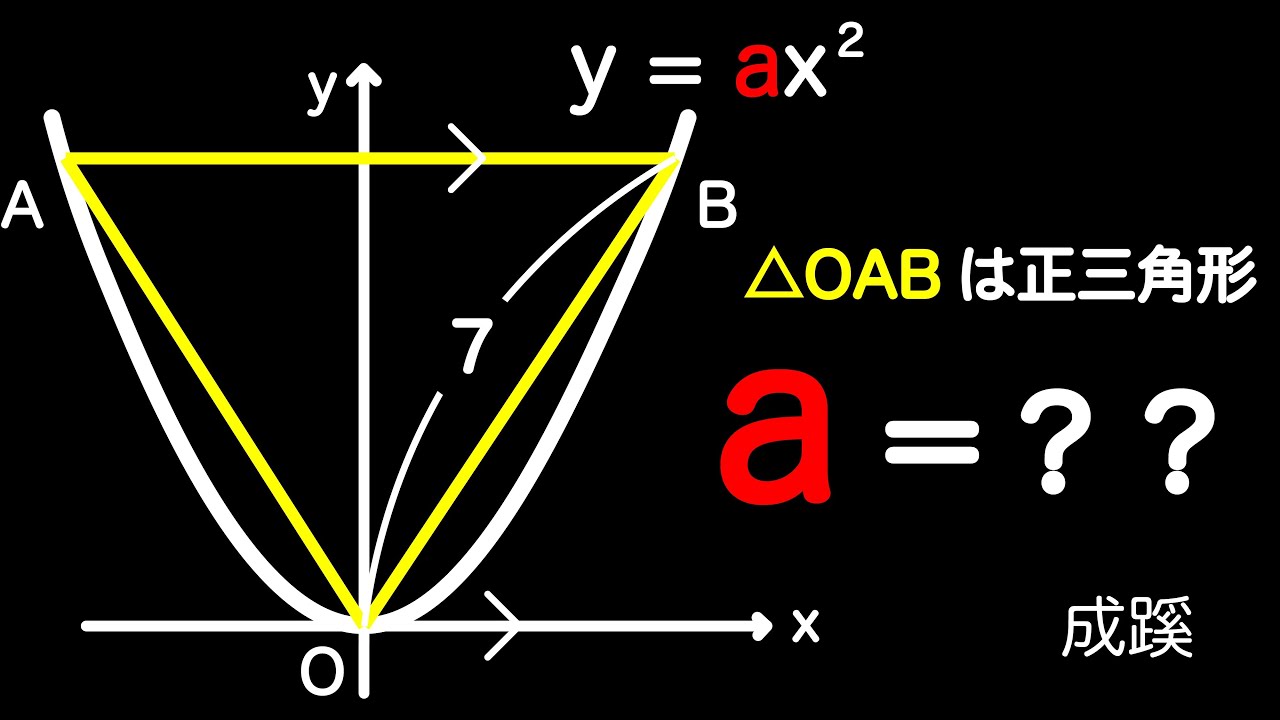
△OABは正三角形
a=?
*図は動画内参照
成蹊高等学校
この動画を見る
△OABは正三角形
a=?
*図は動画内参照
成蹊高等学校
補助線を引く喜びを
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
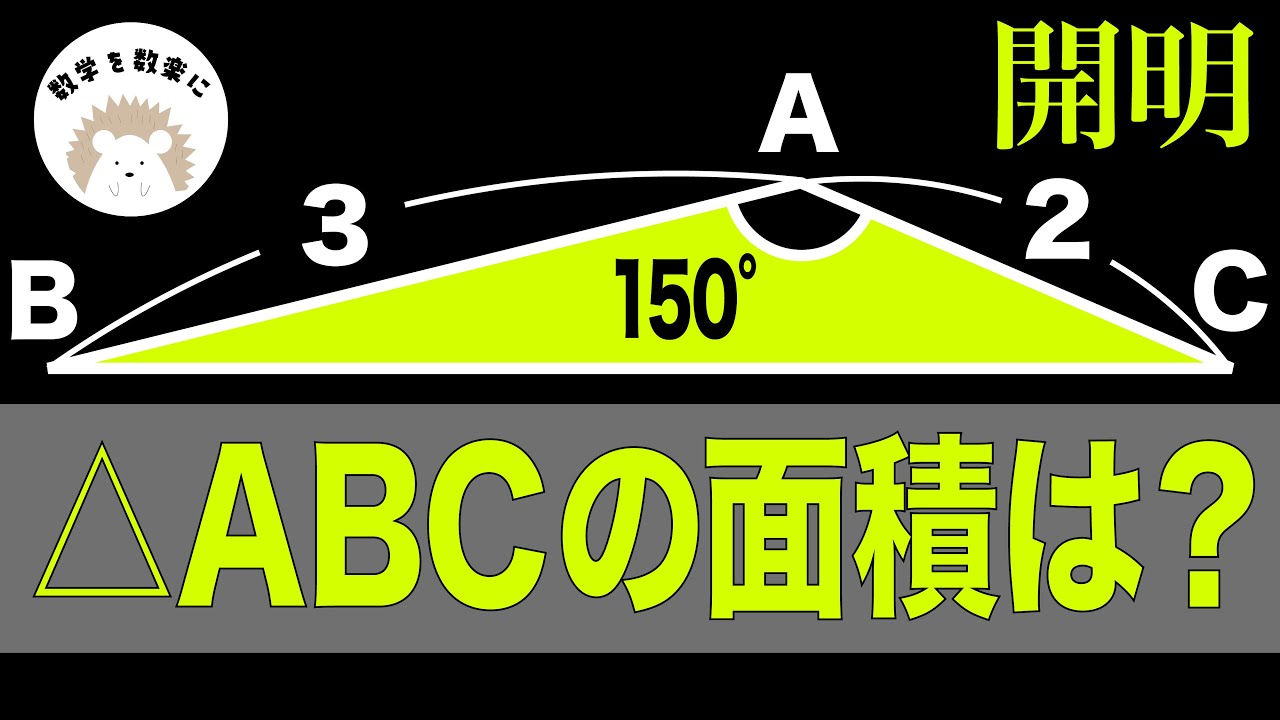
△ABC=?
*図は動画内参照
開明高等学校
この動画を見る
△ABC=?
*図は動画内参照
開明高等学校
【順番を守れば怖くない!】チェバ・メネラウスの定理はこう攻略する!〔高校数学 数学〕

おうぎ形と円

単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
赤い円の面積=?
*図は動画内参照
この動画を見る
赤い円の面積=?
*図は動画内参照
福田の数学〜明治大学2021年理工学部第2問〜格子点と確率

単元:
#数A#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#大学入試解答速報#数学#明治大学#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$ nを正の整数とする。座標平面上の点でx座標とy座標がともに整数であるもの
を格子点と呼ぶ。$|x|+|y|=2n$を満たす格子点(x,\ y)全体の集合を$D_{2n}$とする。
(1)$D_4$は$\boxed{\ \ あ\ \ }$個の点からなる。一般に、$D_{2n}$は$\boxed{\ \ い\ \ }$個の点からなる。
(2)$D_{2n}$に属する点$(x,\ y)$で$|x-2n|+|y|=2n$を満たすものは全部で$\boxed{\ \ う\ \ }$個ある。
(3)$D_{2n}$に属する点$(x,\ y)$で$|x-n|+|y-n|=2n$を満たすものは全部で$\boxed{\ \ え\ \ }$個ある。
(4)$D_{2n}$から異なる2点$(x_1,\ y_1),\ (x_2,\ y_2)$を無作為に選ぶとき、
$|x_1-x_2|+|y_1-y_2|=2n$
が成り立つ確率は$\boxed{\ \ お\ \ }$である。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{2}}$ nを正の整数とする。座標平面上の点でx座標とy座標がともに整数であるもの
を格子点と呼ぶ。$|x|+|y|=2n$を満たす格子点(x,\ y)全体の集合を$D_{2n}$とする。
(1)$D_4$は$\boxed{\ \ あ\ \ }$個の点からなる。一般に、$D_{2n}$は$\boxed{\ \ い\ \ }$個の点からなる。
(2)$D_{2n}$に属する点$(x,\ y)$で$|x-2n|+|y|=2n$を満たすものは全部で$\boxed{\ \ う\ \ }$個ある。
(3)$D_{2n}$に属する点$(x,\ y)$で$|x-n|+|y-n|=2n$を満たすものは全部で$\boxed{\ \ え\ \ }$個ある。
(4)$D_{2n}$から異なる2点$(x_1,\ y_1),\ (x_2,\ y_2)$を無作為に選ぶとき、
$|x_1-x_2|+|y_1-y_2|=2n$
が成り立つ確率は$\boxed{\ \ お\ \ }$である。
2021明治大学理工学部過去問
