 複素数と方程式
複素数と方程式
 複素数と方程式
複素数と方程式
複素数 広島大

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z^2=8+6i$のとき,$z^3-16z-\dfrac{100}{z}$の値を求めよ.
1966広島大過去問
この動画を見る
$z^2=8+6i$のとき,$z^3-16z-\dfrac{100}{z}$の値を求めよ.
1966広島大過去問
n乗根の方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x,y$は実数である.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=10 \\
\sqrt[3]{x}+\sqrt[3]{y}=\dfrac{5}{2}\sqrt[6]{xy}
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.$x,y$は実数である.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=10 \\
\sqrt[3]{x}+\sqrt[3]{y}=\dfrac{5}{2}\sqrt[6]{xy}
\end{array}
\right.
\end{eqnarray}$
三次方程式の実数解 埼玉大

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$12x^3-21x^2+2x+4=0$
(1)正の実数を2つ,負の実数解を1つもつことを示せ.
(2)正の実数解を$\alpha,\beta(\alpha \lt \beta)$とするとき,$\vert \alpha-1 \vert,\vert \beta-1 \vert $の大小比較せよ.
1982埼玉大過去問
この動画を見る
$12x^3-21x^2+2x+4=0$
(1)正の実数を2つ,負の実数解を1つもつことを示せ.
(2)正の実数解を$\alpha,\beta(\alpha \lt \beta)$とするとき,$\vert \alpha-1 \vert,\vert \beta-1 \vert $の大小比較せよ.
1982埼玉大過去問
式の値
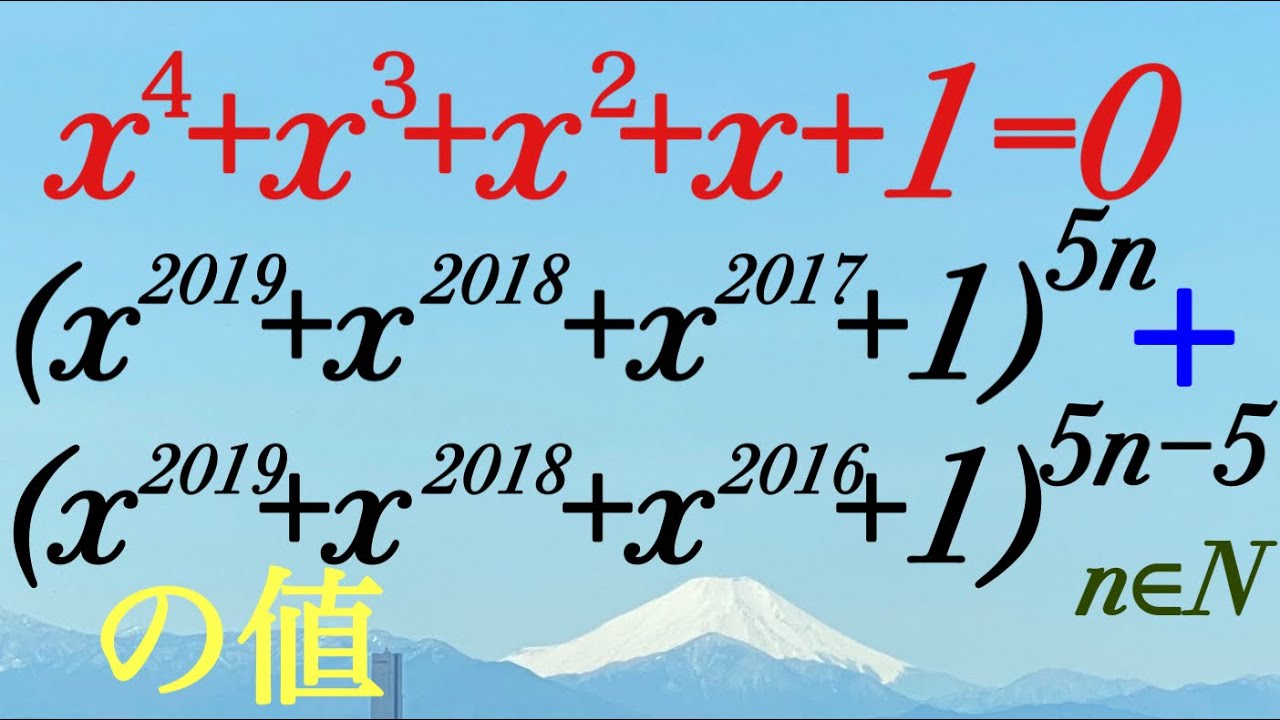
単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^4+x^3+x^2+x+1=0$を満たすとき,
$(x^{2019}+x^{2018}+x^{2017}+1)^{5n}+$
$(x^{2019}+x^{2018}+x^{2016}+1)^{5n-5}$の値を求めよ.
この動画を見る
$x^4+x^3+x^2+x+1=0$を満たすとき,
$(x^{2019}+x^{2018}+x^{2017}+1)^{5n}+$
$(x^{2019}+x^{2018}+x^{2016}+1)^{5n-5}$の値を求めよ.
複素数の3次方程式

複素数の計算 群馬大

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z=\dfrac{\sqrt3-1}{2}+\dfrac{\sqrt3+1}{2}i$である.$z^{12}$の値を求めよ
(1)$\dfrac{z}{1+i}$を$a+bi$の形で表せ.
(2)$z$を極形式で表せ.
群馬大過去問
この動画を見る
$z=\dfrac{\sqrt3-1}{2}+\dfrac{\sqrt3+1}{2}i$である.$z^{12}$の値を求めよ
(1)$\dfrac{z}{1+i}$を$a+bi$の形で表せ.
(2)$z$を極形式で表せ.
群馬大過去問
複素数とは?名古屋工業大

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(\sqrt3+i)^m=(1+i)^n$,最小の自然数$m,n$を求めよ.
1967名古屋工大過去問
この動画を見る
$(\sqrt3+i)^m=(1+i)^n$,最小の自然数$m,n$を求めよ.
1967名古屋工大過去問
複素数 学習院大

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z$は複素数であり,$\dfrac{z-1-3i}{z-2}$が純虚数である.
$\vert z \vert$の最大値と最小値を求めよ.
学習院大過去問
この動画を見る
$z$は複素数であり,$\dfrac{z-1-3i}{z-2}$が純虚数である.
$\vert z \vert$の最大値と最小値を求めよ.
学習院大過去問
京都大 三次方程式の解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$k\gt 0$であるとする.
$x(x+3)(x-3)+3k(x+1)(x-1)=0$が3つ実数解をもつことを示せ.
1967京都大(文理共通)過去問
この動画を見る
$k\gt 0$であるとする.
$x(x+3)(x-3)+3k(x+1)(x-1)=0$が3つ実数解をもつことを示せ.
1967京都大(文理共通)過去問
東工大 三次方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$k \gt 0$である.
$x^3-x+k=0$は絶対値が1の虚数解をもつ.3つの解を求めよ.
1972東工大過去問
この動画を見る
$k \gt 0$である.
$x^3-x+k=0$は絶対値が1の虚数解をもつ.3つの解を求めよ.
1972東工大過去問
京都大 三次方程式有理数解

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3+x-8=0$の解は無理数であることを示せ.
1966京都大過去問
この動画を見る
$x^3+x-8=0$の解は無理数であることを示せ.
1966京都大過去問
北里大 複素数の総和

単元:
#数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z=-1+i$
$\displaystyle \sum_{n=1}^{12} z^n$
出典:2014年北里大学 過去問
この動画を見る
$z=-1+i$
$\displaystyle \sum_{n=1}^{12} z^n$
出典:2014年北里大学 過去問
神戸大 複素数 三次方程式

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z^3-2|z|+1=0$を満たす$z$のうち実数でないものの個数を求めよ
出典:1968年神戸大学 過去問
この動画を見る
$z^3-2|z|+1=0$を満たす$z$のうち実数でないものの個数を求めよ
出典:1968年神戸大学 過去問
神戸大 複素数の2次方程式

単元:
#数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2+i=0$を解け
出典:1971年神戸大学 過去問
この動画を見る
$x^2+i=0$を解け
出典:1971年神戸大学 過去問
名古屋市立大 3次方程式が相違3実数解を持つ条件

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋市立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3-kx+k=0$が相異なる3つの実数解をもつ$k$の範囲を求めよ
出典:名古屋市立大学 過去問
この動画を見る
$x^3-kx+k=0$が相異なる3つの実数解をもつ$k$の範囲を求めよ
出典:名古屋市立大学 過去問
山梨大 複素数の4乗根

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z$複素数
$z^4=-8-8\sqrt{ 3 }i$
出典:山梨大学 過去問
この動画を見る
$z$複素数
$z^4=-8-8\sqrt{ 3 }i$
出典:山梨大学 過去問
指数方程式 指数公式 杏林大

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$4^x-1=2^{x-\displaystyle \frac{1}{2}}$
出典:杏林大学 過去問
この動画を見る
$4^x-1=2^{x-\displaystyle \frac{1}{2}}$
出典:杏林大学 過去問
九州大 三次方程式と無理数

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z=\cos2 0^{ \circ }+i \sin20^{ \circ }$
$\alpha=z+\bar{ z }$
(1)
$\alpha$を解に持つ整数、係数の3次方程式を求めよ
(2)
(1)で求めた方程式は相異なる3つの実数解をもち、それらはすべて無理数となることを示せ
(3)
$\alpha$を解にもつ有理数係数の2次方程式はないことを示せ
出典:2000年九州大学 過去問
この動画を見る
$z=\cos2 0^{ \circ }+i \sin20^{ \circ }$
$\alpha=z+\bar{ z }$
(1)
$\alpha$を解に持つ整数、係数の3次方程式を求めよ
(2)
(1)で求めた方程式は相異なる3つの実数解をもち、それらはすべて無理数となることを示せ
(3)
$\alpha$を解にもつ有理数係数の2次方程式はないことを示せ
出典:2000年九州大学 過去問
横浜国大 三角方程式 4倍角

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$0 \leqq \theta \lt 2\pi$
$1-2\cos 3\theta+\cos4\theta=0$
解の個数を求めよ
出典:2000年横浜国立大学 過去問
この動画を見る
$0 \leqq \theta \lt 2\pi$
$1-2\cos 3\theta+\cos4\theta=0$
解の個数を求めよ
出典:2000年横浜国立大学 過去問
九州大 COS7.5° 複素数
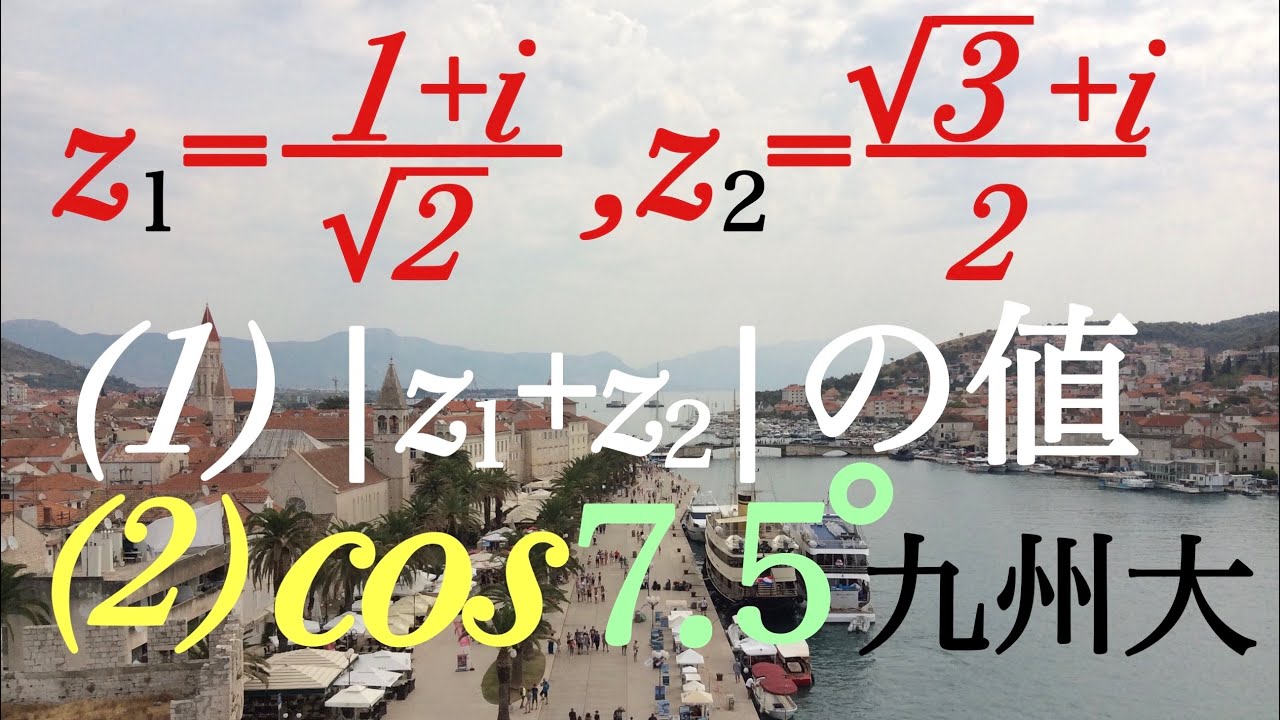
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z_1=\displaystyle \frac{1+i}{\sqrt{ 2 }},z_2=\displaystyle \frac{\sqrt{ 3 }+i}{2}$
(1)
$|z_1+z_2|$の値を求めよ
(2)
$\cos 7.5^{ \circ }$を求めよ
出典:1972年九州大学 過去問
この動画を見る
$z_1=\displaystyle \frac{1+i}{\sqrt{ 2 }},z_2=\displaystyle \frac{\sqrt{ 3 }+i}{2}$
(1)
$|z_1+z_2|$の値を求めよ
(2)
$\cos 7.5^{ \circ }$を求めよ
出典:1972年九州大学 過去問
大阪教育大 複素数の方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#大阪教育大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=1+\sqrt{ 3 }i,\beta=1-\sqrt{ 3 }i$
(1)
$\displaystyle \frac{1}{\alpha^2}+\displaystyle \frac{1}{\beta^2}$の値を求めよ
(2)
$\displaystyle \frac{\beta^8}{\alpha^7}$の値を求めよ
(3)
$z^4=-8\beta$を満たす$z$を求めよ
出典:1999年大阪教育大学 過去問
この動画を見る
$\alpha=1+\sqrt{ 3 }i,\beta=1-\sqrt{ 3 }i$
(1)
$\displaystyle \frac{1}{\alpha^2}+\displaystyle \frac{1}{\beta^2}$の値を求めよ
(2)
$\displaystyle \frac{\beta^8}{\alpha^7}$の値を求めよ
(3)
$z^4=-8\beta$を満たす$z$を求めよ
出典:1999年大阪教育大学 過去問
早稲田大(政)方程式の実数解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$-90^{ \circ } \lt \theta \lt 90^{ \circ }$
$(\sin \theta)x^2+2(\cos2\theta)x+cos2\theta=0$が少なくとも1つの実数解をもつような$\theta$の範囲を求めよ
出典:2001年早稲田大学 政治経済学部 過去問
この動画を見る
$-90^{ \circ } \lt \theta \lt 90^{ \circ }$
$(\sin \theta)x^2+2(\cos2\theta)x+cos2\theta=0$が少なくとも1つの実数解をもつような$\theta$の範囲を求めよ
出典:2001年早稲田大学 政治経済学部 過去問
京都大(文)4次方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^4-x^3+x^2-(a+2)x-a-3=0$が虚軸上の解をもつ実数$a$を求めよ
出典:2001年京都大学 大学院文学研究科 過去問
この動画を見る
$x^4-x^3+x^2-(a+2)x-a-3=0$が虚軸上の解をもつ実数$a$を求めよ
出典:2001年京都大学 大学院文学研究科 過去問
東京都立大 複素数
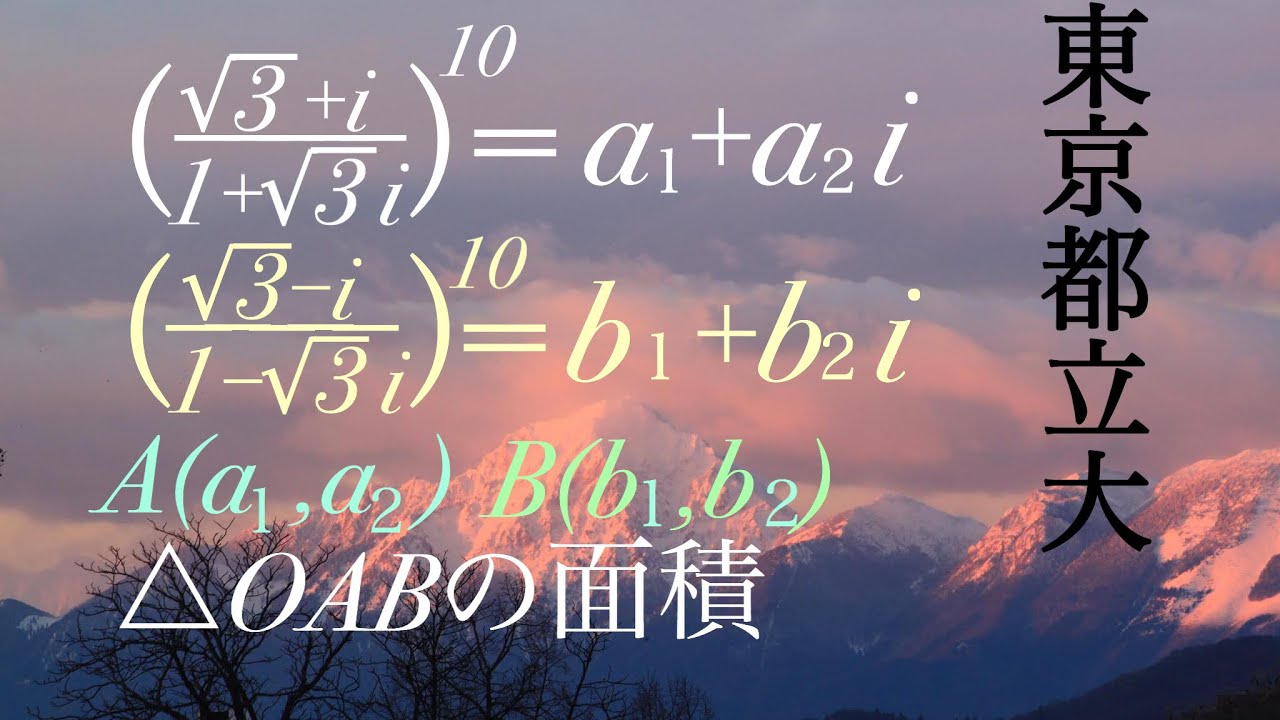
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#東京都立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(\displaystyle \frac{\sqrt{ 3 }+i}{1+\sqrt{ 3 }i})^{10}=a_1+a_2i$
$(\displaystyle \frac{\sqrt{ 3 }-i}{1-\sqrt{ 3 }i})^{10}=b_1+b_2i$
(1)
$a_1,a_2,b_1,b_2$を求めよ
(2)
$A(a_1,a_2)$ $B(b_1,b_2)$
$\triangle OAB$の面積を求めよ
出典:2001年東京都立大学 過去問
この動画を見る
$(\displaystyle \frac{\sqrt{ 3 }+i}{1+\sqrt{ 3 }i})^{10}=a_1+a_2i$
$(\displaystyle \frac{\sqrt{ 3 }-i}{1-\sqrt{ 3 }i})^{10}=b_1+b_2i$
(1)
$a_1,a_2,b_1,b_2$を求めよ
(2)
$A(a_1,a_2)$ $B(b_1,b_2)$
$\triangle OAB$の面積を求めよ
出典:2001年東京都立大学 過去問
九州大 虚数解を持つ4次方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=\sqrt{ 5 }-1+\sqrt{ 10+2\sqrt{ 5 } }i$
$\beta=-\sqrt{ 5 }-1+\sqrt{ 10-2\sqrt{ 5 } }i$
(1)
$\alpha,\beta$の両方を解にもつ実数係数の4次方程式を求めよ
(2)
$\beta^5$の値を求めよ
出典:1999年九州大学 過去問
この動画を見る
$\alpha=\sqrt{ 5 }-1+\sqrt{ 10+2\sqrt{ 5 } }i$
$\beta=-\sqrt{ 5 }-1+\sqrt{ 10-2\sqrt{ 5 } }i$
(1)
$\alpha,\beta$の両方を解にもつ実数係数の4次方程式を求めよ
(2)
$\beta^5$の値を求めよ
出典:1999年九州大学 過去問
光文社新書「中学の知識でオイラー公式がわかる」Vol.15 複素数の絶対値・かけ算

光文社新書「中学の知識でオイラー公式がわかる」Vol14

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2=9$
$(x-2)^2=25$
$x^2=5$
$(x+3)^2=2$
この動画を見る
$x^2=9$
$(x-2)^2=25$
$x^2=5$
$(x+3)^2=2$
岐阜大 積分 3次方程式の実数解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#不定積分・定積分#岐阜大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=2x^3+ax^2-\displaystyle \int_{-2}^{1} x f(t) dt$
$f(x)=0$が異なる3つの実数解をもつ$a$の範囲を求めよ
出典:2013年岐阜大学 過去問
この動画を見る
$f(x)=2x^3+ax^2-\displaystyle \int_{-2}^{1} x f(t) dt$
$f(x)=0$が異なる3つの実数解をもつ$a$の範囲を求めよ
出典:2013年岐阜大学 過去問
センター試験レベル 指数方程式の解 津田塾大

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#津田塾大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x$の方程式
$9^x+2a・3^x+2a^2+a-6=0$が正と負の解を各1つもつ$a$の範囲を求めよ
出典:2000年津田塾大学 過去問
この動画を見る
$x$の方程式
$9^x+2a・3^x+2a^2+a-6=0$が正と負の解を各1つもつ$a$の範囲を求めよ
出典:2000年津田塾大学 過去問
滋賀大 複素数 数列 漸化式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#滋賀大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_n,b_n$整数
$(3+2i)^n=a_n+b_ni$
$a_n,b_n$の一般項を求めよ
出典:滋賀大学 過去問
この動画を見る
$a_n,b_n$整数
$(3+2i)^n=a_n+b_ni$
$a_n,b_n$の一般項を求めよ
出典:滋賀大学 過去問
