 対数関数
対数関数
 対数関数
対数関数
対数の大小比較

練習問題15 教採模試(対数の性質)
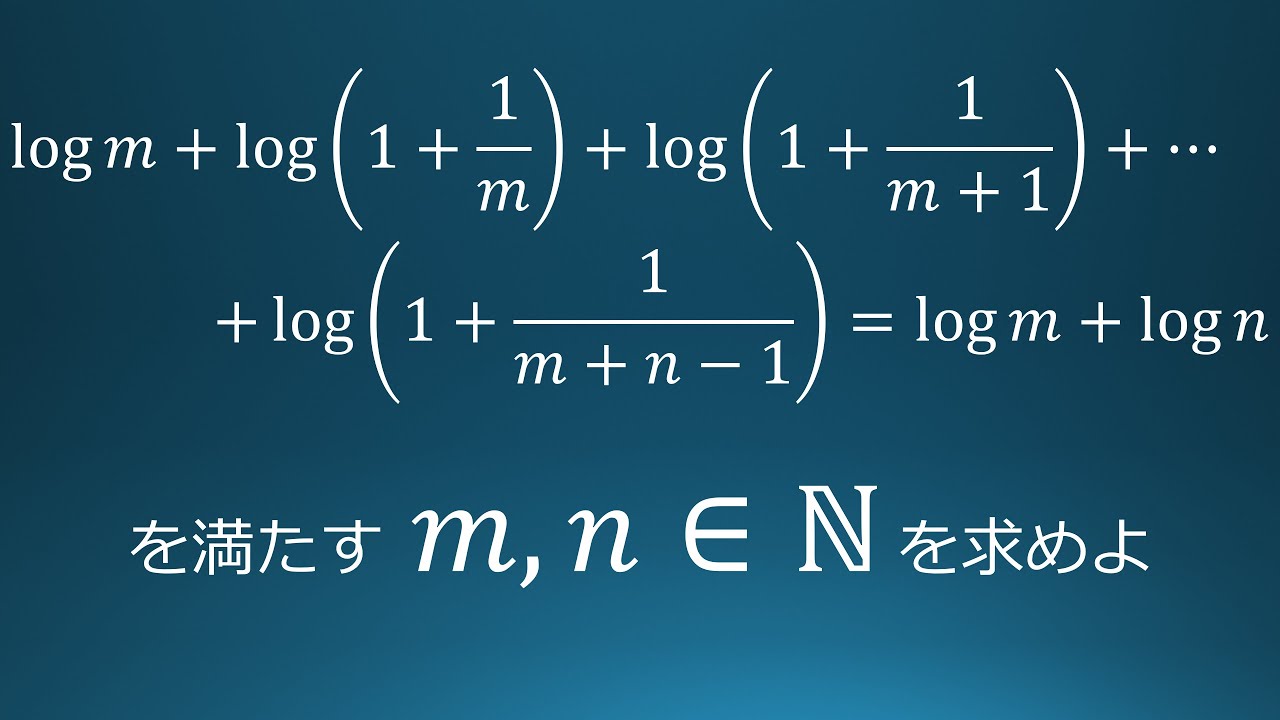
単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$m,n\in IN$
$\log m+\log \left(1+\dfrac{1}{m}\right)+\log \left(1+\dfrac{1}{m+1}\right)$
$+・・・+\log\left(1+\dfrac{1}{m+n-1}\right)$
$=\log \ m+\log\ n$
$m,n$の値を求めよ.
この動画を見る
$m,n\in IN$
$\log m+\log \left(1+\dfrac{1}{m}\right)+\log \left(1+\dfrac{1}{m+1}\right)$
$+・・・+\log\left(1+\dfrac{1}{m+n-1}\right)$
$=\log \ m+\log\ n$
$m,n$の値を求めよ.
共通テスト第2日程2021年数学詳しい解説〜共通テスト第2日程2021年2B第1問〜対数関数と三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#指数関数と対数関数#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第1問}$
[1] (1)$\log_{10}10=\boxed{\ \ ア\ \ }$である。また、$\log_{10}5,\log_{10}15$をそれぞれ
$\log_{10}2と\log_{10}3$を用いて表すと
$\log_{10}5=\boxed{\ \ イ\ \ }\log_{10}2+\boxed{\ \ ウ\ \ }$
$\log_{10}15=$$\boxed{\ \ エ\ \ }\log_{10}2+\log_{10}3+\boxed{\ \ オ\ \ }$
(2)太郎さんと花子さんは、$15^{20}$について話している。
以下では、$\log_{10}2=0.3010、$$\log_{10}3=0.4771$とする。
太郎:$15^{20}$は何桁の数だろう。
花子:$15$の20乗を求めるのは大変だね。$\log_{10}15^{20}$の整数部分に
着目してみようよ。
$\log_{10}15^{20}$は
$\boxed{\ \ カキ\ \ } \lt \log_{10}15^{20}$$ \lt \boxed{\ \ カキ\ \ }+1$
を満たす。よって、$15^{20}は\boxed{\ \ クケ\ \ }$桁の数である。
太郎:$15^{20}$の最高位の数字も知りたいね。だけど、$\log_{10}15^{20}$の
整数部分にだけ着目してもわからないな。
花子:$N・10^{\boxed{カキ}} \lt 15^{20}$$ \lt (N+1)・10^{\boxed{カキ}}$を満たすような
正の整数Nに着目してみたらどうかな。
$\log_{10}15^{20}$の小数部分は$\log_{10}15^{20}-\boxed{\ \ カキ\ \ }$であり
$\log_{10}\boxed{\ \ コ\ \ } \lt \log_{10}15^{20}-\boxed{\ \ カキ\ \ }$$ \lt \log_{10}(\boxed{\ \ コ\ \ }+1)$
が成り立つので、$15^{20}$の最高位の数字は$\boxed{\ \ サ\ \ }$である。
[2]座標平面上の原点を中心とする半径1の円周上に3点$P(\cos\theta,\sin\theta),$
$Q(\cos\alpha,\sin\alpha),R(\cos\beta,\sin\beta)$がある。ただし、$0 \leqq \theta \lt \alpha \lt \beta \lt 2\pi$
とする。このとき、$s$と$t$を次のように定める。
$s=\cos\theta+\cos\alpha+\cos\beta,$$ t=\sin\theta+\sin\alpha+\sin\beta$
(1)$\triangle PQR$が正三角形や二等辺三角形のときの$s$と$t$の値について考察しよう。
考察$1:\triangle PQR$が正三角形である場合を考える。
この場合、$\alpha,\beta$を$\theta$で表すと
$\alpha=\theta+\displaystyle \frac{\boxed{\ \ シ\ \ }}{3}\pi,$$ \beta=\theta+\displaystyle \frac{\boxed{\ \ ス\ \ }}{3}\pi$
であり、加法定理により
$\cos\alpha=\boxed{\boxed{\ \ セ\ \ }}, \sin\alpha=\boxed{\boxed{\ \ ソ\ \ }}$
である。同様に、$\cos\beta$および$\sin\beta$を、$\sin\theta$と$\cos\theta$を用いて表すことができる。
これらのことから、$s=t=\boxed{\ \ タ\ \ }$である。
$\boxed{\boxed{\ \ セ\ \ }},\boxed{\boxed{\ \ ソ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$\displaystyle \frac{1}{2}\sin\theta+\displaystyle \frac{\sqrt3}{2}\cos\theta$
①$\displaystyle \frac{\sqrt3}{2}\sin\theta+\displaystyle \frac{1}{2}\cos\theta$
②$\displaystyle \frac{1}{2}\sin\theta-\displaystyle \frac{\sqrt3}{2}\cos\theta$
③$\displaystyle \frac{\sqrt3}{2}\sin\theta-\displaystyle \frac{1}{2}\cos\theta$
④$-\displaystyle \frac{1}{2}\sin\theta+\displaystyle \frac{\sqrt3}{2}\cos\theta$
⑤$-\displaystyle \frac{\sqrt3}{2}\sin\theta+\displaystyle \frac{1}{2}\cos\theta$
②$-\displaystyle \frac{1}{2}\sin\theta-\displaystyle \frac{\sqrt3}{2}\cos\theta$
③$-\displaystyle \frac{\sqrt3}{2}\sin\theta-\displaystyle \frac{1}{2}\cos\theta$
考察2:$\triangle PQR$が$PQ=PR$となる二等辺三角形である場合を考える。
例えば、点$P$が直線$y=x$上にあり、点$Q,R$が直線$y=x$に関して対称
であるときを考える。このとき、$\theta=\displaystyle \frac{\pi}{4}$である。また、$\alpha$は
$\alpha \lt \displaystyle \frac{5}{4}\pi, \beta$は$\displaystyle \frac{5}{4}\pi \lt \beta$を満たし、点$Q,R$の座標について、
$\sin\beta=\cos\alpha, \cos\beta=\sin\alpha$が成り立つ。よって
$s=t=\displaystyle \frac{\sqrt{\boxed{\ \ チ\ \ }}}{\boxed{\ \ ツ\ \ }}+\sin\alpha+\cos\alpha$
である。
ここで、三角関数の合成により
$\sin\alpha+\cos\alpha=$$\sqrt{\boxed{\ \ テ\ \ }}\sin\left(\alpha+\displaystyle \frac{\pi}{\boxed{\ \ ト\ \ }}\right)$
である。したがって
$\alpha=\displaystyle \frac{\boxed{\ \ ナニ\ \ }}{12}\pi, \beta=\displaystyle \frac{\boxed{\ \ ヌネ\ \ }}{12}\pi$
のとき、$s=t=0$である。
(2)次に、$s$と$t$の値を定めるときの$\theta,\alpha,\beta$の関係について考察しよう。
考察$3:s=t=0$の場合を考える。
この場合、$\sin^2\theta+\cos^2\theta=1$により、$\alpha$と$\beta$について考えると
$\cos\alpha\cos\beta+\sin\alpha\sin\beta=\displaystyle \frac{\boxed{\ \ ノハ\ \ }}{\boxed{\ \ ヒ\ \ }}$
である。
同様に、$\theta$と$\alpha$について考えると
$\cos\theta\cos\alpha+\sin\theta\sin\alpha=\displaystyle \frac{\boxed{\ \ ノハ\ \ }}{\boxed{\ \ ヒ\ \ }}$
であるから、$\theta,\alpha,\beta$の範囲に注意すると
$\beta-\alpha=\alpha-\theta=\displaystyle \frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}\pi$
という関係が得られる。
(3)これまでの考察を振り返ると、次の⓪~③のうち、
正しいものは$\boxed{\boxed{\ \ ホ\ \ }}$であることが分かる。
$\boxed{\boxed{\ \ ホ\ \ }}$の解答群
⓪$\triangle PQR$が正三角形ならば$s=t=0$であり、$s=t=0$ならば
$\triangle PQR$は正三角形である。
①$\triangle PQR$が正三角形ならば$s=t=0$であり、$s=t=0$で
あっても$\triangle PQR$は正三角形でない場合がある。
②$\triangle PQR$が正三角形であっても$s=t=0$でない場合があるが
$s=t=0$ならば$\triangle PQR$は正三角形である。
③$\triangle PQR$が正三角形であっても$s=t=0$でない場合があり、
$s=t=0$であっても$\triangle PQR$が正三角形でない場合がある。
この動画を見る
${\large第1問}$
[1] (1)$\log_{10}10=\boxed{\ \ ア\ \ }$である。また、$\log_{10}5,\log_{10}15$をそれぞれ
$\log_{10}2と\log_{10}3$を用いて表すと
$\log_{10}5=\boxed{\ \ イ\ \ }\log_{10}2+\boxed{\ \ ウ\ \ }$
$\log_{10}15=$$\boxed{\ \ エ\ \ }\log_{10}2+\log_{10}3+\boxed{\ \ オ\ \ }$
(2)太郎さんと花子さんは、$15^{20}$について話している。
以下では、$\log_{10}2=0.3010、$$\log_{10}3=0.4771$とする。
太郎:$15^{20}$は何桁の数だろう。
花子:$15$の20乗を求めるのは大変だね。$\log_{10}15^{20}$の整数部分に
着目してみようよ。
$\log_{10}15^{20}$は
$\boxed{\ \ カキ\ \ } \lt \log_{10}15^{20}$$ \lt \boxed{\ \ カキ\ \ }+1$
を満たす。よって、$15^{20}は\boxed{\ \ クケ\ \ }$桁の数である。
太郎:$15^{20}$の最高位の数字も知りたいね。だけど、$\log_{10}15^{20}$の
整数部分にだけ着目してもわからないな。
花子:$N・10^{\boxed{カキ}} \lt 15^{20}$$ \lt (N+1)・10^{\boxed{カキ}}$を満たすような
正の整数Nに着目してみたらどうかな。
$\log_{10}15^{20}$の小数部分は$\log_{10}15^{20}-\boxed{\ \ カキ\ \ }$であり
$\log_{10}\boxed{\ \ コ\ \ } \lt \log_{10}15^{20}-\boxed{\ \ カキ\ \ }$$ \lt \log_{10}(\boxed{\ \ コ\ \ }+1)$
が成り立つので、$15^{20}$の最高位の数字は$\boxed{\ \ サ\ \ }$である。
[2]座標平面上の原点を中心とする半径1の円周上に3点$P(\cos\theta,\sin\theta),$
$Q(\cos\alpha,\sin\alpha),R(\cos\beta,\sin\beta)$がある。ただし、$0 \leqq \theta \lt \alpha \lt \beta \lt 2\pi$
とする。このとき、$s$と$t$を次のように定める。
$s=\cos\theta+\cos\alpha+\cos\beta,$$ t=\sin\theta+\sin\alpha+\sin\beta$
(1)$\triangle PQR$が正三角形や二等辺三角形のときの$s$と$t$の値について考察しよう。
考察$1:\triangle PQR$が正三角形である場合を考える。
この場合、$\alpha,\beta$を$\theta$で表すと
$\alpha=\theta+\displaystyle \frac{\boxed{\ \ シ\ \ }}{3}\pi,$$ \beta=\theta+\displaystyle \frac{\boxed{\ \ ス\ \ }}{3}\pi$
であり、加法定理により
$\cos\alpha=\boxed{\boxed{\ \ セ\ \ }}, \sin\alpha=\boxed{\boxed{\ \ ソ\ \ }}$
である。同様に、$\cos\beta$および$\sin\beta$を、$\sin\theta$と$\cos\theta$を用いて表すことができる。
これらのことから、$s=t=\boxed{\ \ タ\ \ }$である。
$\boxed{\boxed{\ \ セ\ \ }},\boxed{\boxed{\ \ ソ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$\displaystyle \frac{1}{2}\sin\theta+\displaystyle \frac{\sqrt3}{2}\cos\theta$
①$\displaystyle \frac{\sqrt3}{2}\sin\theta+\displaystyle \frac{1}{2}\cos\theta$
②$\displaystyle \frac{1}{2}\sin\theta-\displaystyle \frac{\sqrt3}{2}\cos\theta$
③$\displaystyle \frac{\sqrt3}{2}\sin\theta-\displaystyle \frac{1}{2}\cos\theta$
④$-\displaystyle \frac{1}{2}\sin\theta+\displaystyle \frac{\sqrt3}{2}\cos\theta$
⑤$-\displaystyle \frac{\sqrt3}{2}\sin\theta+\displaystyle \frac{1}{2}\cos\theta$
②$-\displaystyle \frac{1}{2}\sin\theta-\displaystyle \frac{\sqrt3}{2}\cos\theta$
③$-\displaystyle \frac{\sqrt3}{2}\sin\theta-\displaystyle \frac{1}{2}\cos\theta$
考察2:$\triangle PQR$が$PQ=PR$となる二等辺三角形である場合を考える。
例えば、点$P$が直線$y=x$上にあり、点$Q,R$が直線$y=x$に関して対称
であるときを考える。このとき、$\theta=\displaystyle \frac{\pi}{4}$である。また、$\alpha$は
$\alpha \lt \displaystyle \frac{5}{4}\pi, \beta$は$\displaystyle \frac{5}{4}\pi \lt \beta$を満たし、点$Q,R$の座標について、
$\sin\beta=\cos\alpha, \cos\beta=\sin\alpha$が成り立つ。よって
$s=t=\displaystyle \frac{\sqrt{\boxed{\ \ チ\ \ }}}{\boxed{\ \ ツ\ \ }}+\sin\alpha+\cos\alpha$
である。
ここで、三角関数の合成により
$\sin\alpha+\cos\alpha=$$\sqrt{\boxed{\ \ テ\ \ }}\sin\left(\alpha+\displaystyle \frac{\pi}{\boxed{\ \ ト\ \ }}\right)$
である。したがって
$\alpha=\displaystyle \frac{\boxed{\ \ ナニ\ \ }}{12}\pi, \beta=\displaystyle \frac{\boxed{\ \ ヌネ\ \ }}{12}\pi$
のとき、$s=t=0$である。
(2)次に、$s$と$t$の値を定めるときの$\theta,\alpha,\beta$の関係について考察しよう。
考察$3:s=t=0$の場合を考える。
この場合、$\sin^2\theta+\cos^2\theta=1$により、$\alpha$と$\beta$について考えると
$\cos\alpha\cos\beta+\sin\alpha\sin\beta=\displaystyle \frac{\boxed{\ \ ノハ\ \ }}{\boxed{\ \ ヒ\ \ }}$
である。
同様に、$\theta$と$\alpha$について考えると
$\cos\theta\cos\alpha+\sin\theta\sin\alpha=\displaystyle \frac{\boxed{\ \ ノハ\ \ }}{\boxed{\ \ ヒ\ \ }}$
であるから、$\theta,\alpha,\beta$の範囲に注意すると
$\beta-\alpha=\alpha-\theta=\displaystyle \frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}\pi$
という関係が得られる。
(3)これまでの考察を振り返ると、次の⓪~③のうち、
正しいものは$\boxed{\boxed{\ \ ホ\ \ }}$であることが分かる。
$\boxed{\boxed{\ \ ホ\ \ }}$の解答群
⓪$\triangle PQR$が正三角形ならば$s=t=0$であり、$s=t=0$ならば
$\triangle PQR$は正三角形である。
①$\triangle PQR$が正三角形ならば$s=t=0$であり、$s=t=0$で
あっても$\triangle PQR$は正三角形でない場合がある。
②$\triangle PQR$が正三角形であっても$s=t=0$でない場合があるが
$s=t=0$ならば$\triangle PQR$は正三角形である。
③$\triangle PQR$が正三角形であっても$s=t=0$でない場合があり、
$s=t=0$であっても$\triangle PQR$が正三角形でない場合がある。
ε-δ論法 #2 f(x)=log x が連続
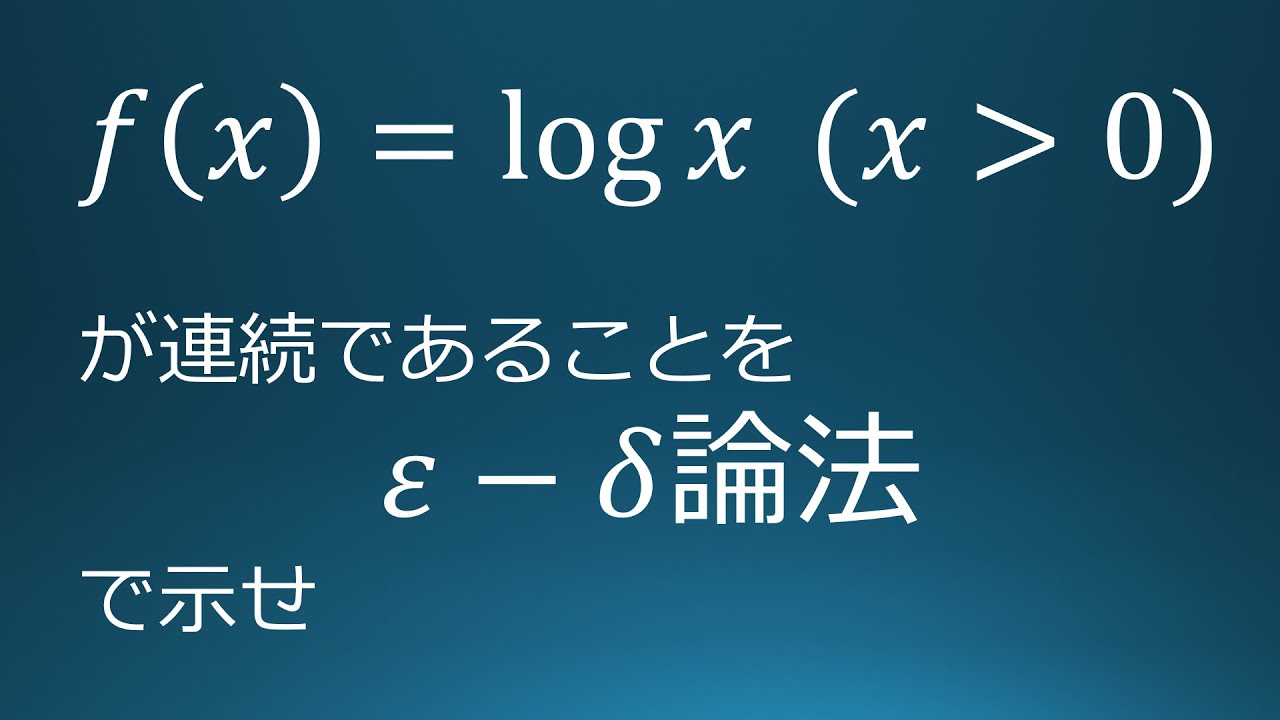
単元:
#数Ⅱ#式と証明#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\log x\ (x\gt 0)$が連続であることを
$ε-δ$論法で示せ.
この動画を見る
$f(x)=\log x\ (x\gt 0)$が連続であることを
$ε-δ$論法で示せ.
2021東京女子医大 対数

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y$は実数であり,$x\gt 0,y\gt 0$である.
$xy^{1+\log_2 x^2}=1$を満たすとき,$xy$のとりうる値の範囲を求めよ.
2021東京女子医大過去問
この動画を見る
$x,y$は実数であり,$x\gt 0,y\gt 0$である.
$xy^{1+\log_2 x^2}=1$を満たすとき,$xy$のとりうる値の範囲を求めよ.
2021東京女子医大過去問
共通テスト2021年数学詳しい解説〜共通テスト2021年2B第1問〜三角関数、指数関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#指数関数と対数関数#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#センター試験・共通テスト関連#共通テスト#センター試験#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第1問}$
[1](1)次の問題$A$について考えよう。
$\boxed{\boxed{問題A} 関数y=\sin\theta+\sqrt3\cos\theta\left(0 \leqq \theta \leqq \displaystyle \frac{\pi}{2}\right)$の最大値を求めよ。}$
$\sin\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}=\displaystyle \frac{\sqrt3}{2},$ $\cos\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}=\displaystyle \frac{1}{2}$
であるから、三角関数の合成により
$y=\boxed{\ \ イ\ \ }\sin\left(\theta+\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}\right)$
と変形できる。よって、$y$は$\theta=\displaystyle \frac{\pi}{\boxed{\ \ ウ\ \ }}$で最大値$\ \boxed{\ \ エ\ \ }\ $をとる。
(2)$p$を定数とし、次の問題$B$について考えよう。
$\boxed{\boxed{問題B} 関数y=\sin\theta+p\cos\theta\left(0 \leqq \theta \leqq \frac{\pi}{2}\right)の最大値を求めよ。}$
$(\textrm{i})$ $p=0$のとき、$y$は$\theta=\displaystyle \frac{\pi}{\boxed{\ \ オ\ \ }}$で最大値$\ \boxed{\ \ カ\ \ }\ $をとる。
$(\textrm{ii})$ $p \gt 0$のときは、加法定理
$\cos(\theta-\alpha)=\cos\theta\cos\alpha$$+\sin\theta\sin\alpha$
を用いると
$y=\sin\theta+p\cos\theta$$=\sqrt{\boxed{\boxed{\ \ キ\ \ }}}\cos(\theta-\alpha)$
と表すことができる。ただし、$\alpha$は
$\sin\alpha=\displaystyle \frac{\boxed{\boxed{\ \ ク\ \ }}}{\sqrt{\boxed{\boxed{\ \ キ\ \ }}}}$、$\cos\alpha=\frac{\boxed{\boxed{\ \ ケ\ \ }}}{\sqrt{\boxed{\boxed{\ \ キ\ \ }}}}$、$0 \lt \alpha \lt \displaystyle \frac{\pi}{2}$
を満たすものとする。このとき、$y$は$\theta=\boxed{\boxed{\ \ コ\ \ }}$で最大値
$\sqrt{\boxed{\boxed{\ \ サ\ \ }}}$をとる。
$(\textrm{iii})$ $p \lt 0$のとき、$y$は$\theta=\boxed{\boxed{\ \ シ\ \ }}$で最大値$\boxed{\boxed{\ \ ス\ \ }}$をとる。
$\boxed{\boxed{\ \ キ\ \ }}~\boxed{\boxed{\ \ ケ\ \ }}、\boxed{\boxed{\ \ サ\ \ }}、\boxed{\boxed{\ \ ス\ \ }}$の解答群(同じものを繰り返
し選んでもよい。)
⓪$-1$
①$1$
②$-p$
③$p$
④$1-p$
⑤$1+p$
⑥$-p^2$
⑦$p^2$
⑧$1-p^2$
⑨$1+p^2$
ⓐ$(1-p)^2$
ⓑ$(1+p)^2$
$\boxed{\boxed{\ \ コ\ \ }}、\boxed{\boxed{\ \ シ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$0$
①$\alpha$
②$\displaystyle \frac{\pi}{2}$
[2]二つの関数$f(x)=\displaystyle \frac{2^x+2^{-x}}{2}$、$g(x)=\displaystyle \frac{2^x-2^{-x}}{2}$ について考える。
(1)$f(0)=\boxed{\ \ セ\ \ }、g(0)=\boxed{\ \ ソ\ \ }$である。また、$f(x)$は相加平均
と相乗平均の関係から、$x=\boxed{\ \ タ\ \ }$で最小値$\ \boxed{\ \ チ\ \ }$ をとる。
$g(x)=-2$ となる$x$の値は$\log_2\left(\sqrt{\boxed{\ \ ツ\ \ }}-\boxed{\ \ テ\ \ }\right)$である。
(3)次の①~④は、$x$にどのような値を代入しても常に成り立つ。
$f(-x)=\boxed{\boxed{\ \ ト\ \ }}$ $\cdots$①
$g(-x)=\boxed{\boxed{\ \ ナ\ \ }}$ $\cdots$②
$\left\{f(x)\right\}^2-\left\{g(x)\right\}^2=\boxed{\ \ ニ\ \ }$ $\cdots$③
$g(2x)=\boxed{\ \ ヌ\ \ }\ f(x)g(x)$ $\cdots$④
$\boxed{\boxed{\ \ ト\ \ }}、\boxed{\boxed{\ \ ナ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$f(x)$
①$-f(x)$
②$g(x)$
③$-g(x)$
(3)花子さんと太郎さんは、$f(x)$と$g(x)$の性質について話している。
花子:①~④は三角関数の性質に似ているね。
太郎:三角関数の加法定理に類似した式($\textrm{A}$)~($\textrm{D}$)を考えてみたけど、
常に成り立つ式はあるだろうか。
花子:成り立たない式を見つけるために、式($\textrm{A}$)~($\textrm{D}$)の$\beta$に何か具体
的な値を代入して調べてみたらどうかな。
太郎さんが考えた式
$f(\alpha-\beta)=f(\alpha)g(\beta)+g(\alpha)f(\beta)$ $\cdots(\textrm{A})$
$f(\alpha+\beta)=f(\alpha)f(\beta)+g(\alpha)g(\beta)$ $\cdots(\textrm{B})$
$g(\alpha-\beta)=f(\alpha)f(\beta)+g(\alpha)g(\beta)$ $\cdots(\textrm{C})$
$g(\alpha+\beta)=f(\alpha)g(\beta)-g(\alpha)f(\beta)$ $\cdots(\textrm{D})$
(1),(2)で示されたことのいくつかを利用すると、式($\textrm{A}$)~($\textrm{D}$)のうち、
$\boxed{\boxed{\ \ ネ\ \ }}$以外の三つは成り立たないことが分かる。$\boxed{\boxed{\ \ ネ\ \ }}$は左辺と右辺
をそれぞれ計算することによって成り立つことが確かめられる。
$\boxed{\boxed{\ \ ネ\ \ }}$の解答群
⓪$(\textrm{A})$
①$(\textrm{B})$
②$(\textrm{C})$
③$(\textrm{D})$
2021共通テスト過去問
この動画を見る
${\large第1問}$
[1](1)次の問題$A$について考えよう。
$\boxed{\boxed{問題A} 関数y=\sin\theta+\sqrt3\cos\theta\left(0 \leqq \theta \leqq \displaystyle \frac{\pi}{2}\right)$の最大値を求めよ。}$
$\sin\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}=\displaystyle \frac{\sqrt3}{2},$ $\cos\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}=\displaystyle \frac{1}{2}$
であるから、三角関数の合成により
$y=\boxed{\ \ イ\ \ }\sin\left(\theta+\displaystyle \frac{\pi}{\boxed{\ \ ア\ \ }}\right)$
と変形できる。よって、$y$は$\theta=\displaystyle \frac{\pi}{\boxed{\ \ ウ\ \ }}$で最大値$\ \boxed{\ \ エ\ \ }\ $をとる。
(2)$p$を定数とし、次の問題$B$について考えよう。
$\boxed{\boxed{問題B} 関数y=\sin\theta+p\cos\theta\left(0 \leqq \theta \leqq \frac{\pi}{2}\right)の最大値を求めよ。}$
$(\textrm{i})$ $p=0$のとき、$y$は$\theta=\displaystyle \frac{\pi}{\boxed{\ \ オ\ \ }}$で最大値$\ \boxed{\ \ カ\ \ }\ $をとる。
$(\textrm{ii})$ $p \gt 0$のときは、加法定理
$\cos(\theta-\alpha)=\cos\theta\cos\alpha$$+\sin\theta\sin\alpha$
を用いると
$y=\sin\theta+p\cos\theta$$=\sqrt{\boxed{\boxed{\ \ キ\ \ }}}\cos(\theta-\alpha)$
と表すことができる。ただし、$\alpha$は
$\sin\alpha=\displaystyle \frac{\boxed{\boxed{\ \ ク\ \ }}}{\sqrt{\boxed{\boxed{\ \ キ\ \ }}}}$、$\cos\alpha=\frac{\boxed{\boxed{\ \ ケ\ \ }}}{\sqrt{\boxed{\boxed{\ \ キ\ \ }}}}$、$0 \lt \alpha \lt \displaystyle \frac{\pi}{2}$
を満たすものとする。このとき、$y$は$\theta=\boxed{\boxed{\ \ コ\ \ }}$で最大値
$\sqrt{\boxed{\boxed{\ \ サ\ \ }}}$をとる。
$(\textrm{iii})$ $p \lt 0$のとき、$y$は$\theta=\boxed{\boxed{\ \ シ\ \ }}$で最大値$\boxed{\boxed{\ \ ス\ \ }}$をとる。
$\boxed{\boxed{\ \ キ\ \ }}~\boxed{\boxed{\ \ ケ\ \ }}、\boxed{\boxed{\ \ サ\ \ }}、\boxed{\boxed{\ \ ス\ \ }}$の解答群(同じものを繰り返
し選んでもよい。)
⓪$-1$
①$1$
②$-p$
③$p$
④$1-p$
⑤$1+p$
⑥$-p^2$
⑦$p^2$
⑧$1-p^2$
⑨$1+p^2$
ⓐ$(1-p)^2$
ⓑ$(1+p)^2$
$\boxed{\boxed{\ \ コ\ \ }}、\boxed{\boxed{\ \ シ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$0$
①$\alpha$
②$\displaystyle \frac{\pi}{2}$
[2]二つの関数$f(x)=\displaystyle \frac{2^x+2^{-x}}{2}$、$g(x)=\displaystyle \frac{2^x-2^{-x}}{2}$ について考える。
(1)$f(0)=\boxed{\ \ セ\ \ }、g(0)=\boxed{\ \ ソ\ \ }$である。また、$f(x)$は相加平均
と相乗平均の関係から、$x=\boxed{\ \ タ\ \ }$で最小値$\ \boxed{\ \ チ\ \ }$ をとる。
$g(x)=-2$ となる$x$の値は$\log_2\left(\sqrt{\boxed{\ \ ツ\ \ }}-\boxed{\ \ テ\ \ }\right)$である。
(3)次の①~④は、$x$にどのような値を代入しても常に成り立つ。
$f(-x)=\boxed{\boxed{\ \ ト\ \ }}$ $\cdots$①
$g(-x)=\boxed{\boxed{\ \ ナ\ \ }}$ $\cdots$②
$\left\{f(x)\right\}^2-\left\{g(x)\right\}^2=\boxed{\ \ ニ\ \ }$ $\cdots$③
$g(2x)=\boxed{\ \ ヌ\ \ }\ f(x)g(x)$ $\cdots$④
$\boxed{\boxed{\ \ ト\ \ }}、\boxed{\boxed{\ \ ナ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪$f(x)$
①$-f(x)$
②$g(x)$
③$-g(x)$
(3)花子さんと太郎さんは、$f(x)$と$g(x)$の性質について話している。
花子:①~④は三角関数の性質に似ているね。
太郎:三角関数の加法定理に類似した式($\textrm{A}$)~($\textrm{D}$)を考えてみたけど、
常に成り立つ式はあるだろうか。
花子:成り立たない式を見つけるために、式($\textrm{A}$)~($\textrm{D}$)の$\beta$に何か具体
的な値を代入して調べてみたらどうかな。
太郎さんが考えた式
$f(\alpha-\beta)=f(\alpha)g(\beta)+g(\alpha)f(\beta)$ $\cdots(\textrm{A})$
$f(\alpha+\beta)=f(\alpha)f(\beta)+g(\alpha)g(\beta)$ $\cdots(\textrm{B})$
$g(\alpha-\beta)=f(\alpha)f(\beta)+g(\alpha)g(\beta)$ $\cdots(\textrm{C})$
$g(\alpha+\beta)=f(\alpha)g(\beta)-g(\alpha)f(\beta)$ $\cdots(\textrm{D})$
(1),(2)で示されたことのいくつかを利用すると、式($\textrm{A}$)~($\textrm{D}$)のうち、
$\boxed{\boxed{\ \ ネ\ \ }}$以外の三つは成り立たないことが分かる。$\boxed{\boxed{\ \ ネ\ \ }}$は左辺と右辺
をそれぞれ計算することによって成り立つことが確かめられる。
$\boxed{\boxed{\ \ ネ\ \ }}$の解答群
⓪$(\textrm{A})$
①$(\textrm{B})$
②$(\textrm{C})$
③$(\textrm{D})$
2021共通テスト過去問
05神奈川県教員採用試験(数学:2番 対数)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$ $17^{50}$は$62$桁の整数である.
$17^{24}$の桁数を求めよ.
この動画を見る
$\boxed{2}$ $17^{50}$は$62$桁の整数である.
$17^{24}$の桁数を求めよ.
大阪大 対数

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$を自然数とし,$0\lt a \lt 1$とする.
$\log_2 6=m+\dfrac{1}{n+a}$
(1)$m,n$を求めよ.
(2)$a\gt \dfrac{2}{3}$を示せ.
2006大阪大過去問
この動画を見る
$m,n$を自然数とし,$0\lt a \lt 1$とする.
$\log_2 6=m+\dfrac{1}{n+a}$
(1)$m,n$を求めよ.
(2)$a\gt \dfrac{2}{3}$を示せ.
2006大阪大過去問
練習問題3(数検準1級,教員採用試験 対数と相加相乗平均)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#式と証明#指数関数と対数関数#恒等式・等式・不等式の証明#対数関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\sqrt x+ \sqrt y = 20$
$log_{10}x+log_{10}y$の最大値を求めよ。
この動画を見る
$\sqrt x+ \sqrt y = 20$
$log_{10}x+log_{10}y$の最大値を求めよ。
数検準1級2次過去問(1番 指数対数の不等式)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#式と証明#指数関数と対数関数#恒等式・等式・不等式の証明#指数関数#対数関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣
$2^xlog_2x+2^{x+2}-4log_2x-16 < 0$
をみたすxの値の範囲を求めよ。
この動画を見る
1⃣
$2^xlog_2x+2^{x+2}-4log_2x-16 < 0$
をみたすxの値の範囲を求めよ。
東北大 対数方程式
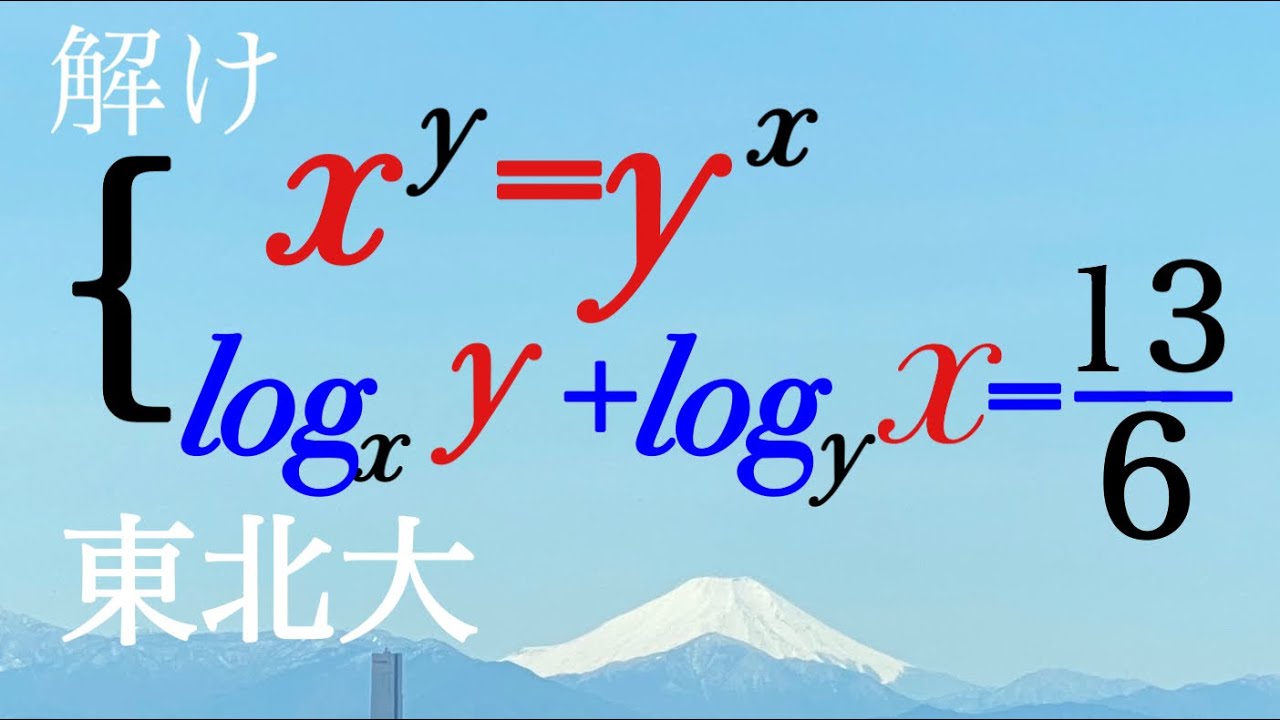
単元:
#数A#数Ⅱ#整数の性質#ユークリッド互除法と不定方程式・N進法#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
連立方程式を解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^y=y^x \\
\log_x y+\log_y x=\dfrac{13}{6}
\end{array}
\right.
\end{eqnarray}$
東北大過去問
この動画を見る
連立方程式を解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^y=y^x \\
\log_x y+\log_y x=\dfrac{13}{6}
\end{array}
\right.
\end{eqnarray}$
東北大過去問
05大阪府教員採用試験(数学:2番 指数対数)

単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣ $x,y,z \in \mathbb{R}$
$2^x=3^y=Z$
$\frac{1}{x}+\frac{1}{y}=\frac{1}{2}$のときZの値を求めよ。
この動画を見る
2⃣ $x,y,z \in \mathbb{R}$
$2^x=3^y=Z$
$\frac{1}{x}+\frac{1}{y}=\frac{1}{2}$のときZの値を求めよ。
三重大 対数と二次関数

単元:
#数Ⅰ#数Ⅱ#2次関数#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha \gt 0$とする.
$f(x)=\log_3 \left(-\dfrac{1}{2}x^2+\dfrac{1}{2}\alpha x+9 \right)$
$f(x)$が整数となる$x$が$0\leqq x\leqq \alpha$の範囲でちょうど$6$個あるような$\alpha$の範囲を求めよ.
三重大過去問
この動画を見る
$\alpha \gt 0$とする.
$f(x)=\log_3 \left(-\dfrac{1}{2}x^2+\dfrac{1}{2}\alpha x+9 \right)$
$f(x)$が整数となる$x$が$0\leqq x\leqq \alpha$の範囲でちょうど$6$個あるような$\alpha$の範囲を求めよ.
三重大過去問
00兵庫県教員採用試験(数学:4番 対数)

単元:
#数Ⅱ#式と証明#図形と方程式#指数関数と対数関数#恒等式・等式・不等式の証明#軌跡と領域#対数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
4⃣$log_xy+2log_yx \leqq 3$
をみたす(x,y)の存在する領域を図示せよ
この動画を見る
4⃣$log_xy+2log_yx \leqq 3$
をみたす(x,y)の存在する領域を図示せよ
10大阪府教員採用試験(数学:2番 微積)意外と沼にハマりがち

単元:
#数Ⅱ#指数関数と対数関数#対数関数#積分とその応用#定積分#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
2⃣ $f(x) = \frac{x}{1+x^2}$
f(α)=f(β) , 0 < α < β のとき$\int_α^β \frac{x}{1+x^2}dx= log_β$を示せ
この動画を見る
2⃣ $f(x) = \frac{x}{1+x^2}$
f(α)=f(β) , 0 < α < β のとき$\int_α^β \frac{x}{1+x^2}dx= log_β$を示せ
岐阜薬科大 対数の不等式 良問

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\log_x y-\log_y x^{\frac{1}{2}}\lt -\dfrac{1}{2}$を満たす点$(x,y)$の領域を図示せよ.
岐阜薬科大過去問
この動画を見る
$\log_x y-\log_y x^{\frac{1}{2}}\lt -\dfrac{1}{2}$を満たす点$(x,y)$の領域を図示せよ.
岐阜薬科大過去問
【解けたら上位!】対数の難問 数学II

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学II】対数の難問解説動画です
-----------------
(1)$log_{10}2 \gt 0.3$を示せ
(2)$log_{10}(M+N) \geqq \displaystyle \frac{1}{2}(log_{10}M+log_{10}N)+log_{10} 2$を示せ
(3)$log_{10} 13\gt 1.1$を示せ
この動画を見る
【数学II】対数の難問解説動画です
-----------------
(1)$log_{10}2 \gt 0.3$を示せ
(2)$log_{10}(M+N) \geqq \displaystyle \frac{1}{2}(log_{10}M+log_{10}N)+log_{10} 2$を示せ
(3)$log_{10} 13\gt 1.1$を示せ
16愛知県教員採用試験(数学:5番 対数,相加平均・相乗平均)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
5⃣$a=log_3x$ , $b=log_4y$
a+2b=3のときx+yの最小値を求めよ。
この動画を見る
5⃣$a=log_3x$ , $b=log_4y$
a+2b=3のときx+yの最小値を求めよ。
13大阪府教員採用試験(数学:1-1番 対数の整数問題)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣(1) 10<x<100
$\log_{ 10 } x$と$\log_{ 10 } x^3$の小数部分が等しいときxの値を求めよ。
この動画を見る
1⃣(1) 10<x<100
$\log_{ 10 } x$と$\log_{ 10 } x^3$の小数部分が等しいときxの値を求めよ。
11兵庫県教員採用試験(数学:1-4番 対数)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣(4)$x \geqq 2$ , $y \geqq \frac{1}{2}$ , $ xy=64$
$(log_2x)(log_2y)$
の最大値、最小値を求めよ。
この動画を見る
1⃣(4)$x \geqq 2$ , $y \geqq \frac{1}{2}$ , $ xy=64$
$(log_2x)(log_2y)$
の最大値、最小値を求めよ。
早稲田大(国際教養)対数とガウス記号

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\gt 0$とする.
$m=\left[\log_{10}\dfrac{3\sqrt x}{20}\right]$
$n=\left[\log_{10}\dfrac{800}{x}\right]$
$3m+n$のとりうる値を求めよ.
早稲田(国際教)過去問
この動画を見る
$x\gt 0$とする.
$m=\left[\log_{10}\dfrac{3\sqrt x}{20}\right]$
$n=\left[\log_{10}\dfrac{800}{x}\right]$
$3m+n$のとりうる値を求めよ.
早稲田(国際教)過去問
16神奈川県教員採用試験(数学:6番 指数対数)
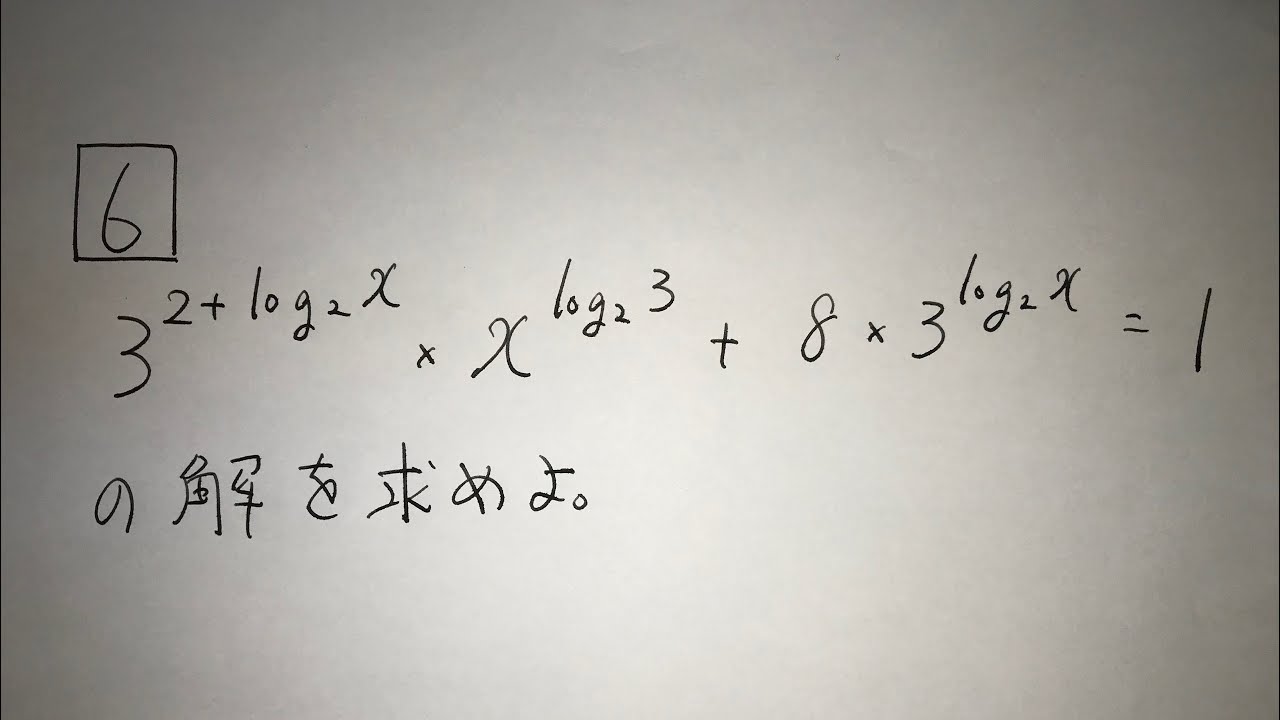
単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
6⃣
$3^{2+log_2x}×x^{log_23}+8×3^{log_2x}=1$の解を求めよ。
この動画を見る
6⃣
$3^{2+log_2x}×x^{log_23}+8×3^{log_2x}=1$の解を求めよ。
一橋大 漸化式&対数

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
数列$a_n,a_1=5,a_{n+1}=2,a_n+3^n$がある.
(1)$a_n$を求めよ.
(2)$a_n\lt 10^{10}$を満たす最大の$n$を求めよ.
$\log_{10}2=0.3010,\log_{10}3=0.4771$
1998一橋大過去問
この動画を見る
数列$a_n,a_1=5,a_{n+1}=2,a_n+3^n$がある.
(1)$a_n$を求めよ.
(2)$a_n\lt 10^{10}$を満たす最大の$n$を求めよ.
$\log_{10}2=0.3010,\log_{10}3=0.4771$
1998一橋大過去問
19神奈川県教員採用試験(数学:10番 数列・対数)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{10}$${a_n}$:等比数列,$a_1=2,r=3$
$10^4 < a_n <10^7$
をみたすnの個数を求めよ。
$log_{10}2=0.301$ , $log_{10}3=0.4771$
この動画を見る
$\boxed{10}$${a_n}$:等比数列,$a_1=2,r=3$
$10^4 < a_n <10^7$
をみたすnの個数を求めよ。
$log_{10}2=0.301$ , $log_{10}3=0.4771$
16大阪府教員採用試験(数学:高校1番 積分)

単元:
#数Ⅰ#数Ⅱ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#対数関数#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
1⃣ $f(x)=\int_1^e |logt-logx|dt (1 \leqq x \leqq e)$
(1)f(x)を求めよ。
(2)f(x)の最大値、最小値を求めよ。
この動画を見る
1⃣ $f(x)=\int_1^e |logt-logx|dt (1 \leqq x \leqq e)$
(1)f(x)を求めよ。
(2)f(x)の最大値、最小値を求めよ。
長崎大 対数の基本

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\log_{2}x^2=2+\log_2 \vert x-2 \vert $を解け.
長崎大過去問
この動画を見る
$\log_{2}x^2=2+\log_2 \vert x-2 \vert $を解け.
長崎大過去問
11奈良県教員採用試験(数学:高校3番 逆関数と積分)

単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#関数と極限#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
3⃣高 $f(x)=\frac{e^x+e^{-x}}{2}$ $(x \geqq 0)$の逆関数をg(x)
(1)g(x)を求めよ。
(2)y=g(x),x=2,x軸で囲まれた面積
この動画を見る
3⃣高 $f(x)=\frac{e^x+e^{-x}}{2}$ $(x \geqq 0)$の逆関数をg(x)
(1)g(x)を求めよ。
(2)y=g(x),x=2,x軸で囲まれた面積
16京都府教員採用試験(数学:2番 背理法)
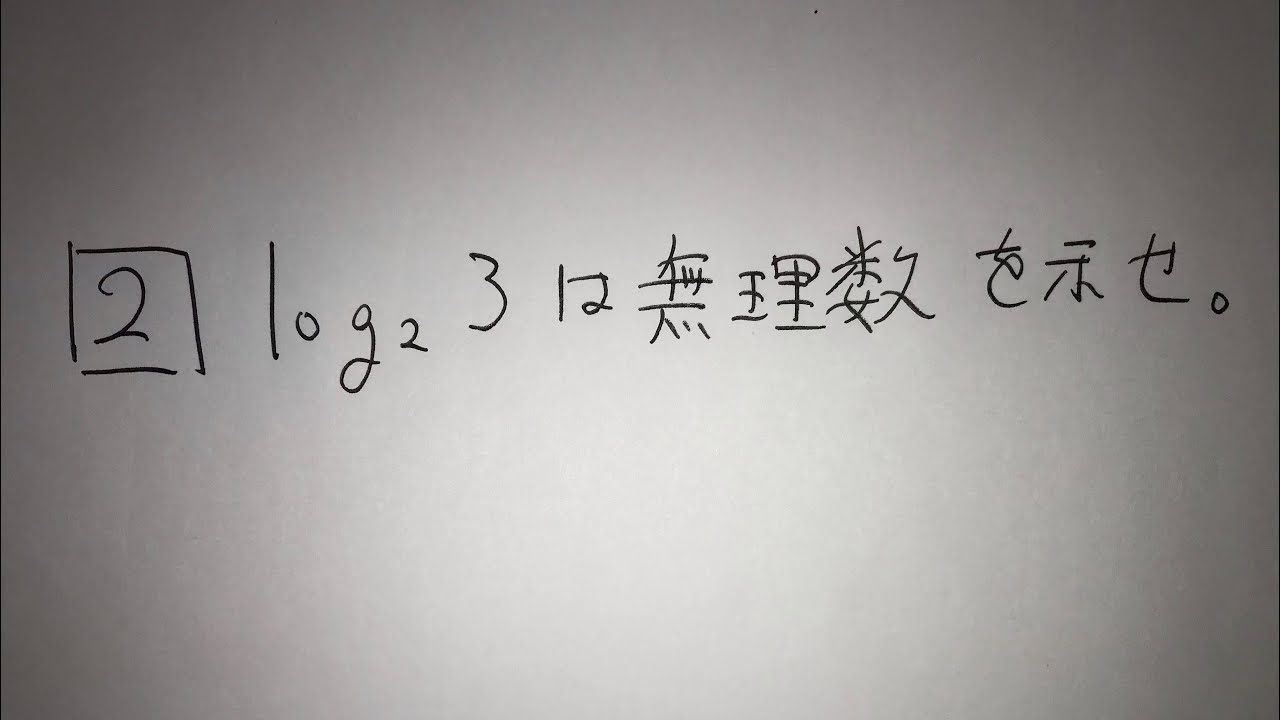
単元:
#数Ⅰ#数Ⅱ#数と式#集合と命題(集合・命題と条件・背理法)#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
2⃣ $\log_{ 2 } 3$は無理数を示せ。
この動画を見る
2⃣ $\log_{ 2 } 3$は無理数を示せ。
17東京都教員採用試験(数学:3番 x軸回転体)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
3⃣$C_1:y=logx , C_2:y=\frac{1}{2}log(x≠2)$
$C_1$,$C_2$の交点x座標をa
(1)aの値
(2)$C_1$,$C_2$,x軸で囲まれた面積S
(3)$C_1$,$C_2$,x軸で囲まれた図形をx軸中心に回転した体積V
この動画を見る
3⃣$C_1:y=logx , C_2:y=\frac{1}{2}log(x≠2)$
$C_1$,$C_2$の交点x座標をa
(1)aの値
(2)$C_1$,$C_2$,x軸で囲まれた面積S
(3)$C_1$,$C_2$,x軸で囲まれた図形をx軸中心に回転した体積V
【東京大学2007[6]】不等式の証明、log2の評価

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#対数関数#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
受験メモ山本
問題文全文(内容文):
$(1)0 \lt x\lt aのとき$
\begin{equation}
\frac{2x}{a} \lt \int^{a+x}_{a-x} \frac{1}{t}dt \lt x(\frac{1}{a+x}+\frac{1}{a-x})
\end{equation}を示せ.
$(2)0.68\lt log2\lt 0.71を示せ.$
この動画を見る
$(1)0 \lt x\lt aのとき$
\begin{equation}
\frac{2x}{a} \lt \int^{a+x}_{a-x} \frac{1}{t}dt \lt x(\frac{1}{a+x}+\frac{1}{a-x})
\end{equation}を示せ.
$(2)0.68\lt log2\lt 0.71を示せ.$
