 不定積分・定積分
不定積分・定積分
 不定積分・定積分
不定積分・定積分
#富山大学推薦2019#定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{\sqrt{ 3 }} \displaystyle \frac{x}{x^2+1} dx$
出典:2019年富山大学推薦
この動画を見る
$\displaystyle \int_{1}^{\sqrt{ 3 }} \displaystyle \frac{x}{x^2+1} dx$
出典:2019年富山大学推薦
大学入試問題#892「数学はやっぱ根性」 #京都工芸繊維大学(2023)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \leq \theta \leq \displaystyle \frac{\pi}{4}$とする
$f(\theta)=\displaystyle \int_{0}^{\frac{\pi}{4}} \displaystyle \frac{|\sin\theta-\sin x|}{\cos^2x} dx$
出典:2023年京都工芸繊維大学
この動画を見る
$0 \leq \theta \leq \displaystyle \frac{\pi}{4}$とする
$f(\theta)=\displaystyle \int_{0}^{\frac{\pi}{4}} \displaystyle \frac{|\sin\theta-\sin x|}{\cos^2x} dx$
出典:2023年京都工芸繊維大学
#広島市立大学2014#不定積分#ますただ
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
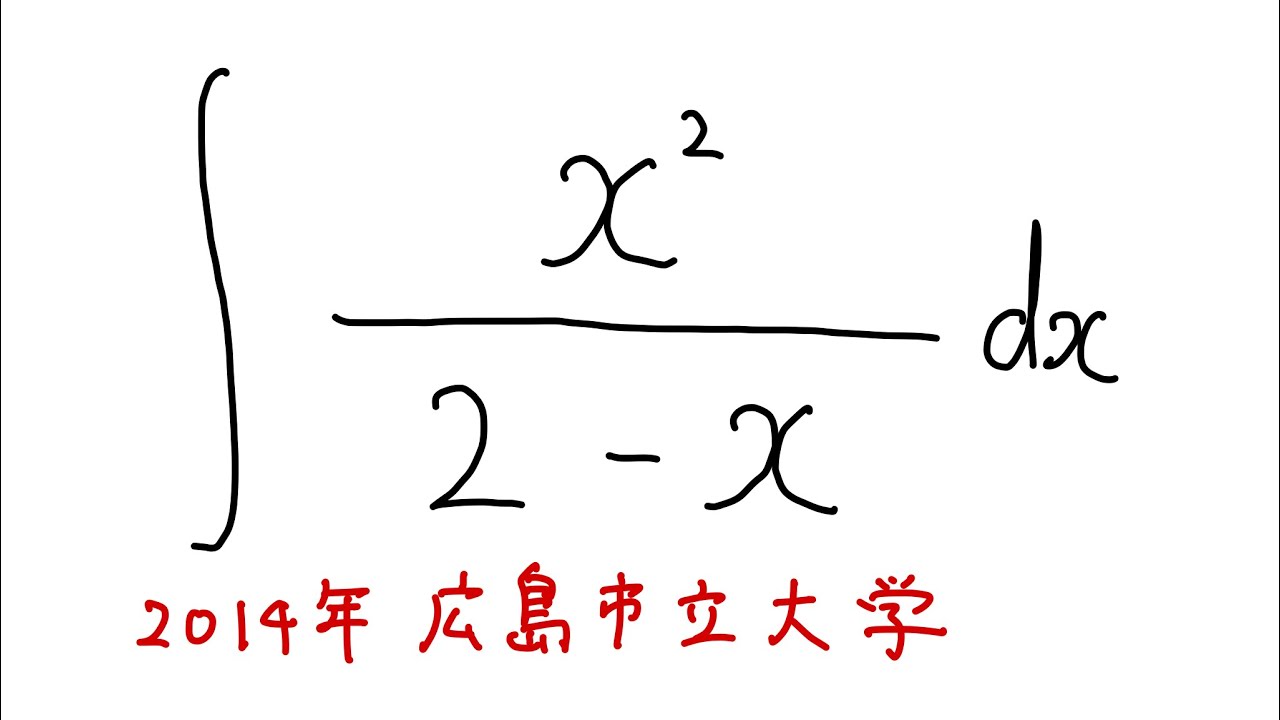
$\displaystyle \int \displaystyle \frac{x^2}{2-x} dx$
出典:2014年広島市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2}{2-x} dx$
出典:2014年広島市立大学
#電気通信大学2015#定積分#ますただ
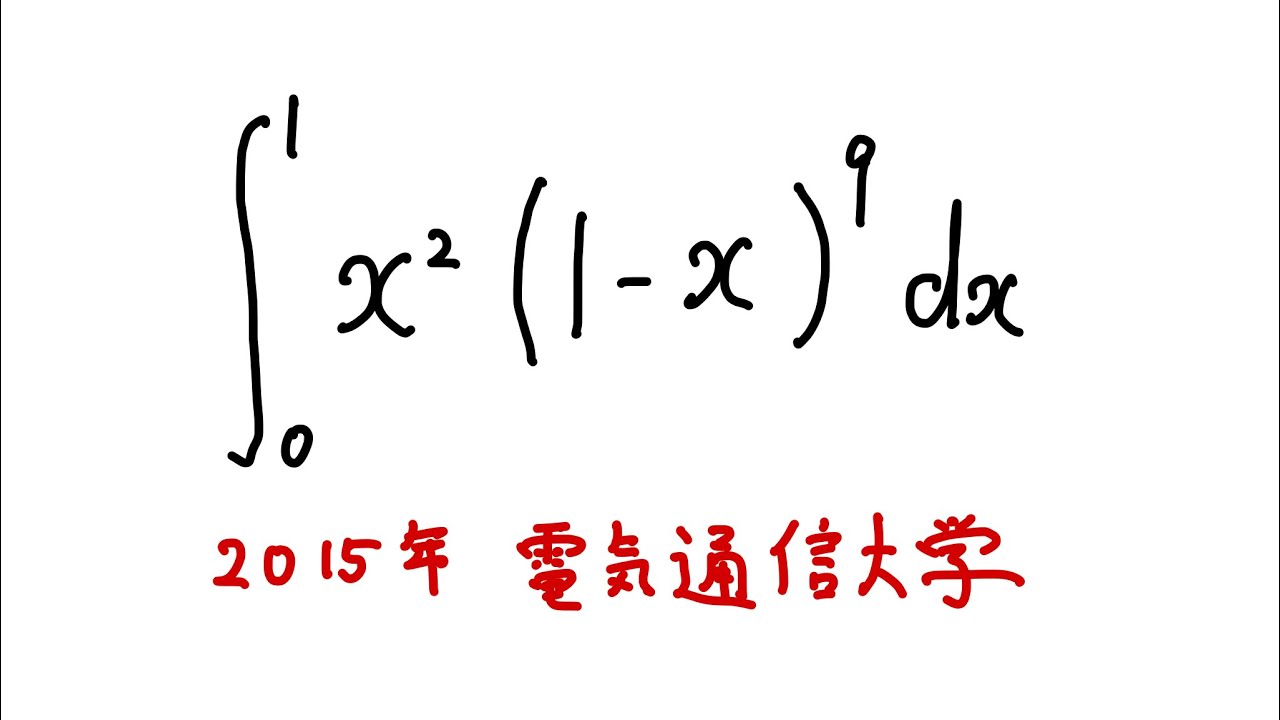
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$
出典:2015年電気通信大学
この動画を見る
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$
出典:2015年電気通信大学
大学入試問題#891「まだこのタイプの問題残ってた」 #信州大学(2023) #キングプロパティ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\pi}^{ \pi } \displaystyle \frac{1}{1+e^{-2\sin x}} dx$
出典:2023年信州大学
この動画を見る
$\displaystyle \int_{-\pi}^{ \pi } \displaystyle \frac{1}{1+e^{-2\sin x}} dx$
出典:2023年信州大学
#富山大学薬学部2018#不定積分
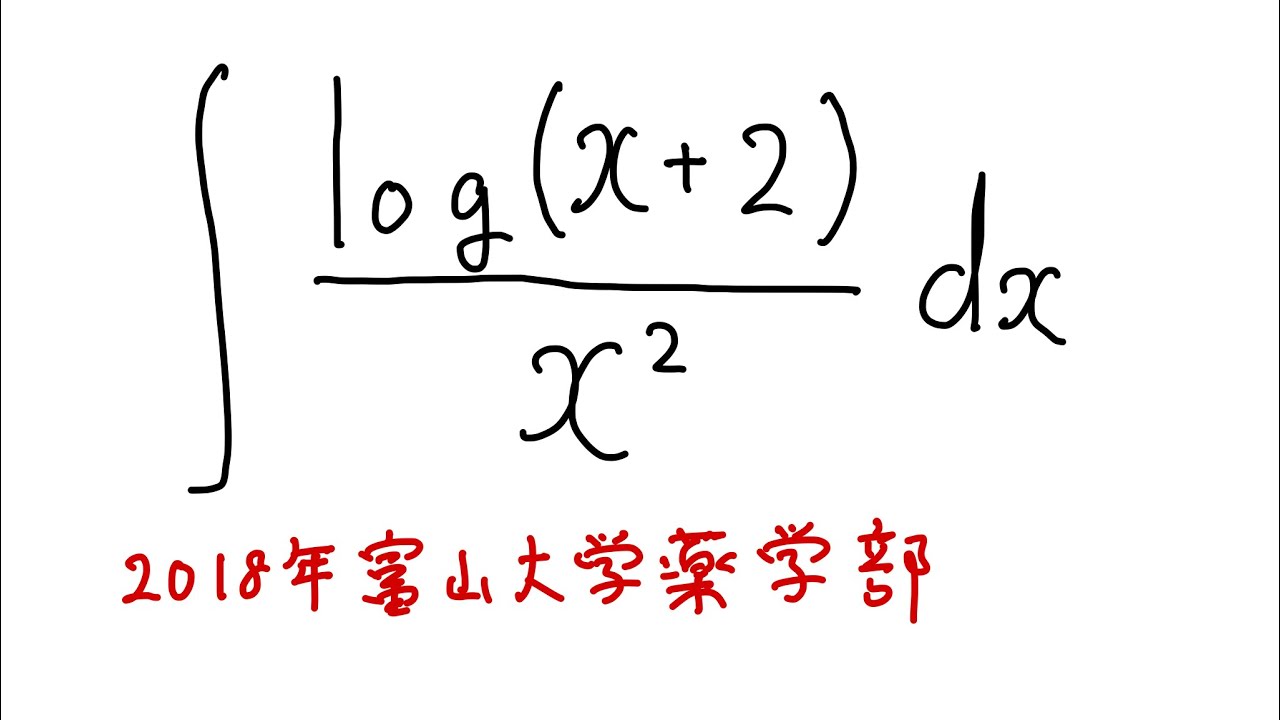
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{log(x+2)}{x^2} dx$
出典:2018年富山大学薬学部
この動画を見る
$\displaystyle \int \displaystyle \frac{log(x+2)}{x^2} dx$
出典:2018年富山大学薬学部
#数検準1級1次_4#不定積分
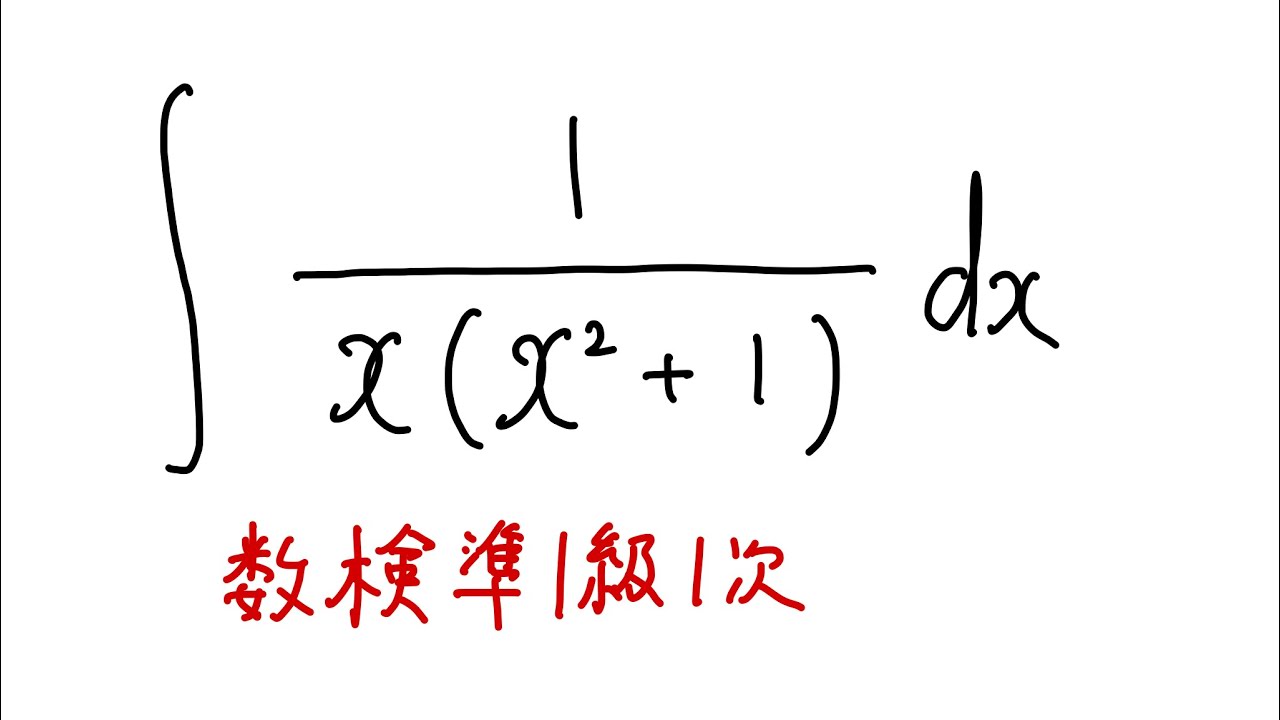
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1}{x(x^2+1)} dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{x(x^2+1)} dx$
出典:数検準1級1次
#藤田医科大学2023#定積分
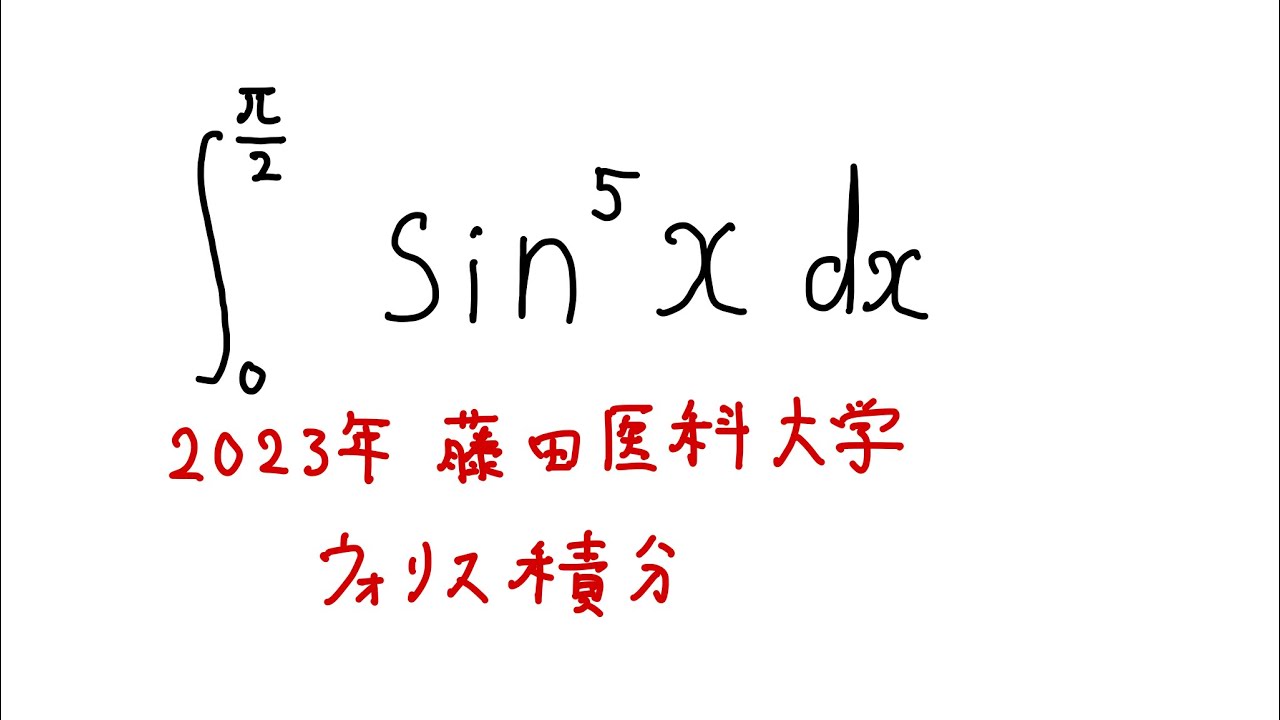
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#藤田医科大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^5x$ $dx$
出典:2023年藤田医科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^5x$ $dx$
出典:2023年藤田医科大学
#数検準1級1次_2 #不定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{e^x}{e^x+e^{-x}} dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int \displaystyle \frac{e^x}{e^x+e^{-x}} dx$
出典:数検準1級1次
大学入試問題#889「丁寧に計算するのみ」 #富山大学(2019)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi} (\cos^2x+x^2\sin^2x) dx$
出典:2019年富山大学推薦
この動画を見る
$\displaystyle \int_{0}^{2\pi} (\cos^2x+x^2\sin^2x) dx$
出典:2019年富山大学推薦
#数検準1級1次 #7
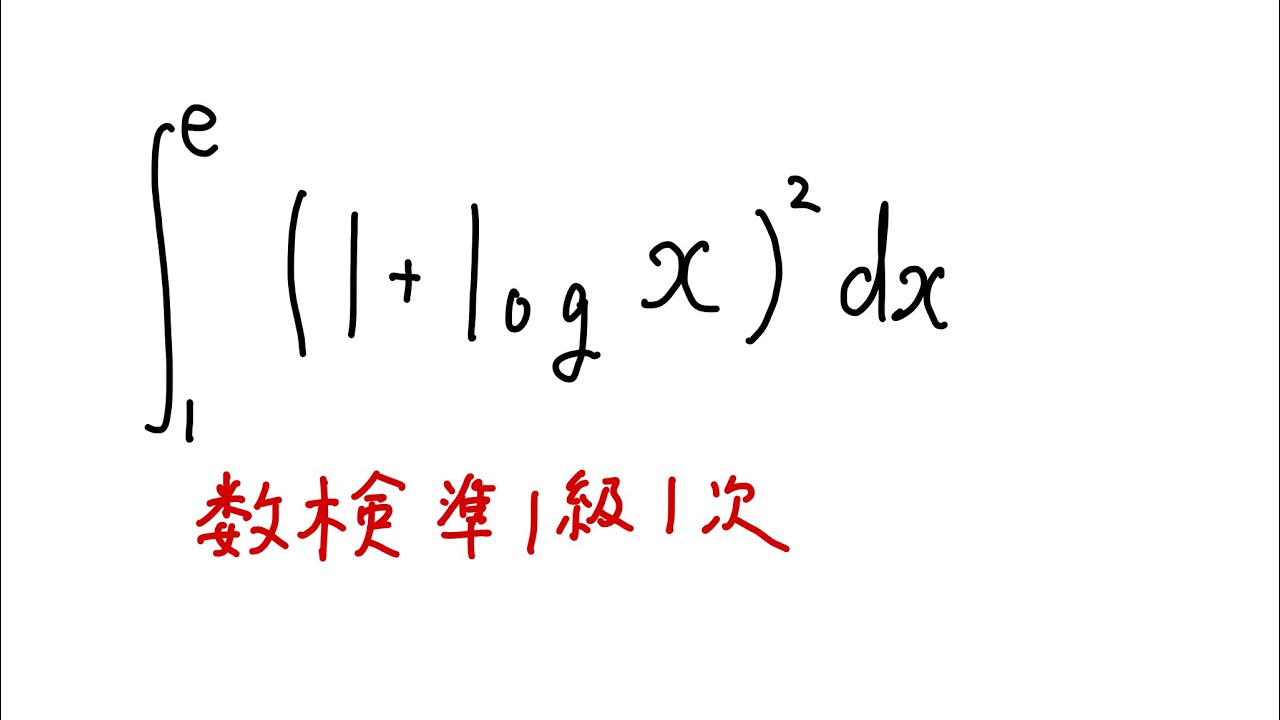
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} (1+log x)^2$ $dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{1}^{e} (1+log x)^2$ $dx$
出典:数検準1級1次
#数検準1級1次-1 #定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{x^4+2x^2+1} dx$
出典:数検準1級1次
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{x^4+2x^2+1} dx$
出典:数検準1級1次
#数学検定準1級2次過去問#70「根性出すしかないんかなー」 #定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^4(1-x)^4}{1+x^2} dx$
出典:数検準1級2次
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x^4(1-x)^4}{1+x^2} dx$
出典:数検準1級2次
#数検準1級1次#5#不定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }} dx$
出典:数検準1級
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }} dx$
出典:数検準1級
#東京理科大学2023#定積分#ますただ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt{ e }} \displaystyle \frac{e}{x^2+e} dx$
出典:2023年東京理科大学
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ e }} \displaystyle \frac{e}{x^2+e} dx$
出典:2023年東京理科大学
#数検準1級-1#定積分#ますただ
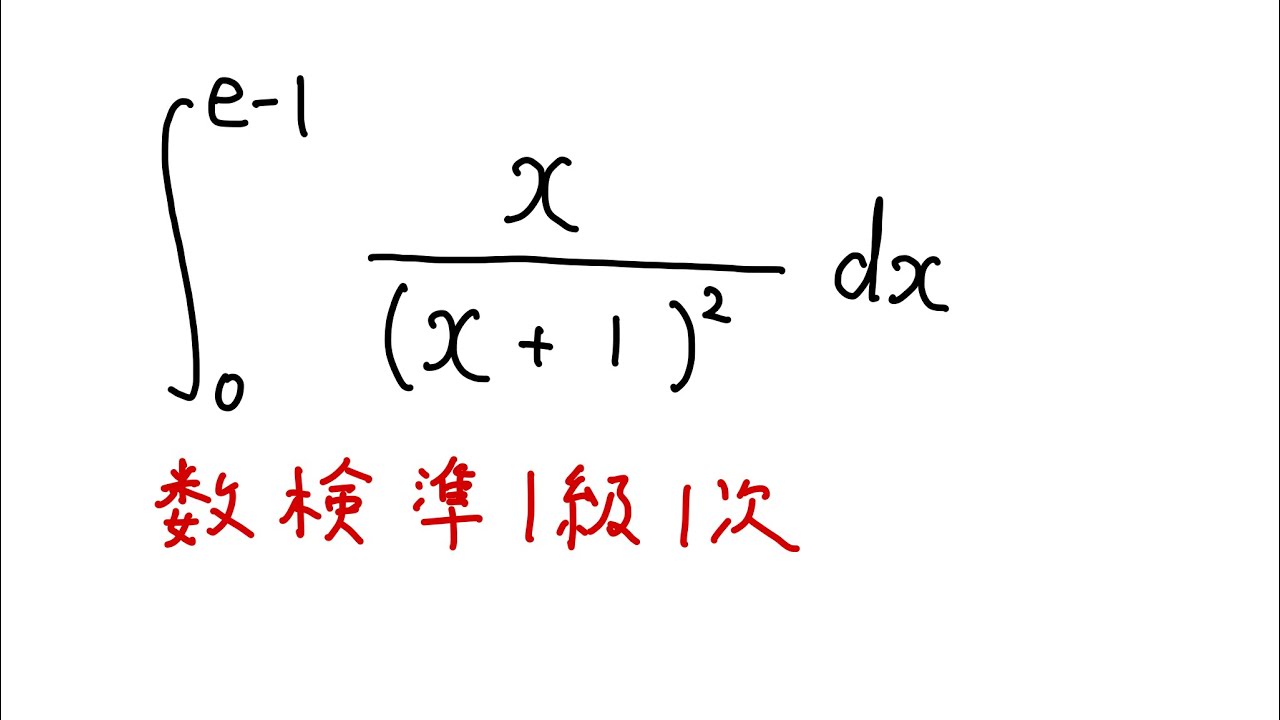
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{e-1} \displaystyle \frac{x}{(x+1)^2} dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{0}^{e-1} \displaystyle \frac{x}{(x+1)^2} dx$
出典:数検準1級1次
#数学検定準1級2次過去問#69「展開が最短かも」 #定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x^4(1-x)^4$ $dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{0}^{1} x^4(1-x)^4$ $dx$
出典:数検準1級1次
#数検準1級1次#定積分#ますただ
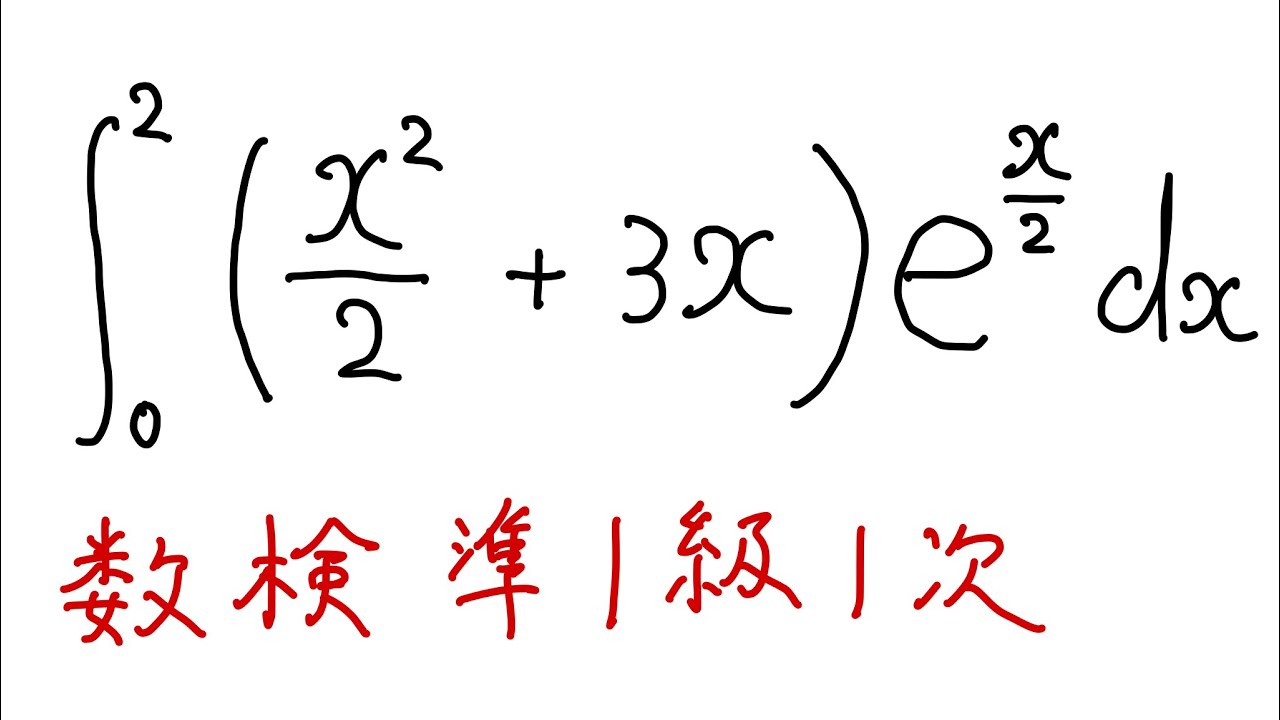
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} (\displaystyle \frac{x^2}{2}+3x)e^{\frac{x}{2}}dx$
出典:
この動画を見る
$\displaystyle \int_{0}^{2} (\displaystyle \frac{x^2}{2}+3x)e^{\frac{x}{2}}dx$
出典:
#山梨大学2013#定積分#ますただ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#山梨大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-10}^{0} \displaystyle \frac{1}{(x+11)(x+12)}$ $dx$
出典:2013年山梨大学
この動画を見る
$\displaystyle \int_{-10}^{0} \displaystyle \frac{1}{(x+11)(x+12)}$ $dx$
出典:2013年山梨大学
#数検準1級1次過去問#定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{e^2-1} log(x+1)$ $dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{0}^{e^2-1} log(x+1)$ $dx$
出典:数検準1級1次
#福岡大学#不定積分#ますただ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#福岡大学
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+1 }}$ $dx$
出典:福岡大学
この動画を見る
以下の不定積分を解け
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+1 }}$ $dx$
出典:福岡大学
#福島大学2013#定積分#ますただ
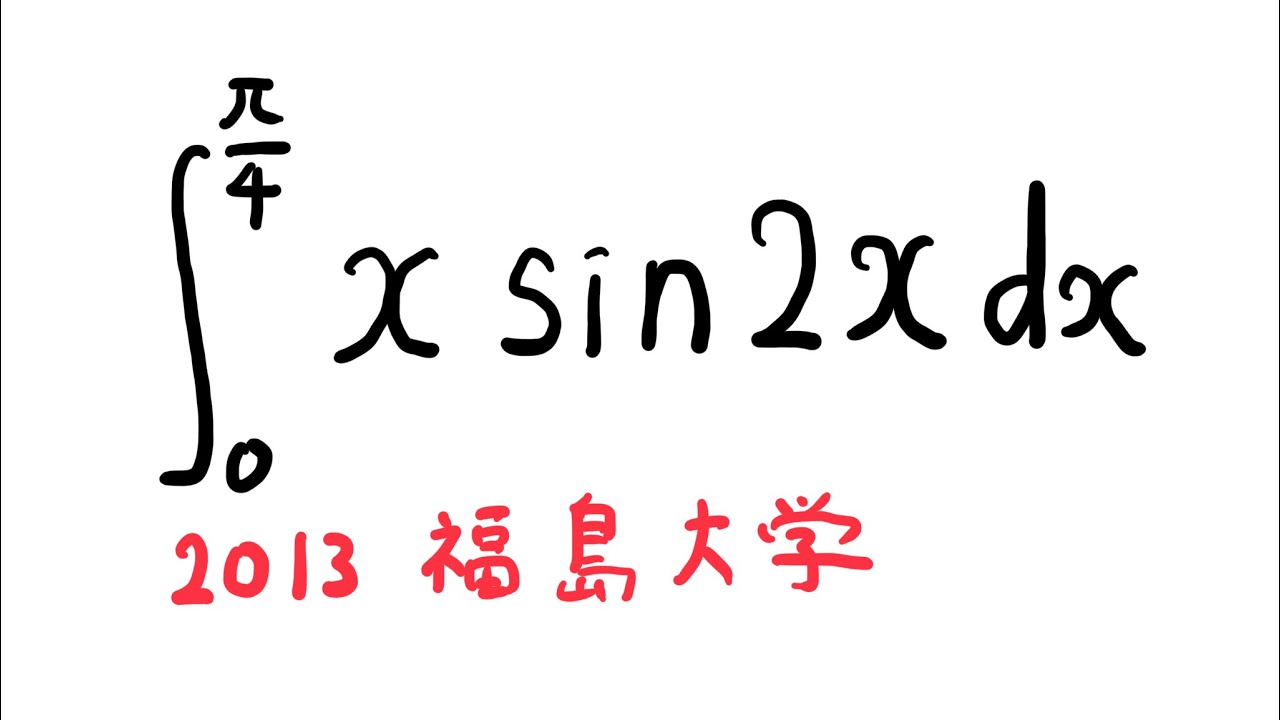
単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} x$ $\sin2$ $x$ $dx$
出典:2013年福島大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} x$ $\sin2$ $x$ $dx$
出典:2013年福島大学
大学入試問題#884「ミスれん」 #東京理科大学(2022) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{x-4}{2x^2+5x+2}$ $dx$
出典:2022年東京理科大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x-4}{2x^2+5x+2}$ $dx$
出典:2022年東京理科大学
#小樽商科大学#不定積分#ますただ
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#小樽商科大学
指導講師:
ますただ
問題文全文(内容文):
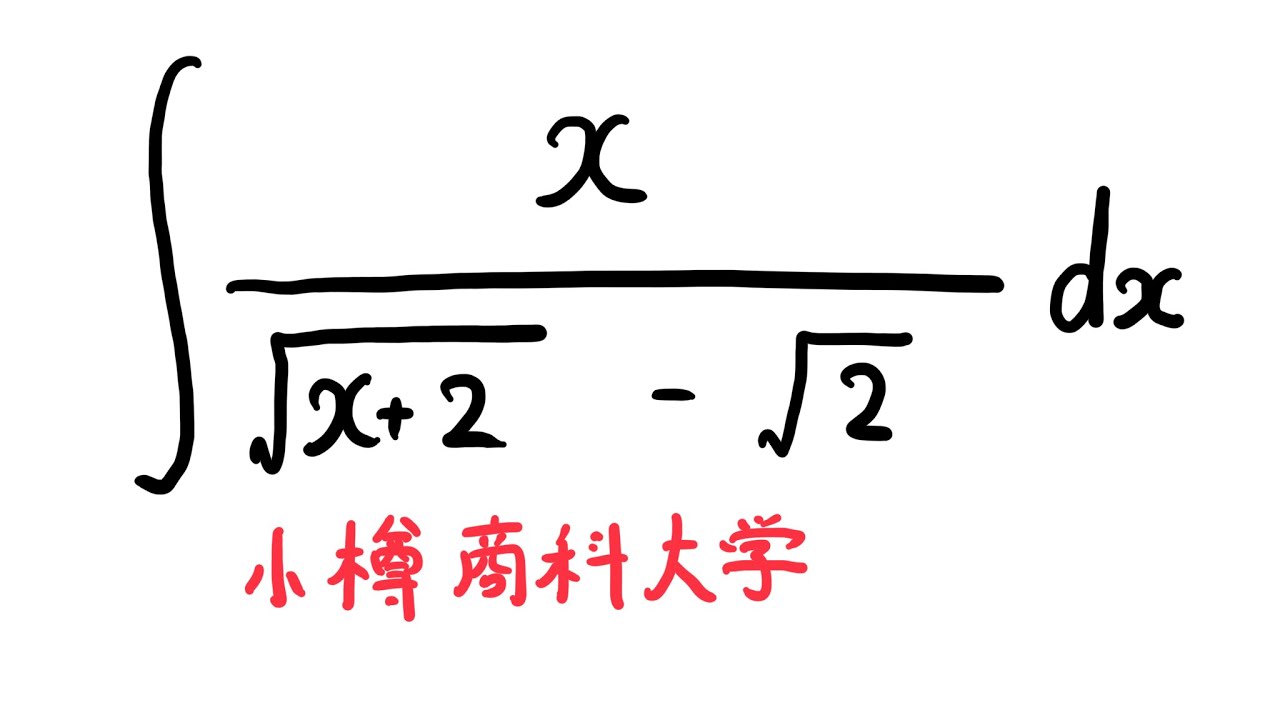
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+2}-\sqrt{ 2 }}$ $dx$
出典:小樽商科大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+2}-\sqrt{ 2 }}$ $dx$
出典:小樽商科大学
【高校数学】数Ⅱ:微分法と積分法:定積分の計算(同じ積分範囲)【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の定積分を求めよ。
$\displaystyle \int_{-2}^{3}(2x^2+4x-3)dx-2 \int_{-2}^{3}(x^2+4x+3)dx$
この動画を見る
次の定積分を求めよ。
$\displaystyle \int_{-2}^{3}(2x^2+4x-3)dx-2 \int_{-2}^{3}(x^2+4x+3)dx$
福田の数学〜立教大学2024年経済学部第1問(6)〜定積分で表された関数

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$0 \leqq x \leqq1$ の範囲において $f(x) \geqq 0$ である $2$ 次関数 $f(x) = ax^2+b$ は、等式
$\displaystyle f(x)(\int_0^1f(t)dt) = x^2+5$
を満たす。このとき、定数 $a,b$ は $a=\fbox{ケ}, b=\fbox{コ}$ である。
この動画を見る
$0 \leqq x \leqq1$ の範囲において $f(x) \geqq 0$ である $2$ 次関数 $f(x) = ax^2+b$ は、等式
$\displaystyle f(x)(\int_0^1f(t)dt) = x^2+5$
を満たす。このとき、定数 $a,b$ は $a=\fbox{ケ}, b=\fbox{コ}$ である。
#立教大学2012 #積分方程式

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#立教大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=x^2+4x-\displaystyle \int_{0}^{1} f(x)$ $dt$を満たす関数$f(x)$を求めよ。
出典:2012年立教大学
この動画を見る
$f(x)=x^2+4x-\displaystyle \int_{0}^{1} f(x)$ $dt$を満たす関数$f(x)$を求めよ。
出典:2012年立教大学
【高校数学】数Ⅱ:微分法と積分法:定積分と面積:1/6公式を用いて曲線で囲まれた図形の面積を求める!【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#面積、体積#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の曲線または直線で囲まれた図形の面積Sを求めよ。
$y=x^2+3x,y=-x^2-x+6$
この動画を見る
次の曲線または直線で囲まれた図形の面積Sを求めよ。
$y=x^2+3x,y=-x^2-x+6$
福田の数学〜大阪大学2024年文系第1問〜絶対値付き放物線と直線で囲まれた2つの面積が等しい条件

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 曲線$y$=|$x^2-1$|を$C$、直線$y$=$2a(x+1)$を$l$とする。ただし、$a$は0<$a$<1を満たす実数とする。
(1)曲線$C$と直線$l$の共有点の座標を全て求めよ。
(2)曲線$C$と直線$l$で囲まれた2つの部分の面積が等しくなる$a$の値を求めよ。
この動画を見る
$\Large\boxed{1}$ 曲線$y$=|$x^2-1$|を$C$、直線$y$=$2a(x+1)$を$l$とする。ただし、$a$は0<$a$<1を満たす実数とする。
(1)曲線$C$と直線$l$の共有点の座標を全て求めよ。
(2)曲線$C$と直線$l$で囲まれた2つの部分の面積が等しくなる$a$の値を求めよ。
#宮崎大学(2016)
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
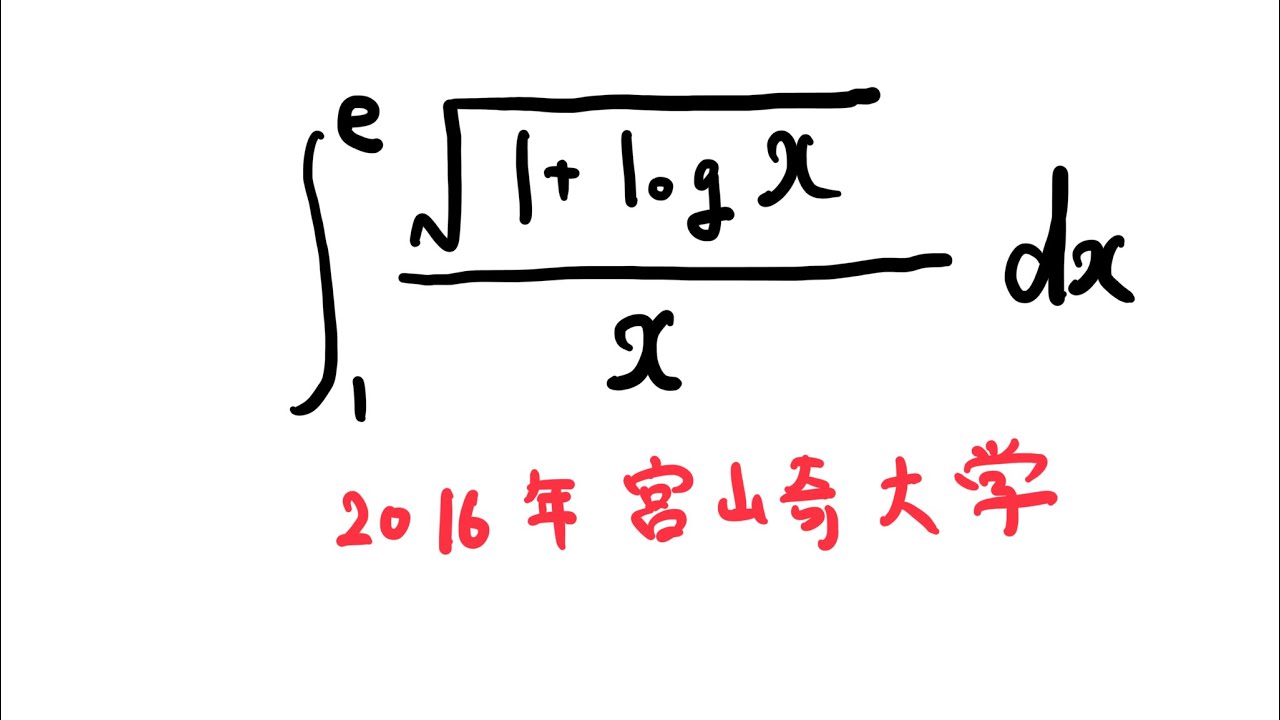
$\displaystyle \int_{1}^{e} \displaystyle \frac{\sqrt{ 1+log\ x }}{x} dx$
出典:2016年宮崎大学
この動画を見る
$\displaystyle \int_{1}^{e} \displaystyle \frac{\sqrt{ 1+log\ x }}{x} dx$
出典:2016年宮崎大学
