 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
福田の数学〜慶應義塾大学2024環境情報学部第4問〜球の一部の体積と距離の最大

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)$xyz$空間において、不等式 $x^2+y^2+z^2\leqq |x|$ が定める立体の体積は$\frac{\fbox{アイ}}{\fbox{ウエ}}\pi$である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は$\fbox{オカ}$である。
(2)$xyz$空間において、不等式 $x^2+y^2+z^2\leqq|x|+|y|$ が定める立体の体積は$\frac{\fbox{キク}}{\fbox{ケコ}}\pi$である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は$\sqrt{\fbox{サシ}}$ である。
(3)$xyz$ 空間において、不等式 $x^2+y^2+z^2\leqq$$ |x| + |y| + |z| - \frac{1}{4}$ が定める立体の体積は$(\fbox{スセ}$$+\frac{\fbox{ソタ}}{\fbox{チツ}}\sqrt{\fbox{テト}})\pi$ である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は $\frac{\fbox{ナニ}}{\fbox{ヌネ}}\sqrt{\fbox{ノハ}}$ $+\frac{\fbox{ヒフ}}{\fbox{ヘホ}}\sqrt{\fbox{マミ}}$ である。(ただし、$\fbox{ノハ} \le \fbox{マミ}$ とする。)
この動画を見る
(1)$xyz$空間において、不等式 $x^2+y^2+z^2\leqq |x|$ が定める立体の体積は$\frac{\fbox{アイ}}{\fbox{ウエ}}\pi$である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は$\fbox{オカ}$である。
(2)$xyz$空間において、不等式 $x^2+y^2+z^2\leqq|x|+|y|$ が定める立体の体積は$\frac{\fbox{キク}}{\fbox{ケコ}}\pi$である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は$\sqrt{\fbox{サシ}}$ である。
(3)$xyz$ 空間において、不等式 $x^2+y^2+z^2\leqq$$ |x| + |y| + |z| - \frac{1}{4}$ が定める立体の体積は$(\fbox{スセ}$$+\frac{\fbox{ソタ}}{\fbox{チツ}}\sqrt{\fbox{テト}})\pi$ である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は $\frac{\fbox{ナニ}}{\fbox{ヌネ}}\sqrt{\fbox{ノハ}}$ $+\frac{\fbox{ヒフ}}{\fbox{ヘホ}}\sqrt{\fbox{マミ}}$ である。(ただし、$\fbox{ノハ} \le \fbox{マミ}$ とする。)
福田のおもしろ数学294〜対数方程式の解の積

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{2024}x^{\log_{2024}x}\ =\ x^2$を満たす実数$x$の積の下3桁を求めよ。
この動画を見る
$\sqrt{2024}x^{\log_{2024}x}\ =\ x^2$を満たす実数$x$の積の下3桁を求めよ。
福田のおもしろ数学293〜三角方程式を満たす正の整数xの最小値

単元:
#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#整数の性質#約数・倍数・整数の割り算と余り・合同式#三角関数とグラフ#加法定理とその応用
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \tan 19x^{\circ}\ =\ \frac{\cos 96^{\circ}+\sin 96^{\circ}}{\cos 96^{\circ}-\sin 96^{\circ}}\ $を満たす最小の正の整数$\ x\ $を求めよ。
この動画を見る
$\displaystyle \tan 19x^{\circ}\ =\ \frac{\cos 96^{\circ}+\sin 96^{\circ}}{\cos 96^{\circ}-\sin 96^{\circ}}\ $を満たす最小の正の整数$\ x\ $を求めよ。
福田の数学〜慶應義塾大学2024環境情報学部第1問(2)〜対数不等式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$
\begin{eqnarray}
実数x, y, zが \\
\left\{
\begin{array}{1}
x > 1, \ y > 1 , \ z > 1\\
log_{x}y + log_{y}x + log_{y}z \leqq 6\\
4xz + 3x - 7y - 5z = -5
\end{array}
\right.
\\を満たしているとき \
x = \frac{\fbox{アイ}}{\fbox{ウエ}}, \
y = \frac{\fbox{オカ}}{\fbox{キク}}, \
z = \frac{\fbox{ケコ}}{\fbox{サシ}},
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
実数x, y, zが \\
\left\{
\begin{array}{1}
x > 1, \ y > 1 , \ z > 1\\
log_{x}y + log_{y}x + log_{y}z \leqq 6\\
4xz + 3x - 7y - 5z = -5
\end{array}
\right.
\\を満たしているとき \
x = \frac{\fbox{アイ}}{\fbox{ウエ}}, \
y = \frac{\fbox{オカ}}{\fbox{キク}}, \
z = \frac{\fbox{ケコ}}{\fbox{サシ}},
\end{eqnarray}
$
#関西学院大学2006#不定積分_68
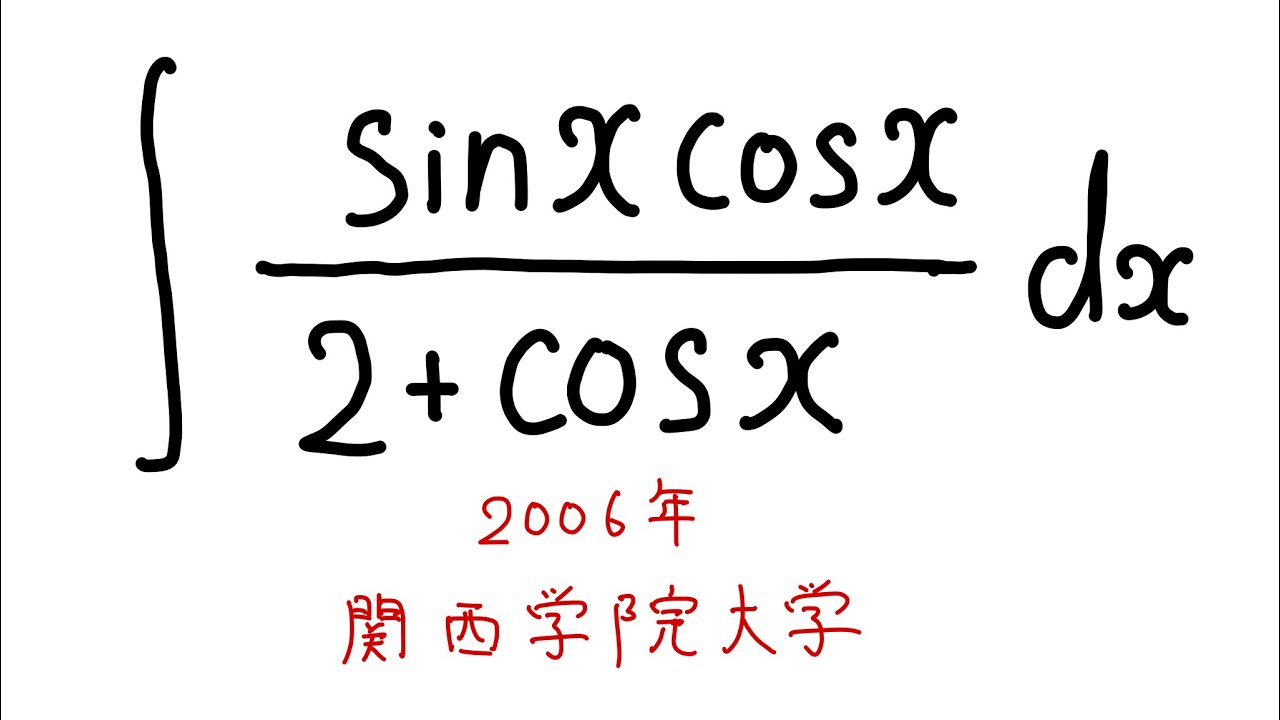
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#関西学院大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \dfrac{\sin x \cos x}{2+\cos \ x} dx$を解け.
2006関西学院大学過去問
この動画を見る
$\displaystyle \int \dfrac{\sin x \cos x}{2+\cos \ x} dx$を解け.
2006関西学院大学過去問
福田の数学〜慶應義塾大学2024環境情報学部第1問(1)〜相加平均と相乗平均の関係

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x,y$ を正の実数とするとき、$\displaystyle 27x + \frac{3x}{y} + \frac{2y}{x}$ は $\displaystyle x=\frac{\fbox{アイ}}{\fbox{ウエ}},$ $\displaystyle y= \frac{\fbox{オカ}}{\fbox{キク}}$ において最小値 $\fbox{ケコ}$ をとる。
この動画を見る
$x,y$ を正の実数とするとき、$\displaystyle 27x + \frac{3x}{y} + \frac{2y}{x}$ は $\displaystyle x=\frac{\fbox{アイ}}{\fbox{ウエ}},$ $\displaystyle y= \frac{\fbox{オカ}}{\fbox{キク}}$ において最小値 $\fbox{ケコ}$ をとる。
#関西学院大学2019#不定積分_67
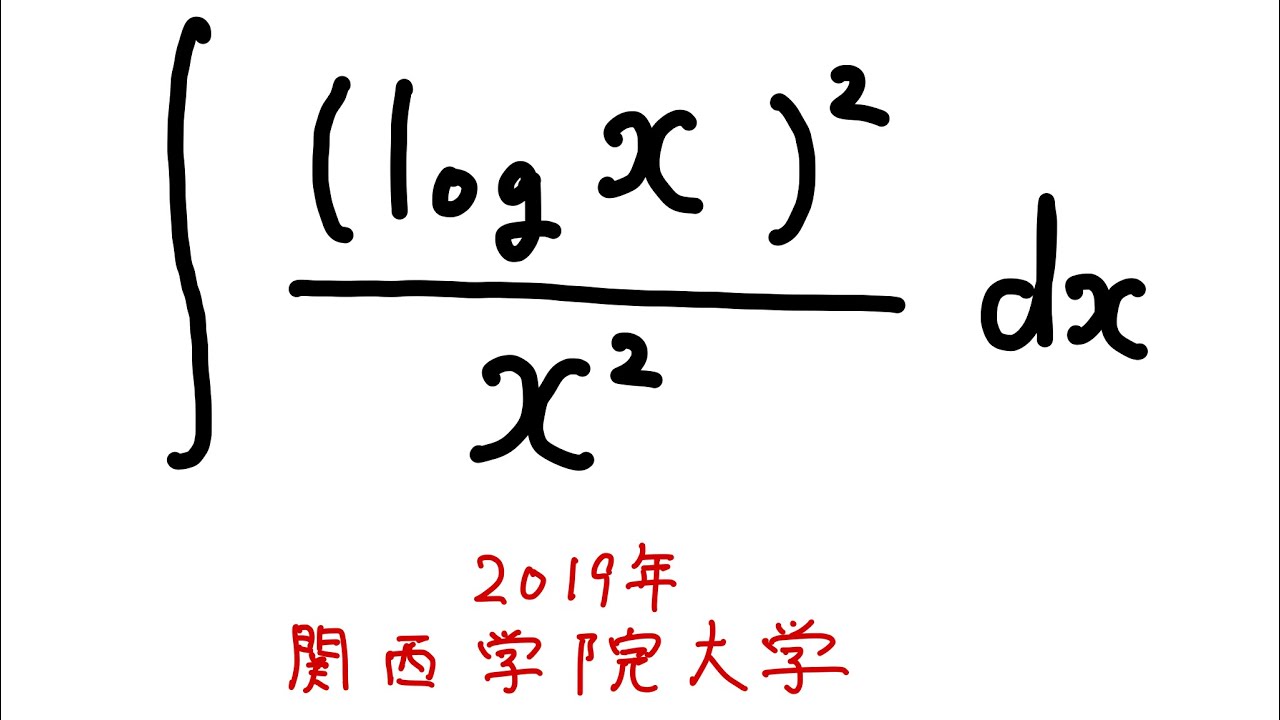
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#関西学院大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \dfrac{(\log x)^2}{x^2} dx$を解け.
2019関西学院大学過去問
この動画を見る
$\displaystyle \int \dfrac{(\log x)^2}{x^2} dx$を解け.
2019関西学院大学過去問
福田の数学〜慶應義塾大学2024総合政策学部第5問〜線形計画法

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
領域 $D$ $ \begin{eqnarray}
\left\{
\begin{array}{l}
x^2 + y^2 \leq 4 \\
(\sqrt{2}x^2 - 2y) (x-2y+2) \leq 0
\end{array}
\right.
\end{eqnarray} $
を点 $(x,y)$ が動くとき $x-2y$ の最大値、最小値を求めよ。
$ax+y$ が $(\frac{6}{5}, \frac{8}{5})$ で最大となる $a$ の範囲は?
そのときの $ax+y$ のとりうる範囲は?
この動画を見る
領域 $D$ $ \begin{eqnarray}
\left\{
\begin{array}{l}
x^2 + y^2 \leq 4 \\
(\sqrt{2}x^2 - 2y) (x-2y+2) \leq 0
\end{array}
\right.
\end{eqnarray} $
を点 $(x,y)$ が動くとき $x-2y$ の最大値、最小値を求めよ。
$ax+y$ が $(\frac{6}{5}, \frac{8}{5})$ で最大となる $a$ の範囲は?
そのときの $ax+y$ のとりうる範囲は?
#関西学院大学2006#不定積分_66
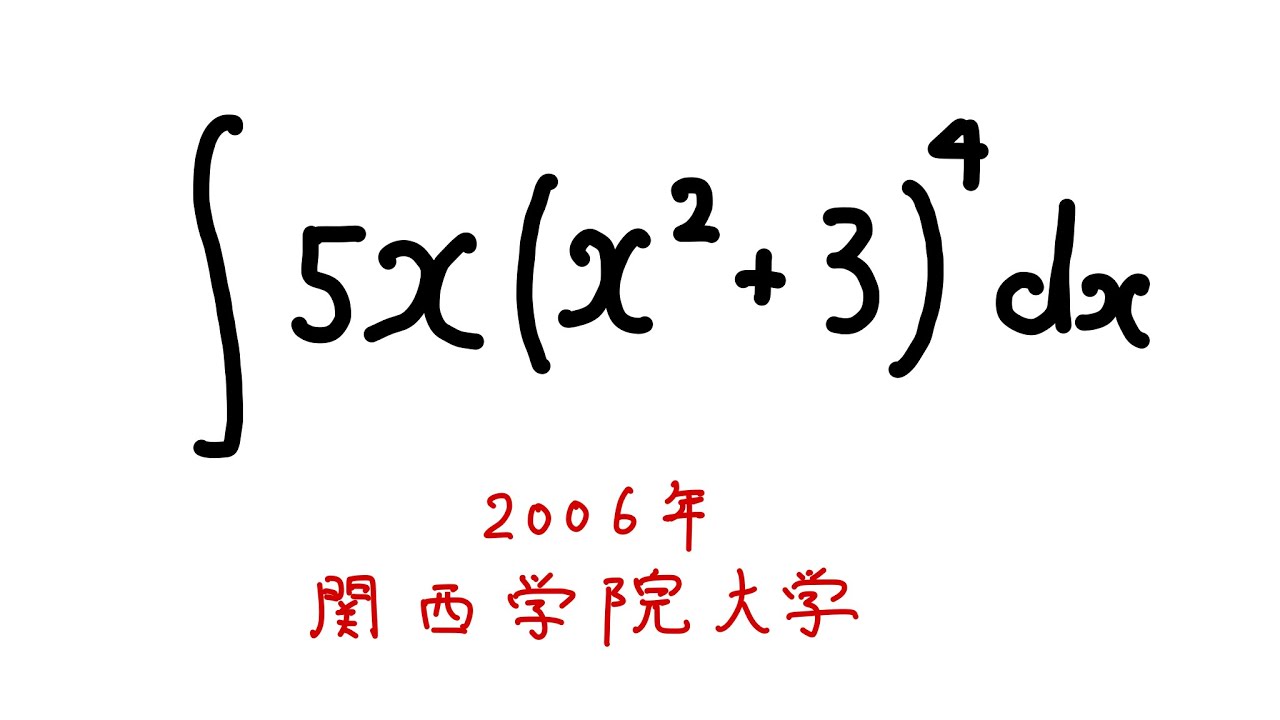
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#関西学院大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$ \int 5x(x^2+3)^4 \ dx$を解け.
2006関西学院大学過去問
この動画を見る
$ \int 5x(x^2+3)^4 \ dx$を解け.
2006関西学院大学過去問
微分法と積分法 数Ⅱ 絶対値を含む関数の最大最小【マコちゃんねるがていねいに解説】

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数f(x)=│x(x-1)(x-2)│ (-1≦x≦3) の最大値,最小値を求めよ。
この動画を見る
関数f(x)=│x(x-1)(x-2)│ (-1≦x≦3) の最大値,最小値を求めよ。
#慶應義塾大学2024#対数_65#Shorts

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$ x\gt 1,y \gt 1,z \gt 1$
$\log_x y +\log_y x+\log_y z+4\log_z y \leqq 6$
$4xz+3x-7y-5z=-5$
を満たす$x,y,z$の値を求めよ.
2024慶應義塾大学環境情報学部過去問題
この動画を見る
$ x\gt 1,y \gt 1,z \gt 1$
$\log_x y +\log_y x+\log_y z+4\log_z y \leqq 6$
$4xz+3x-7y-5z=-5$
を満たす$x,y,z$の値を求めよ.
2024慶應義塾大学環境情報学部過去問題
福田の数学〜慶應義塾大学2024総合政策学部第2問〜定積分で表された関数の最大値

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
負でない実数 $t$ に対して定義される関数 $\displaystyle\frac{9}{2}t-3\int^{1}_{0}|(x-t)(x-2t)|dx$ の最大値と、そのときの $t$ の値は?
この動画を見る
負でない実数 $t$ に対して定義される関数 $\displaystyle\frac{9}{2}t-3\int^{1}_{0}|(x-t)(x-2t)|dx$ の最大値と、そのときの $t$ の値は?
福田の数学〜慶應義塾大学2024総合政策学部第2問〜定積分で表された関数の最大値

単元:
#微分法と積分法#不定積分・定積分
指導講師:
問題文全文(内容文):
負でない実数$\ t\ $に対して定義される関数$\displaystyle \ f(t)\ =\ \frac{9}{2}t-3\int_{0}^{1}|(x-t)(x-2t)|dx\ \ $の最大値を求めよ。
この動画を見る
負でない実数$\ t\ $に対して定義される関数$\displaystyle \ f(t)\ =\ \frac{9}{2}t-3\int_{0}^{1}|(x-t)(x-2t)|dx\ \ $の最大値を求めよ。
福田のおもしろ数学288〜三角関数に関する不等式の証明

単元:
#数Ⅱ#式と証明#三角関数#整式の除法・分数式・二項定理#加法定理とその応用#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$sin^n2x+(sin^xx-cos^nx)^2\leqq1$を証明して下さい。
この動画を見る
$sin^n2x+(sin^xx-cos^nx)^2\leqq1$を証明して下さい。
福田のおもしろ数学286〜f(x+y)=f(x)+f(y)+xyを満たすf(x)を求める

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$
\begin{eqnarray}
連続関数f(x)が任意の点x, \ yに対してf(x+y)=f(x)+f(y)+xy…①を満たし、
\\
f'(0)=1とする。f(x)がすべてのxで微分可能であることを示し、f(x)を求めよ。
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
連続関数f(x)が任意の点x, \ yに対してf(x+y)=f(x)+f(y)+xy…①を満たし、
\\
f'(0)=1とする。f(x)がすべてのxで微分可能であることを示し、f(x)を求めよ。
\end{eqnarray}
$
福田のおもしろ数学285〜(1+1/n)^(n+1)が減少数列である証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$
b_{n}=(1 + \frac{1}{n})^{n+1}
\
で定まる数列 \{ b_{n} \}は減少数列であることを示せ。
$
この動画を見る
$
b_{n}=(1 + \frac{1}{n})^{n+1}
\
で定まる数列 \{ b_{n} \}は減少数列であることを示せ。
$
福田の数学〜慶應義塾大学2024総合政策学部第1問(1)〜2次方程式の作成

福田の数学〜東京慈恵会医科大学2024医学部第4問〜円板を軸の周りに回転してできる立体の体積
単元:
#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
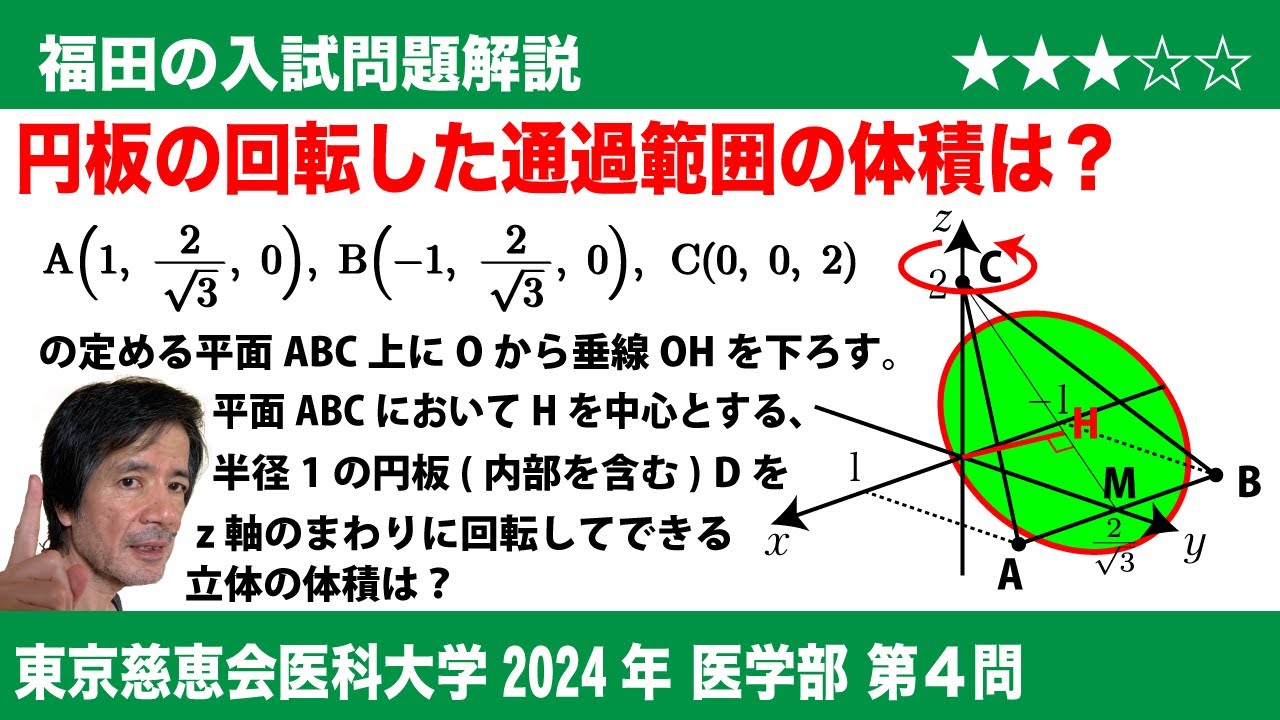
$\mathrm{O}$を原点とする$\mathrm{xyz} $平面において、3点 $\mathrm{A(1,\dfrac{2}{\sqrt{3}}, 0), B(-1, \dfrac{2}{\sqrt{3}}, 0), C(0, 0, 2)}$ の定める平面$\mathrm{ABC}$ 上に$\mathrm{O}$ から垂線$\mathrm{OH}$ を下ろす。平面$\mathrm{ABC}$ において、$\mathrm{H}$ を中心とする半径$\mathrm{1}$の円板(内部を含む)$\mathrm{D}$ を考える。
(1)平面$\mathrm{z = t}$ が$\mathrm{D}$と交わるような$\mathrm{t}$の範囲を求めよ。
(2)$\mathrm{D}$を$\mathrm{z}$軸の周りに$\mathrm{1}$回転させるとき、$\mathrm{D}$が通過してできる立体$\mathrm{K}$の体積$\mathrm{V}$を求めよ。
この動画を見る
$\mathrm{O}$を原点とする$\mathrm{xyz} $平面において、3点 $\mathrm{A(1,\dfrac{2}{\sqrt{3}}, 0), B(-1, \dfrac{2}{\sqrt{3}}, 0), C(0, 0, 2)}$ の定める平面$\mathrm{ABC}$ 上に$\mathrm{O}$ から垂線$\mathrm{OH}$ を下ろす。平面$\mathrm{ABC}$ において、$\mathrm{H}$ を中心とする半径$\mathrm{1}$の円板(内部を含む)$\mathrm{D}$ を考える。
(1)平面$\mathrm{z = t}$ が$\mathrm{D}$と交わるような$\mathrm{t}$の範囲を求めよ。
(2)$\mathrm{D}$を$\mathrm{z}$軸の周りに$\mathrm{1}$回転させるとき、$\mathrm{D}$が通過してできる立体$\mathrm{K}$の体積$\mathrm{V}$を求めよ。
数がでかすぎる!1の位の数字をどう求める?【東京大学】【数学 入試問題】

単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#指数関数#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(10^210)/(10^10+3)の整数部分のけた数と、1の位の数字を求めよ。ただし、3^21=10460353203を用いてよい。
この動画を見る
(10^210)/(10^10+3)の整数部分のけた数と、1の位の数字を求めよ。ただし、3^21=10460353203を用いてよい。
微分法と積分法 数Ⅱ 複合関数の最大最小【マコちゃんねるがていねいに解説】

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
x+3y=9,x≧0,y≧0のとき,x²yの最大値,最小値を求めたい。
(1) x²yをxだけの式で表せ。
(2) xの取り得る範囲を求めよ。
(3) x²yの最大値と最小値と,そのときのx,yの値を求めよ。
この動画を見る
x+3y=9,x≧0,y≧0のとき,x²yの最大値,最小値を求めたい。
(1) x²yをxだけの式で表せ。
(2) xの取り得る範囲を求めよ。
(3) x²yの最大値と最小値と,そのときのx,yの値を求めよ。
福田のおもしろ数学283〜関数不等式を満たす関数を求める

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明
指導講師:
福田次郎
問題文全文(内容文):
任意の実数$x$、$y$、$z$に対して
$f(x+y)+f(y+z)+f(z+x) \geqq 3 f(x+2y+3z)$
が成り立つような実数値をとる関数 $f(x)$をすべて求めよ。
この動画を見る
任意の実数$x$、$y$、$z$に対して
$f(x+y)+f(y+z)+f(z+x) \geqq 3 f(x+2y+3z)$
が成り立つような実数値をとる関数 $f(x)$をすべて求めよ。
微分法と積分法 数Ⅱ 最大最小を利用した関数の決定2【マコちゃんねるがていねいに解説】

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
a,bは定数で、a>0とする。関数f(x)=ax⁴-4ax³+b (1≦x≦4) の最大値が9、最小値がー18になるように,定数a,bの値を定めよ。
この動画を見る
a,bは定数で、a>0とする。関数f(x)=ax⁴-4ax³+b (1≦x≦4) の最大値が9、最小値がー18になるように,定数a,bの値を定めよ。
福田のおもしろ数学279〜関数方程式から関数の値を計算する問題

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
任意の実数$x$に対して$f(x)+f(x-1)=x^2$が成り立ち、$f(19)=94$のとき$f(94)$の値は?
この動画を見る
任意の実数$x$に対して$f(x)+f(x-1)=x^2$が成り立ち、$f(19)=94$のとき$f(94)$の値は?
福田の数学〜東京理科大学2024創域理工学部第2問〜放物線の接線と極限

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$m$を正の実数とし、関数$f(x)$を$f(x)=-mx^2+1$と定める。座標平面上の曲線$y=f(x)$を$C$とおき、負の実数$a$に対して点$\textrm{A}(a,f(a))$における曲線$C$の接線を$l_1$とおく。直線$l_1$と$y$軸との交点を$\textrm{P}$とし、点$\textrm{P}$を通り$l_1$に垂直な直線を$l_2$とおき、$l_2$と$x$軸の交点を$\textrm{Q}$とする。
(1) 点$\textrm{P}$の座標を$a$と$m$を用いて表せ。
(2) 点$\textrm{Q}$の座標を$a$と$m$を用いて表せ。
以下、直線$l_2$が曲線$C$の接線となるときを考える。
(3) $a$を$m$を用いて表せ。
(4) 線分$\textrm{AQ}$の長さは$m$を用いて表される。これを$L(m)$とおく。
(a) $\displaystyle \lim_{m \rightarrow \infty}L(m)$を求めよ。
(b) $\displaystyle \lim_{m \rightarrow 0}mL(m)$を求めよ。
この動画を見る
$m$を正の実数とし、関数$f(x)$を$f(x)=-mx^2+1$と定める。座標平面上の曲線$y=f(x)$を$C$とおき、負の実数$a$に対して点$\textrm{A}(a,f(a))$における曲線$C$の接線を$l_1$とおく。直線$l_1$と$y$軸との交点を$\textrm{P}$とし、点$\textrm{P}$を通り$l_1$に垂直な直線を$l_2$とおき、$l_2$と$x$軸の交点を$\textrm{Q}$とする。
(1) 点$\textrm{P}$の座標を$a$と$m$を用いて表せ。
(2) 点$\textrm{Q}$の座標を$a$と$m$を用いて表せ。
以下、直線$l_2$が曲線$C$の接線となるときを考える。
(3) $a$を$m$を用いて表せ。
(4) 線分$\textrm{AQ}$の長さは$m$を用いて表される。これを$L(m)$とおく。
(a) $\displaystyle \lim_{m \rightarrow \infty}L(m)$を求めよ。
(b) $\displaystyle \lim_{m \rightarrow 0}mL(m)$を求めよ。
#北海道大学1957#因数分解_64

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
ますただ
問題文全文(内容文):
$2x^2-xy-y^2-7x+y+6$を因数分解せよ.
1957北海道大学過去問題
この動画を見る
$2x^2-xy-y^2-7x+y+6$を因数分解せよ.
1957北海道大学過去問題
福田のおもしろ数学277〜ガウス記号の等式の証明

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n$は正の整数とする。
$[\sqrt{n}+\sqrt{n+1}]=[\sqrt{ 4n+2 }]$であることを証明して下さい。
$[n]$は$x$を超えない最大の整数を表します。
この動画を見る
$n$は正の整数とする。
$[\sqrt{n}+\sqrt{n+1}]=[\sqrt{ 4n+2 }]$であることを証明して下さい。
$[n]$は$x$を超えない最大の整数を表します。
福田の数学〜東京理科大学2024創域理工学部第1問(2)〜三角不等式の解法

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(2)0 \leqq θ \lt 2π$のとき、次の不等式を解こう。
$sin2θ \gt 2cos(θ+\frac{π}{6})+\frac{\sqrt{3}}{2}・・・③$
$a=cosθ,b=sinθ$とおくと、次の不等式$③$は
$\boxed{キ}ab-\boxed{ク}\sqrt{\boxed{ケ}}a+\boxed{コ}b-\sqrt{2}\gt0 ・・・④$
となる。不等式$④$の左辺は
$(\boxed{サ}a+\boxed{シ})(\boxed{ス}b-\sqrt{セ})$
と因数分解できる。これより、不等式$③$の解は
$\frac{π}{\boxed{ソ}} \lt θ \lt \frac{\boxed{タ}}{\boxed{チ}}π$または$\frac{\boxed{ツ}}{\boxed{テ}}π \lt θ \lt\frac{\boxed{ト}}{\boxed{ナ}}π$
と求まる。
この動画を見る
$\boxed{1}(2)0 \leqq θ \lt 2π$のとき、次の不等式を解こう。
$sin2θ \gt 2cos(θ+\frac{π}{6})+\frac{\sqrt{3}}{2}・・・③$
$a=cosθ,b=sinθ$とおくと、次の不等式$③$は
$\boxed{キ}ab-\boxed{ク}\sqrt{\boxed{ケ}}a+\boxed{コ}b-\sqrt{2}\gt0 ・・・④$
となる。不等式$④$の左辺は
$(\boxed{サ}a+\boxed{シ})(\boxed{ス}b-\sqrt{セ})$
と因数分解できる。これより、不等式$③$の解は
$\frac{π}{\boxed{ソ}} \lt θ \lt \frac{\boxed{タ}}{\boxed{チ}}π$または$\frac{\boxed{ツ}}{\boxed{テ}}π \lt θ \lt\frac{\boxed{ト}}{\boxed{ナ}}π$
と求まる。
#1 微分空間の圏について: The category of diffeological spaces

福田のおもしろ数学275〜分母の違う項がたくさん並んだ方程式の解

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の方程式を満たす$x$を求めて下さい。
$\frac{x-2020}{1}+\frac{x-2019}{2}+\cdots+\frac{x-2000}{21} = \frac{x-1}{2020}+\frac{x-2}{2019}+\cdots+\frac{x-21}{2000} $
この動画を見る
次の方程式を満たす$x$を求めて下さい。
$\frac{x-2020}{1}+\frac{x-2019}{2}+\cdots+\frac{x-2000}{21} = \frac{x-1}{2020}+\frac{x-2}{2019}+\cdots+\frac{x-21}{2000} $
福田のおもしろ数学274〜底が2の対数のガウスの和が2024を超えるのはいつか

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の式を満たす最小の整数 $n$ を求めて下さい。
$[\log_2{1}]+[\log_2{2}]+[\log_2{3}]+\cdots+[\log_2{n}]>2024$
$[x]$ は $x$ を超えない最大の整数を表します。
この動画を見る
次の式を満たす最小の整数 $n$ を求めて下さい。
$[\log_2{1}]+[\log_2{2}]+[\log_2{3}]+\cdots+[\log_2{n}]>2024$
$[x]$ は $x$ を超えない最大の整数を表します。
