数Ⅱ
数Ⅱ
福田の数学〜慶應義塾大学2022年薬学部第１問(6)〜三角関数の連立方程式
単元：
#連立方程式#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
(6)$0 \leqq x \leqq \pi, 0 \leqq y \leqq \pi$を満たすx,yに対して、等式$2\sin x+\sin y=1$が
成り立つとする。
$(\textrm{i})$この等式を満たすxの範囲は$\boxed{\ \ コ\ \ }$である。
$(\textrm{ii})x,y$が$2\cos x+\cos y=2\sqrt2$を満たすとき、$\sin(x+y)$の値を求めると
$\boxed{\ \ サ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
(6)$0 \leqq x \leqq \pi, 0 \leqq y \leqq \pi$を満たすx,yに対して、等式$2\sin x+\sin y=1$が
成り立つとする。
$(\textrm{i})$この等式を満たすxの範囲は$\boxed{\ \ コ\ \ }$である。
$(\textrm{ii})x,y$が$2\cos x+\cos y=2\sqrt2$を満たすとき、$\sin(x+y)$の値を求めると
$\boxed{\ \ サ\ \ }$である。
2022慶應義塾大学薬学部過去問
Δの読み方知ってる？
福田の数学〜京都大学2022年理系第４問〜四面体に関する証明と線分の長さの最小
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#微分法と積分法#恒等式・等式・不等式の証明#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
四面体OABCが
$OA=4, OB=AB=BC=3, OC=AC=2\sqrt3$
を満たしているとする。Pを辺BC上の点とし、$\triangle OAP$の重心をGとする。
このとき、次の各問いに答えよ。
(1)$\overrightarrow{ PG } ∟ \overrightarrow{ OA }$を示せ。
(2)Pが辺BC上を動くとき、PGの最小値を求めよ。
2022京都大学理系過去問
この動画を見る
四面体OABCが
$OA=4, OB=AB=BC=3, OC=AC=2\sqrt3$
を満たしているとする。Pを辺BC上の点とし、$\triangle OAP$の重心をGとする。
このとき、次の各問いに答えよ。
(1)$\overrightarrow{ PG } ∟ \overrightarrow{ OA }$を示せ。
(2)Pが辺BC上を動くとき、PGの最小値を求めよ。
2022京都大学理系過去問
【ゼロからわかる】二項定理の基本（高校数学Ⅱ）
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
次の式の展開式を求めよ。
（1）
$(x+3)^4$
（2）
$(2a-b)^5$
この動画を見る
次の式の展開式を求めよ。
（1）
$(x+3)^4$
（2）
$(2a-b)^5$
福田の数学〜慶應義塾大学2022年薬学部第１問(5)〜対数方程式と解の個数
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
(5)$x\neq 2$である正の実数xに対して、方程式
$\log_{10}x+\log_{100}x^2-\log_{0.1}|x-2|=\log_{10}a (a \gt 0)$
がある。
$(\textrm{i})x=6$のとき、aの値は$\boxed{\ \ ク\ \ }$である。
$(\textrm{ii})$この方程式が異なる3個の実数解をもつとき、aの値の範囲は$\boxed{\ \ ケ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
(5)$x\neq 2$である正の実数xに対して、方程式
$\log_{10}x+\log_{100}x^2-\log_{0.1}|x-2|=\log_{10}a (a \gt 0)$
がある。
$(\textrm{i})x=6$のとき、aの値は$\boxed{\ \ ク\ \ }$である。
$(\textrm{ii})$この方程式が異なる3個の実数解をもつとき、aの値の範囲は$\boxed{\ \ ケ\ \ }$である。
2022慶應義塾大学薬学部過去問
【誘導あり：概要欄】大学入試問題#131 浜松医科大学(2020) 三角比
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
（1）
$x \gt 0$のとき
$x \gt \sin\ x$を示せ
（2）
$\displaystyle \frac{1}{6} \lt \sin10^{ \circ } \lt \displaystyle \frac{\pi}{18}$を示せ
出典：2020年浜松医科大学 入試問題
この動画を見る
（1）
$x \gt 0$のとき
$x \gt \sin\ x$を示せ
（2）
$\displaystyle \frac{1}{6} \lt \sin10^{ \circ } \lt \displaystyle \frac{\pi}{18}$を示せ
出典：2020年浜松医科大学 入試問題
大阪大の問題の背景 特に文系の人見てください
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\cos\dfrac{2}{7}\pi,\cos\dfrac{4}{7}\pi,\cos\dfrac{6}{7}\pi$を解にもつ3次方程式
$x^3+ax^2+bx+c=0$を求めよ.
ただし,$z^7=1$とする.
2022大阪大過去問
この動画を見る
$\cos\dfrac{2}{7}\pi,\cos\dfrac{4}{7}\pi,\cos\dfrac{6}{7}\pi$を解にもつ3次方程式
$x^3+ax^2+bx+c=0$を求めよ.
ただし,$z^7=1$とする.
2022大阪大過去問
大阪大の問題の背景 特に文系の人見てください
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#図形と計量#三角比（三角比・拡張・相互関係・単位円）#複素数平面#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
(1)$ \cos\dfrac{2}{7}\pi, \cos\dfrac{4}{7}\pi, \cos\dfrac{6}{7}\pi$を解にもつ
$3$次方程式$ x^3+ax^2+bx+c=0$を求めよ.＊$ z^7=1$
(2)$ f(x)=8x^3+4x^2-4x-1$,$f\left(\cos\dfrac{2}{7}\pi \right)=0$を示せ.
この動画を見る
(1)$ \cos\dfrac{2}{7}\pi, \cos\dfrac{4}{7}\pi, \cos\dfrac{6}{7}\pi$を解にもつ
$3$次方程式$ x^3+ax^2+bx+c=0$を求めよ.＊$ z^7=1$
(2)$ f(x)=8x^3+4x^2-4x-1$,$f\left(\cos\dfrac{2}{7}\pi \right)=0$を示せ.
福田の数学〜慶應義塾大学2022年薬学部第１問(4)〜２次関数と積分の確率
単元：
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
(4)f(x)はxの2次関数である。$f(x)$は$x=-2$で極値をとり、$\int_{-3}^0f(x)dx=0$
を満たす。またxy平面上において、f(x)のグラフ$y=f(x)$はx軸と異なる2点で交わり、
$y=f(x)$とx軸で囲まれる部分の面積は$\frac{8}{3}$である。このとき$f(x)=\boxed{\ \ キ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
(4)f(x)はxの2次関数である。$f(x)$は$x=-2$で極値をとり、$\int_{-3}^0f(x)dx=0$
を満たす。またxy平面上において、f(x)のグラフ$y=f(x)$はx軸と異なる2点で交わり、
$y=f(x)$とx軸で囲まれる部分の面積は$\frac{8}{3}$である。このとき$f(x)=\boxed{\ \ キ\ \ }$である。
2022慶應義塾大学薬学部過去問
大阪大2022
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#三角関数#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ \alpha=\dfrac{2}{7}\pi$とする.
(1)$ \cos 4\alpha-\cos 3\alpha$を示せ.
(2)$ f(x)=8x^3+4x^2-4x-1,f(\cos \alpha)=0$を示せ.
(3)$ \cos\dfrac{2}{7}\pi$は無理数であることを示せ.
2022阪大過去問
この動画を見る
$ \alpha=\dfrac{2}{7}\pi$とする.
(1)$ \cos 4\alpha-\cos 3\alpha$を示せ.
(2)$ f(x)=8x^3+4x^2-4x-1,f(\cos \alpha)=0$を示せ.
(3)$ \cos\dfrac{2}{7}\pi$は無理数であることを示せ.
2022阪大過去問
【数Ⅱ】円を表す方程式【図形と方程式の関係】
福田の入試問題解説〜東京大学2022年理系第４問〜３次関数のグラフと直線の囲む2つの部分の面積
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
座標平面上の曲線
$C:y=x^3-x$
を考える。
(1)座標平面上の全ての点Pが次の条件$(\textrm{i})$を満たすことを示せ。
$(\textrm{i})$点Pを通る直線lで、曲線Cと相異なる3点で交わるものが存在する。
(2)次の条件$(\textrm{ii})$を満たす点Pのとりうる範囲を座標平面上に図示せよ。
$(\textrm{ii})$点Pを通る直線lで、曲線Cと相異なる3点で交わり、かつ、直線lと
曲線Cで囲まれた2つの部分の面積が等しくなるものが存在する。
2022東京大学理系過去問
この動画を見る
座標平面上の曲線
$C:y=x^3-x$
を考える。
(1)座標平面上の全ての点Pが次の条件$(\textrm{i})$を満たすことを示せ。
$(\textrm{i})$点Pを通る直線lで、曲線Cと相異なる3点で交わるものが存在する。
(2)次の条件$(\textrm{ii})$を満たす点Pのとりうる範囲を座標平面上に図示せよ。
$(\textrm{ii})$点Pを通る直線lで、曲線Cと相異なる3点で交わり、かつ、直線lと
曲線Cで囲まれた2つの部分の面積が等しくなるものが存在する。
2022東京大学理系過去問
大学入試問題#129 関西学院大学(1991) 二項定理の応用
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$(a+b+\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b})^7$を展開した時の$ab^2$の係数を求めよ。
出典：1991年関西学院大学 入試問題
この動画を見る
$(a+b+\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b})^7$を展開した時の$ab^2$の係数を求めよ。
出典：1991年関西学院大学 入試問題
福田の数学〜慶應義塾大学2022年薬学部第１問(2)〜高次方程式の解
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
(2)a,bは実数とする。xの3次方程式$x^3+(a+4)x^2-3(a+4)x+b=0$
の実数解が$x=3$のみであるとき、aの値の範囲は$\boxed{\ \ エ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
(2)a,bは実数とする。xの3次方程式$x^3+(a+4)x^2-3(a+4)x+b=0$
の実数解が$x=3$のみであるとき、aの値の範囲は$\boxed{\ \ エ\ \ }$である。
2022慶應義塾大学薬学部過去問
指数の方程式 （高校範囲）
福田の数学〜京都大学2022年理系第１問〜対数の値の評価
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$5.4 \lt \log_42022 \lt 5.5$であることを示せ。ただし、$0.301 \lt \log_{10}2 \lt 0.3011$で
あることは用いてよい。
2022京都大学理系過去問
この動画を見る
$5.4 \lt \log_42022 \lt 5.5$であることを示せ。ただし、$0.301 \lt \log_{10}2 \lt 0.3011$で
あることは用いてよい。
2022京都大学理系過去問
大学入試問題#128 東京理科大学(2020) 定積分
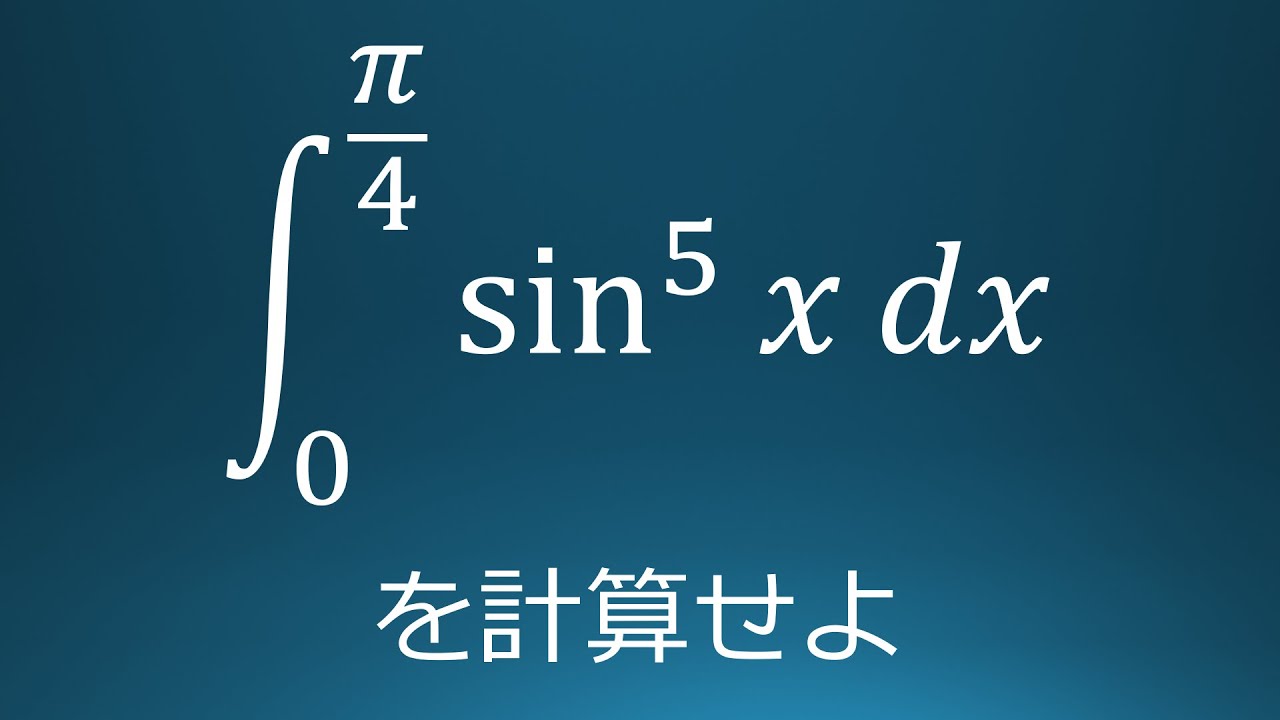
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{4}}\sin^5x\ dx$を計算せよ。
出典：2020年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\sin^5x\ dx$を計算せよ。
出典：2020年東京理科大学 入試問題
埼玉県 令和4年度 数学 関数 2022 入試問題100題解説75問目！
福田の入試問題解説〜東京大学2022年理系第３問〜点の存在する条件と領域の面積
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
Oを原点とする座標平面上で考える。座標平面上の2点$S(x_1,y_1),T(x_2,y_2)$
に対し、点Sが点Tから十分離れているとは、
$|x_1-x_2| \geqq 1$ または $|y_1-y_2| \geqq 1$
が成り立つことと定義する。
不等式
$0 \leqq x \leqq 3, 0 \leqq y \leqq 3$
が表す正方形の領域をDとし、その2つの頂点A(3,0), B(3,3)を考える。
さらに、次の条件$(\textrm{i}),(\textrm{ii})$を共に満たす点Pをとる。
$(\textrm{i})$点Pは領域Dの点であり、かつ、放物線$y=x^2$上にある。
$(\textrm{ii})$点Pは、3点O,A,Bのいずれからも十分離れている。
点Pのx座標をaとする。
(1)aのとりうる値の範囲を求めよ。
(2)次の条件$(\textrm{iii}),(\textrm{iv})$をともに満たす点Qが存在しうる範囲の面積f(a)を求めよ。
$(\textrm{iii})$点Qは領域Dの点である。
$(\textrm{iv})$点Qは、4点O,A,B,Pのいずれからも十分離れている。
(3)aは(1)で求めた範囲を動くとする。(2)のf(a)を最小にするaの値を求めよ。
2022東京大学理系過去問
この動画を見る
Oを原点とする座標平面上で考える。座標平面上の2点$S(x_1,y_1),T(x_2,y_2)$
に対し、点Sが点Tから十分離れているとは、
$|x_1-x_2| \geqq 1$ または $|y_1-y_2| \geqq 1$
が成り立つことと定義する。
不等式
$0 \leqq x \leqq 3, 0 \leqq y \leqq 3$
が表す正方形の領域をDとし、その2つの頂点A(3,0), B(3,3)を考える。
さらに、次の条件$(\textrm{i}),(\textrm{ii})$を共に満たす点Pをとる。
$(\textrm{i})$点Pは領域Dの点であり、かつ、放物線$y=x^2$上にある。
$(\textrm{ii})$点Pは、3点O,A,Bのいずれからも十分離れている。
点Pのx座標をaとする。
(1)aのとりうる値の範囲を求めよ。
(2)次の条件$(\textrm{iii}),(\textrm{iv})$をともに満たす点Qが存在しうる範囲の面積f(a)を求めよ。
$(\textrm{iii})$点Qは領域Dの点である。
$(\textrm{iv})$点Qは、4点O,A,B,Pのいずれからも十分離れている。
(3)aは(1)で求めた範囲を動くとする。(2)のf(a)を最小にするaの値を求めよ。
2022東京大学理系過去問
福田の入試問題解説〜東京大学2022年理系第１問〜最小値の存在と定積分の計算
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
次の関数f(x)を考える。
$f(x)=(\cos x)\log(\cos x)-\cos x+\int_0^x(\cos t)\log(\cos t)dt (0 \leqq x \lt \frac{\pi}{2})$
(1)f(x)は区間$0 \leqq x \lt \frac{\pi}{2}$において最小値を持つことを示せ。
(2)f(x)は区間$0 \leqq x \lt \frac{\pi}{2}$における最小値を求めよ。
2022東京大学理系過去問
この動画を見る
次の関数f(x)を考える。
$f(x)=(\cos x)\log(\cos x)-\cos x+\int_0^x(\cos t)\log(\cos t)dt (0 \leqq x \lt \frac{\pi}{2})$
(1)f(x)は区間$0 \leqq x \lt \frac{\pi}{2}$において最小値を持つことを示せ。
(2)f(x)は区間$0 \leqq x \lt \frac{\pi}{2}$における最小値を求めよ。
2022東京大学理系過去問
千葉県（改） 令和4年度 数学 関数 2022 入試問題100題解説73問目！！
単元：
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
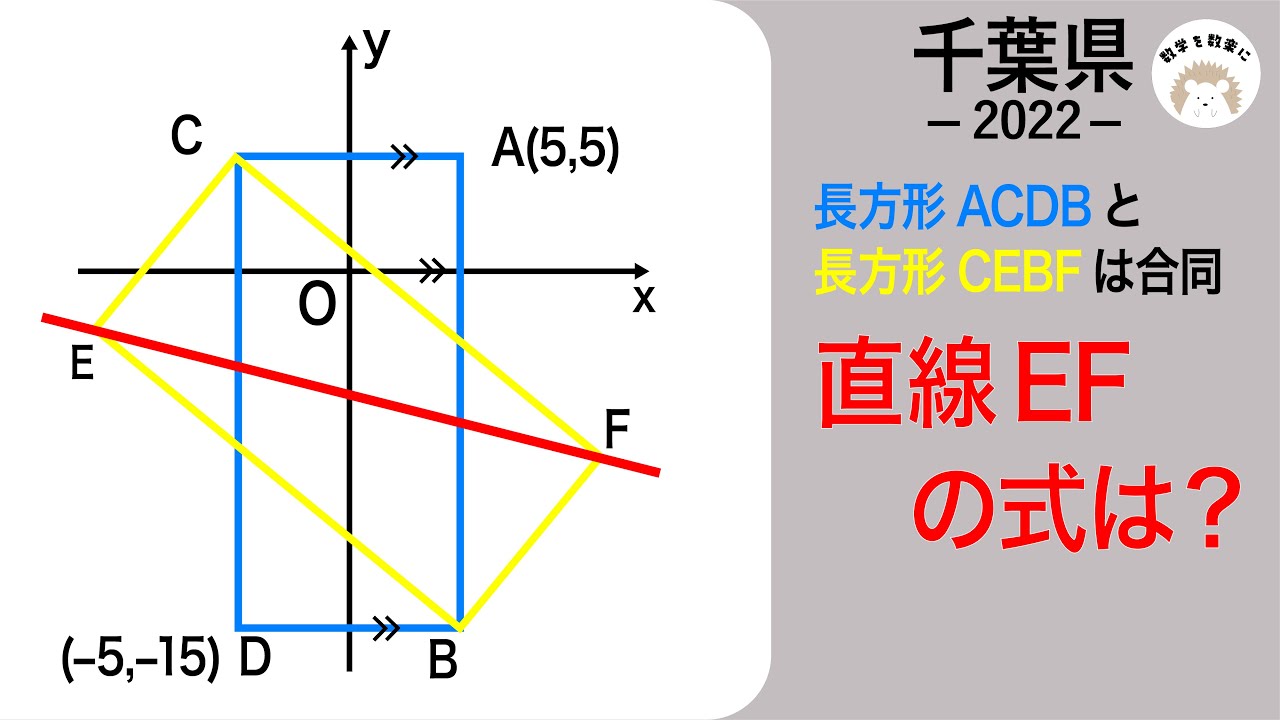
長方形ACDBと長方形CEBFは合同
直線EFの式は？
＊図は動画内参照
2022千葉県
この動画を見る
長方形ACDBと長方形CEBFは合同
直線EFの式は？
＊図は動画内参照
2022千葉県
和積を暗記するのはナンセンスじゃね？
福田の数学〜東京慈恵会医科大学2022年医学部第４問〜複素数平面と図形
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#平面上の曲線#複素数平面#方べきの定理と２つの円の関係#図形と方程式#点と直線#2次曲線#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京慈恵会医科大学
指導講師：
福田次郎
問題文全文(内容文)：
複素数平面上の点zが原点を中心とする半径1の円周上を動くとき、$w=z+\frac{2}{z}$
で表される点wの描く図形をCとする。Cで囲まれた部分の内部(ただし、
境界線は含まない)に定点$\alpha$をとり、$\alpha$を通る直線lがCと交わる2点を$\beta_1,\beta_2$とする。
(1)$w=u+vi$(u,vは実数)とするとき、uとvの間に成り立つ関係式を求めよ。
(2)点$\alpha$を固定したままlを動かすとき、積$|\beta_1-\alpha|・|\beta_2-\alpha|$が最大となる
ようなlはどのような直線のときか調べよ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
複素数平面上の点zが原点を中心とする半径1の円周上を動くとき、$w=z+\frac{2}{z}$
で表される点wの描く図形をCとする。Cで囲まれた部分の内部(ただし、
境界線は含まない)に定点$\alpha$をとり、$\alpha$を通る直線lがCと交わる2点を$\beta_1,\beta_2$とする。
(1)$w=u+vi$(u,vは実数)とするとき、uとvの間に成り立つ関係式を求めよ。
(2)点$\alpha$を固定したままlを動かすとき、積$|\beta_1-\alpha|・|\beta_2-\alpha|$が最大となる
ようなlはどのような直線のときか調べよ。
2022東京慈恵会医科大学医学部過去問
【数学Ⅱ/積分】絶対値を含む定積分
単元：
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
次の定積分を求めよ
$\displaystyle \int_{0}^{3} |x^2-1|dx$
この動画を見る
次の定積分を求めよ
$\displaystyle \int_{0}^{3} |x^2-1|dx$
ざ・見掛け倒しだよ
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+･･･････+\dfrac{32}{33}=\dfrac{a}{33!}$
$a$を17で割った余りを求めよ.
この動画を見る
$\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+･･･････+\dfrac{32}{33}=\dfrac{a}{33!}$
$a$を17で割った余りを求めよ.
福田の数学〜東京慈恵会医科大学2022年医学部第３問〜約数と倍数の性質
単元：
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師：
福田次郎
問題文全文(内容文)：
mは3以上の奇数とし、mの全ての正の約数を$a_1,a_2,\ldots,a_k$と並べる。
ただし、$a_1 \lt a_2 \lt \ldots \lt a_k$とする。
以下の2つの条件$(\textrm{i}),(\textrm{ii})$を満たすmについて考える。
$(\textrm{i})m$は素数ではない。
$(\textrm{ii})i \leqq j,1 \lt i \lt k ,1 \lt j \lt k$を満たす全ての整数i,jについて$a_j-a_i \leqq 3$が
成り立つ。
このとき、次の問いに答えよ。
(1)kは3または4であることを示し、mを$a_2$を用いて表せ。
(2)$k=3$となるとき、全ての正の整数nについて$(a_2n+1)^{a_2}-1$は
mの倍数であることを示せ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
mは3以上の奇数とし、mの全ての正の約数を$a_1,a_2,\ldots,a_k$と並べる。
ただし、$a_1 \lt a_2 \lt \ldots \lt a_k$とする。
以下の2つの条件$(\textrm{i}),(\textrm{ii})$を満たすmについて考える。
$(\textrm{i})m$は素数ではない。
$(\textrm{ii})i \leqq j,1 \lt i \lt k ,1 \lt j \lt k$を満たす全ての整数i,jについて$a_j-a_i \leqq 3$が
成り立つ。
このとき、次の問いに答えよ。
(1)kは3または4であることを示し、mを$a_2$を用いて表せ。
(2)$k=3$となるとき、全ての正の整数nについて$(a_2n+1)^{a_2}-1$は
mの倍数であることを示せ。
2022東京慈恵会医科大学医学部過去問
【数学Ⅱ/積分】関数の決定（定積分）
単元：
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
次の等式を満たす関数$f(x)$を求めよ。
$f(x)=3x^2+4x+\displaystyle \int_{-1}^{1} f(t) dt$
この動画を見る
次の等式を満たす関数$f(x)$を求めよ。
$f(x)=3x^2+4x+\displaystyle \int_{-1}^{1} f(t) dt$
不定方程式
単元：
#数A#複素数と方程式#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x,y$を実数とする.
$ x^3-y^3+(x-y)^3-36xy=3456$のとき,$ x-y$の値を求めよ.
この動画を見る
$x,y$を実数とする.
$ x^3-y^3+(x-y)^3-36xy=3456$のとき,$ x-y$の値を求めよ.
福田の数学〜東京慈恵会医科大学2022年医学部第２問〜微分可能性と最大値と体積
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学
指導講師：
福田次郎
問題文全文(内容文)：
実数aは正の定数とする。実数全体で定義された関数$f(x)=\frac{|x+a|}{\sqrt{x^2+1}}$について、
次の問いに答えよ。
(1)$f(x)$が$x=-a$で微分可能であるかどうか調べよ。
(2)$f(x)$の最大値が$\sqrt2$となるように、定数aの値を定めよ。
(3)定数aは(2)で定めた値とする。$y=f(x)$のグラフとx軸およびy軸で囲まれた部分
をx軸の周りに1回転させてできる立体の体積Vを求めよ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
実数aは正の定数とする。実数全体で定義された関数$f(x)=\frac{|x+a|}{\sqrt{x^2+1}}$について、
次の問いに答えよ。
(1)$f(x)$が$x=-a$で微分可能であるかどうか調べよ。
(2)$f(x)$の最大値が$\sqrt2$となるように、定数aの値を定めよ。
(3)定数aは(2)で定めた値とする。$y=f(x)$のグラフとx軸およびy軸で囲まれた部分
をx軸の周りに1回転させてできる立体の体積Vを求めよ。
2022東京慈恵会医科大学医学部過去問
【数学Ⅱ/積分】定積分で表された関数を求める
単元：
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師：
【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
次の等式を満たす関数$f(x),$および定数$a$の値を求めよ。
$\displaystyle \int_{a}^{x} f(t) dt=x^2-3x-4$
この動画を見る
次の等式を満たす関数$f(x),$および定数$a$の値を求めよ。
$\displaystyle \int_{a}^{x} f(t) dt=x^2-3x-4$