 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
ただの指数・対数方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$5^{\log_{ 10 }x} -50+x^{\log_{ 10 }5}=0$
実数解を求めよ。
この動画を見る
$5^{\log_{ 10 }x} -50+x^{\log_{ 10 }5}=0$
実数解を求めよ。
【数Ⅱ】内分の公式・外分の公式を導出から丁寧に【公式を1つだけにする!?】

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 数直線上の点A(3),B(6)について,線分ABを3:2に内分する点Pの座標を求めよ.$
この動画を見る
$ 数直線上の点A(3),B(6)について,線分ABを3:2に内分する点Pの座標を求めよ.$
大学入試問題#103 東海大学医学部(2017) 二項定理
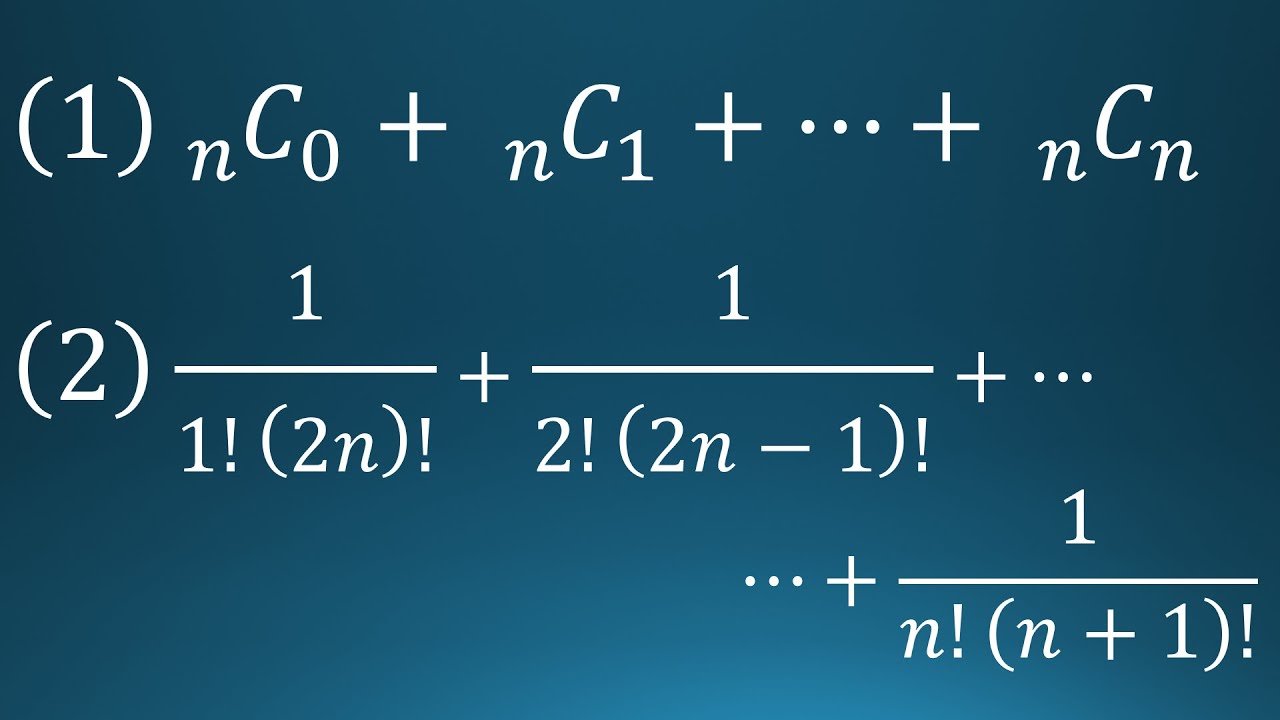
単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師:
ますただ
問題文全文(内容文):
次の和を求めよ。
(1)
${}_{ n }C_0+{}_{ n }C_1+・・・+{}_{ n }C_n$
(2)
$\displaystyle \frac{1}{1!(2n)!}+\displaystyle \frac{1}{2(2n-1)!}+・・・+\displaystyle \frac{1}{n!(n+1)!}$
出典:2017年東海大学医学部 入試問題
この動画を見る
次の和を求めよ。
(1)
${}_{ n }C_0+{}_{ n }C_1+・・・+{}_{ n }C_n$
(2)
$\displaystyle \frac{1}{1!(2n)!}+\displaystyle \frac{1}{2(2n-1)!}+・・・+\displaystyle \frac{1}{n!(n+1)!}$
出典:2017年東海大学医学部 入試問題
指数方程式 解はアレだけじゃないよ

指数方程式 解はアレだけじゃないよ

指数方程式 解はアレだけじゃないよ

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$5^x・16^{\frac{x-1}{x}}=100$
この動画を見る
これを解け.
$5^x・16^{\frac{x-1}{x}}=100$
大学入試問題#100 東京大学(1954) 軌跡・領域

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
点($x,y$)が原点を中心とする半径1の円の内部を動くとき
点($x+y,xy$)の動く範囲を図示せよ。
出典:1954年東京大学 入試問題
この動画を見る
点($x,y$)が原点を中心とする半径1の円の内部を動くとき
点($x+y,xy$)の動く範囲を図示せよ。
出典:1954年東京大学 入試問題
2022東北医科薬科大(医)微分・積分の基本問題

単元:
#数学(中学生)#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^4-4x^3$上の$(P,f(P))$における接線を$\ell $とする.
(1)$f(x)$と$\ell$の共有点が接線のみである$P$の範囲を求めよ.
(2)$P$が最小値のとき,$f(x)$と$\ell$で囲まれる面積を求めよ.
東北医科薬科大(医)過去問
この動画を見る
$f(x)=x^4-4x^3$上の$(P,f(P))$における接線を$\ell $とする.
(1)$f(x)$と$\ell$の共有点が接線のみである$P$の範囲を求めよ.
(2)$P$が最小値のとき,$f(x)$と$\ell$で囲まれる面積を求めよ.
東北医科薬科大(医)過去問
【数Ⅱ】虚数を解に持つ3次方程式【3次方程式の解と係数の関係】

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 3次方程式x^3-4x^2+ax+b=0の解の1つが3+iであるとき,
実際の定数a,bを求めよ.$
この動画を見る
$ 3次方程式x^3-4x^2+ax+b=0の解の1つが3+iであるとき,
実際の定数a,bを求めよ.$
🟨にあてはまる数は? 連分数 渋谷教育学園幕張 2022入試問題解説14問目
単元:
#数学(中学生)#数Ⅱ#式と証明#整式の除法・分数式・二項定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
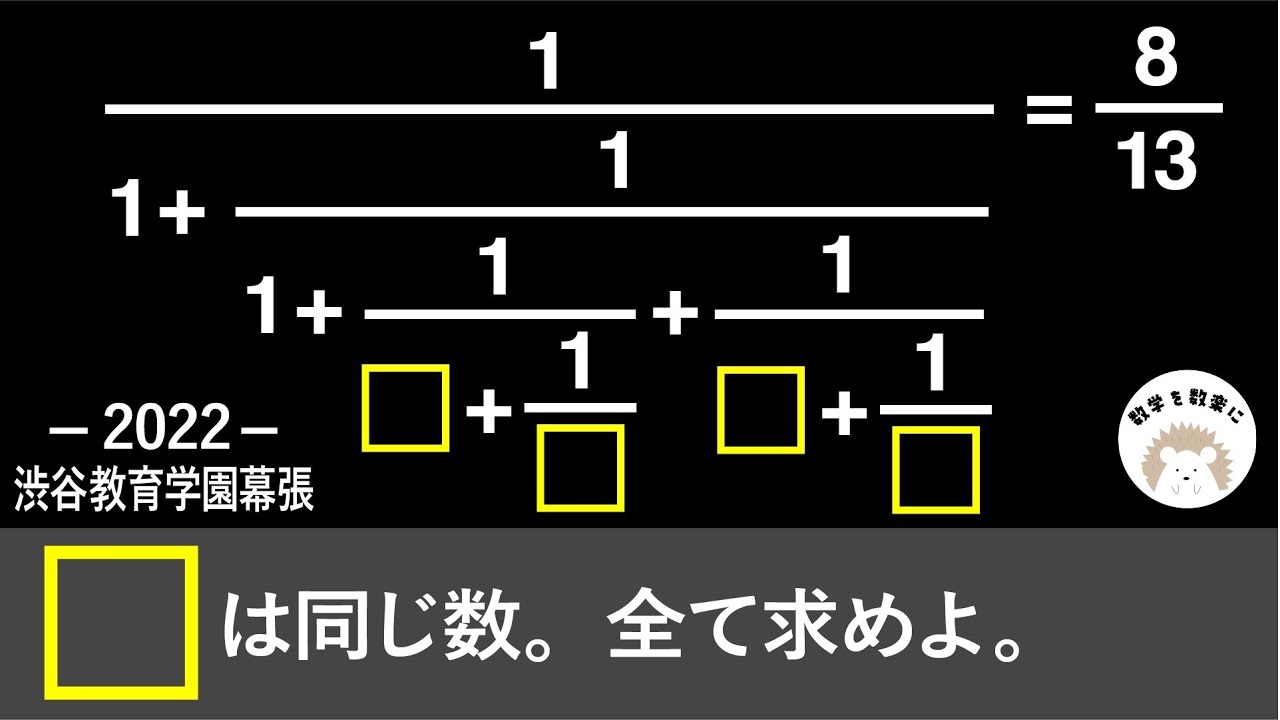
$\frac{1}{1+\frac{1}{1+\frac{1}{▢+\frac{1}{▢}}+\frac{1}{▢+\frac{1}{▢}}}}$=$\frac{8}{13}$
▢は同じ数。全て求めよ。
2022渋谷教育学園幕張
この動画を見る
$\frac{1}{1+\frac{1}{1+\frac{1}{▢+\frac{1}{▢}}+\frac{1}{▢+\frac{1}{▢}}}}$=$\frac{8}{13}$
▢は同じ数。全て求めよ。
2022渋谷教育学園幕張
福田の共通テスト直前演習〜2021年共通テスト数学ⅡB問題2。微分積分の問題。

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#センター試験・共通テスト関連#共通テスト#面積、体積#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
[1]aを実数とし、$f(x)=x^3-6ax+16$
(1)$y=f(x)$のグラフの概形は
$a=0$のとき、$\boxed{\ \ ア\ \ }$
$a \gt 0$のとき、$\boxed{\ \ イ\ \ }$
である.
$\boxed{\ \ ア\ \ },\boxed{\ \ イ\ \ }$については、最も適当なものを、次の⓪~⑤のうちから
1つずつ選べ。ただし、同じものを繰り返し選んでもよい。
(※選択肢は動画参照)
(2)$a \gt 0$とし、pを実数とする。座標平面上の曲線$y=f(x)$と直線$y=p$
が3個の共有点をもつようなpの値の範囲は$\boxed{\ \ ウ\ \ } \lt p \lt \boxed{\ \ エ\ \ }$
である。
$p=\boxed{\ \ ウ\ \ }$のとき、曲線$y=f(x)$と直線$y=p$は2個の共有点をもつ。
それらのx座標を$q,r(q \lt r)$とする。曲線$y=f(x)$と直線$y=p$
が点(r,p)で接することに注意すると
$q=\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キ\ \ }}\ a^{\frac{1}{2}}, r=\sqrt{\boxed{\ \ ク\ \ }}\ a^{\frac{1}{2}}$
と表せる。
$\boxed{\ \ ウ\ \ }, \boxed{\ \ エ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$2\sqrt2a^{\frac{3}{2}}+16$ ①$-2\sqrt2a^{\frac{3}{2}}+16$
②$4\sqrt2a^{\frac{3}{2}}+16$ ③$-4\sqrt2a^{\frac{3}{2}}+16$
④$8\sqrt2a^{\frac{3}{2}}+16$ ⑤$-8\sqrt2a^{\frac{3}{2}}+16$
(3)方程式$f(x)=0$の異なる実数解の個数をnとする。次の⓪~⑤のうち、
正しいものは$\boxed{\ \ ケ\ \ }$と$\boxed{\ \ コ\ \ }$である。
$\boxed{\ \ ケ\ \ }, \boxed{\ \ コ\ \ }$の解答群(解答の順序は問わない。)
$⓪n=1ならばa \lt 0 ①a \lt 0ならばn=1$
$②n=2ならばa \lt 0 ③a \lt 0ならばn=2$
$④n=2ならばa \gt 0 ⑤a \gt 0ならばn=3$
[2]$b \gt 0$とし、$g(x)=x^3-3bx+3b^2, h(x)=x^3-x^2+b^2$とおく。
座標平面上の曲線$y=g(x)$を$C_1$, 曲線$y=h(x)$を$C_2$とする。
$C_1$と$C_2$は2点で交わる。これらの交点のx座標をそれぞれ$\alpha,\beta$
$(\alpha \lt \beta)$とすると、$\alpha=\boxed{\ \ サ\ \ }, \beta=\boxed{\ \ シス\ \ }$である。
$\alpha \leqq x \leqq \beta$の範囲で$C_1$と$C_2$で囲まれた図形の面積をSとする。また、
$t \gt \beta$とし、$\beta \leqq x \leqq t$の範囲で$C_1$と$C_2$および直線$x=t$で囲まれた図形の
面積をTとする。
このとき
$S=\int_{\alpha}^{\beta}\boxed{\ \ セ\ \ }dx$
$T=\int_{\beta}^{t}\boxed{\ \ ソ\ \ }dx$
$S-T=\int_{\alpha}^{t}\boxed{\ \ タ\ \ }dx$
であるので
$S-T=\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テ\ \ }}(2t^3-\ \boxed{\ \ ト\ \ }bt^2+\boxed{\ \ ナニ\ \ }b^2t-\ \boxed{\ \ ヌ\ \ }b^3)$
が得られる。
したがって、$S=T$となるのは$t=\frac{\boxed{\ \ ネ\ \ }}{\boxed{\ \ ノ\ \ }}\ b$のときである。
$\boxed{\ \ セ\ \ }~\boxed{\ \ タ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
$⓪\left\{g(x)+h(x)\right\} ①\left\{g(x)-h(x)\right\}$
$②\left\{h(x)-g(x)\right\} ③\left\{2g(x)+2h(x)\right\}$
$④\left\{2g(x)-2h(x)\right\} ⑤\left\{2h(x)-2g(x)\right\}$
$⑥2g(x) ⑦2h(x)$
2022共通テスト数学過去問
この動画を見る
[1]aを実数とし、$f(x)=x^3-6ax+16$
(1)$y=f(x)$のグラフの概形は
$a=0$のとき、$\boxed{\ \ ア\ \ }$
$a \gt 0$のとき、$\boxed{\ \ イ\ \ }$
である.
$\boxed{\ \ ア\ \ },\boxed{\ \ イ\ \ }$については、最も適当なものを、次の⓪~⑤のうちから
1つずつ選べ。ただし、同じものを繰り返し選んでもよい。
(※選択肢は動画参照)
(2)$a \gt 0$とし、pを実数とする。座標平面上の曲線$y=f(x)$と直線$y=p$
が3個の共有点をもつようなpの値の範囲は$\boxed{\ \ ウ\ \ } \lt p \lt \boxed{\ \ エ\ \ }$
である。
$p=\boxed{\ \ ウ\ \ }$のとき、曲線$y=f(x)$と直線$y=p$は2個の共有点をもつ。
それらのx座標を$q,r(q \lt r)$とする。曲線$y=f(x)$と直線$y=p$
が点(r,p)で接することに注意すると
$q=\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キ\ \ }}\ a^{\frac{1}{2}}, r=\sqrt{\boxed{\ \ ク\ \ }}\ a^{\frac{1}{2}}$
と表せる。
$\boxed{\ \ ウ\ \ }, \boxed{\ \ エ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
⓪$2\sqrt2a^{\frac{3}{2}}+16$ ①$-2\sqrt2a^{\frac{3}{2}}+16$
②$4\sqrt2a^{\frac{3}{2}}+16$ ③$-4\sqrt2a^{\frac{3}{2}}+16$
④$8\sqrt2a^{\frac{3}{2}}+16$ ⑤$-8\sqrt2a^{\frac{3}{2}}+16$
(3)方程式$f(x)=0$の異なる実数解の個数をnとする。次の⓪~⑤のうち、
正しいものは$\boxed{\ \ ケ\ \ }$と$\boxed{\ \ コ\ \ }$である。
$\boxed{\ \ ケ\ \ }, \boxed{\ \ コ\ \ }$の解答群(解答の順序は問わない。)
$⓪n=1ならばa \lt 0 ①a \lt 0ならばn=1$
$②n=2ならばa \lt 0 ③a \lt 0ならばn=2$
$④n=2ならばa \gt 0 ⑤a \gt 0ならばn=3$
[2]$b \gt 0$とし、$g(x)=x^3-3bx+3b^2, h(x)=x^3-x^2+b^2$とおく。
座標平面上の曲線$y=g(x)$を$C_1$, 曲線$y=h(x)$を$C_2$とする。
$C_1$と$C_2$は2点で交わる。これらの交点のx座標をそれぞれ$\alpha,\beta$
$(\alpha \lt \beta)$とすると、$\alpha=\boxed{\ \ サ\ \ }, \beta=\boxed{\ \ シス\ \ }$である。
$\alpha \leqq x \leqq \beta$の範囲で$C_1$と$C_2$で囲まれた図形の面積をSとする。また、
$t \gt \beta$とし、$\beta \leqq x \leqq t$の範囲で$C_1$と$C_2$および直線$x=t$で囲まれた図形の
面積をTとする。
このとき
$S=\int_{\alpha}^{\beta}\boxed{\ \ セ\ \ }dx$
$T=\int_{\beta}^{t}\boxed{\ \ ソ\ \ }dx$
$S-T=\int_{\alpha}^{t}\boxed{\ \ タ\ \ }dx$
であるので
$S-T=\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テ\ \ }}(2t^3-\ \boxed{\ \ ト\ \ }bt^2+\boxed{\ \ ナニ\ \ }b^2t-\ \boxed{\ \ ヌ\ \ }b^3)$
が得られる。
したがって、$S=T$となるのは$t=\frac{\boxed{\ \ ネ\ \ }}{\boxed{\ \ ノ\ \ }}\ b$のときである。
$\boxed{\ \ セ\ \ }~\boxed{\ \ タ\ \ }$の解答群(同じものを繰り返し選んでもよい。)
$⓪\left\{g(x)+h(x)\right\} ①\left\{g(x)-h(x)\right\}$
$②\left\{h(x)-g(x)\right\} ③\left\{2g(x)+2h(x)\right\}$
$④\left\{2g(x)-2h(x)\right\} ⑤\left\{2h(x)-2g(x)\right\}$
$⑥2g(x) ⑦2h(x)$
2022共通テスト数学過去問
福田の共通テスト直前演習〜2021年共通テスト数学ⅡB問題1[2]。対数の大小判定の問題。

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
[2]a,bは正の実数であり、$a\neq 1,b\neq 1$を満たすとする。太郎さんは
$\log_ab$と$\log_ba$の大小関係を調べることにした。
(1)太郎さんは次のような考察をした。
まず、$\log_39=\boxed{\ \ ス\ \ }, \log_93=\frac{1}{\boxed{\ \ ス\ \ }}$である、この場合
$\log_39 \gt \log_93$
が成り立つ。
一方、$\log_{\frac{1}{4}}\boxed{\ \ セ\ \ }=-\frac{3}{2},\log_{\boxed{セ}}\frac{1}{4}=-\frac{2}{3}$である。この場合
$\log_{\frac{1}{4}}\boxed{\ \ セ\ \ } \lt \log_{\boxed{セ}}\frac{1}{4}$
が成り立つ。
(2)ここで
$\log_ab=t \ldots①$
とおく。
(1)の考察をもとにして、太郎さんは次の式が成り立つと推測し、
それが正しいことを確かめることにした。
$\log_ba=\frac{1}{t} \ldots②$
①により、$\boxed{\ \ ソ\ \ }$である。このことにより$\boxed{\ \ タ\ \ }$が得られ、②が
成り立つことが確かめられる。
$\boxed{\ \ ソ\ \ }$の解答群
$⓪a^k=t ①a^t=b ②b^a=t$
$③b^t=a ④t^a=b ⑤t^b=a$
$\boxed{\ \ タ\ \ }$の解答群
$⓪a=t^{\frac{1}{b}} ①a=b^{\frac{1}{t}} ②b=t^{\frac{1}{a}}$
$③b=a^{\frac{1}{t}} ④t=b^{\frac{1}{a}} ⑤t=a^{\frac{1}{b}}$
(3)次に、太郎さんは(2)の考察をもとにして
$t \gt \frac{1}{t} \ldots③$
を満たす実数$t(t\neq 0)$の値の範囲を求めた。
太郎さんの考察
$t \gt 0$ならば、③の両辺にtを掛けることにより、$t^2 \gt 1$を得る。
このような$t(t \gt 0)$の値の範囲は$1 \lt t$である。
$t \lt 0$ならば、③の両辺にtを掛けることにより、$t^2 \lt 1$を得る。
このような$t(t \lt 0)$の値の範囲は$-1 \lt t \lt 0$である。
この考察により、③を満たす$t(t\neq 0)$の値の範囲は
$-1 \lt t \lt 0, 1 \lt t$
であることが分かる。
ここで、aの値を一つ定めたとき、不等式
$\log_ab \gt \log_ba \ldots④$
を満たす実数$b(b \gt 0, b\neq 1)$の値の範囲について考える。
④を満たすbの値の範囲は$a \gt 1$のときは$\boxed{\ \ チ\ \ }$であり、
$0 \lt a \lt 1$のときは$\boxed{\ \ ツ\ \ }$である。
$\boxed{\ \ チ\ \ }$の解答群
$⓪0 \lt b \lt \frac{1}{a}, 1 \lt b \lt a ①0 \lt b \lt \frac{1}{a}, a \lt b$
$②\frac{1}{a} \lt b \lt 1, 1 \lt b \lt a ③\frac{1}{a} \lt b \lt 1, a \lt b$
$\boxed{\ \ ツ\ \ }$の解答群
$⓪0 \lt b \lt a, 1 \lt b \lt \frac{1}{a} ①0 \lt b \lt a, \frac{1}{a} \lt b$
$②a \lt b \lt 1, 1 \lt b \lt \frac{1}{a} ③a \lt b \lt 1, \frac{1}{a} \lt b$
(4)$p=\frac{12}{13}, q=\frac{12}{11}, r=\frac{14}{13}$とする。
次の⓪~③のうち、正しいものは$\boxed{\ \ テ\ \ }$である。
$\boxed{\ \ テ\ \ }$の解答群
$⓪\log_pq \gt \log_qp$かつ$\log_pr \gt \log_rp$
$①\log_pq \gt \log_qp$かつ$\log_pr \lt \log_rp$
$②\log_pq \lt \log_qp$かつ$\log_pr \gt \log_rp$
$③\log_pq \lt \log_qp$かつ$\log_pr \lt \log_rp$
2022共通テスト数学過去問
この動画を見る
[2]a,bは正の実数であり、$a\neq 1,b\neq 1$を満たすとする。太郎さんは
$\log_ab$と$\log_ba$の大小関係を調べることにした。
(1)太郎さんは次のような考察をした。
まず、$\log_39=\boxed{\ \ ス\ \ }, \log_93=\frac{1}{\boxed{\ \ ス\ \ }}$である、この場合
$\log_39 \gt \log_93$
が成り立つ。
一方、$\log_{\frac{1}{4}}\boxed{\ \ セ\ \ }=-\frac{3}{2},\log_{\boxed{セ}}\frac{1}{4}=-\frac{2}{3}$である。この場合
$\log_{\frac{1}{4}}\boxed{\ \ セ\ \ } \lt \log_{\boxed{セ}}\frac{1}{4}$
が成り立つ。
(2)ここで
$\log_ab=t \ldots①$
とおく。
(1)の考察をもとにして、太郎さんは次の式が成り立つと推測し、
それが正しいことを確かめることにした。
$\log_ba=\frac{1}{t} \ldots②$
①により、$\boxed{\ \ ソ\ \ }$である。このことにより$\boxed{\ \ タ\ \ }$が得られ、②が
成り立つことが確かめられる。
$\boxed{\ \ ソ\ \ }$の解答群
$⓪a^k=t ①a^t=b ②b^a=t$
$③b^t=a ④t^a=b ⑤t^b=a$
$\boxed{\ \ タ\ \ }$の解答群
$⓪a=t^{\frac{1}{b}} ①a=b^{\frac{1}{t}} ②b=t^{\frac{1}{a}}$
$③b=a^{\frac{1}{t}} ④t=b^{\frac{1}{a}} ⑤t=a^{\frac{1}{b}}$
(3)次に、太郎さんは(2)の考察をもとにして
$t \gt \frac{1}{t} \ldots③$
を満たす実数$t(t\neq 0)$の値の範囲を求めた。
太郎さんの考察
$t \gt 0$ならば、③の両辺にtを掛けることにより、$t^2 \gt 1$を得る。
このような$t(t \gt 0)$の値の範囲は$1 \lt t$である。
$t \lt 0$ならば、③の両辺にtを掛けることにより、$t^2 \lt 1$を得る。
このような$t(t \lt 0)$の値の範囲は$-1 \lt t \lt 0$である。
この考察により、③を満たす$t(t\neq 0)$の値の範囲は
$-1 \lt t \lt 0, 1 \lt t$
であることが分かる。
ここで、aの値を一つ定めたとき、不等式
$\log_ab \gt \log_ba \ldots④$
を満たす実数$b(b \gt 0, b\neq 1)$の値の範囲について考える。
④を満たすbの値の範囲は$a \gt 1$のときは$\boxed{\ \ チ\ \ }$であり、
$0 \lt a \lt 1$のときは$\boxed{\ \ ツ\ \ }$である。
$\boxed{\ \ チ\ \ }$の解答群
$⓪0 \lt b \lt \frac{1}{a}, 1 \lt b \lt a ①0 \lt b \lt \frac{1}{a}, a \lt b$
$②\frac{1}{a} \lt b \lt 1, 1 \lt b \lt a ③\frac{1}{a} \lt b \lt 1, a \lt b$
$\boxed{\ \ ツ\ \ }$の解答群
$⓪0 \lt b \lt a, 1 \lt b \lt \frac{1}{a} ①0 \lt b \lt a, \frac{1}{a} \lt b$
$②a \lt b \lt 1, 1 \lt b \lt \frac{1}{a} ③a \lt b \lt 1, \frac{1}{a} \lt b$
(4)$p=\frac{12}{13}, q=\frac{12}{11}, r=\frac{14}{13}$とする。
次の⓪~③のうち、正しいものは$\boxed{\ \ テ\ \ }$である。
$\boxed{\ \ テ\ \ }$の解答群
$⓪\log_pq \gt \log_qp$かつ$\log_pr \gt \log_rp$
$①\log_pq \gt \log_qp$かつ$\log_pr \lt \log_rp$
$②\log_pq \lt \log_qp$かつ$\log_pr \gt \log_rp$
$③\log_pq \lt \log_qp$かつ$\log_pr \lt \log_rp$
2022共通テスト数学過去問
加法定理語呂合わせ

福田の共通テスト直前演習〜2021年共通テスト数学ⅡB問題1[1]。直線と円の表す領域とが共有点をもつ条件の問題。

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#図形と方程式#円と方程式#軌跡と領域#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
[1]座標平面上に点A(-8,0)をとる。また、不等式
$x^2+y^2-4x-10y+4 \leqq 0$
の表す領域をDとする。
(1)領域Dは、中心が点$(\boxed{\ \ ア\ \ },\boxed{\ \ イ\ \ })$、半径が$\boxed{\ \ ウ\ \ }$の円の
$\boxed{\ \ エ\ \ }$である。
$\boxed{\ \ エ\ \ }$の解答群
⓪ 周 ① 内部 ② 外部
③ 周および内部 ④ 周および外部
以下、点$(\boxed{\ \ ア\ \ },\boxed{\ \ イ\ \ })$をQとし、方程式
$x^2+y^2-4x-10y+4=0$
の表す図形をCとする。
(2)点Aを通る直線と領域Dが共有点をもつのはどのようなときかを考えよう。
$(\textrm{i})(1)$により、直線$y=\boxed{\ \ オ\ \ }$は点Aを通るCの接線の一つとなること
がわかる。
太郎さんと花子さんは点Aを通るCのもう一つの接線について話している。
点Aを通り、傾きがkの直線をlとする。
太郎:直線lの方程式は$y=k(x+8)$と表すことができるから、
これを
$x^2+y^2-4x-10y+4=0$
に代入することで接線を求められそうだね。
花子:x軸と直線AQのなす角のタンジェントに着目することでも
求められそうだよ。
$(\textrm{ii})$ 太郎さんの求め方について考えてみよう。
$y=k(x+8)$を$x^2+y^2-4x-10y+4=0$に代入すると、
xについての2次方程式
$(k^2+1)x^2+(16k^2-10k-4)x+64k^2-80k+4=0$
が得られる。この方程式が$\boxed{\ \ カ\ \ }$ときのkの値が接線の傾きとなる。
$\boxed{\ \ カ\ \ }$の解答群
⓪重解をもつ
①異なる2つの実数解をもち、1つは0である
②異なる2つの正の実数解をもつ
③正の実数解と負の実数解をもつ
④異なる2つの負の実数解をもつ
⑤異なる2つの虚数解をもつ
$(\textrm{iii})$花子さんの求め方について考えてみよう。
x軸と直線AQのなす角を$\theta(0 \lt \theta \leqq \frac{\pi}{2})$とすると
$\tan\theta=\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}$
であり、直線$y=\boxed{\ \ オ\ \ }$と異なる接線の傾きは$\tan\boxed{\ \ ケ\ \ }$
と表すことができる。
$\boxed{\ \ ケ\ \ }$の解答群
⓪$\theta$ ①$2\theta$ ②$(\theta+\frac{\pi}{2})$
③$(\theta-\frac{\pi}{2})$ ④$(\theta+\pi)$ ⑤$(\theta-\pi)$
⑥$(2\theta+\frac{\pi}{2})$ ⑦$(2\theta-\frac{\pi}{2})$
$(\textrm{iv})$点Aを通るCの接線のうち、直線$y=\boxed{\ \ オ\ \ }$と異なる接線の傾き
を$k_0$とする。このとき、$(\textrm{ii})$または$(\textrm{iii})$の考え方を用いることにより
$k_0=\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$
であることがわかる。
直線lと領域Dが共有点をもつようなkの値の範囲は$\boxed{\ \ シ\ \ }$である。
$\boxed{\ \ シ\ \ }$の解答群
⓪$k \gt k_0$ ①$k \geqq k_0$
②$k \lt k_0$ ③$k \leqq k_0$
④$0 \lt k \lt k_0$ ⑤$0 \leqq k \leqq k_0$
2022共通テスト数学過去問
この動画を見る
[1]座標平面上に点A(-8,0)をとる。また、不等式
$x^2+y^2-4x-10y+4 \leqq 0$
の表す領域をDとする。
(1)領域Dは、中心が点$(\boxed{\ \ ア\ \ },\boxed{\ \ イ\ \ })$、半径が$\boxed{\ \ ウ\ \ }$の円の
$\boxed{\ \ エ\ \ }$である。
$\boxed{\ \ エ\ \ }$の解答群
⓪ 周 ① 内部 ② 外部
③ 周および内部 ④ 周および外部
以下、点$(\boxed{\ \ ア\ \ },\boxed{\ \ イ\ \ })$をQとし、方程式
$x^2+y^2-4x-10y+4=0$
の表す図形をCとする。
(2)点Aを通る直線と領域Dが共有点をもつのはどのようなときかを考えよう。
$(\textrm{i})(1)$により、直線$y=\boxed{\ \ オ\ \ }$は点Aを通るCの接線の一つとなること
がわかる。
太郎さんと花子さんは点Aを通るCのもう一つの接線について話している。
点Aを通り、傾きがkの直線をlとする。
太郎:直線lの方程式は$y=k(x+8)$と表すことができるから、
これを
$x^2+y^2-4x-10y+4=0$
に代入することで接線を求められそうだね。
花子:x軸と直線AQのなす角のタンジェントに着目することでも
求められそうだよ。
$(\textrm{ii})$ 太郎さんの求め方について考えてみよう。
$y=k(x+8)$を$x^2+y^2-4x-10y+4=0$に代入すると、
xについての2次方程式
$(k^2+1)x^2+(16k^2-10k-4)x+64k^2-80k+4=0$
が得られる。この方程式が$\boxed{\ \ カ\ \ }$ときのkの値が接線の傾きとなる。
$\boxed{\ \ カ\ \ }$の解答群
⓪重解をもつ
①異なる2つの実数解をもち、1つは0である
②異なる2つの正の実数解をもつ
③正の実数解と負の実数解をもつ
④異なる2つの負の実数解をもつ
⑤異なる2つの虚数解をもつ
$(\textrm{iii})$花子さんの求め方について考えてみよう。
x軸と直線AQのなす角を$\theta(0 \lt \theta \leqq \frac{\pi}{2})$とすると
$\tan\theta=\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}$
であり、直線$y=\boxed{\ \ オ\ \ }$と異なる接線の傾きは$\tan\boxed{\ \ ケ\ \ }$
と表すことができる。
$\boxed{\ \ ケ\ \ }$の解答群
⓪$\theta$ ①$2\theta$ ②$(\theta+\frac{\pi}{2})$
③$(\theta-\frac{\pi}{2})$ ④$(\theta+\pi)$ ⑤$(\theta-\pi)$
⑥$(2\theta+\frac{\pi}{2})$ ⑦$(2\theta-\frac{\pi}{2})$
$(\textrm{iv})$点Aを通るCの接線のうち、直線$y=\boxed{\ \ オ\ \ }$と異なる接線の傾き
を$k_0$とする。このとき、$(\textrm{ii})$または$(\textrm{iii})$の考え方を用いることにより
$k_0=\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$
であることがわかる。
直線lと領域Dが共有点をもつようなkの値の範囲は$\boxed{\ \ シ\ \ }$である。
$\boxed{\ \ シ\ \ }$の解答群
⓪$k \gt k_0$ ①$k \geqq k_0$
②$k \lt k_0$ ③$k \leqq k_0$
④$0 \lt k \lt k_0$ ⑤$0 \leqq k \leqq k_0$
2022共通テスト数学過去問
大学入試問題#93 昭和大学医学部(2016) 対数
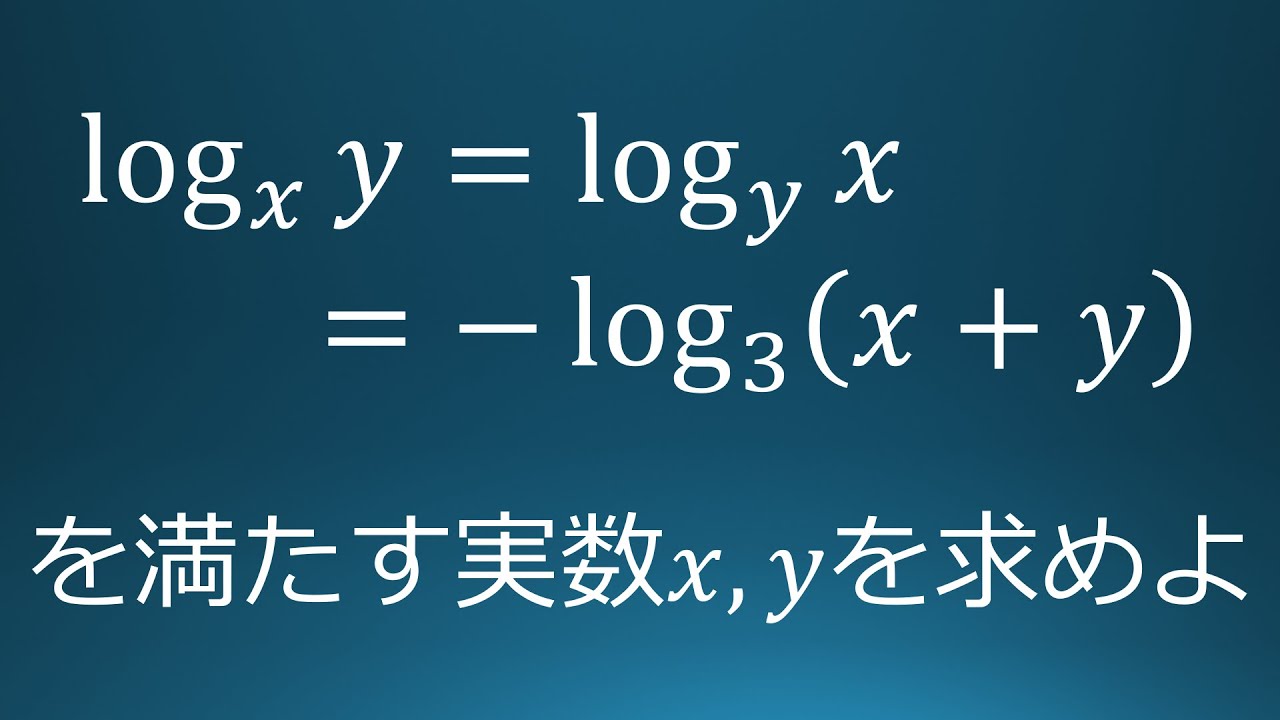
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#昭和大学
指導講師:
ますただ
問題文全文(内容文):
$log_xy=log_yx=-log_3(x+y)$をみたす実数$x,y$を求めよ。
出典:2016年昭和大学医学部 入試問題
この動画を見る
$log_xy=log_yx=-log_3(x+y)$をみたす実数$x,y$を求めよ。
出典:2016年昭和大学医学部 入試問題
【数Ⅱ】虚数を解に持つ2次方程式【最小多項式・解と係数の関係を使う】

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 2次方程式x^2+ax+b=0の解の1つが3+iであるとき,
実数の定数a,bの値を求めよ.$
この動画を見る
$ 2次方程式x^2+ax+b=0の解の1つが3+iであるとき,
実数の定数a,bの値を求めよ.$
福田の共通テスト直前演習〜2021年共通テスト数学ⅡB問題2(2)。3次関数の問題。

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$(2)座標平面上で、次の3つの3次関数のグラフについて考える。$y=4x^3+2x^2+3x+5 \ldots④ y=-2x^3+7x^2+3x+5 \ldots⑤$
$y=5x^3-x^2+3x+5 \ldots⑥$
④,⑤,⑥の3次関数のグラフには次の共通点がある。
共通点:・y軸との交点のy座標は$\boxed{ソ}$である。
・y軸との交点における接線の方程式は $y=\boxed{タ}\ x+\boxed{チ}$ である。
$a,b,c,d$を0でない実数とする。
曲線$y=ax^3+bx^2+cx+d$上の点$(0, \boxed{ツ})$における接線の方程式は
$y=\boxed{テ}\ x+\boxed{ト}$ である。
次に$f(x)=ax^3+bx^2+cx+d, g(x)=\boxed{テ}\ x+\boxed{ト}$とし、
$f(x)-g(x)$について考える。
$h(x)=f(x)-g(x)$とおく。a,b,c,dが正の実数であるとき、$y=h(x)$のグラフ
の概形は$\boxed{ナ}$である。
(※$\boxed{ナ}$の解答群は動画参照)
$y=f(x)$のグラフと$y=g(x)$のグラフの共有点のx座標は$\frac{\boxed{ニヌ}}{\boxed{ネ}}$と$\boxed{ノ}$である。
また、xが$\frac{\boxed{ニヌ}}{\boxed{ネ}}$と$\boxed{ノ}$の間を動くとき、
$|f(x)-g(x)|$の値が最大となるのは、$x=\frac{\boxed{ハヒフ}}{\boxed{ヘホ}}$のときである。
2021共通テスト数学過去問
この動画を見る
${\Large\boxed{2}}$(2)座標平面上で、次の3つの3次関数のグラフについて考える。$y=4x^3+2x^2+3x+5 \ldots④ y=-2x^3+7x^2+3x+5 \ldots⑤$
$y=5x^3-x^2+3x+5 \ldots⑥$
④,⑤,⑥の3次関数のグラフには次の共通点がある。
共通点:・y軸との交点のy座標は$\boxed{ソ}$である。
・y軸との交点における接線の方程式は $y=\boxed{タ}\ x+\boxed{チ}$ である。
$a,b,c,d$を0でない実数とする。
曲線$y=ax^3+bx^2+cx+d$上の点$(0, \boxed{ツ})$における接線の方程式は
$y=\boxed{テ}\ x+\boxed{ト}$ である。
次に$f(x)=ax^3+bx^2+cx+d, g(x)=\boxed{テ}\ x+\boxed{ト}$とし、
$f(x)-g(x)$について考える。
$h(x)=f(x)-g(x)$とおく。a,b,c,dが正の実数であるとき、$y=h(x)$のグラフ
の概形は$\boxed{ナ}$である。
(※$\boxed{ナ}$の解答群は動画参照)
$y=f(x)$のグラフと$y=g(x)$のグラフの共有点のx座標は$\frac{\boxed{ニヌ}}{\boxed{ネ}}$と$\boxed{ノ}$である。
また、xが$\frac{\boxed{ニヌ}}{\boxed{ネ}}$と$\boxed{ノ}$の間を動くとき、
$|f(x)-g(x)|$の値が最大となるのは、$x=\frac{\boxed{ハヒフ}}{\boxed{ヘホ}}$のときである。
2021共通テスト数学過去問
【数IIB】7分で「6分の1公式」をマスターしよう【一夜漬け】【直前に5点UP】

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
積分の1/6公式の具体的な使い方がこの動画を見れば7分でマスターできます!
この動画を見る
積分の1/6公式の具体的な使い方がこの動画を見れば7分でマスターできます!
【数Ⅱ】対数関数:ええ!?マイナスがついていないのにマイナスになる数が存在するのかい!?

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
マイナスがついていないのにマイナスの値になる数があります。
一体その正体とは…????
補足:底が省略されている場合は基底e(約2.7)が省略されています(数Ⅲで習いますが今回の説明にはあまり影響はありません)
この動画を見る
マイナスがついていないのにマイナスの値になる数があります。
一体その正体とは…????
補足:底が省略されている場合は基底e(約2.7)が省略されています(数Ⅲで習いますが今回の説明にはあまり影響はありません)
福田の共通テスト直前演習〜2021年共通テスト数学ⅡB問題2(1)。2次関数の問題。

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#微分法と積分法#接線と増減表・最大値・最小値#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$(1)座標平面上で、次の二つの2次関数のグラフについて考える。
$y=3x^2+2x+3 \ldots① y=2x^2+2x+3 \ldots②$
①、②の2次関数のグラフには次の共通点がある。
共通点:・y軸との交点のy座標は$\boxed{ア}$である。
・y軸との交点における接線の方程式は$y=\boxed{イ}\ x+\boxed{ウ}$である。
次の⓪~⑤の2次関数のグラフのうち、y軸との交点における接線が
$y=\boxed{イ\}\ x+\boxed{ウ}$となるものは
$\boxed{エ}$である。
$\boxed{エ}$の解答群
⓪$y=3x^2-2x-3$ ①$y=-3x^2+2x-3$ ②$y=2x^2+2x-3$
③$y=2x^2-2x+3$ ④$y=-x^2+2x+3$ ⑤$y=-x^2-2x+3$
a,b,cを0でない実数とする。
曲線$y=ax^2+bx+c$上の点$(0,\boxed{オ})$における接線をlとすると、
その方程式は$y=\boxed{カ}\ x+\boxed{キ}$である。
直線lとx軸との交点のx座標は$\frac{\boxed{クケ}}{\boxed{コ}}$である。
a,b,cが正の実数であるとき、曲線$y=ax^2+bx+c$と
直線lおよび直線$x=\frac{\boxed{クケ}}{\boxed{コ}}$で囲まれた図形の
面積を$S$とすると$S=\frac{ac^{\boxed{サ}}}{\boxed{シ}b^{\boxed{ス}}} \ldots③$ である。
③において、$a=1$とし、Sの値が一定となるように正の実数b,cの値を変化させる。
このとき、bとcの関係を表すグラフの概形は$\boxed{セ}$である。
(※$\boxed{セ}$の選択肢は動画参照)
2022共通テスト数学過去問
この動画を見る
${\Large\boxed{2}}$(1)座標平面上で、次の二つの2次関数のグラフについて考える。
$y=3x^2+2x+3 \ldots① y=2x^2+2x+3 \ldots②$
①、②の2次関数のグラフには次の共通点がある。
共通点:・y軸との交点のy座標は$\boxed{ア}$である。
・y軸との交点における接線の方程式は$y=\boxed{イ}\ x+\boxed{ウ}$である。
次の⓪~⑤の2次関数のグラフのうち、y軸との交点における接線が
$y=\boxed{イ\}\ x+\boxed{ウ}$となるものは
$\boxed{エ}$である。
$\boxed{エ}$の解答群
⓪$y=3x^2-2x-3$ ①$y=-3x^2+2x-3$ ②$y=2x^2+2x-3$
③$y=2x^2-2x+3$ ④$y=-x^2+2x+3$ ⑤$y=-x^2-2x+3$
a,b,cを0でない実数とする。
曲線$y=ax^2+bx+c$上の点$(0,\boxed{オ})$における接線をlとすると、
その方程式は$y=\boxed{カ}\ x+\boxed{キ}$である。
直線lとx軸との交点のx座標は$\frac{\boxed{クケ}}{\boxed{コ}}$である。
a,b,cが正の実数であるとき、曲線$y=ax^2+bx+c$と
直線lおよび直線$x=\frac{\boxed{クケ}}{\boxed{コ}}$で囲まれた図形の
面積を$S$とすると$S=\frac{ac^{\boxed{サ}}}{\boxed{シ}b^{\boxed{ス}}} \ldots③$ である。
③において、$a=1$とし、Sの値が一定となるように正の実数b,cの値を変化させる。
このとき、bとcの関係を表すグラフの概形は$\boxed{セ}$である。
(※$\boxed{セ}$の選択肢は動画参照)
2022共通テスト数学過去問
指数
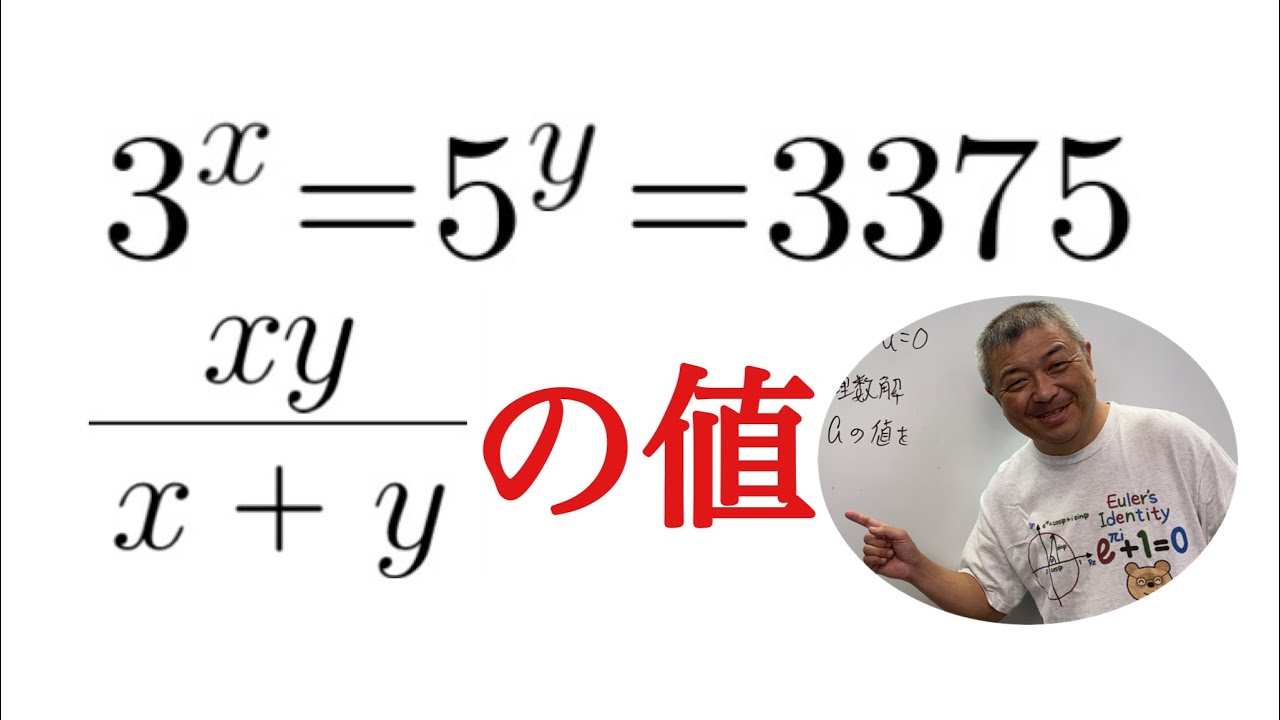
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3^x-5^y=3375$のとき,$\dfrac{xy}{x+y}$の値を求めよ.
この動画を見る
$3^x-5^y=3375$のとき,$\dfrac{xy}{x+y}$の値を求めよ.
福田の共通テスト直前演習〜2021年共通テスト数学ⅡB問題1[2]。指数関数の問題。

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$[2]二つの関数$f(x)=\frac{2^x+2^{-x}}{2}, g(x)=\frac{2^x-2^{-x}}{2}$について考える。
(1)$f(0)=\boxed{セ}, g(0)=\boxed{ソ}$である。また、$f(x)$は
相加平均と相乗平均の関係から、$x=\boxed{タ}$で最小値$\boxed{チ}$をとる。
$g(x)=-2$となるxの値は$\log_2(\sqrt{\boxed{ツ}}-\boxed{テ})$である。
(2)次の①~④は、xにどのような値を代入しても常に成り立つ。
$f(-x)=\boxed{ト} \ldots① g(-x)=\boxed{ナ} \ldots②$
$\left\{f(-x)\right\}^2-\left\{g(-x)\right\}^2=\boxed{ニ} \ldots③$
$g(2x)=\boxed{ヌ}\ f(x)g(x) \ldots④$
$\boxed{ト}、\boxed{ナ}$の解答群
⓪$f(x)$ ①$-f(x)$ ②$g(x)$ ③$-g(x)$
(3)花子:①~④は三角関数の性質に似ているね。
太郎:三角関数の加法定理に類似した式$(\textrm{A})~(\textrm{D})$を考えてみたけど、常に
成り立つ式はあるだろうか。
花子:成り立たない式を見つけるために、式$(\textrm{A})~(\textrm{D})$の$\beta$に
何か具体的な値を代入して調べてみたら?
太郎さんが考えた式
$f(\alpha-\beta)=f(\alpha)g(\beta)+g(\alpha)f(\beta) \ldots(\textrm{A})$
$f(\alpha+\beta)=f(\alpha)g(\beta)+g(\alpha)f(\beta) \ldots(\textrm{B})$
$f(\alpha-\beta)=f(\alpha)g(\beta)+g(\alpha)f(\beta) \ldots(\textrm{C})$
$f(\alpha+\beta)=f(\alpha)g(\beta)-g(\alpha)f(\beta) \ldots(\textrm{D})$
(1),(2)で示されたことのいくつかを利用すると、式$(\textrm{A})~(\textrm{D})$のうち、
$\boxed{ネ}$以外の3つは成り立たないことが分かる。$\boxed{ネ}$は左辺と右辺を
それぞれ計算することによって成り立つことが確かめられる。
$\boxed{ネ}$の解答群
⓪$(\textrm{A})$ ①$(\textrm{B})$ ②$(\textrm{C})$ ③$(\textrm{D})$
2021共通テスト数学過去問
この動画を見る
${\Large\boxed{1}}$[2]二つの関数$f(x)=\frac{2^x+2^{-x}}{2}, g(x)=\frac{2^x-2^{-x}}{2}$について考える。
(1)$f(0)=\boxed{セ}, g(0)=\boxed{ソ}$である。また、$f(x)$は
相加平均と相乗平均の関係から、$x=\boxed{タ}$で最小値$\boxed{チ}$をとる。
$g(x)=-2$となるxの値は$\log_2(\sqrt{\boxed{ツ}}-\boxed{テ})$である。
(2)次の①~④は、xにどのような値を代入しても常に成り立つ。
$f(-x)=\boxed{ト} \ldots① g(-x)=\boxed{ナ} \ldots②$
$\left\{f(-x)\right\}^2-\left\{g(-x)\right\}^2=\boxed{ニ} \ldots③$
$g(2x)=\boxed{ヌ}\ f(x)g(x) \ldots④$
$\boxed{ト}、\boxed{ナ}$の解答群
⓪$f(x)$ ①$-f(x)$ ②$g(x)$ ③$-g(x)$
(3)花子:①~④は三角関数の性質に似ているね。
太郎:三角関数の加法定理に類似した式$(\textrm{A})~(\textrm{D})$を考えてみたけど、常に
成り立つ式はあるだろうか。
花子:成り立たない式を見つけるために、式$(\textrm{A})~(\textrm{D})$の$\beta$に
何か具体的な値を代入して調べてみたら?
太郎さんが考えた式
$f(\alpha-\beta)=f(\alpha)g(\beta)+g(\alpha)f(\beta) \ldots(\textrm{A})$
$f(\alpha+\beta)=f(\alpha)g(\beta)+g(\alpha)f(\beta) \ldots(\textrm{B})$
$f(\alpha-\beta)=f(\alpha)g(\beta)+g(\alpha)f(\beta) \ldots(\textrm{C})$
$f(\alpha+\beta)=f(\alpha)g(\beta)-g(\alpha)f(\beta) \ldots(\textrm{D})$
(1),(2)で示されたことのいくつかを利用すると、式$(\textrm{A})~(\textrm{D})$のうち、
$\boxed{ネ}$以外の3つは成り立たないことが分かる。$\boxed{ネ}$は左辺と右辺を
それぞれ計算することによって成り立つことが確かめられる。
$\boxed{ネ}$の解答群
⓪$(\textrm{A})$ ①$(\textrm{B})$ ②$(\textrm{C})$ ③$(\textrm{D})$
2021共通テスト数学過去問
4次方程式の解の立方の和

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(x+1)(x+2)(x+3)(x+4)=1$の4つの解を$\alpha,\beta,\gamma,\delta$とする.
$\alpha^3+\beta^3+\gamma^3+\delta^3$の値を求めよ.
この動画を見る
$(x+1)(x+2)(x+3)(x+4)=1$の4つの解を$\alpha,\beta,\gamma,\delta$とする.
$\alpha^3+\beta^3+\gamma^3+\delta^3$の値を求めよ.
【数Ⅱ】解と係数の関係と対称式 (2-α)(2-β)の値【もっとも簡単な解き方】
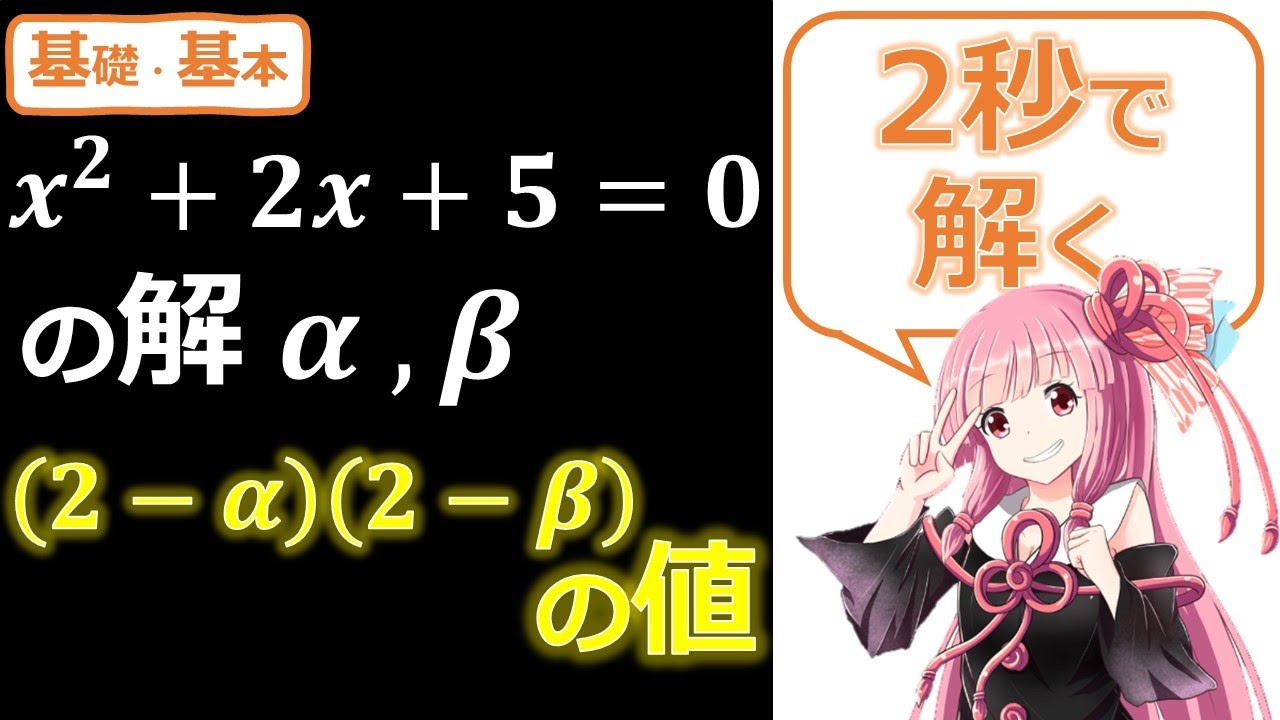
単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ x^2+2x+5=0の解を\alpha,\betaとする.(2-\alpha)(2-\beta)を求めよ.$
この動画を見る
$ x^2+2x+5=0の解を\alpha,\betaとする.(2-\alpha)(2-\beta)を求めよ.$
福田の共通テスト直前演習〜2021年共通テスト数学ⅡB問題1[1]。三角関数の問題。

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#加法定理とその応用#センター試験・共通テスト関連#学校別大学入試過去問解説(数学)#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$[1](1)次の問題Aについて考えよう。
問題A 関数$y=\sin\theta+\sqrt3\cos\theta (0 \leqq \theta \leqq \frac{\pi}{2})$の最大値を求めよ。
$\sin\frac{\pi}{\boxed{ア}}=\frac{\sqrt3}{2}, \cos\frac{\pi}{\boxed{ア}}=\frac{1}{2}$ であるから、三角関数の合成により
$y=\boxed{イ}\sin(\theta+\frac{\pi}{\boxed{ア}})$
と変形できる。よって、yは$\theta=\frac{\pi}{\boxed{ウ}}$で最大値$\boxed{エ}$をとる。
(2)pを定数とし、次の問題Bについて考えよう。
問題B 関数$y=\sin\theta+p\cos\theta (0 \leqq \theta \leqq \frac{\pi}{2})$の最大値を求めよ。
$(\textrm{i})p=0$のとき、yは$\theta=\frac{\pi}{\boxed{オ}}$で最大値$\boxed{カ}$をとる。
$(\textrm{ii})p \gt 0$のときは、加法定理$\cos(\theta-\alpha)=\cos\theta\cos\alpha+\sin\theta\sin\alpha$を用いると
$y=\sin\theta+p\cos\theta=\sqrt{\boxed{キ}}\cos(\theta-\alpha)$
と表すことができる。ただし$\alphaは\sin\alpha=\frac{\boxed{ク}}{\sqrt{\boxed{キ}}}, \cos\alpha=\frac{\boxed{ケ}}{\sqrt{\boxed{キ}}}, 0 \lt \alpha \lt \frac{\pi}{2}$
を満たすものとする。このとき、yは$\theta=\boxed{コ}$で最大値$\sqrt{\boxed{サ}}$をとる。
$(\textrm{iii})p \lt 0$のとき、$y$は$\theta=\boxed{シ}$で最大値$\sqrt{\boxed{ス}}$をとる。
$\boxed{キ}~\boxed{ケ}、\boxed{サ}、\boxed{ス}$の解答群
⓪-1 ①1 ②-p ③p \\
④1-p ⑤1+p ⑥-p^2 ⑦p^2 ⑧1-p^2 \\
⑨1+p^2 ⓐ(1-p)^2 ⓑ(1+p^2) \\
$\boxed{コ}、\boxed{シ}$の解答群
⓪$0$ ①$\alpha$ ②$\frac{\pi}{2}$
2021共通テスト数学過去問
この動画を見る
${\Large\boxed{1}}$[1](1)次の問題Aについて考えよう。
問題A 関数$y=\sin\theta+\sqrt3\cos\theta (0 \leqq \theta \leqq \frac{\pi}{2})$の最大値を求めよ。
$\sin\frac{\pi}{\boxed{ア}}=\frac{\sqrt3}{2}, \cos\frac{\pi}{\boxed{ア}}=\frac{1}{2}$ であるから、三角関数の合成により
$y=\boxed{イ}\sin(\theta+\frac{\pi}{\boxed{ア}})$
と変形できる。よって、yは$\theta=\frac{\pi}{\boxed{ウ}}$で最大値$\boxed{エ}$をとる。
(2)pを定数とし、次の問題Bについて考えよう。
問題B 関数$y=\sin\theta+p\cos\theta (0 \leqq \theta \leqq \frac{\pi}{2})$の最大値を求めよ。
$(\textrm{i})p=0$のとき、yは$\theta=\frac{\pi}{\boxed{オ}}$で最大値$\boxed{カ}$をとる。
$(\textrm{ii})p \gt 0$のときは、加法定理$\cos(\theta-\alpha)=\cos\theta\cos\alpha+\sin\theta\sin\alpha$を用いると
$y=\sin\theta+p\cos\theta=\sqrt{\boxed{キ}}\cos(\theta-\alpha)$
と表すことができる。ただし$\alphaは\sin\alpha=\frac{\boxed{ク}}{\sqrt{\boxed{キ}}}, \cos\alpha=\frac{\boxed{ケ}}{\sqrt{\boxed{キ}}}, 0 \lt \alpha \lt \frac{\pi}{2}$
を満たすものとする。このとき、yは$\theta=\boxed{コ}$で最大値$\sqrt{\boxed{サ}}$をとる。
$(\textrm{iii})p \lt 0$のとき、$y$は$\theta=\boxed{シ}$で最大値$\sqrt{\boxed{ス}}$をとる。
$\boxed{キ}~\boxed{ケ}、\boxed{サ}、\boxed{ス}$の解答群
⓪-1 ①1 ②-p ③p \\
④1-p ⑤1+p ⑥-p^2 ⑦p^2 ⑧1-p^2 \\
⑨1+p^2 ⓐ(1-p)^2 ⓑ(1+p^2) \\
$\boxed{コ}、\boxed{シ}$の解答群
⓪$0$ ①$\alpha$ ②$\frac{\pi}{2}$
2021共通テスト数学過去問
式の値
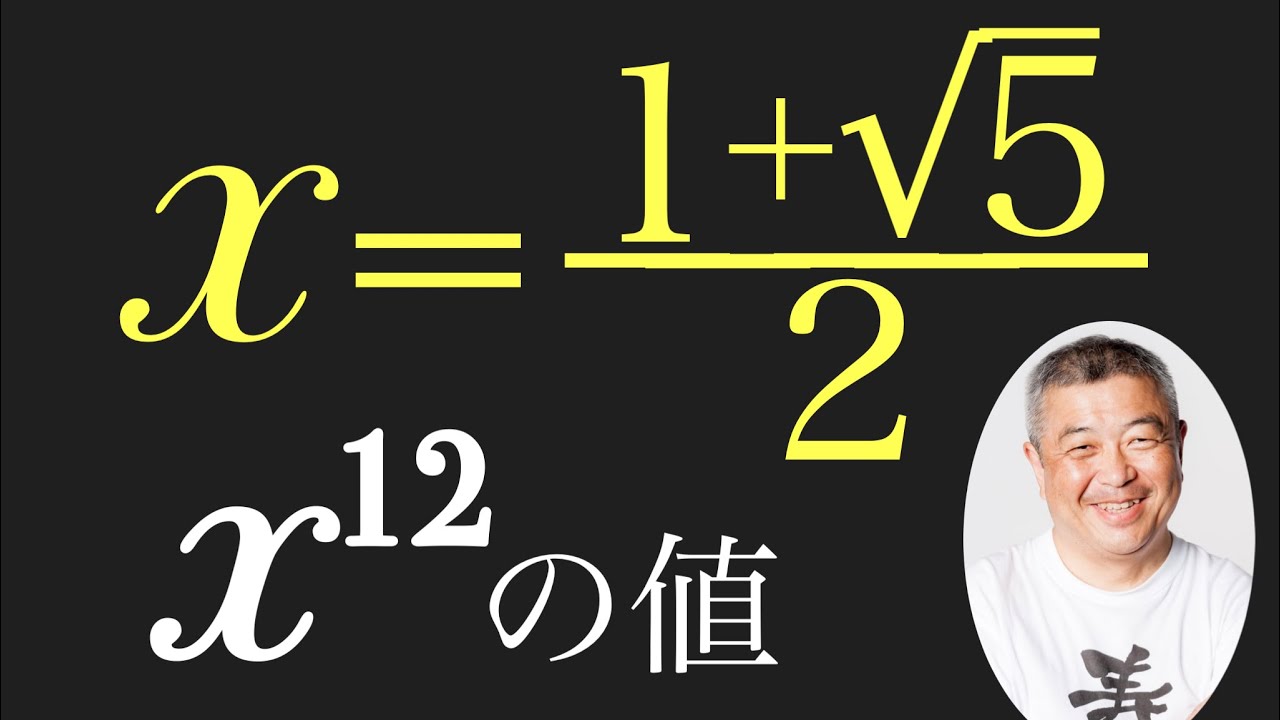
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x=\dfrac{1+\sqrt5}{2}$
$x^{12}$の値を求めよ.
この動画を見る
$x=\dfrac{1+\sqrt5}{2}$
$x^{12}$の値を求めよ.
【ゆっくり丁寧に】数学Ⅱ・微分 3次関数のグラフの書き方

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の関数のグラフをかけ。
(1)
$y=-2x^3+6x^2+12$
(2)
$y=x^3-9x^2+27x+3$
この動画を見る
次の関数のグラフをかけ。
(1)
$y=-2x^3+6x^2+12$
(2)
$y=x^3-9x^2+27x+3$
変な指数方程式
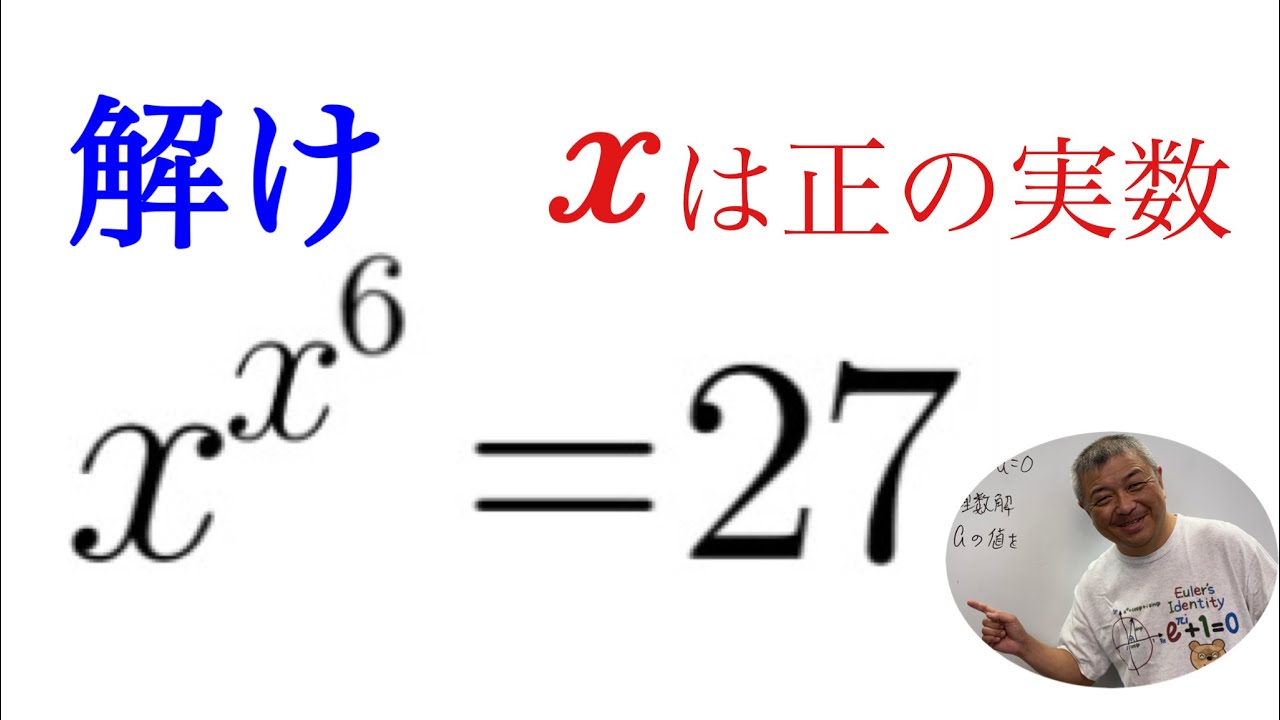
【数学Ⅱ/微分】関数の増減(微分・増減表)

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の関数の増加・減少を調べよ。
(1)
$y=x^3-3x^2-9x+2$
(2)
$y=x^3-3x^2+14x-4$
この動画を見る
次の関数の増加・減少を調べよ。
(1)
$y=x^3-3x^2-9x+2$
(2)
$y=x^3-3x^2+14x-4$
【数学Ⅱ/微分】接線の方程式②

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
点$(-1,-4)$から、曲線$y=x^2-1$に引いた接線の方程式を求めよ。
この動画を見る
点$(-1,-4)$から、曲線$y=x^2-1$に引いた接線の方程式を求めよ。
