数Ⅱ
数Ⅱ
福田のわかった数学〜高校２年生081〜三角関数(20)18°系の三角比(1)
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$ 三角関数(20) 18°系の三角比(1)
$\sin\frac{\pi}{10}$の値を求めよ。
この動画を見る
数学$\textrm{II}$ 三角関数(20) 18°系の三角比(1)
$\sin\frac{\pi}{10}$の値を求めよ。
2021一橋大（経済）補足と別解
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(sin x+1)(cos x+1)=k$の解が$0\leqq x\lt 2\pi$の範囲にちょうど2つある$k$を求めよ.
一橋大（経済）過去問
この動画を見る
$(sin x+1)(cos x+1)=k$の解が$0\leqq x\lt 2\pi$の範囲にちょうど2つある$k$を求めよ.
一橋大（経済）過去問
2021一橋（経済）後期
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(sin x+1)(cos x+1)=k$の解が$0\leqq x\lt 2\pi$の範囲にちょうど2つある$k$を求めよ.
一橋（経済）過去問
この動画を見る
$(sin x+1)(cos x+1)=k$の解が$0\leqq x\lt 2\pi$の範囲にちょうど2つある$k$を求めよ.
一橋（経済）過去問
福田のわかった数学〜高校３年生理系098〜不等式の証明(5)
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{III}$ 不等式の証明(5)
$b(\log a-\log b) \leqq a-b (a \gt 0, b \gt 0)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(5)
$b(\log a-\log b) \leqq a-b (a \gt 0, b \gt 0)$を証明せよ。
福田のわかった数学〜高校２年生080〜三角関数(19)2直線のなす角(3)
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$ 三角関数(19) なす角(3)
2点A(0,2), B(0,8)がある。点P(a,0) $(a \gt 0)$について$\angle APB$が最大となるaは?
この動画を見る
数学$\textrm{II}$ 三角関数(19) なす角(3)
2点A(0,2), B(0,8)がある。点P(a,0) $(a \gt 0)$について$\angle APB$が最大となるaは?
【数Ⅱ】相加平均・相乗平均の関係を正しく使いこなそう【よくある間違え方とは】
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
$ (1)x \gt 0のとき,x+\dfrac{9}{x}\geqq 6を示せ.
(2)x \gt 0のとき,x+\dfrac{9}{x}の最小値を求めよ.
(3)x \gt 0のとき,x+\dfrac{6}{x+1}の最小値を求めよ.
(4)x \gt 0のとき,\dfrac{x^2;5x+15}{x+2}の最小値を求めよ.
(5)a \gt 0,b \gt 0のとき\left(a+\frac{1}{b} \right)\left(\frac{16}{a}+b \right)の最小値
を求めよ.$
この動画を見る
$ (1)x \gt 0のとき,x+\dfrac{9}{x}\geqq 6を示せ.
(2)x \gt 0のとき,x+\dfrac{9}{x}の最小値を求めよ.
(3)x \gt 0のとき,x+\dfrac{6}{x+1}の最小値を求めよ.
(4)x \gt 0のとき,\dfrac{x^2;5x+15}{x+2}の最小値を求めよ.
(5)a \gt 0,b \gt 0のとき\left(a+\frac{1}{b} \right)\left(\frac{16}{a}+b \right)の最小値
を求めよ.$
三角関数基本
単元：
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
値を求めよ.
$\cos \dfrac{\pi}{7}・\cos \dfrac{2\pi}{7}・\cos\dfrac{3\pi}{7}$
この動画を見る
値を求めよ.
$\cos \dfrac{\pi}{7}・\cos \dfrac{2\pi}{7}・\cos\dfrac{3\pi}{7}$
福田のわかった数学〜高校３年生理系097〜不等式の証明(4)
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{III}$ 不等式の証明(4)
$(x+2)\log(x+1) \geqq 2x (x \geqq 0)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(4)
$(x+2)\log(x+1) \geqq 2x (x \geqq 0)$を証明せよ。
福田のわかった数学〜高校２年生079〜三角関数(18)2直線のなす角(2)
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$ 三角関数(18) なす角(2)
$y=3x+1$と$\frac{\pi}{6}$の角をなし、原点を通る直線の方程式を求めよ。
この動画を見る
数学$\textrm{II}$ 三角関数(18) なす角(2)
$y=3x+1$と$\frac{\pi}{6}$の角をなし、原点を通る直線の方程式を求めよ。
4次方程式
【数Ⅱ】不等式の証明・基本パターン【書き出しに注意！】
高校範囲だけど中3生も解けるし
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\frac{x^2-2}{x-1} + \frac{1}{x-1}$
この動画を見る
$\frac{x^2-2}{x-1} + \frac{1}{x-1}$
福田のわかった数学〜高校３年生理系096〜不等式の証明(3)
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{III}$ 不等式の証明(3)
$\sqrt{ab} \lt \frac{b-a}{\log b-\log a} \lt \frac{a+b}{2} (0 \lt a \lt b)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(3)
$\sqrt{ab} \lt \frac{b-a}{\log b-\log a} \lt \frac{a+b}{2} (0 \lt a \lt b)$を証明せよ。
【2次方程式の知識はこれで完ペキ！】複素数と2次方程式の関係を解説！〔数学、高校数学〕
0の0乗ってなに？
福田のわかった数学〜高校２年生078〜三角関数(17)2直線のなす角(1)
単元：
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$ 三角関数(17) なす角(1)
2直線$y=3x-1, y=-2x+4$
のなす角$\theta(0 \lt \theta \lt \frac{\pi}{2})$を求めよ。
この動画を見る
数学$\textrm{II}$ 三角関数(17) なす角(1)
2直線$y=3x-1, y=-2x+4$
のなす角$\theta(0 \lt \theta \lt \frac{\pi}{2})$を求めよ。
#38 数検1級1次 過去問 解と係数の関係
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$z^3+2z^2+2z+1=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^{2019}+\beta^{2019}+\gamma^{2019}$の値を求めよ。
この動画を見る
$z^3+2z^2+2z+1=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^{2019}+\beta^{2019}+\gamma^{2019}$の値を求めよ。
#37 数検1級1次 過去問 重積分
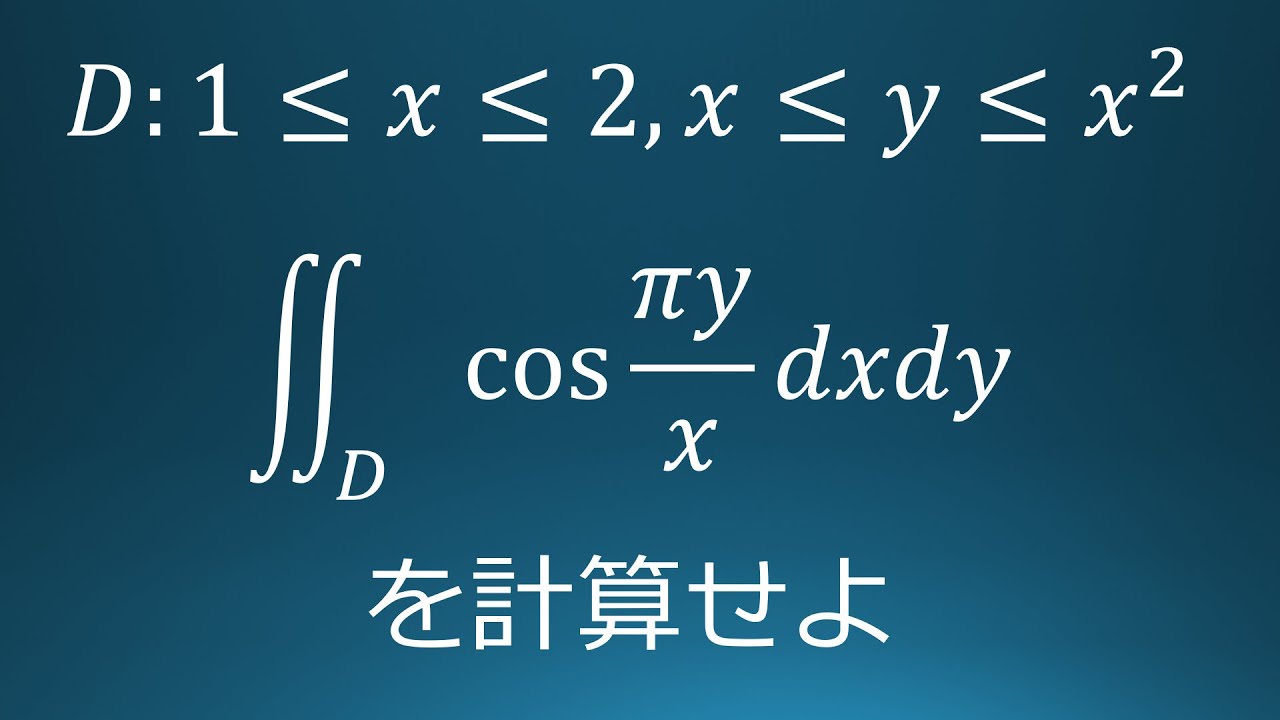
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$D:1 \leqq x \leqq 2,x \leqq y \leqq x^2$
$\displaystyle \int \displaystyle \int \cos\displaystyle \frac{\pi y}{x}\ dxdy$を計算せよ。
この動画を見る
$D:1 \leqq x \leqq 2,x \leqq y \leqq x^2$
$\displaystyle \int \displaystyle \int \cos\displaystyle \frac{\pi y}{x}\ dxdy$を計算せよ。
福田のわかった数学〜高校３年生理系095〜不等式の証明(2)
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{III}$ 不等式の証明(2)
$x\log x \geqq (x-1)\log(x+1) (x \geqq 1)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(2)
$x\log x \geqq (x-1)\log(x+1) (x \geqq 1)$を証明せよ。
#36 数検1級1次 過去問 積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{1}\sqrt{ \displaystyle \frac{1+x}{1-x} }\ dx$を計算せよ。
この動画を見る
$\displaystyle \int_{-1}^{1}\sqrt{ \displaystyle \frac{1+x}{1-x} }\ dx$を計算せよ。
【数Ⅱ】「少なくとも1つが1」「すべてが1」を等式で証明する。【主張を言い換える】
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
$ a+b+c=1,ab+bc+ca=abcが成り立つとき,
a,b,cのうち少なくとも1つは1であることを示せ.$
この動画を見る
$ a+b+c=1,ab+bc+ca=abcが成り立つとき,
a,b,cのうち少なくとも1つは1であることを示せ.$
大学入試じゃないよ 高校入試だよ ３通りで解説 成城学園
単元：
#数学(中学生)#数Ⅱ#指数関数と対数関数#指数関数#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$2^{56}と5^{24}$はどっちが大きい？
成城学園高等学校
この動画を見る
$2^{56}と5^{24}$はどっちが大きい？
成城学園高等学校
指数法則のいい復習になる問題
福田のわかった数学〜高校２年生077〜三角関数(16)三角関数の最大最小
単元：
#数Ⅱ#三角関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{II}$ 三角関数(16) 最大最小(6)
$y=\frac{\sin x+2}{\cos x+1} (0 \leqq x \leqq \frac{2\pi}{3})$の最大値、最小値を求めよ。
この動画を見る
数学$\textrm{II}$ 三角関数(16) 最大最小(6)
$y=\frac{\sin x+2}{\cos x+1} (0 \leqq x \leqq \frac{2\pi}{3})$の最大値、最小値を求めよ。
#35 数検１級１次 過去問 複素数
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数平面#複素数#複素数平面#数学検定#数学検定1級#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt{ 1+\sqrt{ 3 }i }+\sqrt{ 1-\sqrt{ 3 }i }$を簡単にせよ
ただし、外側の平方根の実数部の値は正とする。
この動画を見る
$\sqrt{ 1+\sqrt{ 3 }i }+\sqrt{ 1-\sqrt{ 3 }i }$を簡単にせよ
ただし、外側の平方根の実数部の値は正とする。
【数Ⅱ】式と証明：相加相乗平均の使い方その②
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
aを実数とするとき、$a^2-6a+\dfrac{1}{a^2-6a+10}$の最小値を求めよ。
この動画を見る
aを実数とするとき、$a^2-6a+\dfrac{1}{a^2-6a+10}$の最小値を求めよ。
#34 数検1級1次 過去問 積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\infty}\displaystyle \frac{1}{(x^2+1)^4}\ dx$を計算せよ。
この動画を見る
$\displaystyle \int_{0}^{\infty}\displaystyle \frac{1}{(x^2+1)^4}\ dx$を計算せよ。
【数Ⅱ】式と証明：相加相乗平均の使い方 その①
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$a\gt ０$のとき（１）$a＋\dfrac{9}{a}$（２）$a＋\dfrac{16}{a+2}$（３）$3a＋\dfrac{1}{a}$ の最小値をそれぞれ求めよ。
この動画を見る
$a\gt ０$のとき（１）$a＋\dfrac{9}{a}$（２）$a＋\dfrac{16}{a+2}$（３）$3a＋\dfrac{1}{a}$ の最小値をそれぞれ求めよ。
福田のわかった数学〜高校３年生理系094〜不等式の証明(1)
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
数学$\textrm{III}$ 不等式の証明(1)
$\cos x \lt 1-\frac{x^2}{2}+\frac{x^4}{24} (x \gt 0)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(1)
$\cos x \lt 1-\frac{x^2}{2}+\frac{x^4}{24} (x \gt 0)$を証明せよ。
#33 数検1級1次 過去問 区分求積法
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{1}{\sqrt{ 2nk-k^2 }}$の極限値を求めよ。
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{1}{\sqrt{ 2nk-k^2 }}$の極限値を求めよ。