 数B
数B
 数B
数B
誘導がなければ素晴らしい解法も出てくるんじゃね?

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#大阪教育大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
点Pは原点を出発して,「確率pで+1,確率1-pで+2」の移動を繰り返す.
ただし$0\leqq p \leqq 1$とする.このような移動を繰り返して自然数nの点に到達する確率を$p_n$と表す.次の問に答えよ.
(1)$p_1,p_2,p_3$を$p$を用いて表せ.
(2)$p_n,p_{n+1},p_{n+2}$の間の関係式を求めよ.
(3)$a_n=p_{n+1}-p_n(n \geqq 1)$とおくとき,数列${a_n}$が満たす漸化式を求めよ.
(4)pとnを用いて,一般項$p_n$を表せ.
(5)数列${p_n}$の極限を調べよ.
この動画を見る
点Pは原点を出発して,「確率pで+1,確率1-pで+2」の移動を繰り返す.
ただし$0\leqq p \leqq 1$とする.このような移動を繰り返して自然数nの点に到達する確率を$p_n$と表す.次の問に答えよ.
(1)$p_1,p_2,p_3$を$p$を用いて表せ.
(2)$p_n,p_{n+1},p_{n+2}$の間の関係式を求めよ.
(3)$a_n=p_{n+1}-p_n(n \geqq 1)$とおくとき,数列${a_n}$が満たす漸化式を求めよ.
(4)pとnを用いて,一般項$p_n$を表せ.
(5)数列${p_n}$の極限を調べよ.
この答えあっているのか?指数関数と等差数列 自治医科大
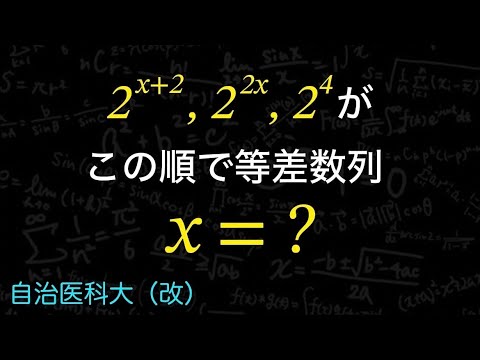
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{x+2} , 2^x , 2^4$がこの順で等差数列をなすとき、x=?
(自治医科大学(改))
この動画を見る
$2^{x+2} , 2^x , 2^4$がこの順で等差数列をなすとき、x=?
(自治医科大学(改))
超不人気!確率漸化式だよ

単元:
#数Ⅰ#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
点Pは原点を出発して確率$p(0\leqq P\leqq 1)$で$+1$, $1-p$で$+2$進む.
自然数nの地点に到達する確率$P_n$を求めよ.
大阪教育大過去問
この動画を見る
点Pは原点を出発して確率$p(0\leqq P\leqq 1)$で$+1$, $1-p$で$+2$進む.
自然数nの地点に到達する確率$P_n$を求めよ.
大阪教育大過去問
福田の数学〜東北大学2023年理系第3問〜漸化式と数列の和

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ sを実数とし、数列$\left\{a_n\right\}$を
$a_1$=s, (n+2)$a_{n+1}$=n$a_n$+2 (n=1,2,3,...)
で定める。以下の問いに答えよ。
(1)$a_n$をnとsを用いて表せ。
(2)ある正の整数$m$に対して、$\displaystyle\sum_{n=1}^ma_n$=0が成り立つとする。sをmを用いて表せ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{3}$ sを実数とし、数列$\left\{a_n\right\}$を
$a_1$=s, (n+2)$a_{n+1}$=n$a_n$+2 (n=1,2,3,...)
で定める。以下の問いに答えよ。
(1)$a_n$をnとsを用いて表せ。
(2)ある正の整数$m$に対して、$\displaystyle\sum_{n=1}^ma_n$=0が成り立つとする。sをmを用いて表せ。
2023東北大学理系過去問
大学入試問題#538「数列のバリューセット」 室蘭工業大学(2018) #数列

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#室蘭工業大学
指導講師:
ますただ
問題文全文(内容文):
$a_1=\displaystyle \frac{1}{2}$
$a_{n+1}=\displaystyle \frac{(n+1)a_n}{n+3^na_n}$のとき
一般項$a_n$を求めよ
出典:2018年室蘭工業大学 入試問題
この動画を見る
$a_1=\displaystyle \frac{1}{2}$
$a_{n+1}=\displaystyle \frac{(n+1)a_n}{n+3^na_n}$のとき
一般項$a_n$を求めよ
出典:2018年室蘭工業大学 入試問題
【短時間でマスター!!】和と一般項の問題の求め方を解説!(数列)〔現役講師解説、数学〕

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
数学2B
和と一般項
数列$\{a_n\}$の初項から第$n$項までの和$S_n$が$S_n=3n(n+5)$で表されるとき、一般項$a_n$を求めよ。
この動画を見る
数学2B
和と一般項
数列$\{a_n\}$の初項から第$n$項までの和$S_n$が$S_n=3n(n+5)$で表されるとき、一般項$a_n$を求めよ。
福田の数学〜慶應義塾大学2023年看護医療学部第2問(3)〜推定して数学的帰納法

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (3) 次の条件によって定められる数列$\left\{a_n\right\}$がある。
$a_1$=1, $a_{n+1}$=$\sqrt{a_n^2+1}$ ($n$=1,2,3,...)
(i)$a_2$=$\boxed{\ \ シ\ \ }$, $a_3$=$\boxed{\ \ ス\ \ }$であり、一般項$a_n$を推定すると$a_n$=$\boxed{\ \ セ\ \ }$である。
(ii)一般項$a_n$が$a_n$=$\boxed{\ \ セ\ \ }$であることの数学的帰納法による証明を述べよ。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{2}$ (3) 次の条件によって定められる数列$\left\{a_n\right\}$がある。
$a_1$=1, $a_{n+1}$=$\sqrt{a_n^2+1}$ ($n$=1,2,3,...)
(i)$a_2$=$\boxed{\ \ シ\ \ }$, $a_3$=$\boxed{\ \ ス\ \ }$であり、一般項$a_n$を推定すると$a_n$=$\boxed{\ \ セ\ \ }$である。
(ii)一般項$a_n$が$a_n$=$\boxed{\ \ セ\ \ }$であることの数学的帰納法による証明を述べよ。
2023慶應義塾大学看護医療学部過去問
埼玉大(経済)典型的な連立漸化式
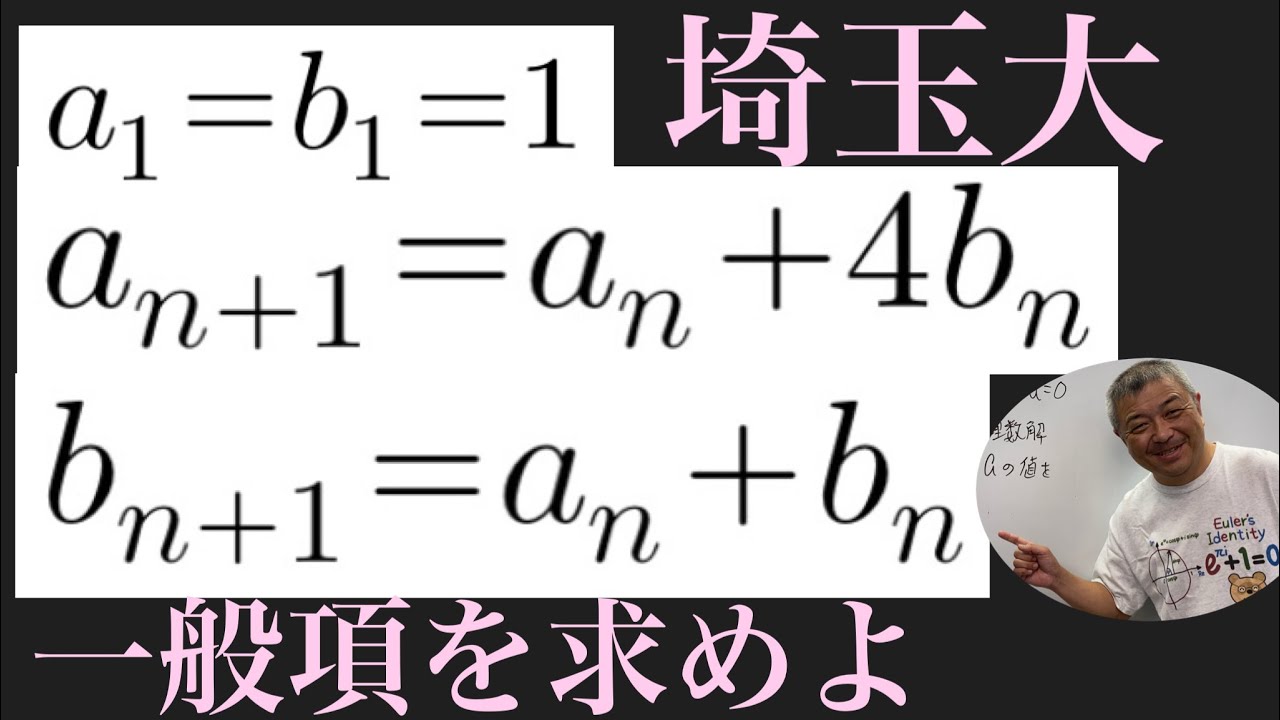
単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_n$の一般項
$a_1=b_1=1$
$a_{n+1}=a_n+4b_n$
$b_{n+1}=a_n+b_n$を求めよ.
埼玉大過去問
この動画を見る
$a_n$の一般項
$a_1=b_1=1$
$a_{n+1}=a_n+4b_n$
$b_{n+1}=a_n+b_n$を求めよ.
埼玉大過去問
福田の数学〜慶應義塾大学2023年看護医療学部第1問(5)〜整式の割り算の余り

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (5)整式P(x)を
P(x)=$\displaystyle\sum_{n=1}^{20}nx^n$=20$x^{20}$+19$x^{19}$+18$x^{18}$+...+2$x^2$+$x$
と定める。このとき、P(x)をx-1で割った時の余りは$\boxed{\ \ ク\ \ }$である。
また、P(x)を$x^2$-1で割った時の余りは$\boxed{\ \ ケ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{1}$ (5)整式P(x)を
P(x)=$\displaystyle\sum_{n=1}^{20}nx^n$=20$x^{20}$+19$x^{19}$+18$x^{18}$+...+2$x^2$+$x$
と定める。このとき、P(x)をx-1で割った時の余りは$\boxed{\ \ ク\ \ }$である。
また、P(x)を$x^2$-1で割った時の余りは$\boxed{\ \ ケ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
大学入試問題#520「これは綺麗や~~」 東北大学(2023) #数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=S$:実数
$(n+2)a_{n+1}=n\ a_n+2$
(1)
$a_n$を求めよ
(2)
$\displaystyle \sum_{n=1}^m a_n=0$のとき$S$を$m$で表せ
出典:2023年東北大学 入試問題
この動画を見る
$a_1=S$:実数
$(n+2)a_{n+1}=n\ a_n+2$
(1)
$a_n$を求めよ
(2)
$\displaystyle \sum_{n=1}^m a_n=0$のとき$S$を$m$で表せ
出典:2023年東北大学 入試問題
【数B】第1項から第10項までの和が4、第1項から第20項までの和が24である等比数列について、第1項から第40項までの和を求めよ

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1項から第10項までの和が4、第1項から第20項までの和が24である等比数列について、第1項から第40項までの和を求めよ
この動画を見る
第1項から第10項までの和が4、第1項から第20項までの和が24である等比数列について、第1項から第40項までの和を求めよ
【短時間でマスター!!】階差数列の求め方を解説!〔現役講師解説、数学〕

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
数学2B
階差数列
$5,11,23,41,65,95,\cdots$の一般項は?
この動画を見る
数学2B
階差数列
$5,11,23,41,65,95,\cdots$の一般項は?
福田の数学〜早稲田大学2023年理工学部第2問〜玉を取り出す確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数学的帰納法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 赤玉と黒玉が入っている袋の中から無作為に玉を1つ取り出し、取り出した玉を袋に戻した上で、取り出した玉と同じ色の玉をもう1つ袋に入れる操作を繰り返す。以下の問いに答えよ。
(1)初めに袋の中に赤玉が1個、黒玉が1個入っているとする。n回の操作を行ったとき、赤玉をちょうどk回取り出す確率を$P_n(k)$(k=0,1,...,n)とする。
$P_1(k)$と$P_2(k)$を求め、さらに$P_n(k)$を求めよ。
(2)初めに袋の中に赤玉がr個、黒玉がb個(r≧1, b≧1)入っているとする。n回の操作を行ったとき、k回目に赤玉が、それ以外ではすべて黒玉が取り出される確率$Q_n(k)$(k=1,2,..., n)とする。$Q_n(k)$はkによらないことを示せ。
2023早稲田大学理工学部過去問
この動画を見る
$\Large\boxed{2}$ 赤玉と黒玉が入っている袋の中から無作為に玉を1つ取り出し、取り出した玉を袋に戻した上で、取り出した玉と同じ色の玉をもう1つ袋に入れる操作を繰り返す。以下の問いに答えよ。
(1)初めに袋の中に赤玉が1個、黒玉が1個入っているとする。n回の操作を行ったとき、赤玉をちょうどk回取り出す確率を$P_n(k)$(k=0,1,...,n)とする。
$P_1(k)$と$P_2(k)$を求め、さらに$P_n(k)$を求めよ。
(2)初めに袋の中に赤玉がr個、黒玉がb個(r≧1, b≧1)入っているとする。n回の操作を行ったとき、k回目に赤玉が、それ以外ではすべて黒玉が取り出される確率$Q_n(k)$(k=1,2,..., n)とする。$Q_n(k)$はkによらないことを示せ。
2023早稲田大学理工学部過去問
福田の数学〜早稲田大学2023年理工学部第1問〜整式の割り算の商に関する論証

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数列#漸化式#数学的帰納法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ nを自然数として、整式$(3x+2)^n$を$x^2$+$x$+1で割った余りを$a_nx$+$b_n$とおく。
(1)$a_{n+1}$と$b_{n+1}$を、それぞれ$a_n$と$b_n$を用いて表せ。
(2)全てのnに対して、$a_n$と$b_n$は7で割り切れないことを示せ。
(3)$a_n$と$b_n$を$a_{n+1}$と$b_{n+1}$で表し、全てのnに対して、2つの整数$a_n$と$b_n$は互いに素であることを示せ。
2023早稲田大学理工学部過去問
この動画を見る
$\Large\boxed{1}$ nを自然数として、整式$(3x+2)^n$を$x^2$+$x$+1で割った余りを$a_nx$+$b_n$とおく。
(1)$a_{n+1}$と$b_{n+1}$を、それぞれ$a_n$と$b_n$を用いて表せ。
(2)全てのnに対して、$a_n$と$b_n$は7で割り切れないことを示せ。
(3)$a_n$と$b_n$を$a_{n+1}$と$b_{n+1}$で表し、全てのnに対して、2つの整数$a_n$と$b_n$は互いに素であることを示せ。
2023早稲田大学理工学部過去問
福田の数学〜慶應義塾大学2023年薬学部第1問(5)〜確率漸化式の基本

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (5)地点Aと地点Bがあり、Kさんは時刻0に地点Aにいる。Kさんは1秒ごとに以下の確率で移動し、時刻0からn秒後に地点Aか地点Bにいる。
$\left\{\begin{array}{1}
・地点Aにいるとき\\
\frac{1}{2}の確率で地点Aにとどまり、\frac{1}{2}の確率で地点Bに移動する。\\
・地点Bにいるとき
\frac{1}{6}の確率で地点Bにとどまり、\frac{5}{6}の確率で地点Aに移動する。\\
\end{array}\right.$
Kさんが時刻0からn秒後に地点Aにいる確率を$a_n$、地点Bにいる確率を$b_n$で表す。ただし、nは0以上の整数とする。
(i)$a_{n+1}$を$a_n$と$b_n$で表すと$a_{n+1}$=$\boxed{\ \ サ\ \ }$$a_n$+$\boxed{\ \ シ\ \ }$$b_n$であり、$a_4$=$\boxed{\ \ ス\ \ }$
(ii)数列{$a_n$}の一般項$a_n$をnの式で表すと$\boxed{\ \ セ\ \ }$である。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (5)地点Aと地点Bがあり、Kさんは時刻0に地点Aにいる。Kさんは1秒ごとに以下の確率で移動し、時刻0からn秒後に地点Aか地点Bにいる。
$\left\{\begin{array}{1}
・地点Aにいるとき\\
\frac{1}{2}の確率で地点Aにとどまり、\frac{1}{2}の確率で地点Bに移動する。\\
・地点Bにいるとき
\frac{1}{6}の確率で地点Bにとどまり、\frac{5}{6}の確率で地点Aに移動する。\\
\end{array}\right.$
Kさんが時刻0からn秒後に地点Aにいる確率を$a_n$、地点Bにいる確率を$b_n$で表す。ただし、nは0以上の整数とする。
(i)$a_{n+1}$を$a_n$と$b_n$で表すと$a_{n+1}$=$\boxed{\ \ サ\ \ }$$a_n$+$\boxed{\ \ シ\ \ }$$b_n$であり、$a_4$=$\boxed{\ \ ス\ \ }$
(ii)数列{$a_n$}の一般項$a_n$をnの式で表すと$\boxed{\ \ セ\ \ }$である。
2023慶應義塾大学薬学部過去問
大学入試問題#510「よくある形」 #防衛医科大学(2015) #数列

単元:
#大学入試過去問(数学)#数列#学校別大学入試過去問解説(数学)#数学(高校生)#数B#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,\ a_2=e$
$a_{n+2}=a_n^{-2}・a_{n+1}^3$
一般項$a_n$を求めよ
出典:2015年防衛医科大学 入試問題
この動画を見る
$a_1=1,\ a_2=e$
$a_{n+2}=a_n^{-2}・a_{n+1}^3$
一般項$a_n$を求めよ
出典:2015年防衛医科大学 入試問題
2023年京大の漸化式!典型的なパターンが詰まった問題です【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
{${ a_n}$}は次の条件を満たしている。
${ a_1}=3$、${ a_n}=\displaystyle \frac{{ S_n}}{n}+(n-1)・2^{n}(n=2,3,4…)$
ただし,${ S_n}={ a_1}+{ a_2}+・・・+{ a_n}$である。このとき、数列{${ a_n}$}の一般項を求めよ。
京都大過去問
この動画を見る
{${ a_n}$}は次の条件を満たしている。
${ a_1}=3$、${ a_n}=\displaystyle \frac{{ S_n}}{n}+(n-1)・2^{n}(n=2,3,4…)$
ただし,${ S_n}={ a_1}+{ a_2}+・・・+{ a_n}$である。このとき、数列{${ a_n}$}の一般項を求めよ。
京都大過去問
仮説検定を分かりやすく!頻度確率を用いて計算しよう!

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ダーツの矢を投げて、統計を取ると20に入る頻度が1000回中800回のプレイヤーが、10回投げたところ9回、20に入った。このプレイヤーは調子が良いか?
この動画を見る
ダーツの矢を投げて、統計を取ると20に入る頻度が1000回中800回のプレイヤーが、10回投げたところ9回、20に入った。このプレイヤーは調子が良いか?
仮説検定を分かりやすく!概念から計算まで

【数B】特殊な数列の一般項

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の数列の一般項を求めなさい。
$a_1=1$
$a_2=2+3+2$
$a_3=3+4+5+4+3$
$a_4=4+5+6+7+6+5+4$
この動画を見る
次の数列の一般項を求めなさい。
$a_1=1$
$a_2=2+3+2$
$a_3=3+4+5+4+3$
$a_4=4+5+6+7+6+5+4$
福田の数学〜大阪大学2023年理系第5問〜確率漸化式と整数の性質

単元:
#数A#大学入試過去問(数学)#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 1個のさいころをn回投げて、k回目に出た目を$a_k$とする。$b_n$を
$b_n$=$\displaystyle\sum_{k=1}^na_1^{n-k}a_k$
により定義し、b_nが7の倍数とする確率を$p_n$とする。
(1)$p_1$, $p_2$を求めよ。
(2)数列$\left\{p_n\right\}$の一般項を求めよ。
2023大阪大学理系過去問
この動画を見る
$\Large\boxed{5}$ 1個のさいころをn回投げて、k回目に出た目を$a_k$とする。$b_n$を
$b_n$=$\displaystyle\sum_{k=1}^na_1^{n-k}a_k$
により定義し、b_nが7の倍数とする確率を$p_n$とする。
(1)$p_1$, $p_2$を求めよ。
(2)数列$\left\{p_n\right\}$の一般項を求めよ。
2023大阪大学理系過去問
【0≦θ≦πを問題文に追加】微分すると大変かも・・・ By ~らん~
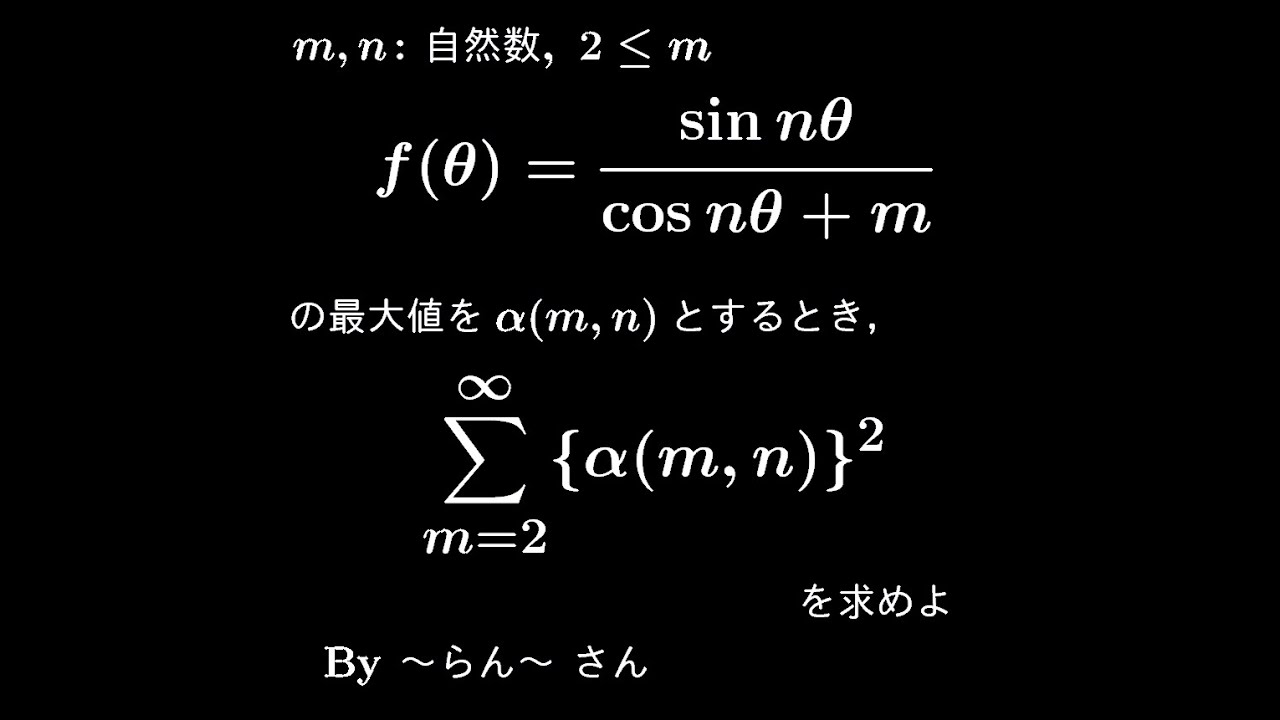
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$m,n$:自然数
$m \geqq 2$
$f(\theta)=\displaystyle \frac{\sin\ n\theta}{\cos\ n\theta+m}$の最大値を$\alpha(m,n)$とする
$\displaystyle \sum_{m=2}^\infty \{\alpha(m,n)\}^2$を求めよ
この動画を見る
$m,n$:自然数
$m \geqq 2$
$f(\theta)=\displaystyle \frac{\sin\ n\theta}{\cos\ n\theta+m}$の最大値を$\alpha(m,n)$とする
$\displaystyle \sum_{m=2}^\infty \{\alpha(m,n)\}^2$を求めよ
関西医科大 三項間漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a_1=0,a_2=1$
$a_{n+2}=10a_{n+1}+51a_{n}$とする。
①一般項$a_n$を求めよ。
②$a_n$を10で割ったあまりを$b_n$とする。
$\displaystyle \sum_{k=1}^{2m} b_k$を求めよ。
関西医科大過去問
この動画を見る
$ a_1=0,a_2=1$
$a_{n+2}=10a_{n+1}+51a_{n}$とする。
①一般項$a_n$を求めよ。
②$a_n$を10で割ったあまりを$b_n$とする。
$\displaystyle \sum_{k=1}^{2m} b_k$を求めよ。
関西医科大過去問
福田の数学〜京都大学2023年文系第4問〜部分和を含んだ漸化式の解法

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 数列{$a_n$}は次の条件を満たしている。
$a_1$=3, $a_n$=$\frac{S_n}{n}$+$(n-1)・2^n$ (n=2,3,4,...)
ただし、$S_n$=$a_1$+$a_2$+...+$a_n$である。このとき、数列{$a_n$}の一般項を求めよ。
2023京都大学文系過去問
この動画を見る
$\Large\boxed{4}$ 数列{$a_n$}は次の条件を満たしている。
$a_1$=3, $a_n$=$\frac{S_n}{n}$+$(n-1)・2^n$ (n=2,3,4,...)
ただし、$S_n$=$a_1$+$a_2$+...+$a_n$である。このとき、数列{$a_n$}の一般項を求めよ。
2023京都大学文系過去問
日本医科大 漸化式 自由に解かせてくれ!

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=-6,
a_{n+1}=2a_n+3n+4^n$
これを求めよ。
日本医科大過去問
この動画を見る
$a_1=-6,
a_{n+1}=2a_n+3n+4^n$
これを求めよ。
日本医科大過去問
大学入試問題#483「作成時間がありませんでした」 近畿大学医学部(2023) #解と係数の関係

単元:
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係#数列#漸化式#数B
指導講師:
ますただ
問題文全文(内容文):
$x^2-x+1=0$の解を$\alpha,\beta$とする
$\alpha^9+\beta^9$の値を求めよ
出典:2023年近畿大学医学 入試問題
この動画を見る
$x^2-x+1=0$の解を$\alpha,\beta$とする
$\alpha^9+\beta^9$の値を求めよ
出典:2023年近畿大学医学 入試問題
東京女子医大 漸化式の基本問題

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#東京女子医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=1,S_n=\displaystyle \sum_{k=1}^n a_k$
$S_{n+1}=3S_n+4n^3+1$
これの一般項aを求めよ.
東京女子医大過去問
この動画を見る
$a_1=1,S_n=\displaystyle \sum_{k=1}^n a_k$
$S_{n+1}=3S_n+4n^3+1$
これの一般項aを求めよ.
東京女子医大過去問
2023久留米大(医)確率漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
無作為に1個取り出して戻すを繰り返す.
n回取り出したときの数の合計が3の倍数になる確率$P_{n}$を求めよ.
久留米大(医)過去問
この動画を見る
無作為に1個取り出して戻すを繰り返す.
n回取り出したときの数の合計が3の倍数になる確率$P_{n}$を求めよ.
久留米大(医)過去問
2023昭和大(医)漸化式の基本問題

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#昭和大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=4$
$\displaystyle \sum_{k=1}^{n+1} a_k=4,a_n+8$
一般項$a_n$を求めよ.
昭和大(医)過去問
この動画を見る
$a_1=4$
$\displaystyle \sum_{k=1}^{n+1} a_k=4,a_n+8$
一般項$a_n$を求めよ.
昭和大(医)過去問
【わかりやすく解説】和の記号Σ(シグマ)(数学B/数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の和を求めよ。
(4)$\displaystyle \sum_{k=1}^n (k^2+3k+2)$
この動画を見る
次の和を求めよ。
(4)$\displaystyle \sum_{k=1}^n (k^2+3k+2)$
