 数Ⅲ
数Ⅲ
 数Ⅲ
数Ⅲ
【高校数学】毎日積分53日目 実践編④回転体シリーズ~斜めの回転軸~【難易度:★★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線$y=\frac{x^2}{\sqrt{2}}-x$と直線$y=x$で囲まれた部分を、直線$y=x$の周りに1回転させてできる立体の体積を求めよ
この動画を見る
放物線$y=\frac{x^2}{\sqrt{2}}-x$と直線$y=x$で囲まれた部分を、直線$y=x$の周りに1回転させてできる立体の体積を求めよ
【高校数学】毎日積分52日目 実践編③回転体シリーズ~軸からの最長距離と最短距離~【難易度:★★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
2つの関数$f(x)=e^{-x} \sin x(0\leqq x\leqq 2\pi)$と$g(x)=-e^{-x}(0\leqq x\leqq 2\pi)$について、次の問いに答えよ。
(1)$f(x)$が最小値をとるときの$x$の値を求めよ。
(2)$f(x)=g(x)$をみたす$x$の値を求めよ。
(3)曲線$C1:y=f(x),C2:y=g(x)$と$y$軸で囲まれる部分を$x$軸のまわり
に1回転してできる立体の体積$V$を求めよ。
この動画を見る
2つの関数$f(x)=e^{-x} \sin x(0\leqq x\leqq 2\pi)$と$g(x)=-e^{-x}(0\leqq x\leqq 2\pi)$について、次の問いに答えよ。
(1)$f(x)$が最小値をとるときの$x$の値を求めよ。
(2)$f(x)=g(x)$をみたす$x$の値を求めよ。
(3)曲線$C1:y=f(x),C2:y=g(x)$と$y$軸で囲まれる部分を$x$軸のまわり
に1回転してできる立体の体積$V$を求めよ。
【高校数学】分数関数の漸近線とグラフの簡単な求め方!
単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
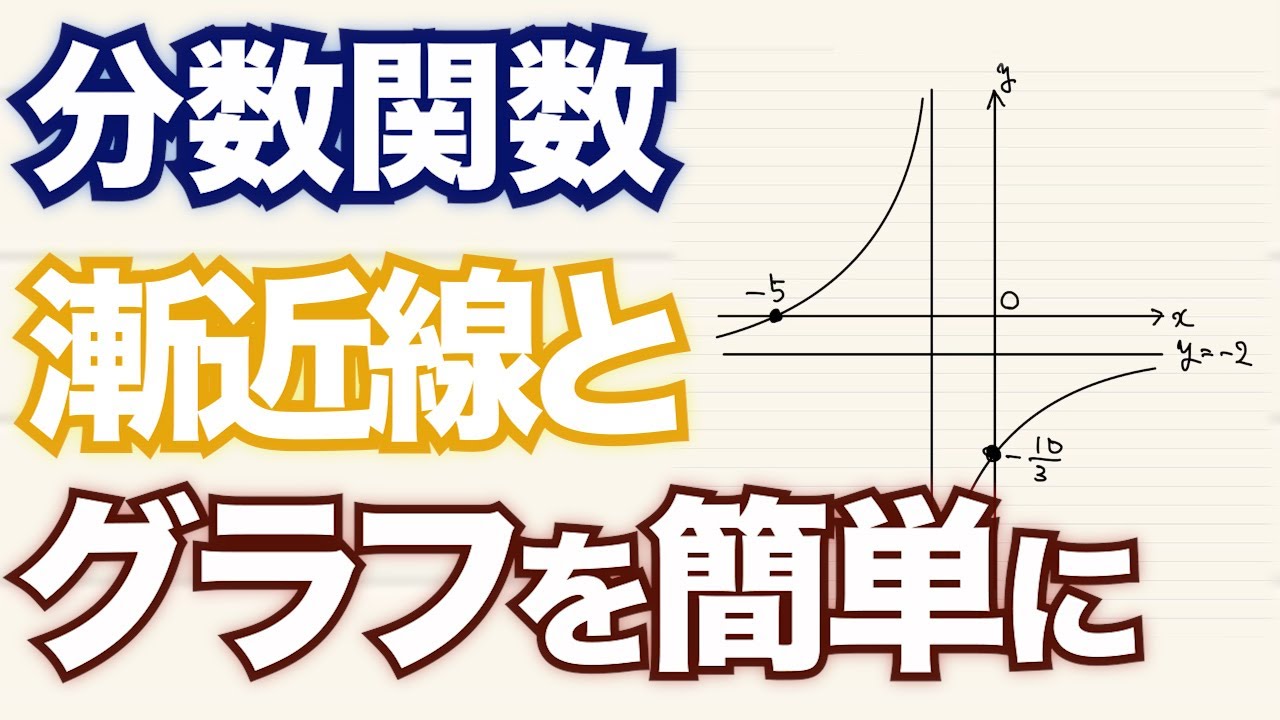
次の関数のグラフをかけ。また,その漸近線を求めよ。
$y=\dfrac{-2x–10}{x+3}$
この動画を見る
次の関数のグラフをかけ。また,その漸近線を求めよ。
$y=\dfrac{-2x–10}{x+3}$
【高校数学】分数関数の漸近線とグラフの簡単な求め方!
単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
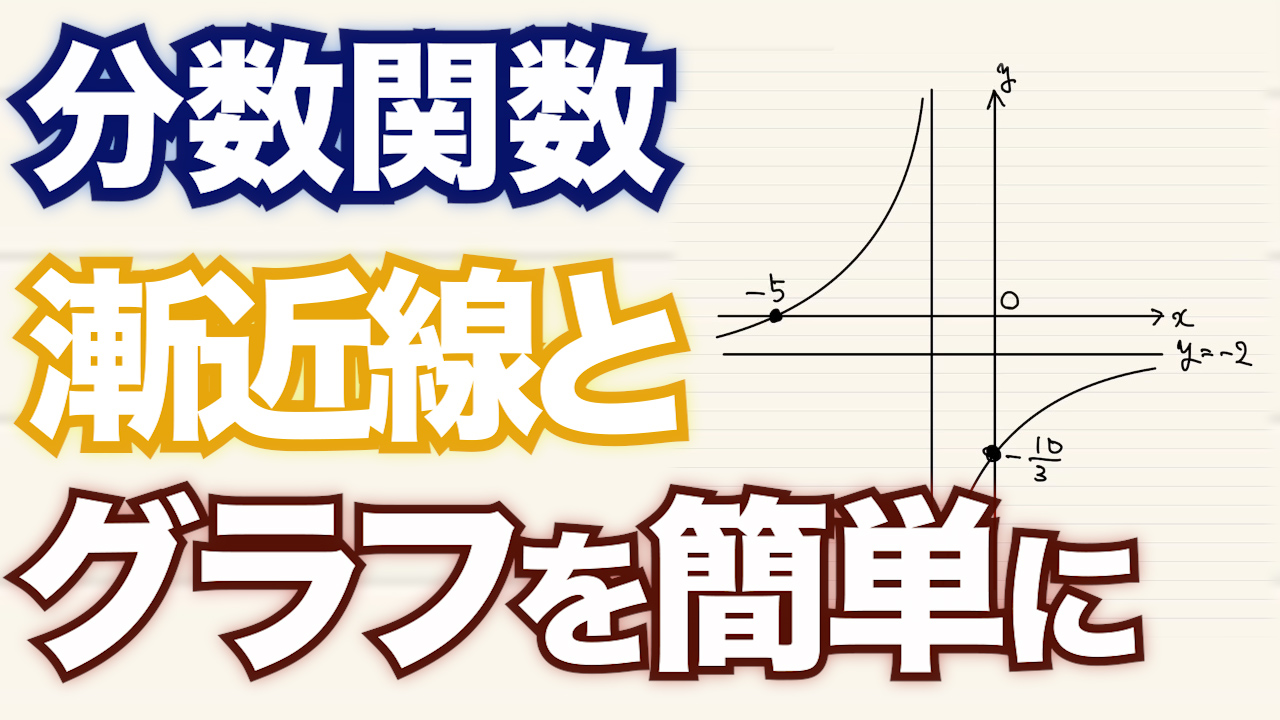
次の関数のグラフをかけ。また,その漸近線を求めよ。
$y=\frac{–2x–10}{x+3}$
この動画を見る
次の関数のグラフをかけ。また,その漸近線を求めよ。
$y=\frac{–2x–10}{x+3}$
【高校数学】毎日積分51日目 実践編②回転体シリーズ~場合分け~【難易度:★★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
座標空間において,連立不等式
$x^2+y^2\leqq 1$
$|x|\leqq \sin z $
$|y|\leqq \sin z $
$0\leqq z \leqq \dfrac{\pi}{2}$
で定められる立体を$K$とする。
(1)$t$を$0\leqq t \leqq \dfrac{\pi}{2}$を満たす定数として、立体$K$を$z$軸に垂直な平面$z=t$で切ったときの断面積を$S(t)$とする。必要に応じて場合分けをして、$S(t)$を$t$の式で表せ。
(2)立体$K$のうち、2つの平面$z=0$と$z=\dfrac{\pi}{4}$ではさまれた部分の体積$V$を求めよ。
(3) 立体$K$の体積$W$を求めよ。
この動画を見る
座標空間において,連立不等式
$x^2+y^2\leqq 1$
$|x|\leqq \sin z $
$|y|\leqq \sin z $
$0\leqq z \leqq \dfrac{\pi}{2}$
で定められる立体を$K$とする。
(1)$t$を$0\leqq t \leqq \dfrac{\pi}{2}$を満たす定数として、立体$K$を$z$軸に垂直な平面$z=t$で切ったときの断面積を$S(t)$とする。必要に応じて場合分けをして、$S(t)$を$t$の式で表せ。
(2)立体$K$のうち、2つの平面$z=0$と$z=\dfrac{\pi}{4}$ではさまれた部分の体積$V$を求めよ。
(3) 立体$K$の体積$W$を求めよ。
【高校数学】毎日積分50日目 実践編①回転体シリーズ~必要な平面を図示~【難易度:★★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$xyz$空間内で4点(0,0,0),(1,0,0),(1,1,0),(0,1,0)を頂点とする正方形の周および内部をKとし、Kをx軸のまわりに1回転させてできる立体をKx,Kをy軸のまわりに1回転させてできる立体をKyとする。さらに、KxとKyの共通部分をLとし、KxとKyの少なくともどちらか一方に含まれる点全体からなる立体をMとする。このとき、以下の問いに答えよ。
(1) Kxの体積を求めよ。
(2)平面$z=t$がKxと共有点をもつような実数tの値の範囲を答えよ。またこのとき、Kxを平面$z=t$で切った断面積A(t)を求めよ。
(3)平面$z=t$がLと共有点をもつような実数tの値の範囲を答えよ。また、このとき、Lを平面$z=t$で切った断面積B(t)を求めよ。
(4) Lの体積を求めよ。
(5) Mの体積を求めよ。
この動画を見る
$xyz$空間内で4点(0,0,0),(1,0,0),(1,1,0),(0,1,0)を頂点とする正方形の周および内部をKとし、Kをx軸のまわりに1回転させてできる立体をKx,Kをy軸のまわりに1回転させてできる立体をKyとする。さらに、KxとKyの共通部分をLとし、KxとKyの少なくともどちらか一方に含まれる点全体からなる立体をMとする。このとき、以下の問いに答えよ。
(1) Kxの体積を求めよ。
(2)平面$z=t$がKxと共有点をもつような実数tの値の範囲を答えよ。またこのとき、Kxを平面$z=t$で切った断面積A(t)を求めよ。
(3)平面$z=t$がLと共有点をもつような実数tの値の範囲を答えよ。また、このとき、Lを平面$z=t$で切った断面積B(t)を求めよ。
(4) Lの体積を求めよ。
(5) Mの体積を求めよ。
福田のおもしろ数学037〜相加相乗平均の罠〜2変数関数の最小値

単元:
#数Ⅰ#2次関数#式と証明#恒等式・等式・不等式の証明#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$x>1,y>1$のとき、
$x+y+\frac{2}{x+y}+\frac{1}{2xy}$の最小値を求めよ
この動画を見る
$x>1,y>1$のとき、
$x+y+\frac{2}{x+y}+\frac{1}{2xy}$の最小値を求めよ
【高校数学】毎日積分49日目【難易度:★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\displaystyle \int_{\frac{π}{3}}^{\frac{π}{2}}\frac{sin\frac{x}{2}}{1+sin\frac{x}{2}}dx$
これを解け.
この動画を見る
$\displaystyle \int_{\frac{π}{3}}^{\frac{π}{2}}\frac{sin\frac{x}{2}}{1+sin\frac{x}{2}}dx$
これを解け.
【高校数学】毎日積分48日目【難易度:★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\displaystyle \int_1^4\frac{1}{\sqrt{x}(\sqrt{x}+1)}dx$
これを解け.
この動画を見る
$\displaystyle \int_1^4\frac{1}{\sqrt{x}(\sqrt{x}+1)}dx$
これを解け.
中学からの極限(応用編)~全国入試問題解法 #shorts #数学 #高校入試 #頭の体操

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \displaystyle \lim_{x \to 1}\dfrac{x^2+2x-3}{x^2+x-2}$を求めよ.
この動画を見る
$ \displaystyle \lim_{x \to 1}\dfrac{x^2+2x-3}{x^2+x-2}$を求めよ.
【高校数学】毎日積分47日目~③前の結果を用いて計算~【難易度:★★★★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_{-\sqrt{2}}^{\sqrt{2}}\frac{8}{x^4+4}dx$
(3)前の結果を用いて計算せよ
この動画を見る
$\int_{-\sqrt{2}}^{\sqrt{2}}\frac{8}{x^4+4}dx$
(3)前の結果を用いて計算せよ
【高校数学】毎日積分46日目~②tan1/8π,tan3/8πを求めよ~【難易度:★★★★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_{-\sqrt{2}}^{\sqrt{2}}\frac{8}{x^4+4}dx$
(2)$tan\frac{1}{8}π,tan\frac{3}{8}π$を求めよ
この動画を見る
$\int_{-\sqrt{2}}^{\sqrt{2}}\frac{8}{x^4+4}dx$
(2)$tan\frac{1}{8}π,tan\frac{3}{8}π$を求めよ
【積分】「積分って結局なにしてるの?」について解説しました!【数学III】

【高校数学】毎日積分45日目~①まずは部分分数分解せよ~【難易度:★★★★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_{-\sqrt{2}}^{\sqrt{2}}\frac{8}{x^4+4}dx$
(1)部分分数分解せよ
この動画を見る
$\int_{-\sqrt{2}}^{\sqrt{2}}\frac{8}{x^4+4}dx$
(1)部分分数分解せよ
【高校数学】毎日積分44日目【難易度:★★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_1^{\sqrt{3}}\frac{1}{x^2}log\sqrt{1+x^2}dx$
これを解け.
この動画を見る
$\int_1^{\sqrt{3}}\frac{1}{x^2}log\sqrt{1+x^2}dx$
これを解け.
【高校数学】毎日積分43日目【難易度:★★】【毎日17時投稿】

【高校数学】毎日積分42日目【難易度:★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^\frac{π}{2}\frac{1}{sinx+cosx+1}dx$
これを解け.
この動画を見る
$\int_0^\frac{π}{2}\frac{1}{sinx+cosx+1}dx$
これを解け.
【高校数学】毎日積分41日目【球の体積を積分で考えてみよう】【毎日17時投稿】

中学からの極限(発展編)~全国入試問題解法 #shorts #数学 #極限 #頭の体操

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \displaystyle \lim_{x \to 1}\dfrac{ax-1}{x-a}$を求めよ.
この動画を見る
$ \displaystyle \lim_{x \to 1}\dfrac{ax-1}{x-a}$を求めよ.
【高校数学】毎日積分40日目【なぜ定積分で面積が求められるの?】【毎日17時投稿】

【高校数学】毎日積分39日目【難易度:★★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_1^2\frac{logx}{1+x^2}dx $
これを解け.
この動画を見る
$\int_1^2\frac{logx}{1+x^2}dx $
これを解け.
福田のおもしろ数学030〜調和級数は発散しない?〜驚くべき事実がここに
単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
調和級数
$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}…$
について解説します
この動画を見る
調和級数
$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}…$
について解説します
【高校数学】毎日積分38日目【難易度:★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_{logπ}^{log2π}e^xsine^xdx$
これを解け.
この動画を見る
$\int_{logπ}^{log2π}e^xsine^xdx$
これを解け.
【高校数学】毎日積分37日目【難易度:★★★☆☆】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^2\frac{2x+1}{\sqrt{x^2+4}}dx$
この動画を見る
$\int_0^2\frac{2x+1}{\sqrt{x^2+4}}dx$
【高校数学】毎日積分36日目【バウムクーヘン積分って実際どれくらい便利なの!?】【毎日17時投稿】

【高校数学】毎日積分35日目【バウムクーヘン積分】【毎日17時投稿】

【高校数学】毎日積分34日目【区分求積法】【毎日17時投稿】

中学からの極限(基礎編)!~全国入試問題解法 #数学 #極限 #微分積分 #頭の体操

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \displaystyle \lim_{x \to \infty}\dfrac{5x^2+x+4}{x^2+2x+3}$を求めよ.
この動画を見る
$ \displaystyle \lim_{x \to \infty}\dfrac{5x^2+x+4}{x^2+2x+3}$を求めよ.
【高校数学】毎日積分33日目【難易度:★★★★★】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式が$1\leqq x\leqq 2$で成り立つような関数f(x)と定数A,Bを求めよ.
$\int_{\frac{1}{x}}^{\frac{2}{x}}|logy|f(xy)dy=3x(logx-1)+A+\frac{B}{x}$
ただし,f(x)は$1\leqq x\leqq 2$に対して定義される連続関数とする.(東京工業大学 2019)
この動画を見る
次の等式が$1\leqq x\leqq 2$で成り立つような関数f(x)と定数A,Bを求めよ.
$\int_{\frac{1}{x}}^{\frac{2}{x}}|logy|f(xy)dy=3x(logx-1)+A+\frac{B}{x}$
ただし,f(x)は$1\leqq x\leqq 2$に対して定義される連続関数とする.(東京工業大学 2019)
【高校数学】毎日積分30日目【難易度:★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^1\sqrt{1+2\sqrt{x}}dx$
これを解け.
この動画を見る
$\int_0^1\sqrt{1+2\sqrt{x}}dx$
これを解け.
