 数Ⅲ
数Ⅲ
 数Ⅲ
数Ⅲ
福田のおもしろ数学438〜定積分の値の評価

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\dfrac{2}{3} \lt \displaystyle \int_{0}^{1} e^{-x^2} dx \lt \dfrac{\pi}{4}$
を証明してください。
この動画を見る
$\dfrac{2}{3} \lt \displaystyle \int_{0}^{1} e^{-x^2} dx \lt \dfrac{\pi}{4}$
を証明してください。
福田のおもしろ数学437〜連立不等式の表す立体の体積

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
x \geqq 0,z \geqq 0 \quad \cdots ① \\
x+y \leqq 1 \qquad \cdots② \\\
z^2\leqq y-x \quad \cdots ③
\end{array}
\right.
\end{eqnarray}$
を満たす点$(x,y,z)$の集合からなる
立体の体積を求めよ。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x \geqq 0,z \geqq 0 \quad \cdots ① \\
x+y \leqq 1 \qquad \cdots② \\\
z^2\leqq y-x \quad \cdots ③
\end{array}
\right.
\end{eqnarray}$
を満たす点$(x,y,z)$の集合からなる
立体の体積を求めよ。
【数Ⅲ】【積分とその応用】定積分部分積分 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
定積分$\displaystyle \int_0^1x^2e^{2x}~dx$を求めよ。
定積分$\displaystyle \int_0^\frac\pi2(ax-\sin x)^2~dx$を最小にする実数$a$の値を求めよ。
定積分$\displaystyle I=\int_0^\frac\pi2e^{-3x}\sin x~dx$を求めよ。
自然数$n$について、$\displaystyle I_n=\int_1^e(\log x)^n~dx$とする。
(1) $I_1$を求めよ。
(2) $I_{n+1}$を$I_n$を用いて表せ。
(3) $I_4$を求めよ。
この動画を見る
定積分$\displaystyle \int_0^1x^2e^{2x}~dx$を求めよ。
定積分$\displaystyle \int_0^\frac\pi2(ax-\sin x)^2~dx$を最小にする実数$a$の値を求めよ。
定積分$\displaystyle I=\int_0^\frac\pi2e^{-3x}\sin x~dx$を求めよ。
自然数$n$について、$\displaystyle I_n=\int_1^e(\log x)^n~dx$とする。
(1) $I_1$を求めよ。
(2) $I_{n+1}$を$I_n$を用いて表せ。
(3) $I_4$を求めよ。
【数Ⅲ】【積分とその応用】定積分置換積分 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の定積分を求めよ。
(1) $\displaystyle \int_{-1}^0 (x+2)\sqrt{3x+4}~dx$
(2) $\displaystyle \int_{0}^4 \frac{x^2}{\sqrt{x+1}}~dx$
(3) $\displaystyle \int_{0}^1 \frac{x^3}{\sqrt{1+x^2}}~dx$
(4) $\displaystyle \int_{1}^3 \frac{dx}{x\sqrt{x+1}}$
(5) $\displaystyle \int_{1}^2 \frac{dx}{e^x-1}$
(6) $\displaystyle \int_{0}^{\frac\pi4} \frac{\sin^3x}{\cos^2x}~dx$
次の定積分を求めよ。ただし、$a$は正の定数とする。
(1) $\displaystyle \int_{0}^1 \sqrt{2x-x^2}~dx$
(2) $\displaystyle \int_{1}^{\frac12} \frac{dx}{\sqrt{2x-x^2}}$
(3) $\displaystyle \int_{1}^{\frac a2} \frac{dx}{(a^2-x^2)^{\frac32}}$
(4) $\displaystyle \int_{1}^{2} \frac{dx}{x^2-2x+2}$
(5) $\displaystyle \int_{3}^{5} \frac{dx}{x^2-4x+4}$
(6) $\displaystyle \int_{6}^{12} \frac{dx}{x^2-3x-10}$
(7) $\displaystyle \int_{0}^{a} \frac{dx}{(x^2+a^2)^2}$
(8) $\displaystyle \int_{1}^{\sqrt3} \frac{2x+1}{x^2+1}~dx$
次のことが成り立つことを証明せよ。
(1) $\displaystyle \int_a^b f(x)~dx=\int_a^bf(a+b-x)~dx$
(2) $\displaystyle\int_{-a}^af(x)~dx=\int_0^a\{f(x)+f(-x)\}~dx$
(3) $\displaystyle \int_0^af(x)~dx=\int_0^{\frac a 2}\{f(x)+f(a-x)\}~dx$
(4) $f(a+x)=f(a-x)$のとき$\displaystyle \int_{a-b}^{a+b}f(x)~dx=2\int_a^{a+b}f(x)~dx$
この動画を見る
次の定積分を求めよ。
(1) $\displaystyle \int_{-1}^0 (x+2)\sqrt{3x+4}~dx$
(2) $\displaystyle \int_{0}^4 \frac{x^2}{\sqrt{x+1}}~dx$
(3) $\displaystyle \int_{0}^1 \frac{x^3}{\sqrt{1+x^2}}~dx$
(4) $\displaystyle \int_{1}^3 \frac{dx}{x\sqrt{x+1}}$
(5) $\displaystyle \int_{1}^2 \frac{dx}{e^x-1}$
(6) $\displaystyle \int_{0}^{\frac\pi4} \frac{\sin^3x}{\cos^2x}~dx$
次の定積分を求めよ。ただし、$a$は正の定数とする。
(1) $\displaystyle \int_{0}^1 \sqrt{2x-x^2}~dx$
(2) $\displaystyle \int_{1}^{\frac12} \frac{dx}{\sqrt{2x-x^2}}$
(3) $\displaystyle \int_{1}^{\frac a2} \frac{dx}{(a^2-x^2)^{\frac32}}$
(4) $\displaystyle \int_{1}^{2} \frac{dx}{x^2-2x+2}$
(5) $\displaystyle \int_{3}^{5} \frac{dx}{x^2-4x+4}$
(6) $\displaystyle \int_{6}^{12} \frac{dx}{x^2-3x-10}$
(7) $\displaystyle \int_{0}^{a} \frac{dx}{(x^2+a^2)^2}$
(8) $\displaystyle \int_{1}^{\sqrt3} \frac{2x+1}{x^2+1}~dx$
次のことが成り立つことを証明せよ。
(1) $\displaystyle \int_a^b f(x)~dx=\int_a^bf(a+b-x)~dx$
(2) $\displaystyle\int_{-a}^af(x)~dx=\int_0^a\{f(x)+f(-x)\}~dx$
(3) $\displaystyle \int_0^af(x)~dx=\int_0^{\frac a 2}\{f(x)+f(a-x)\}~dx$
(4) $f(a+x)=f(a-x)$のとき$\displaystyle \int_{a-b}^{a+b}f(x)~dx=2\int_a^{a+b}f(x)~dx$
【数Ⅲ】【積分とその応用】定積分置換積分、部分積分 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次を求めよ
(1) $\displaystyle \int_0^1 \sqrt{e^{1-t}}~dt$
(2) $\displaystyle \int_0^{\frac{\pi}2}\frac{\cos{2\theta}}{\sin \theta+\cos\theta}~d\theta$
(3) $\displaystyle\int_0^\pi \sin^4x~dx$
(4) $\displaystyle \int_1^2 \frac{\sqrt{x^2-4x+4}}{x}~dx$
次を求めよ
(1) $\displaystyle \int_0^\pi |\cos2\theta|~d\theta$
(2) $\displaystyle \int_0^\pi|\sin x+\cos x|~dx$
$m,n$は正の整数とする。次の定積分を求めよ。
(1) $\displaystyle \int_0^\pi \cos mx\cos nx~dx$
(2) $\displaystyle \int_0^\pi \sin mx\sin nx~dx$
(3) $\displaystyle \int_0^\pi \sin mx\cos nx~dx$
定積分$\displaystyle \int_0^\pi (1-a\sin x-b\sin2x)^2~dx$を最小にする定数$a,b$の値を求めよ。
この動画を見る
次を求めよ
(1) $\displaystyle \int_0^1 \sqrt{e^{1-t}}~dt$
(2) $\displaystyle \int_0^{\frac{\pi}2}\frac{\cos{2\theta}}{\sin \theta+\cos\theta}~d\theta$
(3) $\displaystyle\int_0^\pi \sin^4x~dx$
(4) $\displaystyle \int_1^2 \frac{\sqrt{x^2-4x+4}}{x}~dx$
次を求めよ
(1) $\displaystyle \int_0^\pi |\cos2\theta|~d\theta$
(2) $\displaystyle \int_0^\pi|\sin x+\cos x|~dx$
$m,n$は正の整数とする。次の定積分を求めよ。
(1) $\displaystyle \int_0^\pi \cos mx\cos nx~dx$
(2) $\displaystyle \int_0^\pi \sin mx\sin nx~dx$
(3) $\displaystyle \int_0^\pi \sin mx\cos nx~dx$
定積分$\displaystyle \int_0^\pi (1-a\sin x-b\sin2x)^2~dx$を最小にする定数$a,b$の値を求めよ。
【数Ⅲ】【積分とその応用】不定積分置換積分、部分積分3 ※問題文は概要欄

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{\sqrt x}{\sqrt[4]{x^3}+1}~dx$
(2) $\displaystyle \int \frac{dx}{x\sqrt{x+1}}$
(3) $\displaystyle \int \log|x^2-1|~dx$
(4) $\displaystyle \int \frac{e^x}{e^x-e^{-x}}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \tan^4x~dx$
(2) $\displaystyle \int \frac{dx}{\sin{2x}}$
(3) $\displaystyle \int \frac{1}{1-\sin x}~dx$
(4) $\displaystyle \int (\sin^3x-\cos^3x)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int e^x\cos x~dx$
(2) $\displaystyle \int e^{-x}\sin x~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \sin x\log(\cos x)~dx$
(2) $\displaystyle \int x\tan^2x~dx$
(3) $\displaystyle \int \frac{1}{1-e^x}~dx$
この動画を見る
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{\sqrt x}{\sqrt[4]{x^3}+1}~dx$
(2) $\displaystyle \int \frac{dx}{x\sqrt{x+1}}$
(3) $\displaystyle \int \log|x^2-1|~dx$
(4) $\displaystyle \int \frac{e^x}{e^x-e^{-x}}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \tan^4x~dx$
(2) $\displaystyle \int \frac{dx}{\sin{2x}}$
(3) $\displaystyle \int \frac{1}{1-\sin x}~dx$
(4) $\displaystyle \int (\sin^3x-\cos^3x)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int e^x\cos x~dx$
(2) $\displaystyle \int e^{-x}\sin x~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \sin x\log(\cos x)~dx$
(2) $\displaystyle \int x\tan^2x~dx$
(3) $\displaystyle \int \frac{1}{1-e^x}~dx$
【数Ⅲ】【積分とその応用】不定積分置換積分、部分積分2 ※問題文は概要欄

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x^2+x+1}{x^2+1}~dx$
(2) $\displaystyle \int \frac{x^4}{x^2-1}~dx$
(1)次の等式が成り立つように、定数$a,b,c$の値を定めよ。
$\dfrac{3x+2}{x(x+1)^2}=\dfrac{a}{x}+\dfrac{b}{x+1}+\dfrac{c}{(x+1)^2}$
(2)不定積分$\displaystyle \int \dfrac{3x+2}{x(x+1)^2}~dx$を求めよ。
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{x(x^2-1)}$
(2) $\displaystyle \int \frac{dx}{x^2(x+2)}$
(3) $\displaystyle \int \frac{dx}{x(x^2+1)}$
(4) $\displaystyle \int \frac{x^2+1}{x^4-5x^2+4}~dx$
(5) $\displaystyle \int \frac{3x+2}{x(x+1)^3}~dx$
(6) $\displaystyle \int \frac{x^4}{x^3-3x+2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{\sqrt{x+1}-\sqrt x}$
(2) $\displaystyle \int \frac{x}{\sqrt{3x+4}-2}~dx$
この動画を見る
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x^2+x+1}{x^2+1}~dx$
(2) $\displaystyle \int \frac{x^4}{x^2-1}~dx$
(1)次の等式が成り立つように、定数$a,b,c$の値を定めよ。
$\dfrac{3x+2}{x(x+1)^2}=\dfrac{a}{x}+\dfrac{b}{x+1}+\dfrac{c}{(x+1)^2}$
(2)不定積分$\displaystyle \int \dfrac{3x+2}{x(x+1)^2}~dx$を求めよ。
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{x(x^2-1)}$
(2) $\displaystyle \int \frac{dx}{x^2(x+2)}$
(3) $\displaystyle \int \frac{dx}{x(x^2+1)}$
(4) $\displaystyle \int \frac{x^2+1}{x^4-5x^2+4}~dx$
(5) $\displaystyle \int \frac{3x+2}{x(x+1)^3}~dx$
(6) $\displaystyle \int \frac{x^4}{x^3-3x+2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{\sqrt{x+1}-\sqrt x}$
(2) $\displaystyle \int \frac{x}{\sqrt{3x+4}-2}~dx$
【数Ⅲ】【積分とその応用】不定積分置換積分、部分積分1 ※問題文は概要欄

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不定積分を求めよ。
(1) $\displaystyle \int x\sqrt[3]{1+x}~dx$
(2) $\displaystyle \int \sin x \cos^4x~dx$
(3) $\displaystyle \int \frac {dx}{\cos^4x}$
(4) $\displaystyle \int (2x+1)e^{x^2+x+5}~dx$
(5) $\displaystyle \int \frac{e^{2x}}{(e^x+2)^2}~dx$
(6) $\displaystyle \int \frac{\log x}{x(\log x-1)^2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x}{\cos^2x}~dx$
(2) $\displaystyle \int x\log(x-2)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int x\log(x^2-2)~dx$
(2) $\displaystyle \int e^x\log(e^x+1)~dx$
不定積分$\displaystyle \int (\log x)^3~dx$を求めよ。
この動画を見る
次の不定積分を求めよ。
(1) $\displaystyle \int x\sqrt[3]{1+x}~dx$
(2) $\displaystyle \int \sin x \cos^4x~dx$
(3) $\displaystyle \int \frac {dx}{\cos^4x}$
(4) $\displaystyle \int (2x+1)e^{x^2+x+5}~dx$
(5) $\displaystyle \int \frac{e^{2x}}{(e^x+2)^2}~dx$
(6) $\displaystyle \int \frac{\log x}{x(\log x-1)^2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x}{\cos^2x}~dx$
(2) $\displaystyle \int x\log(x-2)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int x\log(x^2-2)~dx$
(2) $\displaystyle \int e^x\log(e^x+1)~dx$
不定積分$\displaystyle \int (\log x)^3~dx$を求めよ。
福田の数学〜京都大学2025理系第3問〜関数の増減と値域

単元:
#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$e$は自然対数の底とする。
$x\gt \dfrac{1}{\sqrt e}$において定義された次の関数
$f(x),g(x)$を考える。
$f(x)=x^2 \log x$
$g(x)=x^2\log x - \dfrac{1}{1+2\log x}$
実数$t$は$t\gt \dfrac{1}{\sqrt e}$を満たすとする。
曲線$y=f(x)$上の店$(t,f(t))$における接線に垂直で、
点$(t,g(t))$を通る直線を$l_t$とする。
直線$l_t$が$x$軸と交わる点の$x$座標を$p(t)$とする。
$t$が$\dfrac{1}{\sqrt e} \lt t \leqq e$の範囲を動くとき、
$p(t)$の取りうる値の範囲を求めよ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{3}$
$e$は自然対数の底とする。
$x\gt \dfrac{1}{\sqrt e}$において定義された次の関数
$f(x),g(x)$を考える。
$f(x)=x^2 \log x$
$g(x)=x^2\log x - \dfrac{1}{1+2\log x}$
実数$t$は$t\gt \dfrac{1}{\sqrt e}$を満たすとする。
曲線$y=f(x)$上の店$(t,f(t))$における接線に垂直で、
点$(t,g(t))$を通る直線を$l_t$とする。
直線$l_t$が$x$軸と交わる点の$x$座標を$p(t)$とする。
$t$が$\dfrac{1}{\sqrt e} \lt t \leqq e$の範囲を動くとき、
$p(t)$の取りうる値の範囲を求めよ。
$2025$年京都大学理系過去問題
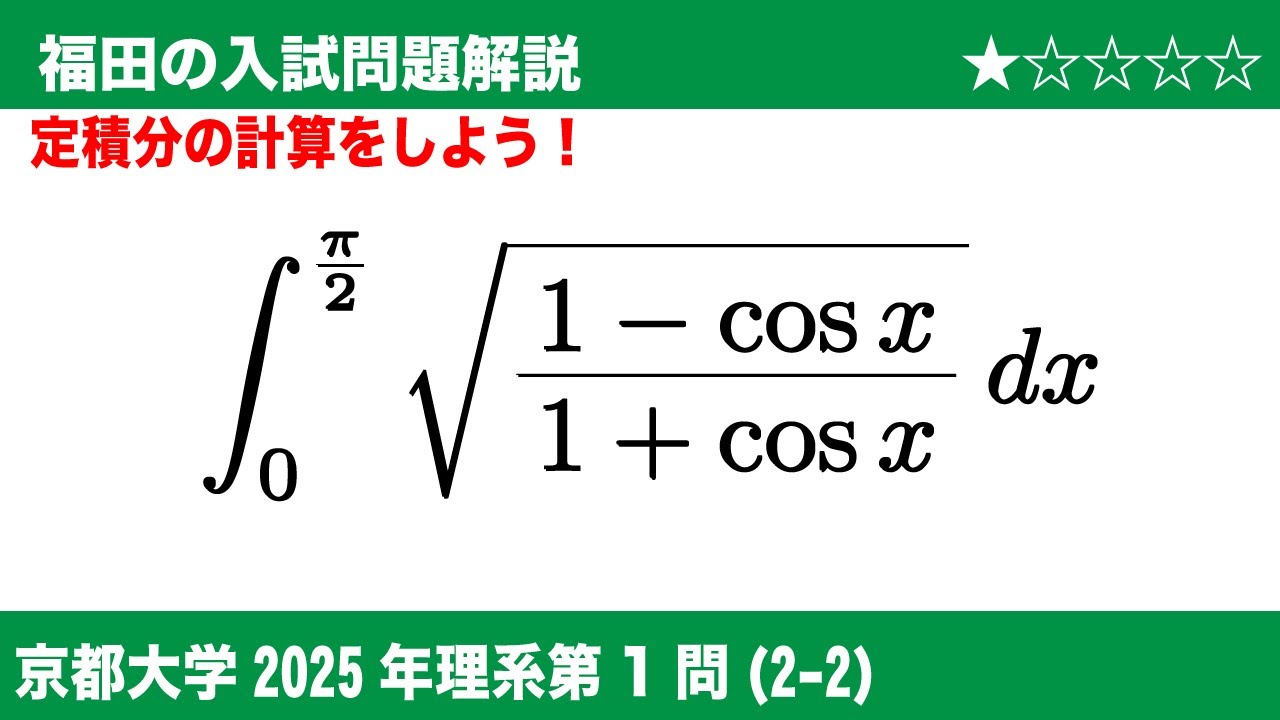
福田の数学〜京都大学2025理系第1問(2−2)〜定積分の計算
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(2-2)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{\dfrac{1-\cos x}{1+\cos x}}dx$
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{1}$
(2-2)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{\dfrac{1-\cos x}{1+\cos x}}dx$
$2025$年京都大学理系過去問題
福田のおもしろ数学429〜複雑な無理関数の最大値

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$xy+x\sqrt{1-y^2}+y\sqrt{1-x^2}$
$\qquad -\sqrt{(1-x^2)(1-y^2)}$
の最大値を求めよ。
この動画を見る
$xy+x\sqrt{1-y^2}+y\sqrt{1-x^2}$
$\qquad -\sqrt{(1-x^2)(1-y^2)}$
の最大値を求めよ。
【数Ⅲ】【微分とその応用】関数のグラフ5 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
1.4次関数$y=f(x)$のグラフの2つの変曲点の座標は
$(-1,1),(1,8)$であり、点$(1,8)$における接線は
直線$y=x$に平行である。関数$f(x)$を求めよ。
2.$a$は定数とする。
曲線$y=(x^2+2x+a)e^x$の変曲点の個数を調べよ
この動画を見る
1.4次関数$y=f(x)$のグラフの2つの変曲点の座標は
$(-1,1),(1,8)$であり、点$(1,8)$における接線は
直線$y=x$に平行である。関数$f(x)$を求めよ。
2.$a$は定数とする。
曲線$y=(x^2+2x+a)e^x$の変曲点の個数を調べよ
【数Ⅲ】【微分とその応用】関数のグラフ4 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
1.関数$y=-x^3+3x^2$のグラフはただ1つの変曲点をもち、
その点に関して対象であることを示せ。
2.関数$y=x^3+3ax^2+3bx+c$は$x=1$で極小となり、
点$(0,3)$はそのグラフの変曲点である。定数$a,b,c$の値を求めよ。
3.右の図は、関数$y=ax^3+bx^2+cx+d~~(0< x <5)$のグラフで、
$x=2$で極大、$x=4$で極小となり、点$(3,5)$は変曲点である。
定数$a,b,c,d$を求めずに、次のものを求めよ。
(1) $y' > 0$となる$x$の値の範囲
(2) $y'' > 0$となる$x$の値の範囲
(3) $y'$が最小となる$x$の値
この動画を見る
1.関数$y=-x^3+3x^2$のグラフはただ1つの変曲点をもち、
その点に関して対象であることを示せ。
2.関数$y=x^3+3ax^2+3bx+c$は$x=1$で極小となり、
点$(0,3)$はそのグラフの変曲点である。定数$a,b,c$の値を求めよ。
3.右の図は、関数$y=ax^3+bx^2+cx+d~~(0< x <5)$のグラフで、
$x=2$で極大、$x=4$で極小となり、点$(3,5)$は変曲点である。
定数$a,b,c,d$を求めずに、次のものを求めよ。
(1) $y' > 0$となる$x$の値の範囲
(2) $y'' > 0$となる$x$の値の範囲
(3) $y'$が最小となる$x$の値
【数Ⅲ】【微分とその応用】関数のグラフ3 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数$f(x)$について、$f'(0)=f''(0)=0$であることを示せ。
また、$f(x)$は$x=0$で極値をとるかどうかを調べよ。
(1) $f(x)=x^4$
(2) $f(x)=x^2\sin x$
この動画を見る
次の関数$f(x)$について、$f'(0)=f''(0)=0$であることを示せ。
また、$f(x)$は$x=0$で極値をとるかどうかを調べよ。
(1) $f(x)=x^4$
(2) $f(x)=x^2\sin x$
【数Ⅲ】【微分とその応用】関数のグラフ2 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数のグラフの概形をかけ。
(1) $y=\dfrac{x^3}{x^2-4}$
(2) $y=x+\sqrt{1-x^2}$
(3) $y=x\sqrt{1-x^2}$
(4) $y=e^{\frac1x}$
(5) $y=e^{-x}\cos x\quad (0\leqq x \leqq 2\pi)$
この動画を見る
次の関数のグラフの概形をかけ。
(1) $y=\dfrac{x^3}{x^2-4}$
(2) $y=x+\sqrt{1-x^2}$
(3) $y=x\sqrt{1-x^2}$
(4) $y=e^{\frac1x}$
(5) $y=e^{-x}\cos x\quad (0\leqq x \leqq 2\pi)$
【数Ⅲ】【微分とその応用】関数のグラフ1 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の曲線の漸近線の方程式を求めよ。
(1) $y=\dfrac{x}{\sqrt{x^2+1}}$
(2) $y=2x+\sqrt{x^2-1}$
この動画を見る
次の曲線の漸近線の方程式を求めよ。
(1) $y=\dfrac{x}{\sqrt{x^2+1}}$
(2) $y=2x+\sqrt{x^2-1}$
【数Ⅲ】【微分とその応用】関数の最大と最小11 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
一直線をなす海岸の地点Aから海岸線に垂直に9km離れた沖の船にいる人が、Aから海岸にそって15km離れた地点Bに最短時間で到着するためには、AB間のAからどれだけ離れた地点に上陸すればよいか。ただし、地点B以外で上陸した場合、上陸した後は歩いて地点Bに向かうものとし、船の速さは4km/h、人の歩く速さは5km/hとする。
この動画を見る
一直線をなす海岸の地点Aから海岸線に垂直に9km離れた沖の船にいる人が、Aから海岸にそって15km離れた地点Bに最短時間で到着するためには、AB間のAからどれだけ離れた地点に上陸すればよいか。ただし、地点B以外で上陸した場合、上陸した後は歩いて地点Bに向かうものとし、船の速さは4km/h、人の歩く速さは5km/hとする。
【数Ⅲ】【微分とその応用】関数の最大と最小10 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
半径rの球に外接する直円錐について
(1) 体積の最小値を求めよ
(2) 表面積の最小値を求めよ
この動画を見る
半径rの球に外接する直円錐について
(1) 体積の最小値を求めよ
(2) 表面積の最小値を求めよ
【数Ⅲ】【微分とその応用】関数の最大と最小9 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
定点A(a,b)を通る傾きが負の直線と、x軸およびy軸とが作る三角形の面積Sの最小値を求めよ。ただし、a>0,b>0とする。
この動画を見る
定点A(a,b)を通る傾きが負の直線と、x軸およびy軸とが作る三角形の面積Sの最小値を求めよ。ただし、a>0,b>0とする。
【数Ⅲ】【微分とその応用】関数の最大と最小8 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数 $y=a(x-\sin 2x)$ $ \displaystyle(-\frac{\pi}{2} \leqq x \leqq \frac{\pi}{2})$の最大値が$\pi$であるように、定数$a$の値を定めよ。
この動画を見る
関数 $y=a(x-\sin 2x)$ $ \displaystyle(-\frac{\pi}{2} \leqq x \leqq \frac{\pi}{2})$の最大値が$\pi$であるように、定数$a$の値を定めよ。
【数Ⅲ】【微分とその応用】関数の最大と最小7 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の最大値、最小値を求めよ。
(1) $ \displaystyle y= \frac{x-1}{x^2+1}$
(2) $y=x- \sqrt{x^2-1}$
(3) $y= \sqrt{x^2+1}+ \sqrt{(x-3)^2+4}$
(4) $y=|x|e^x$
この動画を見る
次の関数の最大値、最小値を求めよ。
(1) $ \displaystyle y= \frac{x-1}{x^2+1}$
(2) $y=x- \sqrt{x^2-1}$
(3) $y= \sqrt{x^2+1}+ \sqrt{(x-3)^2+4}$
(4) $y=|x|e^x$
【数Ⅲ】【微分とその応用】関数の最大と最小6 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数 $f(x)=x+ \dfrac{a}{x-1}$の極大値が$-1$となるように、定数$a$の値を定めよ。ただし、$a \neq 0$とする。
この動画を見る
関数 $f(x)=x+ \dfrac{a}{x-1}$の極大値が$-1$となるように、定数$a$の値を定めよ。ただし、$a \neq 0$とする。
【数Ⅲ】【微分とその応用】関数の最大と最小5 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1) 関数 $y=xe^{-x^2+x}$の極値を求めよ。
(2) $2$次関数 $f(x)=ax^2+bx+c$に対して、$F(x)=xe^{f(x)}$で定義された関数$y=F(x)$が極値を持つための、定数$a,b,c$についての必要十分条件を求めよ。
この動画を見る
(1) 関数 $y=xe^{-x^2+x}$の極値を求めよ。
(2) $2$次関数 $f(x)=ax^2+bx+c$に対して、$F(x)=xe^{f(x)}$で定義された関数$y=F(x)$が極値を持つための、定数$a,b,c$についての必要十分条件を求めよ。
【数Ⅲ】【微分とその応用】関数の最大と最小4 ※問題文は概要欄

単元:
#微分とその応用#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数 $ \displaystyle f(x)= \frac{ax^2+bx+1}{x^2+1}$ が $x=2$で極小値$-1$をとるように、定数$a,b$の値を定めよ。また、$f(x)$の極大値を求めよ。
この動画を見る
関数 $ \displaystyle f(x)= \frac{ax^2+bx+1}{x^2+1}$ が $x=2$で極小値$-1$をとるように、定数$a,b$の値を定めよ。また、$f(x)$の極大値を求めよ。
【数Ⅲ】【微分とその応用】関数の最大と最小3 ※問題文は概要欄

単元:
#微分とその応用#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数 $ \displaystyle f(x)= \frac{x-a}{x^2+x+1}$ が $x=-1$で極値をとるように、定数$a$の値を定めよ。
この動画を見る
関数 $ \displaystyle f(x)= \frac{x-a}{x^2+x+1}$ が $x=-1$で極値をとるように、定数$a$の値を定めよ。
【数Ⅲ】【微分とその応用】関数の最大と最小2 ※問題文は概要欄

単元:
#微分とその応用#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の極値を求めよ。
(1) $ \displaystyle y= \frac{(1-x)^3}{1-2x}$
(2) $ \displaystyle y= \frac{\sin x}{1- \cos x}$ $(0 \lt x \lt 2 \pi)$
(3) $ y=x^3e^{-3x}$
この動画を見る
次の関数の極値を求めよ。
(1) $ \displaystyle y= \frac{(1-x)^3}{1-2x}$
(2) $ \displaystyle y= \frac{\sin x}{1- \cos x}$ $(0 \lt x \lt 2 \pi)$
(3) $ y=x^3e^{-3x}$
【数Ⅲ】【微分とその応用】関数の最大と最小1 ※問題文は概要欄

単元:
#微分とその応用#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数 $ \displaystyle y=( \frac{1}{x})^{ \frac{1}{x}}$ $(x \gt e)$の増減を調べよ。
この動画を見る
関数 $ \displaystyle y=( \frac{1}{x})^{ \frac{1}{x}}$ $(x \gt e)$の増減を調べよ。
【数Ⅲ】【微分とその応用】平均値の定理の利用4 ※問題文は概要欄

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
平均値の定理を用いて、次の極限を求めよ。
(1) lim[x→+0](e^x-e^(tanx))/(x-tanx)
(2) lim[x→ 0](e^x-e^(sinx))/(x-sinx)
(3) lim[x→∞]x{log(x+2)-logx}
この動画を見る
平均値の定理を用いて、次の極限を求めよ。
(1) lim[x→+0](e^x-e^(tanx))/(x-tanx)
(2) lim[x→ 0](e^x-e^(sinx))/(x-sinx)
(3) lim[x→∞]x{log(x+2)-logx}
【数Ⅲ】【微分とその応用】平均値の定理の利用3 ※問題文は概要欄

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
k、αは定数、関数f(x)は微分可能であるとする。
lim[x→∞]f'(x)=αのとき、lim[x→∞]{f(x+k)-f(x)}を求めよ。
この動画を見る
k、αは定数、関数f(x)は微分可能であるとする。
lim[x→∞]f'(x)=αのとき、lim[x→∞]{f(x+k)-f(x)}を求めよ。
【数Ⅲ】【微分とその応用】平均値の定理の利用2 ※問題文は概要欄

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
平均値の定理を用いて、次のことが成り立つことを証明せよ。
(1) 1/e²<a<b<1のとき、a-b<blogb-aloga<b-a
(2) |sinα-sinβ|≦|αーβ|
この動画を見る
平均値の定理を用いて、次のことが成り立つことを証明せよ。
(1) 1/e²<a<b<1のとき、a-b<blogb-aloga<b-a
(2) |sinα-sinβ|≦|αーβ|
