 平面上の曲線
平面上の曲線
 平面上の曲線
平面上の曲線
福田のわかった数学〜高校3年生理系058〜微分(3)媒介変数表示の微分

単元:
#平面上の曲線#微分とその応用#色々な関数の導関数#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数列$\textrm{III}$ 微分(3) 媒介変数表示
$x=a(\theta-\sin\theta), y=a(1-\cos\theta)$のとき、$\frac{dy}{dx},\frac{d^2y}{dx^2}$を$\theta$で表せ。
この動画を見る
数列$\textrm{III}$ 微分(3) 媒介変数表示
$x=a(\theta-\sin\theta), y=a(1-\cos\theta)$のとき、$\frac{dy}{dx},\frac{d^2y}{dx^2}$を$\theta$で表せ。
【数Ⅲ】式と曲線:楕円の基礎

福田のわかった数学〜高校2年生042〜軌跡(9)媒介変数表示の軌跡(2)

単元:
#数Ⅱ#平面上の曲線#図形と方程式#軌跡と領域#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 軌跡(9) 媒介変数表示(2)
tが実数値をとって変化するとき、
$x=\frac{t^2-1}{t^2+1} y=\frac{2t}{t^2+1}$
はどんな曲線を表すか。
この動画を見る
数学$\textrm{II}$ 軌跡(9) 媒介変数表示(2)
tが実数値をとって変化するとき、
$x=\frac{t^2-1}{t^2+1} y=\frac{2t}{t^2+1}$
はどんな曲線を表すか。
福田のわかった数学〜高校2年生041〜軌跡(8)媒介変数表示の軌跡(1)

単元:
#数Ⅱ#平面上の曲線#図形と方程式#軌跡と領域#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 軌跡(8) 媒介変数表示(1)
$\left\{\begin{array}{1}
x=2\cos\theta+\sin\theta\\
y=\cos\theta-2\sin\theta
\end{array}\right.
(0 \leqq \theta \leqq \pi)$
を満たす$(x,y)$の軌跡を図示せよ。
また、$0 \leqq \theta \leqq \frac{3}{2}\pi$のときはどうか。
この動画を見る
数学$\textrm{II}$ 軌跡(8) 媒介変数表示(1)
$\left\{\begin{array}{1}
x=2\cos\theta+\sin\theta\\
y=\cos\theta-2\sin\theta
\end{array}\right.
(0 \leqq \theta \leqq \pi)$
を満たす$(x,y)$の軌跡を図示せよ。
また、$0 \leqq \theta \leqq \frac{3}{2}\pi$のときはどうか。
高専数学 微積I #258 媒介変数表示曲線の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$1 \leqq t \leqq 2$である.
曲線$x=t+\dfrac{1}{t},y=t-\dfrac{1}{t}$と
$x$軸,直線$x=\dfrac{5}{2}$で
囲まれた図形の面積$S$を求めよ.
この動画を見る
$1 \leqq t \leqq 2$である.
曲線$x=t+\dfrac{1}{t},y=t-\dfrac{1}{t}$と
$x$軸,直線$x=\dfrac{5}{2}$で
囲まれた図形の面積$S$を求めよ.
高専数学 微積I #248(2) 極座標表示曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq \theta \leqq 4\pi$である.
極座標による曲線$r=\sin^4\dfrac{\theta}{4}$
の長さを求めよ.
この動画を見る
$0\leqq \theta \leqq 4\pi$である.
極座標による曲線$r=\sin^4\dfrac{\theta}{4}$
の長さを求めよ.
高専数学 微積I #243(2) 媒介変数表示関数のx軸回転体

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq t \leqq 1$である.
曲線$x=t^2,y=e^t$
$x$軸,$y$軸,直線$x=1$で囲まれた図形を
$x$軸を中心とした回転体の体積$V$を求めよ.
この動画を見る
$0 \leqq t \leqq 1$である.
曲線$x=t^2,y=e^t$
$x$軸,$y$軸,直線$x=1$で囲まれた図形を
$x$軸を中心とした回転体の体積$V$を求めよ.
高専数学 微積I #243(1) 媒介変数曲線(x軸回転体)

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$-1\leqq t\leqq 1$である.
曲線$x=t^3,y=t^2-1$と$x$軸で囲まれた
図形を$x$軸中心に回転した体積$V$を求めよ.
この動画を見る
$-1\leqq t\leqq 1$である.
曲線$x=t^3,y=t^2-1$と$x$軸で囲まれた
図形を$x$軸中心に回転した体積$V$を求めよ.
福田の数学〜慶應義塾大学2021年医学部第3問〜見上げる角が等しい点の軌跡と2次曲線

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#図形と方程式#軌跡と領域#2次曲線#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$
水平な平面上の異なる2点${\rm A(0,1),Q}(x,y)$にそれぞれ高さ$h \gt 0,g \gt 0$の塔が平面に垂直に立っている。この平面上にあって$\rm A,Q$とは異なる点$\rm P$から2つの塔の先端を見上げる角度が等しくなる状況を考える。ただし、$h \neq g$とする。
(1)点$\rm Q$の座標が$ (t,1)$ (ただし$t \gt 0$)のとき、2つの塔を見上げる角度が等しくなるような点$\rm P$は、中心の座標が($\boxed{\ \ (あ)\ \ },\boxed{\ \ (い)\ \ }$)、半径が$\boxed{\ \ (う)\ \ }$の円周上にある。
(2)2つの塔を見上げる角度が等しくなるような点$\rm P$のうち、$y$軸上にあるものがただ1つあるとする。このとき$h$と$g$の間には不等式$\boxed{\ \ (え)\ \ }$が成り立ち、点$\textrm{Q}(x,y)$は2直線$y=\boxed{\ \ (お)\ \ }$, $y=\boxed{\ \ (か)\ \ }$のいずれかの上にある。
(3)2つの塔を見上げる角度が等しくなるような点$\rm P$のうち、$x$軸上にあるものがただ1つであるとする。このとき点$\textrm{Q}(x,y)$は方程式
$\boxed{\ \ (き)\ \ }x^2+\boxed{\ \ (く)\ \ }x+$$\boxed{\ \ (け)\ \ }y^2+$$\boxed{\ \ (こ)\ \ }y=1$
で表される2次曲線$C$の上にある。$C$が楕円であるのは$h$と$g$の間に不等式$\boxed{\ \ (さ)\ \ }$が成り立つときであり、そのとき$C$の2つの焦点の座標は$(\boxed{\ \ (し)\ \ },\boxed{\ \ (す)\ \ })$,$(\boxed{\ \ (せ)\ \ },\boxed{\ \ (そ)\ \ })$である。$\boxed{\ \ (さ)\ \ }$が成り立たないとき$C$は双曲線となり、その2つの焦点の座標は$(\boxed{\ \ (た)\ \ },\boxed{\ \ (ち)\ \ })$,$(\boxed{\ \ (つ)\ \ },\boxed{\ \ (て)\ \ })$である。さらに$\dfrac{h}{g}=\boxed{\ \ (と)\ \ }$のとき$C$は直角双曲線となる。
2021慶應義塾大学医学部過去問
この動画を見る
${\Large\boxed{3}}$
水平な平面上の異なる2点${\rm A(0,1),Q}(x,y)$にそれぞれ高さ$h \gt 0,g \gt 0$の塔が平面に垂直に立っている。この平面上にあって$\rm A,Q$とは異なる点$\rm P$から2つの塔の先端を見上げる角度が等しくなる状況を考える。ただし、$h \neq g$とする。
(1)点$\rm Q$の座標が$ (t,1)$ (ただし$t \gt 0$)のとき、2つの塔を見上げる角度が等しくなるような点$\rm P$は、中心の座標が($\boxed{\ \ (あ)\ \ },\boxed{\ \ (い)\ \ }$)、半径が$\boxed{\ \ (う)\ \ }$の円周上にある。
(2)2つの塔を見上げる角度が等しくなるような点$\rm P$のうち、$y$軸上にあるものがただ1つあるとする。このとき$h$と$g$の間には不等式$\boxed{\ \ (え)\ \ }$が成り立ち、点$\textrm{Q}(x,y)$は2直線$y=\boxed{\ \ (お)\ \ }$, $y=\boxed{\ \ (か)\ \ }$のいずれかの上にある。
(3)2つの塔を見上げる角度が等しくなるような点$\rm P$のうち、$x$軸上にあるものがただ1つであるとする。このとき点$\textrm{Q}(x,y)$は方程式
$\boxed{\ \ (き)\ \ }x^2+\boxed{\ \ (く)\ \ }x+$$\boxed{\ \ (け)\ \ }y^2+$$\boxed{\ \ (こ)\ \ }y=1$
で表される2次曲線$C$の上にある。$C$が楕円であるのは$h$と$g$の間に不等式$\boxed{\ \ (さ)\ \ }$が成り立つときであり、そのとき$C$の2つの焦点の座標は$(\boxed{\ \ (し)\ \ },\boxed{\ \ (す)\ \ })$,$(\boxed{\ \ (せ)\ \ },\boxed{\ \ (そ)\ \ })$である。$\boxed{\ \ (さ)\ \ }$が成り立たないとき$C$は双曲線となり、その2つの焦点の座標は$(\boxed{\ \ (た)\ \ },\boxed{\ \ (ち)\ \ })$,$(\boxed{\ \ (つ)\ \ },\boxed{\ \ (て)\ \ })$である。さらに$\dfrac{h}{g}=\boxed{\ \ (と)\ \ }$のとき$C$は直角双曲線となる。
2021慶應義塾大学医学部過去問
高専数学 微積I #242(2) 媒介変数表示曲線の長さ
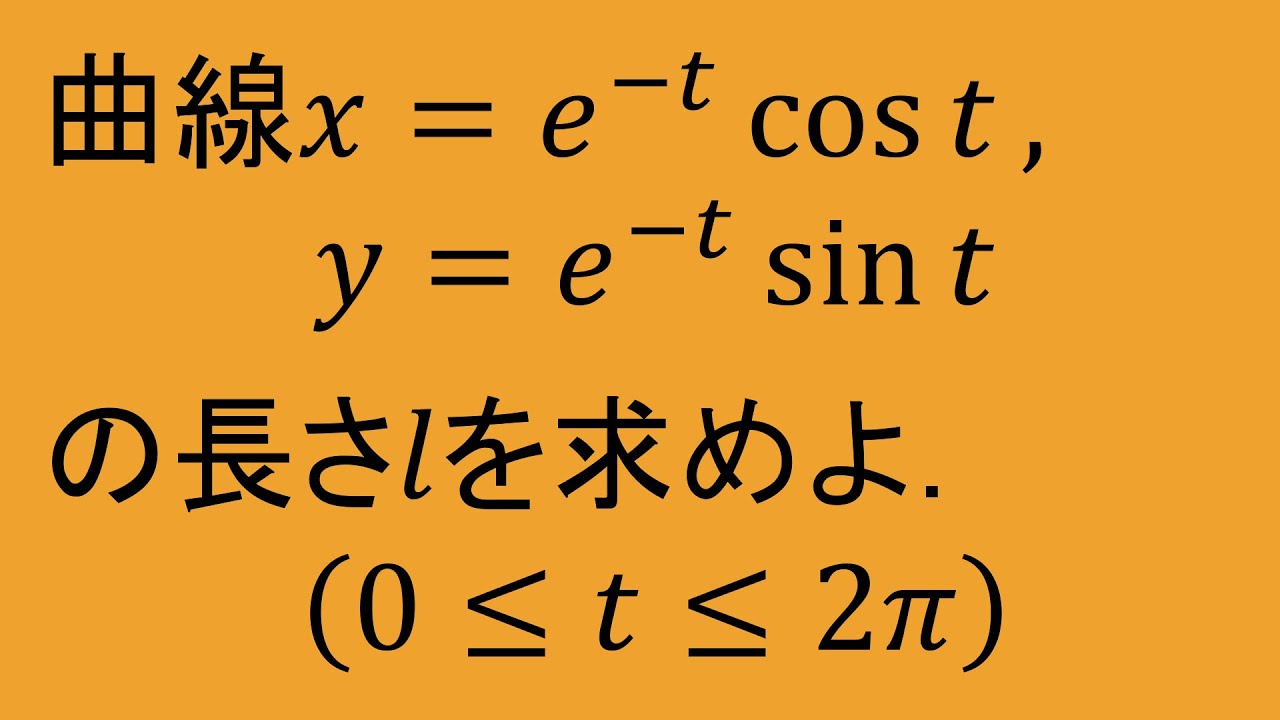
単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq 2\pi$とする.
曲線$x=e^{-t}\cos t,y=e^{-t}\sin t$
の長さ$\ell$を求めよ.
この動画を見る
$0\leqq t\leqq 2\pi$とする.
曲線$x=e^{-t}\cos t,y=e^{-t}\sin t$
の長さ$\ell$を求めよ.
高専数学 微積I #242(1) 媒介変数表示曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
曲線$x=t^3,y=3t^2(0\leqq t\leqq 1)$の
長さ$\ell$を求めよ.
この動画を見る
曲線$x=t^3,y=3t^2(0\leqq t\leqq 1)$の
長さ$\ell$を求めよ.
福田の数学〜早稲田大学2021年人間科学部第7問〜双曲線と図形問題

単元:
#数Ⅰ#大学入試過去問(数学)#平面上の曲線#図形と計量#2次曲線#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{7}}$ 原点を$O$とする座標平面上で、2点$(\sqrt5,0),$$(-\sqrt5,0)$を焦点とし、2点$A(1,0),$$A'(-1,0)$を頂点とする双曲線を$H$とする。$H$の方程式を$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$と表すとき、$a^2=\boxed{\ \ ネ\ \ },$ $b^2=\boxed{\ \ ノ\ \ }$である。双曲線Hの漸近線のうち、傾きが正であるものの方程式は$y=\boxed{\ \ ハ\ \ }x$である。$点P(p,q)$は双曲線$H$の$第1象限$の部分を動く点とする。$点P$から$x軸$に下ろした垂線の足を$Q$、$直線PQ$と$双曲線H$の漸近線との交点のうち、$第1象限$にあるものを$R$とする。$点P$における$H$の接線と$直線x=1$との交点を$M$とし、$直線OM$と$直線AP$との交点を$N$とする。$三角形OQR$の面積を$S$、$三角形OAN$の面積を$T$とするとき、$\frac{T}{S}$は、$p=\boxed{\ \ ヒ\ \ }$のとき、最大値$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}$をとる。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{7}}$ 原点を$O$とする座標平面上で、2点$(\sqrt5,0),$$(-\sqrt5,0)$を焦点とし、2点$A(1,0),$$A'(-1,0)$を頂点とする双曲線を$H$とする。$H$の方程式を$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$と表すとき、$a^2=\boxed{\ \ ネ\ \ },$ $b^2=\boxed{\ \ ノ\ \ }$である。双曲線Hの漸近線のうち、傾きが正であるものの方程式は$y=\boxed{\ \ ハ\ \ }x$である。$点P(p,q)$は双曲線$H$の$第1象限$の部分を動く点とする。$点P$から$x軸$に下ろした垂線の足を$Q$、$直線PQ$と$双曲線H$の漸近線との交点のうち、$第1象限$にあるものを$R$とする。$点P$における$H$の接線と$直線x=1$との交点を$M$とし、$直線OM$と$直線AP$との交点を$N$とする。$三角形OQR$の面積を$S$、$三角形OAN$の面積を$T$とするとき、$\frac{T}{S}$は、$p=\boxed{\ \ ヒ\ \ }$のとき、最大値$\frac{\boxed{\ \ フ\ \ }}{\boxed{\ \ ヘ\ \ }}$をとる。
2021早稲田大学人間科学部過去問
高専数学 微積I #234(1)(2) 極座標表示の曲線の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
(1)曲線$r=\theta^2\left(0\leqq \theta \leqq \dfrac{\theta}{2}\right)$と
半直線$\theta=\dfrac{\theta}{2}$で囲まれた図形の面積を求めよ.
(2)曲線$r=\cos\theta+2(0\leqq \theta \leqq 2\pi)$で囲まれた
図形の面積を求めよ.
この動画を見る
(1)曲線$r=\theta^2\left(0\leqq \theta \leqq \dfrac{\theta}{2}\right)$と
半直線$\theta=\dfrac{\theta}{2}$で囲まれた図形の面積を求めよ.
(2)曲線$r=\cos\theta+2(0\leqq \theta \leqq 2\pi)$で囲まれた
図形の面積を求めよ.
高専数学 微積I #229(2) 媒介変数表示関数のx軸回転体の体積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \dfrac{\pi}{2}$である.
$x=\sin t$
$y=\sin 2t$
と$x$軸で囲まれた図形を$x$軸のまわりに回転して
できる回転体の体積$V$を求めよ.
この動画を見る
$0\leqq t\leqq \dfrac{\pi}{2}$である.
$x=\sin t$
$y=\sin 2t$
と$x$軸で囲まれた図形を$x$軸のまわりに回転して
できる回転体の体積$V$を求めよ.
高専数学 微積I #229(1) 媒介変数表示関数のx軸回転体の体積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq 1$とする.
$x=\sqrt t$
$y=\sqrt t-t$
と$x$軸で囲まれた図形を
$x$軸のまわりに回転してできる回転体の
体積$V$を求めよ.
この動画を見る
$0\leqq t\leqq 1$とする.
$x=\sqrt t$
$y=\sqrt t-t$
と$x$軸で囲まれた図形を
$x$軸のまわりに回転してできる回転体の
体積$V$を求めよ.
高専数学 微積I #227(3) 媒介変数表示関数の曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \pi$とする.
$x=\cos t+ \cos 2t$
$y=2\sin t- \sin 2t$
の曲線の長さ$L$を求めよ.
この動画を見る
$0\leqq t\leqq \pi$とする.
$x=\cos t+ \cos 2t$
$y=2\sin t- \sin 2t$
の曲線の長さ$L$を求めよ.
高専数学 微積I #227(2) 媒介変数表示関数の曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \pi$とする.
$x=\cos t+t \sin t$
$y=\sin t-t \cos t$
の曲線の長さ$L$を求めよ.
この動画を見る
$0\leqq t\leqq \pi$とする.
$x=\cos t+t \sin t$
$y=\sin t-t \cos t$
の曲線の長さ$L$を求めよ.
高専数学 微積I #227(1) 媒介変数表示の曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t \leqq \sqrt3$である.
$x=3t^2,y=3t-t^3$の曲線の長さ$L$を求めよ.
この動画を見る
$0\leqq t \leqq \sqrt3$である.
$x=3t^2,y=3t-t^3$の曲線の長さ$L$を求めよ.
高専数学 微積I #226(3) 媒介変数表示の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \dfrac{\pi}{2}$
曲線$x=\cos t,\cos 2t+1$
$x$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
この動画を見る
$0\leqq t\leqq \dfrac{\pi}{2}$
曲線$x=\cos t,\cos 2t+1$
$x$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
高専数学 微積I #226(2) 媒介変数表示の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \dfrac{\pi}{4}$とする.
曲線$x=\tan t,y=\sin t+1$と
$x$軸,$y$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
この動画を見る
$0\leqq t\leqq \dfrac{\pi}{4}$とする.
曲線$x=\tan t,y=\sin t+1$と
$x$軸,$y$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
高専数学 微積I #226(1) 媒介変数表示の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq 1$とする.
曲線$x=t^2,y=t^2-2t+1$
$x$軸,$y$軸で囲まれた図形の
面積$S$を求めよ.
この動画を見る
$0\leqq t\leqq 1$とする.
曲線$x=t^2,y=t^2-2t+1$
$x$軸,$y$軸で囲まれた図形の
面積$S$を求めよ.
高専数学 微積I #210(2) 曲線の長さ
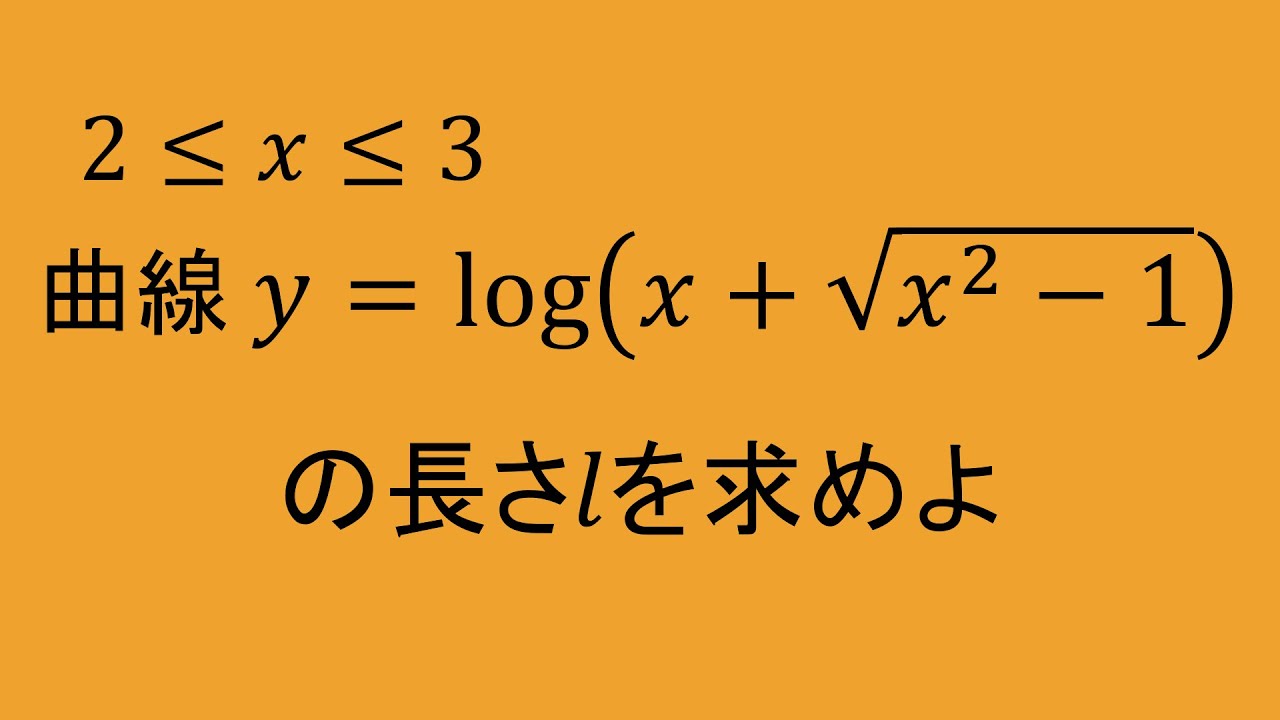
単元:
#数Ⅱ#平面上の曲線#微分法と積分法#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$2\leqq x\leqq 3$
曲線$y=\log (x+\sqrt{x^2-1})$の長さ$\ell$を求めよ.
この動画を見る
$2\leqq x\leqq 3$
曲線$y=\log (x+\sqrt{x^2-1})$の長さ$\ell$を求めよ.
高専数学 微積I #210(1) 曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
曲線$y=(x-1)^{\frac{3}{2}} \ (1\leq x \leq 6)$
の長さ$\ell$を求めよ.
この動画を見る
曲線$y=(x-1)^{\frac{3}{2}} \ (1\leq x \leq 6)$
の長さ$\ell$を求めよ.
福田の数学〜早稲田大学2021年社会科学部第1問〜三角関数で表された点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#三角関数#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ a,bを定数とし、関数$f(x)=x^2+ax+b$ とする。方程式$f(x)=0$の2つの解$\alpha,\beta\\$
が次式で与えられている。
$\alpha=\frac{\sin\theta}{1+\cos\theta}$, $\beta=\frac{\sin\theta}{1-\cos\theta}\\$
ここで$\theta$は、$0 \lt \theta \lt \pi$の定数である。次の問いに答えよ。
$(1)a,b$を$\theta$を用いて表せ。
$(2)\theta$が$0$ $\lt \theta \pi$で変化するとき、放物線$y=f(x)$の頂点の軌跡を求めよ。
$(3)\int_0^{2\sin\theta}f(x)dx=0$ となる$\theta$の値を全て求めよ。
2021早稲田大学社会科学部過去問
この動画を見る
${\Large\boxed{1}}$ a,bを定数とし、関数$f(x)=x^2+ax+b$ とする。方程式$f(x)=0$の2つの解$\alpha,\beta\\$
が次式で与えられている。
$\alpha=\frac{\sin\theta}{1+\cos\theta}$, $\beta=\frac{\sin\theta}{1-\cos\theta}\\$
ここで$\theta$は、$0 \lt \theta \lt \pi$の定数である。次の問いに答えよ。
$(1)a,b$を$\theta$を用いて表せ。
$(2)\theta$が$0$ $\lt \theta \pi$で変化するとき、放物線$y=f(x)$の頂点の軌跡を求めよ。
$(3)\int_0^{2\sin\theta}f(x)dx=0$ となる$\theta$の値を全て求めよ。
2021早稲田大学社会科学部過去問
18岡山県教員使用試験(数学:5番 媒介変数表示のグラフ・面積)

単元:
#平面上の曲線#その他#媒介変数表示と極座標#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$ $ 0\leqq t\leqq \pi$,
$x=\cos t,y=\sin 2t+2\sin t$とする.
(1)曲線の概形
(2)曲線とx軸で囲まれた面積を求めよ.
この動画を見る
$\boxed{5}$ $ 0\leqq t\leqq \pi$,
$x=\cos t,y=\sin 2t+2\sin t$とする.
(1)曲線の概形
(2)曲線とx軸で囲まれた面積を求めよ.
15岡山県教員採用試験(数学:6番 サイクロイドの長さ)

単元:
#平面上の曲線#2次曲線#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
曲線$c$ $\begin{eqnarray}
\left\{
\begin{array}{l}
x=r(\theta-\sin\theta) \\
y-r(1-\cos\theta)
\end{array}
\right.
\end{eqnarray}$
の長さ$\ell$を求めよ.
$r\gt 0,0\leqq \theta 2\pi$とする.
この動画を見る
$\boxed{6}$
曲線$c$ $\begin{eqnarray}
\left\{
\begin{array}{l}
x=r(\theta-\sin\theta) \\
y-r(1-\cos\theta)
\end{array}
\right.
\end{eqnarray}$
の長さ$\ell$を求めよ.
$r\gt 0,0\leqq \theta 2\pi$とする.
二次曲線:東京~全国入試問題解法

単元:
#平面上の曲線#2次曲線#数学(高校生)#数C
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京
【別解付き!】
$x^2-xy+y^2=3$
の囲む面積を求めよ。
この動画を見る
入試問題 東京
【別解付き!】
$x^2-xy+y^2=3$
の囲む面積を求めよ。
05愛知県教員採用試験(数学:9番 曲線の長さ)

単元:
#平面上の曲線#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{9}$ $x=2\cos^3t,y=2\sin^3t(0\leqq t\leqq 2\pi)$
で表される曲線の長さ$\ell$を求めよ.
この動画を見る
$\boxed{9}$ $x=2\cos^3t,y=2\sin^3t(0\leqq t\leqq 2\pi)$
で表される曲線の長さ$\ell$を求めよ.
数検準1級1次過去問【2020年12月】5番:極方程式

単元:
#数学検定・数学甲子園・数学オリンピック等#平面上の曲線#媒介変数表示と極座標#数学検定#数学検定準1級#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
5⃣ 極方程式
r=4sinθ+6cosθ
で表される図形を求めよ。
この動画を見る
5⃣ 極方程式
r=4sinθ+6cosθ
で表される図形を求めよ。
数検準1級1次過去問(6番 楕円)

単元:
#数学検定・数学甲子園・数学オリンピック等#平面上の曲線#2次曲線#数学検定#数学検定準1級#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
6⃣
楕円$x^2-4x+2y^2+12y+14=0$
の焦点の座標を求めよ。
この動画を見る
6⃣
楕円$x^2-4x+2y^2+12y+14=0$
の焦点の座標を求めよ。
