 数C
数C
 数C
数C
虚数の3乗根 島根大
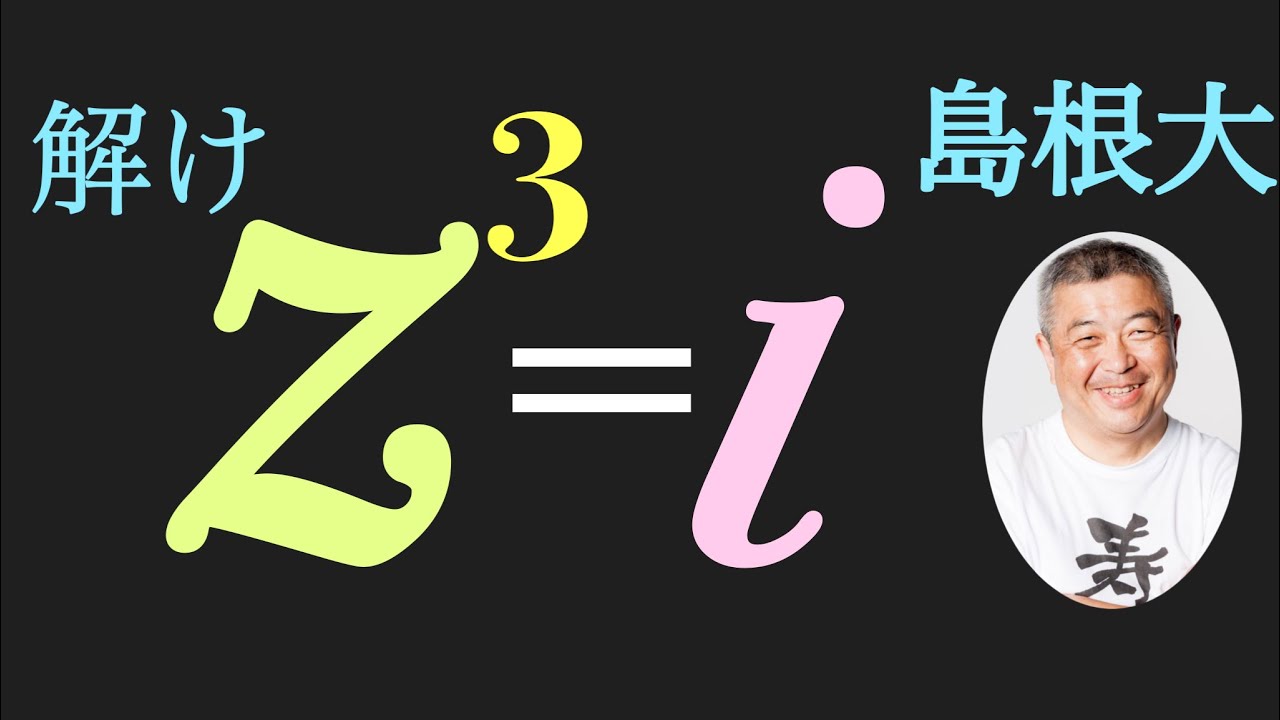
単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z^3=i$
島根大過去問
この動画を見る
$z^3=i$
島根大過去問
福田の数学〜相反方程式の扱い方を知っていますか〜明治大学2023年理工学部第1問(2)〜相反方程式

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (2)(a)$t$を実数とする。$x$についての方程式$x$+$\frac{1}{x}$=$t$ が実数解をもつための必要十分条件は$t$≦$-\boxed{\ \ カ\ \ }$または$t$≧$\boxed{\ \ キ\ \ }$ である。
(b)$k$を実数と定数とし、$f(x)$=$7x^4$+$2x^3$+$kx^2$+$2x$+7 とする。
$x$=$a$が$f(x)$=0 の解であるとき、$t$=$a$+$\frac{1}{a}$ とおくと
$\boxed{\ \ ク\ \ }t^2$+$\boxed{\ \ ケ\ \ }t$+$(k-\boxed{\ \ コサ\ \ })$=0
が成り立つ。方程式$f(x)$=0 の異なる実数解の個数が3個となるような$k$の値は$k$=$-\boxed{\ \ シス\ \ }$ である。
この動画を見る
$\Large{\boxed{1}}$ (2)(a)$t$を実数とする。$x$についての方程式$x$+$\frac{1}{x}$=$t$ が実数解をもつための必要十分条件は$t$≦$-\boxed{\ \ カ\ \ }$または$t$≧$\boxed{\ \ キ\ \ }$ である。
(b)$k$を実数と定数とし、$f(x)$=$7x^4$+$2x^3$+$kx^2$+$2x$+7 とする。
$x$=$a$が$f(x)$=0 の解であるとき、$t$=$a$+$\frac{1}{a}$ とおくと
$\boxed{\ \ ク\ \ }t^2$+$\boxed{\ \ ケ\ \ }t$+$(k-\boxed{\ \ コサ\ \ })$=0
が成り立つ。方程式$f(x)$=0 の異なる実数解の個数が3個となるような$k$の値は$k$=$-\boxed{\ \ シス\ \ }$ である。
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
ここに補助線!! 関数だけど図形で解く!!東京学芸大学附属
10次方程式の解

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\frac{x^{11}-1}{x-1}=0$の解の1つをαとする.
$(1-α)(1-α^2)(1-α^3)\cdots(1-α^{10})$の値を求めよ.
この動画を見る
$\frac{x^{11}-1}{x-1}=0$の解の1つをαとする.
$(1-α)(1-α^2)(1-α^3)\cdots(1-α^{10})$の値を求めよ.
福島大 複素数の基本問題

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$
\begin{eqnarray}
&&2023福島大\\
&&Z=1+\sqrt{3}iの時\\
&&1+Z+Z^2+Z^3+Z^4+Z^5
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&2023福島大\\
&&Z=1+\sqrt{3}iの時\\
&&1+Z+Z^2+Z^3+Z^4+Z^5
\end{eqnarray}
$
大学入試問題#625「根性がためされている」 横浜市立大学医学部(2005) #複素数

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$Z$:複素数
$Z^6+Z^3+1=0$のとき、
$|Z+\displaystyle \frac{1+i}{\sqrt{ 2 }}|^2+|Z-\displaystyle \frac{1+i}{\sqrt{ 2 }}|^2$の値を求めよ
出典:2005年横浜市立大学 入試問題
この動画を見る
$Z$:複素数
$Z^6+Z^3+1=0$のとき、
$|Z+\displaystyle \frac{1+i}{\sqrt{ 2 }}|^2+|Z-\displaystyle \frac{1+i}{\sqrt{ 2 }}|^2$の値を求めよ
出典:2005年横浜市立大学 入試問題
福田の数学〜早稲田大学2023年教育学部第1問(3)〜連立漸化式と複素数平面

単元:
#大学入試過去問(数学)#複素数平面#数列#漸化式#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
$x_0=0,y_0=-1$のとき、非負整数$n\geqq 0$に対して、
$x_{n+1}=(\cos \frac{3\pi}{11})x_n-(\sin \frac{3\pi}{11)}y_n$
$y_{n+1}=(\cos \frac{3\pi}{11})x_n+(\sin \frac{3\pi}{11)}y_n$
のとき、$x_n$が最小となる最初のnを求めよ。
2023早稲田大学教育学部過去問
この動画を見る
$x_0=0,y_0=-1$のとき、非負整数$n\geqq 0$に対して、
$x_{n+1}=(\cos \frac{3\pi}{11})x_n-(\sin \frac{3\pi}{11)}y_n$
$y_{n+1}=(\cos \frac{3\pi}{11})x_n+(\sin \frac{3\pi}{11)}y_n$
のとき、$x_n$が最小となる最初のnを求めよ。
2023早稲田大学教育学部過去問
山口大 1の十乗根の問題

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$
\begin{eqnarray}
&&2023山口大\\
&&2Z^4+(1-\sqrt{5})Z^2+2=0\\
&&①Z^{10}=1 を示せ\\
&&②Z+Z^3+Z^5+Z^7+Z^9の値\\
&&③\cos\frac{\pi}{5}\cos\frac{2\pi}{5} = \frac{1}{4}を示せ
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&2023山口大\\
&&2Z^4+(1-\sqrt{5})Z^2+2=0\\
&&①Z^{10}=1 を示せ\\
&&②Z+Z^3+Z^5+Z^7+Z^9の値\\
&&③\cos\frac{\pi}{5}\cos\frac{2\pi}{5} = \frac{1}{4}を示せ
\end{eqnarray}
$
横浜市立(医・理)

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023横浜市立(医・理)
$
\\
Z^4=Z^2-1をみたす\\
Z^{40}+2Z^{10}+\frac{1}{Z^{20}}
$
この動画を見る
2023横浜市立(医・理)
$
\\
Z^4=Z^2-1をみたす\\
Z^{40}+2Z^{10}+\frac{1}{Z^{20}}
$
福田の数学〜中央大学2023年理工学部第1問〜複素数平面と確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#複素数平面#確率#複素数平面#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ さいころを2回ふって出た目の数を順に$a$, $b$とし、複素数$\alpha$, $\beta$を
$\alpha$=$\displaystyle\cos\frac{a\pi}{3}$+$\displaystyle i\sin\frac{a\pi}{3}$, $\beta$=$\displaystyle\cos\frac{b\pi}{3}$+$\displaystyle i\sin\frac{b\pi}{3}$
と定める($i$は虚数単位)。また、$\alpha$-$\beta$の絶対値を$d$=|$\alpha$-$\beta$|とおく。
(1)$d$のとりうる値は、小さいものから順に0, $\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$, $\boxed{\ \ ウ\ \ }$である。
$d$=0, $\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$, $\boxed{\ \ ウ\ \ }$が成り立つ確率はそれぞれ$\boxed{\ \ エ\ \ }$, $\boxed{\ \ オ\ \ }$, $\boxed{\ \ カ\ \ }$, $\boxed{\ \ キ\ \ }$である。
(2)$\alpha$-$\beta$が実数となる確率は$\boxed{\ \ ク\ \ }$であり、$\alpha$-$\beta$が実数という条件の下で$d$<$\boxed{\ \ ウ\ \ }$が成り立つ条件付き確率は$\boxed{\ \ ケ\ \ }$である。
(3)$\alpha^2$=$\beta^3$という条件の下で$\alpha+\beta$の虚部が正となる条件付き確率は$\boxed{\ \ コ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ さいころを2回ふって出た目の数を順に$a$, $b$とし、複素数$\alpha$, $\beta$を
$\alpha$=$\displaystyle\cos\frac{a\pi}{3}$+$\displaystyle i\sin\frac{a\pi}{3}$, $\beta$=$\displaystyle\cos\frac{b\pi}{3}$+$\displaystyle i\sin\frac{b\pi}{3}$
と定める($i$は虚数単位)。また、$\alpha$-$\beta$の絶対値を$d$=|$\alpha$-$\beta$|とおく。
(1)$d$のとりうる値は、小さいものから順に0, $\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$, $\boxed{\ \ ウ\ \ }$である。
$d$=0, $\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$, $\boxed{\ \ ウ\ \ }$が成り立つ確率はそれぞれ$\boxed{\ \ エ\ \ }$, $\boxed{\ \ オ\ \ }$, $\boxed{\ \ カ\ \ }$, $\boxed{\ \ キ\ \ }$である。
(2)$\alpha$-$\beta$が実数となる確率は$\boxed{\ \ ク\ \ }$であり、$\alpha$-$\beta$が実数という条件の下で$d$<$\boxed{\ \ ウ\ \ }$が成り立つ条件付き確率は$\boxed{\ \ ケ\ \ }$である。
(3)$\alpha^2$=$\beta^3$という条件の下で$\alpha+\beta$の虚部が正となる条件付き確率は$\boxed{\ \ コ\ \ }$である。
福田の数学〜中央大学2023年経済学部第1問(5)〜平面ベクトルの成分と絶対値

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#平面上のベクトル#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\vec{a}+\vec{b}=(3,4),\vec{a}-\vec{b}=(1,2)$
のとき
$|2\vec{a}-3\vec{b}|$
の値を求めよ。
2023中央大学経済学部過去問
この動画を見る
$\vec{a}+\vec{b}=(3,4),\vec{a}-\vec{b}=(1,2)$
のとき
$|2\vec{a}-3\vec{b}|$
の値を求めよ。
2023中央大学経済学部過去問
福田の数学〜上智大学2023年理工学部第1問(1)〜複素数平面と確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#複素数平面#確率#複素数平面#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (1)次の6つの複素数が1つずつ書かれた6枚のカードがある。
$\frac{1}{2}$, 1, 2, $\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}$, $\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}$, $\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}$
これらから無作為に3枚選び、カードに書かれた3つの複素数を掛けた値に対応する複素数平面上の点をPとする。
(i)点Pが虚軸上にある確率は$\displaystyle\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$である。
(ii)点Pの原点からの距離が1である確率は$\displaystyle\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。
この動画を見る
$\Large{\boxed{1}}$ (1)次の6つの複素数が1つずつ書かれた6枚のカードがある。
$\frac{1}{2}$, 1, 2, $\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}$, $\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}$, $\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}$
これらから無作為に3枚選び、カードに書かれた3つの複素数を掛けた値に対応する複素数平面上の点をPとする。
(i)点Pが虚軸上にある確率は$\displaystyle\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$である。
(ii)点Pの原点からの距離が1である確率は$\displaystyle\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。
福田の数学〜上智大学2023年TEAP利用型理系第2問〜立方体の切断と位置ベクトル

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#立体図形#立体切断#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 一辺の長さが2である立方体OADB-CFGEを考える。
$\overrightarrow{OA}$=$\overrightarrow{a}$, $\overrightarrow{OB}$=$\overrightarrow{b}$, $\overrightarrow{OC}$=$\overrightarrow{c}$とおく。辺AFの中点をM、辺BDの中点をNとし、3点O,M,Nを通る平面$\pi$で立方体を切断する。
(1)平面$\pi$は辺AF,BD以外に辺$\boxed{\ \ あ\ \ }$とその両端以外で交わる。
(2)平面$\pi$と辺$\boxed{\ \ あ\ \ }$との交点をPとすると$\overrightarrow{OP}$=$\boxed{\ \ い\ \ } \overrightarrow{a}$+$\boxed{\ \ う\ \ } \overrightarrow{b}$+$\boxed{\ \ え\ \ } \overrightarrow{c}$
(3)断面の面積は$\displaystyle\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}\sqrt{\boxed{\ \ ケ\ \ }}$である。
(4)切断されてできる立体のうち、頂点Aを含むものの体積は$\displaystyle\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。
(5)平面$\pi$と線分CDとの交点をQとする。
(i)点Qは線分CDを$\boxed{\ \ お\ \ }$に内分する。
(ii)$\overrightarrow{OQ}$=$\boxed{\ \ か\ \ } \overrightarrow{a}$+$\boxed{\ \ き\ \ } \overrightarrow{b}$+$\boxed{\ \ く\ \ } \overrightarrow{c}$である。
$\boxed{\ \ い\ \ }~\boxed{\ \ え\ \ }$, $\boxed{\ \ か\ \ }~\boxed{\ \ く\ \ }$の選択肢
(a)0 (b)1 (c)$\frac{1}{2}$ (d)$\frac{1}{3}$ (e)$\frac{2}{3}$ (f)$\frac{1}{4}$ (g)$\frac{3}{4}$ (h)$\frac{1}{5}$
(i)$\frac{2}{5}$ (j)$\frac{3}{5}$ (k)$\frac{4}{5}$ (l)$\frac{1}{6}$ (m)$\frac{5}{6}$
$\boxed{\ \ お\ \ }$の選択肢
(a)1:1 (b)2:1 (c)1:2 (d)3:1 (e)1:3 (f)4:1 (g)3:2
(h)2:3 (i)1:4 (j)5:1 (k)1:5
この動画を見る
$\Large{\boxed{2}}$ 一辺の長さが2である立方体OADB-CFGEを考える。
$\overrightarrow{OA}$=$\overrightarrow{a}$, $\overrightarrow{OB}$=$\overrightarrow{b}$, $\overrightarrow{OC}$=$\overrightarrow{c}$とおく。辺AFの中点をM、辺BDの中点をNとし、3点O,M,Nを通る平面$\pi$で立方体を切断する。
(1)平面$\pi$は辺AF,BD以外に辺$\boxed{\ \ あ\ \ }$とその両端以外で交わる。
(2)平面$\pi$と辺$\boxed{\ \ あ\ \ }$との交点をPとすると$\overrightarrow{OP}$=$\boxed{\ \ い\ \ } \overrightarrow{a}$+$\boxed{\ \ う\ \ } \overrightarrow{b}$+$\boxed{\ \ え\ \ } \overrightarrow{c}$
(3)断面の面積は$\displaystyle\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}\sqrt{\boxed{\ \ ケ\ \ }}$である。
(4)切断されてできる立体のうち、頂点Aを含むものの体積は$\displaystyle\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。
(5)平面$\pi$と線分CDとの交点をQとする。
(i)点Qは線分CDを$\boxed{\ \ お\ \ }$に内分する。
(ii)$\overrightarrow{OQ}$=$\boxed{\ \ か\ \ } \overrightarrow{a}$+$\boxed{\ \ き\ \ } \overrightarrow{b}$+$\boxed{\ \ く\ \ } \overrightarrow{c}$である。
$\boxed{\ \ い\ \ }~\boxed{\ \ え\ \ }$, $\boxed{\ \ か\ \ }~\boxed{\ \ く\ \ }$の選択肢
(a)0 (b)1 (c)$\frac{1}{2}$ (d)$\frac{1}{3}$ (e)$\frac{2}{3}$ (f)$\frac{1}{4}$ (g)$\frac{3}{4}$ (h)$\frac{1}{5}$
(i)$\frac{2}{5}$ (j)$\frac{3}{5}$ (k)$\frac{4}{5}$ (l)$\frac{1}{6}$ (m)$\frac{5}{6}$
$\boxed{\ \ お\ \ }$の選択肢
(a)1:1 (b)2:1 (c)1:2 (d)3:1 (e)1:3 (f)4:1 (g)3:2
(h)2:3 (i)1:4 (j)5:1 (k)1:5
福田の数学〜上智大学2023年TEAP利用型文系第2問〜空間ベクトルと正八面体

単元:
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 図のような一辺の長さが1の正八面体ABCDEFがある。
2点P,Qはそれぞれ辺AD, BC上にあり
$\overrightarrow{PQ}$$\bot$$\overrightarrow{AD}$かつ$\overrightarrow{PQ}$$\bot$$\overrightarrow{BC}$
を満たすとする。
(1)$\overrightarrow{AD}$と$\overrightarrow{BC}$のなす角は$\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$である。
(2)|$\overrightarrow{AP}$|=$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$, |$\overrightarrow{BQ}$|=$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$である。
(3)|$\overrightarrow{PQ}$|=$\frac{\boxed{\ \ テ\ \ }}{\boxed{\ \ ト\ \ }}\sqrt{\boxed{\ \ ナ\ \ }}$である。
(4)平面EPQと直線BFの交点をRとすると|$\overrightarrow{BR}$|=$\frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌ\ \ }}$である。
この動画を見る
$\Large\boxed{2}$ 図のような一辺の長さが1の正八面体ABCDEFがある。
2点P,Qはそれぞれ辺AD, BC上にあり
$\overrightarrow{PQ}$$\bot$$\overrightarrow{AD}$かつ$\overrightarrow{PQ}$$\bot$$\overrightarrow{BC}$
を満たすとする。
(1)$\overrightarrow{AD}$と$\overrightarrow{BC}$のなす角は$\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$である。
(2)|$\overrightarrow{AP}$|=$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$, |$\overrightarrow{BQ}$|=$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$である。
(3)|$\overrightarrow{PQ}$|=$\frac{\boxed{\ \ テ\ \ }}{\boxed{\ \ ト\ \ }}\sqrt{\boxed{\ \ ナ\ \ }}$である。
(4)平面EPQと直線BFの交点をRとすると|$\overrightarrow{BR}$|=$\frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌ\ \ }}$である。
福田の数学〜青山学院大学2023年理工学部第1問〜空間ベクトルとと四面体の体積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#数C#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 座標空間の3点A(0,1,2), B(3,-2,2), C(-1,4,1)が定める平面を$\alpha$とする。
原点Oから平面$\alpha$に垂線を下ろし、$\alpha$との交点をHとする。
(1)$\overrightarrow{AB}$・$\overrightarrow{AC}$=$\boxed{\ \ アイウ\ \ }$
(2)$\triangle$ABCの面積は$\frac{\boxed{\ \ エ\ \ }\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}$である。
(3)$\overrightarrow{AH}$=$\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ クケ\ \ }}$$\overrightarrow{AB}$+$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$$\overrightarrow{AC}$, $\overrightarrow{OH}$=$\frac{\boxed{\ \ シ\ \ }\sqrt{\boxed{\ \ ス\ \ }}}{\boxed{\ \ セ\ \ }}$
(4)四面体OHBCの体積は$\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}$である。
この動画を見る
$\Large\boxed{1}$ 座標空間の3点A(0,1,2), B(3,-2,2), C(-1,4,1)が定める平面を$\alpha$とする。
原点Oから平面$\alpha$に垂線を下ろし、$\alpha$との交点をHとする。
(1)$\overrightarrow{AB}$・$\overrightarrow{AC}$=$\boxed{\ \ アイウ\ \ }$
(2)$\triangle$ABCの面積は$\frac{\boxed{\ \ エ\ \ }\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}$である。
(3)$\overrightarrow{AH}$=$\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ クケ\ \ }}$$\overrightarrow{AB}$+$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$$\overrightarrow{AC}$, $\overrightarrow{OH}$=$\frac{\boxed{\ \ シ\ \ }\sqrt{\boxed{\ \ ス\ \ }}}{\boxed{\ \ セ\ \ }}$
(4)四面体OHBCの体積は$\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}$である。
福田の数学〜慶應義塾大学2023年理工学部第5問(1)〜複素数平面上の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ (1)$\alpha$を±1ではない複素数とする。複素数平面上で$\displaystyle\left|\frac{\alpha z+1}{z+\alpha}\right|$=2 を満たす点$z$全体からなる図形を$C$とする。$C$は$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき直線となり、$\boxed{\ \ チ\ \ }$を満たさないとき円となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たさないとき、円$C$の中心を$\alpha$を用いて表すと$\boxed{\ \ ツ\ \ }$となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき、直線$C$上の点$z$のうち、
その絶対値が最小となるものを$\alpha$を用いて表すと$\boxed{\ \ テ\ \ }$となる。
この動画を見る
$\Large\boxed{5}$ (1)$\alpha$を±1ではない複素数とする。複素数平面上で$\displaystyle\left|\frac{\alpha z+1}{z+\alpha}\right|$=2 を満たす点$z$全体からなる図形を$C$とする。$C$は$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき直線となり、$\boxed{\ \ チ\ \ }$を満たさないとき円となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たさないとき、円$C$の中心を$\alpha$を用いて表すと$\boxed{\ \ ツ\ \ }$となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき、直線$C$上の点$z$のうち、
その絶対値が最小となるものを$\alpha$を用いて表すと$\boxed{\ \ テ\ \ }$となる。
福田の数学〜慶應義塾大学2023年理工学部第2問〜空間ベクトルと2直線から等距離にある点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#図形と方程式#軌跡と領域#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $k$を正の実数とし、空間内に点O(0,0,0), A(4$k$, $-4k$, $-4\sqrt 2k$), B(7, 5, $-\sqrt 2$)をとる。点CはO, A, Bを含む平面上の点であり、OA=4BCで、四角形OACBはOAを底辺とする台形であるとする。
(1)$\cos\angle$AOB=$\boxed{\ \ ア\ \ }$である。台形OACBの面積を$k$を用いて表すと$\boxed{\ \ イ\ \ }$となる。
また、線分ACの長さを$k$を用いて表すと$\boxed{\ \ ウ\ \ }$となる。
(2)台形OACBが円に内接するとき、$k$=$\boxed{\ \ エ\ \ }$である。
(3)$k$=$\boxed{\ \ エ\ \ }$であるとし、直線OBと直線ACの交点をDとする。△OBPと△ACPの面積が等しい、という条件を満たす空間内の点P全体は、点Dを通る2つの平面上の点全体から点Dを除いたものとなる。これら2つの平面のうち、線分OAと交わらないものを$\alpha$とする。点Oから平面$\alpha$に下ろした垂線の長さは$\boxed{\ \ オ\ \ }$である。
この動画を見る
$\Large\boxed{2}$ $k$を正の実数とし、空間内に点O(0,0,0), A(4$k$, $-4k$, $-4\sqrt 2k$), B(7, 5, $-\sqrt 2$)をとる。点CはO, A, Bを含む平面上の点であり、OA=4BCで、四角形OACBはOAを底辺とする台形であるとする。
(1)$\cos\angle$AOB=$\boxed{\ \ ア\ \ }$である。台形OACBの面積を$k$を用いて表すと$\boxed{\ \ イ\ \ }$となる。
また、線分ACの長さを$k$を用いて表すと$\boxed{\ \ ウ\ \ }$となる。
(2)台形OACBが円に内接するとき、$k$=$\boxed{\ \ エ\ \ }$である。
(3)$k$=$\boxed{\ \ エ\ \ }$であるとし、直線OBと直線ACの交点をDとする。△OBPと△ACPの面積が等しい、という条件を満たす空間内の点P全体は、点Dを通る2つの平面上の点全体から点Dを除いたものとなる。これら2つの平面のうち、線分OAと交わらないものを$\alpha$とする。点Oから平面$\alpha$に下ろした垂線の長さは$\boxed{\ \ オ\ \ }$である。
福田の数学〜早稲田大学2023年人間科学部第7問〜空間ベクトルと回転体の体積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{7}$ 座標空間に点C(0,1,1)を中心とする半径1の球面Sがある。点P(0,0,3)からSに引いた接線と$xy$平面との交点をQとする。$\overrightarrow{PC}・\overrightarrow{PQ}$=$t|\overrightarrow{PQ}|$と表すとき、
$t$=$\boxed{\ \ テ \ \ }$である。点Qは楕円状にあり、この楕円を
$\displaystyle\frac{(x+b)^2}{a}$+$\displaystyle\frac{(y+d)^2}{c}$=1
とするとき、$a$=$\boxed{\ \ ト\ \ }$, $b$=$\boxed{\ \ ナ\ \ }$, $c$=$\boxed{\ \ ニ\ \ }$, $d$=$\boxed{\ \ ヌ\ \ }$ である。
また、点Pに光源があるとき、球面Sで光が当たる部分を点Rが動く。ただし、
球面Sは光を通さない。このとき線分PRが通過してできる図形の体積は
2$\pi$・$\displaystyle\frac{\boxed{ネ}+\boxed{ノ}\sqrt{\boxed{ハ}}}{\boxed{ヒ}}$
である。
この動画を見る
$\Large\boxed{7}$ 座標空間に点C(0,1,1)を中心とする半径1の球面Sがある。点P(0,0,3)からSに引いた接線と$xy$平面との交点をQとする。$\overrightarrow{PC}・\overrightarrow{PQ}$=$t|\overrightarrow{PQ}|$と表すとき、
$t$=$\boxed{\ \ テ \ \ }$である。点Qは楕円状にあり、この楕円を
$\displaystyle\frac{(x+b)^2}{a}$+$\displaystyle\frac{(y+d)^2}{c}$=1
とするとき、$a$=$\boxed{\ \ ト\ \ }$, $b$=$\boxed{\ \ ナ\ \ }$, $c$=$\boxed{\ \ ニ\ \ }$, $d$=$\boxed{\ \ ヌ\ \ }$ である。
また、点Pに光源があるとき、球面Sで光が当たる部分を点Rが動く。ただし、
球面Sは光を通さない。このとき線分PRが通過してできる図形の体積は
2$\pi$・$\displaystyle\frac{\boxed{ネ}+\boxed{ノ}\sqrt{\boxed{ハ}}}{\boxed{ヒ}}$
である。
福田の数学〜早稲田大学2023年人間科学部第3問〜対称点とベクトルの絶対値の最小値

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 空間座標における2点A(2,-3,-1)とB(3,0,1)を通る直線を$l_1$とし、直線$l_1$に関して点C(1,5,-2)と対称な点をDとすると、Dの座標は($\boxed{\ \ ク\ \ }$, $\boxed{\ \ ケ\ \ }$, $\boxed{\ \ コ\ \ }$)である。また、点Dを通り$l_1$と平行な直線を$l_2$とし、点Pが直線$l_2$上を、点Qが$xy$平面上の直線$y$=$-x$+4 上をそれぞれ自由に動くとき、$|\overrightarrow{PQ}|^2$の最小値は$\boxed{\ \ サ\ \ }$である。
この動画を見る
$\Large\boxed{3}$ 空間座標における2点A(2,-3,-1)とB(3,0,1)を通る直線を$l_1$とし、直線$l_1$に関して点C(1,5,-2)と対称な点をDとすると、Dの座標は($\boxed{\ \ ク\ \ }$, $\boxed{\ \ ケ\ \ }$, $\boxed{\ \ コ\ \ }$)である。また、点Dを通り$l_1$と平行な直線を$l_2$とし、点Pが直線$l_2$上を、点Qが$xy$平面上の直線$y$=$-x$+4 上をそれぞれ自由に動くとき、$|\overrightarrow{PQ}|^2$の最小値は$\boxed{\ \ サ\ \ }$である。
福田の数学〜浜松医科大学2023医学部年第3問〜複素数平の絶対値と偏角Part2

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
Sを実部、虚部ともに整数であるような0以外の複素数全体の集合、Tを偏角 が0以上$\displaystyle \frac{π}{2}$未満であるようなSの要素全体の集合とする。またiは虚数単位とする。以下の問いに答えよ。
(1)$α=2$, $β=1+i$, $γ=1$のとき、 $|αβγ|$ の値を求めよ。
(2)複素数zについて、 arg z = $\displaystyle \frac{π}{8}$のとき arg(iz) の値を求めよ。
(3) α, ß, γ を Tの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ を満たす α, ß, γ の
組の総数kの値を求めよ。
(4)α, ß, γをSの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ および
$\displaystyle \frac{π}{8} ≦arg(αßγ) < \displaystyle \frac{5π}{8}$
を満たす α, β, yの組の総数をmとするとき、mをkで割った商と余りを求め
よ。
2023浜松医科大学医過去問
この動画を見る
Sを実部、虚部ともに整数であるような0以外の複素数全体の集合、Tを偏角 が0以上$\displaystyle \frac{π}{2}$未満であるようなSの要素全体の集合とする。またiは虚数単位とする。以下の問いに答えよ。
(1)$α=2$, $β=1+i$, $γ=1$のとき、 $|αβγ|$ の値を求めよ。
(2)複素数zについて、 arg z = $\displaystyle \frac{π}{8}$のとき arg(iz) の値を求めよ。
(3) α, ß, γ を Tの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ を満たす α, ß, γ の
組の総数kの値を求めよ。
(4)α, ß, γをSの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ および
$\displaystyle \frac{π}{8} ≦arg(αßγ) < \displaystyle \frac{5π}{8}$
を満たす α, β, yの組の総数をmとするとき、mをkで割った商と余りを求め
よ。
2023浜松医科大学医過去問
福田の数学〜浜松医科大学2023年医学部第3問〜複素数平の絶対値と偏角Part1

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
Sを実部、虚部ともに整数であるような0以外の複素数全体の集合、Tを偏角 が0以上$\displaystyle \frac{π}{2}$未満であるようなSの要素全体の集合とする。またiは虚数単位とする。以下の問いに答えよ。
(1)$α=2$, $β=1+i$, $γ=1$のとき、 $|αβγ|$ の値を求めよ。
(2)複素数zについて、 arg z = $\displaystyle \frac{π}{8}$のとき arg(iz) の値を求めよ。
(3) α, ß, γ を Tの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ を満たす α, ß, γ の
組の総数kの値を求めよ。
(4)α, ß, γをSの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ および
$\displaystyle \frac{π}{8} ≦arg(αßγ) < \displaystyle \frac{5π}{8}$
を満たす α, β, yの組の総数をmとするとき、mをkで割った商と余りを求め
よ。
2023浜松医科大学医過去問
この動画を見る
Sを実部、虚部ともに整数であるような0以外の複素数全体の集合、Tを偏角 が0以上$\displaystyle \frac{π}{2}$未満であるようなSの要素全体の集合とする。またiは虚数単位とする。以下の問いに答えよ。
(1)$α=2$, $β=1+i$, $γ=1$のとき、 $|αβγ|$ の値を求めよ。
(2)複素数zについて、 arg z = $\displaystyle \frac{π}{8}$のとき arg(iz) の値を求めよ。
(3) α, ß, γ を Tの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ を満たす α, ß, γ の
組の総数kの値を求めよ。
(4)α, ß, γをSの要素とする。このとき、$0 < |αβγ| ≦ \sqrt{5}$ および
$\displaystyle \frac{π}{8} ≦arg(αßγ) < \displaystyle \frac{5π}{8}$
を満たす α, β, yの組の総数をmとするとき、mをkで割った商と余りを求め
よ。
2023浜松医科大学医過去問
福田の数学〜千葉大学2023年第8問〜iのn乗根Part2

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{8}$ 実数$a$,$b$と虚数単位$i$を用いて複素数$z$が$z$=$a$+$bi$の形で表されるとき、$a$を$z$の実部、$b$を$z$の虚部と呼び、それぞれ$a$=$Re(z)$,$b$=$Im(z)$と表す。
(1)$z^3$=$i$を満たす複素数$z$をすべて求めよ。
(2)$z^{100}$=$i$を満たす複素数$z$のうち、$Re(z)$≦$\frac{1}{2}$かつ$Im(z)$≧0を満たすものの個数を求めよ。
(3)$n$を正の整数とする。$z^n$=$i$を満たす複素数$z$のうち、$Re(z)$≧$\frac{1}{2}$を満たすものの個数を$N$とする。$N$>$\frac{n}{3}$となるための$n$に関する必要十分条件を求めよ。
この動画を見る
$\Large\boxed{8}$ 実数$a$,$b$と虚数単位$i$を用いて複素数$z$が$z$=$a$+$bi$の形で表されるとき、$a$を$z$の実部、$b$を$z$の虚部と呼び、それぞれ$a$=$Re(z)$,$b$=$Im(z)$と表す。
(1)$z^3$=$i$を満たす複素数$z$をすべて求めよ。
(2)$z^{100}$=$i$を満たす複素数$z$のうち、$Re(z)$≦$\frac{1}{2}$かつ$Im(z)$≧0を満たすものの個数を求めよ。
(3)$n$を正の整数とする。$z^n$=$i$を満たす複素数$z$のうち、$Re(z)$≧$\frac{1}{2}$を満たすものの個数を$N$とする。$N$>$\frac{n}{3}$となるための$n$に関する必要十分条件を求めよ。
福田の数学〜千葉大学2023年第8問〜iのn乗根Part1

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{8}$ 実数$a$,$b$と虚数単位$i$を用いて複素数$z$が$z$=$a$+$bi$の形で表されるとき、$a$を$z$の実部、$b$を$z$の虚部と呼び、それぞれ$a$=$Re(z)$,$b$=$Im(z)$と表す。
(1)$z^3$=$i$を満たす複素数$z$をすべて求めよ。
(2)$z^{100}$=$i$を満たす複素数$z$のうち、$Re(z)$≦$\frac{1}{2}$かつ$Im(z)$≧0を満たすものの個数を求めよ。
(3)$n$を正の整数とする。$z^n$=$i$を満たす複素数$z$のうち、$Re(z)$≧$\frac{1}{2}$を満たすものの個数を$N$とする。$N$>$\frac{n}{3}$となるための$n$に関する必要十分条件を求めよ。
この動画を見る
$\Large\boxed{8}$ 実数$a$,$b$と虚数単位$i$を用いて複素数$z$が$z$=$a$+$bi$の形で表されるとき、$a$を$z$の実部、$b$を$z$の虚部と呼び、それぞれ$a$=$Re(z)$,$b$=$Im(z)$と表す。
(1)$z^3$=$i$を満たす複素数$z$をすべて求めよ。
(2)$z^{100}$=$i$を満たす複素数$z$のうち、$Re(z)$≦$\frac{1}{2}$かつ$Im(z)$≧0を満たすものの個数を求めよ。
(3)$n$を正の整数とする。$z^n$=$i$を満たす複素数$z$のうち、$Re(z)$≧$\frac{1}{2}$を満たすものの個数を$N$とする。$N$>$\frac{n}{3}$となるための$n$に関する必要十分条件を求めよ。
高校の範囲で解ける積分 By 英語orドイツ語シはBかHか さん #定積分

単元:
#複素数平面#積分とその応用#複素数平面#定積分#数学(高校生)#数C#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} arg(1+\sqrt{ -x }) dx$
$-\pi \leqq arg(1+\sqrt{ -x }) \lt \pi$
この動画を見る
$\displaystyle \int_{0}^{1} arg(1+\sqrt{ -x }) dx$
$-\pi \leqq arg(1+\sqrt{ -x }) \lt \pi$
福田の数学〜千葉大学2023年第5問〜垂線の足の位置ベクトル

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 点Oを原点とする座標平面において、点Aと点Bが$\overrightarrow{OA}$・$\overrightarrow{OA}$=5, $\overrightarrow{OB}$・$\overrightarrow{OB}$=2, $\overrightarrow{OA}$・$\overrightarrow{OB}$=3を満たすとする。
(1)$\overrightarrow{OB}$=$k\overrightarrow{OA}$ となるような実数$k$は存在しないことを示せ。
(2)点Bから直線OAに下ろした垂線とOAとの交点をHとする。$\overrightarrow{HB}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
(3)実数$t$に対し、直線OA上の点Pを$\overrightarrow{OP}$=$t\overrightarrow{OA}$となるようにとる。同様に直線OB上の点Qを$\overrightarrow{OQ}$=(1-$t$)$\overrightarrow{OB}$となるようにとる。点Pを通り直線OAと直交する直線を$l_1$とし、点Qを通り直線OBと直交する直線を$l_2$とする。
$l_1$と$l_2$の交点をRとするとき、$\overrightarrow{OR}$を$\overrightarrow{OA}$,$\overrightarrow{OB}$,$t$を用いて表せ。
(4)3点O,A,Bを通る円の中心をCとするとき、$\overrightarrow{OC}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
この動画を見る
$\Large\boxed{5}$ 点Oを原点とする座標平面において、点Aと点Bが$\overrightarrow{OA}$・$\overrightarrow{OA}$=5, $\overrightarrow{OB}$・$\overrightarrow{OB}$=2, $\overrightarrow{OA}$・$\overrightarrow{OB}$=3を満たすとする。
(1)$\overrightarrow{OB}$=$k\overrightarrow{OA}$ となるような実数$k$は存在しないことを示せ。
(2)点Bから直線OAに下ろした垂線とOAとの交点をHとする。$\overrightarrow{HB}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
(3)実数$t$に対し、直線OA上の点Pを$\overrightarrow{OP}$=$t\overrightarrow{OA}$となるようにとる。同様に直線OB上の点Qを$\overrightarrow{OQ}$=(1-$t$)$\overrightarrow{OB}$となるようにとる。点Pを通り直線OAと直交する直線を$l_1$とし、点Qを通り直線OBと直交する直線を$l_2$とする。
$l_1$と$l_2$の交点をRとするとき、$\overrightarrow{OR}$を$\overrightarrow{OA}$,$\overrightarrow{OB}$,$t$を用いて表せ。
(4)3点O,A,Bを通る円の中心をCとするとき、$\overrightarrow{OC}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
大学入試問題#594「やばいのは見た目だけ」 東京帝国大学(1926) #複素数

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$\sqrt[ 3 ]{ i }$を求めよ。
$(i^2=-1)$
出典:1926年東京帝国大学医学部 入試問題
この動画を見る
$\sqrt[ 3 ]{ i }$を求めよ。
$(i^2=-1)$
出典:1926年東京帝国大学医学部 入試問題
福田の数学〜立教大学2023年経済学部第1問(5)〜共面条件

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (5)$t$を実数とする。座標空間において、3点O(0,0,0), A(1,0,2), B(2,-1,0)の定める平面OAB上に点C($t$+1,$t$,1-$t$)があるとき、$t$=$\boxed{\ \ オ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (5)$t$を実数とする。座標空間において、3点O(0,0,0), A(1,0,2), B(2,-1,0)の定める平面OAB上に点C($t$+1,$t$,1-$t$)があるとき、$t$=$\boxed{\ \ オ\ \ }$である。
福田の数学〜立教大学2023年理学部第2問〜ベクトルの共面条件と共線条件

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 0<$k$1とする。座標空間内の四面体OABCについて、線分ACの中点をD、線分BCの中点をE、線分DEを1:2に内分する点をPとする。また、
線分OPを$k$:1-$k$に内分する点をQとし、Rを$\overrightarrow{CR}$=$l\overrightarrow{CQ}$を満たす点とする。
$\overrightarrow{a}$=$\overrightarrow{OA}$, $\overrightarrow{b}$=$\overrightarrow{OB}$, $\overrightarrow{c}$=$\overrightarrow{OC}$とおいたとき、次の問いに答えよ。
(1)$\overrightarrow{OD}$, $\overrightarrow{OE}$, $\overrightarrow{OP}$を$\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$を用いて表せ。
(2)$\overrightarrow{OR}$を$\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$, $k$, $l$を用いて表せ。
(3)Rが平面OAB上にあるとき、$l$を$k$を用いて表せ。
(4)線分OAの中点をF、線分OBの中点をGとする。Rが線分FG上にあるときの$k$の値を求めよ。
この動画を見る
$\Large\boxed{2}$ 0<$k$1とする。座標空間内の四面体OABCについて、線分ACの中点をD、線分BCの中点をE、線分DEを1:2に内分する点をPとする。また、
線分OPを$k$:1-$k$に内分する点をQとし、Rを$\overrightarrow{CR}$=$l\overrightarrow{CQ}$を満たす点とする。
$\overrightarrow{a}$=$\overrightarrow{OA}$, $\overrightarrow{b}$=$\overrightarrow{OB}$, $\overrightarrow{c}$=$\overrightarrow{OC}$とおいたとき、次の問いに答えよ。
(1)$\overrightarrow{OD}$, $\overrightarrow{OE}$, $\overrightarrow{OP}$を$\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$を用いて表せ。
(2)$\overrightarrow{OR}$を$\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$, $k$, $l$を用いて表せ。
(3)Rが平面OAB上にあるとき、$l$を$k$を用いて表せ。
(4)線分OAの中点をF、線分OBの中点をGとする。Rが線分FG上にあるときの$k$の値を求めよ。
自治医大 三次方程式の解

単元:
#数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023自治医科大学過去問題
kは実数
$x^3-6x^2+kx-7 = 0$
の3つの解は複素数平面で1辺の長さが$\sqrt{3}$の正三角形の頂点となる
kの値
この動画を見る
2023自治医科大学過去問題
kは実数
$x^3-6x^2+kx-7 = 0$
の3つの解は複素数平面で1辺の長さが$\sqrt{3}$の正三角形の頂点となる
kの値
