 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【数C】ベクトルの基本⑭係数比較、メネラウスの定理でベクトルを求める

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD,BEの交点をPとする。ABをb,ACをcとするとき、APをb,cを用いて表せ
この動画を見る
三角形ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD,BEの交点をPとする。ABをb,ACをcとするとき、APをb,cを用いて表せ
【数B】ベクトル:ベクトルの基本⑭係数比較、メネラウスの定理でベクトルを求める

単元:
#数A#図形の性質#平面上のベクトル#内心・外心・重心とチェバ・メネラウス#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD,BEの交点をPとする。ABをb,ACをcとするとき、APをb,cを用いて表せ.
この動画を見る
三角形ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD,BEの交点をPとする。ABをb,ACをcとするとき、APをb,cを用いて表せ.
福田の数学〜杏林大学2022年医学部第3問〜空間図形と球面の方程式

単元:
#数Ⅱ#大学入試過去問(数学)#空間ベクトル#図形と方程式#円と方程式#軌跡と領域#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数C
指導講師:
福田次郎
問題文全文(内容文):
(1)座標平面上の3点A(-1,0),B(1,0),Cを頂点とする三角形について考える。
点Cのy座標は正であり、原点をOとして、以下の問いに答えよ。
$(\textrm{a})\angle BAC \lt \angle ABC$を満たす場合、点Cは第$\boxed{ア}$象限に存在する。
$(\textrm{b})\angle ABC \lt \angle ACB$を満たす場合、点Cは$\boxed{イ}$の$\boxed{ウ}$に存在する。
$(\textrm{c})\angle ACB \lt \frac{\pi}{2}$を満たす場合、点Cは$\boxed{エ}$の$\boxed{オ}$に存在する。
$(\textrm{d})\angle BAC \leqq \angle ABC \leqq ACB \leqq \frac{\pi}{2}$を満たす点Cが存在する領域(境界を含む)
の面積は$\frac{\boxed{カ}}{\boxed{キク }}\pi-\frac{\sqrt{\boxed{ケ }}}{\boxed{コ }}$である。
$\boxed{イ},\boxed{エ}$の解答群
①点Aを中心とし点Bを通る円
②点Bを中心とし点Aを通る円
③線分ABを直径とする円
④離心率が0.5で2点O,Aを焦点とする楕円
⑤離心率が0.5で2点O,Bを焦点とする楕円
⑥離心率が0.5で2点A,Bを焦点とする楕円
⑦線分ABを一辺にもち、重心のy座標が正である正三角形
⑧線分ABを一辺にもち、重心のy座標が正である正方形
$\boxed{ウ},\boxed{オ}$の解答群
①内部 ②周上 ③外部 ④重心
(2)座標空間内の4点$A(-1,0,0),B(1,0,0),C(s,t,0),D$を原点とし、
$\angle BAC \lt \angle ABC \lt \angle ACB$
を満たす四面体を考える。$t \gt 0$であり、点Dのz座標は正であるとする。
$(\textrm{a})\angle ADC=\frac{\pi}{2}$を満たす場合、点Dは$\boxed{サ }$に存在する。
$(\textrm{b})\angle ADC=\angle BDC=\frac{\pi}{2}$を満たす場合、
点Dのx座標はsであり、点Dは$(s,\boxed{シ},0)$を中心とする
半径$\boxed{ス}$の円周上にある。
$(\textrm{c})$以下では$t=\frac{4}{3}$とする。設問(1)の結果から、点Cのx座標sは
$\boxed{セ} \lt s \lt -\boxed{ソ}+\frac{\boxed{タ}\sqrt{\boxed{チ}}}{\boxed{ツ}}$の範囲をとりうる。この範囲でsが変化
するとき、$\angle ADB=\angle ADC =\angle BDC=\frac{\pi}{2}$を満たす四面体ABCDの体積は
$s=\frac{\boxed{テ}}{\boxed{エ}}$のとき最大値$\frac{\boxed{ナ}}{\boxed{二ヌ }}$をとる。
2022杏林大学医学部過去問
この動画を見る
(1)座標平面上の3点A(-1,0),B(1,0),Cを頂点とする三角形について考える。
点Cのy座標は正であり、原点をOとして、以下の問いに答えよ。
$(\textrm{a})\angle BAC \lt \angle ABC$を満たす場合、点Cは第$\boxed{ア}$象限に存在する。
$(\textrm{b})\angle ABC \lt \angle ACB$を満たす場合、点Cは$\boxed{イ}$の$\boxed{ウ}$に存在する。
$(\textrm{c})\angle ACB \lt \frac{\pi}{2}$を満たす場合、点Cは$\boxed{エ}$の$\boxed{オ}$に存在する。
$(\textrm{d})\angle BAC \leqq \angle ABC \leqq ACB \leqq \frac{\pi}{2}$を満たす点Cが存在する領域(境界を含む)
の面積は$\frac{\boxed{カ}}{\boxed{キク }}\pi-\frac{\sqrt{\boxed{ケ }}}{\boxed{コ }}$である。
$\boxed{イ},\boxed{エ}$の解答群
①点Aを中心とし点Bを通る円
②点Bを中心とし点Aを通る円
③線分ABを直径とする円
④離心率が0.5で2点O,Aを焦点とする楕円
⑤離心率が0.5で2点O,Bを焦点とする楕円
⑥離心率が0.5で2点A,Bを焦点とする楕円
⑦線分ABを一辺にもち、重心のy座標が正である正三角形
⑧線分ABを一辺にもち、重心のy座標が正である正方形
$\boxed{ウ},\boxed{オ}$の解答群
①内部 ②周上 ③外部 ④重心
(2)座標空間内の4点$A(-1,0,0),B(1,0,0),C(s,t,0),D$を原点とし、
$\angle BAC \lt \angle ABC \lt \angle ACB$
を満たす四面体を考える。$t \gt 0$であり、点Dのz座標は正であるとする。
$(\textrm{a})\angle ADC=\frac{\pi}{2}$を満たす場合、点Dは$\boxed{サ }$に存在する。
$(\textrm{b})\angle ADC=\angle BDC=\frac{\pi}{2}$を満たす場合、
点Dのx座標はsであり、点Dは$(s,\boxed{シ},0)$を中心とする
半径$\boxed{ス}$の円周上にある。
$(\textrm{c})$以下では$t=\frac{4}{3}$とする。設問(1)の結果から、点Cのx座標sは
$\boxed{セ} \lt s \lt -\boxed{ソ}+\frac{\boxed{タ}\sqrt{\boxed{チ}}}{\boxed{ツ}}$の範囲をとりうる。この範囲でsが変化
するとき、$\angle ADB=\angle ADC =\angle BDC=\frac{\pi}{2}$を満たす四面体ABCDの体積は
$s=\frac{\boxed{テ}}{\boxed{エ}}$のとき最大値$\frac{\boxed{ナ}}{\boxed{二ヌ }}$をとる。
2022杏林大学医学部過去問
大学入試問題#355「定番の定食」 山梨大学2019 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \sqrt{ 4-3x^2 }\ dx$
出典:2019年山梨大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \sqrt{ 4-3x^2 }\ dx$
出典:2019年山梨大学 入試問題
解けるように作られた方程式

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,y,zを実数とするとき,これを解け.
$x+y+z=2(\sqrt x +\sqrt{y-1}+\sqrt{z-2})$
中国中等学校過去問
この動画を見る
x,y,zを実数とするとき,これを解け.
$x+y+z=2(\sqrt x +\sqrt{y-1}+\sqrt{z-2})$
中国中等学校過去問
【数C】ベクトルの大きさを自由自在に扱おう!

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#アドバンスプラス#アドバンスプラス数Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
アドバンスプラス数学B
問題617
vec(a)=(2,-1)について、
(1) vec(a)と平行な単位ベクトルを求めよ。
(2) vec(a)と同じ向きで、大きさが5であるvec(b)を求めよ。
この動画を見る
アドバンスプラス数学B
問題617
vec(a)=(2,-1)について、
(1) vec(a)と平行な単位ベクトルを求めよ。
(2) vec(a)と同じ向きで、大きさが5であるvec(b)を求めよ。
【数B】ベクトル:ベクトルの大きさを自由自在に扱おう!

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
アドバンスプラス数学B
問題617
$\vec{a}=(2,-1)$について、
(1)$\vec{a}$と平行な単位ベクトルを求めよ。
(2)$\vec{a}$と同じ向きで、大きさが5である$\vec{b}$を求めよ。
この動画を見る
アドバンスプラス数学B
問題617
$\vec{a}=(2,-1)$について、
(1)$\vec{a}$と平行な単位ベクトルを求めよ。
(2)$\vec{a}$と同じ向きで、大きさが5である$\vec{b}$を求めよ。
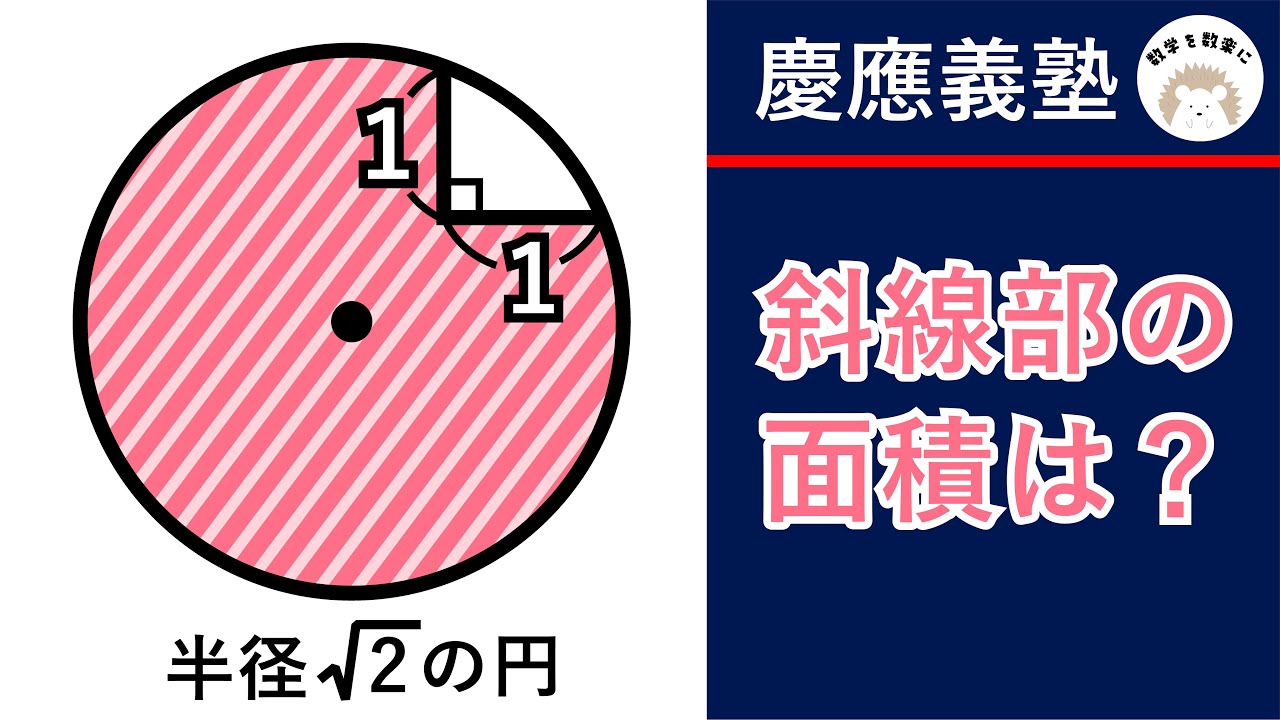
引っかけ問題!? 円 斜線部の面積を求めよ 慶應義塾
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
半径$\sqrt 2$の円
斜線部の面積は?
*図は動画内参照
慶應義塾高等学校
この動画を見る
半径$\sqrt 2$の円
斜線部の面積は?
*図は動画内参照
慶應義塾高等学校
福田の数学〜杏林大学2022年医学部第2問〜定積分と関数の増減

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(1)Cを積分定数として、指数関数とたんっ公式の席の不定積分について、次式が成り立つ。
$\int xe^{-3x}dx = -(\frac{\boxed{ア}\ x+\boxed{イ}}{\boxed{ウ}})\ e^{-3x}+C$
$\int x^2e^{-3x}dx = -(\frac{\boxed{エ}\ x^2+\boxed{オ}\ x+\boxed{カ}}{\boxed{キク}})\ e^{-3x}+C$
また、定積分について、
$\int_0^1|(9x^2-1)e^{-3x}|dx=\frac{1}{\boxed{ケ}}(-1+\boxed{コ}\ e^{\boxed{サシ}}-\boxed{スセ}\ e^{-3})$
が成り立つ。
(2)p,q,rを実数の定数とする。関数$f(x)=(px^2+qx+r)e^{-3x}$が$x=0$で極大、
$x=1$で極小となるための必要十分条件は
$p=\boxed{ソタ}\ r,\ \ \ q=\boxed{チ}\ r,\ \ \ \boxed{ツ}$
である。さらに、$f(x)$の極小値が-1であるとすると、$f(x)$の極大値は$\frac{e^{\boxed{テ}}}{\boxed{ト }}$となる.
このとき、$\int_0^1f(x)dx=\frac{\boxed{ナ}}{\boxed{二}}$である。
$\boxed{ツ}$の解答群
$①\ r\gt 0\ \ \ \ ②\ r=0\ \ \ \ ③\ r \lt 0\ \ \ \ ④\ r \gt 1\ \ \ \ ⑤\ r=1$
$⑥\ r \lt 1\ \ \ \ ⑦\ r \gt \frac{1}{3}\ \ \ \ ⑧\ r =\frac{1}{3}\ \ \ \ ⑨r \lt \frac{1}{3}$
2022杏林大学医学部過去問
この動画を見る
(1)Cを積分定数として、指数関数とたんっ公式の席の不定積分について、次式が成り立つ。
$\int xe^{-3x}dx = -(\frac{\boxed{ア}\ x+\boxed{イ}}{\boxed{ウ}})\ e^{-3x}+C$
$\int x^2e^{-3x}dx = -(\frac{\boxed{エ}\ x^2+\boxed{オ}\ x+\boxed{カ}}{\boxed{キク}})\ e^{-3x}+C$
また、定積分について、
$\int_0^1|(9x^2-1)e^{-3x}|dx=\frac{1}{\boxed{ケ}}(-1+\boxed{コ}\ e^{\boxed{サシ}}-\boxed{スセ}\ e^{-3})$
が成り立つ。
(2)p,q,rを実数の定数とする。関数$f(x)=(px^2+qx+r)e^{-3x}$が$x=0$で極大、
$x=1$で極小となるための必要十分条件は
$p=\boxed{ソタ}\ r,\ \ \ q=\boxed{チ}\ r,\ \ \ \boxed{ツ}$
である。さらに、$f(x)$の極小値が-1であるとすると、$f(x)$の極大値は$\frac{e^{\boxed{テ}}}{\boxed{ト }}$となる.
このとき、$\int_0^1f(x)dx=\frac{\boxed{ナ}}{\boxed{二}}$である。
$\boxed{ツ}$の解答群
$①\ r\gt 0\ \ \ \ ②\ r=0\ \ \ \ ③\ r \lt 0\ \ \ \ ④\ r \gt 1\ \ \ \ ⑤\ r=1$
$⑥\ r \lt 1\ \ \ \ ⑦\ r \gt \frac{1}{3}\ \ \ \ ⑧\ r =\frac{1}{3}\ \ \ \ ⑨r \lt \frac{1}{3}$
2022杏林大学医学部過去問
大学入試問題#354「思った以上に大変でした・・・」 弘前大学 改 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{log\ x} \displaystyle \frac{(e^x-1)(e^x-2)}{e^x+1} dx$
出典:広前大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{log\ x} \displaystyle \frac{(e^x-1)(e^x-2)}{e^x+1} dx$
出典:広前大学 入試問題
指数法則
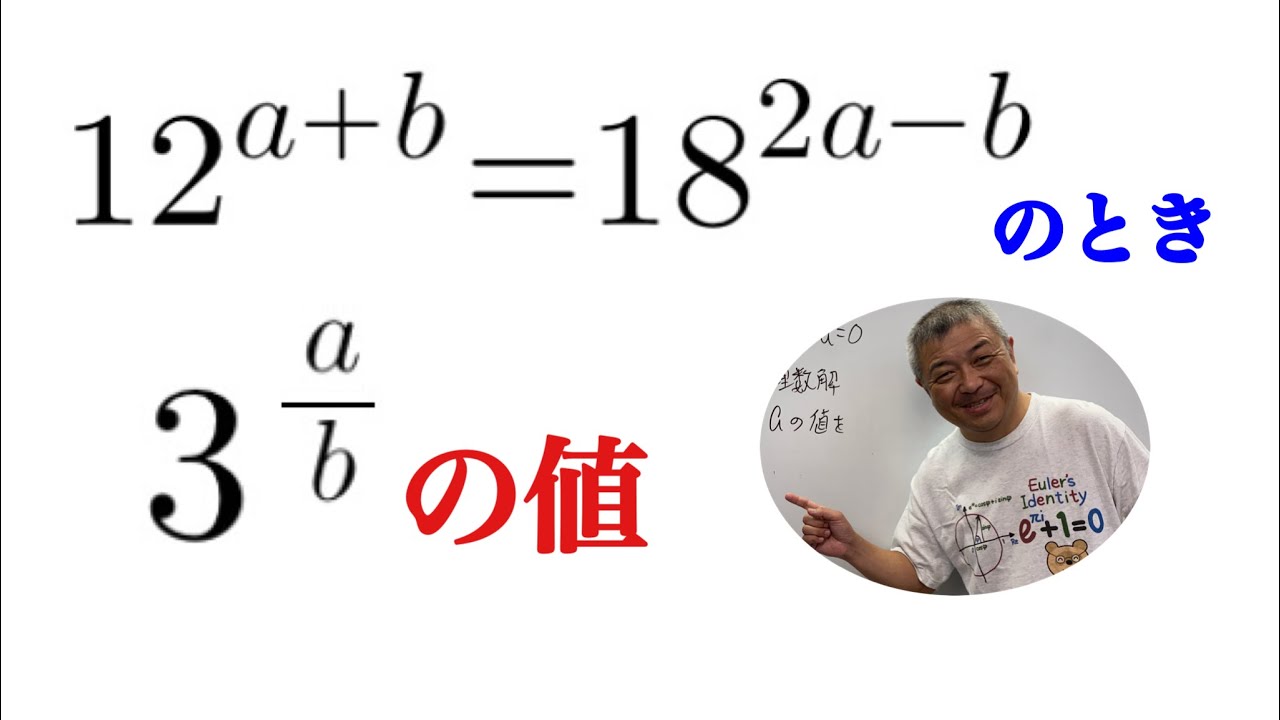
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 12^{a+b}=18^{2a-b}$とするとき,
$3^{\frac{a}{b}}$はいくつか?
この動画を見る
$ 12^{a+b}=18^{2a-b}$とするとき,
$3^{\frac{a}{b}}$はいくつか?
長方形と円 愛知県

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
長方形ABCDの面積=?
*図は動画内参照
愛知県
この動画を見る
長方形ABCDの面積=?
*図は動画内参照
愛知県
絶対に落としたくない問題です【自治医科大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
関数$f(x)$は,等式$f(x)=3x^2 \displaystyle \int_{-1}^{1} f(t) dt+x+\displaystyle \int_{0}^{1} [{f(t)}]^{2} dt+$
$\displaystyle \int_{0}^{1} f(t) dt$を満たす。
$\displaystyle \int_{0}^{1} f(t) dt \neq 0$とするとき,$f(0)$の値を求めよ。
自治医科大過去問
この動画を見る
関数$f(x)$は,等式$f(x)=3x^2 \displaystyle \int_{-1}^{1} f(t) dt+x+\displaystyle \int_{0}^{1} [{f(t)}]^{2} dt+$
$\displaystyle \int_{0}^{1} f(t) dt$を満たす。
$\displaystyle \int_{0}^{1} f(t) dt \neq 0$とするとき,$f(0)$の値を求めよ。
自治医科大過去問
福田の数学〜杏林大学2022年医学部第1問〜三角関数の最大最小と極値

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#加法定理とその応用#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学
指導講師:
福田次郎
問題文全文(内容文):
(1)三角関数について、次の等式が成り立つ。
$\cos2θ=\boxed{アイ}\sin^2θ+\boxed{ウ}$
$\sin3θ=\boxed{エオ}\sin^3θ+\boxed{カ}\sinθ$
(2)$0 \leqq θ \lt 2\pi$のとき、関数
$y=-\frac{1}{12}\sin3θ+\frac{3}{8}\cos2θ-\frac{3}{4}\sinθ$
は$θ=\frac{\boxed{キ}}{\boxed{ク}}\pi$で最小値$\frac{\boxed{ケコサ}}{\boxed{シス}}$をとり、
$\sinθ=\frac{\boxed{セソ}}{\boxed{タ}}$のとき最大値$\frac{\boxed{チツ}}{\boxed{テト}}$
をとる。また、yの極致を与えるθの個数は$\boxed{ナ}$である。
2022杏林大学医学部過去問
この動画を見る
(1)三角関数について、次の等式が成り立つ。
$\cos2θ=\boxed{アイ}\sin^2θ+\boxed{ウ}$
$\sin3θ=\boxed{エオ}\sin^3θ+\boxed{カ}\sinθ$
(2)$0 \leqq θ \lt 2\pi$のとき、関数
$y=-\frac{1}{12}\sin3θ+\frac{3}{8}\cos2θ-\frac{3}{4}\sinθ$
は$θ=\frac{\boxed{キ}}{\boxed{ク}}\pi$で最小値$\frac{\boxed{ケコサ}}{\boxed{シス}}$をとり、
$\sinθ=\frac{\boxed{セソ}}{\boxed{タ}}$のとき最大値$\frac{\boxed{チツ}}{\boxed{テト}}$
をとる。また、yの極致を与えるθの個数は$\boxed{ナ}$である。
2022杏林大学医学部過去問
大学入試問題#353「依頼により誘導通りに解いてみた」 埼玉大学2013 #定積分 #キングプロパティ

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$f(x)$連続
$\displaystyle \int_{0}^{\pi} x\ f(\sin\ x)dx=\displaystyle \frac{\pi}{2}\displaystyle \int_{0}^{\pi} f(\sin\ x) dx$
(2)
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{x(a^2-4\cos^2\ x)\sin\ x}{a^2-\cos^2x} dx$
出典:2013年埼玉大学 入試問題
この動画を見る
(1)
$f(x)$連続
$\displaystyle \int_{0}^{\pi} x\ f(\sin\ x)dx=\displaystyle \frac{\pi}{2}\displaystyle \int_{0}^{\pi} f(\sin\ x) dx$
(2)
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{x(a^2-4\cos^2\ x)\sin\ x}{a^2-\cos^2x} dx$
出典:2013年埼玉大学 入試問題
3乗根の方程式
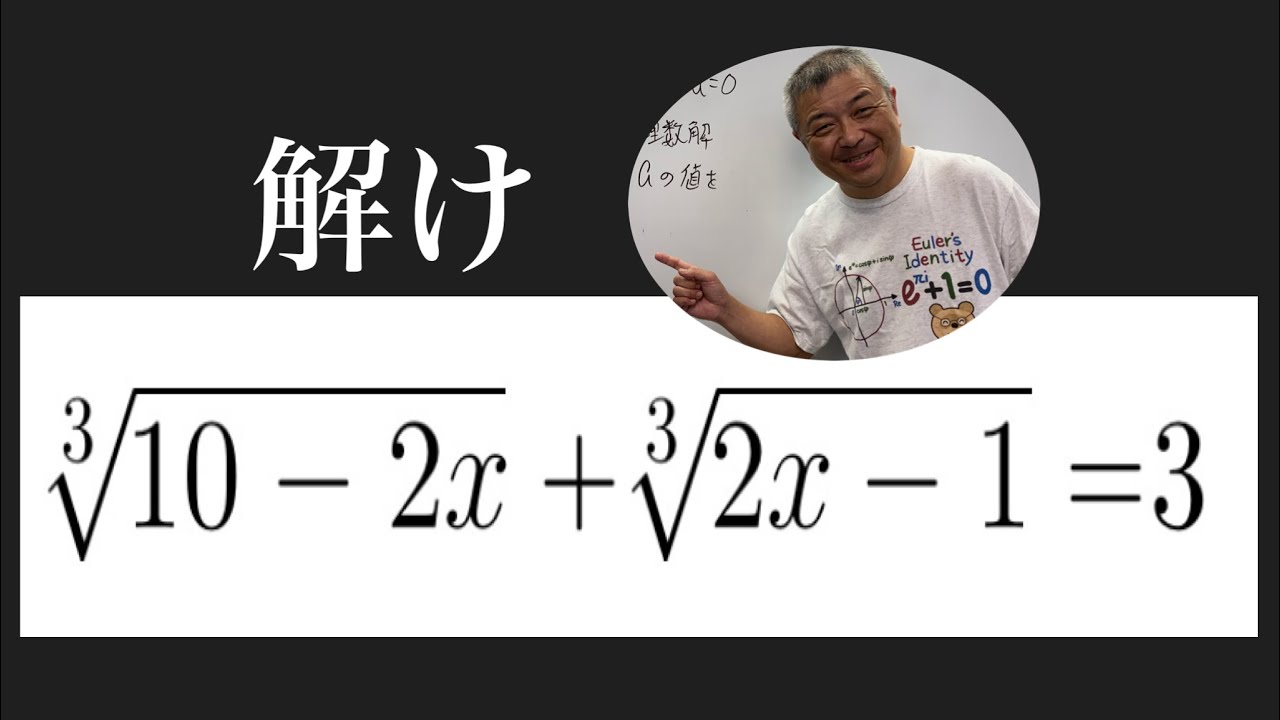
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt[3]{10-2x}+\sqrt[3]{2x-1}=3$
これを解け.
この動画を見る
$ \sqrt[3]{10-2x}+\sqrt[3]{2x-1}=3$
これを解け.
もう一つの解はどうやってだすか。二次方程式

正方形と150度

【いかに論理的に説明するか…!】整数:法政大学高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#整数の性質#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$n$を8で割ったときの余り$r$について$n=7r$が成り立つ.
$n$の値を求めなさい.
法政大高校過去問
この動画を見る
$n$を8で割ったときの余り$r$について$n=7r$が成り立つ.
$n$の値を求めなさい.
法政大高校過去問
渋ハロどれくらい人多いか計算した結果がやばい

単元:
#その他#その他#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
徳島の高校生です。
渋ハロ知らないんですが,どれくらい人多いんですか?
教えて!とんとん!
この動画を見る
徳島の高校生です。
渋ハロ知らないんですが,どれくらい人多いんですか?
教えて!とんとん!
福田の数学〜北里大学2022年医学部第3問〜確率と漸化式の融合問題

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
1つの箱を置ける台と2つの箱A, Bがある。箱Aには赤玉2個、青玉2個が
入っており、箱Bには白玉3個、青玉1個が入っている。台の上に箱Aを置き、
次の操作を繰り返す。
(操作) 台に置かれている箱から玉を1個取り出して色を調べてから箱に戻し、台
に置かれている箱を台から降ろす。取りだした玉が青球であれば箱Bを台
に置き、それ以外の色の玉であれば箱Aを台に置く。
正の整数nに対し、n回目の操作を終えたときに、台に箱Aが置かれている確率
をa_n、箱Bが置かれている確率をb_nとおく。次の問いに答えよ。
(1) 正の整数nに対し、$b_n$と$a_{n+1}$をそれぞれ $a_n$ を用いて表せ。
(2) 正の整数nに対し、$a_n$をnを用いて表せ。
(3) 正の整数nに対し、1回目からn回目までのn回の操作で白玉を1回も取り出
さない確率をnを用いて表せ。
(4)正の整数nに対し、1回目からn回目までのn回の操作で白玉をちょうど1回
だけ取り出す確率をnを用いて表せ。
2022北里大学医学部過去問
この動画を見る
1つの箱を置ける台と2つの箱A, Bがある。箱Aには赤玉2個、青玉2個が
入っており、箱Bには白玉3個、青玉1個が入っている。台の上に箱Aを置き、
次の操作を繰り返す。
(操作) 台に置かれている箱から玉を1個取り出して色を調べてから箱に戻し、台
に置かれている箱を台から降ろす。取りだした玉が青球であれば箱Bを台
に置き、それ以外の色の玉であれば箱Aを台に置く。
正の整数nに対し、n回目の操作を終えたときに、台に箱Aが置かれている確率
をa_n、箱Bが置かれている確率をb_nとおく。次の問いに答えよ。
(1) 正の整数nに対し、$b_n$と$a_{n+1}$をそれぞれ $a_n$ を用いて表せ。
(2) 正の整数nに対し、$a_n$をnを用いて表せ。
(3) 正の整数nに対し、1回目からn回目までのn回の操作で白玉を1回も取り出
さない確率をnを用いて表せ。
(4)正の整数nに対し、1回目からn回目までのn回の操作で白玉をちょうど1回
だけ取り出す確率をnを用いて表せ。
2022北里大学医学部過去問
大学入試問題#352「よく出題されそうな綺麗な問題」 京都工芸繊維大学(2011) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (\displaystyle \frac{log\ x}{x})^2 dx$
出典:2011年京都工芸繊維大学 入試問題
この動画を見る
$\displaystyle \int (\displaystyle \frac{log\ x}{x})^2 dx$
出典:2011年京都工芸繊維大学 入試問題
ただの計算
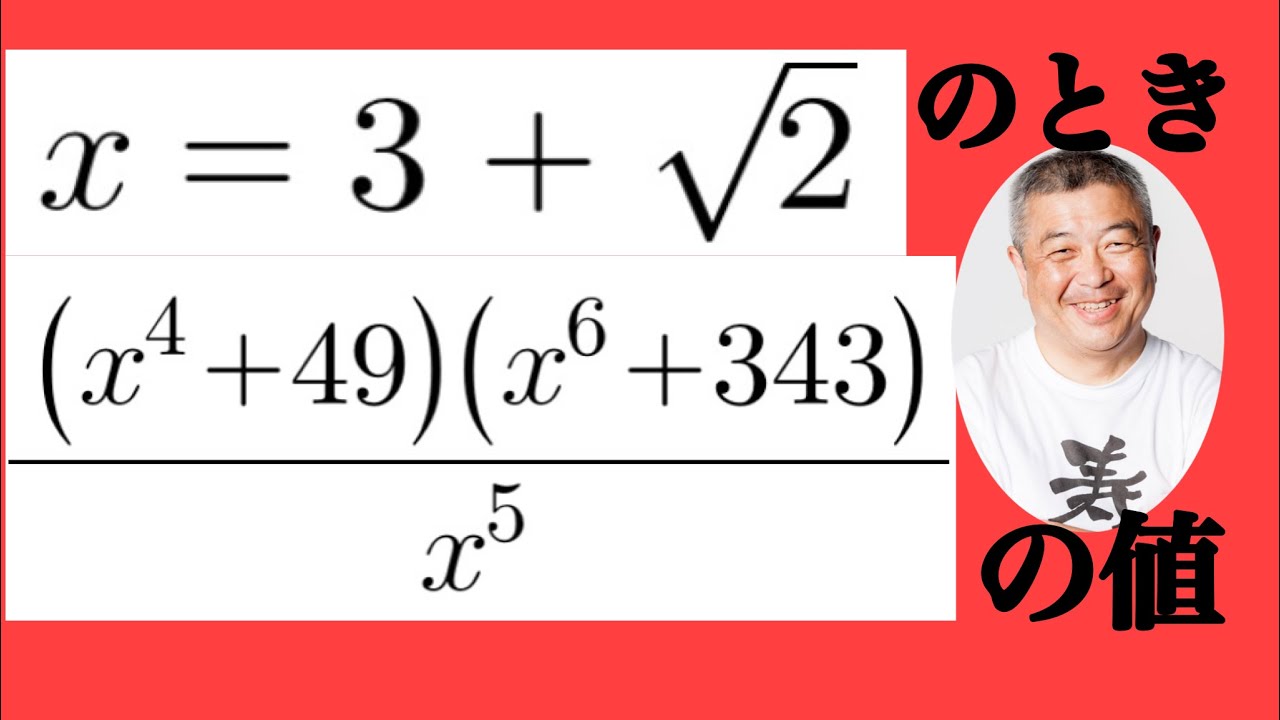
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x=3+\sqrt2,\dfrac{(x^4+49)(x^6+343)}{x^5}$の値を求めよ.
この動画を見る
$ x=3+\sqrt2,\dfrac{(x^4+49)(x^6+343)}{x^5}$の値を求めよ.
3通りで解ける!因数分解 早稲田本庄

単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2+b^2-3c^2+2(ab-bc-ca)$を因数分解せよ。
早稲田大学 本庄高等学院
この動画を見る
$a^2+b^2-3c^2+2(ab-bc-ca)$を因数分解せよ。
早稲田大学 本庄高等学院
シャンクスの帽子の贈与税は?

【数C】単位ベクトルを成分で表そう!

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#アドバンスプラス#アドバンスプラス数Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
アドバンスプラス数学B
問題616
vec(a)=(-3,4)と同じ向きの単位ベクトルvec(e)を求めよ。
この動画を見る
アドバンスプラス数学B
問題616
vec(a)=(-3,4)と同じ向きの単位ベクトルvec(e)を求めよ。
【数B】ベクトル:単位ベクトルを成分で表そう!

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
アドバンスプラス数学B
問題616
$\vec{a}=(-3,4)$と同じ向きの単位ベクトル$\vec{e}$を求めよ。
この動画を見る
アドバンスプラス数学B
問題616
$\vec{a}=(-3,4)$と同じ向きの単位ベクトル$\vec{e}$を求めよ。
福田の数学〜北里大学2022年医学部第2問〜定積分と不等式

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
次の各問いに答えよ。
(1)定積分\int^1_0\frac{1}{1+x^2}dxを求めよ。
(2)$x≠0$を満たすすべての実数xに対して、$e^x \gt 1+x$と$e^{-x^2} \lt \frac{1}{1+x^2}$が
成り立つことを証明せよ。
(3)$\frac{2}{3} \lt \int^1_0e^{-x^2}dx \lt \frac{\pi}{4}$が成り立つことを証明せよ。
2022北里大学医学部過去問
この動画を見る
次の各問いに答えよ。
(1)定積分\int^1_0\frac{1}{1+x^2}dxを求めよ。
(2)$x≠0$を満たすすべての実数xに対して、$e^x \gt 1+x$と$e^{-x^2} \lt \frac{1}{1+x^2}$が
成り立つことを証明せよ。
(3)$\frac{2}{3} \lt \int^1_0e^{-x^2}dx \lt \frac{\pi}{4}$が成り立つことを証明せよ。
2022北里大学医学部過去問
大学入試問題#351「積分できて満足できない問題」 電気通信大学(2013) #定積分 #極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n}\displaystyle \int_{-n}^{n} (\displaystyle \frac{e^x}{e^x+e^{-x}})^2 dx$
出典:2013年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n}\displaystyle \int_{-n}^{n} (\displaystyle \frac{e^x}{e^x+e^{-x}})^2 dx$
出典:2013年電気通信大学 入試問題
(x-y)⁵+(y-z)⁵+(z-x)⁵を因数分解せよ

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(x-y)^5+(y-z)^5+(z-x)^5$を因数分解せよ.
この動画を見る
$(x-y)^5+(y-z)^5+(z-x)^5$を因数分解せよ.
