 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
これ解けますか?

【ニガテな人が多い】通過領域の攻略法を6分で比較・解説!〔数学、高校数学〕

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$a$がすべての実数をとるとき、
$y=(a-1)x+a^2$
の通過する領域を求めよ。
この動画を見る
$a$がすべての実数をとるとき、
$y=(a-1)x+a^2$
の通過する領域を求めよ。
福田の数学〜早稲田大学2022年教育学部第1問(3)〜四面体と四面体の共通部分の切り口の面積

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形と方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(3)座標空間内の4点$(2,0,0),\ (-1,\sqrt3,0),\ (-1,-\sqrt3,0),\ (0,0,2)$を頂点と
する四面体をP、4点$(-2,0,1),\ (1,-\sqrt3,1),\ (1,\sqrt3,1),\ (0,0,-1)$を頂点
とする四面体をQとする。RをPとQの共通部分とする。Rを平面$z=\frac{1}{3}$で
切ったときの切り口の面積を求めよ。
2022早稲田大学教育学部過去問
この動画を見る
${\large\boxed{1}}$(3)座標空間内の4点$(2,0,0),\ (-1,\sqrt3,0),\ (-1,-\sqrt3,0),\ (0,0,2)$を頂点と
する四面体をP、4点$(-2,0,1),\ (1,-\sqrt3,1),\ (1,\sqrt3,1),\ (0,0,-1)$を頂点
とする四面体をQとする。RをPとQの共通部分とする。Rを平面$z=\frac{1}{3}$で
切ったときの切り口の面積を求めよ。
2022早稲田大学教育学部過去問
7で割ったあまり 札幌大谷

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$10^{2021}$を7で割った余りは?
札幌大谷高等学校(改)
この動画を見る
$10^{2021}$を7で割った余りは?
札幌大谷高等学校(改)
大学入試問題#277 横浜国立大学後期(2012) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1}(1-x^2)e^{-2x}dx$を求めよ
出典:2010年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1}(1-x^2)e^{-2x}dx$を求めよ
出典:2010年横浜国立大学 入試問題
愛のある二次方程式

変形できるかできないかが分かれ目 聖望学園

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{6 \sqrt n}{n}$が自然数となる自然数nは何個?
聖望学園高等学校
この動画を見る
$\frac{6 \sqrt n}{n}$が自然数となる自然数nは何個?
聖望学園高等学校
福田の数学〜早稲田大学2022年教育学部第1問(2)〜定積分で表された関数

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}\ (2)t \geqq 0$に対して
$f(t)=2\pi\int_0^{2t}|x-t|\cos(2\pi x)dx-t\sin(4\pi t)$
と定義する。このとき、
$f(t)=0$
を満たすtのうち、閉区間[0,1]に属する相異なるものはいくつあるか
早稲田大学教育学部過去問
この動画を見る
${\large\boxed{1}}\ (2)t \geqq 0$に対して
$f(t)=2\pi\int_0^{2t}|x-t|\cos(2\pi x)dx-t\sin(4\pi t)$
と定義する。このとき、
$f(t)=0$
を満たすtのうち、閉区間[0,1]に属する相異なるものはいくつあるか
早稲田大学教育学部過去問
ルートが入ってる方程式 日大三

単元:
#数学(中学生)#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$\sqrt 2 x = \frac{1}{\sqrt 2} - \frac{1}{\sqrt 3}$
日本大学第三高等学校
この動画を見る
方程式を解け
$\sqrt 2 x = \frac{1}{\sqrt 2} - \frac{1}{\sqrt 3}$
日本大学第三高等学校
大学入試問題#276 信州大学医学部後期 改 (2012) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$0 \lt a \lt 1$
$\displaystyle \int_{0}^{\sqrt{ 1-a^2 }}x\ log(x^2+a^2)dx$
出典:2012年信州大学医学部後期 入試問題
この動画を見る
$0 \lt a \lt 1$
$\displaystyle \int_{0}^{\sqrt{ 1-a^2 }}x\ log(x^2+a^2)dx$
出典:2012年信州大学医学部後期 入試問題
指数方程式
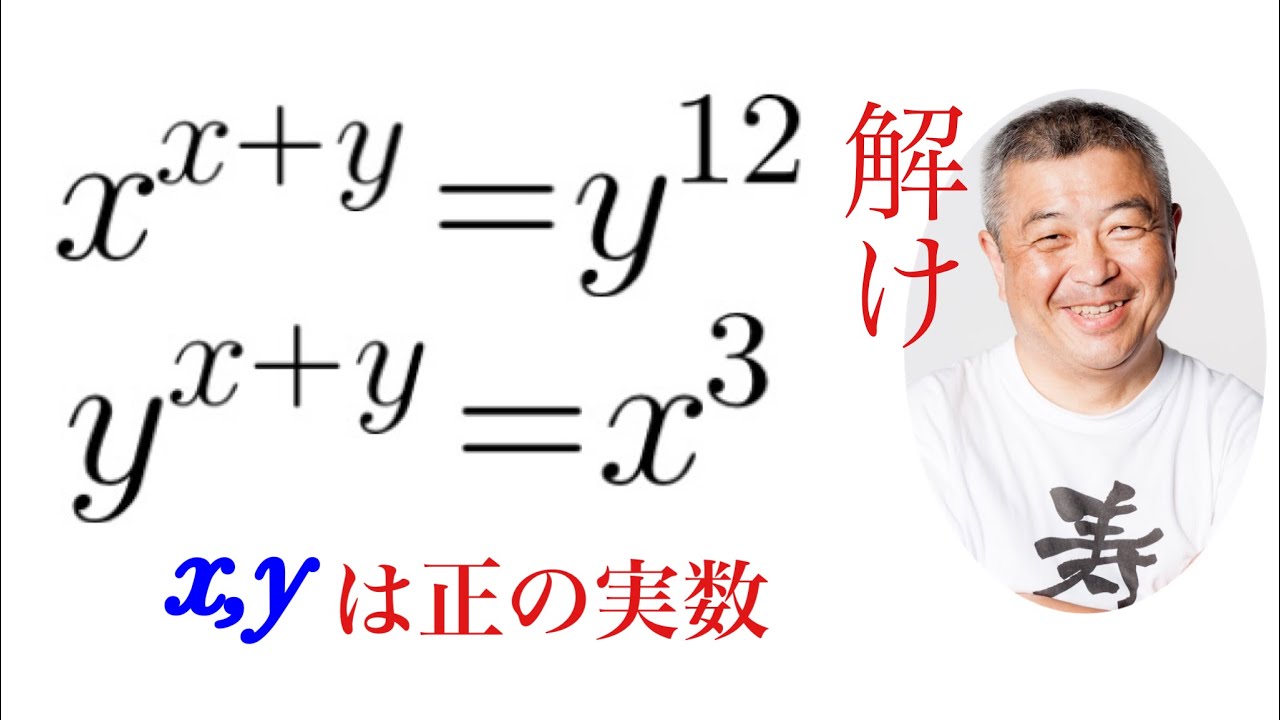
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yは正の実数である.
$x^{x+y}=y^{12},y^{x+y}=x^3$
これを解け.
この動画を見る
x,yは正の実数である.
$x^{x+y}=y^{12},y^{x+y}=x^3$
これを解け.
普通の中学生が解くには難しい 興南高校

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
5つの数字0,1,2,6,7から異なる3つの数字を選び、並べて3ケタの数を作とき
5で割ると2余る数は何個できるか?
興南高等学校
この動画を見る
5つの数字0,1,2,6,7から異なる3つの数字を選び、並べて3ケタの数を作とき
5で割ると2余る数は何個できるか?
興南高等学校
差がつく問題!記号が多くても焦らずに解けば大丈夫!【お茶の水女子大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$m$を2以上の自然数,$n$を自然数とするとき,次の不等式
${}_{mn} \mathrm {C}_n≧m^n>\displaystyle \sum_{i=0}^{n-1} m^i$
が成り立つことを示せ。
お茶の水女子大過去問
この動画を見る
$m$を2以上の自然数,$n$を自然数とするとき,次の不等式
${}_{mn} \mathrm {C}_n≧m^n>\displaystyle \sum_{i=0}^{n-1} m^i$
が成り立つことを示せ。
お茶の水女子大過去問
『lim』極限の解説します

福田の数学〜早稲田大学2022年教育学部第1問(1)〜空間ベクトルと球面の方程式

単元:
#数Ⅱ#大学入試過去問(数学)#空間ベクトル#図形と方程式#円と方程式#空間ベクトル#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(1)座標空間内に3点A$(2,0,0),\ B(0,4,0),\ C(0,0,8)$をとる。
2つのベクトル$\overrightarrow{ AP }$と$\overrightarrow{ BP }+\overrightarrow{ CP }$の内積が0となるような点$P(x,y,z)$
のうち、$|\overrightarrow{ AP }$|が最大となる点Pの座標を求めよ。
2022早稲田大学教育学部過去問
この動画を見る
${\large\boxed{1}}$(1)座標空間内に3点A$(2,0,0),\ B(0,4,0),\ C(0,0,8)$をとる。
2つのベクトル$\overrightarrow{ AP }$と$\overrightarrow{ BP }+\overrightarrow{ CP }$の内積が0となるような点$P(x,y,z)$
のうち、$|\overrightarrow{ AP }$|が最大となる点Pの座標を求めよ。
2022早稲田大学教育学部過去問
整数問題 海星高校(長崎)
単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
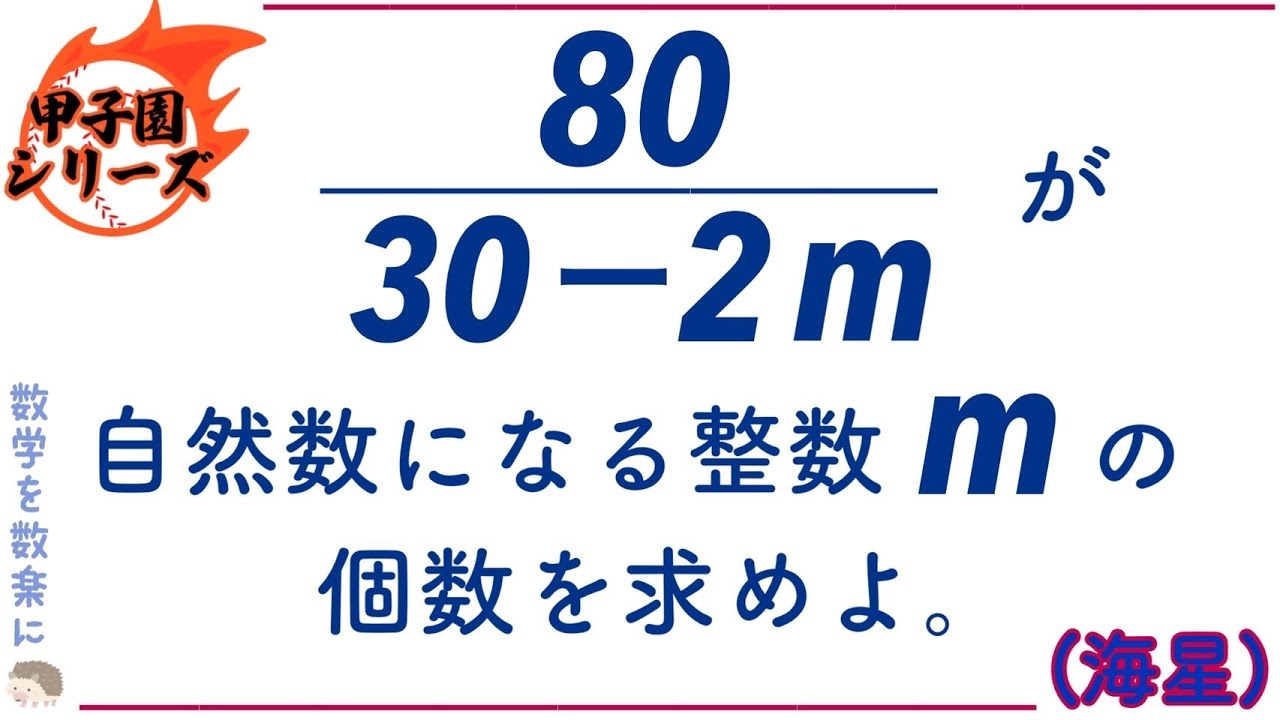
$\frac{80}{30 - 2m}$が自然数になる整数mの個数を求めよ。
海星高校
この動画を見る
$\frac{80}{30 - 2m}$が自然数になる整数mの個数を求めよ。
海星高校
大学入試問題#275 産業医科大学(2013) #区分求積法

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{\displaystyle \sum_{k=1}^{2n} (k+n)^2}{\displaystyle \sum_{k=1}^{2n} k^2}$
出典:2013年産業医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{\displaystyle \sum_{k=1}^{2n} (k+n)^2}{\displaystyle \sum_{k=1}^{2n} k^2}$
出典:2013年産業医科大学 入試問題
整数問題
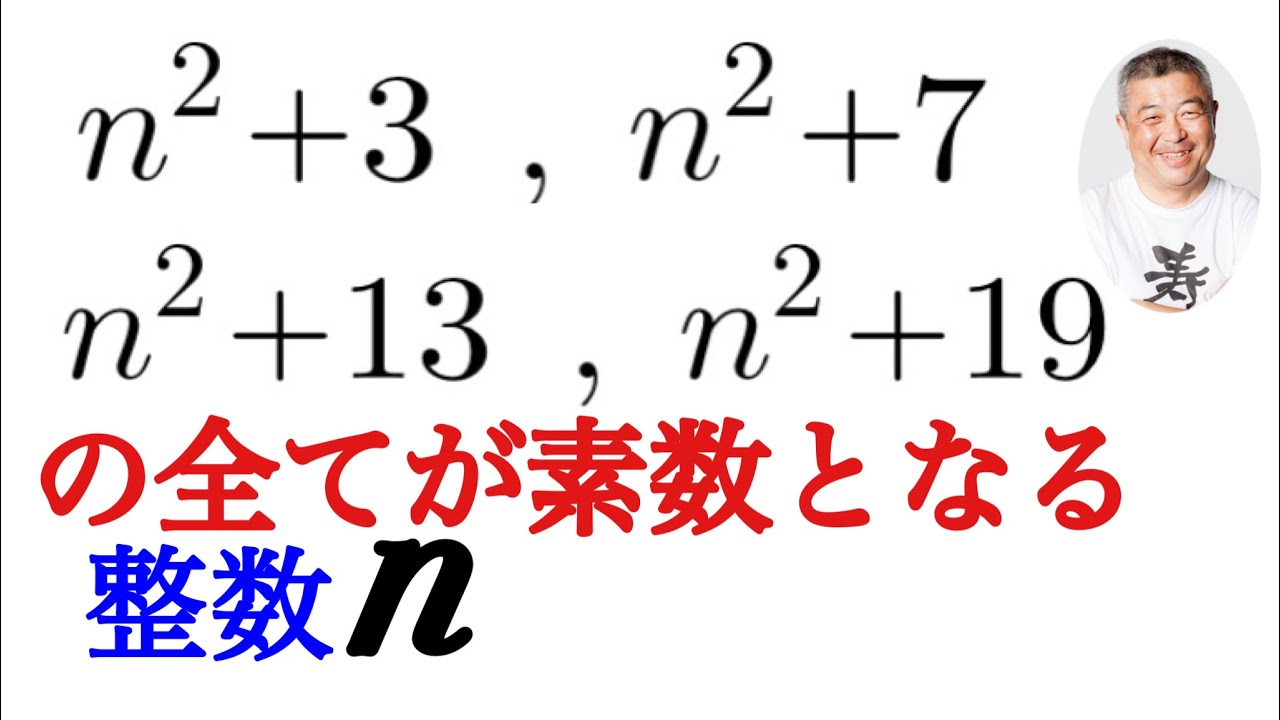
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ n^2+3,n^2+7,n^2+13,n^2+19$のすべてが素数となる整数nをすべて求めよ.
この動画を見る
$ n^2+3,n^2+7,n^2+13,n^2+19$のすべてが素数となる整数nをすべて求めよ.
【高校数学】n進法の足し算引き算をどこよりも丁寧に 5-12【数学A】

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle (1)\,
11011_{(2)} + 111_{(2)}
$
$\displaystyle (2)\,
1323_{(5)} + 402_{(5)}
$
$\displaystyle (3)\,
100101_{(2)} + 1011_{(2)}
$
$\displaystyle (4)\,
2143_{(6)} + 452_{(6)}
$
この動画を見る
$\displaystyle (1)\,
11011_{(2)} + 111_{(2)}
$
$\displaystyle (2)\,
1323_{(5)} + 402_{(5)}
$
$\displaystyle (3)\,
100101_{(2)} + 1011_{(2)}
$
$\displaystyle (4)\,
2143_{(6)} + 452_{(6)}
$
【数学ネタ】近似値を信用しない人 #Shorts

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$2^{30}$の桁数を求めよ。
ただし、$\log_{10}2$=0.3010とする。
この動画を見る
$2^{30}$の桁数を求めよ。
ただし、$\log_{10}2$=0.3010とする。
福田の数学〜早稲田大学2022年人間科学部第7問〜複素数平面上の点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#円と方程式#軌跡と領域#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{7}}\ i$を虚数単位とする。$\alpha=-1+i$とし、zは次の条件をともに満たす複素数とする。
条件1.$\frac{z-\alpha}{z-\bar{\alpha}}$の実部は0である。
条件2.zの虚部は0以上である。
このとき、複素数平面上でzがとりうる値全体の集合を表す図形Cと、実軸で
囲まれる部分の面積は$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\pi$である。
また、$w=\frac{iz}{z+1}$で表される点wがとりうる値全体の集合を表す図形と、
図形Cで囲まれる部分の面積は$\frac{\boxed{\ \ ウ\ \ }\ \pi+\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{7}}\ i$を虚数単位とする。$\alpha=-1+i$とし、zは次の条件をともに満たす複素数とする。
条件1.$\frac{z-\alpha}{z-\bar{\alpha}}$の実部は0である。
条件2.zの虚部は0以上である。
このとき、複素数平面上でzがとりうる値全体の集合を表す図形Cと、実軸で
囲まれる部分の面積は$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\pi$である。
また、$w=\frac{iz}{z+1}$で表される点wがとりうる値全体の集合を表す図形と、
図形Cで囲まれる部分の面積は$\frac{\boxed{\ \ ウ\ \ }\ \pi+\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$である。
2022早稲田大学人間科学部過去問
大学入試問題#274 横浜国立大学後期2012 #区分求積法 #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\{\displaystyle \frac{(2n)!}{n!n^n}\}^{\frac{1}{n}}$を求めよ
出典:2010年横浜国立大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\{\displaystyle \frac{(2n)!}{n!n^n}\}^{\frac{1}{n}}$を求めよ
出典:2010年横浜国立大学 入試問題
解けるようにできた4次方程式 要工夫
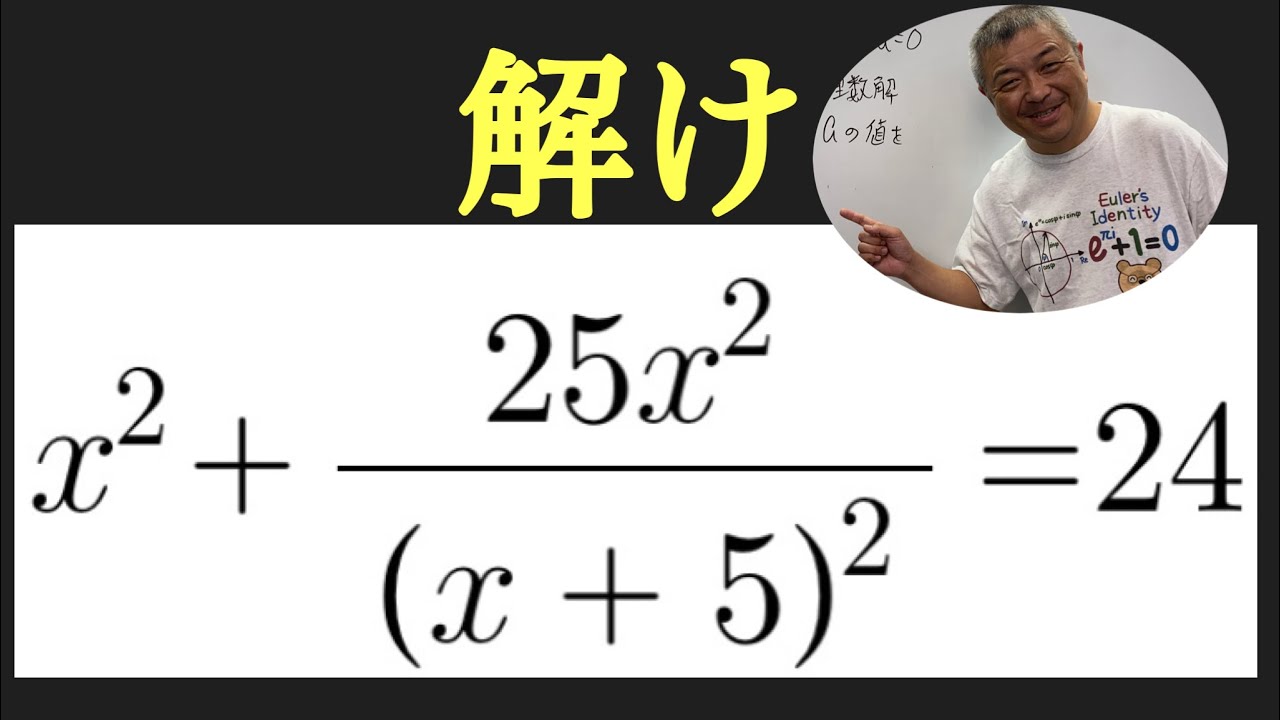
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^2+\dfrac{25x^2}{(x+5)^2}=24$
これを解け.
この動画を見る
$ x^2+\dfrac{25x^2}{(x+5)^2}=24$
これを解け.
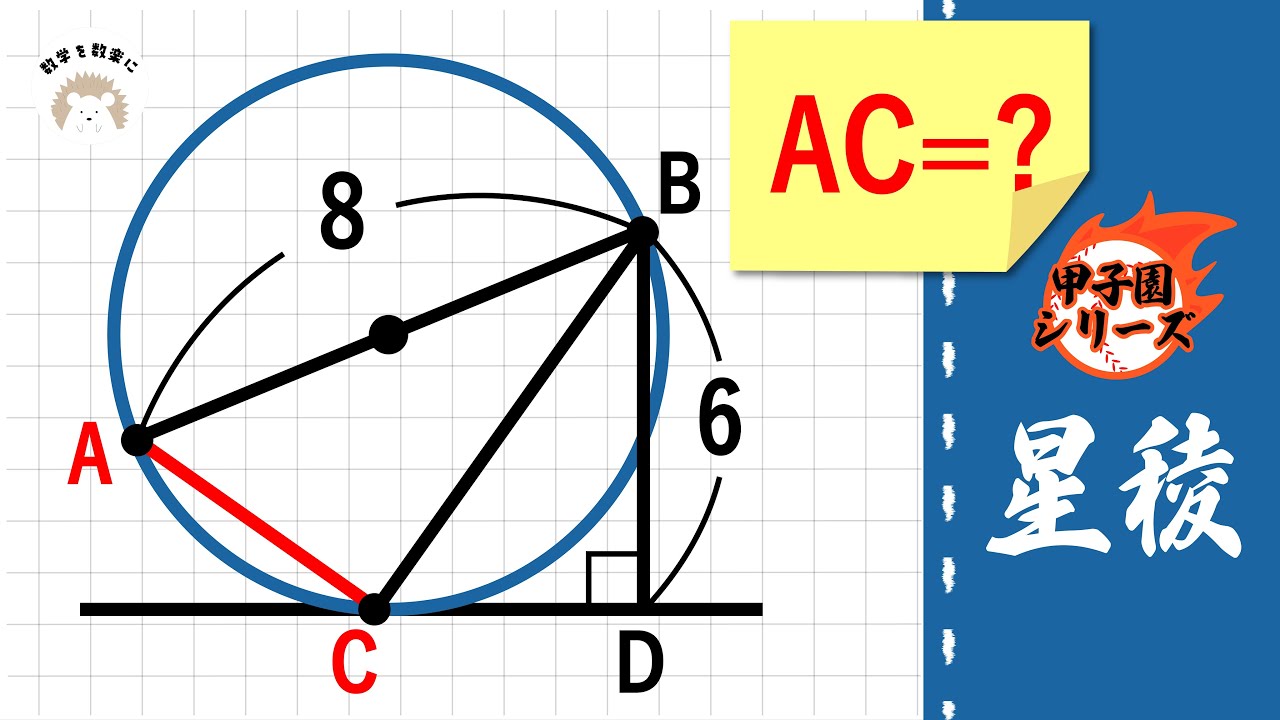
円 星稜
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AC=?
*図は動画内参照
星稜高等学校
この動画を見る
AC=?
*図は動画内参照
星稜高等学校
【頻出】あれを使う!落としてはいけない問題です【数学 入試問題】【茨城大学】

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$21^{2015}$を400で割ったときの余りを求めよ。
茨城大過去問
この動画を見る
$21^{2015}$を400で割ったときの余りを求めよ。
茨城大過去問
福田の数学〜早稲田大学2022年人間科学部第6問〜楕円を軸以外の直線で回転させた立体の体積

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#微分法と積分法#接線と増減表・最大値・最小値#微分とその応用#積分とその応用#2次曲線#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{6}}$直線$x+y=1$に接する楕円$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a \gt 0,\ b \gt 0)$がある。
このとき、$b^2=\boxed{\ \ ア\ \ }\ a^2+\boxed{\ \ イ\ \ }$である。
この楕円を直線$y=b$のまわりに1回転してできる立体の体積は、
$a=\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$のとき、
最大値$\frac{\boxed{\ \ オ\ \ }\sqrt{\boxed{\ \ カ\ \ }}}{\boxed{\ \ キ\ \ }}\pi^2$をとる。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{6}}$直線$x+y=1$に接する楕円$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a \gt 0,\ b \gt 0)$がある。
このとき、$b^2=\boxed{\ \ ア\ \ }\ a^2+\boxed{\ \ イ\ \ }$である。
この楕円を直線$y=b$のまわりに1回転してできる立体の体積は、
$a=\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$のとき、
最大値$\frac{\boxed{\ \ オ\ \ }\sqrt{\boxed{\ \ カ\ \ }}}{\boxed{\ \ キ\ \ }}\pi^2$をとる。
2022早稲田大学人間科学部過去問
大学入試問題#273 日本大学(2010) #微分 #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq x \leqq \pi$
$f(x)=e^{-\frac{3}{4}\sin^2x}\sin2x$
$x=\alpha$で$f(x)$は最大値をとる
(1)$\sin\alpha$の値
(2)$\displaystyle \int_{0}^{\alpha}f(x)dx$
出典:2013年日本大学 入試問題
この動画を見る
$0 \leqq x \leqq \pi$
$f(x)=e^{-\frac{3}{4}\sin^2x}\sin2x$
$x=\alpha$で$f(x)$は最大値をとる
(1)$\sin\alpha$の値
(2)$\displaystyle \int_{0}^{\alpha}f(x)dx$
出典:2013年日本大学 入試問題
ただの分数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{3}{m}+\dfrac{4}{n}=\dfrac{1}{12}$,自然数(m,n)をすべて求めよ.
ただし,$\dfrac{3}{m},\dfrac{4}{m}$は既約分数である.
この動画を見る
$ \dfrac{3}{m}+\dfrac{4}{n}=\dfrac{1}{12}$,自然数(m,n)をすべて求めよ.
ただし,$\dfrac{3}{m},\dfrac{4}{m}$は既約分数である.
福田の数学〜早稲田大学2022年人間科学部第5問〜2次関数の区間の動く最大最小

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#面積、体積#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{5}}$aを実数とする。関数
$f(x)=-x^2+6x(a-2 \leqq x \leqq a)$
の最大値をg(a)、最小値をh(a)とする。このとき、
$ab$平面において$b=g(a)$のグラフとa軸によって囲まれる部分の面積は$\boxed{\ \ ア\ \ }$であり、
ab平面において$b=h(a)$のグラフとa軸によって囲まれる部分の面積は$\boxed{\ \ イ\ \ }$である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{5}}$aを実数とする。関数
$f(x)=-x^2+6x(a-2 \leqq x \leqq a)$
の最大値をg(a)、最小値をh(a)とする。このとき、
$ab$平面において$b=g(a)$のグラフとa軸によって囲まれる部分の面積は$\boxed{\ \ ア\ \ }$であり、
ab平面において$b=h(a)$のグラフとa軸によって囲まれる部分の面積は$\boxed{\ \ イ\ \ }$である。
2022早稲田大学人間科学部過去問
大学入試問題#272 慶應義塾大学(2010) #y軸回転体 #定積分 #バームクーヘン積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
曲線$y=\displaystyle \frac{x}{\sqrt{ 1-x^2 }}$
$x$軸、$x=\displaystyle \frac{1}{2}$で囲まれた部分を$y$軸中心に回転した体積$V$を求めよ。
出典:2010年慶應義塾大学 入試問題
この動画を見る
曲線$y=\displaystyle \frac{x}{\sqrt{ 1-x^2 }}$
$x$軸、$x=\displaystyle \frac{1}{2}$で囲まれた部分を$y$軸中心に回転した体積$V$を求めよ。
出典:2010年慶應義塾大学 入試問題
