 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【数C】【空間ベクトル】点A(3,-4,2)に関して、点P(1,2,3)と対称な点Qの座標を求めよ

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
点A(3,-4,2)に関して、点P(1,2,3)と対称な点Qの座標を求めよ
この動画を見る
点A(3,-4,2)に関して、点P(1,2,3)と対称な点Qの座標を求めよ
【数Ⅲ】【関数と極限】無限級数1-(x+y)+(x+y)²-(x+y)³+…+{-(x+y)}^n-1 +…が収束し、その和が1/1-xであるとき、yをxの式で表し、そのグラフをかけ。

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
$|r| \lt 1$ のとき $\displaystyle\lim_{n \to \infty} n r^n = 0$ である。
このことを利用して$,$ 次の無限級数の和を求めよ。ただし$,$ $|x| < 1$ とする。
$(1)$ $\displaystyle \frac{1}{3}$ $+ \displaystyle \frac{2}{9}$ $+\displaystyle \frac{3}{27}$ $+ \cdots \cdots$ $
+\displaystyle \frac{n}{3^n}$ $ + \cdots \cdots$
$(2)$ $1 + 2x + 3x^2 $$ + \cdots \cdots $$ + n x^{n-1} + \cdots \cdots$
この動画を見る
$|r| \lt 1$ のとき $\displaystyle\lim_{n \to \infty} n r^n = 0$ である。
このことを利用して$,$ 次の無限級数の和を求めよ。ただし$,$ $|x| < 1$ とする。
$(1)$ $\displaystyle \frac{1}{3}$ $+ \displaystyle \frac{2}{9}$ $+\displaystyle \frac{3}{27}$ $+ \cdots \cdots$ $
+\displaystyle \frac{n}{3^n}$ $ + \cdots \cdots$
$(2)$ $1 + 2x + 3x^2 $$ + \cdots \cdots $$ + n x^{n-1} + \cdots \cdots$
【数C】【空間ベクトル】4点A(1,0,0)、B(0,1,0)、C(0,0,2)、D(1,2,3)がある。△ABCの面積Sと、四面体ABCDの体積Vを求めよ。

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
4点A(1,0,0)、B(0,1,0)、C(0,0,2)、D(1,2,3)がある。△ABCの面積Sと、四面体ABCDの体積Vを求めよ。
この動画を見る
4点A(1,0,0)、B(0,1,0)、C(0,0,2)、D(1,2,3)がある。△ABCの面積Sと、四面体ABCDの体積Vを求めよ。
【数Ⅲ】【関数】垂線AA1, A1A2 ,A2A3, …を下ろすとき、△CAA1, △CA1A2, △CA2A3,…の面積の総和が△ABCの面積を超えないためには∠Cの大きさはどんな範囲にあればよいか

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のような直角三角形ABCの直角の頂点Aから、
順に、垂線AA1, A1A2 ,A2A3, …を下ろすとき、△CAA1,
△CA1A2, △CA2A3,…の面積の総和が△ABCの面積を
超えないためには、∠Cの大きさはどんな範囲に
あればよいか。
この動画を見る
図のような直角三角形ABCの直角の頂点Aから、
順に、垂線AA1, A1A2 ,A2A3, …を下ろすとき、△CAA1,
△CA1A2, △CA2A3,…の面積の総和が△ABCの面積を
超えないためには、∠Cの大きさはどんな範囲に
あればよいか。
【数Ⅲ】【関数】次の条件によって定められる数列{an}の極限を求めよ。 a1=10, an+1=2√an

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件によって定められる数列$\{a_n\}$の極限を求めよ。
$a_1=10, a_{n+1}=2\sqrt{a_n}\quad (n=1,2,3,\cdots)$
この動画を見る
次の条件によって定められる数列$\{a_n\}$の極限を求めよ。
$a_1=10, a_{n+1}=2\sqrt{a_n}\quad (n=1,2,3,\cdots)$
【数Ⅲ】【関数】数列{an}に対して、lim(n→∞)(an+5)/(2an+1)=3であるとき、lim(n→∞)anを求めよ。

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
数列$\{a_n\}$に対して、
$\displaystyle \lim_{n\rightarrow\infty}\dfrac{a_n+5}{2a_n+1}=3$であるとき、$\displaystyle \lim_{n\rightarrow\infty}a_n$を求めよ。
この動画を見る
数列$\{a_n\}$に対して、
$\displaystyle \lim_{n\rightarrow\infty}\dfrac{a_n+5}{2a_n+1}=3$であるとき、$\displaystyle \lim_{n\rightarrow\infty}a_n$を求めよ。
【総集編】三角形の合同の証明まとめ~テスト前これだけ見よ~

【数Ⅲ】【関数】次の関数のグラフをかけ。(1) y=√(4-x²)(2) y=-2/3 √(9-x² )(3) y=3/2 √(x²+4)

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数のグラフをかけ。
(1) $y=\sqrt{4-x^2}$
(2) $y=-\dfrac23\sqrt{9-x^2}$
(3) $y=\dfrac32\sqrt{x^2+4}$
この動画を見る
次の関数のグラフをかけ。
(1) $y=\sqrt{4-x^2}$
(2) $y=-\dfrac23\sqrt{9-x^2}$
(3) $y=\dfrac32\sqrt{x^2+4}$
理論化学基礎演習26 水素吸蔵合金

単元:
#大学入試過去問(数学)#化学#学校別大学入試過去問解説(数学)#無機#典型金属元素の単体と化合物#芝浦工業大学#数学(高校生)#理科(高校生)
指導講師:
ぺんぎん高校化学問題集
この動画を見る
【数Ⅲ】【関数】2つの関数 y=√(x+1), y= x+ kのグラフの共有点の個数を調べよ。

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
2つの関数
$y=\sqrt{x+1}$
$y=x+k$
のグラフの共有点の個数を調べよ。
この動画を見る
2つの関数
$y=\sqrt{x+1}$
$y=x+k$
のグラフの共有点の個数を調べよ。
【数Ⅲ】【関数】次の不等式を解け。(1) (x-4)/(x²+x-6) >0 (2) 2/(x-1) - 2/x ≧1

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不等式を解け。
(1) $\dfrac{x-4}{x^2+x-6}>0$
(2) $\dfrac2{x-1}-\dfrac2x\geqq1$
この動画を見る
次の不等式を解け。
(1) $\dfrac{x-4}{x^2+x-6}>0$
(2) $\dfrac2{x-1}-\dfrac2x\geqq1$
【高校数学】三角比を使った三角形の面積の求め方 3-9【数学Ⅰ】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【高校数学】三角比を使った三角形の面積の求め方を解説していきます。
$\triangle ABC$の面積$S$を求めよ。
(1)$b=4,c=7,A=45°$
(2)$a=7,b=5,c=8$
この動画を見る
【高校数学】三角比を使った三角形の面積の求め方を解説していきます。
$\triangle ABC$の面積$S$を求めよ。
(1)$b=4,c=7,A=45°$
(2)$a=7,b=5,c=8$
【数Ⅲ】【関数と極限】無限級数1-(x+y)+(x+y)²-(x+y)³+…+{-(x+y)}^n-1 +…が収束し、その和が1/1-xであるとき、yをxの式で表し、そのグラフをかけ。

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
無限級数
$1- (x+y) $$ + (x+y)^2 - (x+y)^3 $$ + \cdots \cdots + \{ -(x+y) \}^{n-1} $$ + \cdots \cdots$
が収束し、その和が $\displaystyle \frac{1}{1-x}$ であるとき、
$y$ を $x$ で表し、そのグラフをかけ。
この動画を見る
無限級数
$1- (x+y) $$ + (x+y)^2 - (x+y)^3 $$ + \cdots \cdots + \{ -(x+y) \}^{n-1} $$ + \cdots \cdots$
が収束し、その和が $\displaystyle \frac{1}{1-x}$ であるとき、
$y$ を $x$ で表し、そのグラフをかけ。
【数Ⅲ】【関数と極限】次のものが収束するような実数xの値の範囲を求めよ。(1) 無限数列{(x²-2x)^n}(2) 無限級数Σ(x²-2x)^n

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のものが収束するような実数 $x$ の値の範囲を求めよ。
$(1)$ 無限数列 $ \{ (x^2-2x)^n \}$
$(2)$ 無限級数 $\displaystyle \sum_{n=1}^\infty \{ (x^2-2x)^n \}$
この動画を見る
次のものが収束するような実数 $x$ の値の範囲を求めよ。
$(1)$ 無限数列 $ \{ (x^2-2x)^n \}$
$(2)$ 無限級数 $\displaystyle \sum_{n=1}^\infty \{ (x^2-2x)^n \}$
【数Ⅲ】【関数と極限】次の無限級数の和を求めよ。(1) Σ(1/3)^n・cos nπ(2) Σ(-1/3)^n・sin nπ/2

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の無限級数の和を求めよ。
(1)$\displaystyle\sum_{n=1}^{\infty} \left( \dfrac{1}{3} \right)^n \cos n\pi$
(2) $\displaystyle\sum_{n=1}^{\infty} \left( -\dfrac{1}{3} \right)^n \sin \dfrac{n\pi}{2}$
この動画を見る
次の無限級数の和を求めよ。
(1)$\displaystyle\sum_{n=1}^{\infty} \left( \dfrac{1}{3} \right)^n \cos n\pi$
(2) $\displaystyle\sum_{n=1}^{\infty} \left( -\dfrac{1}{3} \right)^n \sin \dfrac{n\pi}{2}$
【数Ⅲ】【関数と極限】無限等比級数で表された関数 f(x)=sinx・cosx + sin³x・cosx + sin⁵x・cosx + …について、y=f(x)のグラフをかけ。

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
無限等比級数で表された関数
$f(x) = \sin x \cos x + \sin^3 x \cos x + \sin^5 x \cos x + \cdots$
について、y=f(x)のグラフをかけ。
この動画を見る
無限等比級数で表された関数
$f(x) = \sin x \cos x + \sin^3 x \cos x + \sin^5 x \cos x + \cdots$
について、y=f(x)のグラフをかけ。
【数Ⅲ】【関数と極限】次の無限級数が0以上の実数xに対して収束することを示せ。和のf(x)のグラフをかけ。√x + √x/1+√x + √x/(1+√x)² + … + √x/(1+√x)^n-1 …

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の無限級数が$0$以上のすべての実数$x$に対して収束することを示せ。
また,その和を$f(x)$とおくとき,関数$y=f(x)$のグラフをかけ。
$\frac{\sqrt{x}}{1+\sqrt{x}} + \frac{\sqrt{x}}{(1+\sqrt{x})^2} + \cdots + \frac{\sqrt{x}}{(1+\sqrt{x})^{n-1}} + \cdots$
この動画を見る
次の無限級数が$0$以上のすべての実数$x$に対して収束することを示せ。
また,その和を$f(x)$とおくとき,関数$y=f(x)$のグラフをかけ。
$\frac{\sqrt{x}}{1+\sqrt{x}} + \frac{\sqrt{x}}{(1+\sqrt{x})^2} + \cdots + \frac{\sqrt{x}}{(1+\sqrt{x})^{n-1}} + \cdots$
【数Ⅲ】【関数と極限】次の式を計算し、結果を循環小数で表せ。(1) 0.36×0.32(2) 1.25÷0.05

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式を計算し,結果を循環小数で表せ。
(1)$0.\dot{3}\dot{6} \times 0.3\dot{2}$
(2) $1.\dot{2}\dot{5} \div 0.0\dot{5}$
この動画を見る
次の式を計算し,結果を循環小数で表せ。
(1)$0.\dot{3}\dot{6} \times 0.3\dot{2}$
(2) $1.\dot{2}\dot{5} \div 0.0\dot{5}$
【数C】【空間ベクトル】3点A(3,6,0)、B(1,4,0)、C(0,5,4)の定める平面ABCに、点P(3,4,5)から垂線PHを下ろす。線分PHの長さを求めよ。

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
3点A(3,6,0)、B(1,4,0)、C(0,5,4)の定める平面ABCに、点P(3,4,5)から垂線PHを下ろす。線分PHの長さを求めよ。
この動画を見る
3点A(3,6,0)、B(1,4,0)、C(0,5,4)の定める平面ABCに、点P(3,4,5)から垂線PHを下ろす。線分PHの長さを求めよ。
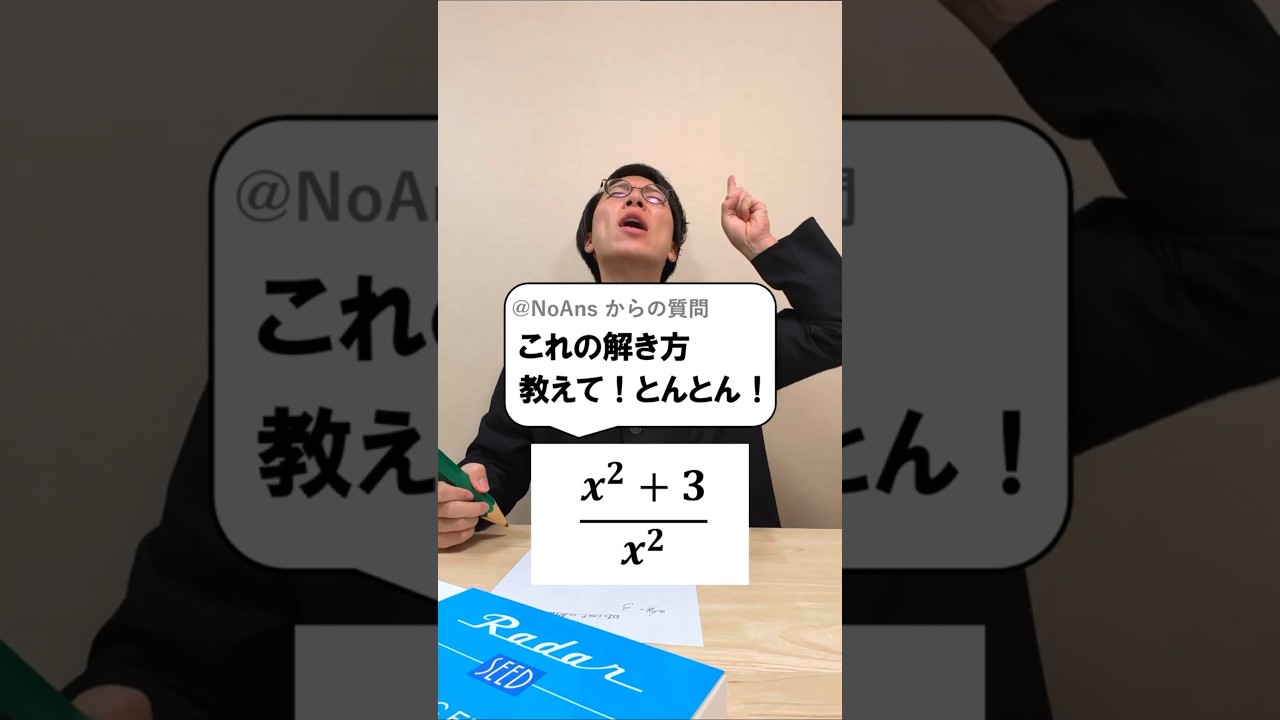
間違い説明できる?
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
この計算の解き方を解説していきます。
$\dfrac{x^2+3}{x^2}$
この動画を見る
この計算の解き方を解説していきます。
$\dfrac{x^2+3}{x^2}$
【数C】【空間ベクトル】(1) 2点A(5,-2,-3)、B(8,0,-4)を通る直線に垂線OHを下ろす。点Hの座標と線分OHの長さを求めよ。他1問

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1) 2点A(5,-2,-3)、B(8,0,-4)を通る直線に、原点Oから垂線OHを下ろす。このとき、点Hの座標と線分OHの長さを求めよ。
(2) 2点A(0.-2,-3)、B(8,4,7)を通る直線に、点P(3,-1,4)から垂線PHを下ろす。このとき、点Hの座標と線分PHの長さを求めよ
この動画を見る
(1) 2点A(5,-2,-3)、B(8,0,-4)を通る直線に、原点Oから垂線OHを下ろす。このとき、点Hの座標と線分OHの長さを求めよ。
(2) 2点A(0.-2,-3)、B(8,4,7)を通る直線に、点P(3,-1,4)から垂線PHを下ろす。このとき、点Hの座標と線分PHの長さを求めよ
計算しないで答えを出せ!奈良教育大

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#奈良教育大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m, n$は自然数、$m$は定数
$S(n)=1+2+3+...+mn$
$T(n)=S(n)-(1~mn間のmの倍数の和)$
$\displaystyle \lim_{ n \to \infty } \frac {T(n)}{S(n)}$
この動画を見る
$m, n$は自然数、$m$は定数
$S(n)=1+2+3+...+mn$
$T(n)=S(n)-(1~mn間のmの倍数の和)$
$\displaystyle \lim_{ n \to \infty } \frac {T(n)}{S(n)}$
【数C】【空間ベクトル】四面体OABCにおいて、OA=OB、→OC⊥→ABとする。(1) AC=BCであることを証明せよ(2) 三角形ABCの重心をGとするとき、→OG⊥→ABであることを証明せよ

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
四面体OABCにおいて、OA=OB、
OC⊥ABとする。
(1) AC=BCであることを証明せよ
(2) 三角形ABCの重心をGとするとき、OG⊥ABであることを証明せよ
この動画を見る
四面体OABCにおいて、OA=OB、
OC⊥ABとする。
(1) AC=BCであることを証明せよ
(2) 三角形ABCの重心をGとするとき、OG⊥ABであることを証明せよ
【数C】【空間ベクトル】四面体ABCDにおいて、次のことを証明せよ。(1) →AB・→AC=→AC・→AD=→AD・→AB(2) AB⊥CD

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
正四面体 $\mathrm{ABCD}$ において、次のことを証明せよ。
(1) $\vec{\mathrm{AB}}\cdot\vec{\mathrm{AC}} = \vec{\mathrm{AC}}\cdot\vec{\mathrm{AD}} = \vec{\mathrm{AD}}\cdot\vec{\mathrm{AB}}$
(2) $\mathrm{AB}\perp\mathrm{CD}$
この動画を見る
正四面体 $\mathrm{ABCD}$ において、次のことを証明せよ。
(1) $\vec{\mathrm{AB}}\cdot\vec{\mathrm{AC}} = \vec{\mathrm{AC}}\cdot\vec{\mathrm{AD}} = \vec{\mathrm{AD}}\cdot\vec{\mathrm{AB}}$
(2) $\mathrm{AB}\perp\mathrm{CD}$
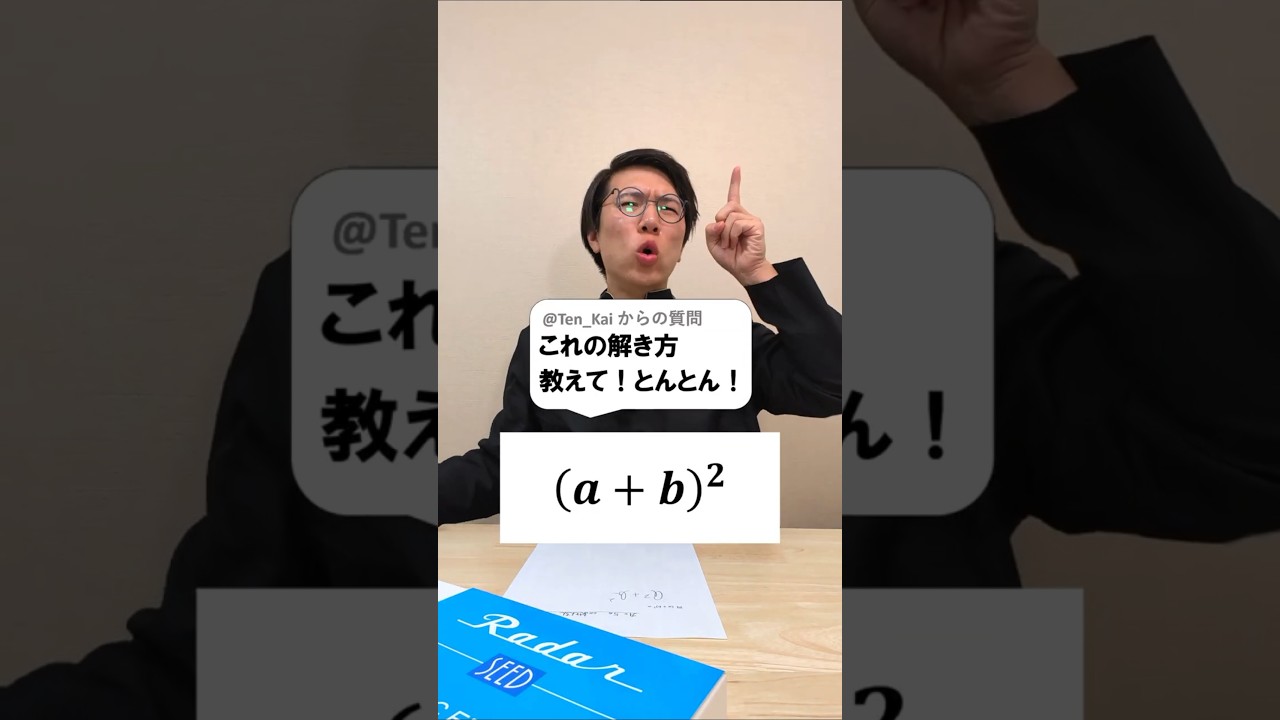
これなにが間違い?
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$(a+b)^2$のどこが間違いか解説していきます。
この動画を見る
$(a+b)^2$のどこが間違いか解説していきます。
【数C】【空間ベクトル】a,bはベクトルとする。a=(3,4,0)とb=(0,x,-√7)のなす角が45°であるとき,xの値を求めよ。

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\vec{a}=(3, \, 4, \, 0)$ と $\vec{b}=(0, \, x, \, -\sqrt{7})$ のなす角が $45^{\circ}$ であるとき、$x$ の値を求めよ。
この動画を見る
$\vec{a}=(3, \, 4, \, 0)$ と $\vec{b}=(0, \, x, \, -\sqrt{7})$ のなす角が $45^{\circ}$ であるとき、$x$ の値を求めよ。
【数C】【空間ベクトル】4点A(1,1,2)、B(0,-4,0)、C(-1,1,-2)、D(2,3,5)がある。線分AB,AC,ADを3辺とする平行六面体の他の頂点の座標を求めよ。

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
4点A(1,1,2)、B(0,-4,0)、C(-1,1,-2)、D(2,3,5)がある。線分AB,AC,ADを3辺とする平行六面体の他の頂点の座標を求めよ。
この動画を見る
4点A(1,1,2)、B(0,-4,0)、C(-1,1,-2)、D(2,3,5)がある。線分AB,AC,ADを3辺とする平行六面体の他の頂点の座標を求めよ。
【数C】【空間ベクトル】a=(1,-1,-3)、b=(2,2,1)、c=(-1,-1,0)とする。|a+xb+yc|を最小にする実数x,yの値を求めよ。

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
a,b,cをベクトルとする。a=(1,-1,-3)、b=(2,2,1)、c=(-1,-1,0)とする。|a+xb+yc|を最小にする実数x,yの値を求めよ。
この動画を見る
a,b,cをベクトルとする。a=(1,-1,-3)、b=(2,2,1)、c=(-1,-1,0)とする。|a+xb+yc|を最小にする実数x,yの値を求めよ。
【数C】【空間ベクトル】a=(0,1,2)、b=(2,4,6)とする。x=a+tb(tは実数)について、|x|の最小値を求めよ。また、その時のxを成分表示せよ。

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
a,b,xをベクトルとする。
a=(0,1,2)、b=(2,4,6)とする。
x=a+tb(tは実数)について、|x|の最小値を求めよ。また、その時のxを成分表示せよ。
この動画を見る
a,b,xをベクトルとする。
a=(0,1,2)、b=(2,4,6)とする。
x=a+tb(tは実数)について、|x|の最小値を求めよ。また、その時のxを成分表示せよ。
【数C】【空間ベクトル】平行四辺形の3つの頂点がA(3,0,-4)、B(-2,5,-1)、C(4,3,2)のとき、第4の頂点の座標を求めよ。

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
平行四辺形の3つの頂点がA(3,0,-4)、B(-2,5,-1)、C(4,3,2)のとき、第4の頂点の座標を求めよ。
この動画を見る
平行四辺形の3つの頂点がA(3,0,-4)、B(-2,5,-1)、C(4,3,2)のとき、第4の頂点の座標を求めよ。
