 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【数Ⅱ】【三角関数】加法定理の応用6 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数のグラフをかけ。また、その周期をいえ。
(1) y=cos² x
(2) y=3sin² x+cos² x
この動画を見る
次の関数のグラフをかけ。また、その周期をいえ。
(1) y=cos² x
(2) y=3sin² x+cos² x
【数Ⅱ】【三角関数】加法定理の応用5 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
-π/2≦x≦π/2 とする。関数 y=2sinx-cos2x の最大値、最小値と、そのときのxの値を求めよ。
この動画を見る
-π/2≦x≦π/2 とする。関数 y=2sinx-cos2x の最大値、最小値と、そのときのxの値を求めよ。
【数Ⅱ】【三角関数】加法定理の応用4 ※問題文は概要欄
単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
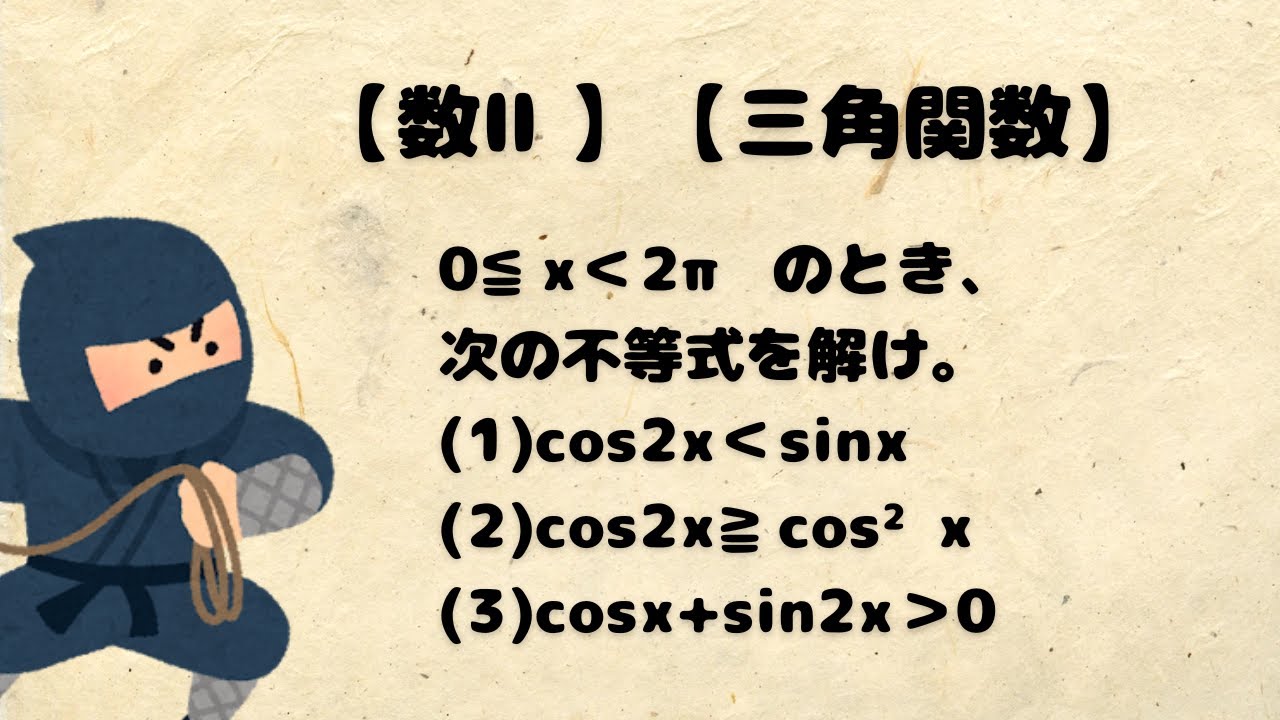
0≦x<2π のとき、次の不等式を解け。
(1)cos2x<sinx
(2)cos2x≧cos² x
(3)cosx+sin2x>0
この動画を見る
0≦x<2π のとき、次の不等式を解け。
(1)cos2x<sinx
(2)cos2x≧cos² x
(3)cosx+sin2x>0
【数Ⅱ】【三角関数】加法定理の応用3 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
0≦x<2π のとき、次の方程式を解け。
(1)cos2x=cosx
(2)sin2x=cosx
(3)2cos2x+4cosx-1=0
(4)sinx(1+cos2x)+sin2x(1+cosx)=0
この動画を見る
0≦x<2π のとき、次の方程式を解け。
(1)cos2x=cosx
(2)sin2x=cosx
(3)2cos2x+4cosx-1=0
(4)sinx(1+cos2x)+sin2x(1+cosx)=0
【数Ⅱ】【三角関数】加法定理の応用2 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
tanα=t のときcos² α ,sin2α ,cos2α を t で表せ。
この動画を見る
tanα=t のときcos² α ,sin2α ,cos2α を t で表せ。
【数Ⅱ】【三角関数】加法定理の応用1 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
等式cos3α+sin3α=(cosα-sinα)(1+2sin2α)を証明せよ。
この動画を見る
等式cos3α+sin3α=(cosα-sinα)(1+2sin2α)を証明せよ。
2025年高校別東京大学合格者ランキング #shorts

単元:
#大学入試過去問(数学)#物理#学校別大学入試過去問解説(数学)#大学入試過去問(物理)#英語(高校生)#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#東京大学#数学(高校生)#理科(高校生)#東京大学#東京大学
指導講師:
Morite2 English Channel
問題文全文(内容文):
2025年版!高校別東大合格者数ランキング速報がヤバい!
このランキングはまだ暫定版で、筑駒の数字はまだ出ていないが、激アツな順位が明らかになったぞ。
栄えある第1位は、今年も駒の数字はまだ出ていないが、激アツな順位が明らかになったぞ。
栄えある第1位は、今年も**開成高校**で149人合格の圧倒的な強さを見せつけた。
そして注目すべきは公立高校の躍進だ!
* 第3位には**日比谷高校**がランクインし、公立ながら東大に81人も合格させている。
* 第7位には**横浜翠嵐高校**(神奈川県)が74人で食い込む。
* 第14位には**県立浦和**が41人で登場だ。
* さらに、**旭丘**(愛知)が28人、**千葉高校**(県立)が21人、**宇都宮**(栃木)が20人、**岡崎**(愛知)も20人と、全国の公立高校が猛追している!
私立ももちろん強い。2位が**聖光学院**(神奈川)で95人、4位**麻布**(79人)、5位**灘**(76人)、6位**渋谷教育学園幕張**(千葉、75人)と続く。神奈川勢は、聖光学院、横浜翠嵐、栄光学園(8位、55人)、浅野(9位、51人)と大健闘だ。
**渋渋(渋谷教育学園渋谷)が50人で10位**に入り、今年も伸びを見せつけているぞ。
このランキングを見れば、どの高校が東大合格戦線をリードしているのか一目瞭然だ。お前らの高校は何位だ!?
この動画を見る
2025年版!高校別東大合格者数ランキング速報がヤバい!
このランキングはまだ暫定版で、筑駒の数字はまだ出ていないが、激アツな順位が明らかになったぞ。
栄えある第1位は、今年も駒の数字はまだ出ていないが、激アツな順位が明らかになったぞ。
栄えある第1位は、今年も**開成高校**で149人合格の圧倒的な強さを見せつけた。
そして注目すべきは公立高校の躍進だ!
* 第3位には**日比谷高校**がランクインし、公立ながら東大に81人も合格させている。
* 第7位には**横浜翠嵐高校**(神奈川県)が74人で食い込む。
* 第14位には**県立浦和**が41人で登場だ。
* さらに、**旭丘**(愛知)が28人、**千葉高校**(県立)が21人、**宇都宮**(栃木)が20人、**岡崎**(愛知)も20人と、全国の公立高校が猛追している!
私立ももちろん強い。2位が**聖光学院**(神奈川)で95人、4位**麻布**(79人)、5位**灘**(76人)、6位**渋谷教育学園幕張**(千葉、75人)と続く。神奈川勢は、聖光学院、横浜翠嵐、栄光学園(8位、55人)、浅野(9位、51人)と大健闘だ。
**渋渋(渋谷教育学園渋谷)が50人で10位**に入り、今年も伸びを見せつけているぞ。
このランキングを見れば、どの高校が東大合格戦線をリードしているのか一目瞭然だ。お前らの高校は何位だ!?
福田のおもしろ数学435〜正三角形の内部の点の位置から面積を求める
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
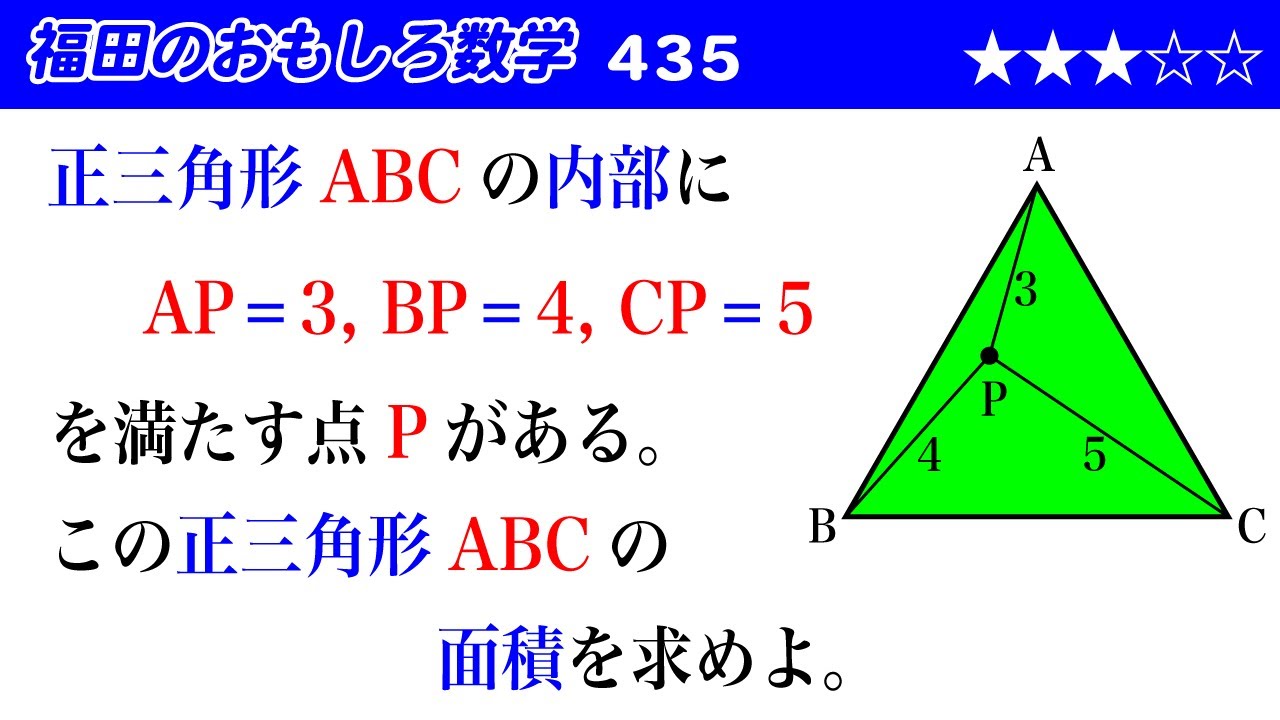
正三角形$ABC$の内部に
$AP=3,BP=4,CP=5$を満たす点$P$がある。
この正三角形$ABC$の面積を求めよ。
図は動画内参照
この動画を見る
正三角形$ABC$の内部に
$AP=3,BP=4,CP=5$を満たす点$P$がある。
この正三角形$ABC$の面積を求めよ。
図は動画内参照
福田の数学〜京都大学2025理系第4問〜平面が定点を通過する条件

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
座標空間の$4$点$O,A,B,C$は同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、
直線$OB$上の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA },\overrightarrow{ OM }=t\overrightarrow{ OB },\overrightarrow{ ON }=u\overrightarrow{ OC }$が
成り立つようにとる。
(1)$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点$P$を通ることを示せ。
さらに、そのような点$P$はただ一つに定まることを示せ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{4}$
座標空間の$4$点$O,A,B,C$は同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、
直線$OB$上の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA },\overrightarrow{ OM }=t\overrightarrow{ OB },\overrightarrow{ ON }=u\overrightarrow{ OC }$が
成り立つようにとる。
(1)$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点$P$を通ることを示せ。
さらに、そのような点$P$はただ一つに定まることを示せ。
$2025$年京都大学理系過去問題
【数Ⅲ】【積分とその応用】定積分部分積分 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
定積分$\displaystyle \int_0^1x^2e^{2x}~dx$を求めよ。
定積分$\displaystyle \int_0^\frac\pi2(ax-\sin x)^2~dx$を最小にする実数$a$の値を求めよ。
定積分$\displaystyle I=\int_0^\frac\pi2e^{-3x}\sin x~dx$を求めよ。
自然数$n$について、$\displaystyle I_n=\int_1^e(\log x)^n~dx$とする。
(1) $I_1$を求めよ。
(2) $I_{n+1}$を$I_n$を用いて表せ。
(3) $I_4$を求めよ。
この動画を見る
定積分$\displaystyle \int_0^1x^2e^{2x}~dx$を求めよ。
定積分$\displaystyle \int_0^\frac\pi2(ax-\sin x)^2~dx$を最小にする実数$a$の値を求めよ。
定積分$\displaystyle I=\int_0^\frac\pi2e^{-3x}\sin x~dx$を求めよ。
自然数$n$について、$\displaystyle I_n=\int_1^e(\log x)^n~dx$とする。
(1) $I_1$を求めよ。
(2) $I_{n+1}$を$I_n$を用いて表せ。
(3) $I_4$を求めよ。
【数Ⅲ】【積分とその応用】定積分置換積分 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の定積分を求めよ。
(1) $\displaystyle \int_{-1}^0 (x+2)\sqrt{3x+4}~dx$
(2) $\displaystyle \int_{0}^4 \frac{x^2}{\sqrt{x+1}}~dx$
(3) $\displaystyle \int_{0}^1 \frac{x^3}{\sqrt{1+x^2}}~dx$
(4) $\displaystyle \int_{1}^3 \frac{dx}{x\sqrt{x+1}}$
(5) $\displaystyle \int_{1}^2 \frac{dx}{e^x-1}$
(6) $\displaystyle \int_{0}^{\frac\pi4} \frac{\sin^3x}{\cos^2x}~dx$
次の定積分を求めよ。ただし、$a$は正の定数とする。
(1) $\displaystyle \int_{0}^1 \sqrt{2x-x^2}~dx$
(2) $\displaystyle \int_{1}^{\frac12} \frac{dx}{\sqrt{2x-x^2}}$
(3) $\displaystyle \int_{1}^{\frac a2} \frac{dx}{(a^2-x^2)^{\frac32}}$
(4) $\displaystyle \int_{1}^{2} \frac{dx}{x^2-2x+2}$
(5) $\displaystyle \int_{3}^{5} \frac{dx}{x^2-4x+4}$
(6) $\displaystyle \int_{6}^{12} \frac{dx}{x^2-3x-10}$
(7) $\displaystyle \int_{0}^{a} \frac{dx}{(x^2+a^2)^2}$
(8) $\displaystyle \int_{1}^{\sqrt3} \frac{2x+1}{x^2+1}~dx$
次のことが成り立つことを証明せよ。
(1) $\displaystyle \int_a^b f(x)~dx=\int_a^bf(a+b-x)~dx$
(2) $\displaystyle\int_{-a}^af(x)~dx=\int_0^a\{f(x)+f(-x)\}~dx$
(3) $\displaystyle \int_0^af(x)~dx=\int_0^{\frac a 2}\{f(x)+f(a-x)\}~dx$
(4) $f(a+x)=f(a-x)$のとき$\displaystyle \int_{a-b}^{a+b}f(x)~dx=2\int_a^{a+b}f(x)~dx$
この動画を見る
次の定積分を求めよ。
(1) $\displaystyle \int_{-1}^0 (x+2)\sqrt{3x+4}~dx$
(2) $\displaystyle \int_{0}^4 \frac{x^2}{\sqrt{x+1}}~dx$
(3) $\displaystyle \int_{0}^1 \frac{x^3}{\sqrt{1+x^2}}~dx$
(4) $\displaystyle \int_{1}^3 \frac{dx}{x\sqrt{x+1}}$
(5) $\displaystyle \int_{1}^2 \frac{dx}{e^x-1}$
(6) $\displaystyle \int_{0}^{\frac\pi4} \frac{\sin^3x}{\cos^2x}~dx$
次の定積分を求めよ。ただし、$a$は正の定数とする。
(1) $\displaystyle \int_{0}^1 \sqrt{2x-x^2}~dx$
(2) $\displaystyle \int_{1}^{\frac12} \frac{dx}{\sqrt{2x-x^2}}$
(3) $\displaystyle \int_{1}^{\frac a2} \frac{dx}{(a^2-x^2)^{\frac32}}$
(4) $\displaystyle \int_{1}^{2} \frac{dx}{x^2-2x+2}$
(5) $\displaystyle \int_{3}^{5} \frac{dx}{x^2-4x+4}$
(6) $\displaystyle \int_{6}^{12} \frac{dx}{x^2-3x-10}$
(7) $\displaystyle \int_{0}^{a} \frac{dx}{(x^2+a^2)^2}$
(8) $\displaystyle \int_{1}^{\sqrt3} \frac{2x+1}{x^2+1}~dx$
次のことが成り立つことを証明せよ。
(1) $\displaystyle \int_a^b f(x)~dx=\int_a^bf(a+b-x)~dx$
(2) $\displaystyle\int_{-a}^af(x)~dx=\int_0^a\{f(x)+f(-x)\}~dx$
(3) $\displaystyle \int_0^af(x)~dx=\int_0^{\frac a 2}\{f(x)+f(a-x)\}~dx$
(4) $f(a+x)=f(a-x)$のとき$\displaystyle \int_{a-b}^{a+b}f(x)~dx=2\int_a^{a+b}f(x)~dx$
【数Ⅲ】【積分とその応用】定積分置換積分、部分積分 ※問題文は概要欄

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次を求めよ
(1) $\displaystyle \int_0^1 \sqrt{e^{1-t}}~dt$
(2) $\displaystyle \int_0^{\frac{\pi}2}\frac{\cos{2\theta}}{\sin \theta+\cos\theta}~d\theta$
(3) $\displaystyle\int_0^\pi \sin^4x~dx$
(4) $\displaystyle \int_1^2 \frac{\sqrt{x^2-4x+4}}{x}~dx$
次を求めよ
(1) $\displaystyle \int_0^\pi |\cos2\theta|~d\theta$
(2) $\displaystyle \int_0^\pi|\sin x+\cos x|~dx$
$m,n$は正の整数とする。次の定積分を求めよ。
(1) $\displaystyle \int_0^\pi \cos mx\cos nx~dx$
(2) $\displaystyle \int_0^\pi \sin mx\sin nx~dx$
(3) $\displaystyle \int_0^\pi \sin mx\cos nx~dx$
定積分$\displaystyle \int_0^\pi (1-a\sin x-b\sin2x)^2~dx$を最小にする定数$a,b$の値を求めよ。
この動画を見る
次を求めよ
(1) $\displaystyle \int_0^1 \sqrt{e^{1-t}}~dt$
(2) $\displaystyle \int_0^{\frac{\pi}2}\frac{\cos{2\theta}}{\sin \theta+\cos\theta}~d\theta$
(3) $\displaystyle\int_0^\pi \sin^4x~dx$
(4) $\displaystyle \int_1^2 \frac{\sqrt{x^2-4x+4}}{x}~dx$
次を求めよ
(1) $\displaystyle \int_0^\pi |\cos2\theta|~d\theta$
(2) $\displaystyle \int_0^\pi|\sin x+\cos x|~dx$
$m,n$は正の整数とする。次の定積分を求めよ。
(1) $\displaystyle \int_0^\pi \cos mx\cos nx~dx$
(2) $\displaystyle \int_0^\pi \sin mx\sin nx~dx$
(3) $\displaystyle \int_0^\pi \sin mx\cos nx~dx$
定積分$\displaystyle \int_0^\pi (1-a\sin x-b\sin2x)^2~dx$を最小にする定数$a,b$の値を求めよ。
【数Ⅲ】【積分とその応用】不定積分置換積分、部分積分3 ※問題文は概要欄

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{\sqrt x}{\sqrt[4]{x^3}+1}~dx$
(2) $\displaystyle \int \frac{dx}{x\sqrt{x+1}}$
(3) $\displaystyle \int \log|x^2-1|~dx$
(4) $\displaystyle \int \frac{e^x}{e^x-e^{-x}}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \tan^4x~dx$
(2) $\displaystyle \int \frac{dx}{\sin{2x}}$
(3) $\displaystyle \int \frac{1}{1-\sin x}~dx$
(4) $\displaystyle \int (\sin^3x-\cos^3x)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int e^x\cos x~dx$
(2) $\displaystyle \int e^{-x}\sin x~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \sin x\log(\cos x)~dx$
(2) $\displaystyle \int x\tan^2x~dx$
(3) $\displaystyle \int \frac{1}{1-e^x}~dx$
この動画を見る
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{\sqrt x}{\sqrt[4]{x^3}+1}~dx$
(2) $\displaystyle \int \frac{dx}{x\sqrt{x+1}}$
(3) $\displaystyle \int \log|x^2-1|~dx$
(4) $\displaystyle \int \frac{e^x}{e^x-e^{-x}}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \tan^4x~dx$
(2) $\displaystyle \int \frac{dx}{\sin{2x}}$
(3) $\displaystyle \int \frac{1}{1-\sin x}~dx$
(4) $\displaystyle \int (\sin^3x-\cos^3x)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int e^x\cos x~dx$
(2) $\displaystyle \int e^{-x}\sin x~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \sin x\log(\cos x)~dx$
(2) $\displaystyle \int x\tan^2x~dx$
(3) $\displaystyle \int \frac{1}{1-e^x}~dx$
【数Ⅲ】【積分とその応用】不定積分置換積分、部分積分2 ※問題文は概要欄

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x^2+x+1}{x^2+1}~dx$
(2) $\displaystyle \int \frac{x^4}{x^2-1}~dx$
(1)次の等式が成り立つように、定数$a,b,c$の値を定めよ。
$\dfrac{3x+2}{x(x+1)^2}=\dfrac{a}{x}+\dfrac{b}{x+1}+\dfrac{c}{(x+1)^2}$
(2)不定積分$\displaystyle \int \dfrac{3x+2}{x(x+1)^2}~dx$を求めよ。
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{x(x^2-1)}$
(2) $\displaystyle \int \frac{dx}{x^2(x+2)}$
(3) $\displaystyle \int \frac{dx}{x(x^2+1)}$
(4) $\displaystyle \int \frac{x^2+1}{x^4-5x^2+4}~dx$
(5) $\displaystyle \int \frac{3x+2}{x(x+1)^3}~dx$
(6) $\displaystyle \int \frac{x^4}{x^3-3x+2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{\sqrt{x+1}-\sqrt x}$
(2) $\displaystyle \int \frac{x}{\sqrt{3x+4}-2}~dx$
この動画を見る
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x^2+x+1}{x^2+1}~dx$
(2) $\displaystyle \int \frac{x^4}{x^2-1}~dx$
(1)次の等式が成り立つように、定数$a,b,c$の値を定めよ。
$\dfrac{3x+2}{x(x+1)^2}=\dfrac{a}{x}+\dfrac{b}{x+1}+\dfrac{c}{(x+1)^2}$
(2)不定積分$\displaystyle \int \dfrac{3x+2}{x(x+1)^2}~dx$を求めよ。
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{x(x^2-1)}$
(2) $\displaystyle \int \frac{dx}{x^2(x+2)}$
(3) $\displaystyle \int \frac{dx}{x(x^2+1)}$
(4) $\displaystyle \int \frac{x^2+1}{x^4-5x^2+4}~dx$
(5) $\displaystyle \int \frac{3x+2}{x(x+1)^3}~dx$
(6) $\displaystyle \int \frac{x^4}{x^3-3x+2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{dx}{\sqrt{x+1}-\sqrt x}$
(2) $\displaystyle \int \frac{x}{\sqrt{3x+4}-2}~dx$
【数Ⅲ】【積分とその応用】不定積分置換積分、部分積分1 ※問題文は概要欄

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不定積分を求めよ。
(1) $\displaystyle \int x\sqrt[3]{1+x}~dx$
(2) $\displaystyle \int \sin x \cos^4x~dx$
(3) $\displaystyle \int \frac {dx}{\cos^4x}$
(4) $\displaystyle \int (2x+1)e^{x^2+x+5}~dx$
(5) $\displaystyle \int \frac{e^{2x}}{(e^x+2)^2}~dx$
(6) $\displaystyle \int \frac{\log x}{x(\log x-1)^2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x}{\cos^2x}~dx$
(2) $\displaystyle \int x\log(x-2)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int x\log(x^2-2)~dx$
(2) $\displaystyle \int e^x\log(e^x+1)~dx$
不定積分$\displaystyle \int (\log x)^3~dx$を求めよ。
この動画を見る
次の不定積分を求めよ。
(1) $\displaystyle \int x\sqrt[3]{1+x}~dx$
(2) $\displaystyle \int \sin x \cos^4x~dx$
(3) $\displaystyle \int \frac {dx}{\cos^4x}$
(4) $\displaystyle \int (2x+1)e^{x^2+x+5}~dx$
(5) $\displaystyle \int \frac{e^{2x}}{(e^x+2)^2}~dx$
(6) $\displaystyle \int \frac{\log x}{x(\log x-1)^2}~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int \frac{x}{\cos^2x}~dx$
(2) $\displaystyle \int x\log(x-2)~dx$
次の不定積分を求めよ。
(1) $\displaystyle \int x\log(x^2-2)~dx$
(2) $\displaystyle \int e^x\log(e^x+1)~dx$
不定積分$\displaystyle \int (\log x)^3~dx$を求めよ。
福田のおもしろ数学434〜2025は何番目のGood-numか

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
正の整数で各位の数の和が$9$となるものを
$Good- num$
と呼ぶことにする。すべての$Good-num$を
昇順に並べたとき、
$2025$は何番目にあるか?
この動画を見る
正の整数で各位の数の和が$9$となるものを
$Good- num$
と呼ぶことにする。すべての$Good-num$を
昇順に並べたとき、
$2025$は何番目にあるか?
福田の数学〜京都大学2025理系第3問〜関数の増減と値域

単元:
#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$e$は自然対数の底とする。
$x\gt \dfrac{1}{\sqrt e}$において定義された次の関数
$f(x),g(x)$を考える。
$f(x)=x^2 \log x$
$g(x)=x^2\log x - \dfrac{1}{1+2\log x}$
実数$t$は$t\gt \dfrac{1}{\sqrt e}$を満たすとする。
曲線$y=f(x)$上の店$(t,f(t))$における接線に垂直で、
点$(t,g(t))$を通る直線を$l_t$とする。
直線$l_t$が$x$軸と交わる点の$x$座標を$p(t)$とする。
$t$が$\dfrac{1}{\sqrt e} \lt t \leqq e$の範囲を動くとき、
$p(t)$の取りうる値の範囲を求めよ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{3}$
$e$は自然対数の底とする。
$x\gt \dfrac{1}{\sqrt e}$において定義された次の関数
$f(x),g(x)$を考える。
$f(x)=x^2 \log x$
$g(x)=x^2\log x - \dfrac{1}{1+2\log x}$
実数$t$は$t\gt \dfrac{1}{\sqrt e}$を満たすとする。
曲線$y=f(x)$上の店$(t,f(t))$における接線に垂直で、
点$(t,g(t))$を通る直線を$l_t$とする。
直線$l_t$が$x$軸と交わる点の$x$座標を$p(t)$とする。
$t$が$\dfrac{1}{\sqrt e} \lt t \leqq e$の範囲を動くとき、
$p(t)$の取りうる値の範囲を求めよ。
$2025$年京都大学理系過去問題
【数Ⅱ】【微分法と積分法】接線からの関数決定 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f'(x)=x^2+2x+2$で、曲線$y=f(x)$は$y=-3x+1$に接している。この時、$f(x)$を求めよ。
この動画を見る
$f'(x)=x^2+2x+2$で、曲線$y=f(x)$は$y=-3x+1$に接している。この時、$f(x)$を求めよ。
【数Ⅱ】【微分法と積分法】係数比較から関数の決定 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2次関数$f(x)$の1つの不定積分$F(x)$が$xf(x)-2x^3+3x^2$に等しく、$f(1)=0$であるとき、$f(x)$を求めよ。
この動画を見る
2次関数$f(x)$の1つの不定積分$F(x)$が$xf(x)-2x^3+3x^2$に等しく、$f(1)=0$であるとき、$f(x)$を求めよ。
福田のおもしろ数学433〜四面体に関する計量問題
単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
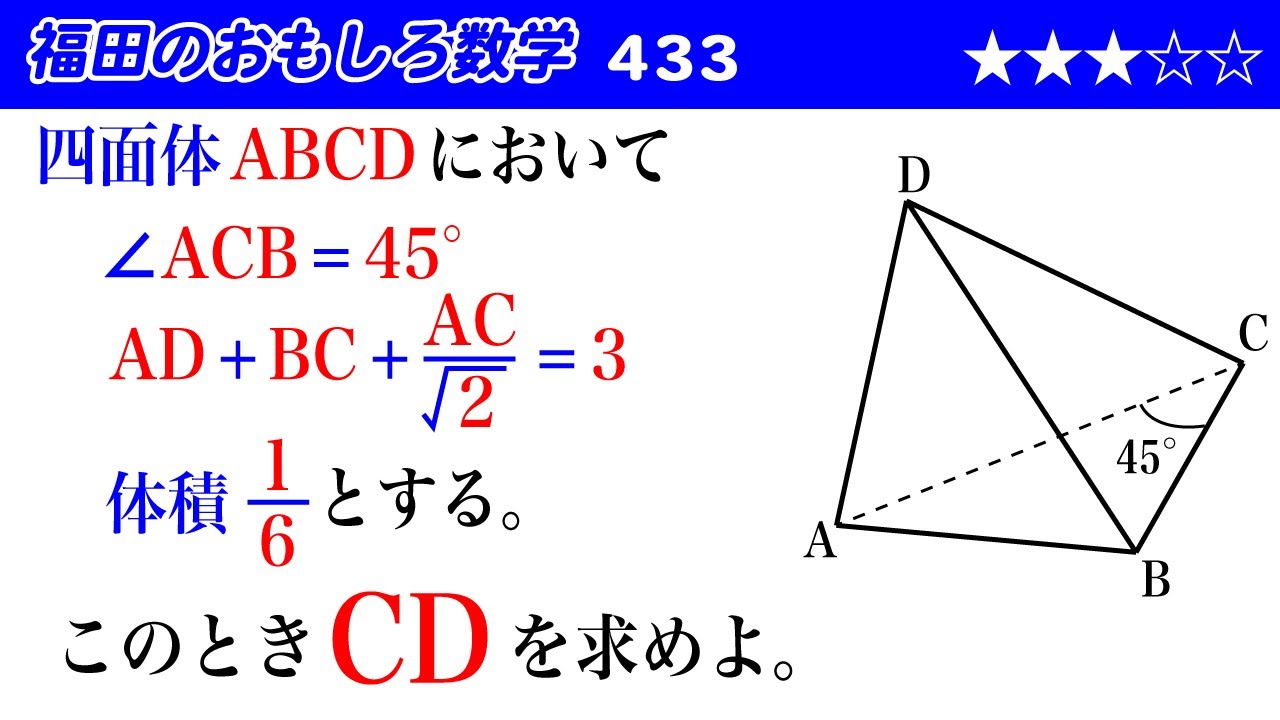
四面体$ABCD$において
$\angle ACB=45°$
$AD+BC+\dfrac{AC}{\sqrt2}=3$
体積$\dfrac{1}{6}$とする。
このとき$CD$を求めよ。
図は動画内参照
この動画を見る
四面体$ABCD$において
$\angle ACB=45°$
$AD+BC+\dfrac{AC}{\sqrt2}=3$
体積$\dfrac{1}{6}$とする。
このとき$CD$を求めよ。
図は動画内参照
福田の数学〜京都大学2025理系第2問〜不定方程式で表された数の最小値

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
正の整数$x,y,z$を用いて
$N=9z^2=x^6+y^4$
と表される正の整数$N$の最小値を求めよ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{2}$
正の整数$x,y,z$を用いて
$N=9z^2=x^6+y^4$
と表される正の整数$N$の最小値を求めよ。
$2025$年京都大学理系過去問題
福田のおもしろ数学432〜ガウス記号を含んだ式が成り立たない条件

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n+\left[\dfrac{n}{2}\right] \neq \left[\dfrac{n}{6}\right]+\left[\dfrac{2n}{3}\right]$
を満たす自然数$n$をすべて求めよ。
この動画を見る
$n+\left[\dfrac{n}{2}\right] \neq \left[\dfrac{n}{6}\right]+\left[\dfrac{2n}{3}\right]$
を満たす自然数$n$をすべて求めよ。
福田の数学〜京都大学2025理系第1問(2−2)〜定積分の計算
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
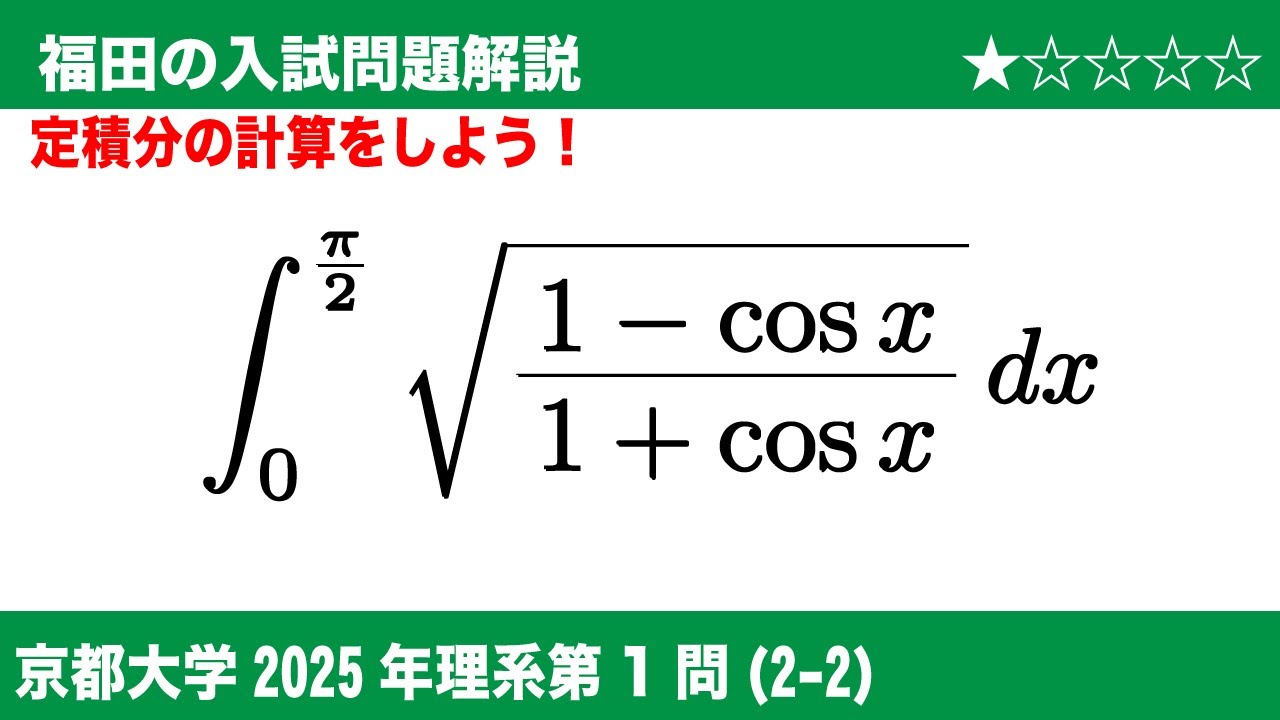
(2-2)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{\dfrac{1-\cos x}{1+\cos x}}dx$
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{1}$
(2-2)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{\dfrac{1-\cos x}{1+\cos x}}dx$
$2025$年京都大学理系過去問題
【数C】【複素数平面】複素数と図形8 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数平面上の2点$\rm A,B$を表す複素数をそれぞれ$\alpha=1-2i,\beta=3+2i$とするとき
線分$\rm AB$を1辺とする正三角形の他の頂点$\rm C$を表す複素数$\gamma$を求めよ。
この動画を見る
複素数平面上の2点$\rm A,B$を表す複素数をそれぞれ$\alpha=1-2i,\beta=3+2i$とするとき
線分$\rm AB$を1辺とする正三角形の他の頂点$\rm C$を表す複素数$\gamma$を求めよ。
【数C】【複素数平面】複素数と図形7 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
原点を${\rm {O}}, \alpha=2-i,\beta=3+(2a-1)i$を表す点をそれぞれ$\rm A,B$とするとき、$\rm \angle AOB=\dfrac\pi4$を満たす実数$a$の値を求めよ。
この動画を見る
原点を${\rm {O}}, \alpha=2-i,\beta=3+(2a-1)i$を表す点をそれぞれ$\rm A,B$とするとき、$\rm \angle AOB=\dfrac\pi4$を満たす実数$a$の値を求めよ。
【数C】【複素数平面】複素数と図形6 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数平面上の異なる4点$\rm A(\alpha),B(\beta),C(\gamma),D(\delta)$
について次のことが成り立つことを証明せよ。
2直線$\rm AB,CD$が垂直に交わる ⇔ $\dfrac{(\delta-\gamma)}{(\beta-\alpha)}$が純虚数
この動画を見る
複素数平面上の異なる4点$\rm A(\alpha),B(\beta),C(\gamma),D(\delta)$
について次のことが成り立つことを証明せよ。
2直線$\rm AB,CD$が垂直に交わる ⇔ $\dfrac{(\delta-\gamma)}{(\beta-\alpha)}$が純虚数
【数C】【複素数平面】複素数と図形5 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
点$z$が、点$-1$を通り実軸に垂直な直線上を動くとき、
点$w=\dfrac1z$ はどのような図形を描くか。
この動画を見る
点$z$が、点$-1$を通り実軸に垂直な直線上を動くとき、
点$w=\dfrac1z$ はどのような図形を描くか。
【数C】【複素数平面】複素数と図形4 ※問題文は概要欄

単元:
#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
点$z$が、原点$\rm O$を中心とする半径1の円から$-1$を除いた図形上を動くとき、
点$w=\dfrac {(z+i)}{(z+1)}$はどのような図形を描くか。
この動画を見る
点$z$が、原点$\rm O$を中心とする半径1の円から$-1$を除いた図形上を動くとき、
点$w=\dfrac {(z+i)}{(z+1)}$はどのような図形を描くか。
【数C】【複素数平面】複素数と図形3 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
点$z$が、原点$\rm O$を中心とする半径1の円上を動くとき、次の点$w$はどのような図形を描くか。
(1) $w=\dfrac{1+i}{z}$ (2) $w=\dfrac{6z-1}{2z-1}$
この動画を見る
点$z$が、原点$\rm O$を中心とする半径1の円上を動くとき、次の点$w$はどのような図形を描くか。
(1) $w=\dfrac{1+i}{z}$ (2) $w=\dfrac{6z-1}{2z-1}$
【数C】【複素数平面】複素数と図形2 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の方程式を満たす点$z$全体の集合はどのような図形か。
(1) $z+\bar{z}=2$ (2) $z-\bar{z}=2i$
この動画を見る
次の方程式を満たす点$z$全体の集合はどのような図形か。
(1) $z+\bar{z}=2$ (2) $z-\bar{z}=2i$
