 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
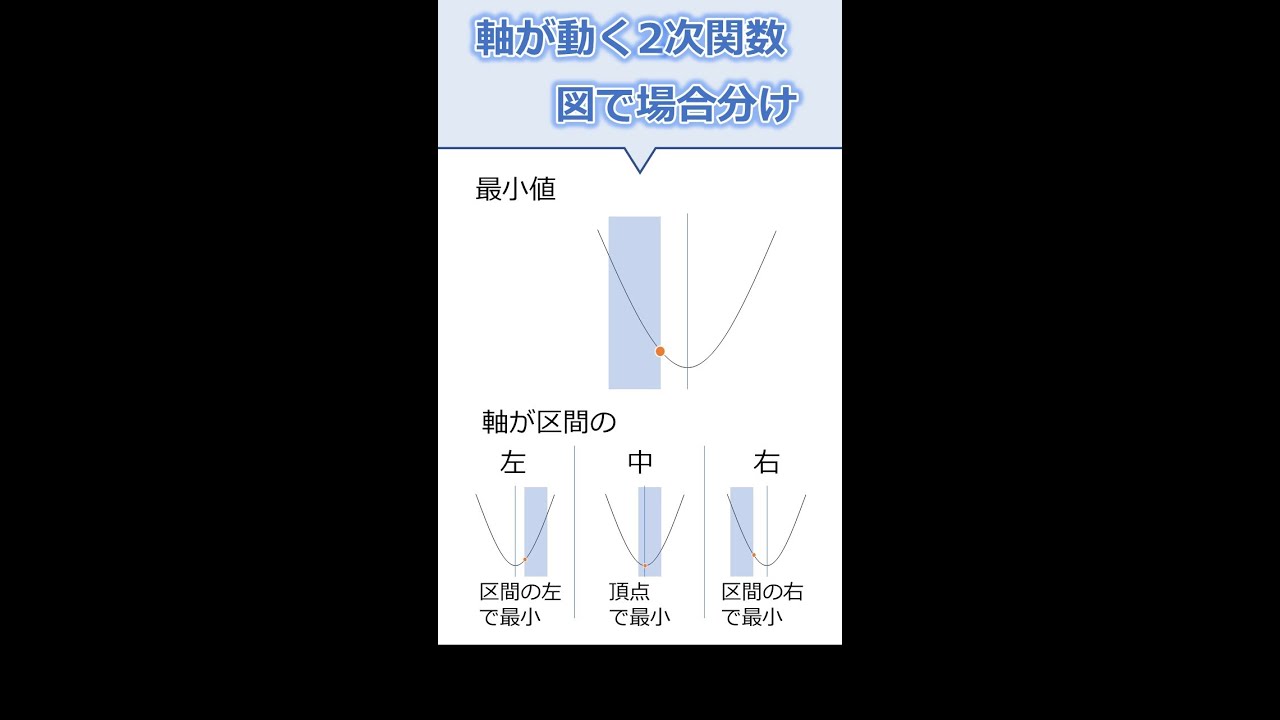
軸が動く2次関数の場合分け 最小値 #Shorts
【数学Ⅱ/積分】定積分で表された関数を微分

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の$x$の関数を微分せよ。
(1)
$\displaystyle \int_{1}^{x} (t^2-3t+2)dt$
(2)
$\displaystyle \int_{x}^{2} (3t^2-1)dt$
この動画を見る
次の$x$の関数を微分せよ。
(1)
$\displaystyle \int_{1}^{x} (t^2-3t+2)dt$
(2)
$\displaystyle \int_{x}^{2} (3t^2-1)dt$
大学入試問題#124 高知大学(2020) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{7}{2}}^{\frac{9}{2}}\displaystyle \frac{2^x}{2^x+\sqrt{ 2 }}\ dx$を計算せよ。
出典:2020年高知大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{7}{2}}^{\frac{9}{2}}\displaystyle \frac{2^x}{2^x+\sqrt{ 2 }}\ dx$を計算せよ。
出典:2020年高知大学 入試問題
xの2022乗の値
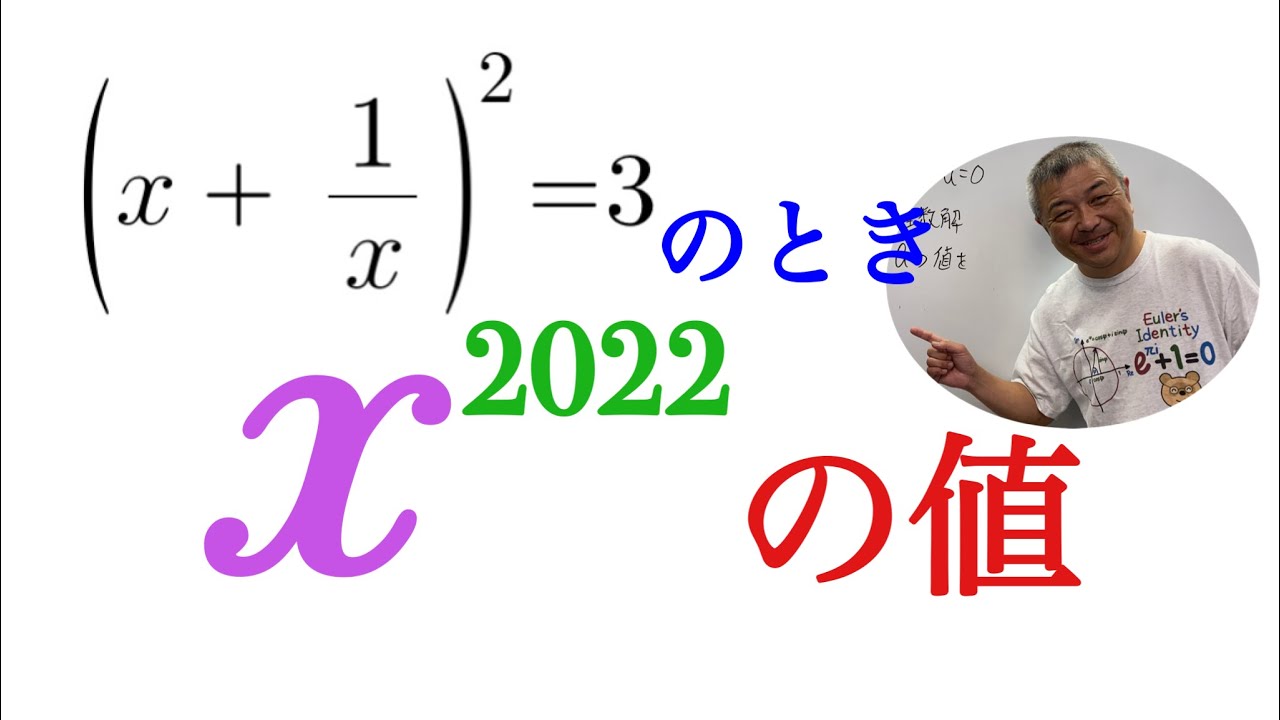
単元:
#数Ⅰ#数と式#2次関数#式の計算(整式・展開・因数分解)#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \left(x+\dfrac{1}{x}\right)^2=3$のとき,$ x^{2022}$の値を求めよ.
この動画を見る
$ \left(x+\dfrac{1}{x}\right)^2=3$のとき,$ x^{2022}$の値を求めよ.
福田の数学〜東京慈恵会医科大学2022年医学部第1問〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
袋Aには白玉2個、赤玉1個、袋Bには白玉1個、赤玉2個が入っている。
この状態から始めて、次の操作を繰り返し行う。
操作
① 袋A、袋Bから玉を1個ずつ取り出す。
② $(\textrm{i})$取り出した2個の玉の色が同じである場合は、取り出した玉を2個とも
袋Aに入れる。
$(\textrm{ii})$取り出した2個の玉の色が異なる場合は、袋Aから取り出した玉は袋B
に入れ、袋Bから取り出した玉は袋Aに入れる。
このとき、
・操作を2回繰り返した後に袋Aに入っている赤玉の個数が1個である確率は$\boxed{\ \ (ア)\ \ }$
・操作を3回繰り返した後に袋Aに入っている赤玉の個数が0個である確率は$\boxed{\ \ (イ)\ \ }$
である。
2022東京慈恵会医科大学医学部過去問
この動画を見る
袋Aには白玉2個、赤玉1個、袋Bには白玉1個、赤玉2個が入っている。
この状態から始めて、次の操作を繰り返し行う。
操作
① 袋A、袋Bから玉を1個ずつ取り出す。
② $(\textrm{i})$取り出した2個の玉の色が同じである場合は、取り出した玉を2個とも
袋Aに入れる。
$(\textrm{ii})$取り出した2個の玉の色が異なる場合は、袋Aから取り出した玉は袋B
に入れ、袋Bから取り出した玉は袋Aに入れる。
このとき、
・操作を2回繰り返した後に袋Aに入っている赤玉の個数が1個である確率は$\boxed{\ \ (ア)\ \ }$
・操作を3回繰り返した後に袋Aに入っている赤玉の個数が0個である確率は$\boxed{\ \ (イ)\ \ }$
である。
2022東京慈恵会医科大学医学部過去問
【数学Ⅱ/積分】定積分の基本

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の定積分を求めよ。
(1)
$\displaystyle \int_{1}^{3} (-4x)dx$
(2)
$\displaystyle \int_{1}^{2} (x^2+3x+2)dx$
(3)
$\displaystyle \int_{-1}^{2} (x^2+3x)dx-\displaystyle \int_{-1}^{2} (x^2-x)dx$
この動画を見る
次の定積分を求めよ。
(1)
$\displaystyle \int_{1}^{3} (-4x)dx$
(2)
$\displaystyle \int_{1}^{2} (x^2+3x+2)dx$
(3)
$\displaystyle \int_{-1}^{2} (x^2+3x)dx-\displaystyle \int_{-1}^{2} (x^2-x)dx$
【数学Ⅱ/積分】原始関数を求める

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$F'(x)=6x^2+4x+3,F(0)=1$を満たす関数$F(x)$を求めよ。
この動画を見る
$F'(x)=6x^2+4x+3,F(0)=1$を満たす関数$F(x)$を求めよ。
2022都立入試 整数問題証明(11の倍数)

単元:
#数学(中学生)#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数列#数列とその和(等差・等比・階差・Σ)#高校入試過去問(数学)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
2022都立入試 整数問題証明に関して解説していきます.
この動画を見る
2022都立入試 整数問題証明に関して解説していきます.
大学入試問題#123 鳥取大学 改 (2020) Σの計算

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#鳥取大学#数B
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \sum_{k=1}^n k^2 2^k$を計算せよ。
出典:2020年鳥取大学 入試問題
この動画を見る
$\displaystyle \sum_{k=1}^n k^2 2^k$を計算せよ。
出典:2020年鳥取大学 入試問題
小数第2022位の数は?!

単元:
#数Ⅰ#数と式#2次関数#式の計算(整式・展開・因数分解)#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ (6+\sqrt{37})^{2023}$の小数第$2022$位数は?
この動画を見る
$ (6+\sqrt{37})^{2023}$の小数第$2022$位数は?
【数学Ⅱ/積分】不定積分の基本

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の不定積分を求めよ。
(1)
$\displaystyle \int (-2)dx$
(2)
$\displaystyle \int (3x+4)dx$
(3)
$\displaystyle \int (2t-1)^2dx$
この動画を見る
次の不定積分を求めよ。
(1)
$\displaystyle \int (-2)dx$
(2)
$\displaystyle \int (3x+4)dx$
(3)
$\displaystyle \int (2t-1)^2dx$
【高校数学】和の記号・シグマの公式の証明 3-8.5【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
次式を証明せよ。
$\displaystyle \sum_{i=1}^n k^2=\frac{1}{6}n(n+1)(2n+1)$
$\displaystyle \sum_{i=1}^n k^3=\{ \frac{1}{2}n(n+1)\}^2$
この動画を見る
次式を証明せよ。
$\displaystyle \sum_{i=1}^n k^2=\frac{1}{6}n(n+1)(2n+1)$
$\displaystyle \sum_{i=1}^n k^3=\{ \frac{1}{2}n(n+1)\}^2$
【数学】横浜国立大2018年度(理系前期)第5問の解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大(理系)2018年度前期入試
第5問
xy平面上に双曲線$C1:y=\dfrac{1}{x}$がある。C1上の点P$(t,\dfrac{1}{t})$(ただし$t>0$)におけるC1の接線をlとする。
放物線$C2:y=x^2+ax+b$(a,bは実数)は点Pを通りC1と第3象限において共有点をただ一つ持つ。C2とlで囲まれた部分の面積をSとする。
(1) lの方程式を求めよ。
(2) a,bをそれぞれtの式で表せ。
(3) Sをtの式で表せ。
(4) tが正の実数全体を動くとき、Sの最小値を求めよ。
この動画を見る
横浜国立大(理系)2018年度前期入試
第5問
xy平面上に双曲線$C1:y=\dfrac{1}{x}$がある。C1上の点P$(t,\dfrac{1}{t})$(ただし$t>0$)におけるC1の接線をlとする。
放物線$C2:y=x^2+ax+b$(a,bは実数)は点Pを通りC1と第3象限において共有点をただ一つ持つ。C2とlで囲まれた部分の面積をSとする。
(1) lの方程式を求めよ。
(2) a,bをそれぞれtの式で表せ。
(3) Sをtの式で表せ。
(4) tが正の実数全体を動くとき、Sの最小値を求めよ。
【数学Ⅰ/三角比】円に内接する四角形②
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
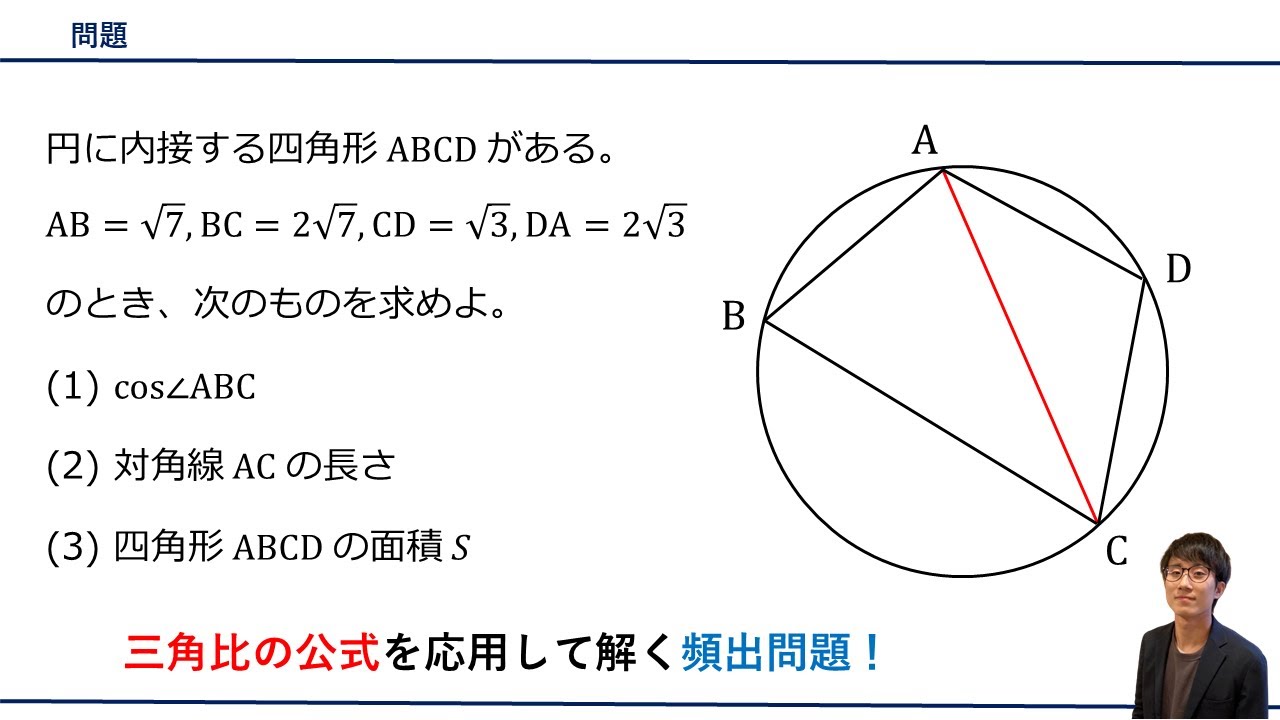
円に内接する四角形$ABCD$がある。
$AB=\sqrt{ 7 },BC=2\sqrt{ 7 },CD=\sqrt{ 3 },DA=2\sqrt{ 3 }$のとき、次のものを求めよ。
(1)
$\cos\angle ABC$
(2)
対角線$AC$の長さ
(3)
四角形$ABCD$の面積$S$
この動画を見る
円に内接する四角形$ABCD$がある。
$AB=\sqrt{ 7 },BC=2\sqrt{ 7 },CD=\sqrt{ 3 },DA=2\sqrt{ 3 }$のとき、次のものを求めよ。
(1)
$\cos\angle ABC$
(2)
対角線$AC$の長さ
(3)
四角形$ABCD$の面積$S$
大学入試問題#122 愛知県立大学(2020) 極限
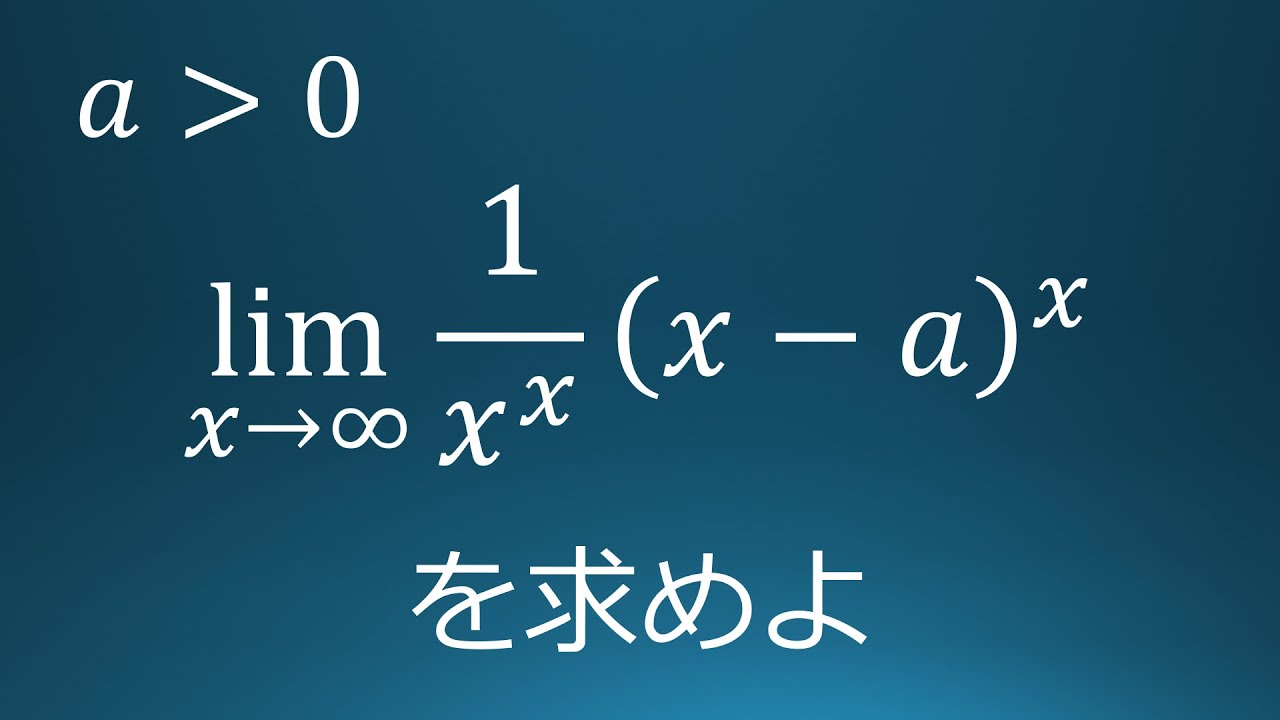
単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0$
$\displaystyle \lim_{ x \to \infty }\displaystyle \frac{1}{x^x}(x-a)^x$を求めよ。
出典:2020年愛知県立大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \lim_{ x \to \infty }\displaystyle \frac{1}{x^x}(x-a)^x$を求めよ。
出典:2020年愛知県立大学 入試問題
3乗根をはずせ

単元:
#数Ⅰ#数と式#2次関数#式の計算(整式・展開・因数分解)#2次方程式と2次不等式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3$乗根をはずせ.
$\sqrt[3]{8+\sqrt{189}}$
この動画を見る
$3$乗根をはずせ.
$\sqrt[3]{8+\sqrt{189}}$
3乗根をはずせ

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
3乗根をはずせ.
$\sqrt[3]{8+\sqrt{189}}$
この動画を見る
3乗根をはずせ.
$\sqrt[3]{8+\sqrt{189}}$
【数学】横浜国立大2018年度(理系前期)第1問の解説

単元:
#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大(理系)2018年度前期入試
第1問
(1) 定積分$\displaystyle \int_{0}^{\frac{\pi}{3}}\dfrac{x}{\cos(x)^2} dx$を求めよ。
(2) $\dfrac{-\pi}{2}\lt x\lt \dfrac{\pi}{2}$で定義された関数f(x)が
$f(x)\cos(x)^2 =\pi-\dfrac{x}{\log2}\displaystyle \int_{0}^{\frac{\pi}{3}f(t)dt$
をみたすとき、f(x)を求めよ。
この動画を見る
横浜国立大(理系)2018年度前期入試
第1問
(1) 定積分$\displaystyle \int_{0}^{\frac{\pi}{3}}\dfrac{x}{\cos(x)^2} dx$を求めよ。
(2) $\dfrac{-\pi}{2}\lt x\lt \dfrac{\pi}{2}$で定義された関数f(x)が
$f(x)\cos(x)^2 =\pi-\dfrac{x}{\log2}\displaystyle \int_{0}^{\frac{\pi}{3}f(t)dt$
をみたすとき、f(x)を求めよ。
フェルマーの最終定理の証明

【数学Ⅰ/三角比】円に内接する四角形①
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
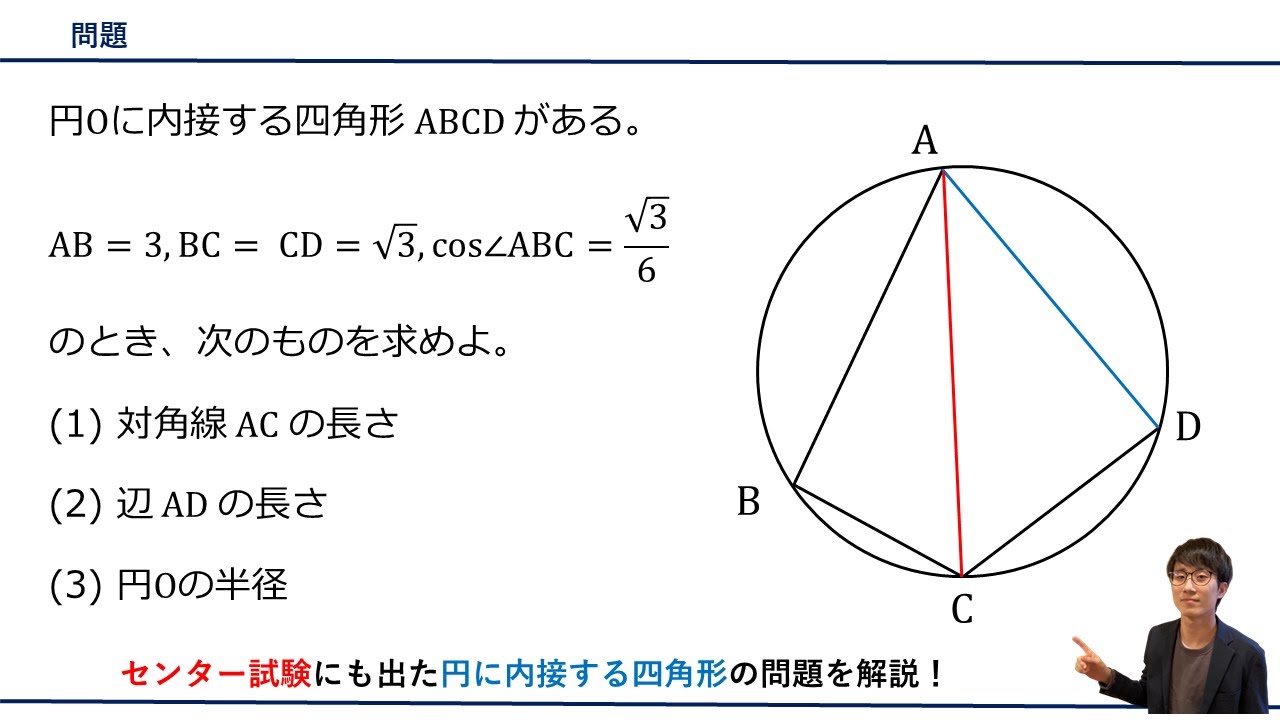
円$O$に内接する四角形$ABCD$がある。
$AB=3,$ $BC=CD=\sqrt{ 3 },$ $\cos\angle ABC=\displaystyle \frac{\sqrt{ 3 }}{6}$のとき、次のものを求めよ。
(1)対角線$AC$の長さ
(2)辺$AD$の長さ
(3)円$O$の半径
この動画を見る
円$O$に内接する四角形$ABCD$がある。
$AB=3,$ $BC=CD=\sqrt{ 3 },$ $\cos\angle ABC=\displaystyle \frac{\sqrt{ 3 }}{6}$のとき、次のものを求めよ。
(1)対角線$AC$の長さ
(2)辺$AD$の長さ
(3)円$O$の半径
大学入試問題#121 横浜国立大学(2004) 定積分
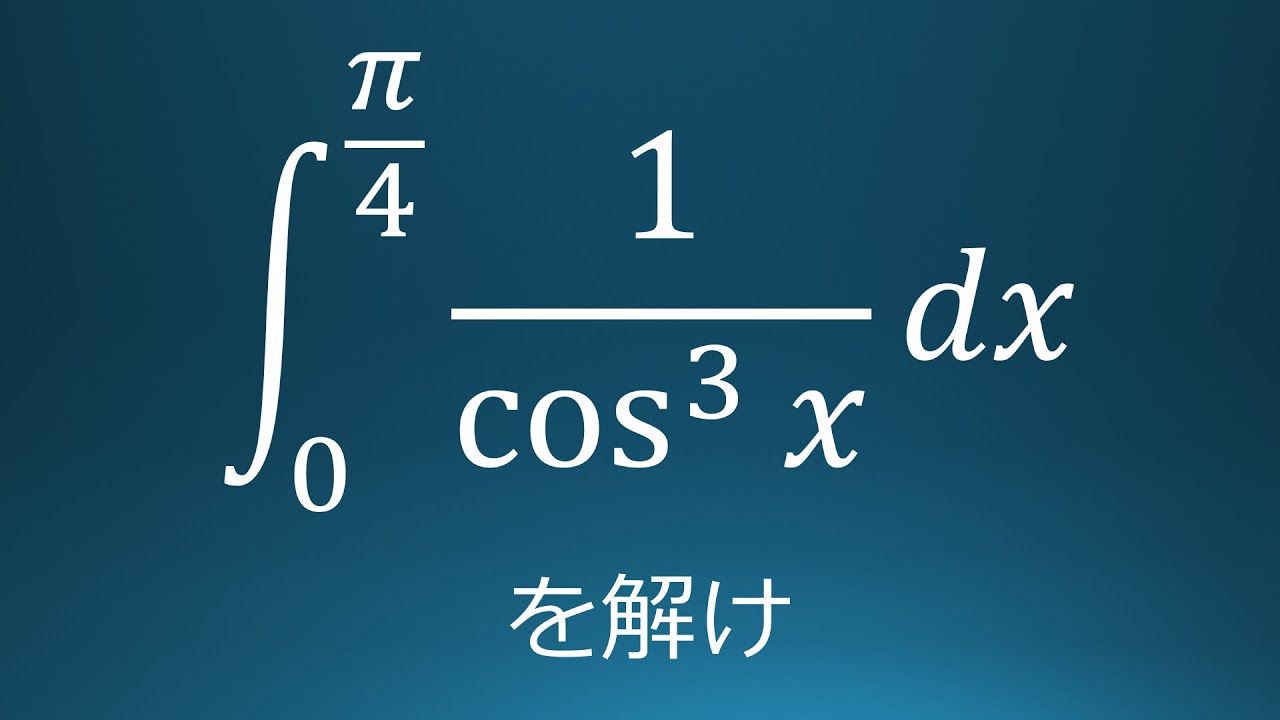
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{1}{\cos^3\ x}\ dx$を計算せよ。
出典:2004年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{1}{\cos^3\ x}\ dx$を計算せよ。
出典:2004年横浜国立大学 入試問題
平方根&分数式の方程式
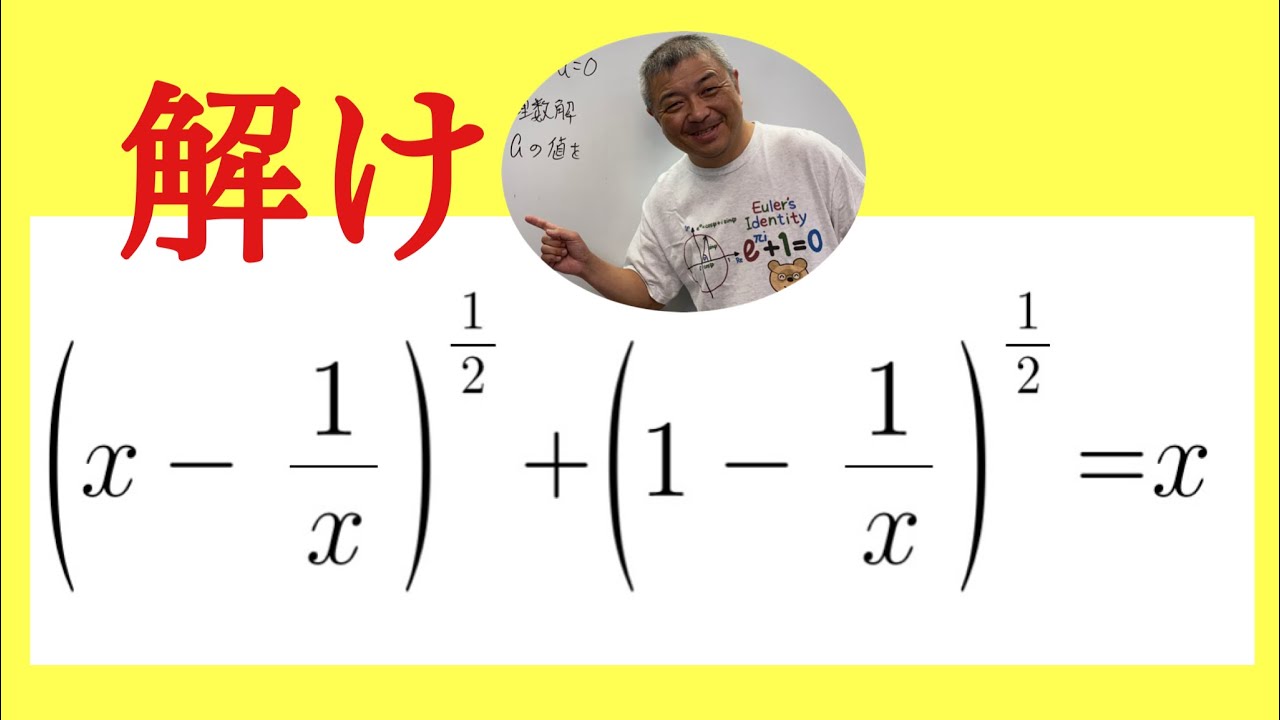
単元:
#数Ⅰ#数と式#2次関数#式の計算(整式・展開・因数分解)#2次関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$ \left(x-\dfrac{1}{x}\right)^{\frac{1}{2}}+\left(1-\dfrac{1}{x}\right)^{\frac{1}{2}}=x$
この動画を見る
これを解け.
$ \left(x-\dfrac{1}{x}\right)^{\frac{1}{2}}+\left(1-\dfrac{1}{x}\right)^{\frac{1}{2}}=x$
三角関数の方程式
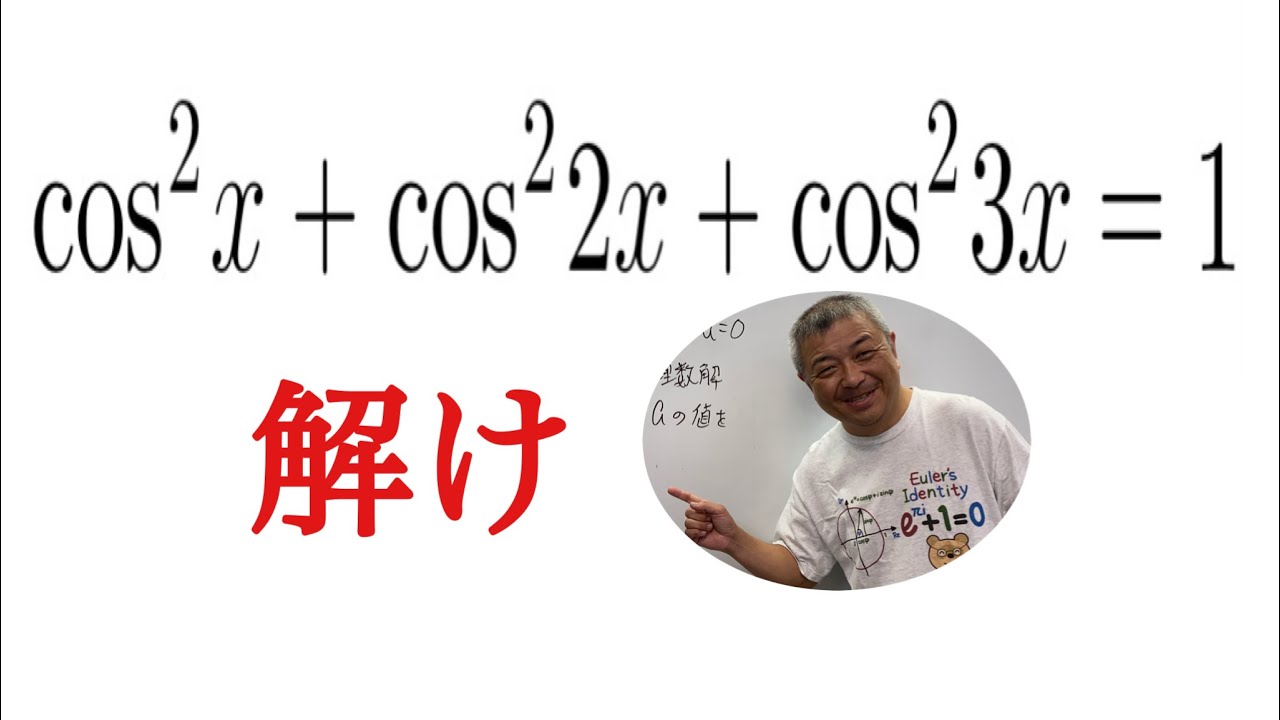
単元:
#数Ⅱ#三角関数#三角関数とグラフ#加法定理とその応用#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$ \cos^2x+\cos^22x+\cos^23x=1$
この動画を見る
これを解け.
$ \cos^2x+\cos^22x+\cos^23x=1$
大学入試問題#120 早稲田大学(2003) 対数の不等式
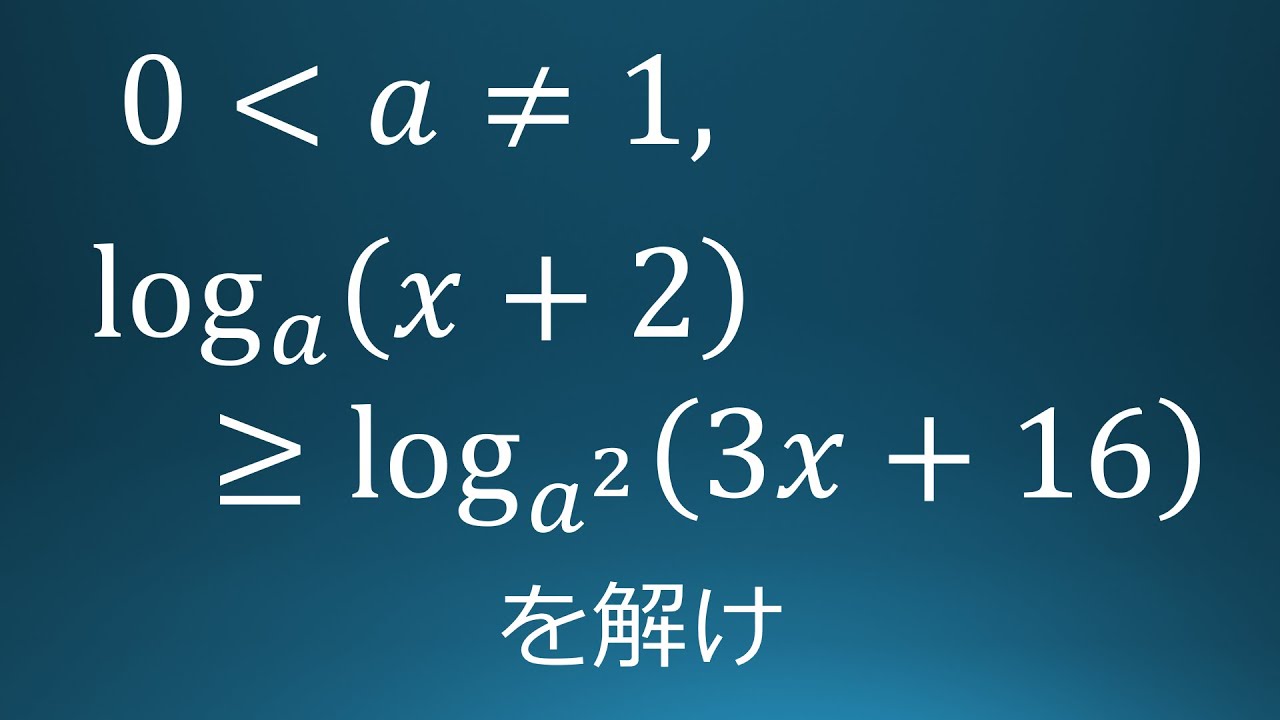
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0,\ a \neq 1$
$log\ a(x+2) \geqq log\ a^2(3x+16)$を解け
出典:2003年早稲田大学 入試問題
この動画を見る
$a \gt 0,\ a \neq 1$
$log\ a(x+2) \geqq log\ a^2(3x+16)$を解け
出典:2003年早稲田大学 入試問題
大学入試問題#119 横浜国立大学(2020) 定積分
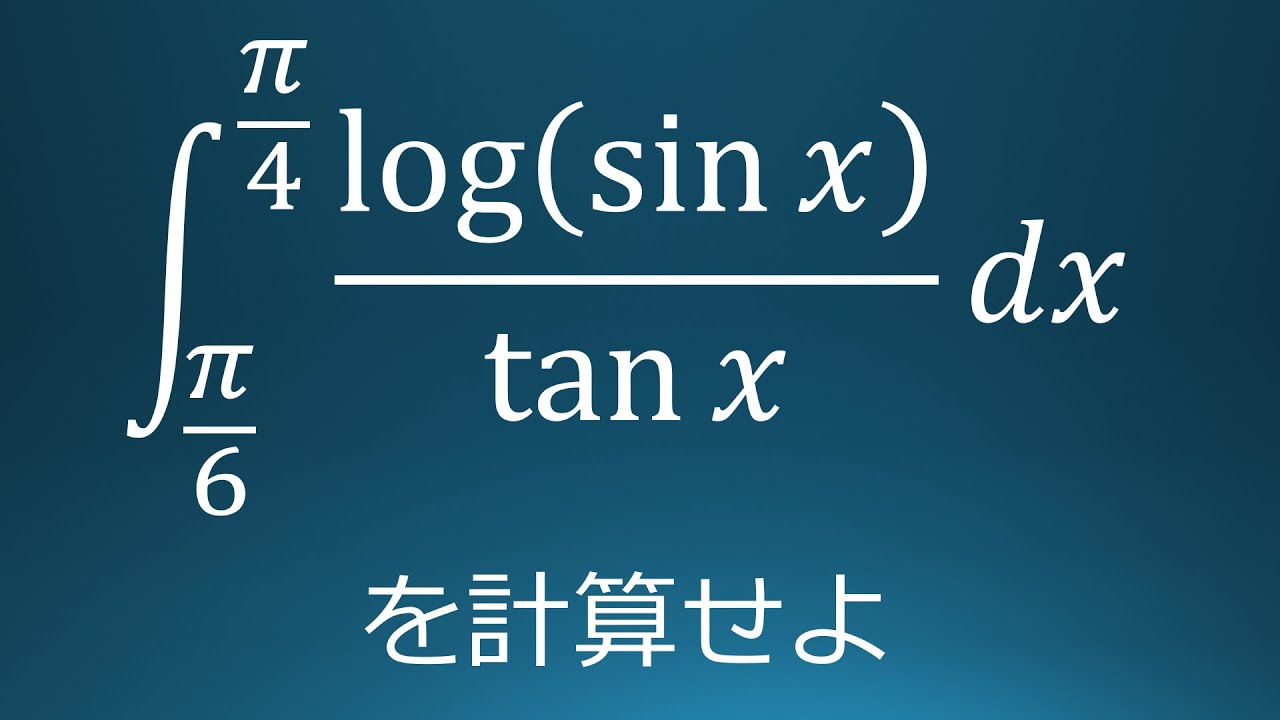
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\displaystyle \frac{log(\sin\ x)}{\tan\ x}\ dx$を計算せよ。
出典:2020年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\displaystyle \frac{log(\sin\ x)}{\tan\ x}\ dx$を計算せよ。
出典:2020年横浜国立大学 入試問題
3次方程式の解の公式 順天堂大(医)

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#順天堂大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$ x^3+9x+6=0$
*誘導あり
解には$ \omega^3=1$の$\omega$を用いる$(\omega\neq 1)$
順天堂大(医)過去問
この動画を見る
これを解け.
$ x^3+9x+6=0$
*誘導あり
解には$ \omega^3=1$の$\omega$を用いる$(\omega\neq 1)$
順天堂大(医)過去問
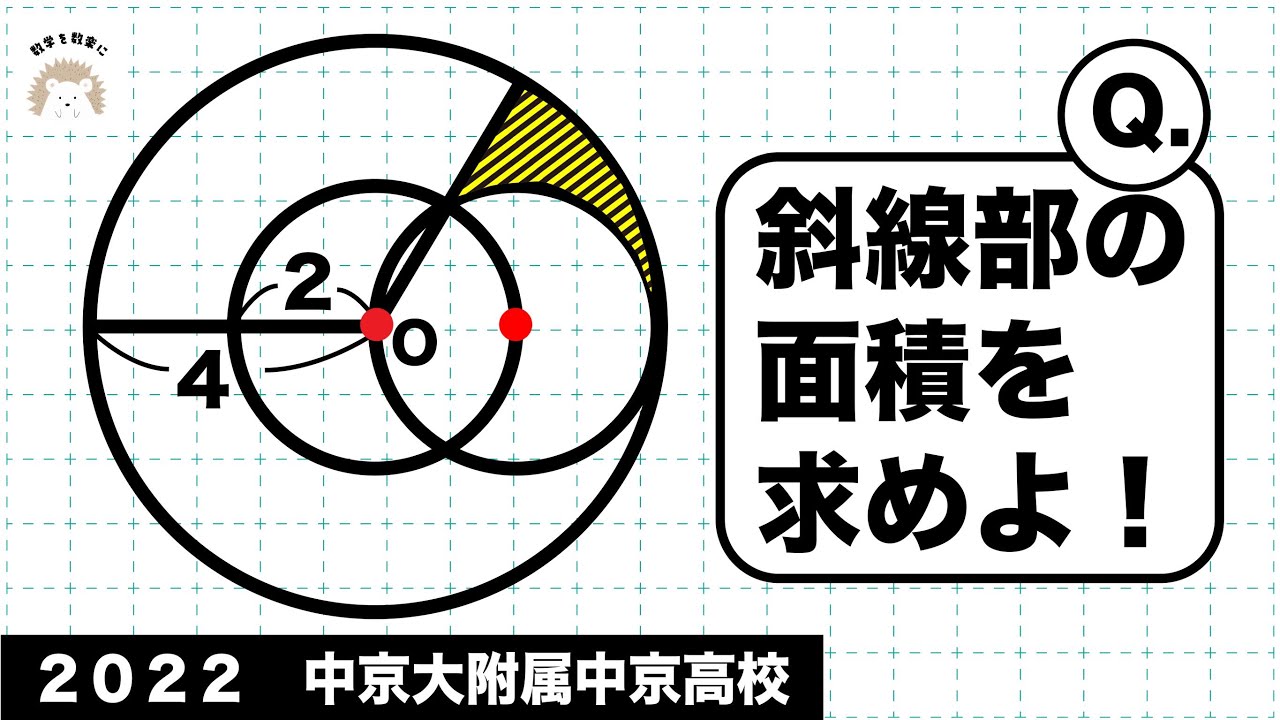
斜線部の面積 中京大附属中京 2022入試問題解説100問解説59問目!
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積を求めよ。
*図は動画内参照
2022中京大学附属中京高等学校
この動画を見る
斜線部の面積を求めよ。
*図は動画内参照
2022中京大学附属中京高等学校
大学入試問題#118 防衛医科大学(2012) 区分求積法

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ \displaystyle \frac{(4n)!}{(3n)!} }$を求めよ。
出典:2012年防衛医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ \displaystyle \frac{(4n)!}{(3n)!} }$を求めよ。
出典:2012年防衛医科大学 入試問題
簡単な根号のついた方程式

単元:
#数Ⅰ#数Ⅱ#数と式#2次関数#複素数と方程式#式の計算(整式・展開・因数分解)#2次方程式と2次不等式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$ \sqrt{3x^2-4x+11}-\sqrt{3x^2-4x-4}=3$
この動画を見る
これを解け.
$ \sqrt{3x^2-4x+11}-\sqrt{3x^2-4x-4}=3$
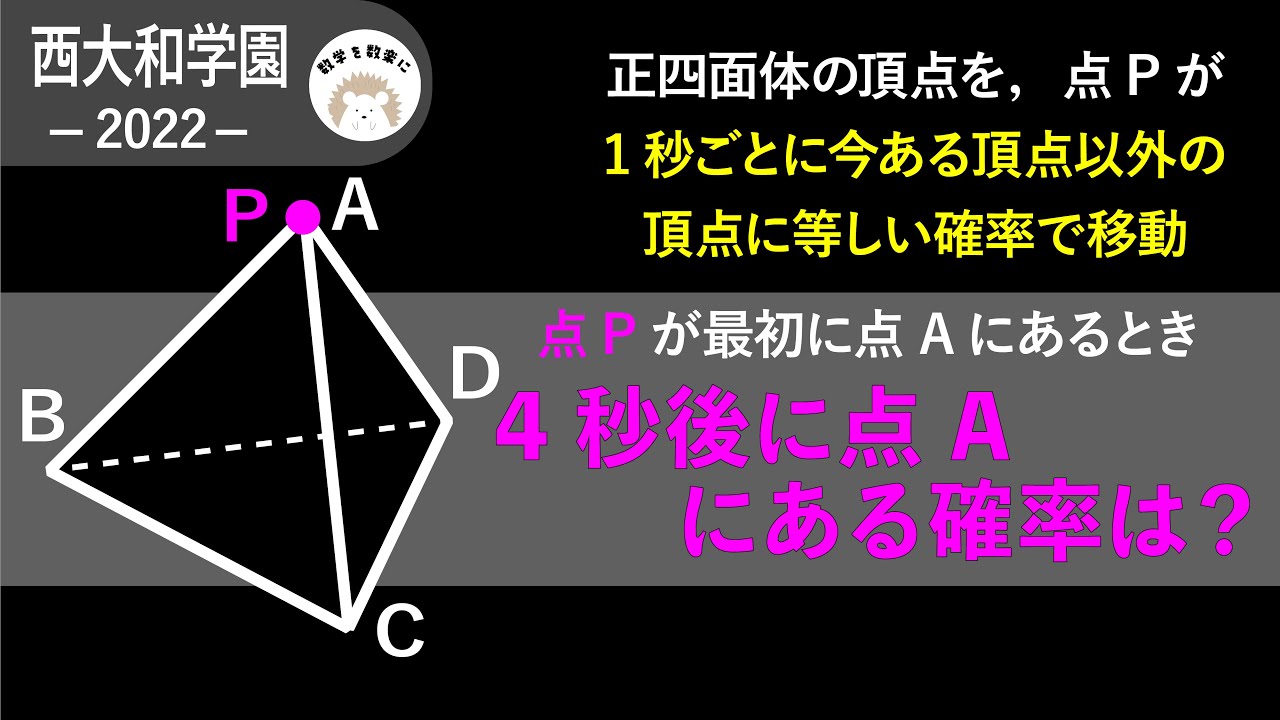
高校入試だけど確率漸化式!?西大和学園2022入試問題解説100問解説!!58問目
単元:
#数学(中学生)#中2数学#確率#数列#漸化式#高校入試過去問(数学)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
正四面体の頂点を、点Pが1秒ごとに今ある頂点以外の頂点に等しい確率で移動する
点Pが最初に点Aにあるとき4秒後に点Aにある確率は?
*図は動画内参照
2022西大和学園高等学校
この動画を見る
正四面体の頂点を、点Pが1秒ごとに今ある頂点以外の頂点に等しい確率で移動する
点Pが最初に点Aにあるとき4秒後に点Aにある確率は?
*図は動画内参照
2022西大和学園高等学校
