 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【数Ⅱ】多項式の割り算【無理数の代入をかんたんに計算!】

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ (1)\begin{array}{r}7\enclose{longdiv}{95\phantom{0}} \\[-3pt]\end{array}
これを解け.
(2)f(x)=x^3+2x^2+3x+6とおく.
f(1+\sqrt2)を求めよ.$
この動画を見る
$ (1)\begin{array}{r}7\enclose{longdiv}{95\phantom{0}} \\[-3pt]\end{array}
これを解け.
(2)f(x)=x^3+2x^2+3x+6とおく.
f(1+\sqrt2)を求めよ.$
福田のわかった数学〜高校1年生074〜場合の数(13)整数解の個数

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(13) 整数解の個数
次の条件を満たす整数の組(x,y,z,u)は何個あるか。
(1)$x+y+z+u=10, x \geqq 0, y \geqq 0, z \geqq 0, u \geqq 0$
(2)$x+y+z+u=10, x \geqq 1, y \geqq 1, z \geqq 1, u \geqq 1$
(3)$x+y+z+u \leqq 10, x \geqq 0, y \geqq 0, z \geqq 0, u \geqq 0$
この動画を見る
数学$\textrm{I}$ 場合の数(13) 整数解の個数
次の条件を満たす整数の組(x,y,z,u)は何個あるか。
(1)$x+y+z+u=10, x \geqq 0, y \geqq 0, z \geqq 0, u \geqq 0$
(2)$x+y+z+u=10, x \geqq 1, y \geqq 1, z \geqq 1, u \geqq 1$
(3)$x+y+z+u \leqq 10, x \geqq 0, y \geqq 0, z \geqq 0, u \geqq 0$
大学入試問題#43 津田塾大学(2021) 複素数

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#津田塾大学
指導講師:
ますただ
問題文全文(内容文):
$|z-5|=|z+5i|$
$|z-2i|=2$を満たす複素数$z$に対して$z^4$を求めよ。
出典:2021年津田塾大学 入試問題
この動画を見る
$|z-5|=|z+5i|$
$|z-2i|=2$を満たす複素数$z$に対して$z^4$を求めよ。
出典:2021年津田塾大学 入試問題
整数問題の基本
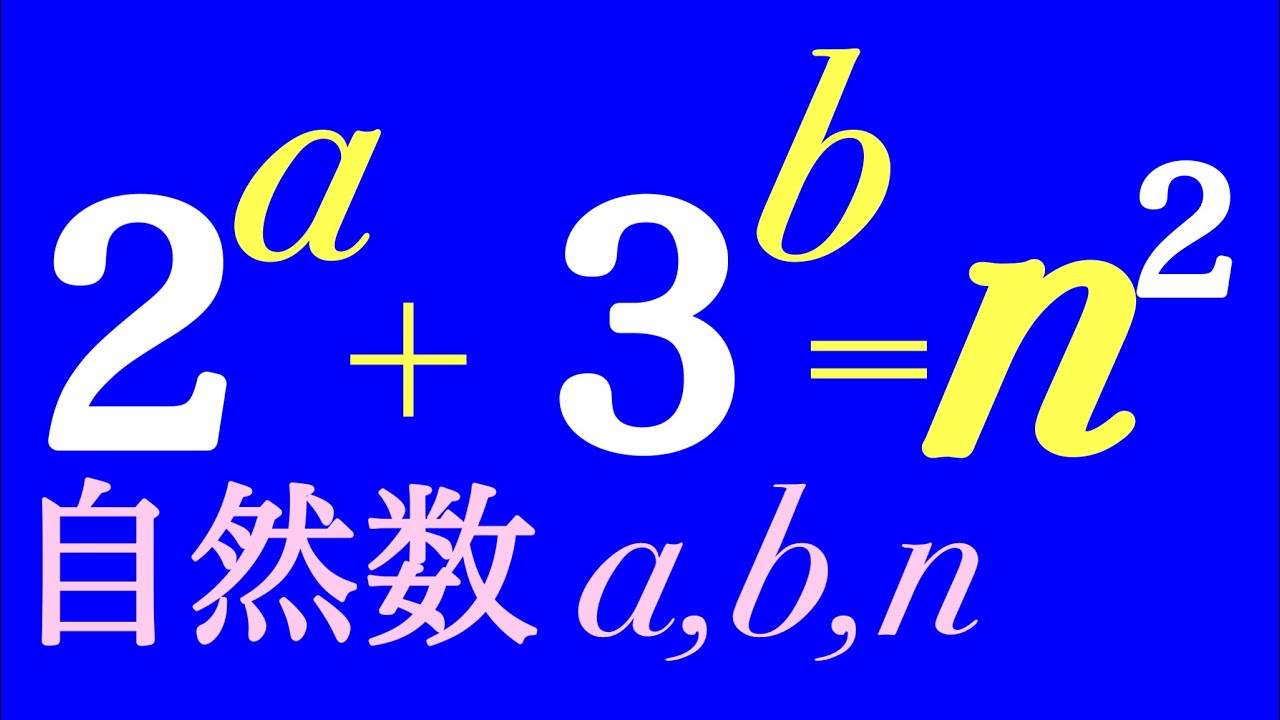
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$a,b,n$をすべて求めよ.
$2^a+3^b=n^2$
この動画を見る
自然数$a,b,n$をすべて求めよ.
$2^a+3^b=n^2$
3=4が成り立つ世界

福田のわかった数学〜高校3年生理系091〜グラフを描こう(13)指数関数、凹凸、漸近線

単元:
#数Ⅱ#指数関数と対数関数#指数関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(13)
$y=e^{\frac{1}{x^2-1}} (-1 \lt x \lt 1)$
のグラフを描け。凹凸、漸近線を調べよ。
この動画を見る
数学$\textrm{III}$ グラフを描こう(13)
$y=e^{\frac{1}{x^2-1}} (-1 \lt x \lt 1)$
のグラフを描け。凹凸、漸近線を調べよ。
大学入試問題#42 慶應義塾大学(2021) 絶対値の定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a:$実数
$f(x)=|x|+a$に対して$\displaystyle \int_{-5}^{5}|f(x)|dx$が最小となる$a$の値を求めよ。
出典:2021年慶應義塾大学 入試問題
この動画を見る
$a:$実数
$f(x)=|x|+a$に対して$\displaystyle \int_{-5}^{5}|f(x)|dx$が最小となる$a$の値を求めよ。
出典:2021年慶應義塾大学 入試問題
どっちがでかい?

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt2 $ vs $\sqrt[3]{3}$
どちらが大きいか?
この動画を見る
$\sqrt2 $ vs $\sqrt[3]{3}$
どちらが大きいか?
【除法はこれでマスター】整式の除法のやり方となんで必要なのかを解説!〔高校数学 数学〕

数学「大学入試良問集」【14−15 折れ線の最小値と空間ベクトル】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#鳥取大学#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
点$A(1,2,4)$を通り、ベクトル$\vec{ n }=(-3,1,2)$に垂直な平面を$\alpha$とする。
平面$\alpha$に関して同じ側に2点$P(-2,1,7),Q(1,3,7)$がある。
次の問いに答えよ。
(1)
平面$\alpha$に関して点$P$と対称な点$R$の座標を求めよ。
(2)
平面$\alpha$上の点で、$PS+QS$を最小にする点$S$の座標とそのときの最小値を求めよ。
この動画を見る
点$A(1,2,4)$を通り、ベクトル$\vec{ n }=(-3,1,2)$に垂直な平面を$\alpha$とする。
平面$\alpha$に関して同じ側に2点$P(-2,1,7),Q(1,3,7)$がある。
次の問いに答えよ。
(1)
平面$\alpha$に関して点$P$と対称な点$R$の座標を求めよ。
(2)
平面$\alpha$上の点で、$PS+QS$を最小にする点$S$の座標とそのときの最小値を求めよ。
福田のわかった数学〜高校2年生073〜三角関数(12)三角関数の最大最小

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 三角関数(12) 最大最小(2)
$y=\cos2x+2a\sin x+1$
の$0 \leqq x \leqq \pi$における最大値、最小値を求めよ。
この動画を見る
数学$\textrm{II}$ 三角関数(12) 最大最小(2)
$y=\cos2x+2a\sin x+1$
の$0 \leqq x \leqq \pi$における最大値、最小値を求めよ。
大学入試問題#41 東海大学医学部(2021) 因数分解

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師:
ますただ
問題文全文(内容文):
$(a+b+c)^3-a^3-b^3-c^3$を因数分解せよ。
出典:2021年東海大学医学部 入試問題
この動画を見る
$(a+b+c)^3-a^3-b^3-c^3$を因数分解せよ。
出典:2021年東海大学医学部 入試問題
整数の基本問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ab+cd$が$a-c$の倍数ならば,
$ad+bc$も$a-c$の倍数であることを示せ.
$a,b,c,d$は自然数である.
この動画を見る
$ab+cd$が$a-c$の倍数ならば,
$ad+bc$も$a-c$の倍数であることを示せ.
$a,b,c,d$は自然数である.
3つの半円の面積の和 東北学院
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
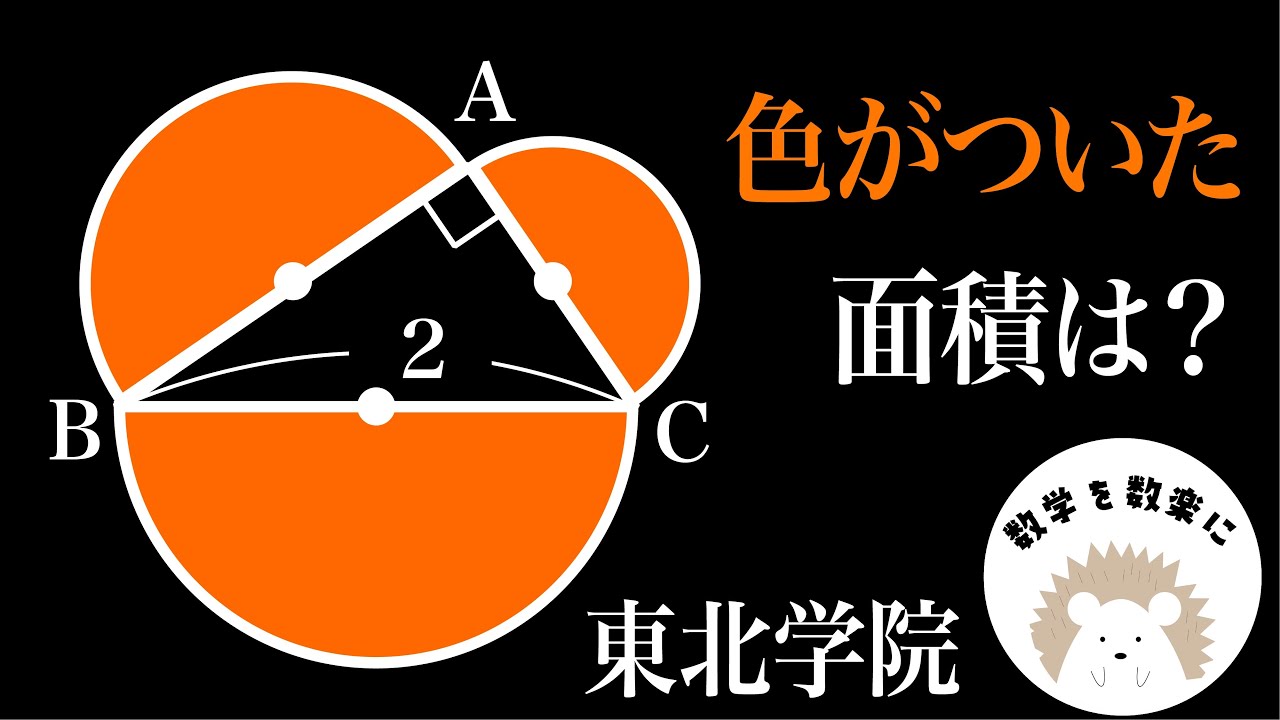
3つの半円の面積の和=?
*図は動画内参照
東北学院高等学校
この動画を見る
3つの半円の面積の和=?
*図は動画内参照
東北学院高等学校
【数Ⅱ】二項定理・多項定理の導出と使い方【ストーリーがわかれば暗記不要!】

この数字すごない?

福田のわかった数学〜高校1年生073〜場合の数(12)組み分け
単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
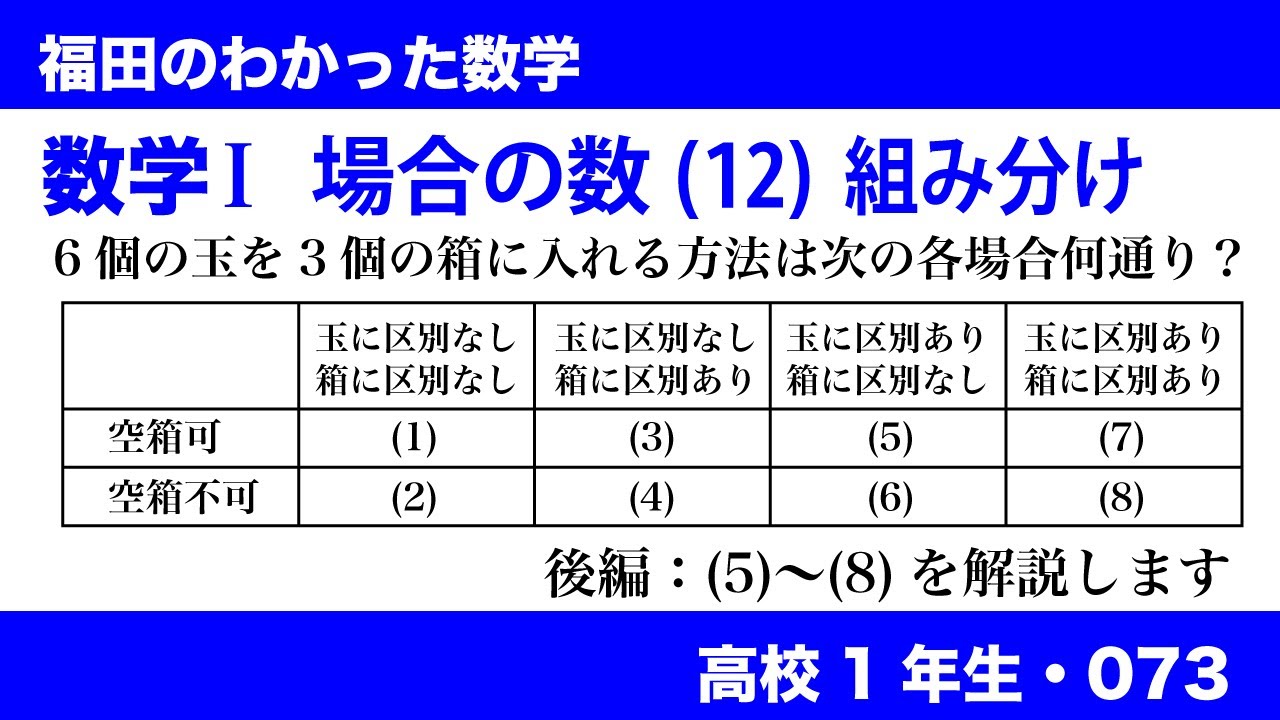
数学$\textrm{I}$ 場合の数(12) 組み分け
6個の玉を3個の箱に入れる方法は次の各場合に何通りあるか。
\begin{array}{|c|c|c|c|c|}
\hline
& 玉に区別なし & 玉に区別なし & 玉に区別あり &玉に区別あり\\
& 箱に区別なし & 箱に区別あり & 箱に区別なし &箱に区別あり\\
\hline
空箱可 & (1) & (3) & (5) & (7)\\
\hline
空箱不可 & (2) & (4) & (6) & (8)\\
\hline
\end{array}
\end{eqnarray}
この動画を見る
数学$\textrm{I}$ 場合の数(12) 組み分け
6個の玉を3個の箱に入れる方法は次の各場合に何通りあるか。
\begin{array}{|c|c|c|c|c|}
\hline
& 玉に区別なし & 玉に区別なし & 玉に区別あり &玉に区別あり\\
& 箱に区別なし & 箱に区別あり & 箱に区別なし &箱に区別あり\\
\hline
空箱可 & (1) & (3) & (5) & (7)\\
\hline
空箱不可 & (2) & (4) & (6) & (8)\\
\hline
\end{array}
\end{eqnarray}
大学入試問題#40 東京理科大学(2021) 数列と極限
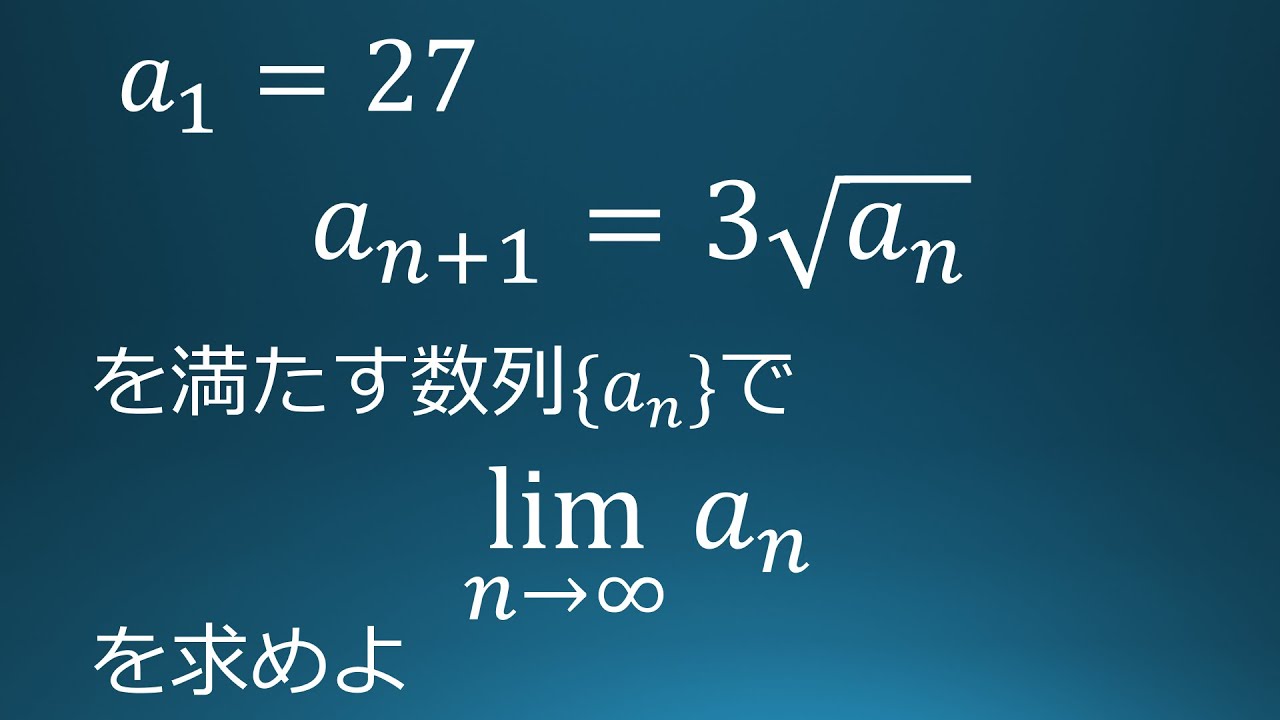
単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1=27$
$a_{n+1}=3\sqrt{ a_n }$を満たす数列$\{a_n\}$において
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典:2021年東京理科大学 入試問題
この動画を見る
$a_1=27$
$a_{n+1}=3\sqrt{ a_n }$を満たす数列$\{a_n\}$において
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典:2021年東京理科大学 入試問題
スッキリ解こう!対数・指数方程式
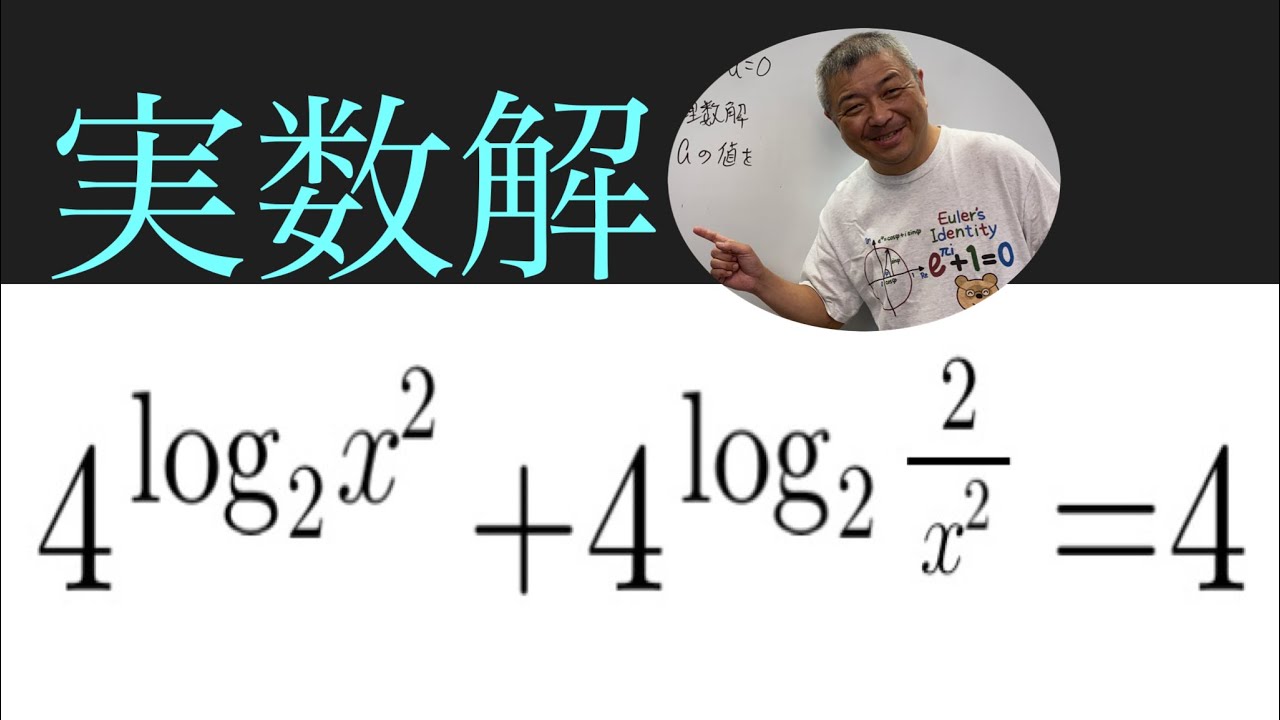
単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$4^{\log_2 x^2}$$+4^{\log_2 \frac{2}{x^2}}=4$
この動画を見る
実数解を求めよ.
$4^{\log_2 x^2}$$+4^{\log_2 \frac{2}{x^2}}=4$
これ便利すぎ

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\sin 330^{ \circ }=-\displaystyle \frac{1}{2}$
面白い有名角の覚え方紹介動画です
この動画を見る
$\sin 330^{ \circ }=-\displaystyle \frac{1}{2}$
面白い有名角の覚え方紹介動画です
3乗根

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
${}^3\sqrt {\sqrt{64}}=$
この動画を見る
${}^3\sqrt {\sqrt{64}}=$
福田のわかった数学〜高校3年生理系090〜グラフを描こう(12)無理関数、凹凸、漸近線

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう。(12)
$y=\sqrt[3]{x^3-x^2}$ のグラフを描け。ただし凹凸、漸近線も調べよ。
この動画を見る
数学$\textrm{III}$ グラフを描こう。(12)
$y=\sqrt[3]{x^3-x^2}$ のグラフを描け。ただし凹凸、漸近線も調べよ。
大学入試問題#39 東海大学医学部(2021) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師:
ますただ
問題文全文(内容文):
$n:$自然数
$n^3+100$が$n+10$で割り切れるような最大の$n$の値を求めよ。
出典:2021年東海大学医学部 入試問題
この動画を見る
$n:$自然数
$n^3+100$が$n+10$で割り切れるような最大の$n$の値を求めよ。
出典:2021年東海大学医学部 入試問題
ただの三次方程式
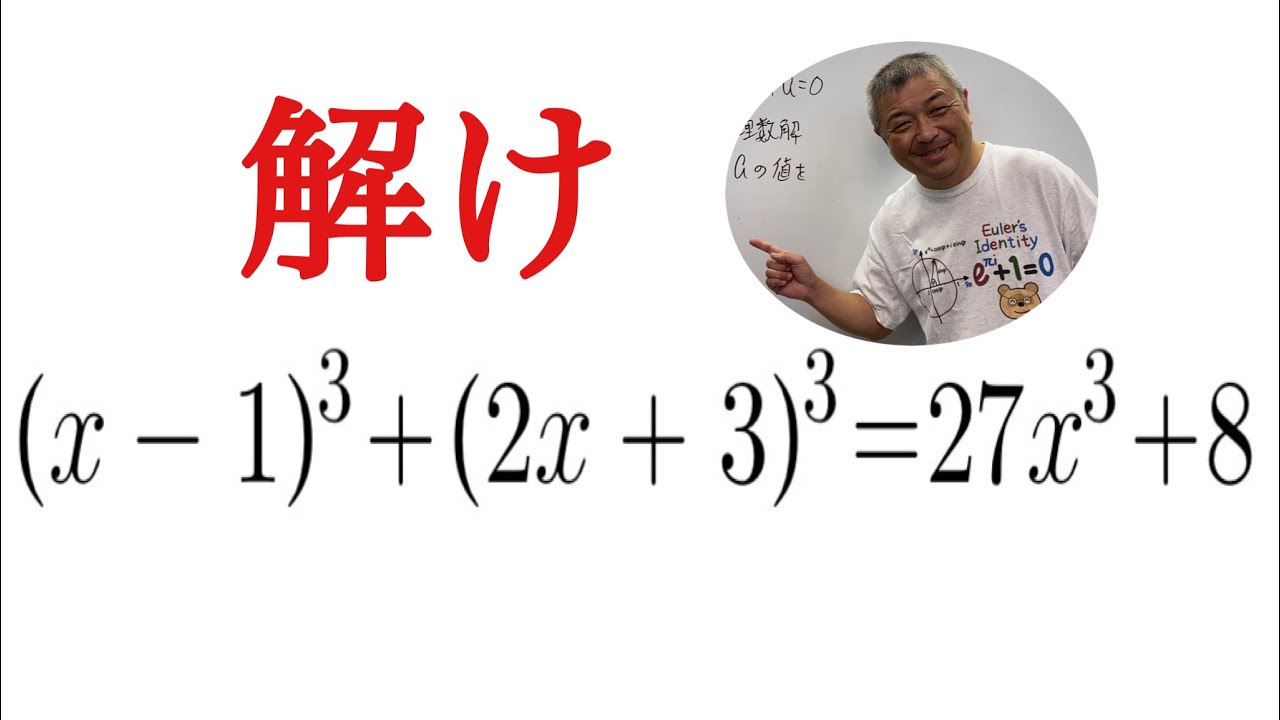
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$(x-1)^3+(2x+3)^3=27x^3+8$
この動画を見る
これを解け.
$(x-1)^3+(2x+3)^3=27x^3+8$
数学「大学入試良問集」【14−14四面体の体積•平面と垂直な直線】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#大分大学#数学(高校生)#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
空間内に4点$A(0,0,0),B(2,1,1),C(-2,2,-4),D(1,2,-4)$がある。
(1)
$\angle BAC=\theta$とおくとき、$\cos\theta$の値と$\triangle ABC$の面積を求めよ。
(2)
$\overrightarrow{ AB }$と$\overrightarrow{ AC }$の両方に垂直なベクトルを1つ求めよ。
(3)
点$D$から、3点$A,B,C$を含む平面に垂直な直線を引き、その交点を$E$とするとき、線分$DE$の長さを求めよ。
(4)
四面体$ABCD$の体積を求めよ。
この動画を見る
空間内に4点$A(0,0,0),B(2,1,1),C(-2,2,-4),D(1,2,-4)$がある。
(1)
$\angle BAC=\theta$とおくとき、$\cos\theta$の値と$\triangle ABC$の面積を求めよ。
(2)
$\overrightarrow{ AB }$と$\overrightarrow{ AC }$の両方に垂直なベクトルを1つ求めよ。
(3)
点$D$から、3点$A,B,C$を含む平面に垂直な直線を引き、その交点を$E$とするとき、線分$DE$の長さを求めよ。
(4)
四面体$ABCD$の体積を求めよ。
福田のわかった数学〜高校2年生072〜三角関数(11)三角関数の最大最小

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 三角関数(11) 最大最小(1)
$y=3\cos x+4\sin x (0 \leqq x \leqq \frac{\pi}{2})$
(1)右辺を$\cos$で合成せよ。
(2)yの最大値、最小値を求めよ。
この動画を見る
数学$\textrm{II}$ 三角関数(11) 最大最小(1)
$y=3\cos x+4\sin x (0 \leqq x \leqq \frac{\pi}{2})$
(1)右辺を$\cos$で合成せよ。
(2)yの最大値、最小値を求めよ。
#27 数検1級1次 過去問 整数問題

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x,y:$正の整数
$x+y=316$
$x:13$の倍数
$y:11$の倍数
をみたす組$(x,y)$をすべて求めよ。
この動画を見る
$x,y:$正の整数
$x+y=316$
$x:13$の倍数
$y:11$の倍数
をみたす組$(x,y)$をすべて求めよ。
ただの分母の有理化
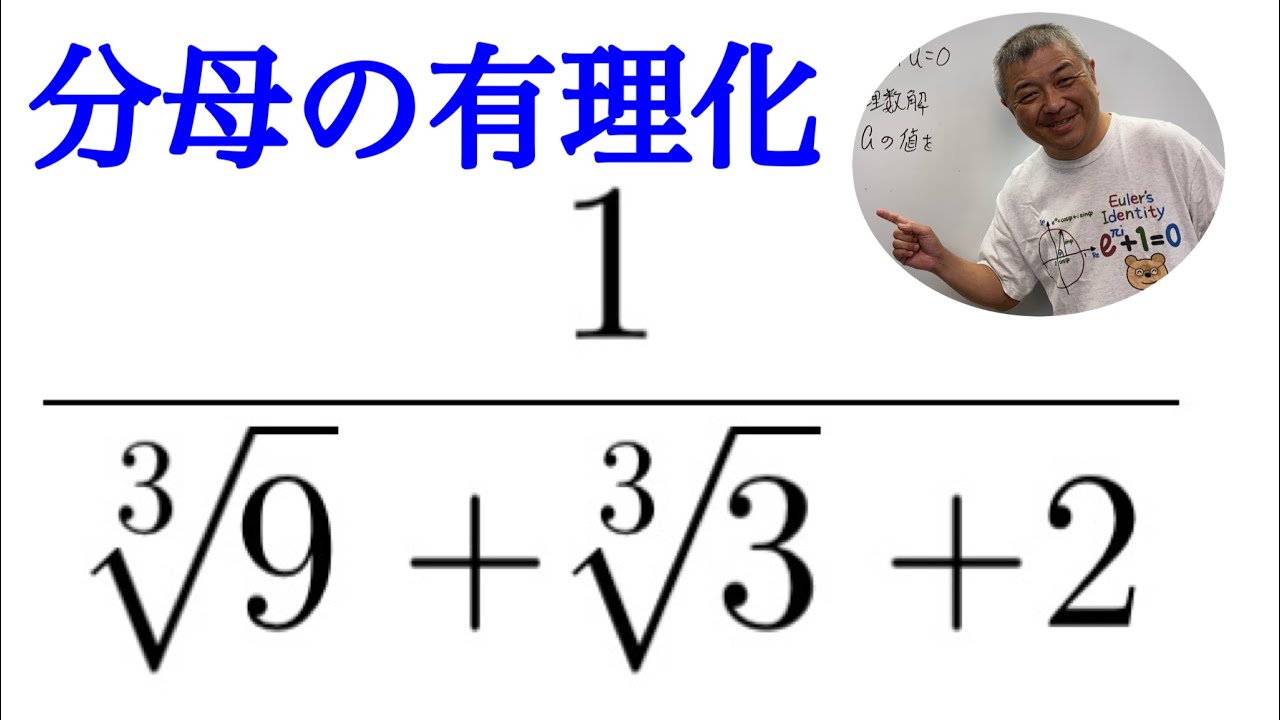
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
分母を有理化せよ.
$\dfrac{1}{\sqrt[3]{9}+\sqrt[3]{3}+2}$
この動画を見る
分母を有理化せよ.
$\dfrac{1}{\sqrt[3]{9}+\sqrt[3]{3}+2}$
福田のわかった数学〜高校1年生072〜場合の数(11)組み分け
単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
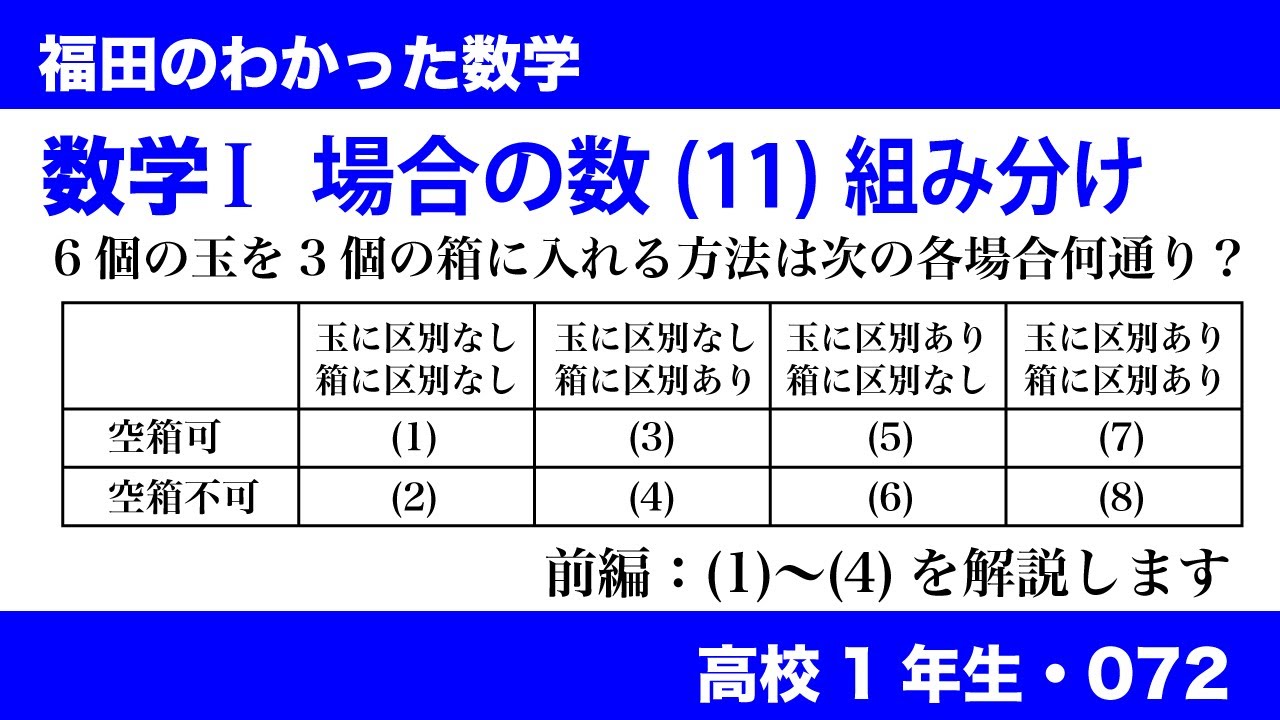
数学$\textrm{I}$ 場合の数(11) 組み分け
6個の玉を3個の箱に入れる方法は次の各場合に何通りあるか。
\begin{array}{|c|c|c|c|c|}
\hline
& 玉に区別なし & 玉に区別なし & 玉に区別あり &玉に区別あり\\
& 箱に区別なし & 箱に区別あり & 箱に区別なし &箱に区別あり\\
\hline
空箱可 & (1) & (3) & (5) & (7)\\
\hline
空箱不可 & (2) & (4) & (6) & (8)\\
\hline
\end{array}
\end{eqnarray}
この動画を見る
数学$\textrm{I}$ 場合の数(11) 組み分け
6個の玉を3個の箱に入れる方法は次の各場合に何通りあるか。
\begin{array}{|c|c|c|c|c|}
\hline
& 玉に区別なし & 玉に区別なし & 玉に区別あり &玉に区別あり\\
& 箱に区別なし & 箱に区別あり & 箱に区別なし &箱に区別あり\\
\hline
空箱可 & (1) & (3) & (5) & (7)\\
\hline
空箱不可 & (2) & (4) & (6) & (8)\\
\hline
\end{array}
\end{eqnarray}
〇〇を教えるときに注意していること
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
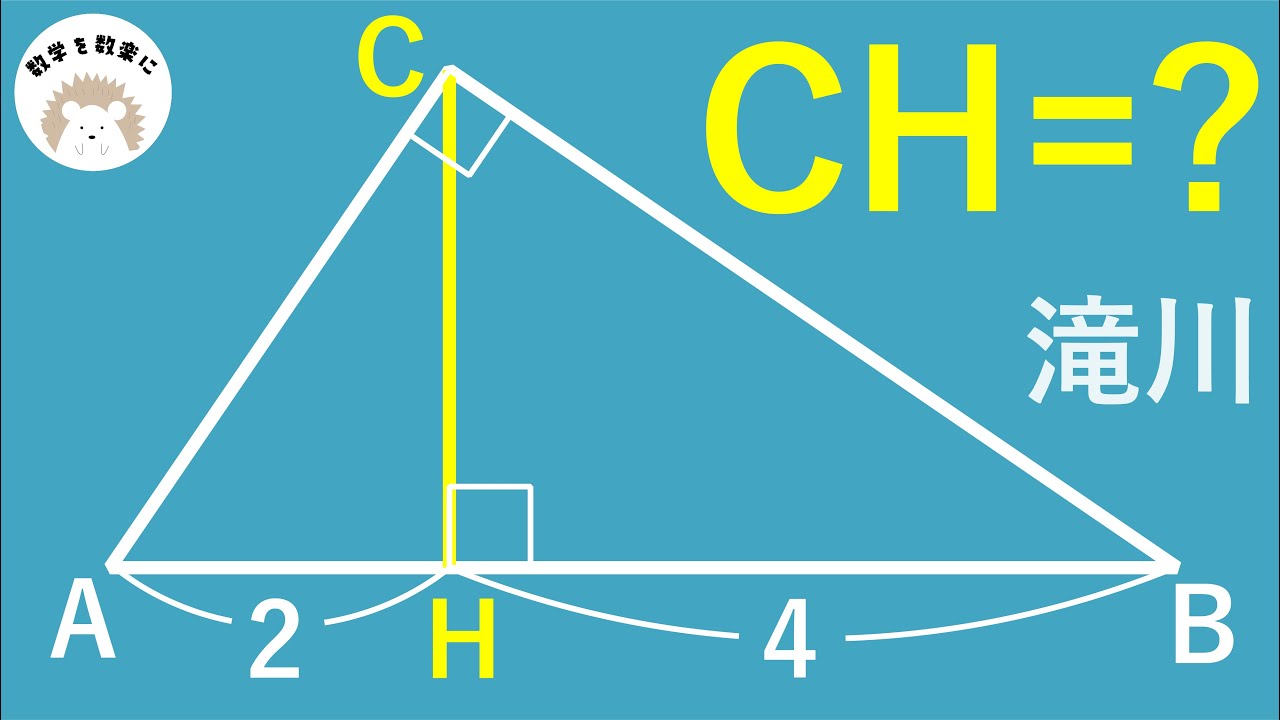
問題文全文(内容文):
CH=?
*図は動画内参照
滝川高等学校
この動画を見る
CH=?
*図は動画内参照
滝川高等学校
