 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
補助線引けるかな?
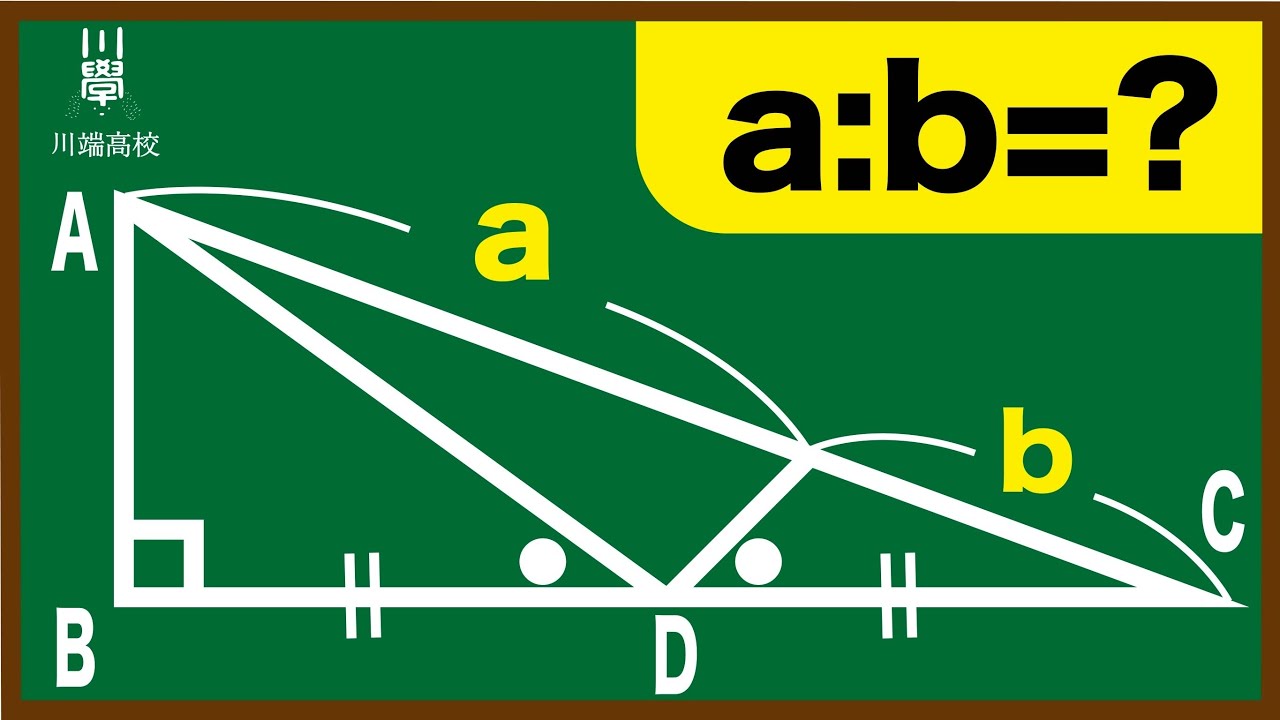
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a:b=?
*図は動画内参照
川端高校
この動画を見る
a:b=?
*図は動画内参照
川端高校
【数学】(高2生必見!!)2019年度 第3回 K塾高2模試 全問解説

単元:
#大学入試過去問(数学)#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
大問1:小問集合
(1)2次不等式$x^2+5x-6\lt 0$を解け。
(2)9人の生徒を3人ずつA,B,Cの3つの組に分けるとき、分け方は何通りか。
(3)次のデータがある。3,5,5,6,7,10.このデータの平均値を求めよ。また、分散を求めよ。
(4)$(4x+1)^5$を展開したとき、$x^2$の係数を求めよ。
(5)xの整式$x^3-3x^2+ax-a$ (aは定数)がx-2で割り切れるとき、aの値を求めよ。
(6)$a\neq 0,b\neq 0$とする。 $(ab)^5\times (a^2)^{-3}\div (b^2)^2$を計算せよ。
(7)整数m,nについて、$m+n$が偶数であることは、mnが偶数であるための$\Box$である。
(選択肢)
①必要十分条件である
②必要条件であるが、十分条件ではない
③十分条件であるが、必要条件ではない
④必要条件でも十分条件でもない
大問2[1]:式と証明
次のような問題がある。
問1 すべての実数xに対して、不等式 $x^2+x+1\geqq 3x-2 …$(*)が成り立つことを証明せよ。
問2 $x\geqq 2$のとき、関数$ f(x)=\dfrac{x+2}{x}$ の最小値を求めよ。
太郎さんはこの問題の解答を次のように書いた。
問1 $(x^2+x+1)-(3x-2)=x^2-2x+3=(a-1)^2+2$ すべての実数xに対して、$(x-1)^2\geqq 0$であるから、$(a-1)^2+2\geqq 0$ よって、$x^2+x+1\geqq 3x-2$ は成り立つ。
問2 $x\geqq 2$のとき、$x\gt 0,\dfrac{2}{x}\gt 0$であるから、相加平均と相乗平均の大小関係より、$\dfrac{x+2}{x}\geqq 2\sqrt x\times \dfrac{2}{x}$ これより、$f(x)\geqq 2\sqrt2$ よって、f(x)の最小値は$2\sqrt2$である。
(1)太郎さんの問1の解答は正しいか、正しくないか答えよ(答えのみでよい)。また、xが実数のとき、問1の不等式(*)において、等号が成り立つか成り立たないか答えよ。さらに、その理由を「実数」「実数解」のいずれかの単語を用いて説明せよ。
大問2[2]:確率
1~4の数字が書かれたカードが1枚ずつ計4枚のカードが入っている袋がある。この袋の中から1枚のカードを無作為に取り出し、カードに書かれた数を記録して袋に戻すことを繰り返し4回行う。
(1)4回とも1が記録される確率を求めよ。
(2)4回とも2以上の数が記録される確率を求めよ。
(3)記録された4個の数の最小値が2である確率を求めよ。
大問3:図形と方程式
aは実数の定数とする。xy平面上に2点A(1,0)、B(-1,4)と円C:$x^2+y^2-2(a+1)x-4ay+5a^2+2a=0$があり、Cの中心をPとする。
(1)線分ABの長さと、直線ABの方程式を求めよ。
(2)$a=1$のとき、Pの座標を求めよ。また、このときのPと直線ABの距離を求めよ。
(3)aが実数全体を変化するとき、Pの軌跡を求めよ。
(4)aの値が$1\leqq a\leqq 3$の範囲を変化するとき、Cが通過する領域をDとする。点QがDを動くとき、三角形ABQの面積の最小値と最大値をそれぞれ求めよ。
大問4:三角関数
座標平面上に2点A(8,0)、B(0,8)と、原点を中心とする半径3の円がある。この円上に、x座標、y座標がともに正である点P($3\cos\theta,3\sin\theta)\left(0\lt\theta\lt \dfrac{\pi}{2}\right)$をとる。Pからx軸に下した垂線とx軸の交点をQ、Pからy軸に下した垂線とy軸の交点をRとし、△APQと△BPRの面積の和をSとする。
(1)線分AB、BRの長さをそれぞれ$\sin\theta、\cos\theta$を用いて表せ。
(2)Sを$\sin\theta、\cos\theta$を用いて表せ。
(3)$t=\sin\theta+\cos\theta$とする。$\theta$が$0\lt\theta\lt\dfrac{\pi}{2}$の範囲を変化するとき、tのとり得る値の範囲を求めよ。
(4)(i)θが$0\lt\theta\lt\dfrac{\pi}{2}$の範囲を変化するとき、Sの最大値を求めよ。
(ii)Sが最大となる$\theta$は2つあり、それらを$\theta_1,\theta_2\left(0\lt\theta_1\lt\theta_2\lt\dfrac{\pi}{2}\right)$とする。このとき、$\dfrac{\pi}{8}\lt \theta_1\lt\dfrac{\pi}{6}$であることを証明せよ。
大問5:微分法
3次関数 $f(x)=2x^3+3(1-a)x^2-6ax+8a$ がある。ただし、aは実数の定数である。
(1)a=2とする。
(i)f(x)の増減を調べて、f(x)の極大値と極小値を求めよ。
(ii)xの方程式$f(x)=0$の解で、$1\lt x\lt2$を満たすものの個数を求めよ。
(2)f(x)が$1\lt x\lt 2$において極値をもたないようなaの値の範囲を求めよ。
(3)xの方程式$f(x)=0$が$1\lt x\lt 2$の範囲に少なくとも1つの解をもつようなaの値の範囲を求めよ。
大問6:ベクトル
Oを原点とする座標空間に、3点A(1,2,2)、B(3,-4,0)、C(a,b,5)があり、$OA⊥OC$かつ$OB⊥OC$が成り立っている。
(1)$\vert OA\vert$、$\vert OB\vert$、内積$OA・OB、\cos\angle AOB$の値をそれぞれ求めよ。
(2)a,bの値を求めよ。
(3)四面体OABCの体積を求めよ。
(4)Oを中心とする半径rの球面Sがある。Sが3点A,B,Cを通る平面と交わってできる円の半径が2であるとき、rの値を求めよ。
大問7:数列
数列{$a_n$}$(n=1,2,3,…)$を$a_1=7, a_{n+1}=a_n+4(n=1,2,3,…)$によって定める。
(1)$a_4$の値を求めよ。また、数列{$a_n$}の一般項$a_n$を求めよ。
(2)$\displaystyle \sum_{k=1}^n a_k$を求めよ。
(3)数列{$b_n$}$(n=1,2,3,…)$を$b_1=3, b_{n+1}-b_n=a_n(n=1,2,3,…)$によって定める。数列{$b_n$}の一般項$b_n$を求めよ。
(4)数列{$c_n$}$(n=1,2,3,…)$を(3)の$b_n$を用いて、$c_1=\dfrac{1}{5}, c_{n+1}=b_n\times \dfrac{c_n}{(b_{n+1}-3)}(n=1,2,3,…)$によって定める。数列${c_n}$の一般項$c_n$を求めよ。また、$\displaystyle \sum_{k=1}^n c_k$を求めよ。
この動画を見る
大問1:小問集合
(1)2次不等式$x^2+5x-6\lt 0$を解け。
(2)9人の生徒を3人ずつA,B,Cの3つの組に分けるとき、分け方は何通りか。
(3)次のデータがある。3,5,5,6,7,10.このデータの平均値を求めよ。また、分散を求めよ。
(4)$(4x+1)^5$を展開したとき、$x^2$の係数を求めよ。
(5)xの整式$x^3-3x^2+ax-a$ (aは定数)がx-2で割り切れるとき、aの値を求めよ。
(6)$a\neq 0,b\neq 0$とする。 $(ab)^5\times (a^2)^{-3}\div (b^2)^2$を計算せよ。
(7)整数m,nについて、$m+n$が偶数であることは、mnが偶数であるための$\Box$である。
(選択肢)
①必要十分条件である
②必要条件であるが、十分条件ではない
③十分条件であるが、必要条件ではない
④必要条件でも十分条件でもない
大問2[1]:式と証明
次のような問題がある。
問1 すべての実数xに対して、不等式 $x^2+x+1\geqq 3x-2 …$(*)が成り立つことを証明せよ。
問2 $x\geqq 2$のとき、関数$ f(x)=\dfrac{x+2}{x}$ の最小値を求めよ。
太郎さんはこの問題の解答を次のように書いた。
問1 $(x^2+x+1)-(3x-2)=x^2-2x+3=(a-1)^2+2$ すべての実数xに対して、$(x-1)^2\geqq 0$であるから、$(a-1)^2+2\geqq 0$ よって、$x^2+x+1\geqq 3x-2$ は成り立つ。
問2 $x\geqq 2$のとき、$x\gt 0,\dfrac{2}{x}\gt 0$であるから、相加平均と相乗平均の大小関係より、$\dfrac{x+2}{x}\geqq 2\sqrt x\times \dfrac{2}{x}$ これより、$f(x)\geqq 2\sqrt2$ よって、f(x)の最小値は$2\sqrt2$である。
(1)太郎さんの問1の解答は正しいか、正しくないか答えよ(答えのみでよい)。また、xが実数のとき、問1の不等式(*)において、等号が成り立つか成り立たないか答えよ。さらに、その理由を「実数」「実数解」のいずれかの単語を用いて説明せよ。
大問2[2]:確率
1~4の数字が書かれたカードが1枚ずつ計4枚のカードが入っている袋がある。この袋の中から1枚のカードを無作為に取り出し、カードに書かれた数を記録して袋に戻すことを繰り返し4回行う。
(1)4回とも1が記録される確率を求めよ。
(2)4回とも2以上の数が記録される確率を求めよ。
(3)記録された4個の数の最小値が2である確率を求めよ。
大問3:図形と方程式
aは実数の定数とする。xy平面上に2点A(1,0)、B(-1,4)と円C:$x^2+y^2-2(a+1)x-4ay+5a^2+2a=0$があり、Cの中心をPとする。
(1)線分ABの長さと、直線ABの方程式を求めよ。
(2)$a=1$のとき、Pの座標を求めよ。また、このときのPと直線ABの距離を求めよ。
(3)aが実数全体を変化するとき、Pの軌跡を求めよ。
(4)aの値が$1\leqq a\leqq 3$の範囲を変化するとき、Cが通過する領域をDとする。点QがDを動くとき、三角形ABQの面積の最小値と最大値をそれぞれ求めよ。
大問4:三角関数
座標平面上に2点A(8,0)、B(0,8)と、原点を中心とする半径3の円がある。この円上に、x座標、y座標がともに正である点P($3\cos\theta,3\sin\theta)\left(0\lt\theta\lt \dfrac{\pi}{2}\right)$をとる。Pからx軸に下した垂線とx軸の交点をQ、Pからy軸に下した垂線とy軸の交点をRとし、△APQと△BPRの面積の和をSとする。
(1)線分AB、BRの長さをそれぞれ$\sin\theta、\cos\theta$を用いて表せ。
(2)Sを$\sin\theta、\cos\theta$を用いて表せ。
(3)$t=\sin\theta+\cos\theta$とする。$\theta$が$0\lt\theta\lt\dfrac{\pi}{2}$の範囲を変化するとき、tのとり得る値の範囲を求めよ。
(4)(i)θが$0\lt\theta\lt\dfrac{\pi}{2}$の範囲を変化するとき、Sの最大値を求めよ。
(ii)Sが最大となる$\theta$は2つあり、それらを$\theta_1,\theta_2\left(0\lt\theta_1\lt\theta_2\lt\dfrac{\pi}{2}\right)$とする。このとき、$\dfrac{\pi}{8}\lt \theta_1\lt\dfrac{\pi}{6}$であることを証明せよ。
大問5:微分法
3次関数 $f(x)=2x^3+3(1-a)x^2-6ax+8a$ がある。ただし、aは実数の定数である。
(1)a=2とする。
(i)f(x)の増減を調べて、f(x)の極大値と極小値を求めよ。
(ii)xの方程式$f(x)=0$の解で、$1\lt x\lt2$を満たすものの個数を求めよ。
(2)f(x)が$1\lt x\lt 2$において極値をもたないようなaの値の範囲を求めよ。
(3)xの方程式$f(x)=0$が$1\lt x\lt 2$の範囲に少なくとも1つの解をもつようなaの値の範囲を求めよ。
大問6:ベクトル
Oを原点とする座標空間に、3点A(1,2,2)、B(3,-4,0)、C(a,b,5)があり、$OA⊥OC$かつ$OB⊥OC$が成り立っている。
(1)$\vert OA\vert$、$\vert OB\vert$、内積$OA・OB、\cos\angle AOB$の値をそれぞれ求めよ。
(2)a,bの値を求めよ。
(3)四面体OABCの体積を求めよ。
(4)Oを中心とする半径rの球面Sがある。Sが3点A,B,Cを通る平面と交わってできる円の半径が2であるとき、rの値を求めよ。
大問7:数列
数列{$a_n$}$(n=1,2,3,…)$を$a_1=7, a_{n+1}=a_n+4(n=1,2,3,…)$によって定める。
(1)$a_4$の値を求めよ。また、数列{$a_n$}の一般項$a_n$を求めよ。
(2)$\displaystyle \sum_{k=1}^n a_k$を求めよ。
(3)数列{$b_n$}$(n=1,2,3,…)$を$b_1=3, b_{n+1}-b_n=a_n(n=1,2,3,…)$によって定める。数列{$b_n$}の一般項$b_n$を求めよ。
(4)数列{$c_n$}$(n=1,2,3,…)$を(3)の$b_n$を用いて、$c_1=\dfrac{1}{5}, c_{n+1}=b_n\times \dfrac{c_n}{(b_{n+1}-3)}(n=1,2,3,…)$によって定める。数列${c_n}$の一般項$c_n$を求めよ。また、$\displaystyle \sum_{k=1}^n c_k$を求めよ。
【数Ⅰ】円に内接する四角形【余弦定理を使い倒せ!】

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 四角形ABCDは円に内接しており,AB=2,BC=4,CD=3,DA=3である.
(1)cosA,BDの長さを求めよ.
(2)四角形ABCDの面積を求めよ.$
この動画を見る
$ 四角形ABCDは円に内接しており,AB=2,BC=4,CD=3,DA=3である.
(1)cosA,BDの長さを求めよ.
(2)四角形ABCDの面積を求めよ.$
座標平面上の角の二等分線
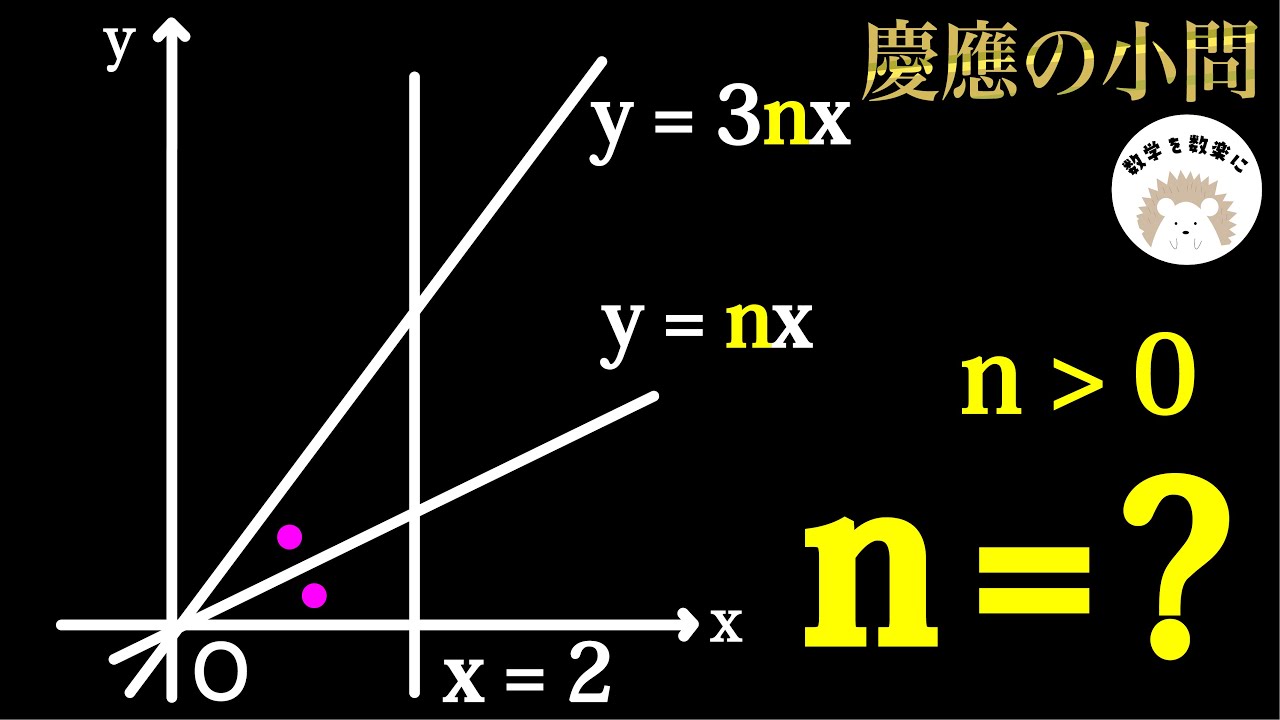
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
y=3nx
y=nx
*図は動画内参照
n=? (n>0)
慶應義塾高等学校
この動画を見る
y=3nx
y=nx
*図は動画内参照
n=? (n>0)
慶應義塾高等学校
福田のわかった数学〜高校2年生069〜三角関数(8)三角不等式

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 三角関数(8) 三角不等式
aは2以上の整数、$0 \lt x \leqq \pi$のとき次の連立不等式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\cos x \leqq \cos2ax \ldots① \\
\sin2ax \leqq 0 \ldots②
\end{array}
\right.
\end{eqnarray}$
この動画を見る
数学$\textrm{II}$ 三角関数(8) 三角不等式
aは2以上の整数、$0 \lt x \leqq \pi$のとき次の連立不等式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\cos x \leqq \cos2ax \ldots① \\
\sin2ax \leqq 0 \ldots②
\end{array}
\right.
\end{eqnarray}$
06兵庫県教員採用試験(数学:3番 円と直線の関係)

単元:
#数Ⅱ#図形と方程式#円と方程式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
円$c:x^2+y^2=1+m$と直線$l:y=-3x+m$が異なる2点$A,B$で交わる。
$m$は定数
(1)
$m$の値の範囲を求めよ
(2)
弦$AB$の長さの最大値とそのときの$m$の値を求めよ。
この動画を見る
円$c:x^2+y^2=1+m$と直線$l:y=-3x+m$が異なる2点$A,B$で交わる。
$m$は定数
(1)
$m$の値の範囲を求めよ
(2)
弦$AB$の長さの最大値とそのときの$m$の値を求めよ。
九州大の過去問をパクって問題作ってみた

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^3+3b^3=7c^3$を満たす整数$(a,b,c)$の組をすべて求めよ.
この動画を見る
$a^3+3b^3=7c^3$を満たす整数$(a,b,c)$の組をすべて求めよ.
数学「大学入試良問集」【14−10空間ベクトルと正四面体】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
各辺の長さが1の正四面体$OABC$に対し、$OB$を$2:1$に内分する点を$D,OC$を2等分する点を$E,BC$を2等分にする点を$F$とする。
$DE$と$OF$の交点を$G$とするとき、以下の各問いに答えよ。
(1)$OG$の長さを求めよ。
(2)$AG$の長さを求めよ。
この動画を見る
各辺の長さが1の正四面体$OABC$に対し、$OB$を$2:1$に内分する点を$D,OC$を2等分する点を$E,BC$を2等分にする点を$F$とする。
$DE$と$OF$の交点を$G$とするとき、以下の各問いに答えよ。
(1)$OG$の長さを求めよ。
(2)$AG$の長さを求めよ。
福田のわかった数学〜高校1年生069〜場合の数(8)円順列その2

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(8) 円順列(2)
次のような玉を円形に並べる方法は何通りか。
(1)白玉1個、黄玉2個、赤玉3個
(2)白玉2個、赤玉4個
(3)白玉2個、黄玉2個、赤玉2個
この動画を見る
数学$\textrm{I}$ 場合の数(8) 円順列(2)
次のような玉を円形に並べる方法は何通りか。
(1)白玉1個、黄玉2個、赤玉3個
(2)白玉2個、赤玉4個
(3)白玉2個、黄玉2個、赤玉2個
大学入試問題#38 日本大学(2021) 三角関数
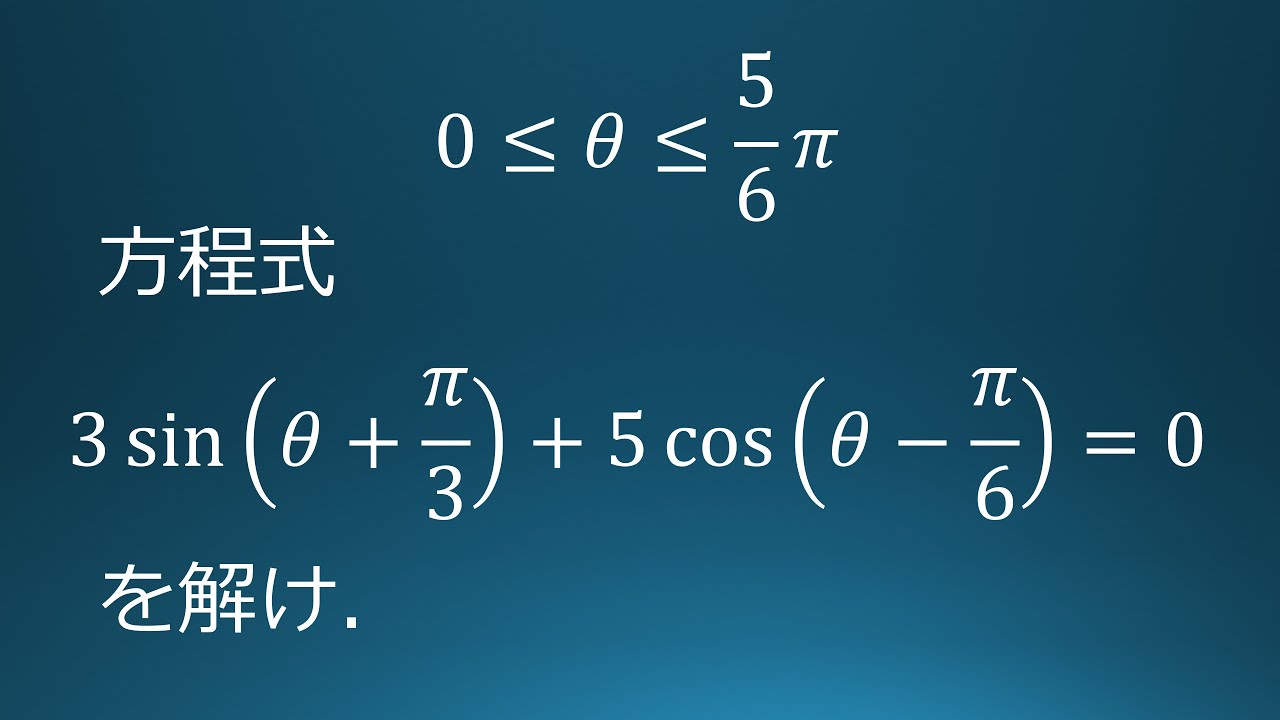
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq \theta \leqq \displaystyle \frac{5}{6}\pi$において
方程式
$3\sin(\theta+\displaystyle \frac{\pi}{3})+5\ \cos(\theta-\displaystyle \frac{\pi}{6})=0$を解け。
出典:2021年日本大学 入試問題
この動画を見る
$0 \leqq \theta \leqq \displaystyle \frac{5}{6}\pi$において
方程式
$3\sin(\theta+\displaystyle \frac{\pi}{3})+5\ \cos(\theta-\displaystyle \frac{\pi}{6})=0$を解け。
出典:2021年日本大学 入試問題
千葉大2002

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$を自然数とする.
$\log_2 n$が整数でない有理数となることを調べよ.
千葉大過去問
この動画を見る
$n$を自然数とする.
$\log_2 n$が整数でない有理数となることを調べよ.
千葉大過去問
【共通テスト】数学ⅡB公式出題ランキング!この公式はおさえておけ!

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
共通テストⅡBでおさえておくべき公式は??ランキングでまとめました
この動画を見る
共通テストⅡBでおさえておくべき公式は??ランキングでまとめました
【数Ⅱ】三角関数:方程式6x²-xy-y²=0は交わる2直線を表す。このとき、2直線のなす角θ(0≦θ≦π/2)を求めよ。

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
方程式$6x^2-xy-y^2=0$は交わる2直線を表す。このとき、2直線のなす角$\theta(0\leqq\theta\leqq \dfrac{\pi}{2}$)を求めよ。
この動画を見る
方程式$6x^2-xy-y^2=0$は交わる2直線を表す。このとき、2直線のなす角$\theta(0\leqq\theta\leqq \dfrac{\pi}{2}$)を求めよ。
感覚と違うくない?

福田のわかった数学〜高校3年生理系086〜グラフを描こう(8)媒介変数表示のグラフ

単元:
#平面上の曲線#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(8)
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=t^3-3t^2\\
y=t^2-2t
\end{array}
\right.
\end{eqnarray}$
のグラフを描け。
ただし凹凸は調べなくてよい。
この動画を見る
数学$\textrm{III}$ グラフを描こう(8)
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=t^3-3t^2\\
y=t^2-2t
\end{array}
\right.
\end{eqnarray}$
のグラフを描け。
ただし凹凸は調べなくてよい。
大学入試問題#37 早稲田大学(2021) 整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a,b,c:$実数
$0 \leqq a \leqq b \leqq c$
$a+b+c=7$を満たすとき
$ab,bc,ca$の最大値を求めよ。
出典:2021年早稲田大学 入試問題
この動画を見る
$a,b,c:$実数
$0 \leqq a \leqq b \leqq c$
$a+b+c=7$を満たすとき
$ab,bc,ca$の最大値を求めよ。
出典:2021年早稲田大学 入試問題
【数Ⅱ】三角関数:方程式sin(θ+40°)=sinθ(ただし0°≦θ≦90°)をみたすθを求めよ。

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
方程式$\sin(\theta+40°)=\sin\theta$(ただし$0°\leqq\theta\leqq90°$)をみたす$\theta$を求めよ。
この動画を見る
方程式$\sin(\theta+40°)=\sin\theta$(ただし$0°\leqq\theta\leqq90°$)をみたす$\theta$を求めよ。
指数・対数の基本問題
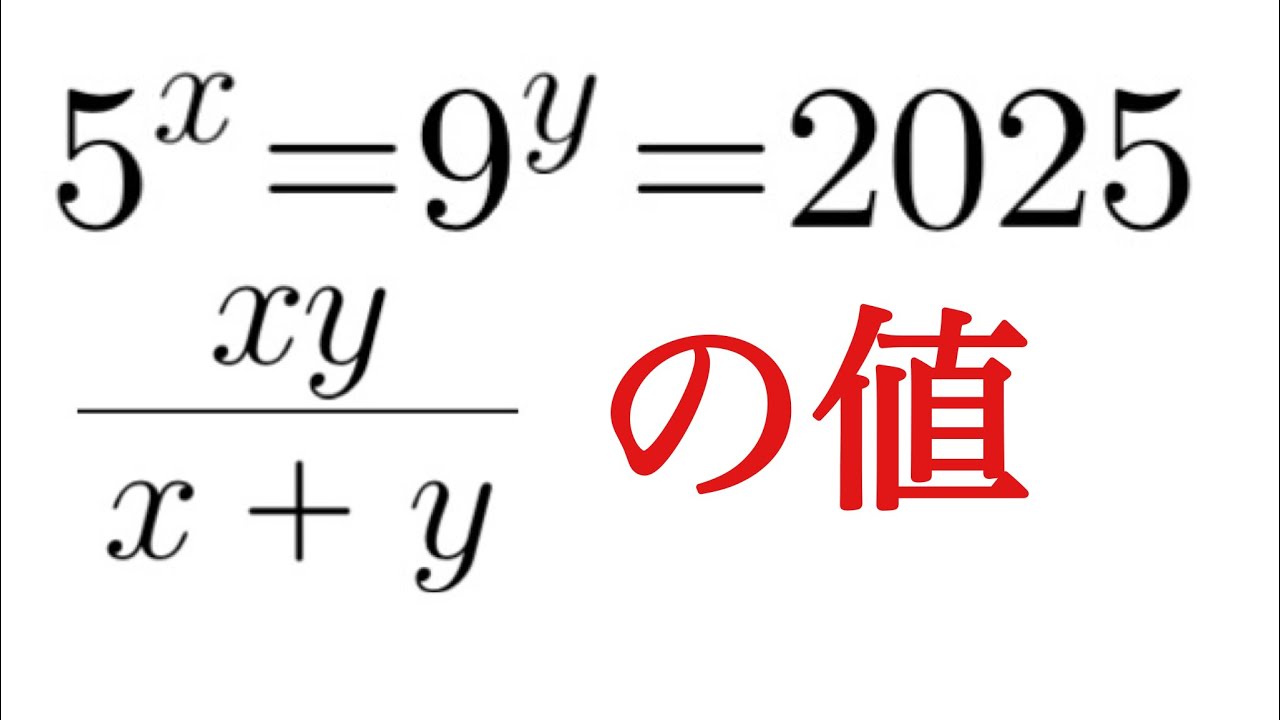
単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$5^x=9^y=2025$である.
$\dfrac{xy}{x+y}$の値を求めよ.
この動画を見る
$5^x=9^y=2025$である.
$\dfrac{xy}{x+y}$の値を求めよ.
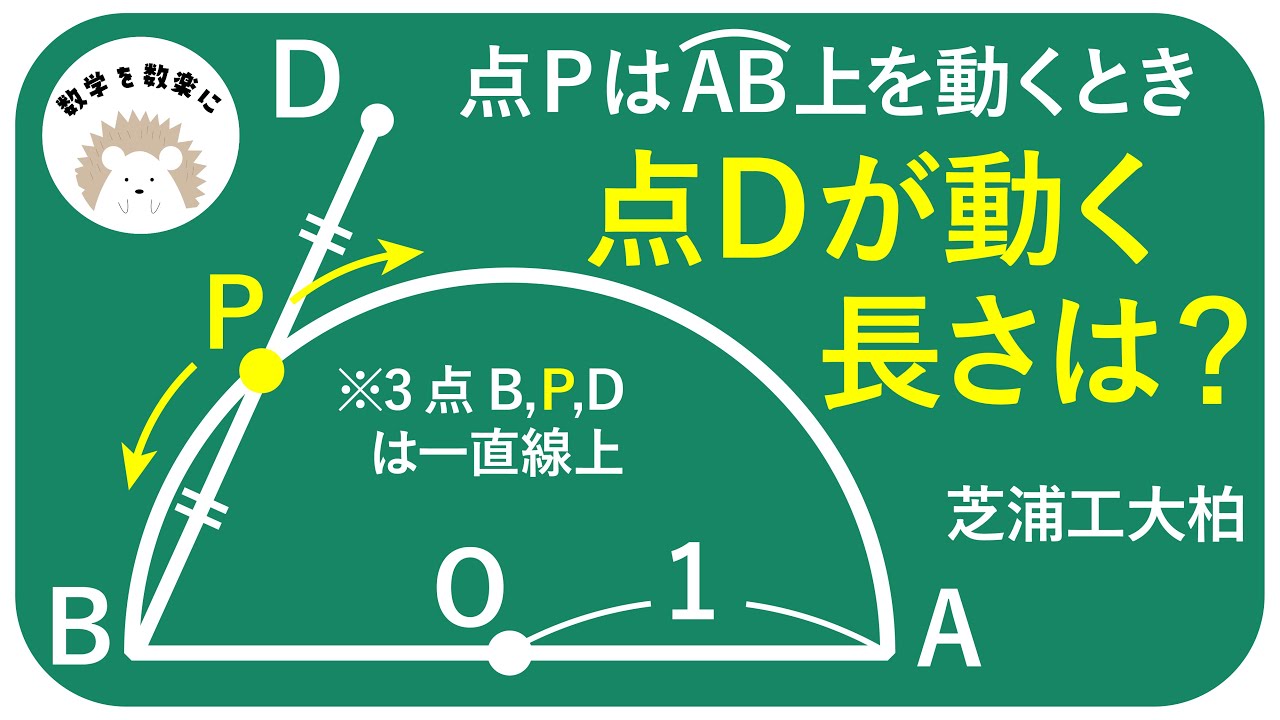
高校入試の軌跡の問題
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点Pは$\stackrel{\huge\frown}{AB}$上を動く。
BP=DPとなるように点Dを定めるとき点Dが動く長さは?
芝浦工業大学柏高等学校
この動画を見る
点Pは$\stackrel{\huge\frown}{AB}$上を動く。
BP=DPとなるように点Dを定めるとき点Dが動く長さは?
芝浦工業大学柏高等学校
数学「大学入試良問集」【14−9ベクトルと反転】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$xy$平面において、原点$O$を通る半径$r(r \gt 0)$の円を$C$とし、その中心を$A$とする。
$O$を除く$C$上の点$P$に対し、次の2つの条件$(a),(b)$で定まる点$Q$を考える。
(a)$\overrightarrow{ OP }$と$\overrightarrow{ OQ }$の向きが同じ。
(b)$|\overrightarrow{ OP }||\overrightarrow{ OQ }|=1$
以下の問いに答えよ。
(1)
点$P$が$O$を除く$C$上を動くとき、点$Q$は$\overrightarrow{ OA }$に直交する直線状を動くことを示せ。
(2)
(1)の直線を$l$とする。
$l$が$C$と2点で交わるとき、$r$のとり得る値の範囲を求めよ。
この動画を見る
$xy$平面において、原点$O$を通る半径$r(r \gt 0)$の円を$C$とし、その中心を$A$とする。
$O$を除く$C$上の点$P$に対し、次の2つの条件$(a),(b)$で定まる点$Q$を考える。
(a)$\overrightarrow{ OP }$と$\overrightarrow{ OQ }$の向きが同じ。
(b)$|\overrightarrow{ OP }||\overrightarrow{ OQ }|=1$
以下の問いに答えよ。
(1)
点$P$が$O$を除く$C$上を動くとき、点$Q$は$\overrightarrow{ OA }$に直交する直線状を動くことを示せ。
(2)
(1)の直線を$l$とする。
$l$が$C$と2点で交わるとき、$r$のとり得る値の範囲を求めよ。
【数Ⅰ】面積公式・ヘロンの公式・内接円の半径【小学生からの脱却!】

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
面積公式・ヘロンの公式・内接円の半径に関して解説していきます.
この動画を見る
面積公式・ヘロンの公式・内接円の半径に関して解説していきます.
三角比この覚え方はどうでしょうか?

福田のわかった数学〜高校2年生068〜三角関数(7)三角方程式とグラフ

単元:
#数Ⅱ#複素数と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 三角関数(7) 三角方程式
$0 \leqq x \leqq 2\pi, 0 \leqq y \leqq 2\pi$において
$\cos y=\sin2x$ のグラフを描け。
この動画を見る
数学$\textrm{II}$ 三角関数(7) 三角方程式
$0 \leqq x \leqq 2\pi, 0 \leqq y \leqq 2\pi$において
$\cos y=\sin2x$ のグラフを描け。
16高知県教員採用試験(数学:2-(4) 複素数)

単元:
#複素数平面#複素数平面#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\fcolorbox{black}{ #fffff }{$2$}-(4)$
$z^3=8i$
をみたす複素数$z$をすべて求めよ。
この動画を見る
$\fcolorbox{black}{ #fffff }{$2$}-(4)$
$z^3=8i$
をみたす複素数$z$をすべて求めよ。
指数方程式 解は1つではない

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^x・2^{\frac{6}{x}}=72$
この動画を見る
実数解を求めよ.
$3^x・2^{\frac{6}{x}}=72$
解が整数じゃなくても解けるよ
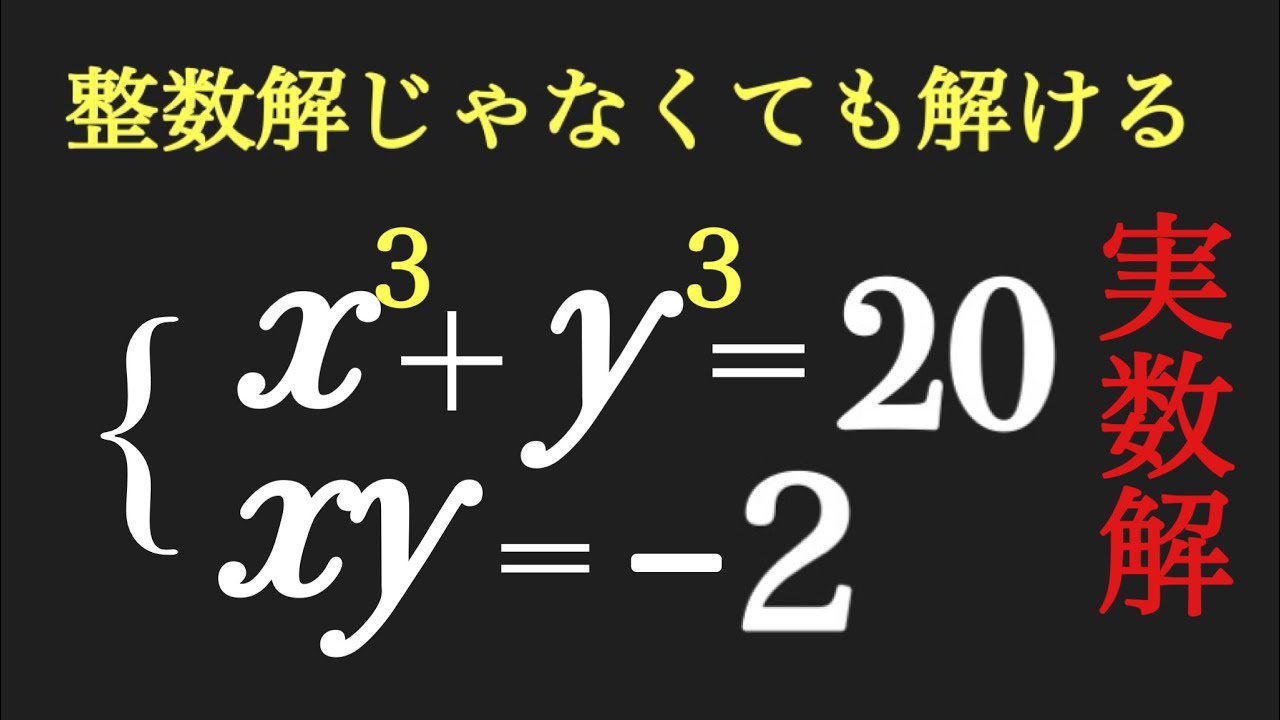
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3+y^3-91 \\
xy=12
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3+y^3=20 \\
xy=-2
\end{array}
\right.
\end{eqnarray}$
この動画を見る
実数解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3+y^3-91 \\
xy=12
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3+y^3=20 \\
xy=-2
\end{array}
\right.
\end{eqnarray}$
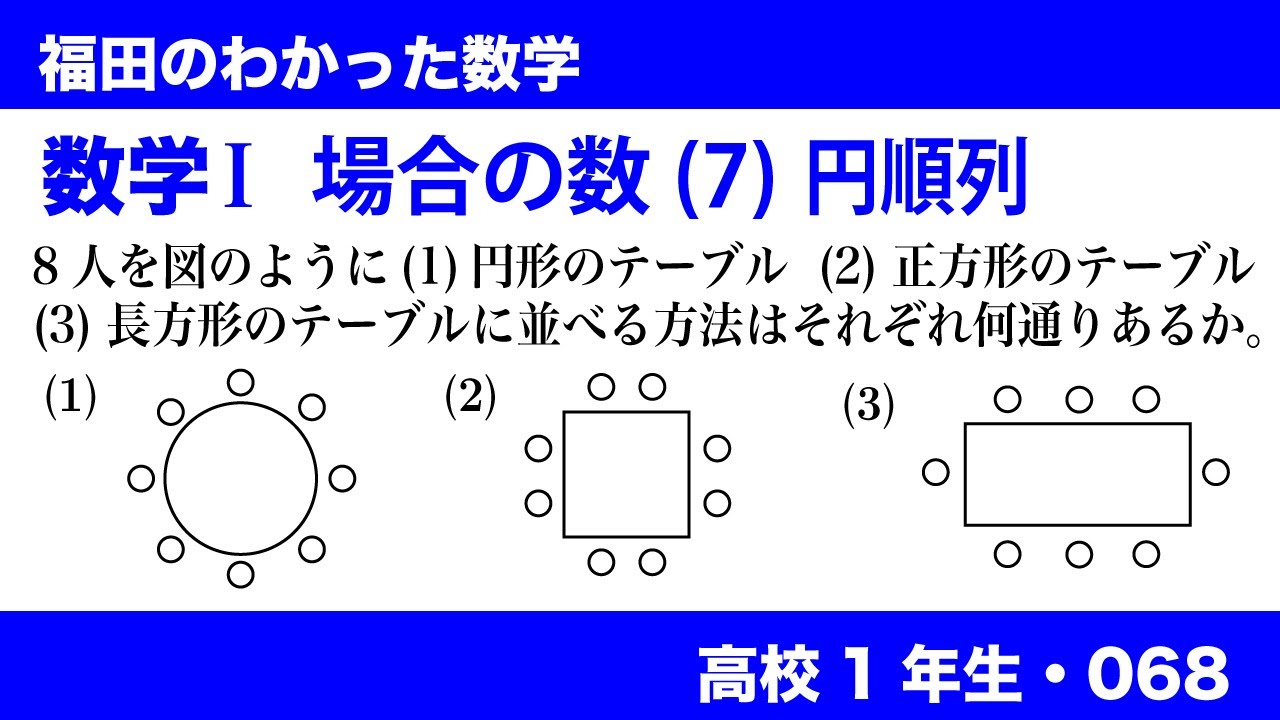
福田のわかった数学〜高校1年生068〜場合の数(7)円順列
単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(7) 円順列
8人を図のように(1)円形のテーブル (2)正方形のテーブル (3)長方形のテーブルに並べる方法は
それぞれ何通りあるか。
(※図は動画参照)
この動画を見る
数学$\textrm{I}$ 場合の数(7) 円順列
8人を図のように(1)円形のテーブル (2)正方形のテーブル (3)長方形のテーブルに並べる方法は
それぞれ何通りあるか。
(※図は動画参照)
微分方程式 高専数学 p 100(1)(2)
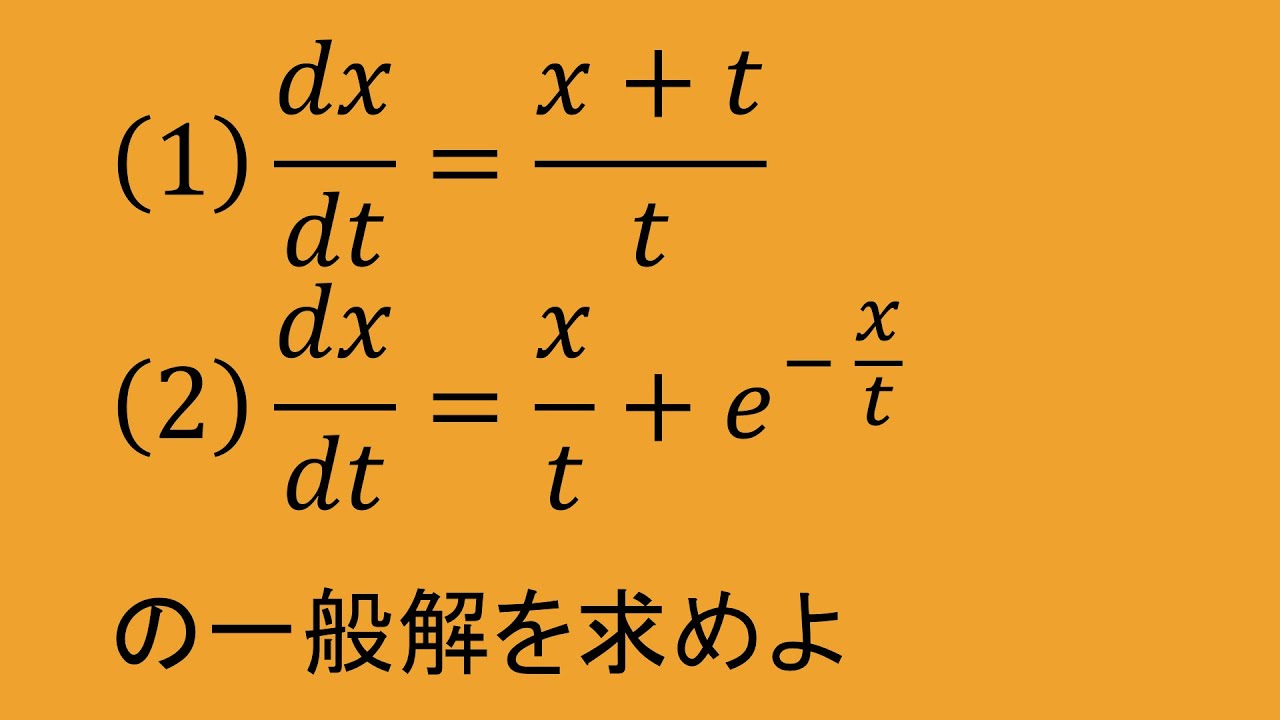
単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
微分方程式
(1)$\displaystyle \frac{dx}{dt}=\displaystyle \frac{x+t}{t}$
(2)$\displaystyle \frac{dx}{dt}=\displaystyle \frac{x}{t}+e^\frac{x}{t}$
の一般解を求めよ。
この動画を見る
微分方程式
(1)$\displaystyle \frac{dx}{dt}=\displaystyle \frac{x+t}{t}$
(2)$\displaystyle \frac{dx}{dt}=\displaystyle \frac{x}{t}+e^\frac{x}{t}$
の一般解を求めよ。
【数B】確率分布と統計的推測:母集団と標本:復元抽出と非復元抽出は何が違うの?

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
1,2,3が書かれたカードが1枚ずつあり、この中から大きさ2の標本を抜き出すとき、「復元抽出」「非復元抽出」の違いは?
この動画を見る
1,2,3が書かれたカードが1枚ずつあり、この中から大きさ2の標本を抜き出すとき、「復元抽出」「非復元抽出」の違いは?
数学「大学入試良問集」【14−8ベクトルと軌跡と等式・不等式】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#数学(高校生)#鳥取大学#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
平面上において同一直線上にない3点$A,B,C$があるとき、次の各問いに対して、それぞれの式をみたす点$P$の集合を求めよ。
(1)$\overrightarrow{ AP }+\overrightarrow{ BP }+\overrightarrow{ CP }=\overrightarrow{ AC }$
(2)$\overrightarrow{ AB }・\overrightarrow{ AP }=\overrightarrow{ AB }・\overrightarrow{ AB }$
(3)$\overrightarrow{ AB }・\overrightarrow{ AC }+\overrightarrow{ AP }・\overrightarrow{ AP } \leqq \overrightarrow{ AB }・\overrightarrow{ AP }+\overrightarrow{ AC }・\overrightarrow{ AP }$
この動画を見る
平面上において同一直線上にない3点$A,B,C$があるとき、次の各問いに対して、それぞれの式をみたす点$P$の集合を求めよ。
(1)$\overrightarrow{ AP }+\overrightarrow{ BP }+\overrightarrow{ CP }=\overrightarrow{ AC }$
(2)$\overrightarrow{ AB }・\overrightarrow{ AP }=\overrightarrow{ AB }・\overrightarrow{ AB }$
(3)$\overrightarrow{ AB }・\overrightarrow{ AC }+\overrightarrow{ AP }・\overrightarrow{ AP } \leqq \overrightarrow{ AB }・\overrightarrow{ AP }+\overrightarrow{ AC }・\overrightarrow{ AP }$
