 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
高専数学 微積I #229(2) 媒介変数表示関数のx軸回転体の体積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \dfrac{\pi}{2}$である.
$x=\sin t$
$y=\sin 2t$
と$x$軸で囲まれた図形を$x$軸のまわりに回転して
できる回転体の体積$V$を求めよ.
この動画を見る
$0\leqq t\leqq \dfrac{\pi}{2}$である.
$x=\sin t$
$y=\sin 2t$
と$x$軸で囲まれた図形を$x$軸のまわりに回転して
できる回転体の体積$V$を求めよ.
連立二元二次方程式
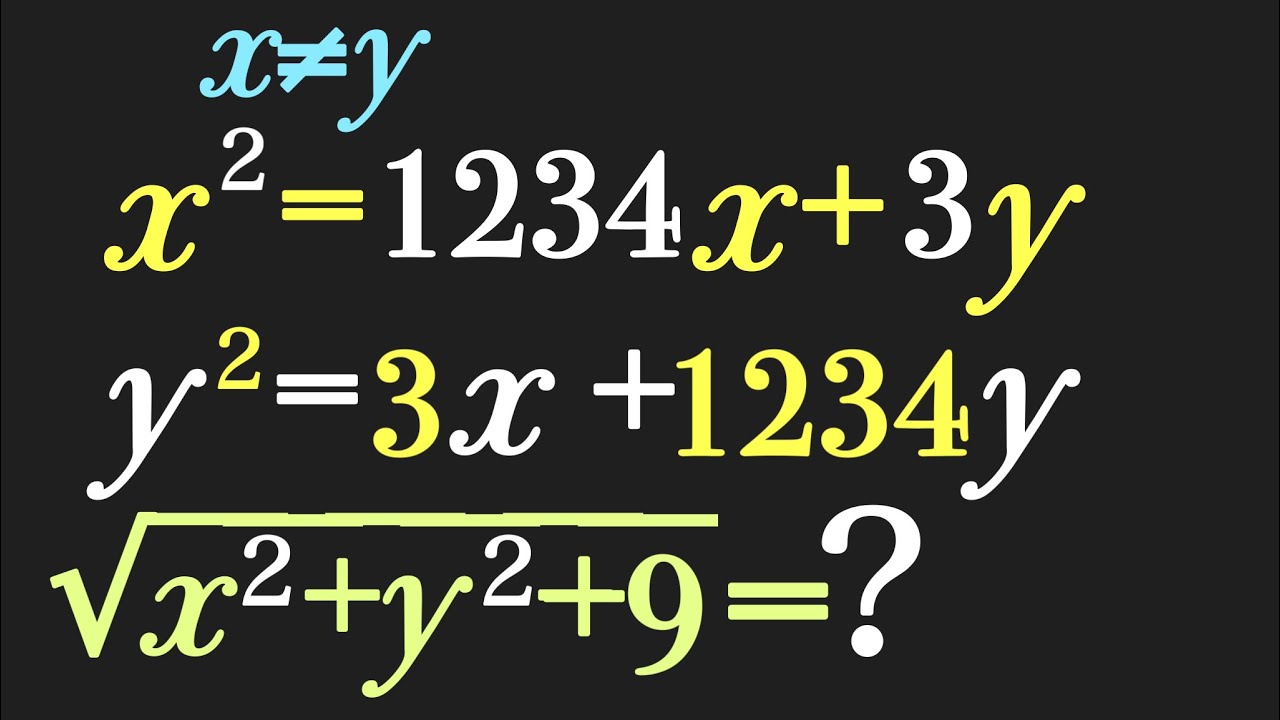
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x\neq y$である.
$x^2=1234x+3y$
$y^2=3x+1234y$
$\sqrt{x^2+y^2+9}=?$
この動画を見る
これを解け.$x\neq y$である.
$x^2=1234x+3y$
$y^2=3x+1234y$
$\sqrt{x^2+y^2+9}=?$
弧の長さの和=❓
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
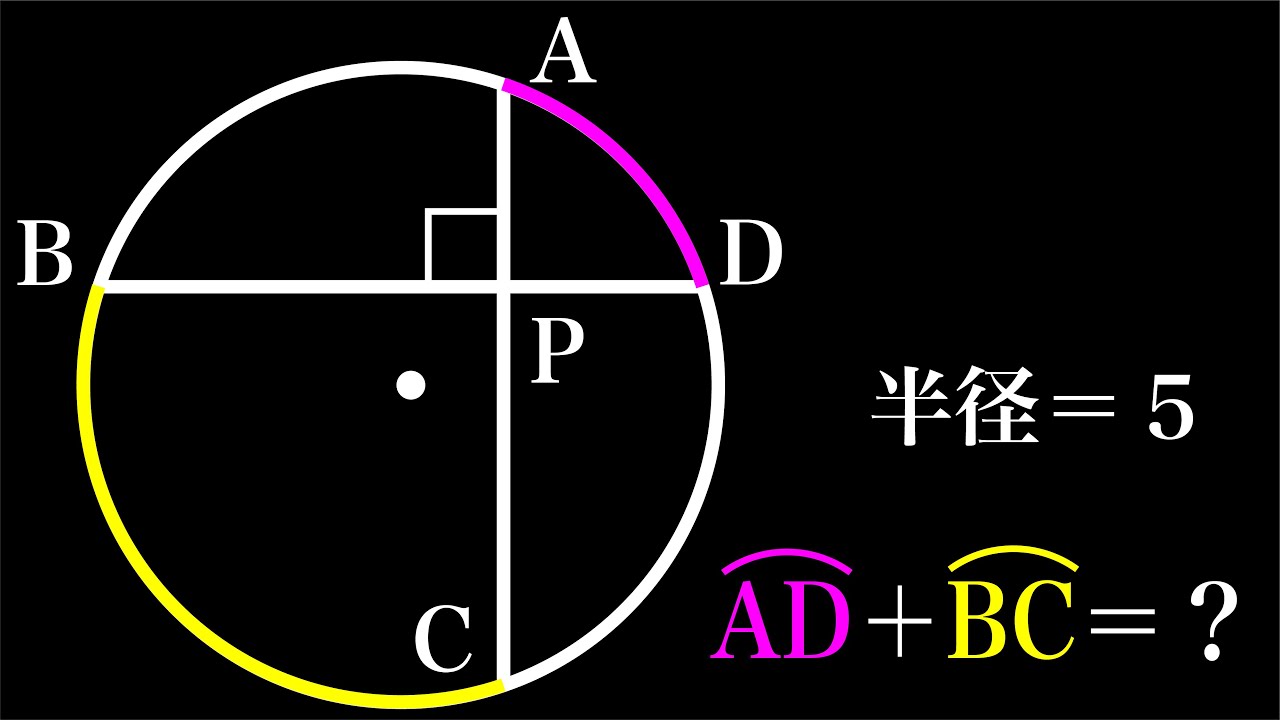
$\stackrel{\huge\frown}{AB}+\stackrel{\huge\frown}{BC} =?$
*図は動画内参照
この動画を見る
$\stackrel{\huge\frown}{AB}+\stackrel{\huge\frown}{BC} =?$
*図は動画内参照
数学「大学入試良問集」【17−3② 解けない漸化式とはさみうちの原理】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$a_1=2,a_{n+1}=\displaystyle \frac{4a_n^2+9}{8a_n}(n=1,2,3,・・・)$で定義される数列$\{a_n\}$について以下の問いに答えよ。
(1)$a_n \gt \displaystyle \frac{3}{2}(n=1,2,3,・・・)$を証明せよ。
(2)$a_{n+1}-\displaystyle \frac{3}{2} \lt \displaystyle \frac{1}{3}\left[ a_n-\dfrac{ 3 }{ 2 } \right]^2(n=1,2,3,・・・)$を証明せよ。
(3)$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
この動画を見る
$a_1=2,a_{n+1}=\displaystyle \frac{4a_n^2+9}{8a_n}(n=1,2,3,・・・)$で定義される数列$\{a_n\}$について以下の問いに答えよ。
(1)$a_n \gt \displaystyle \frac{3}{2}(n=1,2,3,・・・)$を証明せよ。
(2)$a_{n+1}-\displaystyle \frac{3}{2} \lt \displaystyle \frac{1}{3}\left[ a_n-\dfrac{ 3 }{ 2 } \right]^2(n=1,2,3,・・・)$を証明せよ。
(3)$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
【高校数学】三角関数の性質の裏技~先生には怒られるかもしれません~ 4-3.5【数学Ⅱ】

福田の数学〜早稲田大学2021年人間科学部第4問〜領域における最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$
不等式$(x-6)^2+(y-4)^2 \leqq 4$の表す領域を点$\textrm{P}(x,y)$が動くものとする。
このとき、$x^2+y^2$の最大値は$\boxed{\ \ タ\ \ }+\boxed{\ \ チ\ \ }\sqrt{\boxed{\ \ ツ\ \ }}$、$\dfrac{y}{x}$の最小値は$\dfrac{\boxed{\ \ テ\ \ }-\sqrt{\boxed{\ \ ト\ \ }}}{\boxed{\ \ ナ\ \ }}$、$x+y$の最大値は$\boxed{\ \ ニ\ \ }+\boxed{\ \ ヌ\ \ }\sqrt{\boxed{\ \ ネ\ \ }}$となる。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{4}}$
不等式$(x-6)^2+(y-4)^2 \leqq 4$の表す領域を点$\textrm{P}(x,y)$が動くものとする。
このとき、$x^2+y^2$の最大値は$\boxed{\ \ タ\ \ }+\boxed{\ \ チ\ \ }\sqrt{\boxed{\ \ ツ\ \ }}$、$\dfrac{y}{x}$の最小値は$\dfrac{\boxed{\ \ テ\ \ }-\sqrt{\boxed{\ \ ト\ \ }}}{\boxed{\ \ ナ\ \ }}$、$x+y$の最大値は$\boxed{\ \ ニ\ \ }+\boxed{\ \ ヌ\ \ }\sqrt{\boxed{\ \ ネ\ \ }}$となる。
2021早稲田大学人間科学部過去問
福田のわかった数学〜高校2年生032〜知って得する平行・垂直条件(1)

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 知って得する平行・垂直条件(1)
2直線
$ax-y-a+1=0 \ldots①$
$(a+2)x-ay+2a=0 \ldots②$
が次の条件を満たすとき、定数$a$の値を求めよ。
(1)平行である (2)垂直である
この動画を見る
数学$\textrm{II}$ 知って得する平行・垂直条件(1)
2直線
$ax-y-a+1=0 \ldots①$
$(a+2)x-ay+2a=0 \ldots②$
が次の条件を満たすとき、定数$a$の値を求めよ。
(1)平行である (2)垂直である
灘高校の式の値 伝えたいこと、たくさん
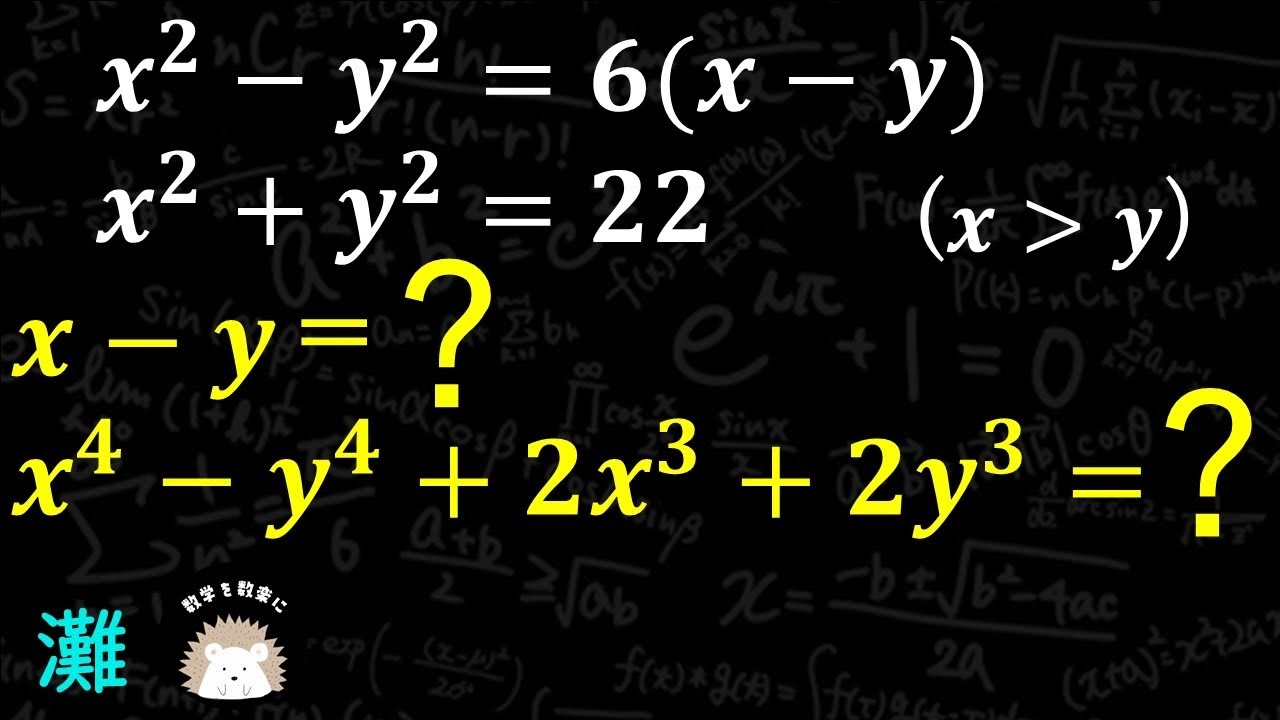
単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-y^2=6(x-y)$ , $x^2+y^2 = 22$ (x>y)
$x-y=?$
$x^4-y^4+2x^3+2y^3=?$
灘高等学校
この動画を見る
$x^2-y^2=6(x-y)$ , $x^2+y^2 = 22$ (x>y)
$x-y=?$
$x^4-y^4+2x^3+2y^3=?$
灘高等学校
高専数学 微積I #229(1) 媒介変数表示関数のx軸回転体の体積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq 1$とする.
$x=\sqrt t$
$y=\sqrt t-t$
と$x$軸で囲まれた図形を
$x$軸のまわりに回転してできる回転体の
体積$V$を求めよ.
この動画を見る
$0\leqq t\leqq 1$とする.
$x=\sqrt t$
$y=\sqrt t-t$
と$x$軸で囲まれた図形を
$x$軸のまわりに回転してできる回転体の
体積$V$を求めよ.
11和歌山県教員採用試験(数学:4番 微分と微分方程式)

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
$f(x)$:微分可能
任意の実数$x,y$に対して
$f(x+y)=f(x),f(y),f`(0)=2$
(1)$f(0)$を求めよ.
(2)$f(x)$を求めよ.
この動画を見る
$\boxed{4}$
$f(x)$:微分可能
任意の実数$x,y$に対して
$f(x+y)=f(x),f(y),f`(0)=2$
(1)$f(0)$を求めよ.
(2)$f(x)$を求めよ.
有名問題だよ(多分)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt[n]{n}$が最大となる自然数$n$を求めよ.
この動画を見る
$\sqrt[n]{n}$が最大となる自然数$n$を求めよ.
数学「大学入試良問集」【17−3① 解けない漸化式とはさみうちの原理】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#岐阜大学#数学(高校生)#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$a_1=2,a_{n+1}=\displaystyle \frac{1}{2}a_n+\displaystyle \frac{1}{a_n}$ $n=1,2,3,・・・$で定義される数列$\{a_n\}$について以下の問いに答えよ。
(1)$a_n \gt \sqrt{ 2 }(n=1,2,3,・・・)$を証明せよ。
(2)$a_{n+1}-\sqrt{ 2 } \lt \displaystyle \frac{1}{2}(a_n-\sqrt{ 2 })(n=1,2,3,・・・)$を証明せよ。
(3)$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
この動画を見る
$a_1=2,a_{n+1}=\displaystyle \frac{1}{2}a_n+\displaystyle \frac{1}{a_n}$ $n=1,2,3,・・・$で定義される数列$\{a_n\}$について以下の問いに答えよ。
(1)$a_n \gt \sqrt{ 2 }(n=1,2,3,・・・)$を証明せよ。
(2)$a_{n+1}-\sqrt{ 2 } \lt \displaystyle \frac{1}{2}(a_n-\sqrt{ 2 })(n=1,2,3,・・・)$を証明せよ。
(3)$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
【数Ⅲ】積分法:楕円で構成された図形の面積

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#チャート式#青チャートⅢ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
【高校数学 数学Ⅲ 積分法の応用】
2つの楕円$x^2+3y^2=4・・・①、3x^2+y^2=4・・・②$がある。
(1)2つの楕円の4つの交点の座標を求めよ。
(2)2つの楕円の内部の重なった部分の面積を求めよ。
(出典元)青チャート数学Ⅲより
この動画を見る
【高校数学 数学Ⅲ 積分法の応用】
2つの楕円$x^2+3y^2=4・・・①、3x^2+y^2=4・・・②$がある。
(1)2つの楕円の4つの交点の座標を求めよ。
(2)2つの楕円の内部の重なった部分の面積を求めよ。
(出典元)青チャート数学Ⅲより
【中学数学】平方根・ルートの足し算をどこよりも分かりやすく 2-4.5【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$5 \times 2\sqrt{ 3 }$
2⃣
$5\sqrt{ 2 }+7\sqrt{ 2 }$
3⃣
$2\sqrt{ 3 }+5\sqrt{ 2 }+3\sqrt{ 3 }+\sqrt{ 2 }$
この動画を見る
1⃣
$5 \times 2\sqrt{ 3 }$
2⃣
$5\sqrt{ 2 }+7\sqrt{ 2 }$
3⃣
$2\sqrt{ 3 }+5\sqrt{ 2 }+3\sqrt{ 3 }+\sqrt{ 2 }$
田の数学〜早稲田大学2021年人間科学部第3問〜格子点の個数

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$
自然数$n$について、連立不等式
$\left\{\begin{array}{1}
x \geqq 0\\
\displaystyle\frac{1}{4}x+\frac{1}{5}|y| \leqq n\\
\end{array}\right.$
を満たす整数の組$(x, y)$の個数は、$n=1$のときは$\boxed{\ \ シ\ \ }$であり、$n$の式で表すと$\boxed{\ \ ス\ \ }n^2+\boxed{\ \ セ\ \ }n+\boxed{\ \ ソ\ \ }$となる。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{3}}$
自然数$n$について、連立不等式
$\left\{\begin{array}{1}
x \geqq 0\\
\displaystyle\frac{1}{4}x+\frac{1}{5}|y| \leqq n\\
\end{array}\right.$
を満たす整数の組$(x, y)$の個数は、$n=1$のときは$\boxed{\ \ シ\ \ }$であり、$n$の式で表すと$\boxed{\ \ ス\ \ }n^2+\boxed{\ \ セ\ \ }n+\boxed{\ \ ソ\ \ }$となる。
2021早稲田大学人間科学部過去問
福田のわかった数学〜高校3年生理系035〜極限(35)関数の極限、色々な極限(5)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 色々な極限(5)\\
\lim_{x \to 0}\frac{a^x-1}{x} (a \gt 1)\\
を2通りの方法で求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 色々な極限(5)\\
\lim_{x \to 0}\frac{a^x-1}{x} (a \gt 1)\\
を2通りの方法で求めよ。
\end{eqnarray}
高専数学 微積I #227(3) 媒介変数表示関数の曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \pi$とする.
$x=\cos t+ \cos 2t$
$y=2\sin t- \sin 2t$
の曲線の長さ$L$を求めよ.
この動画を見る
$0\leqq t\leqq \pi$とする.
$x=\cos t+ \cos 2t$
$y=2\sin t- \sin 2t$
の曲線の長さ$L$を求めよ.
練習問題33 数検1級1次 微分方程式
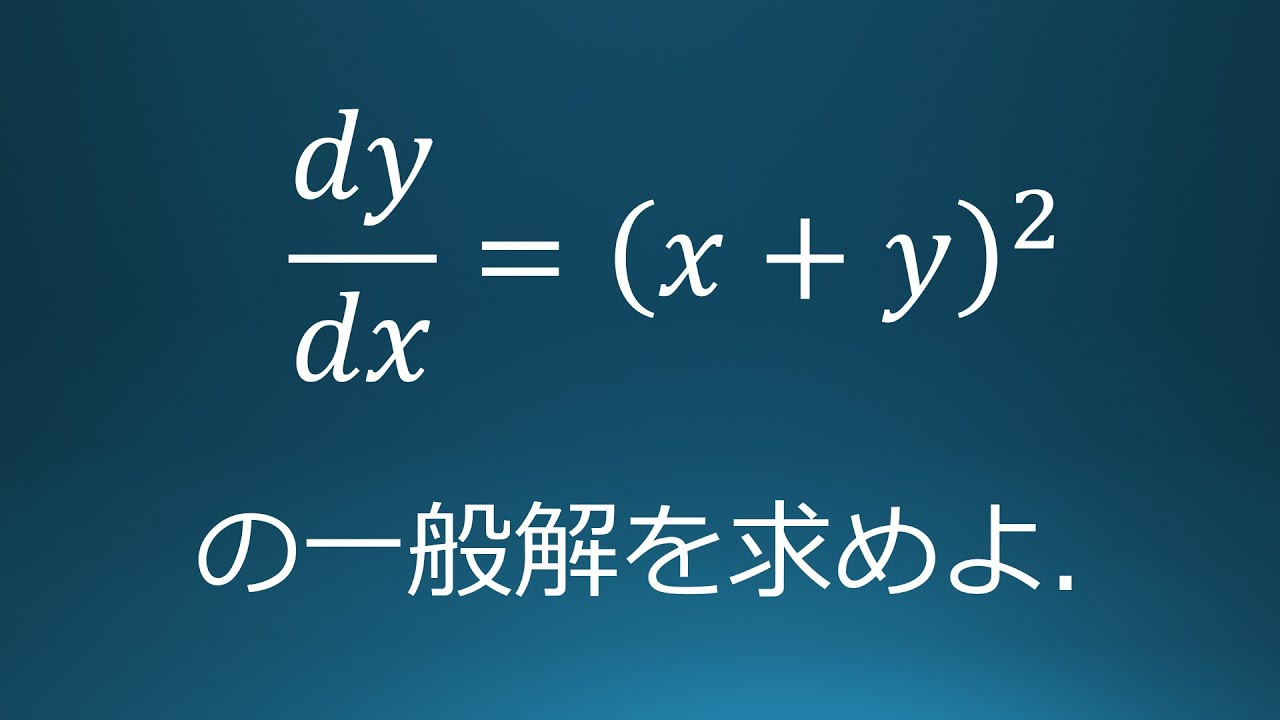
単元:
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\dfrac{dy}{dx}=(x+y)^2$
の一般解を求めよ.
この動画を見る
$\dfrac{dy}{dx}=(x+y)^2$
の一般解を求めよ.
【数Ⅱ】三角関数:置換したときの解の個数を考える

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#チャート式#黄チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$0\leqq\theta\lt2\pi$のとき、$\sin^2\theta-\sin\theta=a$ この方程式の解の個数を実数aの値で場合分けして求めよ
この動画を見る
$0\leqq\theta\lt2\pi$のとき、$\sin^2\theta-\sin\theta=a$ この方程式の解の個数を実数aの値で場合分けして求めよ
4の累乗の和で平方数を作れ

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c,n$は自然数である.
$4^a+4^b+4^c=n^2$
$10\lt a\lt b\lt c$を満たす$(a,b,c)$を1組与えよ.
この動画を見る
$a,b,c,n$は自然数である.
$4^a+4^b+4^c=n^2$
$10\lt a\lt b\lt c$を満たす$(a,b,c)$を1組与えよ.
共有点の個数
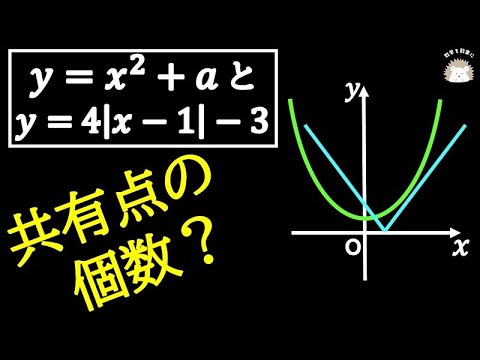
単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
aは定数。放物線$y=x^2+a$と$y=4|x-1|-3$のグラフとの共有点の個数を求めよ。
この動画を見る
aは定数。放物線$y=x^2+a$と$y=4|x-1|-3$のグラフとの共有点の個数を求めよ。
補助線を引け!解説2通り
【高校数学】数列の基礎・言葉の確認~知らないとヤバい知識~ 3-1【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1,4,9,16,25…この一般項を求めよ。
この動画を見る
1,4,9,16,25…この一般項を求めよ。
福田の数学〜早稲田大学2021年人間科学部第2問(3)〜n進法

単元:
#計算と数の性質#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
(3)$n$進法で$2021_{(n)}$と表される数が、素数であるような$n$の最小値を十進法で表すと$\boxed{\ \ コ\ \ }$となり、合成数である(素数ではない)ような$n$の最小値を十進法で表すと$\boxed{\ \ サ\ \ }$となる。
この動画を見る
${\Large\boxed{2}}$
(3)$n$進法で$2021_{(n)}$と表される数が、素数であるような$n$の最小値を十進法で表すと$\boxed{\ \ コ\ \ }$となり、合成数である(素数ではない)ような$n$の最小値を十進法で表すと$\boxed{\ \ サ\ \ }$となる。
福田のわかった数学〜高校1年生032〜否定分の作り方(2)

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 否定分の作り方(2)
次の関数$f(x)$についての命題を否定せよ。
「$N$以上の全ての自然数$n$について$f(n) \leqq 2$」
が成り立つような自然数$N$が存在する。
この動画を見る
数学$\textrm{I}$ 否定分の作り方(2)
次の関数$f(x)$についての命題を否定せよ。
「$N$以上の全ての自然数$n$について$f(n) \leqq 2$」
が成り立つような自然数$N$が存在する。
08岡山県教員採用試験(数学:1-(4) 微分方程式)
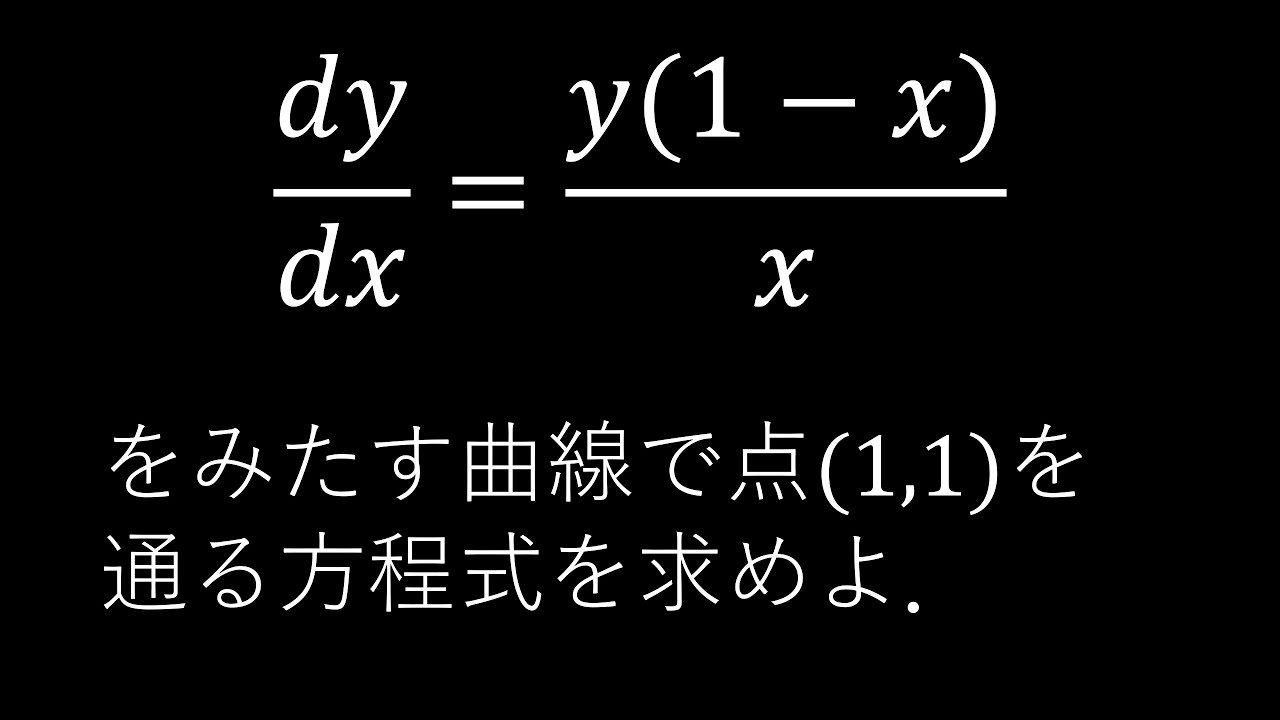
単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(4)$
$\dfrac{dy}{dx}=\dfrac{y(x-1)}{x}$
をみたす曲線で$(1,1)$を通る方程式を求めよ.
この動画を見る
$\boxed{1}-(4)$
$\dfrac{dy}{dx}=\dfrac{y(x-1)}{x}$
をみたす曲線で$(1,1)$を通る方程式を求めよ.
高専数学 微積I #227(2) 媒介変数表示関数の曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \pi$とする.
$x=\cos t+t \sin t$
$y=\sin t-t \cos t$
の曲線の長さ$L$を求めよ.
この動画を見る
$0\leqq t\leqq \pi$とする.
$x=\cos t+t \sin t$
$y=\sin t-t \cos t$
の曲線の長さ$L$を求めよ.
整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
${}_{70} \mathrm{C}_{35}$を$71$で割った余りを求めよ.
${}_{50} \mathrm{C}_{25}$を$51$で割った余りを求めよ.
この動画を見る
${}_{70} \mathrm{C}_{35}$を$71$で割った余りを求めよ.
${}_{50} \mathrm{C}_{25}$を$51$で割った余りを求めよ.
垂線の長さの和=❓ B
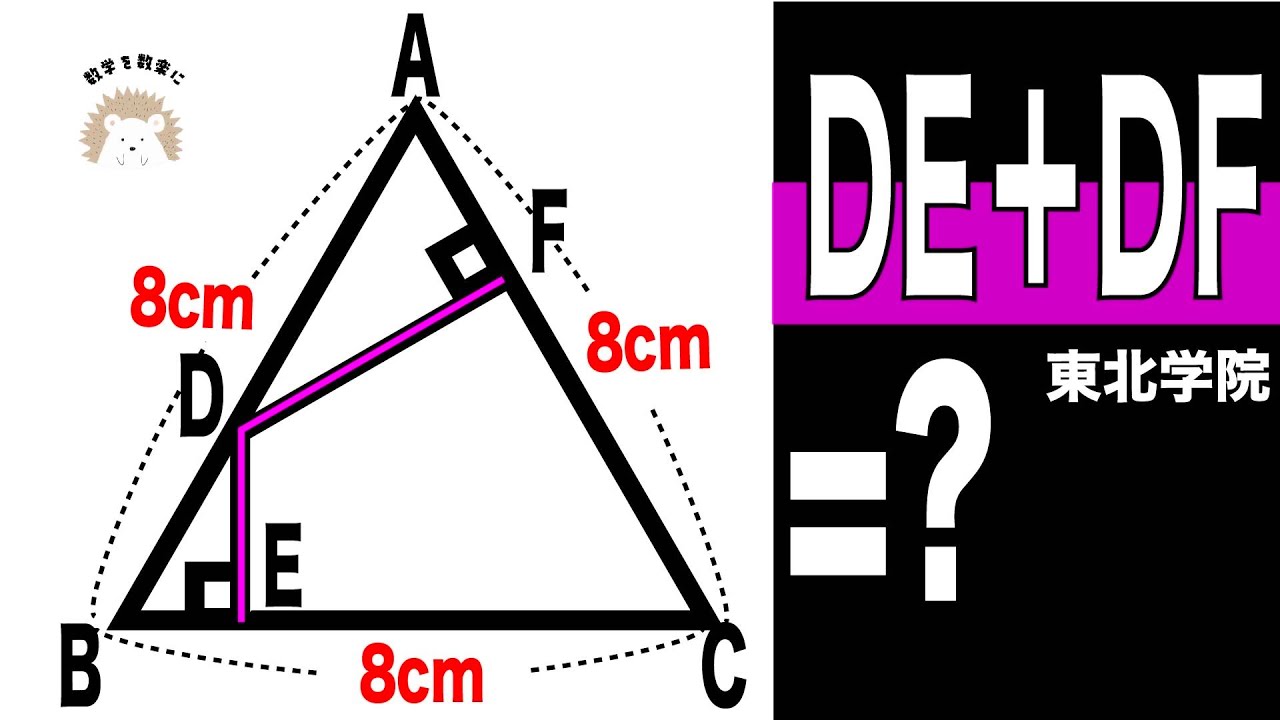
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
DE+EF=?
*図は動画内参照
東北学院高等学校
この動画を見る
DE+EF=?
*図は動画内参照
東北学院高等学校
【背理法はこう解け!】背理法の考え方と解法のテンプレはこうだ!【高校数学 数学】

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$\sqrt{ 3 }$が無理数なことを証明せよ
この動画を見る
$\sqrt{ 3 }$が無理数なことを証明せよ
