 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田の数学〜早稲田大学2021年理工学部第1問〜2直線のなす角の最小

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#微分とその応用#微分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ $xy$平面上の曲線$y=x^3$を$C$とする。$C$上の2点$A(-1,-1), B(1,1)$をとる。
さらに、$C$上で原点$O$と$B$の間に動点$P(t,t^3)(0 \lt t \lt 1)$をとる。このとき、
以下の問いに答えよ。
(1)直線$AP$と$x$軸のなす角を$\alpha$とし、直線$PB$と$x$軸のなす角を$\beta$とするとき、
$\tan\alpha,\tan\beta$を$t$を用いて表せ。ただし、$0 \lt \alpha \lt \displaystyle \frac{\pi}{2},\ 0 \lt \beta \lt \displaystyle \frac{\pi}{2}$とする。
(2)$\tan\angle APB$を$t$を用いて表せ。
(3)$\angle APB$を最小にする$t$の値を求めよ。
2021早稲田大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$ $xy$平面上の曲線$y=x^3$を$C$とする。$C$上の2点$A(-1,-1), B(1,1)$をとる。
さらに、$C$上で原点$O$と$B$の間に動点$P(t,t^3)(0 \lt t \lt 1)$をとる。このとき、
以下の問いに答えよ。
(1)直線$AP$と$x$軸のなす角を$\alpha$とし、直線$PB$と$x$軸のなす角を$\beta$とするとき、
$\tan\alpha,\tan\beta$を$t$を用いて表せ。ただし、$0 \lt \alpha \lt \displaystyle \frac{\pi}{2},\ 0 \lt \beta \lt \displaystyle \frac{\pi}{2}$とする。
(2)$\tan\angle APB$を$t$を用いて表せ。
(3)$\angle APB$を最小にする$t$の値を求めよ。
2021早稲田大学理工学部過去問
福田のわかった数学〜高校3年生理系018〜極限(18)関数の極限、無理関数の極限(3)

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 無理関数の極限(3)
$\displaystyle \lim_{x \to \infty}(\sqrt{x^2+x+1}-$$\sqrt{x^2-x+1})$ を求めよ。
この動画を見る
数学$\textrm{III}$ 無理関数の極限(3)
$\displaystyle \lim_{x \to \infty}(\sqrt{x^2+x+1}-$$\sqrt{x^2-x+1})$ を求めよ。
福田のわかった数学〜高校2年生023〜円の外部から引いた接線の求め方

単元:
#数Ⅱ#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 円と接線
点$A(2,4)$から
円$C:(x+2)^2+(y-2)^2=10$
へ引いた接線の方程式を求めよ。
この動画を見る
数学$\textrm{II}$ 円と接線
点$A(2,4)$から
円$C:(x+2)^2+(y-2)^2=10$
へ引いた接線の方程式を求めよ。
式の値
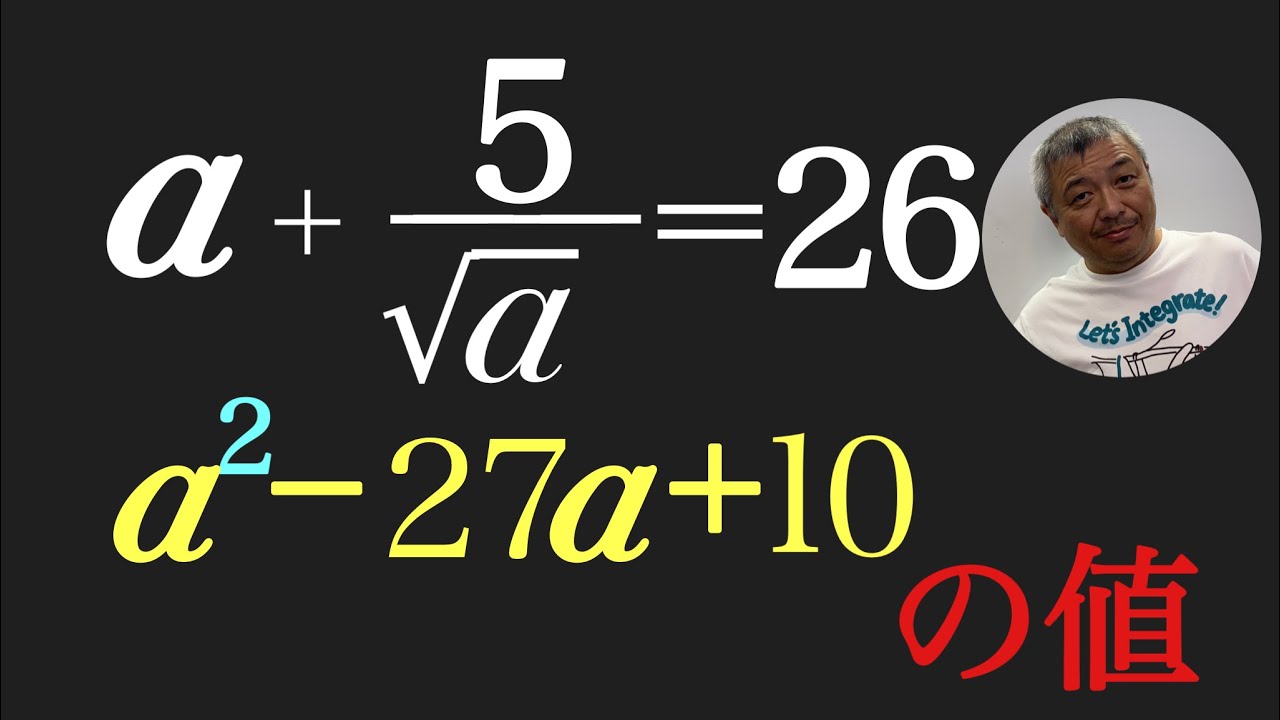
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a+\dfrac{5}{\sqrt a}=26$
$a^2-27a+10$の値を求めよ.
この動画を見る
$a+\dfrac{5}{\sqrt a}=26$
$a^2-27a+10$の値を求めよ.
【理数個別の過去問解説】2021年度東京大学 数学 理科・文科第4問(3)解説

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
東京大学 2021年理科・文科第4問(3)
以下の問いに答えよ。
(1)正の奇数K,Lと正の整数A,BがKA=LBを満たしているとする。Kを4で割った余りがLを4で割った余りと等しいならば、Aを4で割った余りはBを4で割った余りと等しいことを示せ。
(2)正の整数a,bがa>bを満たしているとする。このとき、$A=_{4a+1}C_{4b+1},B=aCb$に対してKA=LBとなるような正の奇数K,Lが存在することを示せ。
(3)a,bは(2)の通りとし、さらにa-bが2で割り切れるとする。$_{4a+1}C_{4b+1}wp4$で割った余りは${}_a\mathrm{C}_b$を4で割った余りと等しいことを示せ。
(4)2021C37を4で割った余りを求めよ。
この動画を見る
東京大学 2021年理科・文科第4問(3)
以下の問いに答えよ。
(1)正の奇数K,Lと正の整数A,BがKA=LBを満たしているとする。Kを4で割った余りがLを4で割った余りと等しいならば、Aを4で割った余りはBを4で割った余りと等しいことを示せ。
(2)正の整数a,bがa>bを満たしているとする。このとき、$A=_{4a+1}C_{4b+1},B=aCb$に対してKA=LBとなるような正の奇数K,Lが存在することを示せ。
(3)a,bは(2)の通りとし、さらにa-bが2で割り切れるとする。$_{4a+1}C_{4b+1}wp4$で割った余りは${}_a\mathrm{C}_b$を4で割った余りと等しいことを示せ。
(4)2021C37を4で割った余りを求めよ。
【数学Ⅱ/中間テスト対策】繫分数式
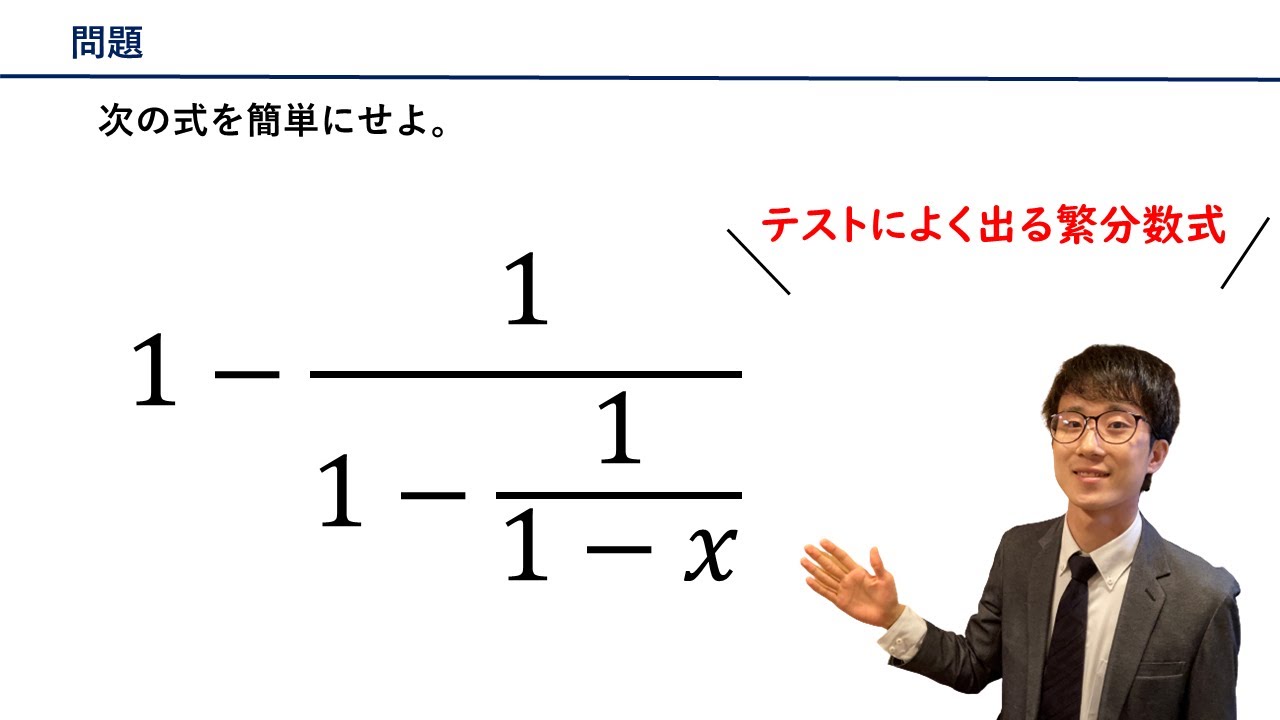
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式を簡単にせよ。
$1-\displaystyle \frac{1}{1-\displaystyle \frac{1}{1-x}}$
この動画を見る
次の式を簡単にせよ。
$1-\displaystyle \frac{1}{1-\displaystyle \frac{1}{1-x}}$
数学基礎40「積分と面積公式」【高校数学ⅡB】を宇宙一わかりやすく

数学「大学入試良問集」【12−4 共通接線と面積】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#名古屋市立大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
2つの関数$f_1(x)=-x^2+8x-9,f_2(x)=-x^2+2x+3$に対して、関数$F(x)$を次のように定義する。
$F(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
f_1(x)(xがf_1(x) \geqq f_2(x)をみたすとき) \\
f_2(x)(xがf_1(x) \lt f_2(x)をみたすとき)
\end{array}
\right.
\end{eqnarray}$
以下の問いに答えよ。
(1)$y=F(x)$のグラフをかけ。
(2)曲線$y=F(x)$上の異なる2点で接する直線$l$を求めよ。
(3)$y=F(x)$と$l$とで囲まれた図形の面積を求めよ。
この動画を見る
2つの関数$f_1(x)=-x^2+8x-9,f_2(x)=-x^2+2x+3$に対して、関数$F(x)$を次のように定義する。
$F(x)=\begin{eqnarray}
\left\{
\begin{array}{l}
f_1(x)(xがf_1(x) \geqq f_2(x)をみたすとき) \\
f_2(x)(xがf_1(x) \lt f_2(x)をみたすとき)
\end{array}
\right.
\end{eqnarray}$
以下の問いに答えよ。
(1)$y=F(x)$のグラフをかけ。
(2)曲線$y=F(x)$上の異なる2点で接する直線$l$を求めよ。
(3)$y=F(x)$と$l$とで囲まれた図形の面積を求めよ。
加法定理の証明をベクトルで

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
cosα・cosβ+sinα・sinβ =
この動画を見る
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
cosα・cosβ+sinα・sinβ =
福田のわかった数学〜高校3年生理系017〜関数の極限、無理関数の極限(2)

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 無理関数の極限(2)
$\lim_{x \to 1}\displaystyle \frac{\sqrt[3]x-1}{\sqrt x-1}$ を求めよ。
この動画を見る
数学$\textrm{III}$ 無理関数の極限(2)
$\lim_{x \to 1}\displaystyle \frac{\sqrt[3]x-1}{\sqrt x-1}$ を求めよ。
福田のわかった数学〜高校1年生023〜連立2次不等式の整数解の個数

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 連立2次不等式
$\left\{\begin{array}{1}
x^2-2x-3 \gt 0\\
x^2-(a+1)x+a \lt 0\\
\end{array}\right.$
をともに満たす整数がただ1つとなる
ようなaの値の範囲を求めよ。
この動画を見る
数学$\textrm{I}$ 連立2次不等式
$\left\{\begin{array}{1}
x^2-2x-3 \gt 0\\
x^2-(a+1)x+a \lt 0\\
\end{array}\right.$
をともに満たす整数がただ1つとなる
ようなaの値の範囲を求めよ。
〇〇に注目すれば一瞬!3通りで解説
#18数検1級1次過去問 3重積分

単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\boxed{7}$
$D:x^2+y^2 \leqq z \leqq 2x$
$ \displaystyle \iiint_D \ dx\ dy\ dz$
の値を求めよ.
この動画を見る
$\boxed{7}$
$D:x^2+y^2 \leqq z \leqq 2x$
$ \displaystyle \iiint_D \ dx\ dy\ dz$
の値を求めよ.
【今見るべき公式集!】高校までに学ぶ「因数分解」の公式~全国入試問題解法

単元:
#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
中学校、高等学校までに学ぶ「因数分解の公式」一覧の解説
①$ma\pm mℓ=m(a \pm ℓ)$
②$x^2 \pm 2xy+y^2=(x \pm y)^2$
③$x^2-y^2=(x-y)(x+y)$
④$x^2 +(a+ℓ) x + aℓ=(x + a)(x+ℓ)$
⑤$acx^2+(ad+ℓc)x+ℓd=(ax+ℓ)(cx+d)$
⑥$x^3\pm y^3=(x+y)(x^2\mp xy+y^2)$
⑦$a^2+ℓ^2+c^2+2aℓ+2ℓc+2ca=(a+ℓ+c)^2$
⑧$a^3\pm 3a^2ℓ+3aℓ^2\pmℓ^3=(a \pmℓ)^3$
⑨$a^3+ℓ^3+c^3-3aℓc=(a+ℓ+c)(a^2+ℓ^2c^2-ℓc-ca-aℓ)$
この動画を見る
中学校、高等学校までに学ぶ「因数分解の公式」一覧の解説
①$ma\pm mℓ=m(a \pm ℓ)$
②$x^2 \pm 2xy+y^2=(x \pm y)^2$
③$x^2-y^2=(x-y)(x+y)$
④$x^2 +(a+ℓ) x + aℓ=(x + a)(x+ℓ)$
⑤$acx^2+(ad+ℓc)x+ℓd=(ax+ℓ)(cx+d)$
⑥$x^3\pm y^3=(x+y)(x^2\mp xy+y^2)$
⑦$a^2+ℓ^2+c^2+2aℓ+2ℓc+2ca=(a+ℓ+c)^2$
⑧$a^3\pm 3a^2ℓ+3aℓ^2\pmℓ^3=(a \pmℓ)^3$
⑨$a^3+ℓ^3+c^3-3aℓc=(a+ℓ+c)(a^2+ℓ^2c^2-ℓc-ca-aℓ)$
数学「大学入試良問集」【12−3 極値と不等式の関係】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$a$を実数とし、関数$f(x)=x^3-3ax+a$を考える。
$0 \leqq x \leqq 1$となるような$a$の値の範囲を求めよ。
この動画を見る
$a$を実数とし、関数$f(x)=x^3-3ax+a$を考える。
$0 \leqq x \leqq 1$となるような$a$の値の範囲を求めよ。
福田のわかった数学〜高校3年生理系016〜極限(16)関数の極限、無理関数の極限

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(16)
$\lim_{x \to 1}\displaystyle \frac{\sqrt{x+8}-3}{\sqrt{x+3}-2}$ を求めよ。
この動画を見る
数学$\textrm{III}$ 極限(16)
$\lim_{x \to 1}\displaystyle \frac{\sqrt{x+8}-3}{\sqrt{x+3}-2}$ を求めよ。
福田のわかった数学〜高校2年生022〜円の外部から引いた接線の求め方

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 円の方程式
円$C:x^2+y^2=4$ の接線で$(2,3)$を通るものと
そのときの接点を次の3通りの方法で求めよ。
(1)接線の公式$x_1x+y_1=r^2$ を利用
(2)点と直線の距離の公式を利用
(3)判別式を利用
この動画を見る
数学$\textrm{II}$ 円の方程式
円$C:x^2+y^2=4$ の接線で$(2,3)$を通るものと
そのときの接点を次の3通りの方法で求めよ。
(1)接線の公式$x_1x+y_1=r^2$ を利用
(2)点と直線の距離の公式を利用
(3)判別式を利用
最短経路 他の問題もあり
単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
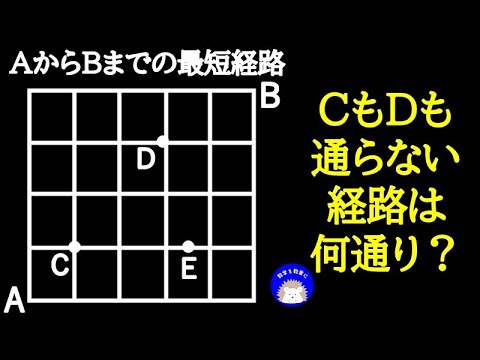
最短経路
AからBまで最短距離で行く。
(1)全部で何通り?
(2)Dを通らない場合は何通り?
(3)Eを通らない場合は何通り?
(4)CもDも通る場合は何通り?
(5)CもDも通らない場合は何通り?
この動画を見る
最短経路
AからBまで最短距離で行く。
(1)全部で何通り?
(2)Dを通らない場合は何通り?
(3)Eを通らない場合は何通り?
(4)CもDも通る場合は何通り?
(5)CもDも通らない場合は何通り?
整数問題 慶應義塾

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a,b,cは1~9の異なる整数
$\frac{a+b+c}{abc}$の最大値は?
$\frac{a+b+c}{abc}$=
慶應義塾高等学校
この動画を見る
a,b,cは1~9の異なる整数
$\frac{a+b+c}{abc}$の最大値は?
$\frac{a+b+c}{abc}$=
慶應義塾高等学校
08岡山県教員採用試験(数学:6番 積分・面積)
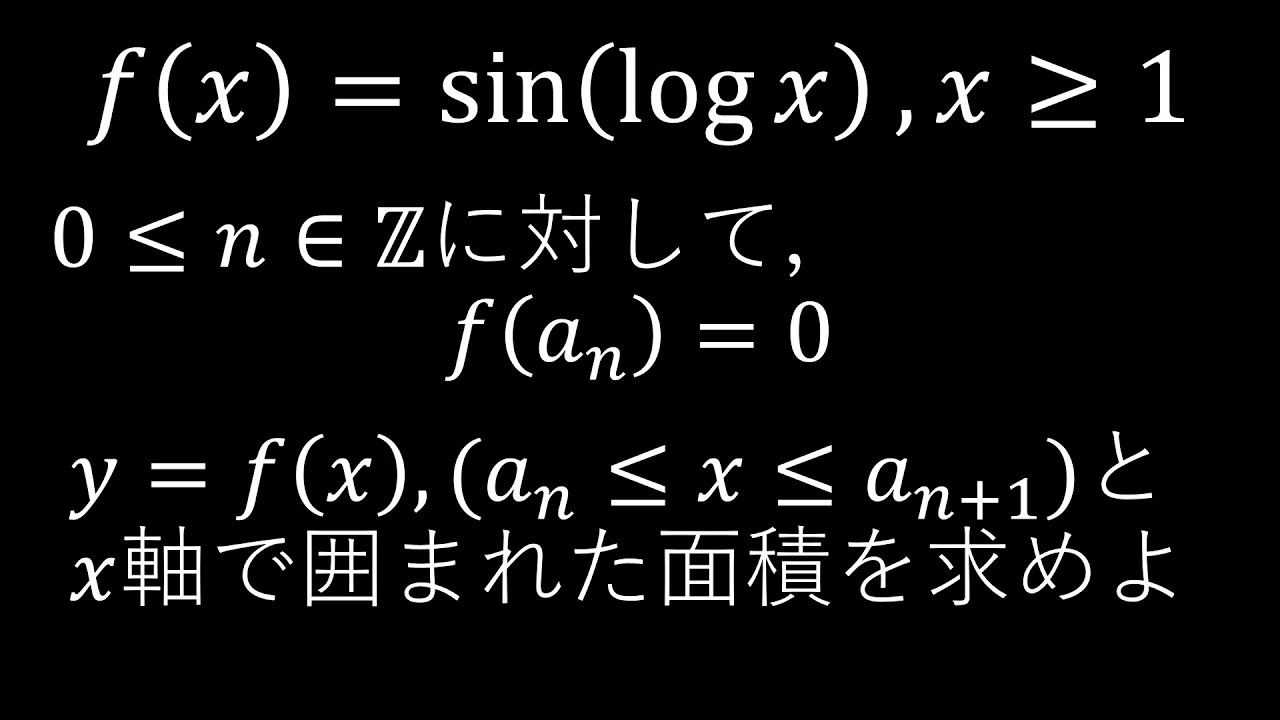
単元:
#積分とその応用#面積・体積・長さ・速度#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$x\geqq 1$とする.
$f(x)=\sin (\log x)$
各$n=0,1,2,・・・$に対して$f(a_n)=0$とする.
曲線$y=f(x)$ $(a_n \leqq x \leqq a_{n+1})$と
$x$軸で囲まれた面積$S_n$を求めよ.
この動画を見る
$\boxed{6}$
$x\geqq 1$とする.
$f(x)=\sin (\log x)$
各$n=0,1,2,・・・$に対して$f(a_n)=0$とする.
曲線$y=f(x)$ $(a_n \leqq x \leqq a_{n+1})$と
$x$軸で囲まれた面積$S_n$を求めよ.
お茶の水女子大 101の100乗の下8桁を求めよ

【数A】整数の性質:φ関数(φ(24)について)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
1~24までの自然数のうち、24と互いに素となる自然数の個数を求めよ。
この動画を見る
1~24までの自然数のうち、24と互いに素となる自然数の個数を求めよ。
【数A】確率:(理系)東京大学1971年 ジャンケンの確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
3人でジャンケンをして勝者をきめることにする。たとえば,1人が"紙"を出し, 他の2人が”石"を出せば,ただ1回でちょうど1人の勝者がきまることになる。
3 人でジャンケンをして,負けた人は次の回に参加しないことにして,ちょうど1 人の勝者がきまるまで,ジャンケンをくり返すことにする。
このとき,n回目 に,はじめてちょうど1人の勝者がきまる確率を求めよう。
この動画を見る
3人でジャンケンをして勝者をきめることにする。たとえば,1人が"紙"を出し, 他の2人が”石"を出せば,ただ1回でちょうど1人の勝者がきまることになる。
3 人でジャンケンをして,負けた人は次の回に参加しないことにして,ちょうど1 人の勝者がきまるまで,ジャンケンをくり返すことにする。
このとき,n回目 に,はじめてちょうど1人の勝者がきまる確率を求めよう。
【高校数学】弧度法を簡単に分かりやすく~ラジアンとは~ 4-1.5【数学Ⅱ】

角度を求める C
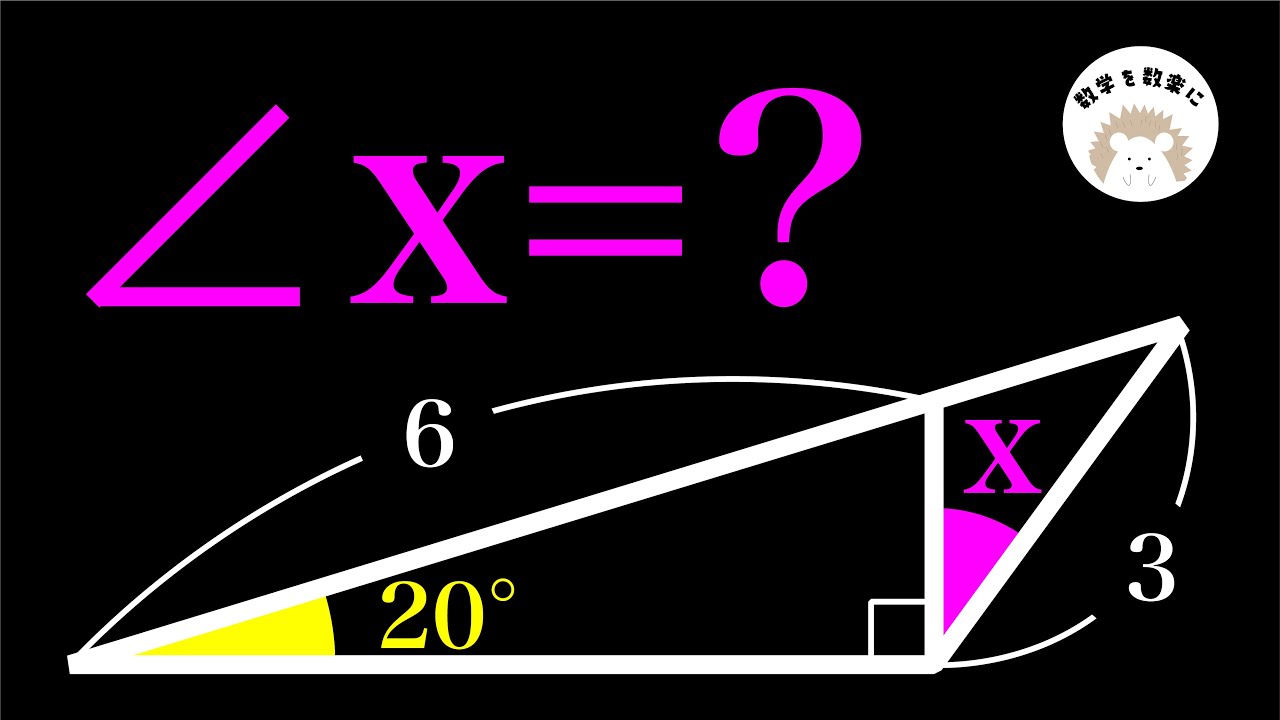
福田のわかった数学〜高校1年生022〜2次方程式の解の分離

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 2次方程式の解の分離
$a \geqq 0$のとき、
$x^2-(a+1)x-a=0$
の実数解の取り得る値の範囲を求めよ。
この動画を見る
数学$\textrm{I}$ 2次方程式の解の分離
$a \geqq 0$のとき、
$x^2-(a+1)x-a=0$
の実数解の取り得る値の範囲を求めよ。
極限値 文系でもできるよ

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\displaystyle \lim_{x\to \infty}\dfrac{\left[\dfrac{x^3}{\pi}\right]}{x^3}$
この動画を見る
これを解け.
$\displaystyle \lim_{x\to \infty}\dfrac{\left[\dfrac{x^3}{\pi}\right]}{x^3}$
【図でイメージする!】2次関数の最大値と最小値の問題はこう解く!【高校数学 数学】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
2次関数の値の範囲と最大値・最小値
①$y=x^2-2x+1$を定義域(0 \leqq x \leqq 3)でグラフをかけ
②$y=2x^2-4x+1$について$-1 \leq z \leq 2$の範囲での最大値と最小値を求めよ
③$y=-3x^2-4x-1$について$1 \leq z \leq 3$の範囲での最大値と最小値を求めよ
この動画を見る
2次関数の値の範囲と最大値・最小値
①$y=x^2-2x+1$を定義域(0 \leqq x \leqq 3)でグラフをかけ
②$y=2x^2-4x+1$について$-1 \leq z \leq 2$の範囲での最大値と最小値を求めよ
③$y=-3x^2-4x-1$について$1 \leq z \leq 3$の範囲での最大値と最小値を求めよ
数学「大学入試良問集」【12−2 微分と直方体の体積】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#朝日大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
縦$x$、横$y$、高さ$z$の和が12、表面積が90であるような直方体を考える。
(1)$y+z$および$yz$を$x$の式で表せ。
(2)このような直方体が存在するための$x$の範囲を求めよ。
(3)このような直方体のうち体積が最大であるものを求めよ。
この動画を見る
縦$x$、横$y$、高さ$z$の和が12、表面積が90であるような直方体を考える。
(1)$y+z$および$yz$を$x$の式で表せ。
(2)このような直方体が存在するための$x$の範囲を求めよ。
(3)このような直方体のうち体積が最大であるものを求めよ。
福田のわかった数学〜高校3年生理系015〜極限(15)級数と区分求積

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(15)
$\lim_{n \to \infty}\displaystyle \sum_{k=0}^{n-1}\displaystyle \frac{1}{\sqrt{4n^2-k^2}}$ を求めよ。
この動画を見る
数学$\textrm{III}$ 極限(15)
$\lim_{n \to \infty}\displaystyle \sum_{k=0}^{n-1}\displaystyle \frac{1}{\sqrt{4n^2-k^2}}$ を求めよ。
